Diffusion tensor magnetic resonance histology reveals microstructural changes in the developing rat brain

Abstract

The postnatal period is a remarkably dynamic phase of brain growth and development characterized by large-scale macrostructural changes, as well as dramatic microstructural changes, including myelination and cortical layering. This crucial period of neurodevelopment is uniquely susceptible to a wide variety of insults that may lead to neurologic disease. MRI is an important tool for studying both normal and abnormal neurodevelopmental changes, and quantitative imaging strategies like diffusion tensor imaging (DTI) allow visualization of many of the complex microstructural changes that occur during postnatal life. Diffusion tensor magnetic resonance histology (DT-MRH) provides particularly unique insight into cytoarchitectural changes in the developing brain. In this study, we used DT-MRH to track microstructural changes in the rat brain throughout normal postnatal neurodevelopment. We provide examples of diffusion tensor parameter changes in both white matter and gray matter structures, and correlate these changes with changes in cytoarchitecture. Finally, we provide a comprehensive database of image sets as a foundation for future studies using DT-MRH to characterize abnormal neurodevelopment in rodent models of neurodevelopmental disease.

1. Introduction and Background

Early postnatal life is a crucial period of mammalian brain growth and development. During this period the neonate is exposed to the extrauterine environment for the first time and must learn to interact with others and process a wide variety of external stimuli (i.e. vision, olfaction, audition). These dramatic functional changes are accompanied by equally dramatic changes in brain structure including massive cell growth and macrostructural changes. Perhaps equally as important are the complex microstructural changes that occur, including cellular differentiation, formation and pruning of axonal connections, and cerebral myelination (Nagy et al., 2004). Alteration of this elaborate microstructural remodeling is increasingly being recognized as a cause of neurodevelopmental disease even in the absence of gross morphologic changes in the brain. In particular, postnatal neurodevelopment seems to be uniquely susceptible to white matter injury. For example, a wide variety of perinatal vascular insults (perinatal hypoxia, cerebral palsy), toxic insults (fetal alcohol exposure, antidepressant exposure), and traumatic insults (shaken baby syndrome) are known to produce white matter injury in the perinatal period in both humans and small animal models (Bonnier et al., 2004; Wang et al., 2009; O'Leary-Moore et al., 2011; Simpson et al., 2011). Unfortunately, these types of white matter injuries are difficult to study in the dynamic background of postnatal neurodevelopment. A need exists for a quantitative understanding of normative microstructural changes that occur during postnatal brain development to allow effective characterization of disease states.

MRI has proven particularly useful in understanding both normal and abnormal fetal and postnatal neurodevelopment (Mori et al., 2001; Zhang et al., 2005; 2006; Chuang et al., 2011). Through the use of Diffusion Tensor Imaging (DTI) techniques, MRI can provide quantitative, brain-wide maps of water diffusion characteristics that reveal underlying tissue microstructure (Basser, 1995). Several of these tissue microstructural parameters are useful for detecting neuropathology. For example, fractional anisotropy (FA) is sensitive to white matter integrity and apparent diffusion coefficient (ADC) is altered in necrosis, edema and gliosis (Mukherjee et al., 2008). Further, several groups have identified DTI parameter changes in animal models of neurodevelopmental disease such as fetal alcohol syndrome, autism and hypoxic ischemic encephalopathy (Wang et al., 2009; Ellegood et al., 2011; Wozniak and Muetzel, 2011).

One benefit of DTI is that it can be performed in-vivo; however the use of diffusion tensor MRI to study fixed, ex-vivo tissue—referred to as Diffusion Tensor Magnetic Resonance Histology (DT-MRH)—may be preferable to serial in-vivo imaging for studying neurodevelopment for a number of reasons. Anesthesia is clearly a confound for in-vivo studies, particularly in the developing brain where it is known to cause widespread apoptosis (Yon et al., 2005). Fixing each specimen at a given time point eliminates any effects from anesthesia, particularly those that might be cumulative.

Lerch et al. (2012) have highlighted the benefits of using fixed tissues over in-vivo studies. Image quality and resolution can be considerably higher, particularly for DTI studies where the long scans required would be prohibitive for in-vivo studies (Lerch et al., 2012). Higher resolution may also reduce the ambiguity associated with intra-voxel fiber crossing and partial volume averaging (Kim et al., 2006). Since the anatomic variability in healthy rodents of the same strain is small (Kovacevic et al., 2005), even in out-bred strains like the Wistar rat (Calabrese et al., 2013), the use of multiple fixed specimens at different ages can provide a more definitive measure of normal neurodevelopment than might be derived from serial in-vivo studies; however, this approach may not be appropriate for disease models where inter-specimen variability is high. Finally, our long-term goal is the development of DT-MRH to provide quantitative assessment of pathology induced by the many sources mentioned previously. Since our end point is fixed tissues, the baseline we are providing should clearly be tissues fixed in the same fashion. It is important to note that the term histology, when used in scientific literature, usually refers to light microscopy studies of fixed tissue. In contrast, the term magnetic resonance histology (MRH) invokes the literal meaning of the word histology—the study of the microscopic structure of tissues—and refers to the use of MRI to study tissue microstructure.

DT-MRH has exciting potential to characterize and quantify the trajectory of postnatal microstructural changes in the brain, particularly in small animal models like the rat where this technology is relatively easy to implement. This use of DT-MRH comes with an important caveat—water diffusion in the brain is changed by cell death, fixation and ambient temperature, so ex-vivo measurements of diffusion tensor parameters are often different from in-vivo measurements (Sun et al., 2005; 2009). Further, inherent biological control of brain environment (i.e. thermoregulation, osmoregulation) is absent in ex-vivo experiments, which allows wider variability in diffusion measurements. Perhaps for these reasons, previous attempts to measure diffusion tensor parameters in the fixed rodent brains brain have yielded widely varying results (Guilfoyle et al., 2003; Verma et al., 2005; Zhang et al., 2005; 2006; Jiang and Johnson, 2011). Despite these issues, DT-MRH remains a valuable technique for studying and quantifying neurodevelopment in animal models and well-defined normal values would allow quantitative characterization of abnormal versus normal neuro-microstructural development.

In this study, we used DT-MRH to reveal postnatal tissue microstructural changes in the developing rat brain at what we believe to be the highest spatial resolution yet attained. We have correlated the observed changes in diffusion tensor parameters with known microstructural developmental processes and compared our results to other diffusion-tensor-based studies of rat neurodevelopment. We show that with careful experimental design and data normalization, DT-MRH measurements of mean diffusivity closely resemble the trajectory, but not necessarily the magnitude, of comparable in-vivo measurements. This study establishes a database of normative changes in DT-MRH microstructural metrics that can be used as a reference for detecting and quantifying neuropathology in rat models of human neurodevelopmental disease.

2. Materials and Methods

2.1 Experimental animals

All experiments were done with the approval of the Duke University Institutional Animal Care and Use Committee. To ensure accurate sampling of postnatal brain development, we selected nine time-points temporally spaced to allow an approximately fixed percentage increase (~30%) in brain mass between samples based on previously published rat brain growth curves (Donaldson, 1915). The nine time-points selected for the atlas were p0, p2, p4, p8, p12, p18, p24, p40, and p80 (where “p” indicates postnatal day and p0 refers to the day of birth). Five male, Wistar rats were selected for imaging at each time-point. All animals were from litters of 10–12 pups (average = 11) and had a body weight within one standard deviation of mean weight for age based on the growth curve provided by the supplier (Charles River, 2013). Each time-point includes animals from at least three different litters, and all animals were raised in complete litters until imaging or weaning (p22), whichever occurred first.

2.2 Specimen preparation

Animals were perfusion-fixed using the active staining technique described more completely in (Johnson et al., 2002). Perfusion fixation was achieved using a 10% solution of Neutral Buffered Formalin (NBF) containing 10% (50 mM) Gadoteridol. After perfusion fixation, rat heads were removed and immersed in 10% NBF for 24 hours. Finally, fixed rat heads were transferred to a 0.1 M solution of Phosphate Buffered Saline containing 1% (5 mM) Gadoteridol and stored at 4° C for 5–7 days. The active staining technique significantly reduces the T1 relaxation time of the brain parenchyma and thus allows high-resolution, high signal-to-noise ratio (SNR) imaging to be achieved with a much shorter TR and, therefore, shorter total scan time. Before imaging, specimens were placed in custom-made, MRI-compatible tubes and immersed in Fomblin liquid fluorocarbon (Ausimont USA, Thorofare, NJ) for susceptibility matching and to prevent specimen dehydration. All imaging experiments were performed with the brain inside the neurocranium.

2.3 Image acquisition

Imaging was performed on a 7T small animal MRI system (Magnex Scientific, Yarnton, Oxford, UK) equipped with 650 mT/m Resonance Research gradient coils (Resonance Research, Inc., Billerica, MA, USA), and controlled with a General Electric Signa console (GE Medical Systems, Milwaukee, WI, USA). RF transmission and reception were achieved using a series of custom solenoid coils ranging from 15 mm diameter by 30 mm long to 30 mm diameter by 50 mm long. Diffusion weighted images were acquired using a spin-echo pulse sequence (TR = 100 ms, TE = 16.2 ms, NEX = 1). Diffusion preparation was accomplished using a modified Tanner-Stejskal diffusion-encoding scheme (Stejskal and Tanner, 1965) with a pair of unipolar, half-sine diffusion gradient waveforms (width δ = 3 ms, separation Δ = 8.5 ms, gradient amplitude = 600 mT/m). One b0 image and 6 high b-value images (b=1492 s/mm²) were acquired with diffusion sensitization along each of six non-colinear diffusion gradient vectors: [1, 1, 0], [1, 0, 1], [0, 1, 1], [−1, 1, 0], [1, 0, −1], and [0, −1, 1]. The acquisition matrix ranged from 512 × 256 × 256 to 800 × 400 × 400 and FOV ranged from 25.6 × 12.8 × 12.8 mm to 40 × 20 × 20 mm. The Nyquist isotropic spatial resolution was 50 µm in all cases, corresponding to the smallest voxel size that we could achieve in the developing rat brain without sacrificing SNR ≥ 30 or dramatically increasing acquisition time. This high-resolution strategy was chosen to reduce the contribution of intra-voxel fiber crossing and partial volume effects on diffusion tensor parameter measurements. All images were derived from fully sampled k-space data. Bore temperature was maintained at a constant 20° C using forced air and water-cooling. Total scan time ranged from 12 hours to 32 hours depending on matrix size.

2.4 Diffusion tensor image processing

Diffusion data were processed with a custom image-processing pipeline comprised of freely available software packages including Perl (http://www.perl.org), ANTs (http://www.picsl.upenn.edu/ANTS/) and Diffusion Toolkit (http://www.trackvis.org). This automated pipeline was created to ensure that all data were processed in the same way, and to reduce the potential for user error. First, diffusion weighted image volumes were spatially normalized to the b0 volume using the ANTs 6-parameter rigid-affine registration to correct for the linear portion of eddy current distortions. Next diffusion tensor estimation, and calculation of tensor-derived data sets were performed using Diffusion Toolkit. Finally, data were organized in to a consistent file architecture and archived in an on-site Oracle database (Johnson et al, 2007).

2.5 Image registration and averaging

Intra-time-point image registration was accomplished with the ANTs software package (Avants et al., 2008). All registration steps were carried out using the mean diffusion-weighted image, which provides high SNR and high image contrast throughout postnatal rat neurodevelopment. Skull-stripped diffusion-weighted images from each set of specimens (five per time-point) were aligned using a six-parameter rigid affine registration, followed by an iterative, viscous fluid model, non-linear registration. We employed a Minimum Deformation Template (MDT) strategy, which uses pairwise, nonlinear image registrations to construct an average template requiring the minimum amount of deformation from each of the starting points (Kochunov et al., 2001). The similarity metric used for registration was cross-correlation computed for a kernel radius of 4 voxels. We used a multi-resolution scheme, and did a maximum of 500 iterations at a down-sampling factor of 3, 500 iterations at a down-sampling factor of 2, and 250 iterations at full resolution. We used the greedy symmetric normalization (SyN) model with a gradient step of 0.5 and a Gaussian regularization with σ = 3 for the similarity gradient, and σ = 1 for the deformation field. The algorithm converged at each step of the registration and in all cases the cross-correlation increased by >10% after registration. We further assessed registration accuracy by manually inspecting population averaged datasets and ensuring good visual agreement between segmented brain regions. The resultant transformations were applied directly to scalar images to create population averages. To create population average tensor volumes we used log-Euclidean mathematics operations (Arsigny et al., 2006). In short, the transformation is applied to the matrix logarithm of the tensor, and then the matrix exponent of the result is taken to create the transformed tensor. This technique provides the best linear approximation of an average tensor.

2.6 Anatomic segmentation and labeling

Manual, whole-brain segmentation was performed on population-averaged images at each of the atlas time-points. We segmented 26 distinct brain regions that are identifiable in MRH volumes throughout postnatal neurodevelopment (Calabrese et al., 2012). All manual segmentation was performed with Avizo 3D segmentation software (Visualization Sciences Group, Burlington, MA, USA). The resulting population-average label sets were propagated back to the individual specimens using the inverse of the affine and diffeomorphic maps used to create the population-average image volumes.

2.7 Calculation of diffusion tensor scalars

Labels were used as 3D regions-of-interest (ROIs) for analysis of diffusion tensor parameters. For each label and at each time point, we calculated the mean value of four different tensor derived scalars: mean diffusivity (MD), radial diffusivity (RD), axial diffusivity (AD) and fractional anisotropy (FA). MD is the mean of the three tensor eigenvalues: (λ₁ + λ ₂ + λ ₃)/3. AD is equivalent to λ₁ and RD is the average of the second and third eigenvalues, (λ₂ + λ ₃)/2. FA was calculated as:

$$FA=\sqrt{\frac{1}{2}}\frac{\sqrt{{({\lambda }_1-{\lambda }_2)}^2+{({\lambda }_2-{\lambda }_3)}^2+{({\lambda }_3-{\lambda }_1)}^2}}{\sqrt{{\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2}}$$

At the reported spatial resolution it is possible for a small fraction of voxels to lie entirely within small air bubbles or fluid filled blood vessels, resulting in outlier measurements that do not represent the actual diffusion parameter of the tissue of interest. To reduce the effect of outliers we discarded the top and bottom 2.5% of voxel intensities within each region before calculating the mean. Data were then imported into JMP Pro 9 statistics software (http://www.jmp.com) for further analysis. ADC, AD and RD values were normalized based on the ADC of the ventricular space. To accomplish this normalization, we manually selected a large region of ventricular space with no visible choroid plexus and measured the average voxel value, which was assumed to represent unhindered diffusion. Each dataset was then normalized by some scalar, such that ventricular diffusion measurement matched the group average ventricular diffusion measurement. This normalization is meant to correct for diffusion measurement error induced by ambient temperature and effective b-value variability and does not account for differences in tissue fixation. Average datasets for each time point, as well as the complete diffusion tensor scalar database, are provided as supplemental material online at http://www.civm.duhs.duke.edu/2013diffratbrain/.

2.8 Transmission electron microscopy

After fixation and MR imaging, a single specimen from each time point was further processed for transmission electron microscopy. In short, brains were manually extracted from the skull, hemisected along the mid sagittal line, and sliced in the sagittal plane using a vibratome. Para-sagittal slices were then prepared for electron microscopy using a standard four-hour microwave processing protocol (Giberson and Demaree, 1999). Individual resin blocks were prepared for the genu of the corpus callosum, and the outer cingulate cortex of each specimen. Tissue blocks were surveyed to identify the tissue of interest, and a series of electron micrographs were acquired at 50,000× and 100,000× display magnification using a Philips CM12 transmission electron microscope. All electron microscopy work was performed at the Duke University electron microscopy facility (http://pathology.mc.duke.edu/Path/Experimental/EM/EM_Main.aspx).

3. Results

3.1 DT-MRH of postnatal rat brain development

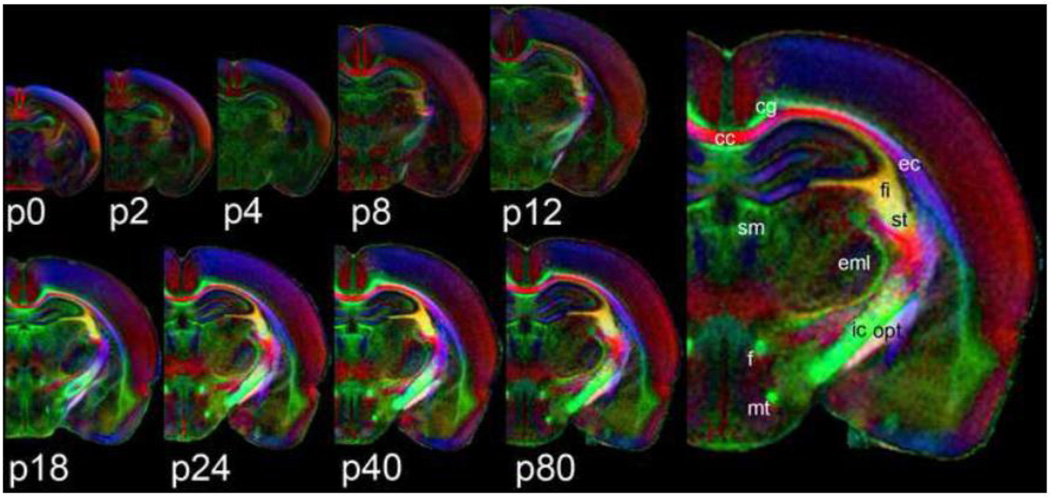
Figure 1 shows population-averaged (n = 5), directionally-encoded color FA maps from all nine time-points included in this study (p0 to p80) in the coronal plane. Pixel intensity indicates fractional anisotropy and color indicates orientation of the primary eigenvector (red = lateral/medial orientation, green = rostral/caudal and blue = dorsal/ventral). All coronal slices are taken from roughly the same anatomic location—through the rostral aspect of the hippocampal formation. On the right side of Figure 1, the p80 image is replicated at 2× magnification to show detail. Several major white matter structures are labeled using the abbreviations and nomenclature of the Paxinos and Watson rat brain atlas (Paxinos and Watson, 2007). FA of white matter structures tends to increase (i.e. higher intensity) with increasing age. In contrast, cortical FA is highest at p0 (average=0.31±0.02) and tends to decrease with increasing age.

Figure 1.

Population averaged, coronal, color FA maps from nine different postnatal time points (p0–p80). Slices are taken from approximately the same location—the rostral aspect of the hippocampal formation. The p80 image is replicated and enlarged (right) to show detail. Several major white matter structures are labeled using the nomenclature and abbreviations of the Paxinos and Watson rat brain atlas (2008); cc – corpus callosum; cg – cingulum; ec – external capsule; eml – external medullary lamina; f – fornix; fi – fimbria; ic – internal capsule; mt – mamillothalamic tract; opt – optic tract; sm – stria medullaris; st – stria terminalis.

3.2 Anatomic labels and white matter segmentation

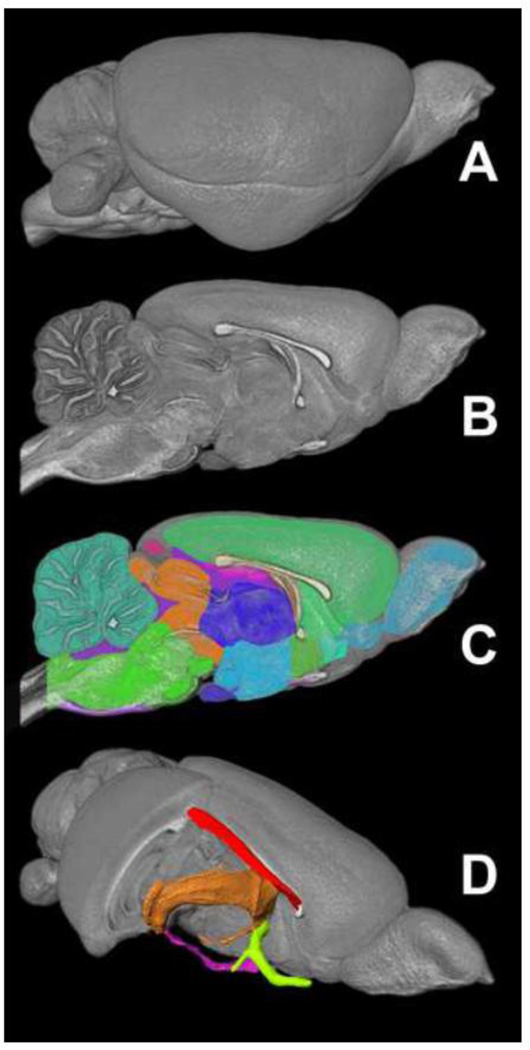
Figure 2 shows the 3D anatomic labels used for region of interest (ROI)-based diffusion tensor parameter analysis. A volume-rendered adult (p80) rat brain (A) is shown next to a mid-sagittal sliced volume-render without labels (B) and with labels as semi-transparent color overlays (C). These labels were generated as part of a related study and the associated color-code and label descriptions can be found in the associated publication (Calabrese et al., 2012) or online at http://neurolex.org/wiki/Category:CIVM_postnatal_rat_brain_atlas_parcellation_scheme. These structures were chosen to be developmentally relevant and easily identifiable in the rat brain throughout postnatal neurodevelopment. All 26 structures were identified and segmented at each of the nine time points included in this study. Figure 2D shows a volume-rendered rat brain with the right anterolateral quadrant removed revealing volume-rendered representations of four of the major white matter structures included in this study: the cingulum bundle (red), the fimbria/fornix (orange), the anterior commissure (green), and the optic tracts (magenta).

Figure 2.

The 3D labels used for diffusion parameter analysis. A volume-rendered p80 rat brain is shown in lateral (A) and mid-sagittal views (B) with labels shown as 2D color overlays (C). Selected white matter labels are shown as 3D surfaces in a cut-away anterolateral view of the brain (D); red – cingulum; orange – fimbria/fornix; magenta – optic tracts; green – anterior commissure.

3.3 White matter regions

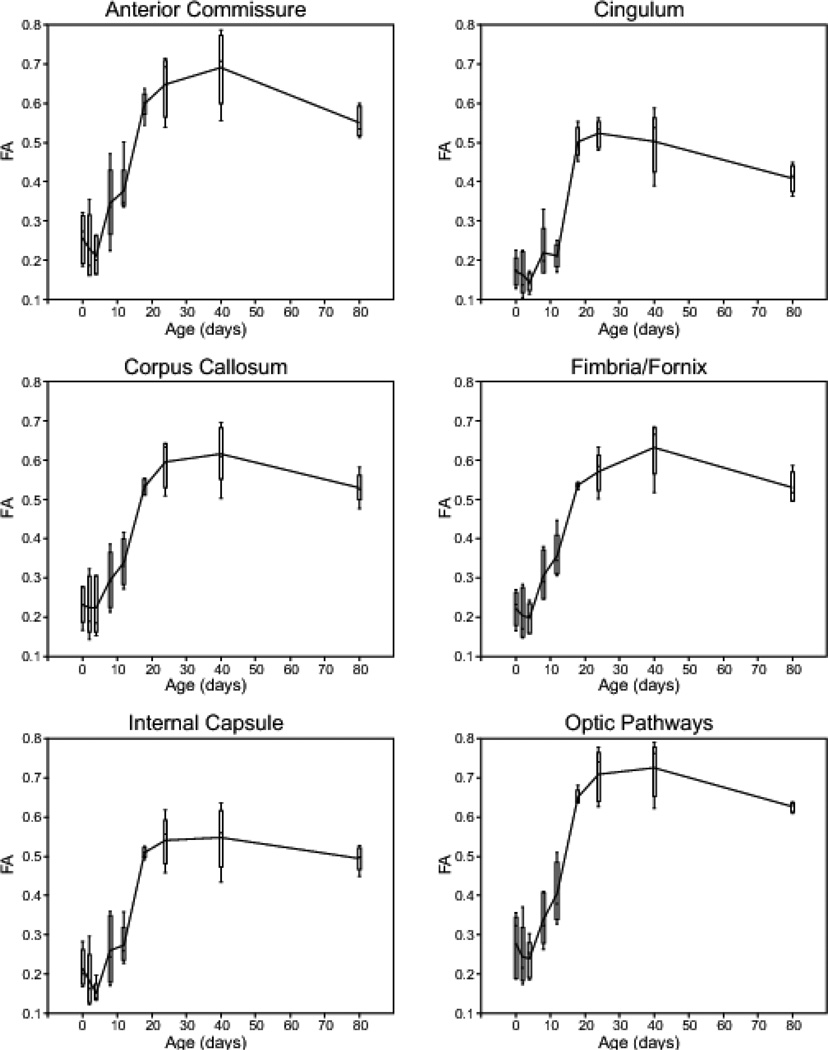
Figure 3 shows plots of FA versus postnatal day for six major white matter structures. Data are displayed as outlier style box-and-whisker plots with a line connecting adjacent means. All six white matter regions exhibit a similar FA trajectory during neurodevelopment; FA is generally low at birth (i.e. less than 0.3), reaches a maximum between p24 and p40, and then decreases slightly, although not significantly at p80. In all cases, the most rapid increase in FA occurs between p12 and p18. The anterior commissure and optic pathways had slightly higher mean FA than other white matter structures at the same age, ranging from ~0.3 at p0 to ~0.7 at p40. The distribution of FA measurements was relatively consistent between time-points; however, the p18 and p80 time-points generally exhibited narrower FA distribution for the six white matter structures shown here.

Figure 3.

Plots of fractional anisotropy (FA) versus postnatal day for six major white matter regions in the postnatal developing rat brain. Data are shown as outlier-style box-and-whisker plots with a line connecting adjacent means.

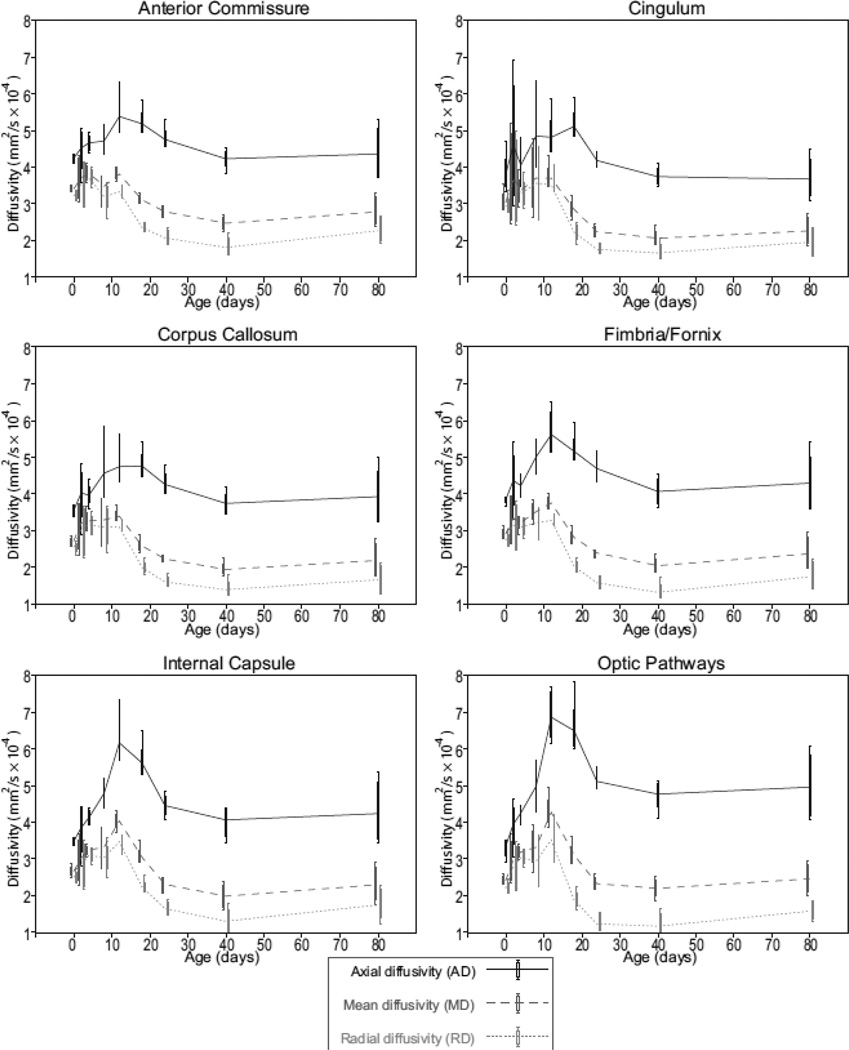
Diffusivity values for the same six white matter regions are displayed in Figure 4. Axial diffusivity (AD, black), mean diffusivity (MD, dark gray), and radial diffusivity (RD, light gray) are shown on the same plot for each structure as outlier style box-and-whisker plots. As is expected for high FA structures like white matter tracts, AD was much greater than MD and RD. All six white matter regions show a similar trend; diffusivities peak around p12 and then stabilize to a minimum near p40. Once again, variability was generally larger near birth (p0) and lowest around p18. In most cases, RD values experienced a net decrease between p0 and adulthood (p80), whereas AD remained the same or slightly increased during this period (optic pathways for example).

Figure 4.

Plots of diffusivity data versus postnatal day for the same six white matter regions shown in Figure 3. Data are shown as outlier-style box-and-whisker plots with a line connecting adjacent means. Each plot includes axial diffusivity (AD, solid black), mean diffusivity (MD, dashed dark gray), and radial diffusivity (RD, dotted light gray).

3.4 Gray matter regions

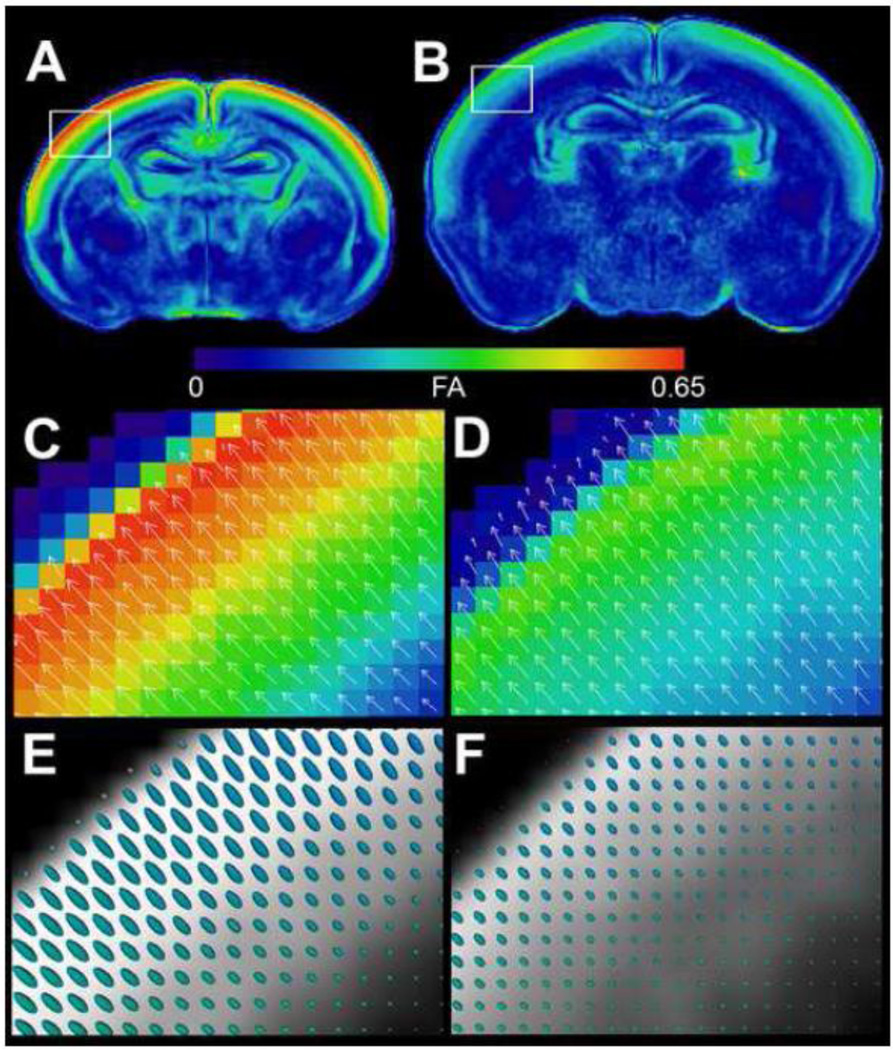
In contrast to the dramatic increases in FA seen in most major white matter structures, a majority of gray matter structures show no significant change in mean FA during postnatal neurodevelopment. The major exception to this trend is the superficial isocortex, which shows a remarkably high FA at birth that rapidly disappears by the 8^th postnatal day. Figure 5 shows a comparison of cortical FA in a p0 (A, C, E) and p4 rat brain (B, D, F). Figure 5 A and B are FA images displayed with a heat-map lookup table to highlight differences (color map shown). The displayed slices were taken at roughly the same location in the p0 and p4 cortex, respectively; however, subcortical structures may not be coplanar between these time points due to different growth trajectories. These data reveal high FA in the p0 isocortex that is substantially reduced by p4. Interestingly, high birth FA only occurs in the outer half of the isocortex, roughly corresponding to cortical layers I–III. Magnified insets spanning the entire cortical thickness (C and D) are displayed along with vector arrows indicating direction of the primary eigenvector and its magnitude (i.e. the axial diffusivity) at each pixel. Despite the large changes in cortical FA between p0 and p4, the orientation of the primary eigenvector remains relatively unchanged. Figure 5 E and F show the same region of cortex in grayscale along with the 3D tensor ellipsoids corresponding to each pixel. The tensor ellipsoids reveal that FA loss in the outer layers of the isocortex is primarily the result of decreasing axial diffusivity (i.e. a shortened long axis of the tensor ellipsoid).

Figure 5.

Fractional anisotropy changes in the neonatal isocortex between p0 (left) and p4 (right). Coronal fractional anisotropy (FA) images through the rostral hippocampal formation from the p0 (A) and p4 (B) rat brain are shown in false color heat-map to highlight differences (scale shown). Magnified insets of the entire cortical thickness are shown with vector arrows indicating direction and magnitude of the primary eigenvector (C–D). The same regions are shown in grayscale along with the 3D tensor ellipsoids corresponding to each voxel (E–F).

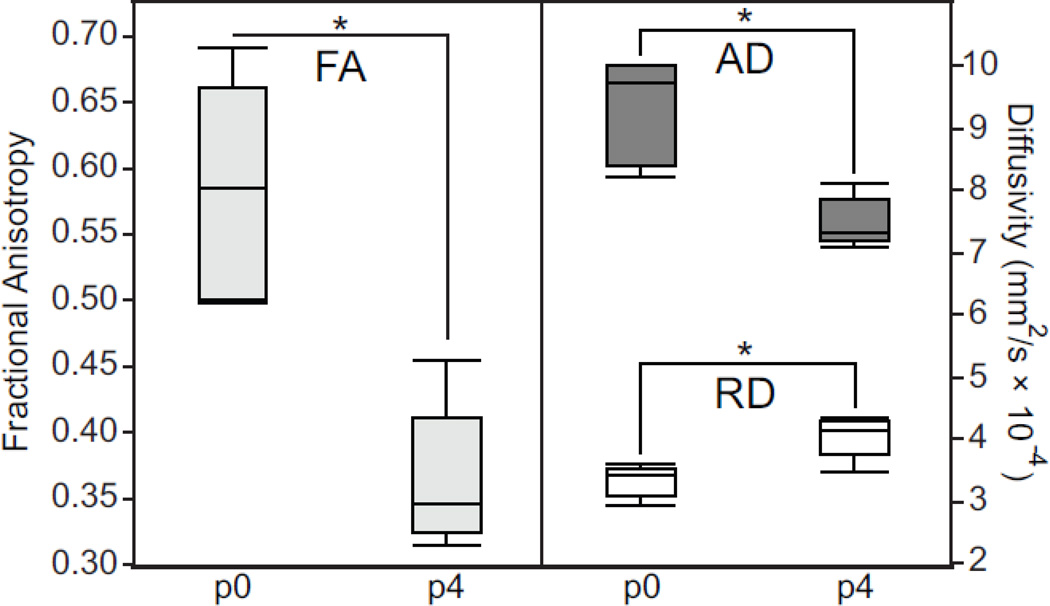
We quantify these findings in Figure 6, which shows data collected from a 2D ROI placed in the outer layers of the isocortex at approximately the same location shown in Figure 5 C and D. We compared FA (left), AD, and RD (right) values for all five specimens at p0 and p4. Statistically significant differences were computed using the student’s T-test. These data show a decrease in FA between p0 and p4 that is due to a large decrease in AD and a modest increase in RD. All three changes reached statistical significance. Similar comparisons of cortical diffusion parameters for all nine time points are included as Supplemental Figure 2.

Figure 6.

Diffusion parameter measurements from a 2D region of interest placed in the outer layers of the p0 and p4 isocortex at approximately the same locations shown in Figure 5 B–C. Fractional anisotropy (FA) is shown (left) next to axial diffusivity (AD) and radial diffusivity (RD) (right). Statistically significant changes in diffusion parameters are denoted with an asterisk.

3.5 Transmission electron microscopy

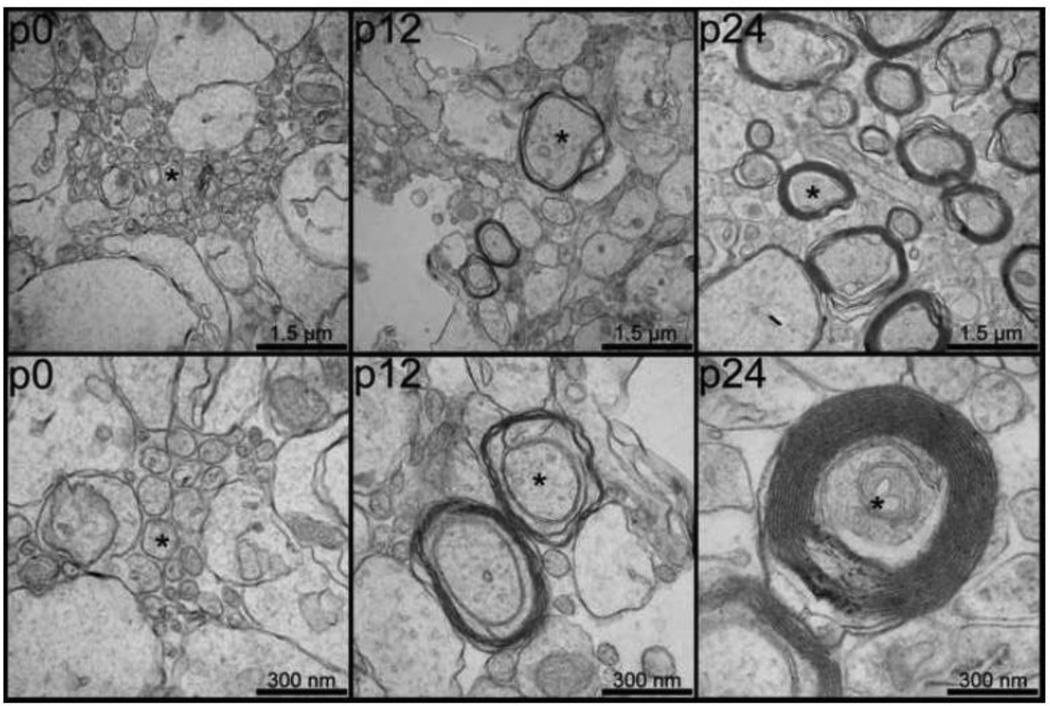
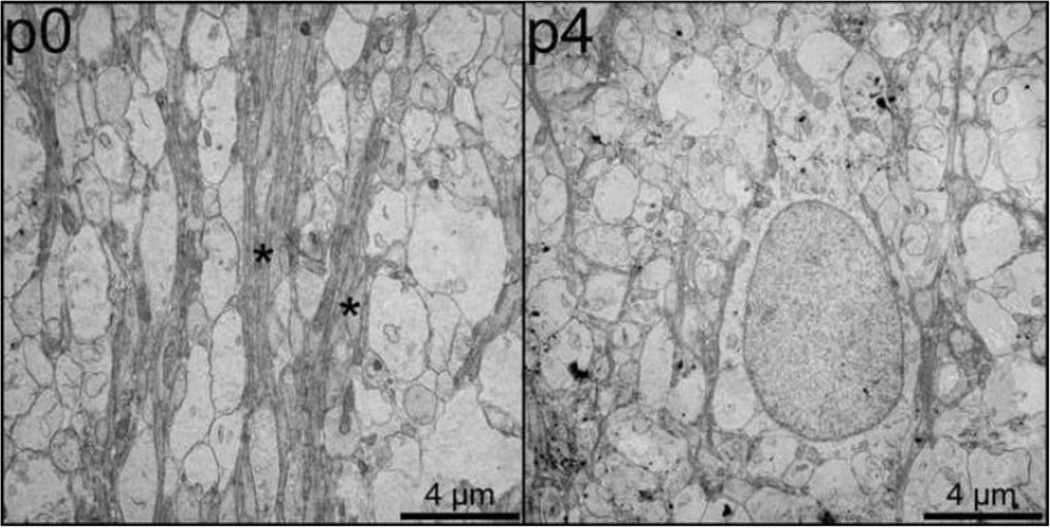
Figure 7 and Figure 8 show electron microscopy results from specimens previously imaged with DT-MRH. Figure 7 compares low-power (top) and high-power (bottom) images of the genu of the corpus callosum at three different postnatal time points: p0 (left), p12 (center), and p24 (right). These three time points correspond to the beginning, middle, and end, respectively, of the period of most rapid change in callosal diffusion tensor parameters. In each image, representative axons are marked with asterisks. The p0 genu is comprised largely of widely spaced clusters of small, unmyelinated axons. The p12 genu consists of slightly larger diameter axons loosely wrapped in immature myelin lamellae with abundant periaxonal cytoplasm. In contrast, the p24 micrographs show several large diameter axons with thick, highly compact myelin sheaths. Figure 8 is a comparison of electron micrographs taken from the outer layers of the cingulate cortex in the p2 and p4 rat brain. The p2 outer cortex (left) is dominated by a complex network of radially oriented glial cell processes (marked with asterisks). This radial glia network is much less prominent in the p4 outer cortex (left) and is virtually absent in later time points.

Figure 7.

Electron micrographs of the genu of the corpus callosum at three postnatal time points (p0, left; p12, center; and p24, right) demonstrating postnatal cerebral myelination. Both low power (50,000× magnification, top) and high-power (100,000× magnification, bottom) are shown for each time point. Representative axons are marked with asterisks and scale bars are shown in the bottom right corner of each image.

Figure 8.

Electron micrographs of the outer layers of the cingulate cortex at two postnatal time points (p0, left; and p4, center) demonstrating differences in radial glial cell processes. Bundles of radial glial cell processes are marked with asterisks and scale bars are shown in the bottom right corner of each image.

4. Discussion

4.1 Diffusion tensor changes reveal white matter maturation

A majority of white matter myelination in the rodent brain occurs during the early postnatal period, and the myelination process is virtually complete by the third postnatal week (Foran and Peterson, 1992). FA is a sensitive (though not specific) imaging biomarker for axonal organization and myelin integrity. The diffusion data collected for this study reveal dramatic microstructural changes during early postnatal development that correlate, both spatially and temporally, with known white matter maturation milestones. For example, FA data from six major cerebral white matter regions (Figure 3) follow a trajectory that is consistent with cerebral myelin maturation. Gene transcription and electron microscopy studies have shown that rodent brain myelination starts by the end of the first week of postnatal life and is largely complete by the end of the third postnatal week (Luse, 1956; Field et al., 1969; Foran and Peterson, 1992). Similarly, all six plots of FA versus postnatal day shown in Figure 3 have positive slope between p8 and p24. Further, the most rapid increase in FA occurs between p12 and p18, which is believed to be the period of most rapid myelination in the rodent brain.

One of the major advantages of diffusion tensor measurements over conventional histologic methods for assessing white matter maturation is that they can be easily quantified. In our study, we were able to show statistically significant increases in FA between p12 and p18 for all six white matter structures included in the analysis (results included as supplementary Figure 1). The quantitative nature of this FA data allows it to be used for quantifying developmental neuropathology in rodent models. Unfortunately, one of the major shortcomings of FA is the fact that it is nonspecific, and is at best a surrogate for myelin integrity. FA is in essence a normalized ratio of water diffusion in one direction to its diffusion the two orthogonal directions (Basser and Pierpaoli, 1996). Many microstructural features can lead to increasing diffusion anisotropy in white matter including; 1) decreased RD from myelination, myelin compaction or the compaction of many axons into a nerve fascicle; 2) increased AD from a reduction in axonal swelling or an increase in inter-axon extracellular space; or 3) a combination of decreased RD and increased AD (Basser, 1995; Mukherjee et al., 2008). Careful analysis of the diffusivity values used to calculate FA, including AD, MD, and RD can reveal further details about underlying tissue changes.

Measurement of diffusion via DT-MRH is inherently problematic because fixation alters tissue diffusivity (Sun et al., 2009). Fortunately, if performed carefully, perfusion fixation produces a spatially and temporally consistent reduction in tissue diffusion that appears to be proportional to in-vivo diffusivity, thus reducing diffusion magnitude but not directionality or proportionality (Sun et al., 2005). Another concern is that ex-vivo tissue does not have any inherent thermoregulation or osmoregulation, which can lead to a spuriously wide inter-specimen data distribution due to subtle changes in perfusate osmolality or magnet bore temperature. This effect can be corrected for by normalizing to a substance of known diffusivity, such as a diffusion phantom, or if image resolution permits, to the ventricular fluid as was done for this study.

Figure 4 shows normalized diffusivity data plotted against age in postnatal days for the same six white matter structures as Figure 3. One of the most striking similarities in these plots is the increase in all three diffusivity parameters that occurs around p12 in all six structures. Interestingly, this diffusivity increase coincides temporally with the start of a rapid increase in FA. Several previous in-vivo studies of rodent white matter diffusivity have shown a similar increase in white matter diffusivity during the second postnatal week followed by a decline and stabilization after the third postnatal week (Chahboune et al., 2007; Larvaron et al., 2007; Bockhorst et al., 2008). Specifically, Bockhorst et al. (2008) showed a similar trend in the corpus callosum and internal capsule, Chahbourne et al. (2007) in the corpus callosum and cingulum and Larvaron et al. (2007) in the corpus callosum and anterior commissure. All three groups reported in-vivo MD change in the corpus callosum from ~0.8×10⁻³ mm²/s to ~0.5×10⁻³ mm²/s during the course of postnatal neurodevelopment, representing a ~37% decrease with age. Our ex-vivo results show corpus callosum MD change from 0.35+0.02×10⁻³ mm²/s to 0.23+0.04×10⁻³ mm²/s, or a 34% decrease during this period. These results indicate that normalized DT-MRH measurements of diffusivity closely match the trajectory and proportionality of comparable in-vivo measurements, though not necessarily the magnitude.

Together, the estimates of white matter diffusion parameters shown in Figure 2 and Figure 3 reveal complex changes in underlying tissue microstructure. The data show a large, but transient, increase in diffusivity around p12 followed by a rapid increase in FA between p12 and adulthood. These diffusivity trends correlate well with previously published microstructural observations in developing white matter (Field et al., 1969) and with the electron microscopy findings presented in Figure 7; axons in the p0 corpus callosum (Figure 7, left) are predominantly unmyelinated, presumably contributing to the low FA observed in p0 DT-MRH data. The p12 corpus callosum (Figure 7, center) has many myelinated axons; however, the myelin lamellae are immature and have large areas of periaxonal cytoplasm. This excess of periaxonal cytoplasm, where diffusion is relatively unhindered, may be the cause of increasing white matter diffusivity values in the context of rapid cerebral myelination. In contrast, axons in the p24 corpus callosum (Figure 7, right) are tightly ensheathed in mature myelin lamellae with very little periaxonal cytoplasm, resulting in relatively low diffusivity and high FA. These data suggest that both the degree of myelination, and the compactness of the myelin layers contribute to diffusion tensor changes during normal neurodevelopment. Despite their lack of specificity, it is clear that diffusion parameters like FA and RD are sensitive, quantitative biomarkers for the range of microstructural changes that occur during normal white matter development.

4.2 Diffusion tensor changes in the developing cerebral cortex

As previously explained, diffusion tensor parameters are not specific for white matter integrity, but rather reflect tissue microstructural organization. In fact, dramatic diffusion tensor changes occur in the developing cerebral cortex as shown in Figure 5 and Figure 6. At birth, the outer layers of the rat isocortex have a remarkably high FA—even higher than major cerebral white matter structures (e.g. Figure 5 A). Interestingly this high cortical anisotropy rapidly decreases and is virtually absent by p8 (see Figure 1 p0-p8). This rapid change in cortical microstructure is characterized by decreasing diffusion anisotropy in the presence of an unchanged primary eigenvector (Figure 5 C–F). The statistical analysis presented in Figure 6 points to a decrease in AD and a proportionally smaller increase in RD as the cause of this early postnatal, cortical anisotropy loss. These diffusion changes in the presence of an unchanged primary eigenvector suggest the loss of a radially organized diffusion pathway in the outer cortex during early postnatal life.

It is likely that several different microstructural processes contribute to the observed FA changes in the developing rat cortex. For example, a number of white matter pathways radiate outwards towards the cortical surface; however, they tend to become more organized, rather than less organized during neurodevelopment (Wise and Jones, 1976; Allendoerfer and Shatz, 1994). In addition, the radial migration of cortical neurons and the later development of cortical interneurons (Noctor et al., 2004) could conceivably alter diffusion properties along the cortical column. Perhaps the major contributor to the observed changes is the disruption of a radially organized network of glial cells that is known to occur during early cortical development (Chanas-Sacre et al., 2000). This highly ordered scaffolding of glial cell processes, often referred to as “radial glia,” provides a pathway for migration of neurons and neuronal precursor cells what will eventually become the six layers of the cerebral cortex (Rakic, 1972). Because of its important organizational role in the developing cortex, damage to the radial glia, as a result of perinatal asphyxia for example, can lead to severe cortical malformation and neurologic disability (Marín-Padilla, 1996). The presence of radial glial cell processes on transmission electron micrographs correlated well with FA changes in the developing neonatal isocortex; we observed an abundance of radial glial cell processes in the p0 outer cortex (Figure 8, left), which was substantially reduced in the p4 outer cortex (Figure 8, right). The ability to quantify spatial and temporal changes in cortical microstructure has exciting potential to advance our understanding of diseases that may be the result of perinatal cortical insults such as hypoxic ischemic encephalopathy or cerebral palsy. For example, perinatal hypoxic ischemic injury has been shown to significantly reduce FA and alter the radial organization of the primary eigenvector in the neonatal rat cerebral cortex (Sizonenko et al., 2007).

These data emphasize that DT-MRH data can be used to quantify microstructural changes in both white matter and gray matter structures. In total, the diffusion parameter database generated from this study comprises 26 distinct brain regions, most of which are at least partially composed of gray matter. In each case, the postnatal trajectory of diffusion tensor changes has the potential to reveal some nuance of brain microstructural development, although an in-depth analysis of each region is beyond the scope of the current study. The entire diffusion parameter database is included in the online supplement (http://www.civm.duhs.duke.edu/2013diffratbrain/) for further analysis.

4.3 Limitations of DT-MRH

There are two important limitations of these data; 1) the diffusion parameter estimates are from fixed ex-vivo tissue; and 2) the diffusion data were acquired using only six gradient directions. Previous studies have shown that brain fixation decreases the magnitude, but not the proportionality or directionality of diffusion, thus leaving FA relatively unchanged (Sun et al., 2005). We replicate these findings in this work by comparing our diffusivity measurements to analogous in-vivo measurements and showing similar trends at lower diffusion magnitudes. We believe that the increased spatial specificity and image quality DT-MRH provides makes it a valuable alternative to in-vivo DTI. Similarly, we favor higher spatial-resolution over higher angular sampling of the diffusion tensor. A number of previous studies have suggested that as many as 30 gradient directions are required for accurate and precise estimates of FA (Ni et al., 2006; Landman et al., 2007); however, these studies are largely based on in-vivo clinical data where patient orientation and motion artifacts are a major source of error. In addition, most clinical diffusion data are acquired with an echo-planar imaging sequence, which is particularly prone to susceptibility artifacts, and generally has lower signal-to-noise ratio (SNR) than DT-MRH data. For these reasons, observations on the effect of the number of gradient directions on diffusion tensor estimation accuracy from clinical studies are not necessarily applicable to DT-MRH studies. Any error resulting from a six-direction strategy is likely compensated for by the increased image quality, SNR, and spatial accuracy that DT-MRH can provide (Alexander et al., 2001; Anderson, 2001).

Another important limitation of our methods is the long scan-time required to acquire high-resolution, high-SNR data. It is currently impractical for most laboratories to acquire the type of data presented here for routine assessment of disease models. Fortunately, this type of data is not always necessary for assessing preclinical models where differences are often evident at substantially lower resolution. Because diffusion-weighted signal is related to the average diffusivity throughout a voxel, the data presented here can be downsampled for direct, voxelwise comparisons with lower resolution data. It is also straightforward to compare average diffusion parameter values of specific brain regions from lower-resolution data. For large ROIs, average diffusion parameter measurements should be very similar regardless of spatial resolution; however, smaller structures may be difficult to reliably segment in low-resolution data and may be more susceptible to partial volume effects. Comparisons with lower-SNR data are also possible with the caveat that low SNR may negatively impact measurement precision.

5. Conclusions

The data presented here represents the most comprehensive and highest-resolution diffusion tensor database of rat neurodevelopment to date. We have collected diffusion tensor data at unprecedented spatial- and temporal-resolution throughout postnatal neurodevelopment and used it to characterize the normal microstructural changes that occur during this crucial period of brain growth and differentiation. Further, we have correlated our findings with known microstructural developmental milestones and compared our diffusion parameter measurements with analogous in-vivo measurements. These data will provide a foundation for future studies investigating diffusion tensor microstructural changes in rat models of neurodevelopmental diseases. The population averaged image sets provided in the supplementary material (http://www.civm.duhs.duke.edu/2013diffratbrain/) will allow registration and spatial normalization of experimental data, and the diffusion tensor parameter database will facilitate quantitative comparisons. We believe that these data demonstrate exciting potential for the use of DT-MRH to quantify microstructural changes during both normal and abnormal neurodevelopment, and we look forward to future studies using DT-MRH to characterize rodent models of neurodevelopmental disease.