SEMIPARAMETRIC ZERO-INFLATED MODELING IN MULTI-ETHNIC STUDY OF ATHEROSCLEROSIS (MESA)

Abstract

We analyze the Agatston score of coronary artery calcium (CAC) from the Multi-Ethnic Study of Atherosclerosis (MESA) using semi-parametric zero-inflated modeling approach, where the observed CAC scores from this cohort consist of high frequency of zeroes and continuously distributed positive values. Both partially constrained and unconstrained models are considered to investigate the underlying biological processes of CAC development from zero to positive, and from small amount to large amount. Different from existing studies, a model selection procedure based on likelihood cross-validation is adopted to identify the optimal model, which is justified by comparative Monte Carlo studies. A shrinkaged version of cubic regression spline is used for model estimation and variable selection simultaneously. When applying the proposed methods to the MESA data analysis, we show that the two biological mechanisms influencing the initiation of CAC and the magnitude of CAC when it is positive are better characterized by an unconstrained zero-inflated normal model. Our results are significantly different from those in published studies, and may provide further insights into the biological mechanisms underlying CAC development in human. This highly flexible statistical framework can be applied to zero-inflated data analyses in other areas.

1. Introduction

The Multi-Ethnic Study of Atherosclerosis (MESA) (Bild et al., 2002) is an ongoing longitudinal study of subclinical cardiovascular disease (CVD) involving a cohort of more than 6,500 men and women from six communities in the United States (http://www.mesa-nhlbi.org/). It was initiated by the National Heart, Lung, and Blood Institute in July 2000 to investigate the prevalence, risk factors and progression of subclinical CVD in a population-based multi-ethnic cohort. Agatston score (Agatston et al., 1990), which measures the amount of coronary artery calcium (CAC), is an important predictor of future coronary heart disease events (Min et al., 2010; Polonsky et al., 2010). However, many healthy people may have no detectable CAC; consequently CAC equals zero with substantial relative frequency, but otherwise it is a continuous positive variable. That CAC has a mixture distribution with an atom at zero hampers its analysis by standard statistical methods. Such data are referred to as “zero-inflated” and require the development of more complex statistical models.

Zero-inflated data actually abound in many areas, for example, in health care cost studies (Blough, Madden and Hornbrook, 1999), environmental science (Agarwal, Gelfand and Citron-Pousty, 2002), ecological applications (Liu et al., 2011), etc. Among various models for analyzing data with excess zeroes, the hurdle model (Mullahy, 1986) has been proposed to handle both zero-inflation and zero-deflation in count data, which consists of two parts: one binary model to determine whether the response outcome is zero or positive and a second part conditional on the positive responses if the “hurdle is crossed”. On the other hand, zero-inflated model (Lambert, 1992) that assumes an underlying mixture distribution of probability mass at zero and some continuous or discrete distribution (e.g., normal, Poisson) has been widely used to analyze zero-inflated continuous data (Couturier and Victoria-Feser, 2010). Note that both the hurdle model and the zero-inflated model are essentially equivalent to the two-part model (Kronmal, 2005; Welsh and Zhou, 2006) when dealing with zero-inflated continuous data as the CAC score in MESA (see Min and Agresti, 2005, for discussion on comparing existing models for zero-inflated count data). Therefore we will not distinguish the aforementioned two models and refer to the approach as the zero-inflated model in the following discussion. Also note that the two-part model for zero-inflated continuous data, with the probit link for the binary model part, is a special case of the Heckman model (also known as Type II To-bit model, see Heckman, 1979; Amemiya, 1984). Most existing zero-inflated models are in the parametric setting, assuming that the covariate effects are linear (on proper link scales). However, the assumption of linearity may not hold in public health or medical research. Instead, semiparametric regression model (Ruppert, Wand and Carroll, 2003) provides a powerful tool to describing nonlinear relationships between the covariates and response variables in such situations. For instance, Lam, Xue and Cheung (2006) used the sieve estimator to analyze zero-inflated count data from a public health survey.

In zero-inflated data analyses, it is often of interest to examine whether the zero and non-zero responses are generated by related mechanisms. In MESA, it may provide useful insights into the biological process on whether or not the risk factors of CVD influence the probability of having positive CAC and the progression of CAC when it is present in a similar way, which could be statistically verified by introducing proportional constraints into the zero-inflated model. Such constrained zero-inflated model can be interpreted by a latent biological mechanism involving an unobservable random threshold and has been studied mostly in a parametric framework. For example, Han and Kronmal (2006) considered proportional constraints in two-part models in MESA to promote better understanding of the mechanism that drives the zero-inflation in CAC, and to estimate the model parameters more accurately (intuitively because fewer parameters need to be estimated in a constrained model) as well. However, they did not take into account the nonlinear relationships between some covariates and the response variable in MESA (McClelland et al., 2006). Ma et al. (2010) incorporated proportional constraints in a semiparametric zero-inflated normal model when analyzing the same data set, but they only considered an universal proportionality parameter on all covariates, which is not flexible enough to handle more complicated zero-inflation processes (see Section 2 for more discussion). Therefore, it becomes necessary to study a more flexible partially constrained semiparametric zero-inflated model to overcome the limitations of the existing investigations. We note that similar techniques of imposing proportional constraints on two sets of regression coefficients in complex models were investigated by Albert, Follmann and Barnhart (1997); Moulton, Curriero and Barroso (2002), among others.

In this paper, we propose a partially constrained semiparametric zero-inflated model to analyze the CAC score in MESA, which provides a highly flexible approach for delineating the zero-inflated data generating process. Under the general partially constrained model framework, the unconstrained and constrained zero-inflated models together make it possible to shed new light on the relationship between the zero and non-zero data generating processes, and the latter promotes estimation efficiency when the postulated constraint holds. Cubic regression spline with shrinkage is adopted to estimate nonparametric regression functions and to select important variables simultaneously. Because of the complex model specification with a mixture distribution, a model selection procedure based on cross-validated likelihood is implemented to examine the prediction performance of the fitted models, and to choose the optimal zero-inflated model from multiple candidate models with various partial proportional constraints, which avoids the problem of multiple testing by treating each candidate model on equal basis. Estimation of the proposed zero-inflated model and statistical inference will also be discussed. The outline of this paper is as follows. We introduce the semi-parametric zero-inflated model methodology in Section 2. Simulation studies are carried out to illustrate the proposed model estimation and selection methods in Section 3. The analytical results of the MESA data analysis are presented in Section 4. Some concluding remarks are discussed in Section 5.

2. Methods

2.1. Semiparametric zero-inflated model

Statistical analysis of zero-inflated data cannot proceed under the assumption of regular probability distribution due to the high frequency of zeroes. If the non-zero responses are continuously distributed, zero-inflated normal (ZIN) model can be utilized, which assumes a mixture distribution of probability mass at zero and a normal distribution, after suitable transformation. Suppose that given the covariate vectors Z = (Z₁, …, Z_m)′ and X = (X₁, …, X_k)′, the conditional distribution of the response variable Y is zero-inflated normal:

$$Y\mid \mathbf{Z},\mathbf{X}~\{\begin{array}{ll}0\hfill & \text{with}\text{probability}(1-p)\hfill \\ \mathcal{N}(\mu ,{\sigma }^2)\hfill & \text{with}\text{probability}p,\hfill \end{array}$$ (2.1)

where the covariate effects of Z are parametric and those of X are nonparametric. The above ZIN model consists of two parts:

$$g(p)={\beta }_0+{\mathit{\beta }}^{\prime }\mathbf{Z}+\sum _{i=1}^k{h}_i(X_i)$$ (2.2)

links the non-zero-inflation probability p to the covariates via a link function g (e.g. logit or probit function) in the binary part, and the linear part

$$\mu ={\gamma }_0+{\mathit{\gamma }}^{\prime }\mathbf{Z}+\sum _{i=1}^k{s}_i(X_i)$$ (2.3)

describes the covariate effects on the normal mean response μ. In the semi-parametric setting, β₀ and γ₀ are two intercept terms, the regression coefficients β = (β₁, …, β_m)′ and γ = (γ₁, …, γ_m)′ correspond to the parametric effects in the two parts respectively, and h_i, s_i, i = 1, …, k, are two sets of nonparametric smooth functions. By setting some parametric coefficients and/or some smooth functions to be identically zero, equations (2.2) and (2.3) subsume the case that the two parts of the model involve different sets of covariates. Each univariate smooth function h_i(X_i) or s_i(X_i), i = 1, …, k, can be estimated nonparametrically using cubic regression spline, which can be readily extended to high-dimensional smoother using thin plate spline (Wood, 2003) to accommodate interaction between several continuous predictor variables.

Equations (2.1), (2.2) and (2.3) formulate an unconstrained semiparametric ZIN model, which assumes that the covariate effects on the probability of having a non-zero response and the magnitude of the non-zero response may follow different data generating mechanisms. However, an interesting research question arises as to whether the two processes are related to some extent such that some covariates influence the two processes similarly. The partially constrained zero-inflated modeling approach (Liu and Chan, 2011) could be used to test the above hypothesis, which assumes that some of the smooth components (operating on the same covariates) in (2.2) and (2.3) bear proportional relationships with the constraints:

$$h_i={\delta }_i{s}_i,i\in \mathcal{C}\subseteq \{1,\dots ,k\},$$ (2.4)

where 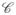is the index set of the constrained smooth components; δ_i, i ∈ 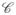are unknown proportionality parameters. The covariates corresponding to those smooth functions with proportional constraints then affect the nonzero-inflation probability and the mean non-zero response proportionally on the link scales. However, the other covariates with indices not in 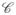may have different impacts on the above two processes, which can be flexibly modeled by the unconstrained components. Note that the unconstrained zero-inflated model is a special case in the general partially constrained model framework with = ∅.

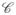We consider proportional constraints in the zero-inflated model not only because they may result in more parsimonious models, but also because they may admit biological interpretation connected to some latent threshold model. To illustrate this connection, suppose that Y^* is a latent response variable following the 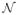(μ, σ²) distribution. The observed response Y is zero if the latent mean response μ is less than a random threshold T which could be due to measurement error or limits of detection, and it is equal to Y^* if μ exceeds the threshold. Hence the non-zero-inflation probability p = Pr(Y = Y^*) = Pr(T ≤ μ) = F_T (μ), where F_T is the cumulative distribution function (CDF) of the random threshold variable T. As a result, we would have g(p) = μ if the link function is taken as the inverse CDF of T, which is, however, generally unknown. Nevertheless, according to Li and Duan (1989), under some mild regularity conditions, any maximum likelihood-type estimator is consistent up to a multiplicative scalar, even under a misspecified link function. More specifically, if we use, for example, a logit link in (2.2), the parameter estimators in the binary part are proportional to the true parameters in (2.3), i.e., β̂ = δγ, and ĥ_i = δs_i, i = 1, …, k, for some scalar δ. Alternatively, assuming the zero-inflation is caused by some other biological characteristic depending on the covariates through ξ(Z, X), i.e., Y = 0 if ξ(Z, X) < T, we may have partial proportionality among the parameters in the two parts. Based on this latent biological process, we further relax the proportionality parameter to be possibly different across the linear and smooth components, leading to the proposed partially proportionally constrained zero-inflated model.

As a closely relevant study in the literature, Ma et al. (2010) compared the unconstrained semiparametric zero-inflated model to a fully proportionally constrained model, which assumed (2.2) and $\mu =\alpha +\tau \{{\mathit{\beta }}^{\prime }\mathbf{Z}+{\sum }_{i=1}^k{h}_i(X_i)\}$, with τ being the universal proportionality scale parameter. The fully constrained model is, however, quite inflexible and it cannot handle the cases with non-identical sets of covariates in (2.2) and (2.3) or more complicated zero-inflation mechanisms (e.g., ξ(Z, X) ≠ μ as discussed above). The partially constrained semiparametric zero-inflated model, on the other hand, is more flexible by untangling the constrained and unconstrained smooth components. In addition, when the postulated proportional constraint holds, the more parsimonious partially constrained zero-inflated model promotes estimation efficiency compared to its unconstrained counterpart. Compared to a more recent study Liu et al. (2012) on similar problems in constrained semi-parametric two-part model, our method is computationally more affordable and more flexible. In this study, we shall focus on the statistical inference and model selection regarding proportional constraints on the nonparametric smooth components, which has not been discussed in the literature to our knowledge. Moreover, the estimation and inference methods proposed below could be readily lifted to the cases where the parametric terms are also (partially) constrained.

2.2. Model estimation and inference

The proposed semiparametric zero-inflated model can be estimated by the penalized likelihood approach, which, in the unconstrained case, maximizes the following penalized log-likelihood function

$${\mathbb{P}}_n\ell ({\beta }_0,\mathit{\beta },{\gamma }_0,\mathit{\gamma },{\sigma }^2,h_1,\dots ,h_k,s_1,\dots ,s_k)-\sum _{i=1}^k{\lambda }_{n,i}^{2}J(h_i)-\sum _{i=1}^k{\varphi }_{n,i}^{2}J(s_i),$$

where ℙ_n is the empirical measure of n observations, $\ell =I(Y=0)log(1-p)+I(Y\ne 0)\left\{logp-\frac{{(Y-\mu )}^2}{2{\sigma }^2}\right\}$ is the log-likelihood function for a single observation, J(f) defines a roughness penalty functional of f, and λ_n,i, ϕ_n,i, i = 1, …, k, are the smoothing parameters corresponding to each penalty term, which control the trade-off between the smoothness of the function estimates and goodness-of-fit of the model. In this study, cubic regression spline is adopted with roughness penalty J(f) = {f⁽²⁾(x)}²dx, where f⁽²⁾(x) denotes the second derivative of a univariate function f(x). The spline estimate can be represented as a linear combination of some basis functions: $\widehat{f}(x)={\theta }_0+{\theta }_{1}x+{\sum }_{j=1}^{K-1}{\theta }_{j+1}{(x-x_j^{\ast })}_{+}^3$, where $x_j^{\ast }$, j = 1, …, K − 1 are fixed knots placed evenly (in terms of percentiles) over the corresponding observed covariate values (see Durrleman and Simon, 1989, for more discussion on the knots selection in cubic splines), (x)₊ = x if x > 0 and (x)₊ = 0 otherwise, θ= (θ₀, …, θ_K)′ is the parameter vector. Accordingly, the roughness penalty could be written as a quadratic form of the corresponding parameters, such that J(f) = θ′Sθ, where S is the penalty matrix. The smoothing parameters can be selected by generalized cross-validation (GCV) or similar procedures. Under the main regularity conditions: (R1) The covariates {Z, X} and the true parametric coefficients β₀, β, γ₀, γ are bounded; (R2) h_i, s_i are non-constant and satisfy J(h_i), J(s_i) < ∞; (R3) λ_n,i, ϕ_n,i = O_P(n^−2/5); (R4) The Fisher information matrix is non-singular, plus some minor technical conditions, the maximum penalized likelihood estimators of the smooth functions can be shown to be n^2/5 consistent, and the parametric coefficient estimators are n^1/2 consistent and asymptotically normal, using similar empirical processes techniques in Liu and Chan (2011).

Statistical inference including construction of the confidence intervals for the parametric coefficients and confidence bands for the smooth functions can be based on the observed Fisher information matrix, which avoids computer-intensive bootstrap methods used in Ma et al. (2010) and Liu et al. (2012). Monte Carlo studies reported in Liu and Chan (2011) showed that such confidence intervals/bands enjoyed desirable empirical properties in that their across-the-function coverage rates were close to their nominal levels. Estimation and inference of partially constrained semiparametric zero-inflated model follows similar procedure. More details of the estimation algorithm and theoretical results can be found in Liu and Chan (2011).

As pointed out by Wood (2006), a disadvantage of the cubic spline smoother is that the estimated smooth is never completely eliminated in the sense of having all corresponding parameters estimated to be zero. In addition, linear components in the smooth function are always un-penalized by the second derivative penalty. From variable selection point of view (Huang, Horowitz and Wei, 2010), it may be desirable to have the smooth to be shrunk completely to zero if the corresponding smoothing parameter is sufficiently large, and preserve the curvature otherwise. Wood (2006) proposed to add an extra small amount of ridge-type of penalty to the original penalty matrix, i.e., S_ε = S + εI was used as the penalty matrix with additional shrinkage. The parameters of a smooth function with large smoothing parameter are set to be exactly zero. But otherwise the additional small fraction of identity matrix has almost no influence on the cubic spline estimate if it is not shrunk to linearity by the roughness penalty. With this slight adjustment, the resulting cubic smooth with additional shrinkage behaves reasonably well in variable selection empirically, which is illustrated in a simulation study in Section 3. In the following discussion, the cubic regression spline with shrinkage is adopted to estimate the nonparametric covariate effects as well as to select relevant variables simultaneously.

2.3. Partial-constraint selection

One remaining issue with the partially constrained zero-inflated model is to choose an optimal model in terms of prediction performance from multiple candidate models with various partial constraints (model (2.1) to (2.3) with constraint (2.4), note that different index sets 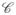correspond to different partially constrained models, including 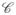= ∅, i.e., the unconstrained model) and justify the selection procedure. Liu and Chan (2011) proposed a model selection criterion for nonparametric zero-inflated model based on the marginal likelihood, which is similar to the Bayesian information criterion (BIC) (Schwarz, 1978). However, although the marginal likelihood criterion was shown to work well for zero-inflated model selection both theoretically and empirically, it was derived for penalized regression splines without additional shrinkage. Little is known about its behavior when applied to the shrinkaged version of cubic spline, as we adopted in this study. Instead, cross-validation works almost universally (Shao, 1993) for most model selection purposes, which assesses the prediction performance of the models under comparison. The model selection method is easier to implement in practice than the hypothesis testing approach used in other studies (see, e.g, Han and Kronmal, 2006), which usually involves step-wise search and whose complexity increases dramatically with the number of candidate models.

Among a variety of cross-validation methodologies (Arlot and Celisse, 2010), we use the Monte Carlo cross-validation (MCCV) (Picard and Cook, 1984) to examine the out-of-sample prediction performances of various partially constrained zero-inflated models under consideration. In particular, the data are randomly partitioned into two disjoint sets, one of which with a fixed fraction 1 − ν of the whole data (training set) are used to build the model, and the remaining ν fraction of the data (validation set) are used to evaluate some goodness-of-fit criterion (or equivalently, the risk) for each candidate model. The partition is repeated independently for B times and the out-of-sample prediction performance of each model is estimated by taking the average over the B validation sets. Furthermore, because of the complexity of the mixture zero-inflated distribution, the goodness-of-fit criterion need to be chosen with caution. We propose to use cross-validated likelihood as the prediction performance criterion, which is advocated in a probabilistic clustering problem using mixture modeling (Smyth, 2000). The cross-validated (log−)likelihood of the kth candidate model is defined as

$${\ell }_k^{\text{cv}}=\frac{1}{B}\sum _{j=1}^B\ell ({\widehat{\mathrm{\Theta }}}_k(D\backslash D_j^{\text{v}})\mid D_j^{\text{v}}),$$

where D denotes the original data, $D_j^{\text{v}}$ is the validation set of the jth partition, ${\widehat{\mathrm{\Theta }}}_k(D\backslash D_j^{\text{v}})$ is the maximum penalized likelihood estimator of the model parameter for the kth candidate model estimated from the jth training set, and ℓ is the (log−)likelihood function evaluated on $D_j^{\text{v}}$. It can be shown that the expected value of the likelihood evaluated on an independent validation data set is related to the Kullback-Leibler divergence between the truth and the model under consideration (Smyth, 2000).

Other possible model selection criteria include the mean squared error (MSE) of the non-zero responses, and the area under the receiver operating characteristic (ROC) curve (AUC, larger is preferred as it indicates better prediction, see, e.g., Miller, Hui and Tierney, 1991) of the binary indicators of zero responses. However, both MSE and AUC have limitations when applied to zero-inflated data. In particular, the MSE only measures the risk for the non-zero responses. Whereas the AUC takes into account of all validation samples, but it fails to assess the accuracy of the predictive value of the nonzero response. Sometimes the two criteria may point to different candidate models, which confounds the model selection. In addition, the bias-corrected MSE (denoted as MSE_c, it is not difficult to see that E(Y) = pμ from (2.1)) of both the zero and non-zero data can be calculated for each validation set as

$${\text{MSE}}_c=\frac{1}{n_{\text{v}}}\sum _{i=1}^{n_{\text{v}}}{({\widehat{p}}_i{\widehat{\mu }}_i-y_i^{\text{v}})}^2,$$

where $y_i^{\text{v}}$ is the ith observed response in the validation set with n_v samples, p̂_i and μ̂_i are the corresponding estimated non-zero-inflation probability and mean non-zero-inflated response from the fitted model respectively. A simulation study is carried out to evaluate the performance in model selection between the partially constrained and unconstrained zero-inflated models based on the cross-validated likelihood, AUC, MSE and MSE_c in Section 3. In practice, it suffices to set the MCCV replication size B to some number between 20 and 50 in most model selection problems in the parametric framework (Shao and Tu, 1995). In the semiparametric setting as in our study, we repeat the partition with equal size (ν = 0.5) for B = 100 times in the simulation study and B = 200 in the MESA data analysis because of its much larger sample size.

3. Simulation study

Before applying the zero-inflated modeling approach to the MESA data analysis, we first conduct a Monte Carlo study to examine the performance of the proposed model selection method based on cross-validated likelihood, as well as other goodness-of-fit criteria discussed in the previous section. The out-of-sample prediction performance is evaluated for two candidate models, i.e., the partially constrained zero-inflated normal model (with the correct model specification) and its unconstrained counterpart.

The simulated data were generated based on three univariate test functions s₁, s₂ and s₃ on [0, 1]:

$$\begin{array}{l}{s}_1(x)=\{0.2x^{11}{(10(1-x))}^6+10{(10x)}^3{(1-x)}^{10}\}/4,\\ s_2(x)=2sin(\pi x),\\ s_3(x)=exp(3x)/10.\end{array}$$

First, n independently uniformly distributed random variables X₁, X₂ and X₃ were generated on [0, 1]. A two-level factor covariate Z was set to be 0 for the first n/2 samples and 1 for the rest. The true non-zero-inflation probability p and non-zero-inflated mean response μ were generated by

$$\text{logit}(p)=0.3Z+0.5{\overline{s}}_1(X_1)+{\overline{s}}_2(X_2),$$ (3.1)

$$\mu =-1+2Z+{\overline{s}}_1(X_1)+{\overline{s}}_3(X_2),$$ (3.2)

where each smooth component was centered at the observed covariate values and denoted as s̄_j, j = 1, 2, 3, respectively. The non-zero-inflated responses $Y_i^{\ast }$, i = 1, …, n, were randomly sampled from normal 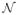(μ_i, σ) distributions. The response variable was then “zero-inflated” according to the indicator random variables E_i, which followed independent Bernoulli(p_i) distributions, i.e., $Y_i=Y_i^{\ast }$ if E_i = 1 and Y_i = 0 if E_i = 0. The simulated data set is denoted as ${\{(Y_i,Z_i,X_{i1},X_{i2},X_{i3})\}}_{i=1}^n$. Note that the above data simulation procedure specifies a partially constrained ZIN with proportional constraint on the s̄₁(X₁) component. But the covariate X₂ affects the probability of non-zero inflation and the mean non-zero response with different functional forms, namely s₂ and s₃ in equations (3.1) and (3.2) respectively. X₃ is a redundant covariate that has no impact in either p or μ.

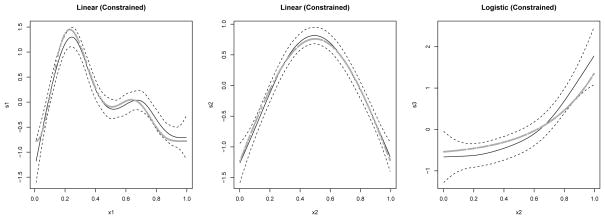
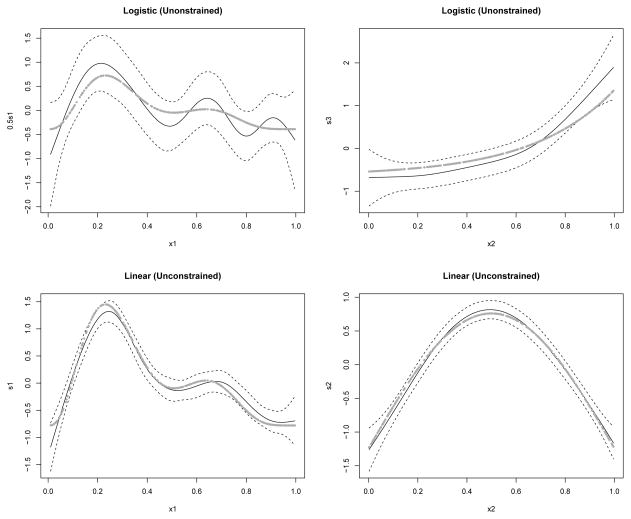
For each simulated data set, we fitted the partially constrained ZIN and the unconstrained counterpart, with nine evenly spaced knots for each cubic spline. We examined seven sample sizes from n = 200 to 800, with two noise levels σ = 0.5 and 1. Figure 1 shows the smooth function estimates by the partially constrained ZIN fitted to one simulated data set with n = 400 and σ = 0.5. The estimated smooth functions by the unconstrained ZIN fitted to the same data set are displayed in Figure 2. The wide confidence band (i.e., large standard errors of the smooth function estimates) in the upper left panel of Figure 2 suggests the lack of efficiency in estimating the logistic part (3.1) by the unconstrained ZIN as compared to the constrained model, if the data were generated from the constrained model (see Liu and Chan, 2011, Section 5, for more discussion on the estimation efficiency). It is worthwhile to mention that in both the constrained and unconstrained models, the covariate effect of the redundant variable X₃ were completely shrunk to zero by the cubic regression splines with shrinkage.

Fig 1.

Estimated smooth functions fitted by the partially constrained zero-inflated normal model, with n = 400 and σ = 0.5. The solid lines show the cubic regression spline estimates, with the dashed lines representing the 95% point-wise confidence bands. The gray dots denote the true functional values.

Fig 2.

Estimated smooth functions with 95% point-wise confidence bands (dashed lines) fitted by the unconstrained zero-inflated normal model, with n = 400 and σ = 0.5. The gray dots denote the true functional values.

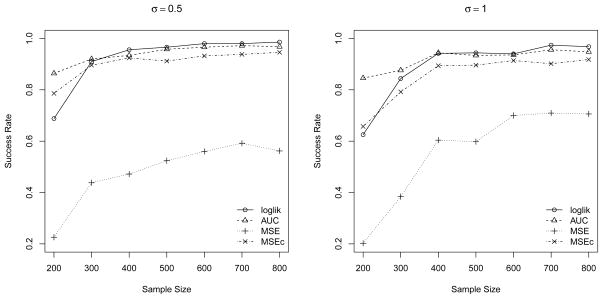
MCCV were conducted for B = 100 times with ν = 0.5 to evaluate the cross-validated likelihood, AUC, MSE and MSE_c for the constrained and unconstrained ZIN models. In each of the aforementioned settings, 500 replications were performed and the success rates in selecting the true model by each of the criteria were compared and summarized in Figure 3. As expected, the success rates of selecting the true model generally increase with the sample size for each criterion. Except for very small sample sizes (n = 200, 300, note that they were zero-inflated data with nearly 50% zeroes), the cross-validated likelihood outperforms all other three criteria. Especially for MSE of the non-zero data, the success rates are significantly lower than the other three in each scenario, which suggests that it is not a reliable measure of the overall prediction performance for zero-inflated model. On the other hand, the bias-corrected version of MSE performs reasonably well. By comparing the levels of error variance, the success rates are observed to be consistently higher across different sample sizes for σ = 0.5 (left panel of Figure 3) than σ = 1 (right panel), except for MSE. This seemingly implausible phenomena of MSE may be explained by the bias-variance trade-off of the imposed constraint in the zero-inflated model. More specifically, the constrained model is more parsimonious and hence has smaller estimation variance as compared to the unconstrained model, which may also introduce bias. When the error variance is reduced, the bias becomes more dominant than the estimation variance in the MSE decomposition. Therefore, the unconstrained model tends to be more favored by MSE when the error variance is smaller.

Fig 3.

Model selection performance of the cross-validated likelihood, AUC, MSE and MSE_c.

We also remark that the average discrepancies of all criteria between the unconstrained and correctly specified constrained models decrease as the sample size increases, which suggests that the relative predictive gain by the constrained ZIN diminishes with increasing sample size. This is not surprising because as the sample size increases, the estimation error becomes smaller relative to the intrinsic variabilities in the data. So if the data were truly generated from a partially constrained zero-inflated model and the sample size is large, we would benefit not as much on the estimation efficiency by fitting a constrained model as for small to moderately large sample sizes. In situations where there are too few observations to carry out an unconstrained semiparametric or nonparametric zero-inflated model analysis, fitting a partially constrained model may provide an elegant alternative –a perspective earlier advanced by Lambert (1992) within the parametric zero-inflated framework.

In summary, as illustrated by the Monte Carlo study, the cross-validated likelihood performs very well in selecting the true model with over 90% success rate under mid to large sample sizes (n ≥ 400), which provides strong justification for the proposed model selection procedure.

4. MESA data analysis

4.1. Model specification

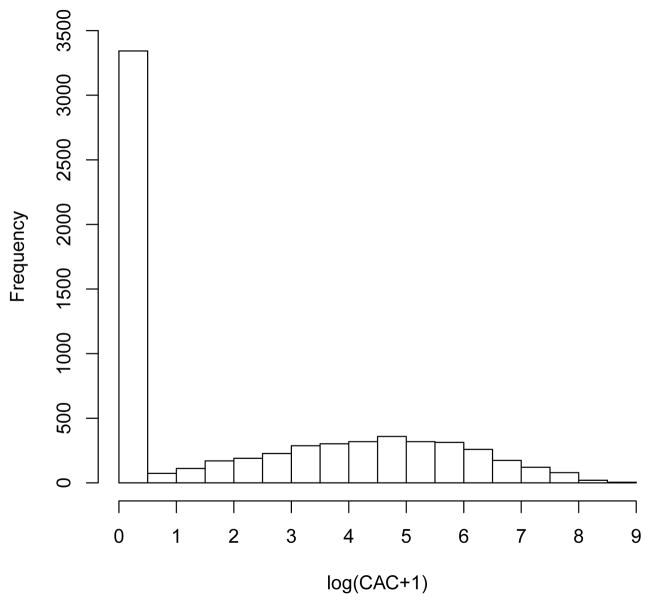
The MESA data consist of 6,672 participants 44 to 84 years old (after removing missing values), among which 3,343 (50.1%) have zero Agatston scores of CAC. We use log(CAC+1) as the response variable (the log-plus-one transformation is commonly used in many applications to avoid long tails and preserve the zeroes), and the covariates include gender (0-female, 1-male), race (0-Caucasian, 1-Chinese, 2-African American, 3-Hispanic), diabetes mellitus (0-normal, 1-otherwise), cigarette smoking status (0-never, 1-former, 2-current), age, body mass index (BMI), diastolic blood pressure (DBP), systolic blood pressure (SBP), high-density lipoprotein (HDL) cholesterol and low-density lipoprotein (LDL) cholesterol, of which the first four could be treated as factor predictors, and the rest are continuous variables. Because approximately half of the CAC scores are zeroes, while the remaining are positive and continuously distributed, we adopt a semiparametric zero-inflated normal regression model for the response variable Y = log(CAC+1) (see Figure 4), with the conditional response distribution as specified by (2.1). The covariate effect of BMI was found to be linear in a preliminary analysis, hence it was modeled as a parametric term. There was only slight interaction between HDL and LDL cholesterol levels, so they were modeled additively for ease of interpretation. As a consequence, the probability of having positive CAC is linked via the logit function (it is referred to as logistic part and henceforth) to the covariates as follows:

$$\begin{array}{l}\text{logit}(p)={\beta }_0+{\beta }_1\mathit{Male}+{\beta }_2\mathit{Chinese}+{\beta }_3\mathit{Black}+{\beta }_4\mathit{Hispanic}\\ +{\beta }_5{\mathit{Cig}}_f+{\beta }_6{\mathit{Cig}}_c+{\beta }_{7}DM+{\beta }_8\mathit{BMI}\\ +h_1(\mathit{Age})+h_2(\mathit{DBP})+h_3(\mathit{SBP})+h_4(\mathit{HDL})+h_5(\mathit{LDL}),\end{array}$$ (4.1)

where β₀ to β₈ are the regression coefficients associated with the parametric terms; DM stands for abnormal diabetes mellitus status; Cig_f and Cig_c are binary indicators of former and current smoker respectively; h_i, i = 1, …, 5, are unknown smooth functions. The mean positive (transformed) CAC level is specified as follows (linear part):

$$\begin{array}{l}\mu ={\gamma }_0+{\gamma }_1\mathit{Male}+{\gamma }_2\mathit{Chinese}+{\gamma }_3\mathit{Black}+{\gamma }_4\mathit{Hispanic}\\ +{\gamma }_5{\mathit{Cig}}_f+{\gamma }_6{\mathit{Cig}}_c+{\gamma }_{7}DM+{\gamma }_8\mathit{BMI}\\ +s_1(\mathit{Age})+s_2(\mathit{DBP})+s_3(\mathit{SBP})+s_4(\mathit{HDL})+s_5(\mathit{LDL}),\end{array}$$ (4.2)

where γ₀ to γ₈ are regression coefficients, s_i, i = 1, …, 5, are smooth functions possibly distinct from h_i. All univariate smooth functions in the logistic and linear parts above were estimated nonparametrically using cubic regression splines with shrinkage and nine evenly spaced knots to identify important risk factors, as discussed in Section 2.

Fig 4.

Histogram of log(CAC+1) from MESA.

The unconstrained ZIN model (4.1) and (4.2) assumes that the covariate effects on the probability of having a positive CAC score and the mean positive (transformed) CAC may be driven by different physiological processes. As discussed earlier, partially constrained zero-inflated model could be used to test whether the two processes are related to some extent. For example, we can add a proportional constraint h₁ = δ₁s₁ to examine whether age acts in a similar manner in affecting CAC from zero to positive, and from small amount to large amount. By comparing the fitted partially constrained and unconstrained models based on their cross-validated likelihoods, we can properly address interesting scientific hypotheses as above, which may help elucidate the biological process responsible for CAC development.

Table 1 lists some partially constrained and unconstrained ZIN models fitted to the MESA data, with corresponding cross-validated (log−) likelihood, AUC, MSE and MSE_c estimated from B = 200 replications (given that the sample size is considerably larger than that in the simulation study) of MCCV with equal size of training set and validation set (ν= 0.5). The DBP effect was found to be completely eliminated in both the logistic and linear parts, and hence it was treated as an unconstrained component. We did not include models with constraints on the HDL and/or LDL components due to convergence problem. This suggests that the HDL and LDL effects are likely to be very different in the two processes, namely, the absence/presence of CAC and the level of CAC when it is present, such that forcing them to be proportional on the link scales will cause numerical problems in the estimation. Therefore, we considered four candidate semiparametric zero-inflated models in the MESA data analysis: M₁ - no constraint imposed, M₂ - proportional constraint on age, M₃ - proportional constraint on SBP, and M₄ - proportional constraints on both age and SBP (with different proportionality parameters).

Table 1.

Comparison of candidate zero-inflated normal models fitted to the MESA data based on Monte Carlo cross-validation with B = 200 and ν = 0.5. “✓” denotes the proportional constrained smooth component; “×” denotes unconstrained smooth component.

Model	Age	DBP	SBP	HDL	LDL	loglik	AUC	MSE	MSEc
M1	×	×	×	×	×	−5018.5	0.79	2.59	4.38
M2	✓	×	×	×	×	−5034.9	0.78	2.60	4.42
M3	×	×	✓	×	×	−5022.3	0.79	2.61	4.38
M4	✓	×	✓	×	×	−5034.6	0.78	2.60	4.42

According to the cross-validated likelihood, the unconstrained ZIN model M₁, has the best prediction performance among all candidate models. The second best model is the constrained model M₃, which imposes a proportional constraint on the SBP component (estimated proportionality parameter is 0.682 with standard deviation 0.157). Note that all other three criteria, i.e, AUC, MSE, and MSE_c, are very close, especially for M₁ and M₃. This is expected because as discussed in the end of Section 3, the discrepancies between these criteria would be very small with large sample size. In fact, the AUC and MSE_c criteria (which are two reasonably reliable measures as demonstrated in the simulation study) of M₁ and M₃ are so close that it is hard to discern any differences. However, there is still some gain in the cross-validated likelihood by fitting an unconstrained ZIN as compared to the constrained models. We also tried other values of the fraction ν between 0.5 and 0.85 with more data in the validation set (ν = 0.85 corresponds to 1000 samples in the training set) to assess the robustness of the likelihood cross-validation procedure. The unconstrained model was consistently selected under various sizes of the validation set. Therefore, according to the prediction performance using cross-validation, the unconstrained model performs better than the partially constrained models, which suggests that the covariates act differently in predicting the presence of positive CAC and its severity when it is positive. The above result is significantly different from existing studies including Han and Kronmal (2006), Ma et al. (2010) and Liu et al. (2012) in the determination of proportional constraint in zero-inflated models of CAC score in MESA.

4.2. Analytical results

We now present the results of the fitted unconstrained semiparametric zero-inflated model to the MESA data, as selected by the model selection procedure based on likelihood cross-validation. Table 2 lists the coefficient estimates of the parametric components. The model results suggest that men have increased risk of having positive CAC and higher mean CAC score when it is present, as compared to women. Both African- and Hispanic Americans have reduced probability of having CAC, as compared with Caucasian. Chinese, African and Hispanic Americans all have lower average CAC level when it is positive. Having abnormal diabetes status will increase both the risk of positive CAC and its progression. Former smokers are more likely to have CAC and, on the average, they have higher positive CAC scores, as compared with non-smokers. Current smokers have even higher risk and mean positive CAC level. BMI is linearly positively associated with both the probability of having positive CAC (on the link scale) and CAC score if it is positive.

Table 2.

Coefficient estimates of the fitted unconstrained zero-inflated normal model defined by equations (4.1) and (4.2)

	Logistic			Linear
	Estimate	SE	p-value	Estimate	SE	p-value
Intercept	−1.13	0.18	< 0.001	3.46	0.19	< 0.001
Male	0.91	0.06	< 0.001	0.67	0.06	< 0.001
Chinese	−0.13	0.10	0.209	−0.28	0.10	0.004
African	−0.79	0.07	< 0.001	−0.37	0.07	< 0.001
Hispanic	−0.63	0.08	< 0.001	−0.34	0.08	< 0.001
DM	0.25	0.07	< 0.001	0.27	0.06	< 0.001
Cigf	0.37	0.06	< 0.001	0.19	0.06	0.002
Cigc	0.61	0.09	< 0.001	0.31	0.09	< 0.001
BMI	0.03	0.01	< 0.001	0.02	0.01	0.002

Among other related MESA studies, Han and Kronmal (2006) included only gender, race and age as the covariates, and their parameter estimates are similar to ours in signs and magnitudes, except that they found Chinese had significantly reduced risk of having positive CAC, as compared to Caucasian. The above findings on the parametric components are consistent with the unconstrained two-part model in Ma et al. (2010).

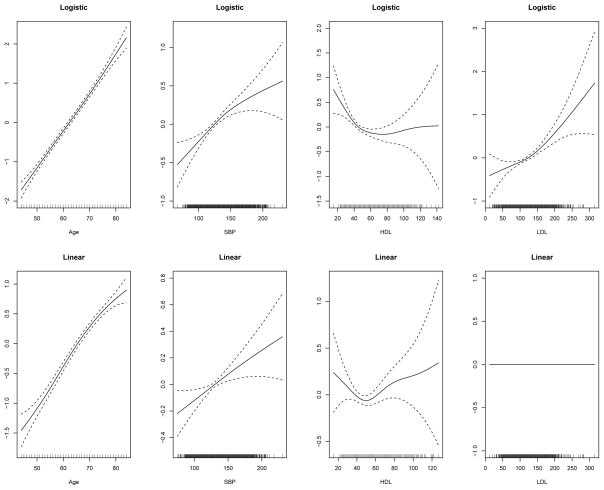
The estimated nonparametric smooth functions are displayed in Figure 5. Table 3 summarizes the significance test results of the nonparametric terms based on F tests with the null hypothesis that the smooth function is identically zero over the observed domain. Age is positively related to both the probability of positive CAC (p < 0.001) and positive CAC level (p < 0.001). However, its effect in the positive mean response μ shows some curvature at the right tail, suggesting that the age effect is not as strong in the old as in mid-aged people. Elevated systolic blood pressure is associated with increased risk of having positive CAC (p < 0.001) and higher CAC score when it is present (p = 0.003). Its effect on the presence of CAC is nonlinear on the logistic scale, whereas it is almost linear in the positive mean response part. The probability of having positive CAC decreases as the HDL cholesterol level increases up to around 60 mg/dL, beyond which the risk then stays stable (p < 0.001). Among the participants who have positive CAC scores, those with HDL between 40 to 60 mg/dL were observed to have lower CAC levels, however, its influence is not statistically significant (p = 0.128). LDL is a pronounced risk factor of CAC initiation (p < 0.001). Nevertheless, the LDL effect on the extent and severity of CAC when it is positive is completely eliminated by the shrinkaged cubic spline. The same was observed as to the diastolic blood pressure effects in both logistic and linear parts (not shown in Figure 5).

Fig 5.

Nonparametric smooth function estimates of the fitted unconstrained zero-inflated normal model defined by equations (4.1) and (4.2). The dashed lines constitute 95% point-wise confidence bands. The DBP effects are estimated to be zero in both the logistic and linear parts (not shown).

Table 3.

Nonparametric smooth function estimates of the fitted unconstrained zero-inflated normal model defined by equations (4.1) and (4.2). EDF stands for effective degrees of freedom.

The p-values are based on F tests for significance.

	Logistic			Linear
	EDF	F statistic	p-value	EDF	F statistic	p-value
s(Age)	2.4	816.6	< 0.001	2.7	116.7	< 0.001
s(DBP)	NA	NA	NA	NA	NA	NA
s(SBP)	1.7	31.1	< 0.001	1.0	7.2	0.003
s(HDL)	3.0	19.5	< 0.001	2.8	1.8	0.128
s(LDL)	2.2	38.0	< 0.001	NA	NA	NA

This study may significantly differ from published MESA studies concerning the nonparametric covariate effects along the following perspectives. First, unconstrained semiparametric zero-inflated model of Agatston score was found to have the best prediction performance based on the likelihood cross-validation procedure. Second, the age effect on the magnitude of CAC when it is positive, and the systolic blood pressure influence on the probability of having positive CAC, were both observed to be nonlinear. Third, LDL was shown to have no effect in predicting CAC level among those with positive CAC. And last, diastolic blood pressure was found not to be a risk factor in human CAC development by the cubic regression spline with shrinkage adopted in our study.

5. Discussion and conclusion

We have presented a highly flexible semiparametric regression model for analyzing zero-inflated data. Possible partial proportional constraints, whose biological interpretation could be traced to some latent threshold model under a possibly misspecified link function, were considered to promote estimation efficiency and help to reveal the connection between the zero and non-zero data generating processes. In order to choose the optimal model specification among multiple candidate models with various partial constraints, a model selection procedure based on cross-validated likelihood was used, which was empirically corroborated by a simulation study. The proposed partially constrained zero-inflated model framework makes it possible to provide evidence-based justification to address research questions concerning the underlying mechanisms that drive the presence and magnitude of the non-zero response. In particular, it can be used to identify closely related covariate effects in the zero and non-zero data generating processes. We have adopted the cubic regression spline with shrinkage to estimate nonparametric smooth functions and select relevant variables simultaneously, which works well empirically in both simulation and real data application. However, its theoretical properties still need to be investigated in the future.

When applied to the MESA data analysis, the semiparametric zero-inflated modeling approach indicates that the initiation of calcium in human coronary artery and the magnitude of positive calcium (measured by Agatston score) in general population are better characterized by an unconstrained zero-inflated model. It is statistically justified that the initiators of coronary artery disease may be different from the factors that are related to extent and progression of the disease which is reflected by the amount of CAC in those with positive CAC scores. In particular, age and systolic blood pressure are both risk factors in influencing the development of CAC from zero to positive, and from small to large amount. But their effects show some extent of nonlinearity at certain stages. HDL and LDL cholesterol levels both have pronounced nonlinear effects in predicting the presence of CAC. However, only HDL has some impact (not statistically significant) on the extent of CAC in those who have positive CAC scores. These results may reflect the fact that the biological mechanisms underlying the initiation and progression of CAC are somehow different. The partially constrained semiparametric zero-inflated modeling approach (including the unconstrained case) with the model selection procedure based on likelihood cross-validation can be applied widely to complex data analysis with zero-inflation problem.