Predictive mechanisms in the control of contour following

Abstract

In haptic exploration, when running a fingertip along a surface, the control system may attempt to anticipate upcoming changes in curvature in order to maintain a consistent level of contact force. Such predictive mechanisms are well known in the visual system, but have yet to be studied in the somatosensory system. Thus the present experiment was designed to reveal human capabilities for different types of haptic prediction. A robot arm with a large 3D workspace was attached to the index fingertip and was programmed to produce virtual surfaces with curvatures that varied within and across trials. With eyes closed, subjects moved the fingertip around elliptical hoops with flattened regions or Limaçon shapes, where the curvature varied continuously. Subjects anticipated the corner of the flattened region rather poorly, but for the Limaçon shapes they varied finger speed with upcoming curvature according to the two-thirds power law. Furthermore, although the Limaçon shapes were randomly presented in various 3D orientations, modulation of contact force also indicated good anticipation of upcoming changes in curvature. The results demonstrate that it is difficult to haptically anticipate the spatial location of an abrupt change in curvature, but smooth changes in curvature may be facilitated by anticipatory predictions.

Introduction

The sensorimotor system uses a combination of feedback and predictive mechanisms to control ongoing movements. For example, smooth pursuit eye movements are usually driven by visual feedback of actual retinal target motion (Krauzlis and Lisberger 1994). However, the system can also generate a prediction of the anticipated retinal target motion, for instance when the target is temporarily occluded (Becker and Fuchs 1985; Mrotek and Soechting 2007) or when the direction of target motion is cued (Barnes 2008). Activity in higher cortical areas such as the frontal eye fields may form predictions based on prior patterns of target motion, which then serve to modulate the gain of smooth pursuit in anticipated directions (Yang et al. 2012). Furthermore, in some situations the retinal target motion may be replaced with cognitively-generated target motion, thus producing a feedback system driven by a cognitive goal trajectory (Tramper et al. 2013).

Like visual guidance of eye movement, haptic guidance of arm movement is a situation where the movement itself alters the sensory input. Thus contour following (Lederman and Klatzky 1987) and haptic tracking (Rosenbaum et al. 2006) are essentially cases of sensory guidance that is accomplished with a somatosensory feedback loop. This was quantified by Weiss and Flanders (2011) using a task where subjects ran a fingertip across spherical virtual surfaces. Subjects reacted to an unexpected change in surface curvature with a compensatory adjustment in contact force at a latency of about 50 ms, which was explained by proposing a spinal control mechanism comparing the actual somatosensory feedback with an expectation provided by efference copy. Other results of this study also suggested longer-latency feedback loops involving the somatosensory cortex, as well as cortical learning and prediction within each trial. The present study aimed to further quantify the predictive mechanisms.

In contrast to visual feedback, somatosensory feedback is complicated by the multiplicity of signal sources, such as tactile and proprioceptive inputs, and their substantial inaccuracies (Biggs et al. 1999; Scott and Loeb 1994). Thus the haptic guidance system should combine feedback and predictive control mechanisms in an efficient fashion. McIntyre and colleagues (1995) tested two control models for the constrained movement of the hand along a short flat surface. Their data favored predictive (feedforward) control and they argued that the inherent delay of the somatosensory feedback loop may preclude its usefulness. While the 2D task used by McIntyre and colleagues (1995) could be accomplished without using feedback of contact force, precisely moving the fingertip in 3D space may be more challenging. When Klein Breteler et al. (2003) asked blindfolded subjects to draw a repeated series of triangles in space, without tactile feedback, the fingertip position drifted and changes in arm posture accumulated across consecutive cycles. Continuous, or at least periodic, tactile feedback presumably would have improved performance.

In a preliminary study (Tramper et al. 2012), we instructed blindfolded subjects to transition from feedback to feedforward performance over the course of several consecutive laps around the same virtual shape. Subjects were instructed to touch the virtual guide as little as possible and eventually to stay just slightly off the surface of the shape. We hypothesized that, as in robotics, the subject would execute the first lap under feedback control and learn the outline of the shape for feedforward execution of subsequent laps. Perhaps due to imprecise movement execution or poor learning and memory, subjects were unable to successfully use this strategy. Thus the current study was designed to test the degree to which subjects could successfully use the alternative strategy of combining ongoing tactile feedback control (i.e., with the finger constantly in contact with the surface) with cortical anticipation of upcoming changes in surface curvature. The design allowed us to investigate two potential types of cortical prediction: learned anticipation (experiment 1) and anticipation due to extrapolation of surface contours (experiment 2).

Methods

Setup

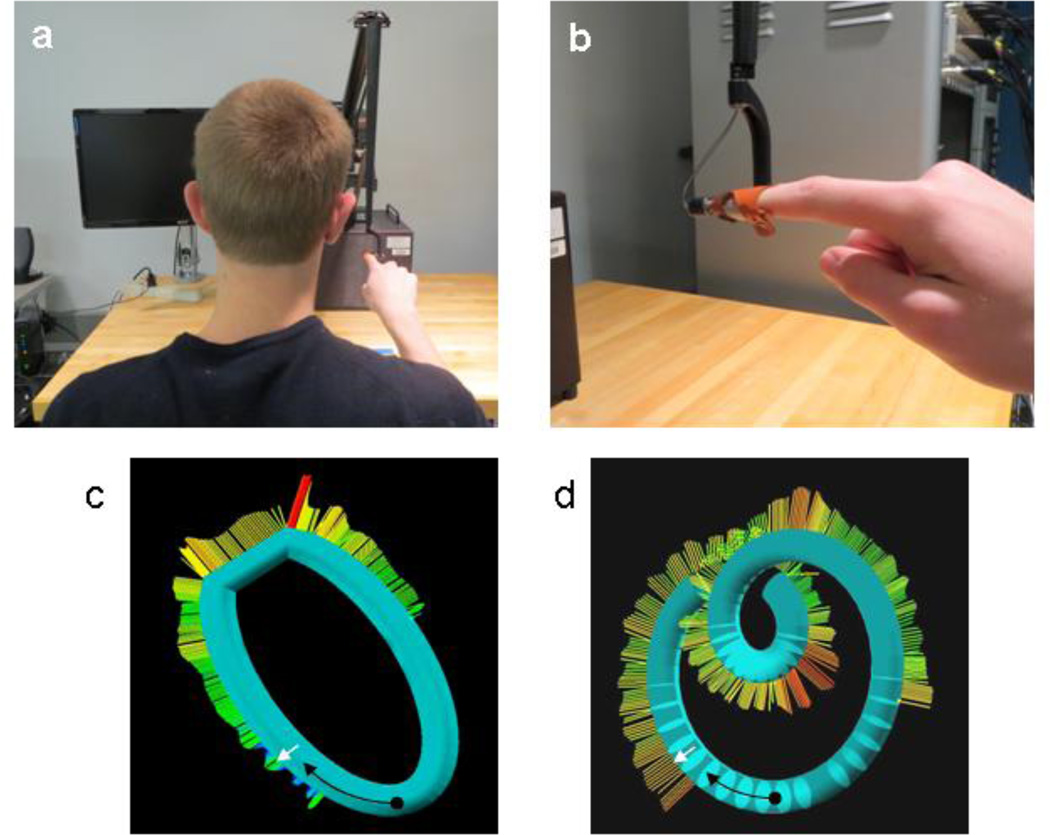
Subjects were seated in a chair with arm rests in front of a Phantom Premium 3.0 Haptic Device with finger sled (Fig. 1a, Sensable Technologies, Inc.), and the right index fingertip was attached to the tip of the light-weight arm of the device (Fig. 1b). Within a workspace of 60 cm wide, 60 cm high, and 30 cm deep, subjects could move the fingertip without restriction unless it encountered a virtual surface, and then the fingertip would slide along the surface. The Phantom device could produce forces with a maximum of 22 N transiently and 3 N sustained when the fingertip attempted to penetrate the surface, and we programmed the stiffness as 1.0 N/mm. Due to the mechanics of the finger sled attachment, when the fingertip pressed into the surface, the subjects experienced compression of the enclosed finger region and resistive force in the arm corresponding to the direction of the applied force (i.e., normal to the virtual surface). In our setup, subjects generally explored 3D shapes with the index finger nearly horizontal (Fig. 1b, also see Weiss and Flanders 2011). Finger position, velocity, and contact force were recorded at 1-ms intervals.

Fig. 1.

Experimental setup. The finger sled attachment (red) is viewed from the back of the subject (panel a) and from the subject’s left side (panel b). Subjects had eyes closed during each trial and their computer monitor was always switched off. Fingertip start position within virtual tubes (black dots), movement direction (black arrows), and contact force direction (white arrows) are indicated for example shapes from experiment 1 (panel c) and experiment 2 (panel d). These screenshots (seen only by the experimenter) also indicate the magnitude of the perpendicular contact forces (by color and length).

Virtual shapes

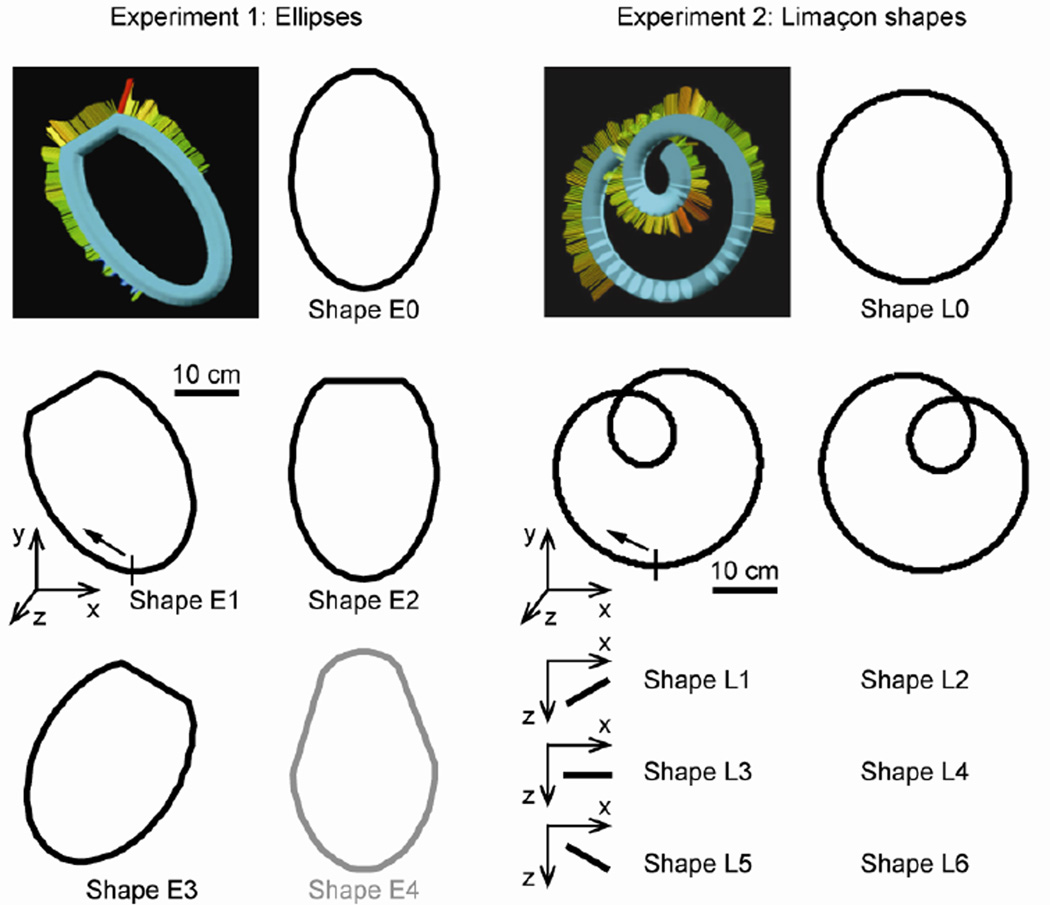
The virtual objects consisted of tubular ellipses (Fig. 1c, experiment 1) and Limaçon shapes (Fig. 1d, experiment 2) approximately 40 cm in length along the long axis and 4 cm in tubular diameter (see Fig. 2). When a trial started, the subject moved his or her index fingertip from the table upward into a virtual funnel guiding the finger to the entrance of the tube at the bottom of the shape (indicated by the small vertical lines in Fig. 2). As soon as the fingertip entered the tube, a tone sounded, the funnel disappeared, and the tube’s entrance became sealed until the end of the trial. In this way, subjects entered the tube and then followed the inner surface, pressing outward.

Fig. 2.

Experimental design. Left column: Tubular ellipses (experiment 1) positioned in the frontal plane. Shapes E1–E3 were rotated 30, 0, or −30 deg around the z-axis and a portion located at the highest point of the major axis was replaced with a straight tubular segment. Shape E4 (gray) was not used in the analyses. Shape E0 was the control condition. Subjects started their movement at the bottom of the shape (indicated by the vertical line in E1) and were instructed to move in a clockwise direction. Right column: Tubular Limaçon shapes (experiment 2). Shapes were rotated 25 deg counterclockwise (L1, L3, L5) or 25 deg clockwise (L2, L4, L6) around the z-axis. These shapes were then rotated −30 deg (L1 and L2), 0 deg (L3 and L4) or 30 deg (L5 and L6) around the y-axis. Shape L0, the control condition, was a circle oriented in the frontal plane.

The ellipses (Fig. 2, left) were positioned in the frontal plane about 9 cm above the surface of a table, with the x-and y-axes representing the cardinal axes, and the z-axis the depth direction from the point of view of the subject. This geometry was chosen based on the results of our preliminary experiment (Tramper et al. 2012), where a similar collection of frontal-plane ellipses provided a very challenging task. We used six different ellipses, all with a 3:2-ratio of major axis (33.8 cm) to minor axis (22.5 cm). Shapes E1–E3 were rotated 30, 0, or −30 deg around the z-axis. A portion of the ellipse, located at the highest point of the major axis, was replaced with a straight tubular segment of 12.3 cm. In shape E4, two curved portions of the ellipse were replaced with straight segments. This shape was included to make the sequence of shapes more unpredictable (see next section), but was not used in the analyses. Shape E0 was an ellipse with 0 deg tilt and no flattening, and acted as a control condition.

The Limaçon shapes (Fig. 2, right) were placed in vertical planes about 9 cm above the table’s surface. The template shape with the small loop located at the top and oriented in the frontal plane was defined by

$$\begin{array}{l}\mathrm{x}(\mathrm{\phi })=-\mathrm{a}(\text{sin}\mathrm{\phi }+\mathrm{k}\text{sin}2\mathrm{\phi })\hfill \\ \mathrm{y}(\mathrm{\phi })=-\mathrm{a}(\text{cos}\mathrm{\phi }+\mathrm{k}\text{cos}2\mathrm{\phi })\hfill \end{array}$$ (1)

where x and y represent coordinates along the cardinal axes, a = 8.0 cm, k = 1.25, and angular position φ = 0 … 360 deg. The Phantom device was programmed with direction sensitivity so that the virtual surface continued without crossing as the fingertip entered and departed the small loop. This allowed subjects to follow continuously along a single curved surface. On different trials, the template shape was rotated 25 deg counterclockwise (L1, L3, L5) or 25 deg clockwise (L2, L4, L6) around the z-axis, followed by a rotation of −30 deg (L1 and L2), 0 deg (L3 and L4) or 30 deg (L5 and L6) around the y-axis, to create a total of six Limaçon shapes in various vertical planes. As a control condition, we added a circle oriented in the frontal plane (Shape L0). The radius of the circle was 10.4 cm, such that the curvature was equal to the average curvature of the Limaçon shapes.

Subjects and experimental procedure

Six human subjects (three males) aged between 22 and 40 years participated in both experiments. All subjects were naive and right-handed, and none of them had any known motor disorder. The subjects gave written informed consent before taking part in the experiments and the protocol was approved by the University of Minnesota IRB. In each experiment, subjects were presented a sequence of shapes starting with three training trials (including a range of tilts and possible shapes), followed by 30 (experiment 1) or 35 (experiment 2) trials using the shapes in random order, and ending with five consecutively repeated trials of shape E2 (experiment 1) or shape L1 (experiment 2). In experiment 1, five repeats of elliptical shapes E0–E3 and ten repeats of shape E4 were used to create the random sequence of 30 trials. In experiment 2, five repeats of Limaçon shapes L0–L6 were used to create the random sequence of 35 trials.

Subjects started each trial with the right fingertip in contact with a start position bump on the table, then raised the fingertip into the shape, and moved in a clockwise direction, making five laps in total. Since each shape occurred five times in the random sequence (ten times for shape E4), this procedure yielded 25 laps per shape. Subjects were instructed to smoothly follow the wall by lightly pressing outward (radial direction) and remaining in constant contact while keeping their eyes closed. We emphasized that the main instruction was to keep moving while pressing as lightly as possible. The screenshots in Figures 1c and 1d show examples of a subject tracing the shapes by pressing outward (arrows), as indicated by the color/length-coded contact force vectors perpendicular to the surface. This computer display was seen only by the experimenter and never by the subjects, who had no visual or verbal information about the types of shapes they felt. After the subject completed the fifth lap, the force field disappeared and the subject returned the fingertip to the start position (and the elbow to the arm rest). A single trial typically took 20 s to complete. Subjects were allowed to rest between trials, which typically took about 10 s. Trials where subjects moved transiently backwards or where the Phantom device malfunctioned (about 10% of trials) were repeated at the end of the random block. Each experiment took about 20 minutes to complete.

Data preprocessing

Data were analyzed using MATLAB (The MathWorks, Inc.). To skip initial transients immediately after subjects entered the tubes, the first 10 cm of each movement was discarded. Then, each trial was subdivided into five consecutive laps, each lap starting 10 cm after the start position of the finger at the bottom of the shape. The tangential velocity, or speed, was calculated as $V=\sqrt{V_x^2+V_y^2+V_z^2}$ with v_x, v_y and v_z the velocity components along the coordinate axes. In experiment 2, speed and force were smoothed with a Savitzky-Golay filter of degree 2 and a span of 199 ms. In experiment 1, we did not smooth the data because we were interested in the abrupt change of speed and force at the onset of a flattened section.

For averaging across repetitions in experiment 2, the speed and force time traces of each lap were mapped to the corresponding spatial locations along the shape (see Figs. 6–7). Therefore, we subdivided the angular position φ (see equation 1) into 1000 equally spaced bins (bin size 0.360 deg). Next, for each finger position (x(t), y(t), z(t)), finger speed and force were mapped onto the center of the nearest bin. In general, each lap contained several thousands of time points, corresponding to a lap duration of several seconds. This resulted in multiple values per bin after the mapping procedure. Therefore, we averaged across these data points to obtain a single value for speed and force per position bin.

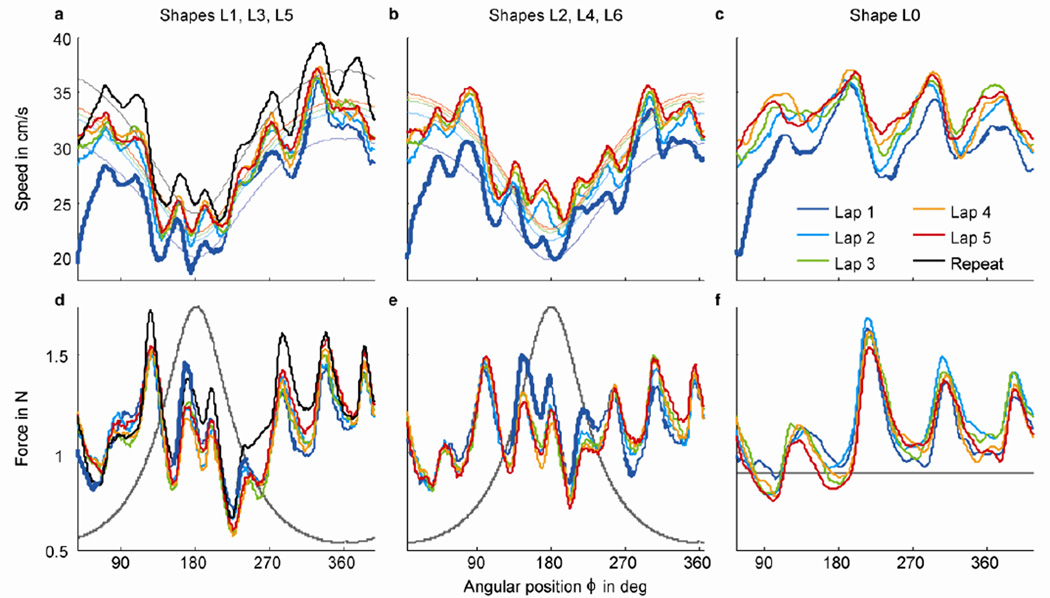
Fig. 6.

Finger speed (panels a–c) and contact force (panels d–f) pooled across subjects (n = 6) and repetitions (n = 5) of counterclockwise rotated shapes L1, L3, L5 (panels a and c), clockwise rotated shapes L2, L4, L6 (panels b and e), and shape L0 (circle; panels c and f). The x-axis represents angular position φ (equation 1); the origin φ = 0 is indicated by the dashed lines in Figure 7. Notice that data analysis started 10 cm from the start position at the bottom of the shape (solid lines in Fig. 7), which is at a different angular position for the counterclockwise shapes, clockwise shapes, and circle. Each color represents data of a single lap. In panels d–f, the gray lines indicate the amount of curvature. In panels a and b, the thin lines show the two-thirds power law fit. In panels a and d, the black lines represent data of shape L3 for a block of five repeated trials presented at the end of the experiment.

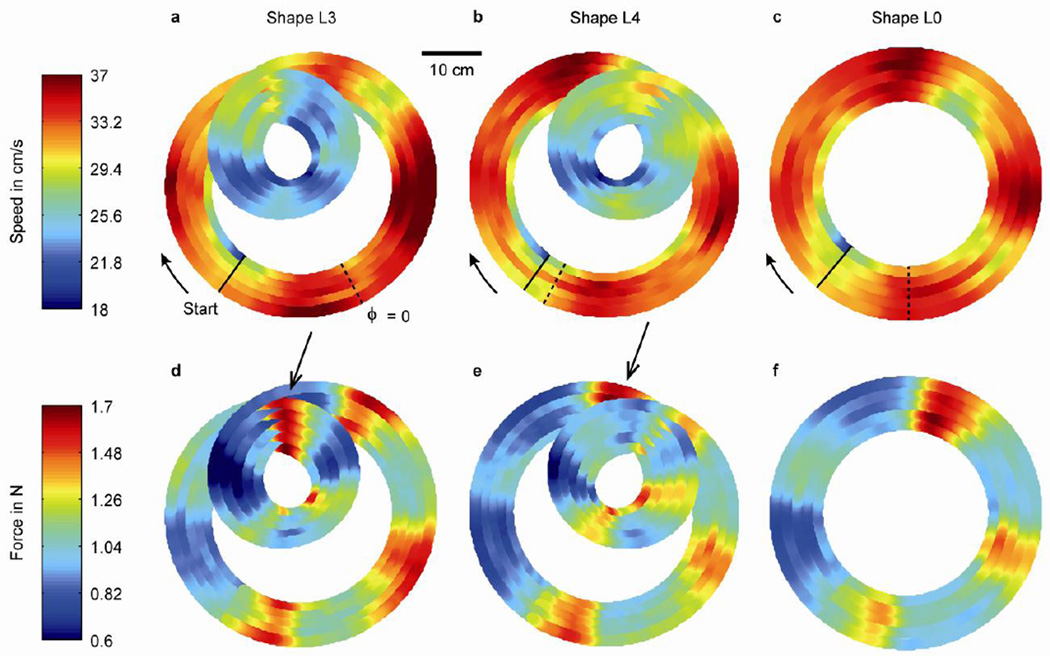
Fig. 7.

Finger speed (panels a–c) and contact force (panels d–f) pooled across subjects (n = 6), and pooled across all repetitions (n = 5) of shape L3 (panels a and d), L4 (panels b and e), L0 (panels c and f). Each drawing consists of five lines representing the laps, where the inner and outer lines correspond to lap 1 and lap 5, respectively. The solid lines indicate the position where the data analysis started, which was 10 cm from the start position of the finger to skip initial transients. The arrows point in the movement direction (clockwise). The dashed lines show the origin of the angular position axes (Fig. 6). The arrows in panels d and e indicate a section of the Limaçon shapes where the contact force was high (see text for further explanation).

Data analysis

In both experiments, we used the average finger speed and average contact force per lap as overall performance indices. A repeated measures ANOVA was used to test whether the subjects’ performance, pooled across repetitions of shapes E1-E3 (experiment 1) or shapes L1-L6 (experiment 2), changed across laps.

In experiment 1, we analyzed finger speed and contact force around the time when subjects hit the first ‘corner’, i.e., the transition from the curved elliptical section to the flattened section. We defined this time as time zero and analyzed the data in a time window from −1000 ms to 500 ms. For each time bin, we tested whether finger speed or contact force (pooled across repetitions of shapes E1-E3) of lap 1 was significantly different from laps 2–5 (Mann-Whitney U test). In addition, we compared speed and contact force between laps 2–5 of shape E2 (flattened ellipse) and laps 2–5 of shape E0 (no flattened section). For each time bin, we tested whether finger speed or contact force (pooled across laps 2–5 and repetitions) of shape E2 was significantly different from shape E0 (Mann-Whitney U test). If finger speed and/or force for shape E2 was lower than for shape E0, this would be an indication that subjects anticipate the corner. To quantify the timing of the anticipation for each subject, we verified that his/her finger speed or contact force for shape E2 at time zero was significantly lower than for shape E0. Then, we obtained the time of anticipation by searching backwards from time zero until the time when the difference in speed or force between shape E2 and shape E0 became not significant. We converted time to position to find the distance of anticipation relative to the location of the first corner.

In experiment 2, we divided the Limaçon shapes into two groups: counterclockwise rotated shapes (L1, L3, L5) and clockwise rotated shapes (L2, L4, L6). For each angular position bin (see Data preprocessing) we tested whether speed or force (pooled across subjects and repetitions of the shapes per group) of lap k was significantly different from lap 1 (Mann-Whitney U test), with k = 2, 3, 4, 5.

For voluntary arm movements, the tangential velocity of the fingertip is often related to the curvature of the fingertip’s trajectory. This relationship is called the two-thirds power law (Viviani and Terzuolo 1982; Lacquaniti et al. 1983) and is given by

$$V=C{\kappa }^{-\frac{1}{3}}$$ (2)

where v is the tangential velocity (or speed), κ is the curvature and c is a constant. (The curvature κ is related to the radius of curvature R as κ =1/R.) For each lap within a group, this equation was fitted to the observed finger speed as a function of angular position along the tube (and thus tube curvature). This procedure yielded 75 individual fits, which were averaged.

Results

Overall performance – both experiments

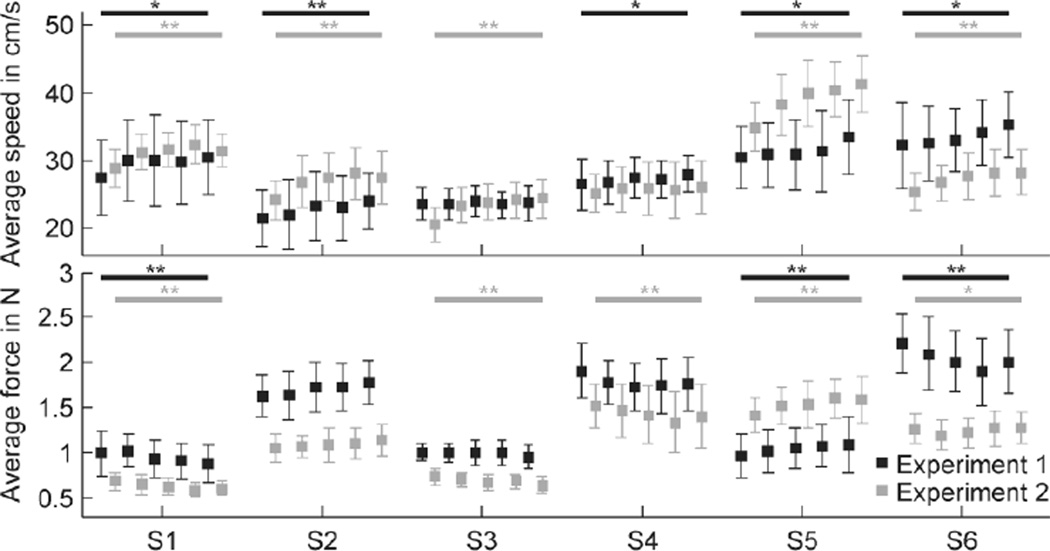
While tracing one of the virtual shapes, subjects may become more familiarized with the shape over time. Therefore, we used the average tracing speed per lap as a general performance index, thinking that the average speed might increase across consecutive laps. Figure 3 (top panel) shows the average tracing speed per lap, pooled across all trials. An average speed of 30 cm/s would correspond to about 3.4 s per lap for ellipses, and 5.3 s per lap for Limaçon shapes. The majority of subjects slightly increased their average speed across laps while exploring the flattened ellipses (E1–E3) in experiment 1 (top panel, black squares; repeated measures ANOVA, p < 0.05 for S1, S4–S6, p < 0.01 for S2; p = 0.69 for S3). This increase was also found for the Limaçon shapes (L1–L6) in experiment 2 (top panel, gray squares; repeated measures ANOVA, p < 0.01 for S1–S3, S5, S6; p = 0.24 for S4). Pooling the data across subjects showed that for both experiments, the subjects’ speed increased across laps (repeated measures ANOVA; p < 0.01, F = 12.4, experiment 1; p < 0.01, F = 89.5, experiment 2).

Fig. 3.

Average tracing speed (top row) and contact force (bottom row) per lap for experiment 1 (black symbols) and experiment 2 (gray symbols). Data are pooled across all repetitions of shapes E1–E3 (experiment 1; n = 15) or shapes L1–L6 (experiment 2; n = 30). Error bars represent the standard deviation. Significant difference between laps (repeated measures ANOVA) were marked with * (p < 0.05) or ** (p < 0.01).

In both experiments, subjects were asked to trace the virtual shape in a smooth fashion by touching the wall as lightly as possible. Therefore, we used the average contact force per lap as a second measure of overall performance and tested whether this average force changed across laps (Fig. 3, bottom panel). In experiment 1 (ellipses), three subjects did not change the average force (bottom panel, black squares; repeated measures ANOVA, p > 0.05 for S2–S4). The other subjects either decreased (p < 0.01 for S1, S6) or increased (p < 0.01 for S5) the amount of contact force across laps. In experiment 2 (Limaçon shapes) S1, S3 and S4 decreased their contact force (bottom panel, gray squares; repeated measures ANOVA, p < 0.01), whereas S5 increased the amount of force (p < 0.01). S2 did not adjust the force (p = 0.06) and S6 did so (p < 0.05), but slightly and without a clear decrease or increase. For both experiments, pooling the data across subjects did not show a significant change in contact force across laps (repeated measures ANOVA; p > 0.05, F = 2.35, experiment 1; p > 0.05, F = 0.81, experiment 2).

To summarize, subjects improved their performance during haptic tracing of a shape by becoming slightly faster across laps. Although speed was not instructed, this is a natural tendency during an experiment with many trials. The average amount of contact force changed very little, suggesting that this aspect of the behavior was more or less maintained across laps.

Anticipation of an abrupt event – experiment 1

The next analyses focused on experiment 1, where subjects explored frontal-plane ellipses with flattened sections. This experiment was designed to investigate whether subjects could learn to anticipate an abrupt, haptic event (the first corner). We analyzed finger speed and contact force around the time of the corner (time zero). Speed always decreased and force increased upon impact with the corner. We hypothesized that subjects would use knowledge of the shape acquired in the first lap to anticipate the corner in the subsequent laps with a preparatory adjustment in speed and/or contact force. This would be in line with the instruction to press as lightly as possible as well as the natural tendency to avoid a hard hit of the flattened surface.

For each subject, we compared lap 1 of shapes E1-E3 to the average values for laps 2–5. At time zero, speed in laps 2–5 was never significantly higher than in lap 1 (Mann-Whitney U test, p < 0.05), despite the fact that average lap speed was higher for most subjects (see Fig. 3). This suggests some degree of anticipation in all subjects. Next, we looked for anticipatory adjustments in contact force. In the laps 2–5, subjects generally did not reduce their force just prior to impact. The only exception was S4 who started to significantly reduce contact force 131 ms before the corner (Mann-Whitney U test, p < 0.05, data not shown).

If subjects successfully anticipated the corner, by slowing, reducing contact force, or reducing stiffness, we would expect that the force of impact would decrease over laps. Subjects S1, S3, S4 and S6 did indeed show a significant reduction of contact force in laps 2–5 at or within 100 ms after the onset of flattening (Mann-Whitney U test, p<0.05, data not shown). Thus most subjects achieved a significant degree of anticipation of the mechanical consequence of impact.

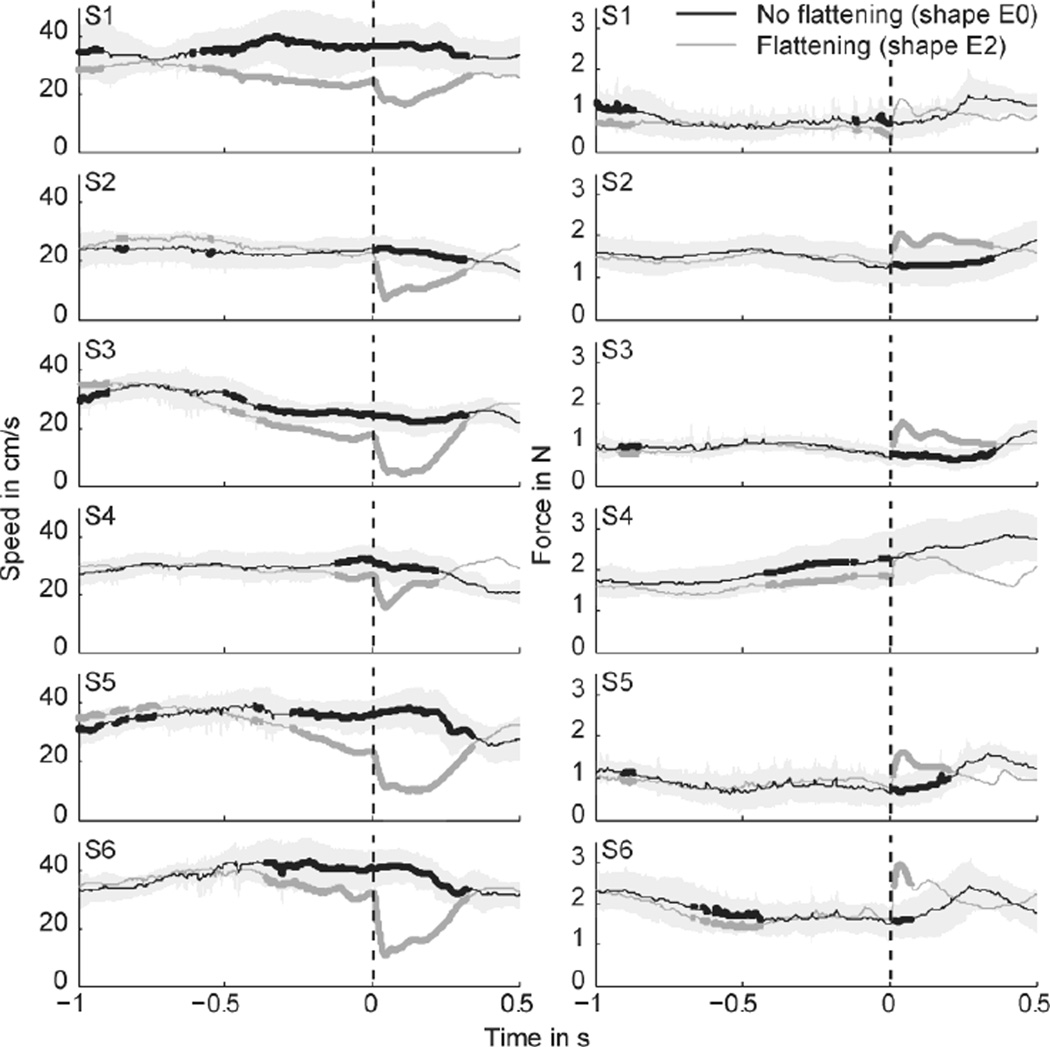
To quantify the timing of the anticipation, we excluded all data from lap 1 and compared speed and contact force between a flattened (E2) and a non-flattened (E0) version of the same shape. In Figure 4, the gray traces represent data of the flattened ellipse with 0 deg tilt (shape E2, see Fig. 2), averaged across laps 2–5 and all repetitions (4 laps × 5 repetitions = 20 time traces). The black traces show data of the ellipse without a flattened section (control shape E0), averaged across laps 2–5 and all repetitions (20 time traces), aligned to the point that corresponded to corner of shape E2. Standard deviations are shown as light gray shaded regions around the black traces, and time intervals with significant differences between the two conditions are shown as thicker traces (Mann-Whitney U test, p < 0.05).

Fig. 4.

Finger speed (left column) and contact force (right column) for subjects exploring the 0-deg tilted ellipse. Black traces show the mean for data of the non-flattened shape (shape E0), pooled across laps 2–5 and repetitions (4 laps × 5 repetitions = 20 time traces). Black traces are aligned to the point that corresponds to the onset of flattening in shape E2 (flattened shape), as indicated by the dashed lines at t = 0. Gray traces show the mean for data of the flattened shape (shape E2) pooled across laps 2–5 and repetitions (20 time traces); they are aligned to the onset of flattening. Shaded area represents the standard deviation. Thick lines indicate significant differences (Mann-Whitney U test, p < 0.05) between the non-flattened shape (black lines) and the flattened shape (gray lines).

For the speed traces (left column of Fig. 4), all subjects except S2 significantly reduced their speed before the onset of flattening. However, the time at which subjects started to decelerate their finger ranged from −578 ms to −128 ms (Table 1). If subjects were attempting to remember the spatial location of the corner, this slowdown point might be more consistent in space, rather than time. We therefore computed the distance from the slowdown point to the corner for each subject (Table 1). This was also rather large and quite variable across subjects, ranging from about −17 cm to −3 cm.

Table 1.

The anticipatory slowdown prior to the first corner of a flattened section, in time and space. Values represent the onset of a significant difference (Mann-Whitney U test) between finger speed in flattened (E2) and non-flattened (E0) shapes.

Subject	Time re. corner	Distance re. corner
S1	−578 ms	−16.8 cm
S2	n.s.	n.s
S3	−390 ms	−5.4 cm
S4	−128 ms	−3.1 cm
S5	−250 ms	−7.9 cm
S6	−365 ms	−2.9 cm

The force analysis (right column of Fig. 4), revealed that most subjects did not adjust the amount of contact force prior to hitting the corner. S4 was the only subject with a sustained decrease in contact force prior to the corner, but contact force for the flattened shape was lower throughout this 1 s interval. As expected, immediately after the onset of flattening, most subjects showed a significant increase compared to the non-flattened shape.

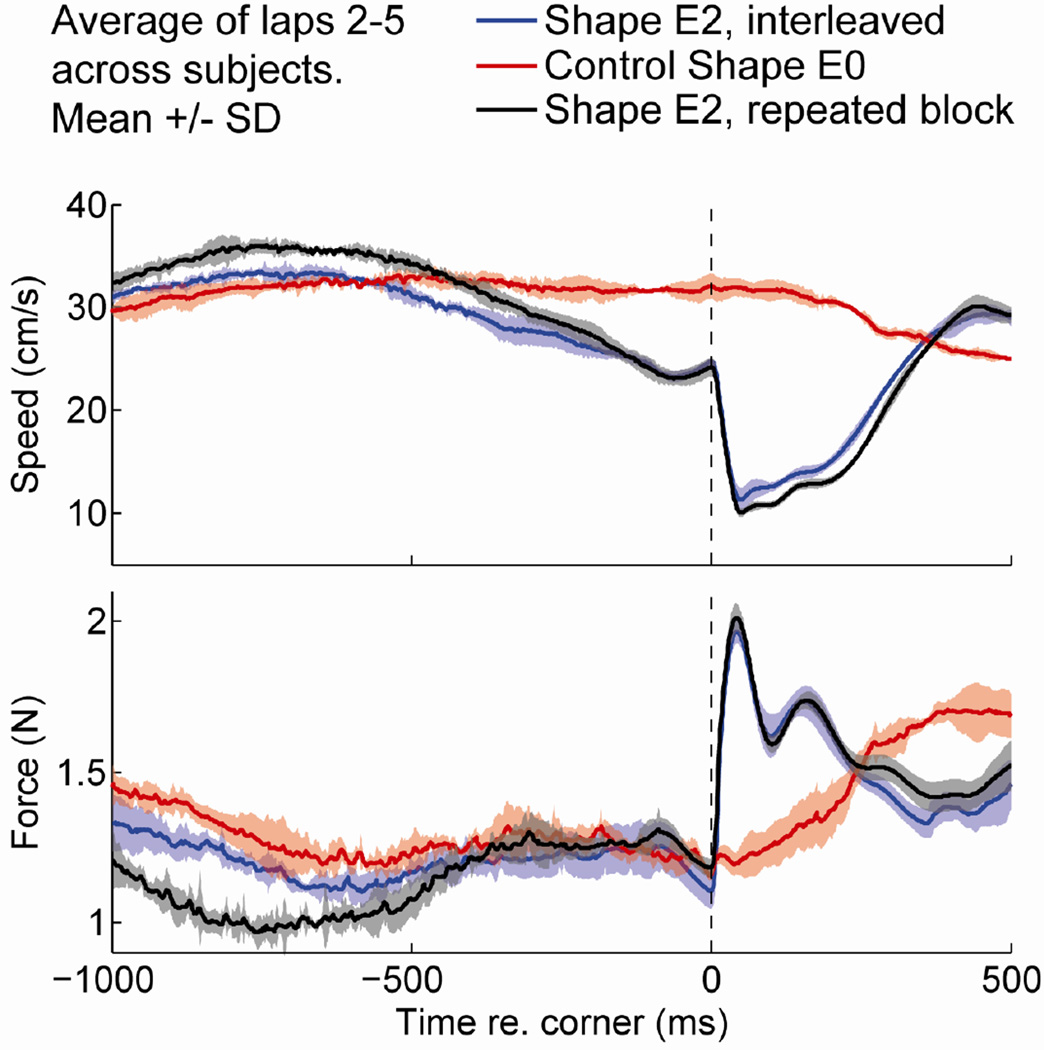
Thus, in consecutive laps around the same shape, subjects failed to exhibit a consistently successful strategy for precisely anticipating time or location of the corner. To further investigate the subjects’ ability to lean to anticipate, at the end of each experiment we presented the very same shape (shape E2) in 5 repeated trials, and subjects were informed accordingly. Within each trial, subjects completed 5 sequential laps (as in the main block of trials where trials with all shapes were presented in random order). We compared the performance during this final block (shape E2, repeated) with the performance for the same shape from the main block (shape E2, interleaved), and with the control shape (shape E0, no flattening). In Figure 5, the traces represent the mean value across subjects (n = 6), trial repetitions (n = 5), and laps 2–5 (n = 4). The shaded areas represent the standard deviations.

Fig. 5.

Finger speed (top) and contact force (bottom) for subjects exploring the 0-deg tilted ellipses in different conditions. The black trace represents shape E2 (0-deg tilted ellipse with flattening) in trials that were interleaved with the other shapes; the red trace represents shape E0 (0-deg tilted ellipse without flattening); the blue trace represents E2 for a block in five consecutively repeated trials presented at the end of the experiment. Each line shows the mean across subjects, repetitions, and laps 2–5 (6 subjects × 5 repetitions × 4 laps = 120 time traces), aligned to the onset of flattening (vertical, dashed line at t = 0). Shaded area represents the standard deviation.

Speed (Fig. 5, top panel) was similar for repeated trials (black traces) and interleaved trials (blue traces). We did not find a significant difference in trial durations between the repeated trials and the interleaved trials: the mean (s.d.) across subjects was 20.5 s (4.2 s) and 19.1 s (2.1 s), respectively, p = 0.11 (two-sided t test)). In both cases, the deceleration of the finger started about 500 ms before the onset of flattening, compared to the control shape (red trace).

The amount of contact force (Fig. 5, bottom panel) just prior to the onset of flattening did not differ between repeated E2 (black trace), interleaved E2 (blue trace) and the control shape E0 (red line). Moreover, we did not find a difference in the force of impact between the repeated and interleaved trials. Before −400 ms, the force was lower for the repeated trials, compared to the other two conditions. Thus, although subjects modulated contact force during the repeated trials, this adjustment was not timed to the onset of flattening.

The comparison of speed and force between a block of repeated trials and the interleaved trials confirmed and extended our conclusion that subjects could not learn to precisely anticipate an abrupt, haptic event. This raised the question of whether subjects have the ability to predict gradual changes in the surface of virtual shapes, which is the topic of the next section.

Anticipation of gradual changes in curvature – experiment 2

In experiment 2, we measured the finger speed and contact force for Limaçon shapes in different orientations, and circles (Fig. 2, right). The Limaçon shape has two important properties. First, it has a continuous change in curvature generated with cosine functions, which allowed us to investigate the effect of a gradual change in surface curvature instead of an abrupt change as in experiment 1. Second, for the sake of discussion, the shape can be subdivided into a small and a large loop. The small loop acted as a single haptic event, analogous to the flattened section of the ellipses in experiment 1.

Figure 6a shows the finger speed as a function of angular position along the shape, for laps 1–5 (cool to warm colors, respectively), averaged across subjects (n = 6), counterclockwise rotated shapes L1, L3, L5 (n = 3), and trial repetitions (n = 5). Speed during the first lap (dark blue) was generally lower than the subsequent laps, with significant differences (Mann-Whitney U test, p < 0.05) indicated by thicker sections of the dark blue lines.

It is known that for various types of voluntary movements, finger speed is inversely related to the curvature of the finger trajectory, following the so-called two-thirds power law (see Methods). Therefore, we hypothesized that if subjects can anticipate the shape of the contour, finger speed might obey this law. In Figure 6a, the thinner lines show the model prediction calculated by fitting equation 2 to individual traces for each lap and then averaging. These fits show that the subject’s finger speed generally followed the prediction of the power law. This was also true for most of the first lap (dark blue), even though subjects did not know which rotation was presented, and hence did not a priori know where the curvature would become the tightest. We found the same result for the clockwise rotated shapes L2, L4, L6 (Fig. 6b). Note that the maximum curvature, and hence the minimum speed, occurred at angular position φ = 180 deg, which was encountered later in clockwise rotated shapes.

The circle (Fig. 6c) had a constant curvature and therefore, one would expect a more or less constant speed. Finger speed indeed had a constant baseline of about 32 cm/s, but on top of that, it showed a stereotypical modulation. Such modulations were also present in the Limaçon shapes (Fig. 6a,b). We will return to this observation after first discussing the analysis of contact force.

The bottom row of Figure 6 shows the corresponding contact force for shapes L1, L3, L5 (panel d), shapes L2, L4, L6 (panel e), and shape L0 (panel f). The gray traces indicate the positional modulation of surface curvature. For both rotations of the Limaçon shape, the force was significantly higher in the beginning of the high curvature section during the first lap (thick dark blue trace) than during the subsequent laps (other colors). Higher force is the mechanical result of moving into a tightening curve (similar to hitting a corner in experiment 1). Thus the reduction in contact force in laps 2–5 indicates improved curvature anticipation across laps.

However, even in lap 1, instead of a single peak in force in the first part of the small loop (the section with most rapidly increasing curvature), we generally found a series of peaks, arranged in a stereotypical way around the shape, also at parts with low curvature (Fig. 6d,e). If subjects did not anticipate the small loop of the Limaçon shapes, one might expect a higher contact force during the high-curvature sections, compared to the contact force when tracing the circle (Fig. 6f). Instead, the peaks in contact force in the first part of the small loop (between φ = 90 and 180 deg in Fig. 6d,e) were significantly lower than the maximum value when tracing the circle (at φ = 215 deg in Fig. 6f) (Mann-Whitney U test, p < 0.05 for L1, L3, L5 and p < 0.001 for L2, L4, L6).

We also measured finger speed and contact force in a block with five repeats of shape L3 (black traces in Fig. 6a,d). In this situation, subjects had ample time to become familiar with the shape, which might explain why finger speed was slightly higher (Fig. 6a). The behavior followed a similar pattern as for the interleaved trials, indicating that the speed and force modulations were not due the subjects’ (lack of) familiarity with the shape.

Notice that in Figure 6, we pooled the data across subjects. The reason is that, unlike in experiment 1, the results of experiment 2 were very consistent across subjects. All subjects had dominant finger speeds corresponding to the two-thirds power law, and had higher frequency speed and force modulations very similar to those shown by the average. For subjects S1, S3, S4, and S6, contact force during the high-curvature section in the first lap was significantly higher than during the subsequent laps. For all subjects, force during the high-curvature sections did not exceed values found during the remaining sections, and during the tracing of the circles. Therefore, the average behavior is representative of each individual subject.

Returning to the higher frequency speed and force modulations, notice that the contact force while tracing the circle (Fig. 6f) showed a similar modulation to finger speed (Fig. 6c), i.e., four peaks and troughs. Furthermore, the oscillation in speed and contact force in Limaçon shapes was not restricted to the high-curvature portions of the shape but was distributed along the whole path. This suggests that this modulation did not originate from the change in curvature. To investigate this in more detail, we present the same data in a spatial format. Figure 7 (top row) shows a heat map of finger speed for shape L3, L4 and L0 (panels a–c), pooled across subjects. Each line represents a single lap, where laps 1 and 5 are the inner and outer lines, respectively. This figure nicely illustrates that speed followed the two-thirds power law, since the speed was always low (blue) when the curvature was large (small loop) and high when the curvature was small (large loop) (Fig. 7a,b).

However, when one of the Limaçon shapes was rotated by 50 deg to match the other shape, the force patterns did not match (Fig. 7d,e). For example, the force was high just after the intersection point for shape L3, but before the intersection point for shape L4, as highlighted by the arrows. This is another indication that this force modulation was not the result of a change in curvature. Rather, the peaks and troughs seemed to occur at fixed positions in workspace, i.e., with respect to the subject.

This conclusion becomes evident when looking at speed and contact force for the circular shape (panels c and f). The speed profile showed four peaks located at approximately 0, 90, 180 and 270 deg, visible as the dark red areas of the circle. Force also showed a modulation with four peaks (yellow/red areas), rotated by approximately 20 deg in clockwise direction with respect to speed (compare panels c and f). Changes in curvature cannot be responsible for this pattern since the curvature of a circle is constant.

Discussion

The goal of this study was to investigate the extent to which the somatosensory system can combine ongoing feedback with predictive mechanisms to guide the hand along unseen surfaces. Therefore, we measured finger speed and contact force during haptic exploration of virtual shapes with abrupt or gradual changes in curvature. Subjects repeated their exploration in sequential laps, which allowed us to dissociate relatively pure feedback control (during the first lap), from feedback combined with learned anticipation of a point in time or space (experiment 1) or anticipation due to extrapolation of surface contours (experiment 2).

Corners

We found that subjects were poor in predicting an abrupt, haptic event (experiment 1). Subjects slowed down before the onset of a flattened section of the shape, but both the timing and the location were quite early and variable (Table 1). Thus, memories were insufficient to precisely anticipate the transition from a curved to a straight section of the shape, even when subjects were allowed 25 consecutive laps (5 consecutive trials with 5 laps each, Fig. 5). These results were consistent with a preliminary study in which subjects had to report whether they encountered the onset of a flattened section (Tramper et al. 2012). Thus, even when subjects were attending to the location of the corner, the ability to predict such a haptic event was poor. Of course, daily training on a task can potentially increase the ability to anticipate. For example, it has been shown that extensive training with a haptic surgical device improves the skills of novices (Eversbusch, and Grantcharov 2004; Ferlitsch et al. 2002). However, our results suggest that it might be important to provide additional cues to warn of the approach of a corner, such as an auditory or textural gradient.

Previous work showed that the somatosensory system can quite accurately extract the shapes of planar virtual objects (Henriques and Soechting 2003). However, when subjects have to judge the shape of complex objects, their percept is biased toward simple geometric shapes and symmetric shapes (Ehrich et al. 2008). Also, people are better in haptically aligning rods along the cardinal axes than along axes with an oblique orientation (Hermens and Gielen 2003; Kappers and Koenderink 1999). Therefore, if subjects used a mental image of the shape’s geometry obtained in the first lap for predicting the exact course of the second lap, it is likely that the localization of the corner between a curved and straight section was also biased, being especially difficult for tilted shapes E1 and E3. However in the present study subjects also had difficulty locating an upcoming corner in a shape symmetric around a cardinal axis (shape E2).

Another potential reason for the poor performance could have been that subjects did not perceive the flattened sections, i.e., they did not notice the corner. Our preliminary experiments showed that subjects can have difficulties in judging whether an ellipse contained a flattened section or not (Tramper et al. 2012). Flattening was poorly detected for relatively elongated ellipses (with a 3:1 or 2:1-ratio of major axis to minor axis). However, flattening was always detected for the ellipses with a 3:2-ratio of major axis to minor axis, and these ellipses were the same as used in the present study.

Smooth curves

Although the Limaçon shapes (experiment 2) were more complex, speed nicely followed the two-thirds power law prediction (Fig. 6a,b). Also, subjects kept the amount of contact force in the same range as for tracing a circle, which is an easy shape to trace (Fig. 6d–f). Since it is known that the percept of complex shapes can be biased (Henriques and Soechting 2005; Soechting et al. 2006), these results cannot be fully explained by the use of memory to guide the movement. If subjects could not anticipate the high-curvature section of the shape, one would expect the force to increase along with the increase in curvature, because subjects would keep hitting the wall of the tube. But this hypothesis did not fit the pattern of force modulation. Therefore, we believe that in this situation, anticipatory predictions came into play.

As outlined in the Introduction, the human visuomotor system combines feedback and predictive mechanisms to control ongoing movements. Soechting et al. (2010) proposed a model with a predictive component for smooth pursuit eye movements, consisting of a low-pass filtered target acceleration signal. Suppose that the somatosensory system uses a similar predictive signal to guide the hand along a surface. In this case, the target is not a moving visual stimulus, but the desired finger movement along the shape. In general, natural movements are smooth and follow the two-thirds power law, that is, the velocity of the controlled limb is inversely related to the curvature of the trajectory. Thus, let us assume that the desired finger trajectory was equal to the shape of the surface with a finger speed that followed the power-law prediction. In experiment 1, the onset of the flattened section was not preceded by an associated change in curvature. Therefore, the predictive component given by the acceleration of the finger was not helpful for the abrupt change in curvature. In experiment 2, we used shapes with a continuous change in curvature. Therefore, acceleration of the finger was a good predictor for the upcoming surface curvature, and hence, subjects were able to predict the high-curvature loop of the Limaçon shape using extrapolation.

When tracing the Limaçon shapes, both finger speed and contact force showed a stereotypical modulation with peaks and troughs that occured at fixed positions in workspace. Such modulations cannot be attributed to noise, which was filtered out (see Methods), or random variability in tracing speed, since Figures 6 and 7 show the average across many trials. The four peaks in the speed profile of the circle, visible as the dark red areas in Figure 7, coincided with the peaks in speed previously reported by Weiss and Flanders (2011) (see Fig. 5c of their study). Thus, as previously discussed by Weiss and Flanders (2011) there is a spatial pattern in the speed/force modulation that is perhaps due to the biomechanics of the finger/hand/arm interacting with the Phantom device in our setup. In the present study, this modulation was clearly not due to a lack of anticipation of the upcoming curvature. Subjects had no difficulty with curvature anticipation in laps 2–5.

Conclusions

To summarize, this study demonstrated that the haptic system is poor in predicting features at a particular spatial location, but in contrast, can successfully anticipate smooth changes in the contour being followed. The quality of predictions depends on whether the haptic input of the preceding surface is informative for the upcoming surface. In order to anticipate an abrupt change in curvature, the subject could potentially have used a memory of the location of the corner, or the position of the arm when the finger reached the corner. But this type of somatosensory memory may be biased and inaccurate (Rincon-Gonzalez et al. 2011).

Although the anatomy and physiology of somatosensory perception is well known, few previous studies have investigated the neural control mechanism for haptic guidance of contour following at the human fingertip. Studies of the neural control of active sensing are perhaps more abundant in the whisker system (Prescott et al. 2011), and it appears that whiskered tetrapods, who often explore during locomotion in darkness, may use different control strategies for accumulating information over space and time compared to humans (Horev et al. 2011). As an approach to the topic of human haptic guidance we make an analogy to control mechanisms for visually-guided eye movements, which have been more thoroughly studied in the past. However, to postulate a negative feedback loop to guide fingertip movements, one must specify a control signal, i.e., the parameter that is fed back and driven toward zero. For smooth pursuit eye movement this is clearly the retinal slip velocity, i.e., the difference between target motion and eye motion (Krauzlis and Lisberger 1994). For haptically exploring the shape of a smooth surface, Weiss and Flanders (2011) suggested that the control may be aimed at keeping a consistent level of contact force, which might serve the purpose of maintaining pressure on tactile receptors within a certain range of their sensitivities (see also McIntyre et al. 1995). This might then be coupled with a strategy for perceiving textures or irregular features of the explored surface (see for example Smith et al. 2002).