Non–invasive Quantification of Intracellular Sodium in Human Brain using Ultra–High–Field MRI

Abstract

In vivo sodium magnetic resonance imaging (MRI) provides a measure of the tissue sodium content in living human brain, but current methods do not allow non–invasive quantitative assessment of intracellular sodium concentration (ISC) – the most useful marker of tissue viability. In this study we report the first non–invasive quantitative in–vivo measurement of the ISC and of the intracellular sodium volume fraction (ISVF) in the healthy human brain made possible by measuring the tissue sodium concentration (TSC) and the intracellular sodium molar fraction (ISMF) at ultra–high–field MRI. The method features the use of single–quantum (SQ) and triple–quantum filtered (TQF) imaging at 7 Tesla to separate intracellular and extracellular sodium signals and to provide quantification of ISMF, ISC and ISVF.

This novel method allows non–invasive quantitative measurement of ISC and ISVF, opening many possibilities for structural and functional metabolic studies in the healthy and diseased brain.

Introduction

Sodium is involved in many critical cellular functions such as regulation of mitosis, cellular proliferation (1), sodium/calcium exchange mediation (2) as well as cellular energy metabolism via active trans–membrane Na+/K+ transport (3). While sodium concentration in extracellular fluid (ESC) is maintained in a narrow range between 136 mmol/L and 142 mmol/L (4) in well perfused tissue, most cell types maintain a large sodium ion concentration gradient across their membranes with an intracellular sodium concentration (ISC) of about 10 – 15 mmol/L. This cross–membrane difference in sodium concentration is essential for the generation and propagation of action potentials (5), cell volume regulation (6), and other cellular homeostatic and regulatory functions. Neurological disease processes may alter intracellular sodium concentration and cell volume fraction (CVF) (7–9). Therefore, non–invasive techniques capable of measuring intracellular sodium concentration and cell volume fraction are needed for monitoring function of healthy and diseased organs, disease development and disease treatment.

Conventional sodium MRI is a non–invasive procedure based on a single–quantum (SQ) sodium signal and can be used for the quantification of the bulk tissue sodium concentration (TSC) (10–12). The TSC represents a weighted average of the extracellular and intracellular sodium content. As a result, TSC is sensitive to changes in the cell volume fraction (cellular death, swelling and proliferation) as well as to changes in ISC due to impaired energy metabolism or other metabolic changes that affect sodium exchange across the cell membrane. For example, neoplastic cell proliferation may disrupt normal cell packing and expand the extracellular volume (7) resulting in increase of TSC. Conversely, the ISC of tumor cells can be higher than in the healthy tissue because of differences in ion homeostasis within tumor cells (8, 9) also leading to TSC increase. In some diseases, such as ischemia, the increase in ISC might be accompanied by cellular swelling (13). This may not lead to any changes in TSC in the early stage of the disease, but rather would cause an increase in intracellular sodium molar fraction (ISMF) defined as the ratio of the intracellular content (in moles) to the total amount of sodium in the tissue. As changes in TSC are not specific to changes in ISC and CVF values, differentiation between the extracellular and intracellular compartments is highly desirable. Furthermore, ISC and CVF rather than TSC are of interest to determine tissue viability.

Unfortunately, the sodium NMR signals from the intracellular and extracellular compartments are isochromatic and cannot be discriminated based on their natural chemical shift (14). The introduction of membrane–impermeable frequency shift reagents (15, 16) may facilitate the monitoring of important trans–membrane sodium concentration gradients. Such shift agents do not cross cell membranes and therefore create a detectible frequency offset for the sodium nuclei in the extracellular space. The intracellular and extracellular compartments are then distinguished by the means of magnetic resonance spectroscopy or spectroscopic imaging. Unfortunately, the shift reagent does not always enter all of the extracellular space causing the unshifted signal to contain some contribution from the extracellular compartment. This leads to an overestimation of ISMF especially in the brain where the reagent is not able to cross the blood–brain–barrier (17). Furthermore, despite their useful properties, currently available shift reagents are toxic (17) and cannot be administered to humans.

Since sodium ions in the extracellular space have a higher mobility than those in the intracellular space, diffusion based methods can be used to separate signals form the two compartments (18). However, the fast signal decay rates of sodium coupled with the low sodium gyromagnetic ratio preclude the effective use of this method in clinical practice. It has been recognized (19, 20) that multi–quantum–filtered NMR sodium signal can be used to study the intracellular compartment. Indeed, the presence of restricted motion and ordered structures in tissue has important consequences for the properties of the sodium NMR signal. In solutions, fast isotropic motion of the sodium ions averages out the dipolar and quadrupolar interactions producing a mono–exponential NMR signal decay. Since viscosity of extracellular space is similar to that of CSF (21), it may be assumed that sodium ions in the extracellular space experience fast isotropic random motion. In slow motion regimes (the rotational correlation time is comparable or larger than the Larmor period) and anisotropic environments, non–zero residual dipolar and quadrupolar interactions lead to the creation of higher order coherences and a bi–exponential NMR signal decay (see (22–27), for example). Since the water diffusion coefficient in cytoplasm is almost ten times lower than that of pure water (28, 29), sodium ions in intracellular space must be experiencing slow isotropic or anisotropic motion. As a result, intracellular and extracellular compartments can be differentiated with triple–quantum filtered (TQF) sodium imaging (14, 23, 24, 30).

Note that NMR compartments, defined as regions of tissue where nuclei have different NMR properties, generally do not coincide with compartments in the physiological sense. For example, extracellular sodium in locally ordered tissues, such as cartilage, muscles, and connective tissue, may produce higher order coherences similar to that of the intracellular sodium (14, 23). However, according to the canonical brain–sodium tissue model (11, 31, 32), sodium is distributed among only two compartments: the intracellular and the extracellular one. Thus, the brain TQF signal may be interpreted as due to the intracellular compartment only (33). Multiple–quantum sodium MRI has been demonstrated in a few studies in experimental models (25, 33, 34) and, as far as we know, in only one study of human brain (24). Unfortunately, these techniques provided a qualitative tissue description due to several instrumental difficulties (35–38).

Finally, it should be recognized that due to possible similarities in NMR properties of cell–membrane sodium and the intracellular one, the canonical brain–sodium model (11, 31, 32, 39) considers cell membrane a part of intracellular space. It is for this reason that we use the term “intracellular sodium volume fraction” (ISVF) and “cell volume fraction” interchangeably.

In this study, we present a non–invasive method which employs single–quantum (SQ) and triple–quantum filtered (TQF) imaging at 7 T to measure intracellular sodium concentration, intracellular sodium volume fraction and intracellular sodium molar fraction in the human brain. The description of the method is organized in three parts. First, based on a well–known two–compartment tissue model, we analyze the relationship of physiologically and clinically relevant ISC and ISVF with the TSC and ISMF. We use this relationship and the ISC and ISVF values known from previous invasive studies for the estimation of TSC and ISMF in the healthy human brain. Then, we employ single–quantum and triple–quantum–filtered imaging to perform the ISMF measurement in healthy human subjects at 7 T MRI. We find that the obtained experimental ISMF values are consistent with the theoretical predictions and previously reported results obtained with invasive techniques. Lastly, we combine ISMF and TSC measurements to obtain maps and histograms of ISC and ISVF in eight healthy volunteers.

Thus, this study demonstrates the feasibility and robustness of non–invasive spatially resolved intracellular sodium and cell volume fraction quantification in vivo, paving the way for future clinical and research applications.

Experimental

Two compartment tissue model

Let us consider the canonical tissue model (11, 31, 32, 39) which is described by a homogeneous intracellular compartment occupying volume V_in and a homogeneous extracellular compartment with volume V_ex respectively. Next, let us use M_in and M_ex to denote respective sodium contents (in moles) in intra– and extracellular compartments. Using these notations, the bulk tissue sodium concentration (ρ_T) and the intracellular sodium concentration (ρ_in) and can be expressed in terms of the above quantities as:

$${\rho }_T=\frac{M_{in}+M_{ex}}{V_{in}+V_{ex}}{\rho }_{in}=\frac{M_{in}}{V_{in}}$$ [1]

Furthermore, the intracellular sodium volume fraction (η_in) and the intracellular sodium molar fraction (χ) are defined as:

$${\eta }_{in}=\frac{V_{in}}{V_{in}+V_{ex}}=\frac{{\rho }_{ex}-{\rho }_T}{{\rho }_{ex}-{\rho }_{in}}\chi =\frac{M_{in}}{M_{in}+M_{ex}}=\frac{{\rho }_{in}}{{\rho }_T}{\eta }_{in}$$ [2]

where ρ_ex stands for the extracellular sodium concentration.

Combining equations [1] and [2], we obtain the intracellular sodium concentration ρ_in and the intracellular sodium volume fraction η_in in terms of tissue sodium concentration ρ_T and the intracellular sodium molar fraction χ:

$$\{\begin{array}{c}{\rho }_{in}=\frac{\chi {\rho }_T{\rho }_{ex}}{{\rho }_{ex}-(1-\chi ){\rho }_T}\\ {\eta }_{in}=1-(1-\chi )\frac{{\rho }_{\text{T}}}{{\rho }_{ex}}\end{array}$$ [3]

This representation of ISC and ISVF in terms of TSC and ISMF is convenient because, as will be shown below (see eqs [6, 7]), TSC and ISMF are MRI–assessable quantities. Therefore, once TSC and ISMF are measured, ISC and ISVF can be computed using equation [3].

Since extracellular sodium concentration is maintained in a narrow range between 136 and 142 mmol/L and does not vary much among subjects (4) throughout this work, we use ρ_ex =140mmol/L. In patients with pathological conditions such as hyper– or hypo–natremia, ρ_ex would have to be determined, for example, using a blood test (4). It is established that there is no significant difference between cerebro–spinal fluid (CSF) and the serum sodium concentration (40, 41).

ISMF and TSC measurements

While ISC and ISVF cannot be assessed directly with MRI, ISMF and TSC can be measured directly. Then, using the equation [3] ISC and ISVF can be computed. Indeed, as stated earlier, it can be assumed that TQF sodium signal arises from the intracellular compartment only (33). As outlined in the Appendix and in references (22, 30, 35–37), the B₀–corrected MRI signals are:

$$S_{SQ}=C\frac{M_{in}}{5}\left(3{\text{e}}^{-\text{TE}/T_{f,in}}+2{\text{e}}^{-\text{TE}/T_{s,in}}\right)sin\alpha +{CM}_{ex}{\text{e}}^{-\text{TE}/T_{s,ex}}sin\alpha$$ [4]

$$S_{\mathit{TQF}}=C\frac{9M_{in}}{40}\left({\text{e}}^{-{\tau }_1/T_{f,in}}-{\text{e}}^{-{\tau }_1/T_{s,in}}\right)\left({\text{e}}^{-\text{TE}/T_{f,in}}-{\text{e}}^{-\text{TE}/T_{s,in}}\right){sin}^5\alpha$$ [5]

where T_s,ex, T_s,in and T_f,in are the slow and fast sodium decay constants for extra– and intracellular components, α is the flip angle, τ₁ and TE are further acquisition parameters (see Figure 1). The proportionality constant C denotes the coil sensitivity and other common factors. The first term in the equation [4] describes the contribution to the SQ signal due to the intracellular compartment, while the second corresponds to the extracellular one. The equation [5] describes TQF signal due to the intracellular compartment. Because SQ and TQF signals depend on the relaxation rates and the flip–angle, B₁–mapping and relaxation measurements will have to be performed to quantitatively interpret the measured signals.

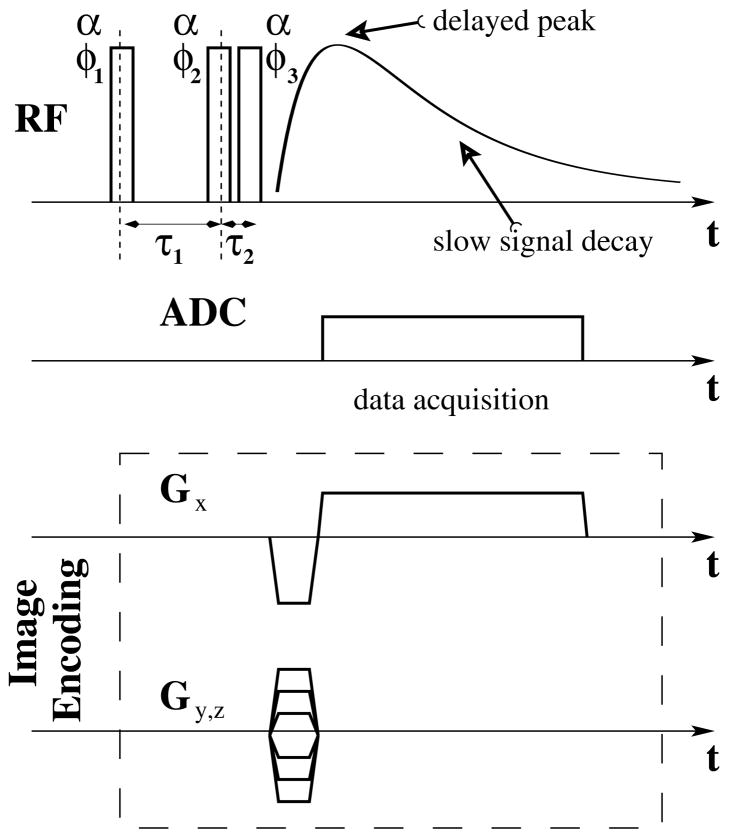
Figure 1.

Schematic diagram of the triple–quantum–filter (TQF) imaging sequence, including TQF excitation block super–posed with TQF signal evolution and imaging readout. Due to delayed peak formation and slow signal decay, Cartesian (GRE) readout is well suited for sodium TQF imaging. For the decay–rate measurements the image encoding block was not executed during the acquisition. For further details about the TQF acquisition used in this work and its B₀ and B₁ stability, see reference (36).

Analysis of eqs [4, 5] suggests a design of the experiments. First of all, the TQF signal is much weaker than the SQ signal and much more averages for TQF would have to be performed. Second, the TQF signal attains its maximum when TE =τ₁ = T_s T_f ln(T_s/T_f)/(T_s–T_f) (30) which is generally much larger than T_f. For example, if T_f = 2 ms and T_s = 45 ms, then TE_opt = 6.5 ms. Since both, TQF and SQ images need to be acquired and because image distortions depend on TE, the same TE will be used for TQF and SQ imaging.

Consequently, from the equations [2, 4, 5], the intracellular sodium molar fraction can be computed based on the measured relaxation constants and the TQF and SQ images according to the expression:

$$\chi =\frac{5{\text{e}}^{-\text{TE}/T_{s,ex}}{S}_{\mathit{TQF}}}{\left(5{\text{e}}^{-\text{TE}/T_{s,ex}}-3{\text{e}}^{-\text{TE}/T_{f,in}}-2{\text{e}}^{-\text{TE}/T_{s,in}}\right)S_{\text{TQF}}+\frac{9S_{SQ}}{8}\left({\text{e}}^{-{\tau }_1/T_{f,in}}-{\text{e}}^{-{\tau }_1/T_{s,in}}\right)\left({\text{e}}^{-\text{TE}/T_{f,in}}-{\text{e}}^{-\text{TE}/T_{s,in}}\right){sin}^4\alpha }$$ [6]

A very important property of ISMF is that this quantity is self calibrated, therefore, no external reference is needed for such quantification. The use of this quantity avoids the need to calibrate the TQF signal which is difficult to achieve.

In contrast to ISMF, the TSC measurement requires an external reference with a known sodium concentration (10–12). The TSC calibration is performed by comparing the SQ and TQF signal intensities from the brain tissue and from the references taking into account possible differences in signal decay rates and B₁–inhomogineities. More specifically, TSC concentration in the brain tissue can be computed from equations [1, 2, 4, 6], by combining the measured relaxation rates, SQ and the intracellular sodium molar fraction images for the brain tissue and for the reference tubes according to:

$${\rho }_T=\frac{S_{SQ}}{S_{SQ,\mathit{ref}}}\frac{{\left[\left(3{\text{e}}^{-\text{TE}/T_{f,in}}+2{\text{e}}^{-\text{TE}/T_{s,in}}\right)\chi +5{\text{e}}^{-\text{TE}/T_{s,ex}}\left(1-\chi \right)\right]}_{\mathit{ref}}\mid C_{\mathit{ref}}\mid sin{\alpha }_{\mathit{ref}}}{\left[\left(3{\text{e}}^{-\text{TE}/T_{f,in}}+2{\text{e}}^{-\text{TE}/T_{s,in}}\right)\chi +5{\text{e}}^{-\text{TE}/T_{s,ex}}\left(1-\chi \right)\right]\mid C\mid sin\alpha }{\rho }_{T,\mathit{ref}}$$ [7]

The reciprocity principle is used to calculate |C_ref/C|=α_ref/α based on the B₁–maps. Here we make use of the facts that a circularly polarized receive/transmit coil is employed, that the sodium resonance frequency at 7 T is only about 76 MHz and the quasistatic approximation applies (42, 43).

MRI acquisition

Eight healthy volunteers 4 elderly (mean age 65.0 ± 1.8 yrs) and 4 young (mean age 27.5 ± 1.3 yrs) were enrolled in this study. Approval for this study was obtained from the Institutional Review Board of New York University Langone Medical Center and written informed consent was obtained from all subjects.

Experiments were performed on a 7 T whole–body MAGNETOM scanner (Siemens Healthcare, Erlangen, Germany) with a custom–built dual tuned TX/RX ¹H/²³Na head coil (see G.C. Wiggins et al. Proc of ISMRM 2010, p1500) and a modified 3D GRE sequence (see Figure 1). To minimize head motion, foam pads were inserted into the space between the subject’s head and the interior of the coil. A vendor–provided semi–automated shimming procedure was performed iteratively 5 to 10 times until it converged and yielded whole–head water linewidth of 45 ± 4 Hz full width at half maximum. The imaging part of the acquisition protocol comprised TQF, SQ/B₀ and B₁ mapping and took about 50 min. Acquisition parameters for the 12–step B₀–corrected TQF imaging sequence (36) were 240×240×240 mm³ FOV with 30×30×24 encoding matrix, TR = 150 ms, TE = 6.8 ms, FA = 90° and τ₁ = 6.8 ms τ₂ = 150μs, 2 averages, leading to an acquisition time of 43.2 min. The TQF RF excitation train consisted of three non–selective pulses with 900μs duration each. The RF pulse duration was chosen as short as possible to satisfy SAR constraints at 150 ms TR on our system. The SQ sodium imaging was performed with the same imaging parameters as the TQF one. This ensures common (if any) distortions in the two images and simplifies data processing. For the purposes of TSC quantification, two reference tubes with known sodium concentrations (50 mmol/L and 100 mmol/L) were placed into the field of view of the SQ imaging. The quantification procedure was similar to the one described in (10–12). For TQF B₀–correction, B₀–maps were computed from the phase difference between two SQ images acquired in 3.6 min (TR = 150 ms) with TE = 6.8 ms and TE = 8.8 ms, respectively. The SQ image with TE = 6.8 ms was used for TSC calculation and did not require a separate acqusition. B₁–maps were computed from the ratio of two additional SQ images acquired in 3.6min with FA=60° and 120°, TR=150ms using the double flip–angle method (44). Using the B₁–maps, B₁–correction was applied to SQ and TQF images according to equations [4] and [5]. A correction for finite RF pulse duration was made according to (45). Since the sodium T₁ relaxation rate is about 50 ms (46) and the data were acquired with TR=150ms, the T₁–weighting leads to a negligible (<5%) quantification error and was ignored.

In addition, anatomical MRI images were acquired from the same subjects using a 3D T₁–weighted magnetization–prepared gradient echo (MPRAGE) on a 3 T system (MAGNETOM Trio, A Tim System, Siemens Medical Solutions,Erlangen, Germany). The parameters of the sequence were: TR = 2400 ms; TE = 2.71 ms; inversion time = 900 ms; flip–angle = 12° covering the whole brain with isotropic spatial resolution of 1 mm. These images were segmented into gray and white matter (GM and WM) masks (threshold above 75 %) and coregistered with the sodium images using FSL (47) in order to measures the ISC and ISVF values of GM and WM separately.

Relaxation Rates measurement

Knowledge of the relaxation rates is needed not only for determination of the optimal τ₁ and TE values for TQF imaging itself (27), but also to obtain ISMF and TSC values (see equations [4, 5] above). While sodium relaxation rates for various tissue types are available in the literature, no such values are reported for human brain at 7 T. Therefore, the intracellular compartment transverse relaxation constants T_s,in and T_f,in were measured from the whole head using a TQF method similar to method (37). The method relies on the free induction decay (FID) data acquired with variable delay constants τ₁ and by processing the data at TE =τ₁ (see Figure 1). The advantage of this method is that it provides a high SNR by collecting data from the whole head and is insensitive to B₁ and B₀ magnetic field inhomogeneities. Therefore, an FID sequence with a TQF cycle was used. The creation time τ₁ was varied in 1 ms increments between 1 ms and 50 ms, TR = 250 ms, sampling interval was 200μs, and 512 complex samples were acquired with 10 averages. Total acquisition time was less than 30 min. These data were acquired in a separate session. The relaxation constant for the extracellular compartment was taken to be T_s,ex = 55 ms (48–51).

Phantom experiments

To validate data acquisition and quantification procedures only, separate measurements were conducted on agar–gel phantoms. Two phantoms (cylinders with 6 cm diameter and 10 cm length) were manufactured with 100 ± 1 mmol/L and 140 ± 1mmol/L sodium concentrations and 4 % agar concentration to create a compartment with slow moving sodium ions. In addition, a phantom (a cylinder with 12 cm diameter and 20 cm length) with 86 ± 1 mmol/L sodium water solution was used as a compartment with fast motion sodium ions. Stricto sensu, there are no cells in the phantoms, nevertheless, it is known that sodium NMR signal from the saline compartment has properties similar to the signal from CSF and extracellular sodium while NMR signal from the agar gels arises mainly from slow tumbling sodium ions as found in the cytoplasm. The advantage of such setup is that the acquisition and quantification procedure can be easily validated by mechanically computing ISC and ISVF values for the phantoms and comparing them with the manufactured numbers. Indeed, owing to the phantom manufacturing process, the phantom’s “intracellular” concentration is equal to TSC and the ISVF values in the two gel phantoms should be high (but below 100 %) and identical. (The exact fraction of fast and slow motion sodium ions in the agar gels is not known.)

The imaging matrix for the phantom scans was 16×16×16 with all other data acquisition parameters and processing steps as described above.

Potential biases in the measurement

To improve SNR and shorten the acquisition time, we assumed that the brain tissue can be characterized by a single pair of T_s and T_f values in the decay rate measurement. We estimate that possible small differences in relaxation properties between gray and white matter will lead to a small (less than 10 %) effect on sodium quantification because of the TE used (52).

Since noise follows the Rice distribution in magnitude reconstructed MR images, a small overestimation in intracellular sodium molar fraction is expected in areas of low TQF signal. As a consequence, it is expected that areas with low ISMF will show intracellular molar fraction of the order of 10 %. Such bias might cause a slight elevation in ISVF value with an associated increase in ISC. Indeed, following the propagation of errors technique (53), equation [8], obtained from the equation [3], relates changes in intracellular sodium volume fraction and intracellular sodium concentration to variations in the input parameters (intracellular sodium molar fraction, tissue sodium concentration and extracellular sodium concentration). From this equation one can see that for most tissue types intracellular sodium volume fraction is robust against ISMF, TSC and ESC variations while intracellular sodium concentration measurement is more sensitive to the errors in the input parameters. Improvements in coil technology and data acquisition strategies will aid in the removal of this low–SNR–related bias.

$$\{\begin{array}{c}\frac{\delta {\rho }_{in}}{{\rho }_{in}}=\frac{{\rho }_{ex}-{\rho }_{in}}{{\rho }_{ex}}·\frac{\delta \chi }{\chi }+\frac{1}{{\eta }_{in}}\frac{\delta {\rho }_T}{{\rho }_T}-\frac{1-{\eta }_{in}}{{\eta }_{in}}\frac{\delta {\rho }_{ex}}{{\rho }_{ex}}\\ \frac{\delta {\eta }_{in}}{{\eta }_{in}}=\frac{{\rho }_{in}}{{\rho }_{ex}}·\frac{\delta \chi }{\chi }+\frac{1-{\eta }_{in}}{{\eta }_{in}}\left(\frac{\delta {\rho }_{ex}}{{\rho }_{ex}}-\frac{\delta {\rho }_T}{{\rho }_T}\right)\end{array}\Rightarrow \left|\begin{array}{l}{\rho }_{ex}=140\mathit{mmol}/L\hfill \\ {\rho }_{in}=12\mathit{mmol}/L\hfill \\ {\eta }_{in}=0.85\hfill \end{array}\right|\Rightarrow \{\begin{array}{l}\frac{\delta {\rho }_{in}}{{\rho }_{in}}\stackrel{\sim }{=}0.9·\frac{\delta \chi }{\chi }+1.18·\frac{\delta {\rho }_T}{{\rho }_T}-0.18·\frac{\delta {\rho }_{ex}}{{\rho }_{ex}}\hfill \\ \frac{\delta {\eta }_{in}}{{\eta }_{in}}\stackrel{\sim }{=}0.09·\frac{\delta \chi }{\chi }+0.18·\left(\frac{\delta {\rho }_{ex}}{{\rho }_{ex}}-\frac{\delta {\rho }_T}{{\rho }_T}\right)\hfill \end{array}$$ [8]

Here, we have selected physiological values for ESC, ISC and ISVF (4, 21, 31, 54–57).

It is important to recognize that intracellular molar content and cell volume are zero in the extracellular tissues leading to an ill–defined ISC. Thus, results of the ISC measurements in CSF, cerebral ventricles and vitreous body of the eyes will be unpredictable and meaningless.

Throughout this work, it is assumed that the TQF signal comes from the intracellular space only (33). If there were a significant contribution to the TQF signal from the extracellular space, it would have caused a bias in ISMF and an overestimation of the ISC and ISVF values (see equation [8]). However, according to the equation [8], an overestimation of ISMF would lead to a small bias in ISVF. The presence of such bias would significantly affect ISC values.

Results

Predictions for intracellular sodium molar fraction and intracellular sodium volume fraction

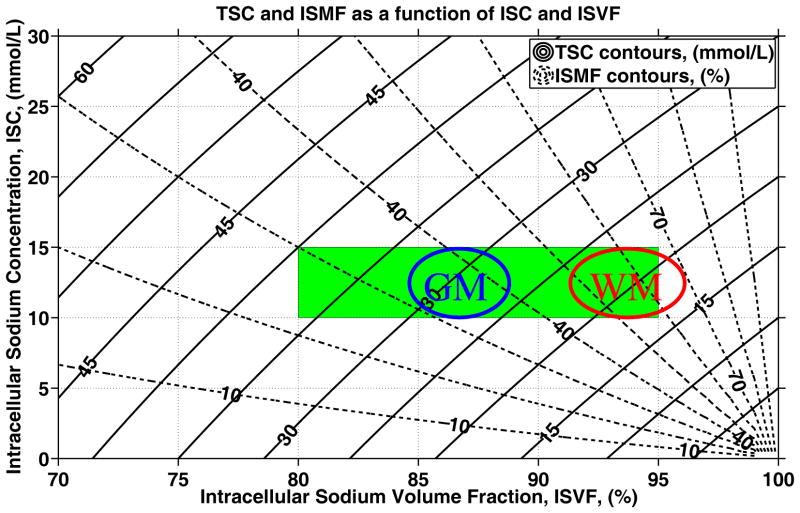
Using equations [3] of the Methods section, it is possible to produce a graph which quantifies the relationship between ISC, ISVF, TSC and ISMF (see Figure 2). This graphical representation of the quantitative relationship given by the equation [3] of the Methods section illustrates how any two out of the four quantities (ISC, ISVF, TSC, ISMF) can be computed using the remaining two. For example, assuming intracellular sodium concentration of 10 – 15 mmol/L (31) and ISVF between 80 % and 95 % (21, 54–57), it can be seen that healthy TSC values are expected in the range of 17 – 40 mmol/L and TSC values above 45 mmol/L (13) are extremely unlikely in healthy tissue as those would require either unreasonably low intracellular volume fractions (21, 54–57) or unreasonably high intracellular sodium concentrations. Furthermore, according to Figure 2, the ISMF values in healthy brain tissue vary over a rather broad range between 25 % and 70 %. Note that the only information used to produce these predictions is that the tissue can be described by two compartments (intra– and extracellular), that the intracellular sodium concentration is 10 – 15 mmol/L, the intracellular sodium volume fraction is 80 – 95 %, and the extracellular sodium concentration is fixed to 140 mmol/L.

Figure 2.

Quantitative relationship among ISC, ISVF, TSC and ISMF (see equation [3]). The solid lines are the contours of constant TSC values, while the dashed lines are the contours of constant ISMF. Note that TSC and ISMF are compound measures of ISC and ISVF and, as a result, are sensitive but not specific to variations in ISC and ISVF. Nevertheless, a combination of TSC and ISMF values can be converted to ISC and ISVF. The rectangular box represents the range of ISC and ISVF values for healthy brain tissue based on invasive measurements in animals or ex–vivo brain tissue (11, 21, 31, 54–57). It is evident that brain–tissue TSC values larger than 45 mmol/L are unlikely in healthy brain tissue as such values would lead to either very low ISVF or very high ISC (11, 13, 21, 31, 54–57). Theoretical predictions for the ISMF and the ISVF values in brain gray and white matter of healthy human subjects based on literature TSC values(10) are also shown using ovals.

Conversely, assuming that TSC is 20 mmol/L for healthy white matter and 30 mmol/L for healthy gray matter, as reported in reference (10), and that ISC is 10 – 15 mmol/L, it is possible to estimate the expected values for ISMF and ISVF in gray and white matter as indicated by ovals in Figure 2. Hence, the predicted ISMF values between 28 – 44 % (gray matter) and 46 – 72 % (white matter) are in good agreement with the previously reported values between 26 % and 57 % (31). Likewise, the predicted ISVF values are between 85 – 88 % (gray matter) and 92 – 96 % (white matter) which is in good agreement with the previously reported range of 80 – 95 % (21, 54–57).

Test of the data acquisition and quantification procedures in phantoms

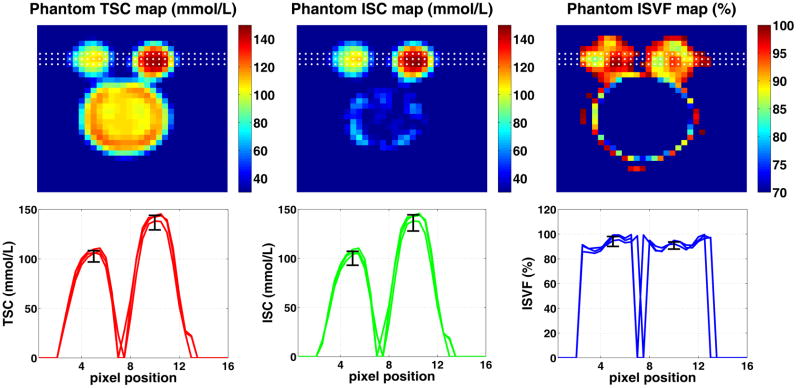
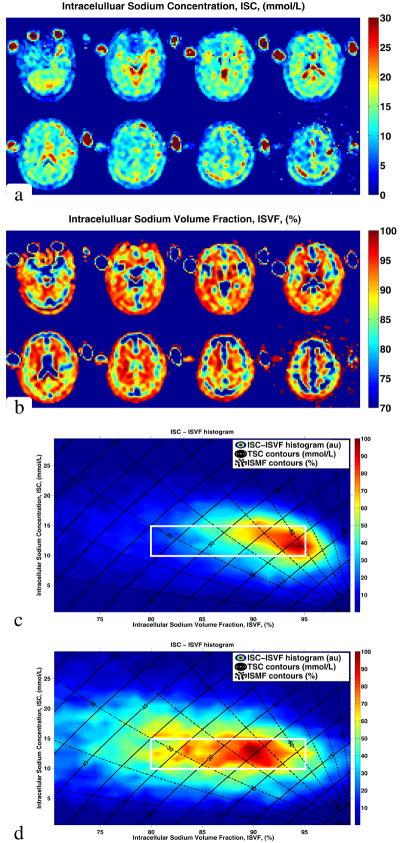
Figure 3 depicts ISC and ISVF maps from the phantom (two agar–gel small bottles and the larger saline bottle). Measured SNR in the raw SQ–image is about 110 in the 140 mmol/L bottle and about 80 in the 100 mmol/L one. Based on these measurements, it is expected that errors in the TSC calibration in the bottles will be 0.9 % and 1.3 %, respectively. Calculated TSC values (mean ± standard deviation) in the phantoms are 137 ± 7 mmol/L and 103 ± 6 mmol/L which are in good agreement with the designed values. (The errors were computed by drawing a region of interest in the center of the phantom bottles.) Nevertheless, the errors are larger than expected. This could be due to Gibbs ringing, B₀–inhomogeneities and possible phantom non–uniformities. Although there is no good reference value for the ISVF in agar gels, owing to the phantom manufacturing process the phantom’s “intracellular” concentration is equal to TSC. Using equations [3, 6, 7] and the measured SQ and TQF signals, the calculated ISCs in the phantom are 136 ± 8 mmol/L and 100 ± 7 mmol/L which is in good agreement with the TSC and design values. It is expected that ISVF values in the two gel phantoms are equal, and they were found to be 91 ± 3 % and 94 ± 4 %. Relaxation constants in the phantoms were 5.9 ± 0.9 ms and 40 ± 4 ms. The errors in T₂ measurements were computed by repeating the data acquisition and reconstruction procedure four times. Note that ISC is not defined in the regions of fast moving sodium ions (both intracellular sodium mass and intracellular sodium volume are zero) causing arbitrary values to be produced in the saline bottle (zero–divided–by–zero problem). Because ISC and ISVF are not defined outside the sample (due to lack of matter), the maps have been masked. The mask was produced from the SQ image by zeroing all pixels with image intensity below 5 % of maximum in that slice.

Figure 3.

An exemplary slice from the phantom setup comprising 2 agar gel bottles (slow–moving sodium ion compartment) and one saline bottle (fast–moving sodium ion compartment). Dotted lines in the TSC, ISC, and ISVF maps illustrate the location of the corresponding 1D profiles shown on the lower panel. As expected, the measured (mean±standard error) TSC (137 ± 7 and 103 ± 6 mmol/L) and ISC (136 ± 8 and 100 ± 7 mmol/L) values are close to the design values of 140 ± 1 and 100 ± 1 mmol/L, respectively. ISVF values in the two gel phantoms, which are expected to be identical due to the phantom preparation process, were 91 ± 3 % and 94 ± 4 %. Note that ISC is not defined in the regions of fast moving sodium ions since both intracellular sodium mass and intracellular sodium volume are zero causing arbitrary values to be produced in the saline bottle (zero–divided–by–zero problem). Similarly, ISC and ISVF are not defined outside the sample. Therefore, the maps have been masked. The mask was produced from SQ image by zeroing all voxels with image intensity below 5% of maximum in that slice.

In vivo intracellular sodium relaxation measurement

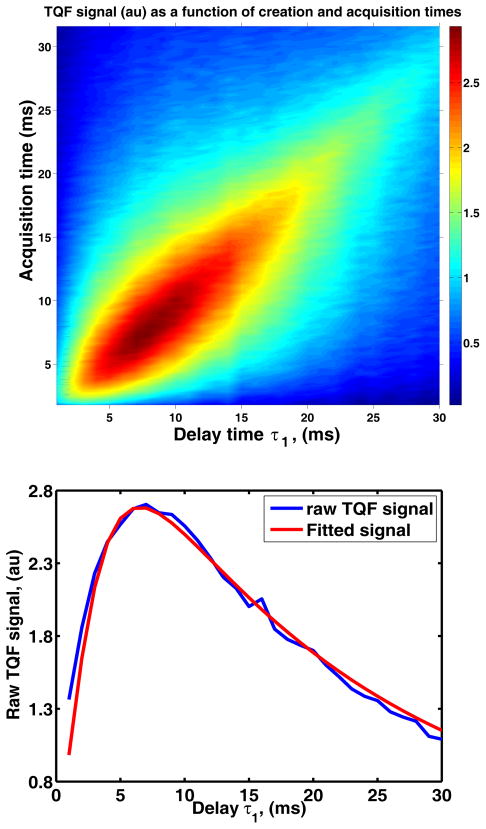
Based on the whole–head TQF measurement, brain tissue sodium relaxation rates T_f,in and T_s,in are T_f,in = 2 ± 0.3 ms T_s,in = 44 ± 6 ms. Figure 4 depicts raw 2D spectroscopic data (top) and fitted data (bottom) from a healthy volunteer. These results are in a good agreement with the previous measurements (Tanase et.al Proc. Intl. Soc Magn Med Reson. 13:2564, 2005). Note that the TQF–based T₂ relaxation measurement is not biased by CSF contamination due to the fact that fast moving sodium ions, as found in CSF, do not produce observable higher–order coherences.

Figure 4.

TQF decay constants measurement in a healthy young, male, 27 year old volunteer: raw data (top) and fitted data (bottom).

In vivo MRI–measured intracellular sodium molar fraction

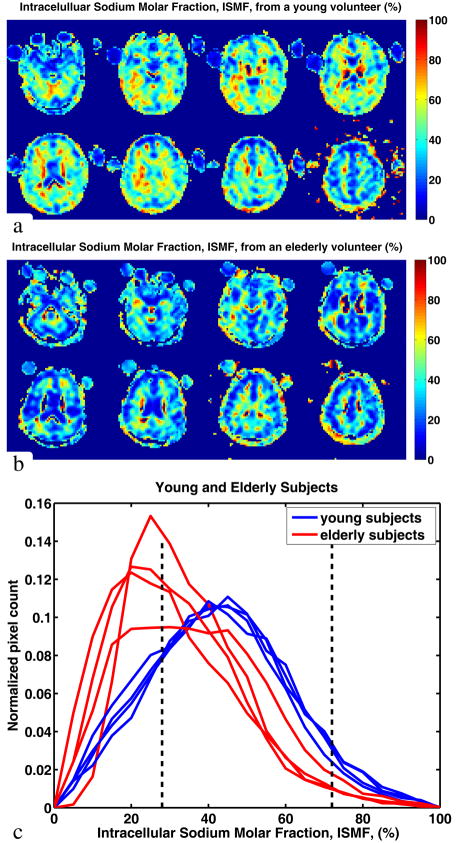
Selected contiguous axial slices of the intracellular sodium molar fraction maps from a 27 year old healthy volunteer are shown in Figure 5, along with whole–brain ISMF histograms from the eight healthy volunteers. As expected, areas with known fast isotropic motion of sodium ions (such as cerebral ventricles or vitreous body of the eyes) show low ISMF (below 10 % due to SNR ~ 5 in TQF and SNR ~ 10 in SQ images) whereas brain tissue, with sodium ions in a slow motion or anisotropic environment shows ISMF values generally between 25 % and 75 %. This is in good agreement with the theoretically predicted values of 28 – 72 % for the young human brain. Based on our data, the mean ISMF value in the young human brain is 43 % which falls within the anticipated values. Note that the ISMF distributions from the various young volunteers are remarkably similar to each other.

Figure 5.

Quantitative ISMF maps from a male, 27 year old volunteer (a), 67 year old volunteer (b) and histograms of the ISMF in each of the eight subjects (c). The dashed lines on the histogram show the theoretically predicted range for gray and white matter (see Figure 2). Contributions with ISMF of less than 25 % are mostly due to the partial volume effect with the CSF, cerebral ventricles and the vitreous body of the eyes.

It is known that healthy aging is associated with brain tissue atrophy caused by death and shrinkage of brain cells (58, 59). Therefore, the intracellular sodium molar fraction in brain tissue should decrease with age if the aging cells maintain ISC at a constant level. Our data presented as histograms in Figure 5 show a similar trend. The distributions of ISMF for the elderly volunteers are shifted towards lower values (to the left) compared to those of younger volunteers.

Using gray and white matter masks we obtained ISMF values of 39 ± 8 % for GM and 56 ± 7 % for WM. These ISMF values are within the anticipated range between 28 % and 44 % for the GM and 46 – 72 % (see Theoretical predictions for ISMF and ISVF section and Figure 2).

In vivo MRI–measured intracellular sodium concentration and intracellular sodium volume fraction

Figure 6 depicts ISC and ISVF maps for a 27 year old volunteer, derived from measured MRI data. The intracellular sodium concentrations of GM and WM regions are relatively uniform at 13 ± 3 mmol/L for the WM and 13 ± 4 mmol/L for the GM. The ISVF values for WM and GM are 94 ± 5 % and 89 ± 6 %, respectively. Figure 6 also depicts a 2–dimensional ISC–ISVF histogram from the whole brain of a young volunteer. The axes and contours in this panel are the same as those on Figure 2. Color in the panel represents voxel frequency count in the brain with corresponding ISMF and TSC values. (The two–dimensional histograms where produced as described in reference (60).) As can be seen from the histogram, ISC and ISVF measured in–vivo are within the expected range. The ISVF for the WM is higher than for the GM consistent with previous findings obtained with invasive methods in animals or ex vivo human brain tissue (11, 31, 54–56) and the ISC remains within the expected range between 10 – 15 mmol/L. The ISC–ISVF histogram for an elderly volunteer is also shown in Figure 6. The ISC values are 13 ± 3 mmol/L and 13 ± 4 mmol/L in WM and GM, similar to those in the young brain, while the ISVF is decreased (ISVF_WM = 87 ± 7 %, ISVF_GM = 83 ± 7 %,). This corresponds to a decrease in intracellular volume caused by normal aging when the intracellular concentration remains constant.

Figure 6.

ISC map (a) and ISVF map (b) derived from MRI measurements in a healthy young, male, 27 year old volunteer. ISC–ISVF histogram from the same volunteer (c). The ISC and ISVF values are within the expected range (see Figure 2) for a healthy brain. For comparison, ISC–ISVF histogram from a healthy elderly, male, 67 year old volunteer is shown in panel (d). The white frame on panels (c) and (d) corresponds to the green box of Figure 2. Comparing (c) and (d), ISC remains constant while ISVF decreases consistent with the normal aging process. Furthermore, as expected, the ISMF values in healthy brain tissue vary over a rather broad range (see Figure 2). Note that ISC is not a well–defined quantity in the areas of pure “extracellular” content such as CSF, cerebral ventricles or vitreous body of the eyes. Consequently, unlike the ISVF, ISC results in such areas are difficult to interpret.

Discussion

Using common assumptions of the intra– and extracellular brain–tissue compartmentalization, we established the quantitative relationship between the clinically meaningful ISC and ISVF and the MRI–measurable tissue–model independent TSC and ISMF values. This relationship can be used to predict TSC and ISMF values for different tissue types and diseases if ISC and ISVF are known from other, often invasive, measurements. For example, we used this relationship to predict TSC and ISMF values for the healthy brain tissue. The results of these predictions are consistent with previous reports (10, 31, 50). Then, combining TQF and SQ imaging we performed in–vivo ISMF measurements in the human brain (Figure 5). As expected from Figure 2, the histogram of the human brain ISMF values is rather wide, indicating gray/white matter heterogeneity. ISMF_GM = 39 ± 8 % and ISMF_WM = 56 ± 7 %, consistent with TSC_GM ~ 30 mmol/L and TSC_WM ~ 20 mmol/L (see Figure 2) reported in references (10) and is in good agreement with theoretically calculated ISMF between 28 % and 72 %. The agreement between independently measured TSC and ISMF values suggests that most of the TQF signal comes from the intracellular compartment.

As can be seen from Figure 2, TSC and ISMF quantifications provide complementary information about the tissue sodium content. For example, increase in ISC accompanied by the cellular death will lead to an increase in TSC while ISMF may remain constant. Conversely, ISC increase accompanied by cellular swelling will lead to an increase in ISMF while TSC may remain constant. Since TSC and ISMF are compound measures of ISC and ISVF, TSC and ISMF are sensitive to changes in ISC and ISVF, but are not specific to any particular one. Therefore, a combination of TSC and ISMF measurements is needed to obtain ISC and ISVF values.

Next, both TSC and ISMF were acquired in a single MRI session from eight healthy volunteers. A typical two–dimensional TSC–ISMF histogram is shown in Figure 6. The data cluster between the 10 – 15 mmol/L ISC and 85 – 95 % ISVF range. In addition, in vivo ISC and ISVF maps were produced. Comparison of ISVF between young and elderly volunteers indicates a decrease of the intracellular space consistent with a 0.1 – 0.2 % decrease of brain volume per year previously reported in healthy volunteers (58, 59). While it is difficult to conclude whether or not the spread of the ISC values observed in Figure 6 is of biological or instrumental origin, we think that the spread of ISVF values is due to differences in gray and white matter architectures. This is because spread of brain ISVF values almost an order of magnitude larger than expected based on the image SNR (see equation [8] of the Methods section).

The quantitative nature of the developed method was validated with phantom studies. A compartment with slow moving sodium ions was prepared using an agar gel, while the compartment with fast moving sodium ions was prepared using saline. The results show good agreement between the designed and the measured values for the ISC. While there is no good reference for the ISVF, there were no significant differences between ISVF values for the two agar phantoms used.

Even though human ISC, ISVF, ISMF and TSC results are in accord with the previous theoretical predictions and experimental works, with exception of TSC measurements, most of the previous sodium related data come from invasive or ex–vivo animal studies. In this work we used these data as a guide in the design of the non–invasive in–vivo measurements in humans. In doing so, we assumed that properties of sodium NMR signal from the tissue are similar between humans and other animals. For example, based on animal studies (21,57), the intracellular volume fraction is 80 – 95 % (with more recently reported data clustering around 80 – 85 %). Our results in human brain indicate a value of 85 – 95 % for the ISVF. This difference may be explained by both biological and methodological factors (such as an affect of the anesthetic on cell volume (61) in animal studies) between the experiments in animal models and humans. Refinements to the technique presented here and/or new techniques are needed to clarify this possible discrepancy.

TSC values measured in our work are in agreement with theoretical predictions (see the green box in Figure 2) and with an independent measurement (ellipses in the Figure 2) in human brain (10) using a different acquisition technique. Nevertheless, it should be pointed out that other groups report higher TSC values (12, 31, 39, 50, 62, 63). The difference is of methodological origin. It is customary to assume that the tissue is described by two homogeneous compartments. If, however, a third compartment with a fast decaying (with T₂ shorter than 2 ms) sodium signal existed, it would have biased our TSC results towards lower values. Acquisition methods sensitive to fast decaying sodium signal such as TPI imaging (12, 24, 27, 39, 62, 64), 3DCones (65) and AWSOS (66) allow for acquisition of fast decaying signals and offer high SNR efficiency. The disadvantage of these approaches was recently discussed in (39, 62) and (66). It was pointed out that those approaches have a much wider point–spread function compared to Fourier encoding. Indeed, based on (39, 62, 66), TPI and AWSOS produce voxels with twice or even larger volume compared with the Fourier encoding for the same nominal spatial resolution. This blurring my also contribute to the apparent increase of the SNR efficiency of the methods and may bias TSC values towards higher values due to possible contamination with CSF. Another difficulty with the approaches is that the point–spread function varies from location to location in the field of view making it even more difficult to perform quantification. Taking this information into account and noting that optimal TE for TQF imaging is usually rather large (30), the Fourier encoding scheme was used in this work.

It is important to mention several other factors that may have affected the relation between ISC and ISVF measured in this study and the physiological ISC and cell volume fraction. The key among those are instrumental (such as low SNR, B₀– and B₁– field inhomogeneities) and molecular environment factors (such as the longitudinal T₁ and transverse T₂ relaxation times). Owing to quite rapid sodium T₁ relaxation in vivo, (T₁ ~< 50 ms) (46) the use of repetition times of 150 ms led to negligible (< 5 %) quantification errors. A B₀–inhomogeneity insensitive TQF acquisition (36) was used to minimize possible B₀–related errors, while B₁–inhomogeneities were corrected in post–processing with the help of the auxiliary B₁–maps as described in the Methods section. Slow and fast T₂ decay rate components were measured using a B₀– and B₁–insensitive method similar to that described in reference (37) and applied to the measured TQF and SQ data as described in the Methods section. The TE in the experiments was chosen to optimize TQF signal (as it is much weaker than SQ one) coming from both slow and fast components of the sodium signal. Since image distortions depend on TE, to keep the distortions the same in TQF and SQ data both TQF and SQ images were acquired with the same TE. While such choice optimized TQF acquisition, it led to an unavoidable signal loss of about 40 % in SQ images. Nevertheless, the use of an intermediate TE in this study reduced the sensitivity of quantification procedure to possible errors in T_f,in and T_s,in. Finally, possible contribution to TQF signal from the extracellular sodium could have biased the results of the measurement. Unfortunately, it is not possible to clarify the magnitude of the bias based on the tissue model and the acquisition used in this work. New models and acquisition schemes may answer this question. Since ISC and ISVF values obtained in our study were within the expected physiological range, we believe that the possible biases remained small. For a more detailed description of the potential biases, please, see the methods section. Development of multi–channel receive arrays for sodium imaging will definitely improve image SNR and will facilitate reduction of imaging time and increase of spatial resolution. Such improvements will increase accuracy and precision of the quantitative measurements. These improvements, however, will come at a cost of a more complex data acquisition and processing associated with the array–sensitivity calibration. Use of more complex tissue models and accounting for partial volume effects may also reduce the errors in the measured parameters. Such improvements will require additional knowledge about tissue parameters and structure and/or additional acquisitions. For example, GM/WM partial volume effect cannot be fully accounted based on a simple GM/WM masks as done in this and many other studies. A better way to account for the effect is to build a tissue model which contains the partial volume effect as part of the model. Given recent increase in publications about sodium TQF techniques, it is reasonable to expect that new acquisition methods will become available which will allow improvement upon results presented here.

Until now the lack of technologies for quantitative mapping of sodium homeostasis has been a major limiting factor in many brain investigations. Our methodology for measuring ISC and ISVF can be applied in neurological disorders such as stroke, cancer, degenerative and inflammatory diseases where accurate non invasive determination of ISC and ISVF is the key for understanding underlying pathophysiological mechanisms. For example, neoplastic cell proliferation may disrupt normal cell packing and expand the extracellular volume (7) resulting in decrease of ISMF and ISVF. Furthermore, the ISC in the tumor cells can be higher than in the healthy tissue because of differences in ion homeostasis within tumor cells (8, 9). The latter information may become of crucial importance for grading the tumor, rule out tumor recurrence and monitor response to medical and surgical treatments. In addition, owing to its sensitivity and specificity to tissue changes at a cellular level, our method has the potential to help elucidating the complex mechanisms underlying physiological and pathological aging.

In conclusion, we used single– and triple–quantum filtered sodium imaging to obtain intracellular sodium molar fraction (ISMF), intracellular sodium concentration (ISC) and intracellular sodium volume fraction (ISVF) maps in–vivo in healthy volunteers at 7 T. ISC and ISVF values measured with the described method are in a good agreement with those from previous invasive and/or ex–vivo studies, indicating potential importance of the developed method for clinical and research applications. The technique allows quantitative mapping of the ISMF, ISVF and ISC in–vivo and may be used in the future for structural and functional studies of healthy and diseased brain, to monitor disease progression and response to current and experimental treatments.

List of Symbols and Abbreviations

ISC ρ_in

Intracellular Sodium Concentration

ESC ρ_ex

Extracellular Sodium Concentration

TQF

Triple Quantum Filter

SQ

Single Quantum

ISMF χ

Intracellular Sodium Molar Fraction

ISVF η_in

Intracellular Sodium Volume Fraction

TSC ρ_T

Tissue Sodium Concentration

CVF

Cell Volume Fraction

Appendix A

Detailed derivation of equations 4 and 5 is described elsewhere (see (37), for example). Nevertheless, we will reproduce the key derivation steps here. SQ and TQF signal amplitudes can be computed using an irreducible tensor operator formalism (22, 30). In this formalism, the density operator σ(t) for a spin 3/2 system is expanded in the form:

$$\sigma (t)=\sum _{l=0}^3\sum _{p=-l}^l{c}_{lp}(t)T_{lp}$$

where T_lp is an irreducible tensor of rank l and coherence order p. The transformation of an T_lp operator under a hard radiofrequency pulse of flip angle α and phase φ is given by (22, 30):

$$T_{lp}\to \sum _{p^{\prime }=-l}^l{d}_{p^{\prime }p}^l(\alpha )e^{-i(p^{\prime }-p)\phi }{T}_{{lp}^{\prime }}$$

where transfer amplitudes d^l_p′p(α) are the elements of the Wigner’s reduced rotation matrix (22, 30). Note that the radiofrequency pulse can cause the change of the coherence order (from p to p′) but does not change the rank l. On the other hand, the evolution of the operator T_lp during time period t is given by:

$$T_{lp}\to \sum _{l^{\prime }=p}^3{f}_{l^{\prime }l}^{(\mid p\mid )}(t)e^{-ip\mathrm{\Omega }t}{T}_{l^{\prime }p}$$

where the functions f_l′l^(p)(t) describe the rank change as a result of relaxation of p–coherence during time t (22, 30) and Ω is the main magnetic field offset.

Combining these facts together and noting that the NMR experiments start in thermal equilibrium (described by T₁₀) and that only components corresponding to T_1–1 can be detected, the first order coherences can be measured after a single excitation pulse (conventional MRI) while a train of at least three RF pulses is needed to measure a contribution due to higher–order coherences. Hence, one obtains expressions for the SQ and TQF signals:

$$\begin{array}{l}{S}_{SQ}-d_{-10}^1(\alpha )f_{11}^{(1)}(t)e^{i\mathrm{\Omega }t}\\ S_{\mathit{TQF}}-\sum _{\begin{array}{l}p=\pm 1\\ p^{\prime }=\pm 3\end{array}}{pd}_{p0}^1(\alpha )f_{31}^{(1)}({\tau }_1)d_{p^{\prime }p}^3(\alpha )d_{-1p^{\prime }}^3(\alpha )f_{13}^{(1)}(t)e^{-ip\mathrm{\Omega }{t}_1}{e}^{i\mathrm{\Omega }t}\end{array}$$

where τ₁ is the delay between the first and the second excitation pulses in the TQF sequence and t is the acquisition time (see Figure 1). Evolution between the second and the third excitation pulses in the TQF sequence (τ₂) has been ignored since the delay is very short. Effect of magnetic field inhomogeneities on signal formation is important and must be taken into account during processing. A more detailed discussion on the B₀–correction and the phase–cycling scheme to select the desired coherence pathways can be found, for example, in (35–37).

Using explicit expressions for d^l_p′p(α) and f_l′l^(p)(t) (22, 30):

$$\begin{array}{l}{d}_{\pm 10}^1(\alpha )=\overline{+}\frac{1}{\sqrt{2}}sin\alpha \\ d_{31}^3(\alpha )=d_{-3-1}^3(\alpha )=\frac{\sqrt{15}}{8}{sin}^2\alpha (1+cos\alpha ),d_{3-1}^3(\alpha )=d_{-31}^3(\alpha )=\frac{\sqrt{15}}{8}{sin}^2\alpha (1-cos\alpha )\\ f_{11}^{(1)}(t)=\frac{1}{5}\left(3e^{-t/T_{2f}}+2e^{-t/T_{2s}}\right)\\ f_{13}^{(1)}(t)=f_{31}^{(1)}(t)=\frac{\sqrt{6}}{5}\left(e^{-t/T_{2f}}-e^{-t/T_{2s}}\right)\end{array}$$

one arrives at equations [4, 5] (37).

Appendix B

Equaiton [4] can be written in the form:

$$S_{SQ}=C\left(D·M_{in}+\text{E}·M_{ex}\right)=C\left(M_{in}+M_{ex}\right)\left(\frac{D·M_{in}}{M_{in}+M_{ex}}+\frac{E·M_{ex}}{M_{in}+M_{ex}}\right)$$

Using the definitions of ρ_T and χ from equations [1] and [2] we obtain:

$$S_{Sq}=C{\rho }_T[D·\chi +\text{E}·(1-\chi )](V_{in}+{\text{V}}_{ex})$$

(V_in + V_ex) is the volume of imaging voxel which is the same for the brain tissue and for the reference tubes. By computing the ratio of SQ signals measured from the tissue and from the reference with known TSC, one obtaines:

$$\frac{S_{SQ}}{S_{SQ,\mathit{ref}}}=\frac{{\rho }_T}{{\rho }_{T,\mathit{ref}}}\frac{C}{C_{\mathit{ref}}}·\frac{\left[D·\chi +\text{E}·(1-\chi )\right]}{{\left[D·\chi +\text{E}·(1-\chi )\right]}_{\mathit{ref}}}$$

Writing out explicit forms of coefficients D and E leads to the equation [7].

By writing equations [4] and [5] in a similar form one obtains:

$$\{\begin{array}{c}{S}_{SQ}=C(D·M_{in}+\text{E}·M_{ex})\\ S_{\mathit{TQF}}=C·F·M_{in}\end{array}\Rightarrow \{\begin{array}{c}C·\left(M_{in}+M_{ex}\right)=\frac{F·S_{SQ}+\left(E-D\right)S_{\mathit{TQF}}}{E·F}\\ C·M_{in}=\frac{S_{\mathit{TQF}}}{F}\end{array}$$

Using ISMF definition from equation [2], we obtain:

$$\chi =\frac{M_{in}}{M_{in}+M_{ex}}=\frac{E·S_{\mathit{TQF}}}{\left(E-D\right)·S_{\mathit{TQF}}+F·S_{SQ}}$$

And writing the explicit forms of coefficients D,E and F leads to the equation [6].