Abstract
More than a simple carrier of the genetic information, messenger RNA (mRNA) coding regions can also harbor functional elements that evolved to control different post-transcriptional processes, such as mRNA splicing, localization and translation. Functional elements in RNA molecules are often encoded by secondary structure elements. In this aticle, we introduce Structural Profile Assignment of RNA Coding Sequences (SPARCS), an efficient method to analyze the (secondary) structure profile of protein-coding regions in mRNAs. First, we develop a novel algorithm that enables us to sample uniformly the sequence landscape preserving the dinucleotide frequency and the encoded amino acid sequence of the input mRNA. Then, we use this algorithm to generate a set of artificial sequences that is used to estimate the Z-score of classical structural metrics such as the sum of base pairing probabilities and the base pairing entropy. Finally, we use these metrics to predict structured and unstructured regions in the input mRNA sequence. We applied our methods to study the structural profile of the ASH1 genes and recovered key structural elements. A web server implementing this discovery pipeline is available at http://csb.cs.mcgill.ca/sparcs together with the source code of the sampling algorithm.
INTRODUCTION
Sequence analysis in the post-genomic era has revealed the multiplicity of selective pressures applied on the genetic code and therefore a frequent overlap of functional elements. Recent studies suggested that coding regions of messenger RNAs (mRNAs) can often include secondary structure elements involved in post-transcriptional regulatory processes (1–3). Although many programs have been developed to analyze folding properties of large non-coding RNAs (4) or untranslated regions of mRNAs (5), these tools cannot be directly applied to study the structural properties in coding regions. Indeed, the sequence of codons that specify the amino acid chain might bias the thermodynamic folding properties of the polynucleotide, thus preventing accurate estimate of the statistical significance of local structural motifs. Similar issues are encountered in the context of large-scale studies and techniques aiming as defining RNA structure characteristics on a genome-wide scale (6,7). Actually, assessing the statistical significance of observed phenomena or patterns requires the definition of a reliable and expressive background model (a.k.a. the null hypothesis). In particular, any sequence property that is a natural consequence of a well-understood mechanism should be captured by the background model so that it will generically appear in random sequences. Including these features in the background model will lead to an increased statistical significance for novel phenomena.
A classic exploratory approach starts with a random generation of sequences that share similar properties as a reference set of sequences. Various metrics can then be evaluated, possibly leading to diverging distributions of values within the random and reference sets. The significance of such an observation can be empirically assessed using classic statistical tools (Z-score, P-value … ). To implement such an approach in the context of mRNAs, one must restrict random sequences to synonymous sequences (i.e. the set of sequences that encode the same amino acid sequence). Such sequences can trivially be generated, uniformly at random, by simply choosing, for each amino acid, one of its alternative codons. Another constraint, essential when analyzing structural properties of RNA molecules, is the preservation of the overall dinucleotide frequencies (DFs). Such a constraint has been popular in the field of RNA bioinformatics following the study of Workman and Krogh (8) and builds on the rationale that preserving the DF maintains the feasibility of stacking base pairs, arguably the main contributor to RNA stability. Efficient methods have been proposed for such a model, drawing an analogy with the random generation of an Euler path in a De Bruijn-like graph, whose edges represent the dinucleotides (9,10).
When attempting to infer an evolutionary pressure from the observation of structural features within mRNA sequences, both constraints should ideally be satisfied. Unfortunately, the algorithms used to capture these two constraints rely on radically different principles and cannot be easily combined into an algorithm that would, at the same time, preserve the DF and an amino acid sequence. For this reason, Katz and Burge (11) proposed DiCodonShuffle, a heuristic algorithm based on a swapping procedure, which repeatedly exchanges codons while preserving the DF. As shown by Shabalina et al. (12), such a model preserves the periodic pattern of base pairing frequencies observed within coding regions of mRNAs. However, this method is only asymptotically uniform, and a bias toward certain sequences may be anticipated in samples produced in finite time (depending on the initial sequence and the number of swaps). Furthermore, as noted by the authors, the codon/DF preserving swaps may disconnect the underlying Markov chain, causing some legit sequences to be completely inaccessible by the sampling procedure. The impact of such limitations turned out to be more than purely theoretical, and we observed (see Figure 1) that the diversity (indicated by the sequence entropy) of generated sequences was much lower for DiCodonShuffle than for our truly uniform procedure, indicating a substantial bias in the method.
Figure 1.
Entropy comparison between sequences generated by DiCodonShuffle (11) and our probabilistic shuffling method. For both methods, 1000 sequences are generated, and, for SPARCS, the relative tolerance was set to 
. Sequences produced using DiCodonShuffle show much less diversity than those generated using SPARCS, either indicating a substantially limited accessibility of compatible sequences or a substantial bias (non-stationarity) owing to the bounded nature of their random walk.
In this article, we introduce Structural Profile Assignment of RNA Coding Sequences (SPARCS), a web server that predicts structured, unstructured and disordered regions in coding RNA sequences. Building on recent algorithmic advances (13,14), we developed a novel sampling algorithm that enables us to sample uniformly random sequences preserving the encoded protein sequence and the DFs. Combined with multiple classical metrics (e.g. base pairing probabilities and base pairing entropy), this sampling algorithm enables the calculation of accurate Z-scores and the prediction of strongly and weakly structured regions, along with disordered regions in exons—an insight that could not be fully achieved using previously existing sampling techniques.
SPARCS takes as input the coding region of an mRNA and proceeds in three steps. First, it generates a set of random sequences preserving the encoded amino acid sequence and the DF of the input sequence. Next, it uses RNAplfold (4) to predict thermodynamic properties (e.g. the sum of base pairing probabilities, base pairing entropy) of each sequence (input RNA and random samples). Lastly, we compare these metrics to calculate, for each position in the input sequence, a Z-score estimating the statistical significance of the secondary structure profile.
SPARCS outputs a graph showing the Z-score of the sum of base pairing probabilities and the base pairing entropy. It also provides a list of segments with predicted strongly and weakly structured segments. In addition, it also predicts disordered regions (i.e. regions with multiple suboptimal structures). To conduct further analysis, the user can also download the set of random sequences generated with SPARCS. The web server and the source code are available at http://csb.cs.mcgill.ca/sparcs.
METHOD OVERVIEW
The methodology of SPARCS is to combine the following procedures, starting from a given RNA sequence:
Use a novel statistical sampling algorithm to generate a set of random sequences that preserve both the encoded amino acid sequence and the DF of the input sequence.
Use RNAplfold (4) to compute thermodynamical properties of the input sequence and all random sequences generated.
Predict regions that are significantly structured, unstructured and disordered, based on a comparison of thermodynamic properties between input and random sequences.
Multivariate Boltzmann sampling of protein-coding sequences under DF constraint
Our approach builds on a multivariate Boltzmann sampling scheme, initially introduced in the context of enumerative combinatorics (13) and previously applied to control the GC-content of sampled RNA sequences within the RNAmutants software (14). This approach initially relaxes the goal of preserving the DF and draws sequences that strictly preserve the amino acid sequence while only achieving, on the average, the prescribed DF. A further rejection of unsuitable sequences, whose DFs differ too much from the targeted DF, filters the generated sequences, reestablishing the uniformity within the selected subset. The produced sequences therefore feature both correct DF and coding capacity while being generated with uniform probability.
Namely, let 
be an amino acid sequence, and 
be the vector of targeted DFs, the algorithm repeats the following steps until the desired number of samples is reached:
Draw a set of structures encoding S, with respect to a weighted distribution;
Estimate expected DF from sample;
Collect suitable sequences;
Update weights to match expected DF with target.
Weighted distribution
We associate a weight 
to each dinucleotide 
. This weight is inherited multiplicatively by any RNA sequence in RNA(S), the set of sequences compatible with a targeted amino acid sequence 
. This implicitly defines a probability distribution over RNA(S) where any RNA sequence w
RNA(S) has probability
 |
Importantly, any pair of sequences having an equal DF will also have equal relative probability. Therefore, generating a set of sequences and retaining only the sequences that do feature the targeted DF, gives an unbiased set of sequences. This property also holds for sequences generated using different weights; therefore, they can be gathered across different iterations of the adaptive sampling without introducing a bias.
Self-adaptive calibration of weights
The weighting scheme may be used to shift the expected number of occurrences of each dinucleotide, as illustrated by Figure 2. Let us denote by 
the number of copies of 
in a random sequence generated in the weighted model. For instance, setting 
to 0 will cancel the probability of any sequence featuring any occurrence of 
, and the expected number of 
will therefore drop to 0. Conversely, setting 
will only grant positive probability to sequences that maximize the number of copies of 
.
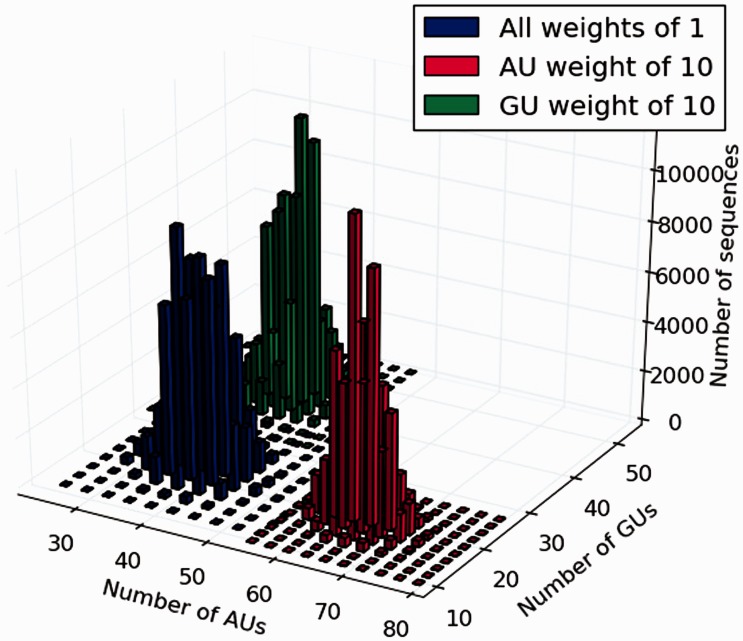
Figure 2.
Impact of weighted distribution on the number of occurrences of dinucleotides 
and 
. Either in the uniform distribution [
, blue] or setting larger weights to AU [π (AU) = 10, red] or GU [π (GU) = 10, green], 100 000 sequences compatible with an mRNA sequence encoding 179 amino acid (the first two exons of oskar gene in Drosophila melanogaster) were randomly generated. The concentration of the distribution and the shift in expected DF observed for different weights are the key ingredients of our method, allowing for an efficient approach based on adaptive sampling.
To find a weight that matches the expected DF with the targeted one, we use a heuristic strategy to figure out weights that achieve, on the average, the targeted DF. To that purpose, we initially set 
and, after each iteration of the adaptive sampling, we update each weight to 
, where 
is the expected value for 
, estimated from the sample. The process typically converges after a few iterations, leading to a good approximation of the best weight set.
Random generation
To draw a sequence of RNA(S) within the weighted distribution, one needs to choose a compatible codon for each of the n amino acid in 
. Such choices cannot be made independently, as the overlap between consecutive codons contributes to an additional dinucleotide, ultimately impacting the weight of a generated sequence.
Following the general principle of the recursive approach for random generation (15,16), we precompute the total weight 
of every sequence accessible on choosing some codon ending with a base 
at the i-th position. Such weights can be efficiently computed using dynamic programming based on
 |
where 
is the set of codons compatible with the i-th amino acid in 
, and 
is the last nucleotide of c. As the first amino acid (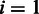
) is not preceded by any nucleotide, it must be treated slightly differently by setting 
Ø and π(Ø
During the random generation, these precomputations are used to assign probabilities to each of the possible codons such that each sequence is generated with respect to the weighted distribution. Namely, one picks a codon 
for the i-th amino acid, in the context of a previous nucleotide b, with probability
 |
The sampling algorithm starts on the first codon (
and 
Ø) and iterates over the amino acid sequence 
in increasing order, picking a codon with the aforementioned probabilities and updating b to the last nucleotide in the elected codon. After picking the last codon, it can be shown that the generated sequence is in RNA(S) and has probability, which is proportional to its weight (cf. Supplementary Material). The complexity of the algorithm is in 
time and space for sampling k sequences, each consisting of n codons.
Overall time and space requirement
We empirically observed, and could formally prove using Drmota theorem (17) for non-degenerate cases, that 
asymptotically follows a Normal law of mean in 
and standard deviation 
in 
. Furthermore, the covariations between numbers for different dinucleotides remain provably limited, and the joint distribution of the 
for every dinucleotide 
asymptotically follows a 16-variate Normal law. Consequently, the probability of generating a sequence having expected DF scales like 
, and it takes, on the average, 
attempts to obtain such a sequence. The average-case complexity of a rejection procedure for the uniform sampling is in 
time, after a linear time and space preprocessing.
Such a large time complexity may be impractical for real-life applications. However, if a small relative tolerance 
is allowed on every targeted dinucleotide count, leading any sequence w to be accepted if its dinucleotide counts are such that
 |
for every dinucleotide 
. Under this setting, the probability of acceptance only decreases like 
, where C is a constant, which only depends on the covariance matrix. In particular, if
 |
then the probability of acceptance becomes greater than 
, and the average-case complexity of the method becomes asymptotically equivalent to 
, at the cost of loss of uniformity, which is typically negligible, and can be efficiently corrected through a post-processing step (13).
Secondary structure prediction
The secondary structures of both the input mRNA sequence and random sequences are predicted using the RNAplfold software, distributed within the Vienna RNA package (18). RNAplfold considers all possible locally stable secondary structures for an input RNA sequence and calculates base pairing probabilities, assuming a Boltzmann equilibrium. As recommended by Lange et al. (19), we use a window size of 
nt (
, the span, is considered to be an optimal choice in the paper), and retain only those base pairs separated by at most W positions, and set a base pairing probability cut off threshold to 0.1.
Characterization of the structural profile
We screen the input sequence with a sliding window of W nucleotides and evaluate the standardized score (Z-score) for each window w on two classical metrics: 
is the sum of base pairing probabilities, and 
is the base pairing entropy. Let 
be the set of all valid base pairs in the sliding window and 
the probability of a base pair (i,j). We define the sum of base pairing probabilities as the sum of all base pairing probabilities assessed by RNAplfold within the frame such that
 |
The sum of base pairing probabilities estimates the stability of the secondary structures in the conformational landscape and thus quantifies the structural potential of the sequence.
Similarly, we define the base pairing entropy as the Shannon entropy of the base pairing probabilities such that
 |
The base pairing entropy aims to evaluate whether many alternate sub-optimal structures exist in the conformational landscape. For each nucleotide position, the Z-scores of all windows are averaged out to give the structural profile at a single nucleotide resolution.
We use these metrics to characterize a structural profile consisting in three, mutally exclusive, types of regions, based on two user-defined thresholds 
and 
:
Structured regions: A region is said to be ‘structured’ when the Z-score of the base pairing probability exceeds
and the Z-score of the base pairing entropy is lower than 
. This configuration indicates stable structures with few competitors.Unstructured regions: A region is ‘unstructured’ when the Z-score of the base pairing probability and the Z-score of the base pairing entropy are, respectively, lower than
and 
. In that case, the energy landscape is ‘flat’ with no dominant structure.Disordered regions: A region is ‘disordered’ when the Z-score of the base pairing probability and the Z-score of the base pairing entropy, respectively, exceed
and 
. This configuration suggests the presence of multiple stable and competing structures in the conformational landscape.
By default, SPARCS uses thresholds on the Z-score of 0.2 to discriminate high or low values. As illustrated in the next section, these settings aim to classify structural domains in the input sequences. Nonetheless, more stringent values can be specified, for instance if the user wishes to detect strongly (un-)structured regions.
Analysis of Ash1 gene in yeast
We illustrate the insights brought by SPARCS on the well-studied ASH1 gene in yeast. Using mutagenesis and comparative sequence analysis, four functional elements have been identified in this mRNA. Each of them has been shown to be sufficient to localize a reporter mRNA to the bud of dividing yeast cells (20). Of the four elements, three (E1, E2A and E2B) are located within the coding region of the mRNA.
Figure 3 shows the output of SPARCS for the ASH1 mRNA coding region. The Z-scores of the sum of base pairing probabilities are represented in magenta, and those of the base pairing entropy are in red. Structured, unstructured and disordered regions are displayed in green, blue and orange, and the functional elements E1, E2A and E2B are indicated at the bottom of the figure with yellow boxes. As aforementioned, here, we aim to detect structural domains and tendencies in the structural profile rather than focusing on the prediction of single elements. Therefore, we used a threshold of 0.
Figure 3.
Analysis of the protein-coding region of the ASH1 gene in yeast. The Z-scores of the base pairing probability are represented in magenta and those of the base pairing entropy in red. Structured, unstructured and disordered regions are displayed in green, blue and orange, and the functional elements E1, E2A and E2B are indicated at the bottom of the figure with yellow boxes. Dashed lines show the thresholds for determining high or low Z-score values.
Our results show that the E1 (positions 625–775) match predicted disordered and structured regions. The presence of disordered region at the beginning of the element could be explained by the presence of internal loops and alternate base pairings in the predicted secondary structure [see (21) and (20)]. Interestingly, the elements E2A (positions 1081–1199) and E2B (positions 1200–1447) are both surrounded by unstructured regions, possibly to avoid interactions between these elements. Noticeably, unlike the E2A element, the E2B element is particularly stable and structured. Outside these functional segments, we identify a large unstructured region (from 200 to 600) before the E1 element, which could help to stabilize the E1 element or, hypothetically, to facilitate translation. By contrast, we identify a strongly structured region between the E1 and E2 elements. This prediction could reveal a buffer that aims to prevent these elements from interacting. Finally, our analysis also suggests a structured region at the beginning of the sequence (positions 50–200). To the best of our knowledge, this region has not been experimentally studied, motivating further comparative studies.
SPARCS SERVER
The SPARCS web server takes an RNA/DNA sequence or a FASTA file as input. On validation, a first set of 1000 random sequences, preserving both the DF and encoded animo acid sequence of the input sequence, is generated. A second set of 1000 random sequences, called the uniform model, is generated to preserve only the amino acid sequence. The input sequence and the 2000 random sequences are then fed to RNAplfold to predict their base pairing properties. The Z-score is computed for a sliding window of user-specified width (defaulting to 150 nt), and all Z-scores are averaged for every position to evaluate the statistical significance of the secondary structure profile.
SPARCS finally outputs a single Z-score plot based on our metrics: sum of base pairing probabilities, base pairing entropy, structural potential region, unstructured potential region and disordered potential region. The dashed line(s) indicates the Z-score thresholds for the sum of base pairing probabilities and base pairing entropy, respectively. Users may specificy custom thresholds for both of the base pairing probability and base pairing entropy metrics.
SPARCS runs on a server hosted at McGill University, which has eight cores and has a total of 63 GB of memory. Each core is an Intel(R) Xeon(R) CPU X5570 at 2.93 GHz, with 8192 KB cache. Figure 4 shows the overall runtime on the server as a function of the mRNA length, for mRNA sequences ranging from 200 to 1000 nt, and reveals a linear trend.
Figure 4.
Typical runtime of SPARCS for sequence lengths varying from 200 to 1000 nt.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR online: Supplementary Methods.
FUNDING
IRCM masters scholarship (to Y.Z.); Natural Sciences and Engineering Council of Canada [NSERC RGPIN 386596-10 to J.W.]; Fonds de Recherche Nature et Technologies du Québec [FQRNT 2012 PR-146375 to J.W.]; Canadian Institute of Health Research [CIHR, operating grant #MOP-230355 to E.L.]; and the French Agence Nationale de la Recherche through the MAGNUM project [ANR 2010 BLAN 0204 to Y.P.]. Funding for open access charge: NSERC of Canada [NSERC RGPIN 386596-10 to J.W.].
Conflict of interest statement. None declared.
REFERENCES
- 1.Chen H, Blanchette M. Detecting non-coding selective pressure in coding regions. BMC Evol. Biol. 2007;7(Suppl. 1):S9. doi: 10.1186/1471-2148-7-S1-S9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Kertesz M, Wan Y, Mazor E, Rinn JL, Nutter RC, Chang HY, Segal E. Genome-wide measurement of rna secondary structure in yeast. Nature. 2010;467:103–107. doi: 10.1038/nature09322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lin MF, Kheradpour P, Washietl S, Parker BJ, Pedersen JS, Kellis M. Locating protein-coding sequences under selection for additional, overlapping functions in 29 mammalian genomes. Genome Res. 2011;21:1916–1928. doi: 10.1101/gr.108753.110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bernhart SH, Hofacker IL, Stadler PF. Local RNA base pairing probabilities in large sequences. Bioinformatics. 2006;22:614–615. doi: 10.1093/bioinformatics/btk014. [DOI] [PubMed] [Google Scholar]
- 5.Rabani M, Kertesz M, Segal E. Computational prediction of RNA structural motifs involved in posttranscriptional regulatory processes. Proc. Natl Acad. Sci. USA. 2008;105:14885–14890. doi: 10.1073/pnas.0803169105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Watts JM, Dang KK, Gorelick RJ, Leonard CW, Bess JW, Swanstrom R, Burch CL, Weeks KM. Architecture and secondary structure of an entire hiv-1 rna genome. Nature. 2009;460:711–716. doi: 10.1038/nature08237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Spitale RC, Crisalli P, Flynn RA, Torre EA, Kool ET, Chang HY. RNA shape analysis in living cells. Nat. Chem. Biol. 2013;9:18–20. doi: 10.1038/nchembio.1131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Workman C, Krogh A. No evidence that mRNAs have lower folding free energies than random sequences with the same dinucleotide distribution. Nucleic Acids Res. 1999;27:4816–4822. doi: 10.1093/nar/27.24.4816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Fitch WM. Random sequences. J. Mol. Biol. 1983;163:171–176. doi: 10.1016/0022-2836(83)90002-5. [DOI] [PubMed] [Google Scholar]
- 10.Altschul SA, Erickson BW. Significance of nucleotide sequence alignments: a method for random sequence permutation that preserves dinucleotide and codon usage. Mol. Biol. Evol. 1985;2:526–538. doi: 10.1093/oxfordjournals.molbev.a040370. [DOI] [PubMed] [Google Scholar]
- 11.Katz L, Burge CB. Widespread selection for local RNA secondary structure in coding regions of bacterial genes. Genome Res. 2003;13:2042–2051. doi: 10.1101/gr.1257503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Shabalina SA, Ogurtsov AY, Spiridonov NA. A periodic pattern of mRNA secondary structure created by the genetic code. Nucleic Acids Res. 2006;34:2428–2437. doi: 10.1093/nar/gkl287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Bodini O, Ponty Y. DMTCS Proceedings—AOFA’10. 2010. Multi-dimensional boltzmann sampling of languages; pp. 49–64. [Google Scholar]
- 14.Waldispühl J, Ponty Y. An unbiased adaptive sampling algorithm for the exploration of RNA mutational landscapes under evolutionary pressure. J. Comput. Biol. 2011;18:1465–1479. doi: 10.1089/cmb.2011.0181. [DOI] [PubMed] [Google Scholar]
- 15.Wilf HS. A unified setting for sequencing, ranking, and selection algorithms for combinatorial objects. Adv. Math. 1977;24:281–291. [Google Scholar]
- 16.Denise A, Ponty Y, Termier M. Controlled non uniform random generation of decomposable structures. Theor. Comput. Sci. 2010;411:3527–3552. [Google Scholar]
- 17.Drmota M. Systems of functional equations. Random Struct. Algorithms. 1997;10:103–124. [Google Scholar]
- 18.Lorenz R, Bernhart S, Honer zu Siederdissen C, Tafer H, Flamm C, Stadler P, Hofacker I. Viennarna package 2.0. Algorithms Mol. Biol. 2011;6:26. doi: 10.1186/1748-7188-6-26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Lange SJ, Maticzka D, Möhl M, Gagnon JN, Brown CM, Backofen R. Global or local? predicting secondary structure and accessibility in mRNAs. Nucleic Acids Res. 2012;40:5215–5226. doi: 10.1093/nar/gks181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Chartrand P, Meng XH, Huttelmaier S, Donato D, Singer RH. Asymmetric sorting of ash1p in yeast results from inhibition of translation by localization elements in the mRNA. Mol. Cell. 2002;10:1319–1330. doi: 10.1016/s1097-2765(02)00694-9. [DOI] [PubMed] [Google Scholar]
- 21.Gonzalez I, Buonomo SB, Nasmyth K, von Ahsen U. ASH1 mRNA localization in yeast involves multiple secondary structural elements and Ash1 protein translation. Curr. Biol. 1999;9:337–340. doi: 10.1016/s0960-9822(99)80145-6. [DOI] [PubMed] [Google Scholar]