Probabilistic Exposure Analysis for Chemical Risk Characterization

Abstract

This paper summarizes the state of the science of probabilistic exposure assessment (PEA) as applied to chemical risk characterization. Current probabilistic risk analysis methods applied to PEA are reviewed. PEA within the context of risk-based decision making is discussed, including probabilistic treatment of related uncertainty, interindividual heterogeneity, and other sources of variability. Key examples of recent experience gained in assessing human exposures to chemicals in the environment, and other applications to chemical risk characterization and assessment, are presented. It is concluded that, although improvements continue to be made, existing methods suffice for effective application of PEA to support quantitative analyses of the risk of chemically induced toxicity that play an increasing role in key decision-making objectives involving health protection, triage, civil justice, and criminal justice. Different types of information required to apply PEA to these different decision contexts are identified, and specific PEA methods are highlighted that are best suited to exposure assessment in these separate contexts.

Exposure assessment provides key input to the process of source-exposure-dose-response-risk characterization that addresses questions concerning the degree to which environmental contaminants pose risks to human and/or ecological health (NRC, 1983, 1994; USEPA, 1997a). A variety of probabilistic risk analysis (PRA) models and methods may be used to characterize uncertainty or lack of knowledge (U); interindividual variability (V) in a specified population at risk; and intraindividual, spatial, temporal, or other non-interindividual types of variability (W) in exposures pertaining to a defined exposure scenario. A probabilistic framework calling for distinctions among uncertainty and different types of “variability” may seem unwieldy, but such systematic distinctions pertaining to inputs (such as exposure characterization) to risk analysis are generally needed to properly characterize the U, the V, and joint U-and-V (JUV) dimensions of predicted risk (Bogen, 1990, 1995; Bogen and Spear, 1987; Cullen and Frey, 1999; NRC, 1994; USEPA, 1997b). Thus to the extent JUV characteristics of predicted risk are relevant to risk management decision making, probabilistic exposure assessment (PEA) must reflect U-, V-, and W-characteristics of exposures that contribute to predicted risk. Examples of U, V, and W that arise in PEA are:

• Uncertainty (U): Uncertainty in the rate at which specific untested chemicals are taken up percutaneously into systemic distribution through human skin; statistical error in the estimated geometric mean and standard deviation of pollutant concentrations in air; model-specification error associated with air-concentration profiles made by alternative air-dispersion models applied to a specific chemical-release scenario; alternative plausible chemical-release scenarios;

• Interindividual variability (V): Interindividual differences in physical and pharmacokinetic characteristics (e.g., gender, body weight, rates of breathing, and metabolism) that result in different corresponding magnitudes of chemical contact or uptake; person-to-person differences in behavioral scenarios (daily shower/bath duration, years of residency at a given location, dietary preferences) that yield differential exposures in a population at risk; person-to-person differences in behavioral scenarios (daily shower/bath duration, years of residency at a given location, dietary preferences) that govern route-specific exposures;

• Other variability (W): Within-person differences in behavior patterns, physical characteristics and pharmacokinetics that occur during different (i.e., neonatal, infant, childhood vs. adult) periods of life; short-term and seasonal variations in meteorological conditions that affect exposure; temporal patterns in prevailing environmental concentrations of specified chemical contaminants (e.g., lead in air, pesticides in crop residues, etc.).

Specific analysis of W may be required in exposure assessment, to distinguish and characterize its U and V dimensions usefully, and/or to provide information needed to model the (dose-response) relation of exposure to risk. For example, although duration-specific time-weighted average air concentrations are often used to assess potential respiratory hazards posed by airborne toxic chemicals, substantial concentration fluctuation (i.e., temporal variability W) that occurs over biologically relevant time periods may be vital when toxicity is better predicted by peak than by mean exposure levels. Likewise, intraindividual variability (W) of inhalation rates per unit body weight over a lifetime may be required to properly assess lifetime average inhalation doses (Salem and Katz, 2006).

Specific methods appropriate to characterize these dimensions of risk, and each of its components, depend on the type of decision to be supported. Section “Decision-Making Paradigm Determines How PRA Should Be Applied for Pea” focuses on the development of different decision contexts. Section “PRA Methods Used In Exposure Assessment” reviews the range of PRA methods applied to enable PEA. Recommendations for improved PEA methodology are presented in section “Conclusion.” Approaches used in the dose-response portion of a chemical assessment may critically affect whether and how PRA is applied in exposure assessment.

DECISION-MAKING PARADIGM DETERMINES HOW PRA SHOULD BE APPLIED FOR PEA

By making explicit the inferences, preferences, facts, and assumptions concerning risk-related information bearing on a decision problem, PRA can facilitate decisions in a variety of different contexts (Parkin and Morgan, 2006; Raiffa, 1968). Problems and progress on technical issues in applying PRA to exposure assessment addressed below are best understood by reference to underlying purposes for which such assessments are conducted. In a research-oriented assessment, comprehensive aspects of exposure and risk may be of interest. More generally, however, the purpose being served tends to define the relevance and utility of different risk-related aspects of exposure information to be characterized. The contribution of PRA to exposure assessments thus depends on how such assessments in turn contribute to solving different kinds of decision-making problems. In practice, most such decisions address four primary decision-making goals: (1) environmental health protection, (2) environmental health triage (as defined below), (3) civil justice, and (4) criminal justice. The decision-making processes used to address these goals may be thought of as decision “paradigms,” because they each entail a number of unique attributes that imply related sets of legal and policy constraints and values, which in turn, imply corresponding sets of characteristic decision-optimization rules. The application of these rules may be facilitated, in turn, by different types of information bearing on U and V in exposure, the corresponding predicted risk, or both. Thus, decision criteria with respect to U and V tend to differ in different decision-making contexts. U and V are present in both the costs and benefits that characterize the range of alternatives being assessed in any decision paradigm.

PRA in Exposure Assessment to Support Environmental Health Protection

The classic paradigm in which PRA is applied to exposure assessment is to develop environmental health protection goals. These goals support the pursuit of public health; environmental protection, regulation, and remediation; occupational health and industrial hygiene; radiation safety; sanitary engineering; food and consumer product safety; regulatory toxicology; and regulatory compliance. The major purpose of these endeavors is protection against human and ecological harm due to toxic environmental exposures. Because public policies developed for managing risks are generally precautionary, rather than being focused on accurate predictions, PEA used to develop these policies must facilitate the characterization of “upper bound” (albeit not unreasonably conservative) estimates of risk (Bogen, 2005; USEPA, 2005a). Inference gaps tend to be bridged by “conservative” “uncertainty” or “safety” factors that err on the side of safety (NRC, 1983), using feasibility and/or cost constraints (as applicable) defined by statute (Bogen, 1982).

Notable exceptions to this generalization occur in the context of regulatory efforts to comply with statutory requirements (Bogen, 1982) or other conventions that involve explicit weighing of costs and benefits. In the field of ionizing radiation protection, for example, a quantitative, predictive approach to PEA (radiation dosimetry) and associated radiological PRA has emerged as a result of scientific deliberation and regulatory processes (Patton, 2000).

Another exception involves quantitative exposure and risk assessments done over the last quarter-century to support decisions about whether to retain or revise the National Ambient Air Quality Standards (NAAQS). The 2007 final rulemaking for the revised ozone 8-h NAAQS included reference to a PEA using the Air Pollution Exposure model. A PRA was also conducted for the PM_2.5 NAAQS (2006) rulemaking. The resulting risk estimates were included in the OAQPS staff paper and discussed in the Federal Register, but were not relied upon to select specific standards (USEPA, 2003, 2006). In its process of reviewing the PM standards, probabilistic risk estimates were considered by the U.S. Environmental Protection Agency (USEPA) as a major component in the recent decision on the PM_2.5 standards. The PM_2.5 risk assessment relied directly on health-effect estimates that were based on epidemiological studies and included statistical uncertainty based on the standard errors reported in those health-effect estimates. Also, a recent USEPA effort to carry out expert elicitation on the relation of annual mortality to annual incremental change in PM_2.5, for example, used expert elicitation to develop distributional information about dose/response to inform benefits analyses (Industrial Economics, 2006). Probabilistic exposure analysis is not generally used when state and local agencies develop State Implementation Plans (SIPs) that lay out implementation measures to attain the NAAQS. Although there is nothing to prevent state or local agencies from including this type of analysis in their SIPs, there are also currently no specific incentives for doing so.

Prior to the advent of major environmental legislation passed starting in the late 1960′s and early 1970′s, regulatory protection from exposure to harmful environmental agents through the application of quantitative, predictive toxicology was largely restricted to the effects of food additives, drugs, and occupational exposures, and uncertainties were addressed primarily by application of conservative assumptions and safety margins. The exception in the field of ionizing radiation protection was noted above. In the mid-1970′s, USEPA adopted a regulatory position that, absent specific data indicating otherwise, environmental chemical carcinogens would be assumed to have a no-threshold dose-response relation analogous to that assumed for ionizing radiation, in view of the plausible role that dose-induced irreversible somatic mutations could play in both chemical and radiogenic cancer (Albert et al., 1977; USEPA, 1976). The regulatory development and adoption of quantitative exposure and risk assessment methods pertaining to a host of environmental chemical exposure scenarios began soon thereafter in the United States, providing a key source of decision problems addressed by increasingly quantitative methods used in the developing fields of environmental exposure and risk analysis (Bogen, 1982; Burmaster and Anderson, 1994; NRC, 1983, 1994; USEPA, 1997b).

PEA methods to support PRA applications to environmental health protection are used to design, or comply with, protective limits on environmental concentrations and exposures, where these methods provide an objective quantitative framework with which to identify acceptable upper bounds with respect to U and V in corresponding predicted risk (Bogen and Spear, 1987; NRC, 1994). Because by definition, upper bounds on V in exposure and associated risk model corresponding heterogeneity, these may be used to express quantitative limits on associated inequity; whereas because those on U model lack of certainty, they may be used to express quantitative goals concerning protection and prevention. A key constraint is that PEA methods used in this context are generally required, as a practical matter, to be reasonably transparent both to understand and to implement. Overly complex methods tend not to be adopted when simpler ones are available that perform adequately in exposure assessments supporting health protection. Application of PEA methods in this context raises a variety of policy and legal issues concerning appropriate interpretation of the output of these analyses (Poulter, 1998).

PRA in Exposure Assessment to Support Environmental Health Triage

Environmental health triage decisions are required when—due to resource constraints and/or exposure-scenario complexity—trade-off decisions must be made about the method, strategy, and/or extent of mitigation or remediation of environmental contamination to be undertaken (Bogen, 2005). A requirement for this decision paradigm may arise ex post facto (or ex ante, for planning purposes) to address situations such as emergency response, homeland security, and military course-of-action problems (NRC, 2004). Exposure and risk analysis needs to be predictive (unbiased) in order to be most effective at ensuring that any triage decisions that must be faced are decisions that minimize expected casualties to the extent feasible (NRC, 1994, 2004). Specifically, emergency and military medical personnel must routinely make triage decisions, which attempt to minimize losses by efficiently allocating limited resources after assessing competing exposures, risks and benefits as accurately as feasible. In contrast, those engaged in assessing and controlling chemical risks have historically operated in an environmental health protection decision-making paradigm, primarily in the fields of occupational and public health, industrial hygiene, sanitary engineering, environmental and regulatory toxicology, with historical emphasis (appropriately) on protection and prevention through exposure limitation—applications that do not routinely involve explicit, life-and-death triage decisions (see “PRA in Exposure Assessment to Support Environmental Health Protection”), rather than on accurate (unbiased) prediction of adverse consequences when required to make effective trade-off decisions (NRC, 1994, 2000, 2004).

Recent homeland-security situations call attention to the fact that methods and resources—analogous to those well established and readily available to support occupational and environmental health protection—do not yet exist specifically to support environmental health triage decisions, but need to be developed to respond effectively to complex scenarios involving large-scale chemical exposures (Bogen, 2005). Methods currently in place for such scenarios either fail to address U probabilistically, or have nonpredictive designs that generally limit meaningful support only to environmental health protection goals, or both. To effectively support triage decisions, PRA methods for exposure assessment must facilitate characterizing the degree of accuracy and precision (i.e., limiting U) in estimated population risk (i.e., in the estimated number of casualties). Time- and population-averaged values of V in exposure can suffice to estimate expected casualties and related error bounds in risk assessments that involve only linear or nearly linear dose-response models (Bogen, 1990; Bogen and Spear, 1987).

PRA in Exposure Assessment to Support Civil Litigation

In Europe, a civil law tradition tends to defer more to “expert” authorities, and to rely heavily on preemptive precautionary regulation rather than on ex post facto liability assignment through litigation. However, a “more likely than not” standard of evidence for harm causation is required by U.S. common law to attain remedies in civil litigation. The U.S. civil litigation model increasingly allows statistical and probabilistic evidence to play a role in presenting legal evidence of harm causation. Because current rules for admissibility of scientific evidence in the United States require a plaintiff to establish and quantify chemical exposure sufficient to cause the alleged harm, chemical exposure and dose reconstruction is becoming a standard technique to evaluate plaintiff claims in toxic tort litigation, particularly when there is substantial uncertainty in exposure history (Brannigan et al., 1992; Finley, 2002). In this decision context, PRA analysis can be used to help estimate the likelihood that one or (any specified number) of cases of harm resulted from a specified exposure of a defined person or class, in direct relation to the burden of proof at issue.

PRA in Exposure Assessment to Support Criminal Prosecution

Criminal prosecution (e.g., for individual or corporate criminal negligence resulting in harmful environmental contamination) in the United States requires a “beyond a reasonable doubt” (forensic) standard of evidence, which increasingly involves or requires probabilistic evidentiary analysis and counter-analysis by plaintiff and defendant (Aitken, 1995). Application of PRA methods to exposure assessment becomes critical in this context, when evidence concerning causality or motive involves uncertain levels of toxic exposure. Again, a key limitation on PRA methods used in this context is that these methods must be readily understood by a lay jury. In this decision context, V may be limited to a specific harmed person or subpopulation, and PRA methods may assist in the design or interpretation of forensic evidence.

PRA METHODS USED IN EXPOSURE ASSESSMENT

Background and History

Explicit techniques for addressing uncertainty and variability in exposure and risk analysis have been introduced in the United States during the past 30–40 years. Probabilistic techniques, in particular, were boosted into the spotlight with the publication of the U.S. Atomic Energy Commission–sponsored “Reactor Safety Study” (U.S. Nuclear Regulatory Commission (USNRC), 1975). Prior to the Study's release, the NRC relied on qualitative safety assessments and goals; however, the Study extended the analysis by including event trees and potential accident scenarios that were assigned probabilities. The step of assigning probabilities transformed the endeavor, but not without introducing significant tension (Lewis et al., 1978). Probabilities were estimated based on both objective information such as historic records, and subjective information such as expert judgment, leading to criticism about their soundness, subjectivity, and reproducibility (Cooke, 1991). Concerns about the degree of uncertainty encompassed in probabilistic judgments, both regarding a potential excess of risk conservatism and a potential lack of such, continue to evoke these early criticisms. In addition, the practice of assigning probabilities to potential adverse consequences stemming from processes, designs, and decisions has continued to evolve despite the challenges.

In 1983, the National Research Council (NRC) outlined the basic steps used to address human health risk analysis in a seminal publication known as “the Red Book,” intended to foster a more systematic, standardized approach to the process of environmental risk management by regulatory agencies (NRC, 1994). The recommended approach involved scientific steps of hazard identification, exposure assessment, dose-response assessment, and risk characterization, which together contribute to a final risk management step that (in accordance with applicable, albeit typically terse and generic, statutory language) renders a societal judgment concerning risk acceptability (NRC, 1983). The report did not mention “variability” at all, and addressed uncertainty primarily through its description of key gaps in knowledge that often impede the process; in order to reach decisions, each such gap had to be surmounted by adopting a corresponding “inference bridge,” typically in the form of a health-conservative default assumption (NRC, 1983).

During the late 1970′s and early 1980′s, spurred by application computer-intensive methods to characterize uncertainty in the field of nuclear safety (discussed above), increased accessibility among the environmental health research community to computational power offered by small-scale (e.g., desktop) computers generated interest in and exploration of more explicit ways to analyze and characterize uncertainty in a wide range of fields, including PEA and PRA. As concepts and recommendations for PEA and PRA methodology were developed (e.g., Bogen, 1990, 1995; Bogen and Spear, 1987; Burmaster and Anderson, 1994; Burmaster and von Stackelberg, 1991; Cox and Baybutt, 1981; Cullen and Frey, 1999; Seiler, 1987; Smith and Charbeneau, 1990; Price and Chaisson, 2005; Price et al., 2003; Frey and Zhao, 2004), scientific, government and international organizations considered these advances and developed guidance for PEA-related U and V analysis (International Programme on Chemical Safety [IPCS], 2000; NRC, 1994, 1996; USEPA, 1985, 1992, 1995; WHO, 2008). A catalyst of transition to this new approach was the clear emphasis placed on U, V, and JUV in exposure and risk analysis by the NRC (1994) “Blue Book” that updated its 1983 “Red Book” mentioned above, based on analytic nomenclature and methods developed specifically to facilitate and communicate such analysis (Bogen and Spear, 1987; Bogen, 1990). In particular, Bogen and Spear (1987) showed how the relationship between JUV in estimated exposures and other inputs used to model individual risks, to U in individual risk, and to U in estimated population risk, can be characterized only if U- and V-related distributions used to characterize these inputs are treated separately in PEA and PRA (e.g., using a two-stage or “nested” Monte Carlo approach). This requirement motivated the NRC (1994) recommendation to distinguish U- from V-related distributions systematically in PEA and PRA.

The combined impact of the new focus on detailed quantitative JUV characterization of toxic exposures and risk has facilitated numerous and growing applications of PEA (e.g., Bosgra et al., 2005; Chen et al., 2007; Citra, 2004; Cullen, 1995, 2002; Driver et al., 2007; Hart et al., 2003; Price and Chaisson, 2005; Slob, 2006; USEPA, 2001; Zartarian et al., 2000). PEA is supported by databases such as the Exposure Factors Handbook (USEPA, 1997a), which includes data and distributions representing variability in many exposure factors (detailed in section “Specifying Variability and Uncertainty in Model Inputs”), along with some information that can be used to characterize uncertainty in these estimates. Probabilistic risk assessment has been adopted in the United States for evaluating food safety (Gibney and van der Voet, 2003; U.S. Food and Drug Administration and U.S. Department of Agriculture [FDA and USDA], 2003). Similarly, PEA methods have increasingly been adopted, developed, and applied worldwide (e.g., IPCS, 2000; Mekel and Fehr, 2001; NRC, 2000; Öberg and Bergbäck, 2005; Okada et al., 2008; U.K. Interdepartmental Liaison Group on Risk Assessment [UK ILGRA], 1996, 1999; WHO, 2008).

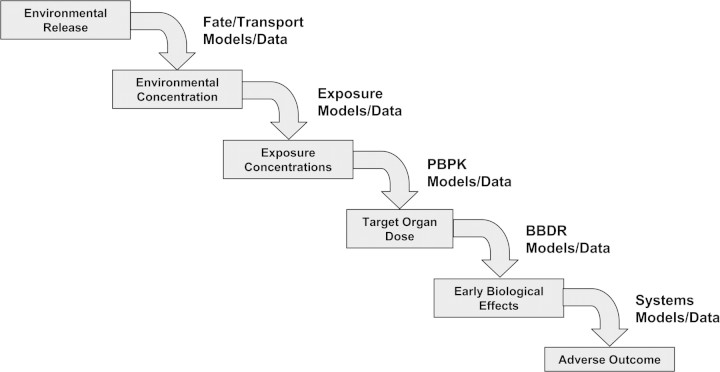
Increasingly routine applications of probabilistic approaches to exposure assessment have been driven by diverse factors, including the rise of toxicological tests that generate large amounts of data (e.g., genomics, proteomics, and metabonomics), the increasing cost of traditional approaches, increased use of physiologically based pharmacokinetic (PBPK) models, new exposure assessment software tools (van Veen, 1996), and increasing reluctance to use animals in testing. By this new approach (Fig. 1), PEA aims to model the source-to-outcome chain using a series of linked models that represent various steps, including physical and chemical processes in the environment, human behavior, and pharmacokinetic and pharmacodynamic processes (USEPA, 2005b). Such models can address the variation in substance concentrations in space and time, and the variation in human behavior, physiology, and dose response. Tools developed for assessing model- or parameter-specific U or V can be applied to each model separately or in combination, though care must be taken to interpret U and V in resulting PEA/PRA characterizations appropriately (Bogen, 1990; Bogen and Spear, 1987; Burmaster and Anderson, 1994; Cullen and Frey, 1999; NRC, 1994; USEPA, 1997a,b).

FIG. 1.

Modeling the chain of sources to outcome (USEPA, 2005b).

Not all exposure or risk assessments need to proceed in a sequential fashion through each link in series, as shown in Figure 1. Decisions about appropriate ambient air or water quality standards, for example, focus on relating exposures to ambient concentrations rather than to sources. Likewise, environmental epidemiology studies often focus on the relationship between ambient concentrations and a measure of health-effect response, without explicit models, or even characterization of intermediate (exposure to dose to effect) steps involved. To develop control strategies that will reduce ambient concentrations, and therefore exposures, source-to-concentration as well as the concentration-to-exposure relationships must be quantified. In particular, more rigorous quantitative characterizations of W and/or V in exposure (as well as in other inputs used to model risk) are generally needed for unbiased assessments whenever risk is modeled as a substantially nonlinear function of exposure and dose. For example, when acute toxicity is predicted better by peak than by time-weighted average exposure concentrations, PEA used to model this endpoint must reflect U, V, and W as these characteristics pertain to the more mechanistically relevant (biologically effective) peak-dose metric. Likewise, if mode of action considerations indicates that a nonlinear function of exposure (and of associated dose rate) best models cancer risk posed by a particular chemical, short-term, less-than-lifetime exposure estimates would be more appropriate than lifetime average daily dose to assess cancer risk in this case (USEPA, 2005a).

Methods for Estimating Uncertainty and Variability in Exposures

No single approach to dealing with U and V is applicable across the broad range of decision contexts discussed above, especially in light of the quality and quantity of available information. Empirical measurements, subjective judgments, model results, historical records, and other information sources all may contribute to our ability to represent uncertainty and variability in an exposure scenario, model input, estimate, or analysis. An array of techniques for addressing U and V exists, including both qualitative and quantitative approaches, and spanning the spectrum from simple bounding to sophisticated numerical analysis. The context of the analysis can inform selections from among these available techniques.

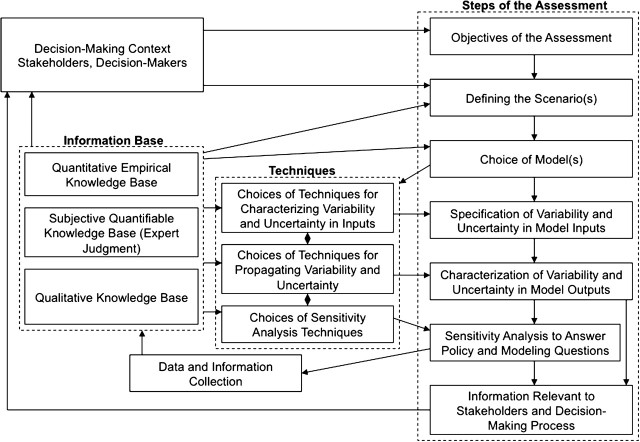
Figure 2 summarizes the relationship among key elements of a risk assessment, including the decision-making context, knowledge base, modeling steps, and choice of techniques. The stakeholders and decision makers typically would define the key objectives of the assessment, as well as the exposure scenario to be assessed. For example, what key subgroups should be included, and what exposure pathways might be of concern to the general public or an exposed population that is demanding action? Of course, the ability to define the scenario will also depend on the information base. The choice of models for the risk assessment will be influenced by the scenario to be analyzed and the availability of information. The choice of techniques for characterizing variability and uncertainty in inputs, propagating such information through a model, and performing sensitivity analysis will depend in part on the information basis and in part on compatibility among these three types of techniques, as well as the characteristics of the model(s) themselves.

FIG. 2.

Simplified influence diagram of the decision-making context, information base, techniques, and steps in a typical risk assessment modeling approach.

PEA should produce various types of information of direct relevance to decision makers and stakeholders. On receiving such information, decision makers and stakeholders may wish to refine or change the objectives of the assessment, leading to another iteration of the basic definition of the problem (discussed in more detail in section “Iterative Tiers of Analysis”). Likewise, the results of the sensitivity analysis might be used to determine key areas of uncertainty for which additional information is needed to reduce uncertainty. Although not shown explicitly, other types of feedback can occur. Furthermore, although the information base is shown as providing input to decision makers and stakeholders, as well as to the assessment itself, the manner in which the information is interpreted and used can be quite different. It cannot be overemphasized that iterative collaboration among exposure and hazard/toxicology professionals working on a specific assessment, starting as early as feasible in the process, can effectively facilitate effective problem formulation and issue identification.

Qualitative analysis.

In situations characterized by fundamental gaps in understanding, for which the time frame or other constraints rule out the acquisition of additional information, it may not be possible to assess exposure and risk quantitatively. However, a qualitative discussion of major assumptions, sources of uncertainty, and their projected impact on the analysis can contribute great insight even in the absence of quantitative treatment. In some cases, it may be possible to develop plausible scenarios and/or decision contexts to qualitatively represent different assumptions about unresolved scientific uncertainty or future events. For example, the International Panel on Climate Change has developed future emissions pathways (i.e., scenarios representing the future use of fossil fuel by the world's population), which are used to drive global climate models (GCMs) (International Panel on Climate Change [IPCC], 2001). The GCMs predict global temperature and precipitation in a future climate conditional on any single assumed emissions scenario. It may be difficult to assign probabilities to alternative possible futures for political, scientific or other reasons; however, this is often done as a practical matter, if only to compare scenario-specific outcomes. Alternative scenarios may be combined assuming equal likelihoods, or by using more sophisticated weighting schemes (Giorgi and Mearns, 2002, 2003; Jones, 2000; Tebaldi et al., 2004, 2005; Markoff and Cullen, 2008; Wigley and Raper, 2001).

Qualitative analysis methods can be classified as unstructured, partially structured, or structured (Frey et al., 2003a). In all three cases, the goal is to develop not only a judgment or estimate of uncertainty, but to understand the basis for that judgment or estimate. Qualitative methods are based on judgments of epistemic status, and they are based on some type of framework for rational argument analysis. In the Classical School, there are formal rules for such analysis (Brown, 1988). In the Dialogical School, rules are also important, but there is more explicit acknowledgment of the possibility of rational disagreement over what the rules might be, and regarding when they should be applied (Bernstein, 1983). Qualitative analysis methods can be used to structure discourse on a particular topic, and they can also be used to make inferences regarding “weight of evidence.” If results of a qualitative analysis (e.g., for the purpose of scenario-identification, model-selection, or parameter-bounding) are to be used to conduct PEA, each such result must ultimately be quantified, at least on a conditional basis, in order for it to have any direct effect on the PEA output.

Quantitative analysis.

Quantitative PEA requires treatment of model uncertainty in addition to relevant exposure scenarios. Each of these requirements is discussed below.

Model Uncertainty. Models are used in all facets of exposure and risk analysis to describe natural and technological systems from which risks emanate, to represent the fate and transport of agents of risk through the environment, to describe interactions of human and other biological systems with agents of risk, and to estimate the ultimate effects of these interactions. Modeling always introduces U to a PEA, because mathematical models are by definition tools used to approximate reality. This source of U may be quite substantial relative all other sources of U characterized in a PEA (Rojas et al., 2008). Key model-U concepts include precision, accuracy, validation, extrapolation, and numerical resolution (see Cullen and Frey, 1999; Frey et al., 2003a, b). Although model validation may be pursued by comparing predictions against observations, a model that predicts accurately or precisely for one setting or purpose may perform poorly for another. For example, a steady-state compartmental model, which may be adequate for predicting long-term average contaminant concentrations distant from a clean-up site, may be inadequate for short-term predictions of average concentration close to the site because of its failure to reflect dynamic, daily fluctuations that drive short-term contaminant transport among media (Cullen, 2002). Model U also arises whenever there are multiple plausible model forms or parameterizations of a single model.

To address model U, analysts may: assign probabilities to each alternative; explore updating of mechanistic models using Bayesian techniques to combine individual or multiple datasets with underlying model structures (Bates et al., 2003); formally assess the relative merits of different model variables by empirical or fully Baysean variable-selection methods applied to single, multiple or fully nested models, for example, using tree models, graphical models, or Markov Chain Monte Carlo methods employing Metropolis-Hastings, Gibbs, reversible-jump, path-ratio, or ratio-importance single-chain sampling algorithms (reviewed by Clyde and George, 2004); or develop scenarios, each of which adopts a single model structure, form, or parameterization as true. These approaches may transform model uncertainty into input or parameter uncertainty, and vice versa. Logical ambiguity between model and parameter uncertainty is a basis for questioning the value of PEA or PRA methods and policies premised on the existence of such a distinction (see NRC, 1994, p. 187, footnote 4). However, the distinction is useful at least insofar as it motivates model improvement.

Scenarios. In analyzing risks posed by human exposures to environmental chemicals, assumptions must be made regarding the exposure scenarios within which chemicals, emission sources, exposed subpopulations, pathways of pollutant transport (e.g., air, groundwater), activity patterns and locations of exposures, exposure pathways (e.g., inhalation, ingestion, dermal), and other considerations (Cullen and Frey, 1999). Failure to properly account for significant factors that affect real-world exposures may lead to substantial biases. For example, if the primary means of exposure to a particular chemical is based on long-range transport and indirect exposure pathways, such as ingestion of local meat and dairy products, but the analysis fails to account for this, then exposure may be severely underestimated.

There are no rigorous methods for dealing with U pertaining to alternative plausible scenarios that may pertain to a specific decision problem (e.g., which scenarios will most likely arise during lifetime exposures to a defined population), A collaboration of persons with varying perspectives on a problem can brainstorm to identify the key dimensions necessary to specify a scenario (such as pollutants, transport pathways, exposure routes, susceptible subpopulations, averaging time, geographic extent, time periods, activity patterns, etc.), and then make decisions regarding how each of these dimensions will be addressed (Frey et al., 2003a). Such scenario U can be explored indirectly by comparing alternative scenarios or by estimating the contribution of individual pathways to total exposure. Often, it is not known a priori which pathways or other aspects of a scenario may be the most important, and resource limitations may dictate that effort be expended only on the most evidently important pathways. A tiered approach to such an analysis, starting with simple screening models and progressing to more refined (and accurate) models, can be used to iteratively evaluate the relative importance of different aspects of a scenario, and to exclude from further analysis those portions that contribute relatively little to total exposure, risk, costs, benefits, or other measures of concern. It is difficult to prove that all, or event the dominant, pathways contributing to potential exposure have been captured. A consensus-building process is thus typically used to define the ultimate scope of scenarios to be considered in PEA, informed by a downward trend toward a negligible magnitude in predicted contributions to exposure arising from consideration of additional scenarios.

Specifying variability and uncertainty in model inputs.

To allow U and V to be characterized in estimated exposures and associated assessment of toxic risk, variability and uncertainty must first be characterized systematically in model inputs (Bogen and Spear, 1987; NRC, 1994). This can be done using empirical approaches, judgment-based approaches, and methods based on underlying mechanisms. In reality, most distribution development of model inputs for application to exposure analysis combines multiple information sources, including judgment. The USEPA (1997a) Exposure Factors Handbook is key compilation of data and derived relationships that may be used to specify V (and to estimate some aspects of U) pertaining to various aspects of exposure, including sex-, age-, ethnicity-, season-, and/or time-of-day–specific reference values and/or distributions for: drinking water ingestion; soil ingestion; inhalation; body/dermal surface area and soil adherence, body weight, lifetime duration, food intakes (fruits and vegetables, fish and shellfish, meat and dairy products, grain products, home-produced food products); breast milk intake; daily activity patterns (bathing, showering, sleeping, occupational and residential durations, time inside/outside the home, time in cars/trucks/etc., doing dishes/laundry, sweeping/dusting, playing in sand/gravel/dirt, playing on grass, working, food preparation, gardening, exercising, swimming, smoking, etc.); use of and exposure to consumer products; and residential building characteristics (volumes and surface areas, ventilation rates, water use, indoor deposition rates and loads for dust and soil, and an overview of generic considerations pertaining to airborne and waterborne residential contaminants).

It may be important to consider statistical U explicitly that pertains to estimates of parameters used to specify plausible or theoretically justified distributions representing U, V, or W in model inputs. In practice, doing this requires using a compound form of each such distribution, in which a U-distribution is used to model U in each estimated parameter required to specify the parent (U, V, or W) distribution. For example, if n measures of pesticide residue log-concentration, log(C), in a particular household garden crop throughout a state are found to be approximately normally distributed with a sample mean and standard deviation of log(C) equal to and s_C, respectively (i.e., ∼N(, s_C)), then variability in log(C) should not be modeled as ∼N(, s_C), but rather JUV in log(C) should be modeled as a doubly compound normal distribution ∼N(μ, σ), with U in parameters μ and σ modeled (using Chochran's Theorem) as (+s_CT) and 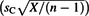, respectively, in which T and X are independent Student's t and chi-square random variables, respectively, each with n – 1 degrees of freedom.

Empirical Methods. Representation of U, V, and/or W in measured or measurable quantities is accomplished by constructing a cumulative distribution function or frequency histogram for actual or potential measurements that faithfully reflects associated U, V, and W, respectively. As long as data reflect a random, representative sample, then empirical statistical methods can be used directly (e.g., Ang and Tang, 1975; Hahn and Shapiro, 1967). An oft-encountered challenge arises when measurements from only a population, species, time frame, or spatial scope, that are slightly or entirely different from those of interest, are available. For example, exposure-factor measurements collected on the general population are not representative of deployed military personnel. A U-, V-, or JUV-distribution fit to measures taken on a broader population may require adjustment in order to accurately reflect these attributes in a specific subpopulation. If bias introduced by relying on data pertaining to a surrogate instead of a target population can be estimated, exposure characterization for the target population may be based on the best available data pertaining to the surrogate population (NRC, 2004). Methods based on expert judgment might be applicable for this purpose. Depending on the exposure factor under consideration, however, this exercise may be complex, and perhaps more costly than collecting exposure data for the target population of interest. Finally, careful characterization of background distributions of contaminant concentrations, human physiological characteristics, and other factors that enter an exposure analysis can be important in PEA. For example, when risk calculations involve nonlinear dose-response models, high-background levels modeled by the upper tails of such distributions may effectively define the “most susceptible” subpopulations.

For many quantities of interest, there may no relevant population of trials of similar events upon which to perform frequentist statistical inference (Morgan and Henrion, 1990). For example, some events may be unique, or in the future, for which it is not possible to obtain empirical sample data. Frequentist statistics are powerful with regard to their domain of applicability, but the domain of applicability is limited compared with the needs of analysts attempting to perform studies relevant to the needs of decision makers.

Judgment-Based Methods (e.g., Heuristics, Biases, Elicitation). An alternative to the frequentist approach to statistics is based on the use of probability to quantify the state of knowledge (or ignorance) regarding a particular value. This view is known as the personalist, subjectivist, or Bayesian view (Morgan and Henrion, 1990). Unlike a frequentist approach, a Bayesian approach does not require assumptions about repeated trials in order to make inferences regarding sampling distributions of statistical estimates (Warren-Hicks and Butcher, 1996). Bayesian methods for statistical inference are based on sample information (e.g., empirical data, when available) and prior information. A prior is a quantitative statement of the degree of certainty with which a person believes that a particular outcome will occur. Because the prior distribution expresses the state of knowledge of a particular expert (or group of experts), this distribution is conditional upon the state of knowledge. Methods for eliciting subjective probability distributions, such as the Stanford/SRI protocol, are intended to produce estimates that accurately reflect the true state of knowledge, free of significant cognitive and motivational biases. Such biases can arise from prevalent propensities to apply simplifying heuristics when people (including experts) make judgments about uncertainty. Elicitation protocols most effectively counteract bias introduced by such heuristics when they involve very careful elicitation of expert exposure characterization judgments in probabilistic form, and when they adjust for intraexpert correlation concerning the statistical significance of assessed characteristics (Walker et al., 2003).

Although the Bayesian approach explicitly acknowledges the role of judgment, the frequentist approach also involves judgment regarding the assumption of a random, representative sample, selection of probability models, evaluation of models using specific goodness-of-fit or diagnostic checks, and other steps in analysis (e.g., Cullen and Frey, 1999). Thus, in a broad sense, all methods for statistical inference require significant judgment on the part of analysts or experts.

Methods based on Underlying Mechanisms. For some uncertain and variable quantities that support exposure modeling, underlying biological, chemical, physical, demographic, economic, and other mechanisms influence the probability associated with specific ranges of values. The literature is rich with presentations of the theoretical bases for individual distributional families and forms (e.g., Bartell and Wittrup, 1996; Brainard and Burmaster, 1992; Cullen, 1995; Enfield and Cid, 1991; Hattis and Burmaster, 1994; Israeli and Nelson, 1992; McKone and Ryan, 1989; Morgan and Henrion, 1990; Ott, 1995; Rubin et al., 1992; Seinfeld, 1986; Thompson et al., 1992). An understanding of the identifiable underlying processes may allow an analyst to select a distributional form to represent a quantity, such as dilution processes leading to a lognormally distributed environmental concentration (Aitchison and Brown, 1957; Ott, 1990). Once a distributional family is selected, the focus shifts to establishing the defining parameters of the distribution using any available data. Of course, there may be multiple distributional forms for which plausible justifications exist—based on either underlying mechanisms or measurements. The ultimate purpose of the analysis, and the role of specific quantities within the analysis, should always guide the process of distilling distributions from available information and developing representations for unknown quantities.

Approaches used to reflect temporal variability (W) in exposure should be selected with recognition that different, complex, or higher-order aspects of temporal variability in exposure that may not typically be characterized in detail nevertheless may be critical when exposure is used, explicitly or implicitly, as input to dose-response models that are sensitive to such temporal variation. For example, statistics concerning the interval between exposure events may be important when modeling endpoints such as asthma or acetylcholinesterase (AChE) inhibition, which may be influenced by long-term exposure history in a complex way. Another example arises when it may be important to model substantial concentration fluctuation (i.e., temporal variability W) that occurs over biologically relevant time periods, because for example, acute chemical toxicity that may arise in relevant exposure scenarios is better predicted by peak exposure levels than by mean exposure levels to specific chemicals of concern (see Introductory section).

Propagating variability and uncertainty through models.

This section briefly describes typical approaches for propagating variability and uncertainty through models based on specification of variability and uncertainty in the inputs to the model. At this point of an analysis, typically the scenario has been specified and models have been selected. Model uncertainties might be incorporated into the analysis in the form of residual distributions that could attempt to quantify the precision and accuracy of the model prediction.

Analytical Solutions and Approximations. For simple additive or multiplicative models, exact solutions can be obtained under specific conditions (such as input variables all normally or lognormally distributed with known covariance) using analytical methods for propagating the mean and covariance of model inputs through the model, to predict the mean and variance of the output of interest (e.g., DeGroot, 1986; Wilson and Crouch, 1981). For example, the product of lognormal distributions is itself a lognormal distribution. This result can be obtained based on the central limit theorem or based on the transformation-of-variables method (e.g., Hahn and Shapiro, 1967). However, for situations in which the model is more complex, or in which the input assumptions do not conform to requirements for obtaining an exact solution for the output, approximation methods based on Taylor series expansions can be used. These methods are often referred to as “error propagation,” “first-order methods,” or “generation of system moments” methods. The purpose of such methods is to estimate the mean, variance, and perhaps higher moments of a model output. Moment information can be used to estimate probability distribution parameters, as well as to identify distributional forms that are consistent with the data analyzed, any one of which (conditional on corresponding moment-based parameter estimates) allows estimation of model-output percentiles of interest. For example, a skewed (e.g., lognormal) distribution would not be appropriate to use to model the univariate distribution of data exhibiting a skewness coefficient (i.e., normalized third central moment) equal to zero. A key limitation of moment-based methods is that they require the model function be differentiable (e.g., involve no Min, Max, or conditional operations). These methods typically require that the second (and potentially higher) derivatives of the model be evaluated. To reduce computational requirements, it is sometimes possible to ignore higher-order terms, but to do so introduces inaccuracies. Information explicitly defining the tails of the input distributions is not propagated. In applications where the shape of the tails is critical, this limitation can be problematic but may generally be addressed by applying methods developed specifically to model extreme values (Coles, 2001; Coles and Pericchi, 2003). With increased application of Monte Carlo methods made feasible by wider access to computational power, analytical solutions and approximations are less frequently pursued, and are nearly obsolete in quantitative exposure analysis today.

Numerical Methods. Numerical methods for propagating distributions through models are used widely because they are flexible. The Monte Carlo method involves sampling input values selected at random from each distribution used to model an input variable, calculating the result of the output function of each sampled set of input variables (Cohen et al., 1994; Cullen and Frey, 1999; Davison and Hinkley, 1997; Efron and Tibshirani, 1993; Metropolis and Ulam, 1949; Morgan and Henrion, 1990). For models that involve linear or monotonically nonlinear relationships between inputs and outputs, a stratified sampling technique known as Latin Hypercube Sampling (LHS) (Iman et al., 1980; McKay et al., 1979; Morgan and Henrion, 1990) provides output distributions, including distributions with user-specified target rank-correlations (Iman and Connover, 1982), similar to those obtained by Monte Carlo sampling but with considerably fewer model evaluations. LHS is carried out by dividing each statistical distribution into segments of equal probability (i.e., with equal area under a probability density function). For each distribution, the standard LHS approach is to sample each segment randomly without replacement, at a random point within that segment, to obtain good coverage of the entire range of potential values. A simpler, “systematic” LHS strategy uses only the average or median value of each segment rather than random samples within each segment, but uses a much larger total number of segments, to obtain good coverage. By using only predefined sample values for each (including each continuous) distribution, the systematic LHS approach can save time; although a drawback of this approach is that exact individual output values generated in different simulations may (unrealistically) recur, such recurrance is rarely relevant to PEA or PRA applications.

LHS sometimes does not outperform Monte Carlo sampling for models with input-output relationships that are non-additive and nonmonotonically nonlinear (Homma and Saltelli, 1995; Saltelli et al., 2000). Quasi-Monte Carlo sampling procedures (Bratley and Fox, 1988; Saltelli et al., 2000), such as Sobol's LP_τ sampling (Saltelli et al., 2000; Sobol, 1967) and the winding stairs method (Jansen et al., 1994; Saltelli et al., 2000), might be considered in such situations. For example, Sobol's LP_τ sampling method is based on more fully satisfying uniformity properties in a multidimensional samping space. These procedures have not yet been widely used by the environmental community, which has instead tended to use Monte Carlo sampling and LHS, and their practicality remains to be explored.

In contrast with the probabilistic basis of sampling in Monte Carlo and Latin Hypercube analyses, importance sampling targets specific events and/or scenarios. Input values related to these critical events and scenarios are sampled disproportionately in the analysis, with the goal of generating output information in proportion to its importance (Morgan and Henrion, 1990).

The Fourier Amplitude Sensitivity Test (FAST) (Cukier et al., 1973; Saltelli et al., 2000) can be used to propagate probability distributions through a model and to generate a sensitivity analysis that quantifies the main and total contributions of each input to the variance of the output (e.g., Mokhtari and Frey, 2005; Patil and Frey, 2004). However, FAST has some practical limitations regarding the number and type of input distributions that can be accommodated.

Sensitivity analysis.

Risk assessment models can be large and complex. Thus, it can be difficult to prioritize controllable variables that are most promising with respect to risk management goals. As a matter of good practice, it is important to evaluate how a model responds to changes in its inputs as part of the process of model development, verification, and validation. Moreover, insight regarding key sources of uncertainty in a model can be used to prioritize additional data collection or research to reduce uncertainty. Sensitivity analysis is a practical tool that helps with all of these policy and modeling needs.

The most commonly used sensitivity analysis methods are those that are built-in features of widely used software tools, such as applying sample or rank correlation coefficients in software packages such as SAS, Crystal Ball, @Risk, or Mathematica. However, many other methods can be used for sensitivity analysis, such as sample regression, rank regression, ANOVA, categorical and regression trees, FAST, Sobol's method, mutual information index, and others. Some methods can quantify the contribution of each input to the linear or nonlinear response of a model output, or to the variance of the output, or to outcomes of the output above a threshold of interest (e.g., high exposure or risk). Saltelli et al. (2000), Frey and Patil (2002), Frey et al. (2003b), and Mokhtari et al. (2006) provide a detailed overview and evaluation of selected methods. Mokhtari and Frey (2005) provide guidance to practitioners regarding how to select and apply sensitivity analysis for risk assessment modeling.

Iterative tiers of analysis.

Modeling is a process of generating insight, and the amount of learning and insight typically improves as one explores more deeply the system of interest, the models, and the inputs used to represent the system (Fig. 2). Thus, as one gains experience with the case study and analysis, opportunities to improve the analysis, or to target resources to the parts of the analysis that matter the most, are typically uncovered. Nearly all guidance documents and handbooks on probabilistic analysis emphasize the importance of an iterative approach to analysis (e.g., Cullen and Frey, 1999; Morgan and Henrion, 1990; USEPA, 1997b; WHO, 2008).

The iterative approach has at least two major considerations: (1) the level of detail, or tier, should be appropriate to the data quality objectives and significance of the analysis to a decision problem; and (2) the analysis should be repeated, with the first iteration intended to determine which components or inputs are most important, and later iterations intended to allow for improvement of those components and inputs and refinement of the results. For example, screening analysis, worst-case bounding analysis, comparison of plausible upper and lower bounds, development of best estimates of interindividual variability, and so on are different modeling objectives that, in turn, imply the need for different tiers of analysis. For any given tier, some degree of iteration can be used to prioritize resources, to preferentially obtain the best possible information for those parts of the analysis that matter the most. In practice, it can be difficult to achieve the ideal for tiers of analysis and iteration, given resource constraints or perceptions that resources do not allow for iteration. Nonetheless, as a matter of good practice, the selection of an appropriate tier (level of detail) and number of iterations is a desirable goal for any analysis. In the long run, a tiered approach to analysis can conserve resources by focusing them on aspects of the analysis that matter the most.

Alternative or complementary techniques.

Although numerical methods such as Monte Carlo simulation, and empirical and judgment-based approaches for quantifying variability and uncertainty in model inputs in the form of probability distributions, appear to be the most widely applied for purposes of dealing with variability and uncertainty in risk assessment, other techniques can be considered and applied as appropriate for dealing with uncertain or imprecise information. Examples of these include interval methods, probability bounds, fuzzy methods, meta-analytical methods, and artificial intelligence.

Interval methods involve specifying a range for each input, without making any additional assumptions regarding the relative likelihood of a value falling within a range, or regarding the type of dependencies that may exist between two or more inputs (Ferson, 1996). In a technique referred to as p-bounds, interval methods can be extended to incorporate probabilistic information about some inputs, and interval information regarding others, while also taking into account all possible dependencies that could exist among the inputs.

Fuzzy methods are intended to deal with situations in which there is “vagueness” but not necessarily statistical uncertainty (Zadeh, 1965). For example, one can deal with vagueness as to whether an individual is a member of a particular group. Although fuzzy methods have found applications in areas such as process control, they are not widely used in human health risk assessment.

Meta-analysis is a technique for quantitatively combining, synthesizing, and summarizing data and results from different studies (Hasselblad, 1995; Putzrath and Ginevan, 1991). A “best estimate” with more confidence can be produced on the basis of summarizing or combining results from different studies, thereby reducing the level of uncertainty compared with that based on any individual study. Meta-analysis is useful, for example, when there are several competing studies regarding dietary patterns, epidemiology, or dose-response effects.

The field of artificial intelligence has produced tools for representing and exploring uncertainty in inputs, models, and the processes by which these interact to yield risk estimates. One tool with great potential for application in the field of risk analysis is the Bayesian Belief Network (BBN) (Pourret et al., 2008). The BBN refers to an influence diagram that graphically represents complex and interlocking relationships among model inputs and outputs. Bidirectional conditionality of probabilities at each node is included explicitly in the network structure. Probabilities in the network can be updated using Bayes’ rule, as new information is introduced.

Modeling exposure and risk using simulation models.

Under the framework presented in Figure 1, exposure assessment is the link between source and PBPK modeling of internal dose and ultimately risk of adverse effects. Increasingly, risk assessors are attempting to construct models that simulate the entire source to response continuum (USEPA, 2005b). A hallmark of these models is that they begin with the definition of the exposed person and place the definition of the person at the center of the model. This process is repeated for other individuals to build up a description of a population (Burke et al., 2001; Price and Chaisson, 2005). There are several reasons for this focus on the person. First, Exposure models represent a breakpoint in modeling domains across the source-to-outcome continuum. Prior to exposure modeling, the process deals with chemicals being released to the environment and moving through various environmental compartments (e.g., fugacity models). After exposure assessment, the scope of the modeling covers absorption, distribution, metabolism, and excretion (ADME) in the human body and ultimately the health outcome of the individual. To correctly link these disparate domains it is critical to both define the person's location over time and behaviors that define their interaction with one or more sources and to define the same person's internal characteristics that define the kinetics, metabolism, and any resulting effects (Price et al., 2004).

To correctly model variation in health outcomes across a population (V), the definition of the individual must be consistent among the exposure, PBPK, and BBDR models. If the use of a product is limited to the elderly, while the physiology used in the PBPK modeling is taken from young adults, and the dose-response model is developed for a child, the resulting outcome predictions will have little value. Different, complex, or higher-order aspects (i.e., not typically characterized details) of temporal variability in exposure may be critical in certain dose-response contexts, such as time between exposure events (in the context of asthma) or AChE depression, that may integrate long-term exposure history in a complex way (see section “Methods based on Underlying Mechanisms”).

Person-oriented models achieve this consistency by defining simulated persons in terms of basic characteristics (demographics) such as age, sex, region where the individual lives, and season of the year when the person interacts with sources. These data are then used to define the probability of interacting with a specific source and the intensity of that interaction. Models of such time- and route-specific estimates of exposure have been developed to meet the needs of the Food Quality Protection Act and the Clean Air Act (Barraj et al., 2000; International Life Sciences Institute [ILSI], 2008; Lifeline Group, Inc. [LifeLine], 2007; USEPA, 2002, 2007). These models also assess exposures that occur by multiple routes and multiple sources (aggregate exposure models). Several models also consider individual activity patterns and their influence on exposure factors such as breathing rates and dermal transfer rates. These data can be passed on to uptake models to produce individually tailored estimates of absorbed dose.

These models provide output in the form of longitudinal exposure histories that define a population of simulated individuals. Each individual's exposure history consists of a series of time steps, the durations of which vary from model to model and can range in length from a few seconds to a year. The models define the dose that an individual receives and the route by which the dose occurs for each time step. These exposure histories (reflecting temporal, or W-type, variability) take place inside a common temporal framework that includes secular trends, such as the long-term decline in sources of lead in the environment, and cyclical changes such as seasonal or weekly chances in human behavior and the environmental factors that influence exposure (Price and Chaisson, 2005). The models define exposures that each individual incurs together with the route(s) by which they occur at each time step, and differences in these modeled exposures are reflected by differences (V) between the various exposure histories. Additional models can also model corresponding sources of uncertainty (U). Thus, the models can be viewed as joint uncertainty, interindividual variability, and intraindividual variability (JUVW) models.

The definition of the person in the exposure modes can be passed on to the PBPK models to provide a basis for defining the physiological characteristics of the exposed individual (Price and Chaisson, 2005; Price et al., 2003, 2004). By defining the individual's basic demographic information (age, sex, ethnicity, etc.) the exposure models provide a basis for assigning characteristics in an internally consistent fashion. For example, height and weight can be assigned based on age and gender. Resting breathing rates and cardiac output can then be modeled based on height, weight, age, and sex (de Simone et al., 1997; Layton, 1993).

This use of contingent relationships between demographics and physiology allows the modeling of temporal variation in physiology (W). By assigning an individual an initial age and height and then modeling the individual over time the height of the individual as they age can be correctly modeled (each year's height a function of the pervious year's height and the age-specific rates of growth). The new height each year can then be used to update the breathing rates and cardiac output.

Finally, the emphasis on the person provides a basis for capturing the age, sex, and genetic components of the variation in ADME kinetics of substances. By assigning each individual demographic characteristics, the model can use information on the frequency of polymorphisms in populations of different ethnicities to define the probability of a person having an unusual sensitivity to a chemical.

Decision context of uncertainty and sensitivity analysis.

Decision analysis is a quantitative framework for assisting decision makers with the process of making a decision, based on principles of rationality (e.g., Watson and Buede, 1987). Decision making typically must contend with several key factors, including: (1) multiple, conflicting objectives; (2) uncertainty; and (3) preferences of a decision maker. In addition, decision analysis provides a theoretical foundation for estimating the value of collecting more information to reduce uncertainty (Evans, 1985; Evans et al., 1988; Finkel and Evans, 1987; Henrion, 1982; Lave et al., 1988; Taylor et al., 1993). Thus, the results of uncertainty and sensitivity analysis can be used as input to a formal decision-making process that could be conducted quantitatively. However, in practice, it is more likely that the quantitative outputs of probabilistic and sensitivity analyses are used as part of a semiquantitative or qualitative decision-making process. Nonetheless, the concepts of multi-attribute decision making and value of information can be used to describe a decision-making process and the types of outcomes that it can produce.

Exposure assessment has usually included modeling the sources of exposure, as well as modeling the actual interaction of a person and a substance. With very few exceptions (e.g., being struck by a meteor), human activity influences either the release of or the exposure to a source. For example, an exposure assessment may begin with the release of a substance at a smoke stack, model the transport to a residence, and then evaluate the inhalation of the substance in an indoor environment. Thus, the problem that risk assessment ultimately tries to address is how decisions concerning a source (e.g., permitting an environmental release, banning fishing in a river, or approving the sale of a product) will affect the health outcomes in a population.

Often, the behavior of the exposed individual affects the source (use of consumer products, choice of transportation, etc.). Where the behavior of the exposed individual is independent of the source (people breathe at the same rate whether or not there is an upwind incinerator), there is a need to connect the exposure assessment to source modeling (e.g., decisions concerning the incinerator may imply imposition of competing risks from alternative waste/landfill management methods). A basis for such a connection is to construct a temporally and spatially defined framework that includes both the source modeling and the exposed individual, as has been done to quantify variability and uncertainty in air pollutant emissions and other discharges to the environment (e.g., Frey and Zhao, 2004; North American Consortium for Atmospheric Research in Support of Air-Quality Management [NARSTO], 2005). Such a framework should identify common pathways, routes of exposure, and potential dose, in a transparent fashion that is useful to toxicological/health-effects assessment.

Ecological risk assessors have developed approaches that are parallel to the person-oriented modeling described above. In these ecological models, species living in a specific environment (fish in a specific river, or birds along a specific portion of shoreline) are modeled by simulating individual animals over time and their ability to survive and reproduce in the face of chemical stressors. The cumulative success of the simulated animals is used to predict whether populations of such species exposed to specific stressors will increase or decline over time. In both human and ecological models of exposure, a temporal framework that addresses seasonal and other cyclical patterns is established. The framework allows the models to represent temporal and spatial variation of stressor exposures and simulates longitudinal exposures of individual human or nonhuman animals over time.

CONCLUSIONS

The state of PEA science was reviewed with reference to experience gained in assessment of human exposures to chemicals in the environment and to key PEA applications and associated design and information needs. A key observation made is that PEA objectives are shaped by the four primary decision-making contexts in which exposure information is used to characterize environmental toxicity risks: protection of public health, environmental health triage, civil justice, and criminal justice. Although information needs differ for these different risk management contexts, and although related methodological improvements continue to be made, existing PRA techniques can be applied to implement PEA to support each area of decision making.

Key barriers, as well as opportunities, exist for improved PEA. Exposure assessments are performed independently by practitioners in diverse fields (industrial hygiene, nuclear power, consumer products, air and water pollution programs, foods, agricultural chemicals, and building design, among others). Different government agencies that deal with these various problem domains typically are the primary sponsors of exposure assessments. Various professional societies as well as regulatory agencies deal with exposure assessment (AIHA, International Society for Exposure Sciences, the Health Physics Society, the Society for Risk Analysis, USEPA, the U.S. Occupational Health and Safety Administration, state environmental protection and occupational health and safety agencies, etc.). Each of the various communities has a unique set of perspectives, historical practices, terminologies, resources, and propensities, governed by overlapping set(s) of problems and decision-making goals, regulatory requirements, and legislative mandates being addressed, directly or indirectly, by these interrelated communities.

Different communities may not be fully aware of the state of best practice in other communities, leading to missed opportunities to more rapidly adopt successful approaches.

PEA can thus be made more effective by actions to improve the characterization of variability and uncertainty in sources; expand interdisciplinary approaches that link with other aspects of chemical risk assessment, including decision context and dose-response assessment; increase the application of iterative analyses proportionate to and at a level of sophistication warranted by the characteristics of the decision under consideration; integrate the ability of PEA to reflect recent advances in toxicology, genomics, and PBPK modeling—all facilitated by improved training of exposure analysts, and more rigorous and systematic peer review of PEA projects to foster their credibility and the general advancement of the state of PEA practice.