Network-based Analysis of Multivariate Gene Expression Data

Abstract

Multivariate microarray gene expression data are commonly collected to study the genomic responses under ordered conditions such as over increasing/decreasing dose levels or over time during biological processes, where the expression levels of a give gene are expected to be dependent. One important question from such multivariate gene expression experiments is to identify genes that show different expression patterns over treatment dosages or over time; these genes can also point to the pathways that are perturbed during a given biological process. Several empirical Bayes approaches have been developed for identifying the differentially expressed genes in order to account for the parallel structure of the data and to borrow information across all the genes. However, these methods assume that the genes are independent. In this paper, we introduce an alternative empirical Bayes approach for analysis of multivariate gene expression data by assuming a discrete Markov random field (MRF) prior, where the dependency of the differential expression patterns of genes on the networks are modeled by a Markov random field. Simulation studies indicated that the method is quite effective in identifying genes and the modified subnetworks and has higher sensitivity than the commonly used procedures that do not use the pathway information, with similar observed false discovery rates. We applied the proposed methods for analysis of a microarray time course gene expression study of TrkA- and TrkB-transfected neuroblastoma cell lines and identified genes and subnetworks on MAPK, focal adhesion and prion disease pathways that may explain cell differentiation in TrkA-transfected cell lines.

1 Introduction

Multivariate microarray gene expression data are commonly collected to investigate dose-dependent alterations in gene expression or time-dependent gene expression during a biological process. For example, dose-dependent gene expression data are often measured in the area of toxicology (Lehmann et al., 2004; Seidel et al., 2006) and time-course gene expression data are often collected during a dynamic biological process. For both the dose-dependent and time-course gene expression experiments, the data can be summarized as multivariate vectors, and one goal of such multivariate gene expression studies is to identify genes that have different overall expression patterns between two experiments; these genes can often lead to the identification of the pathways or subnetworks that are perturbed or activated during a given dose-dependent experiment or a dynamic biological process. Compared to gene expression studies of one single experimental condition, such multivariate gene expression data can potentially identify more genes that are differentially expressed (Yuan and Kendzioski, 2006; Tai and Speed, 2006; Hong and Li, 2006; Wei and Li, 2008).

One important feature of the multivariate gene expression data is that the data are expected to be dependent across dosages or time points. Efficiently utilizing such dependency can lead to a gain in efficiency in identifying the differentially expressed genes. Yuan and Kendzioski (2006) and Wei and Li (2008) developed the hidden Markov model and hidden Markov random field model to identify the differentially expressed genes at each time point for analysis of microarray time-course gene expression data. Instead of identifying genes that are differentially expressed at each time point during a biological process or at a given dosage level, the investigators sometimes are only interested in identifying the genes that show different overall expression patterns during the experiments. Tai and Speed (2006) developed an empirical Bayes method treating the observed time-course gene expression data as multivariate vectors. Hong and Li (2006) developed a functional empirical Bayes method using B-splines. Both approaches treat the data as multivariate vectors to account for possible correlations of gene expressions over different dosages or time points. These empirical Bayes have approved useful for identifying the relevant genes, they all make the assumptions that the genes are independent with respective to their differential expression states. However, we expect that the differential expression states of genes with transcriptional regulatory relationships are dependent.

The goal of this paper is to model such regulatory dependency by using the prior regulatory network information in order to increase the sensitivities of identifying the biologically relevant pathways. Information about gene regulatory dependence has been accumulated from many years of biomedical experiments and is summarized in the form of pathways and networks and assembled into pathway databases. Some well-known pathway databases include KEGG, BioCarta (www.biocarta.com) and BioCyc (www.biocyc.org). The most common way of utilizing the known regulatory network information in analysis of microarray gene expression data is to first identify the differentially expressed genes using methods e.g. of Tai and Speed (2006) or Hong and Li (2006) and then to map these genes to the network to visualize which subnetworks show differential expression or to perform some types of gene set enrichment analysis. One limitation of such an approach is that for many multivariate gene expression data sets, the sample sizes are usually small and therefore the approach often has limited power to identify the relevant subnetworks. Representing the known genetic regulatory network as an undirected graph, Wei and Li (2007) and Wei and Pan (2008) have recently developed hidden Markov random field (MRF)-based models for identifying the subnetworks that show differential expression patterns between two conditions, and have demonstrated using both simulations and applications to real data sets that the procedure is more sensitive in identifying the differentially expressed genes than those procedures that do not utilize the pathway structure information. However, neither of these explicitly models the multivariate expression data. Wei and Li (2008) extended the model of Wei and Li (2007) and the HMM model of Yuan and Kendzioski (2006) to analyze the microarray time course gene expression in the framework of a hidden spatial-temporal MRF model. However, this approach aims to identify the differentially expressed genes at each time point and it assumes the same network-dependency of the gene differential expression states at all the time points.

In this paper, to efficiently identify the differentially expressed genes in the multivariate gene expression experiments, we develop the hidden MRF model of Wei and Li (2007) further into a hidden MRF model for multivariate gene expression data in order to take into account potential dependency of gene expression over time and the known biological pathway information. We treat the multivariate gene expression data as multivariate data, allowing for dependency of the data across the dosage levels or over time points. Different from the popular empirical Bayes methods for analysis of multivariate gene expression data where genes and their differentially expression states are assumed to be independent, this method models the dependency of the differentially expression states using a discrete Markov random field and therefore enables the information of a known network of pathways to be efficiently utilized in order to identify more biologically interpretable results. Although the formulation of the problem is similar to that of Wei and Li (2007), models for multivariate gene expression data are more complicated and require new methods for estimating the model parameters. We propose to use both the moment estimate and maximum likelihood estimates in the iterative conditional mode (ICM) algorithm (Besag, 1974; Besag, 1986).

We first introduce the hidden MRF model for multivariate expression data and present an efficient algorithm for parameter estimation by the ICM algorithm. We then present results from simulation studies to demonstrate the application of the hidden MRF model, to compare with existing methods, and to evaluate the sensitivity of the method to misspecification of the network structure. For a case study, we apply the hidden MRF model to analyze the time-course gene expression data of TrkA- and TrkB-transfected neuroblastoma cell lines in order to identify the pathways that are related to cell differentiation in TrkA-transfected cell lines. Finally, we present a brief discussion of the methods.

2 Statistical Models and Methods

We first introduce a hidden MRF model for multivariate gene expression data, where the network structure is represented as an undirected graph. The model is an extension of the model of Wei and Li (2007) to multivariate gene expression data, where the distribution of latent differential states of the genes is modeled as a discrete MRF defined on the prior network structure, and the empirical Bayes model of Tai and Speed (2006) are used for modeling the emission density for the observed multivariate gene expression data.

2.1 Data observed and representation of genetic networks as undirected graphs

Consider the multivariate gene expression data measured under two different conditions over k dosage levels or time points, with n independent samples measured under one condition and m independent samples measured under another condition. For each experiment, we assume that the expression levels of p genes are measured. For a given gene g, we denote these data as i.i.d. k × 1 random vectors Y_g1, · · · , Y_gn for condition 1 and Z_g1, · · · , Z_gm for condition 2. We further assume that Y_gi ~ N_k(μ_gy, Σ_g) and Z_gi ~ N_k(μ_gz, Σ_g). For a given gene g, the null hypothesis of interest is

$$H_{g0}:{\mu }_{\mathrm{gy}}={\mu }_{\mathrm{gz}}.$$ (1)

Define μ_g = μ_gy – μ_gz. For a given gene g, let I_g take the value of 1 if μ_g ≠ 0 and 0 if μ_g = 0. We call the genes with I_g = 1 the differentially expressed (DE) genes. Our goal is to identify these DE genes among the p genes.

Besides the gene expression data, suppose that we have a network of known pathways that can be represented as an undirected graph G = (V, E), where V is the set of nodes that represent genes or proteins coded by genes and E is the set of edges linking two genes with a regulatory relationship. Let p = |V| be the number of genes that this network contains. Note the gene set V is often a subset of all the genes that are probed on the gene expression arrays. If we want to include all the genes that are probed on the expression arrays, we can expand the network graph G to include isolated nodes, which are those genes that are probed on the arrays but are not part of the known biological network. For two genes g and g′, if there is a known regulatory relationship, we write g ~ g′. For a given gene g, let N_g = {g′ : g ~ g′ ∈ E} be the set of genes that have a regulatory relationship with gene g and d_g = |N_g| be the degree for gene g.

2.2 A discrete Markov random field model for differential expression states for genes on the network

Our goal is to identify the genes on the network G that are multivariate differentially expressed between the two experimental conditions. Since two neighboring genes g and g′ have regulatory relationship on the network, we should expect that the DE states I_g and I_g′ are dependent. In order to model the dependency of I_g over the network, following Wei and Li (2007), we introduce a simple MRF model. Particularly, we assume the following auto-logistic model for the conditional distribution of I_g,

$$Pr(I_g\mid I_{g^{\prime }},g^{\prime }\ne g)=\frac{\text{exp}\left\{I_{g}F\left(I_g\right)\right\}}{1+\text{exp}\left\{F\left(I_g\right)\right\}},$$ (2)

where

$$F\left(I_g\right)=\gamma +\beta \frac{{\sum }_{g^{\prime }\in N_g}(2I_{g^{\prime }}-1)}{d_g},$$

and γ and β ≥ 0 are arbitrary real numbers. Here the parameter β measures the dependency of the differential expression states of the neighboring genes. We assume that the true DE states $\left(I_g^{\ast }\right)=\{I_g^{\ast },g=1,\cdots ,p\}$ is a particular realization of this locally dependent MRF. Note that when β = 0, the model assumes that all the I_gs are independent with the same prior probability exp(γ)/(1 + exp(γ)) of being a DE gene.

2.3 Emission probabilities for multivariate gene expression data and the HMRF model

To relate the differential expression state I_g to the observed gene expression data D_g = (Y_g1, · · · , Y_gn; Z_g1, · · · , Z_gm), we follow the empirical Bayes approach of Tai and Speed (2006) for multivariate gene expression data and use conjugate priors for μ_g and Σ_g, that is, an inverse Wishart prior for Σ_g and a dependent multivariate normal prior for μ_g. To make notation simple, we drop the gene subscript g when introducing the Bayesian model. Let Ȳ = (Y₁ + · · · + Y_n)/n, Z̄ = (Z₁ + · · · + Z_m)/m, X̄ = Ȳ – Z̄, ${\mathbf{S}}_{\mathbf{y}}={(n-1)}^{-1}{\sum }_{i=1}^n({\mathbf{Y}}_i-\stackrel{‒}{\mathbf{Y}}){({\mathbf{Y}}_i-\stackrel{‒}{\mathbf{Y}})}^{\prime }$, ${\mathbf{S}}_{\mathbf{z}}={(m-1)}^{-1}{\sum }_{i=1}^m({\mathbf{Z}}_i-\stackrel{‒}{\mathbf{Z}}){({\mathbf{Z}}_i-\stackrel{‒}{\mathbf{Z}})}^{\prime }$, S = (n+m–2)^–1((n–1)S_y +(m–1)S_z). Following Tai and Speed (2006), we assign independent and identical inverse Wishart priors to Σ, Σ ~ W ^–1((νΛ)^–1, ν). Given Σ, we assign multivariate normal priors for the gene-specific mean difference μ for the two cases (I = 1) and (I = 0):

$$\begin{array}{cc}\hfill \mu \mid \Sigma ,I& =1\sim N_k(0,{\eta }^{-1}\Sigma ),\hfill \\ \hfill \mu \mid \Sigma ,I& =0\equiv 0.\hfill \end{array}$$

Since the statistics (X̄, S) are the sufficient statistics for the parameters (μ, Σ) (Tai and Speed, 2006), the conditional distribution of the data D = (Y₁, · · · , Y_n, Z₁, · · · , Z_m) can be written as

$$P(\mathbf{D}\mid I)=P({\mathbf{Y}}_1,\cdots ,{\mathbf{Y}}_n,{\mathbf{Z}}_1,\cdots ,{\mathbf{Z}}_m\mid I)=P(\stackrel{‒}{\mathbf{X}},\mathbf{S}\mid I).$$

Tai and Speed (2006) further derived

$$P(\mathbf{D}\mid I=1)=\frac{{\Gamma }_k((N+\nu )∕2)}{{\Gamma }_k((N-1)∕2){\Gamma }_k(\nu ∕2)}\times {(N-1)}^{\frac{k(N-1)}{2}}{\nu }^{-\frac{kN}{2}}{\left(\pi (n^{-1}+m^{-1}+{\eta }^{-1})\right)}^{-\frac{k}{2}}\times \frac{{\mid \Lambda \mid }^{-\frac{N}{2}}{\mid \mathbf{S}\mid }^{\frac{N-k-2}{2}}}{\mid {\mathbf{I}}_k+{\left((n^{-1}+m^{-1}+{\eta }^{-1})\nu \Lambda \right)}^{-1}\stackrel{‒}{\mathbf{X}}{\stackrel{‒}{\mathbf{X}}}^{\prime }+S^{\ast }\mid \frac{N+\nu }{2}},$$ (3)

where N = n+m–1 and S* = (νΛ/(N –1))^–1S. Thus, given I = 1, the probability density function of the data is a function of X̄ and S̄ only, which follows a Student-Siegel distribution (Aitchison and Dunsmore, 1975). Following Aitchison and Dunsmore's and Tai and Speed's notation, this distribution is denoted by StSi_k(ν, 0, (n^–1+m^–1+η^–1)Λ, N –1, (N –1)^–1νΛ). Similarly, the distribution of P(D|I = 0) follows StSi_k(ν, 0, (n^–1 + m^–1)Λ, N – 1, (N – 1)^–1νΛ), with the following density function

$$P(\mathbf{D}\mid I=0)=\frac{{\Gamma }_k((N+\nu )∕2)}{{\Gamma }_k((N-1)∕2){\Gamma }_k(\nu ∕2)}\times {(N-1)}^{\frac{k(N-1)}{2}}{\nu }^{-\frac{kN}{2}}{\left(\pi (n^{-1}+m^{-1})\right)}^{-\frac{k}{2}}\times \frac{{\mid \Lambda \mid }^{-\frac{N}{2}}{\mid \mathbf{S}\mid }^{\frac{N-k-2}{2}}}{\mid {\mathbf{I}}_k+{\left((n^{-1}+m^{-1})\nu \Lambda \right)}^{-1}\stackrel{‒}{\mathbf{X}}{\stackrel{‒}{\mathbf{X}}}^{\prime }+S^{\ast }\mid \frac{N+\nu }{2}}.$$ (4)

Together the transition probability (2) and the emission probabilities (3) and (4) define a hidden MRF model for multivariate gene expression data with parameters in the emission probabilities θ = (η, ν, Λ). Define (I_g) = {I₁, · · · , I_p} to be a vector of the differential expression states of the p genes on the network. By Bayes rule, Pr((I_g)|D) ∝ Pr(D|(I_g)) × Pr((I_g)). The estimate (Î_g) that maximizes Pr((I_g)|D) is a maximum a posterior (MAP) estimate under 0-1 loss. In order to estimate the parameters and (I_g), we make the following conditional independence assumption,

Assumption

Given any particular realization (I_g), the random variables (D) = (D₁, D₂, · · · , D_g) are conditionally independent and each D_g has the same unknown conditional density function P(D_g|I_g), dependent only on I_g. The conditional density of the observed gene expression data D, given G and parameter θ = (η, ν, Λ), is simply,

$$L_{\theta }(\left({\mathbf{D}}_g\right)\mid \left(I_g\right))=\prod _{g=1}^{p}P({\mathbf{D}}_g\mid I_g)$$ (5)

where P(D_g|I_g) is defined as (3) or (4).

3 Estimation of the Model Parameters and the Posterior Probabilities of the DE States

When inferring (I_g)*, parameter estimation must be carried out simultaneously. We propose the following ICM algorithm of Besag (1986) to simultaneously estimate the parameter θ = (η, ν, Λ) with a positive definite constraint on the covariance matrix Λ in the emission probability model and the parameter Φ = (γ, β) in the auto-logistic model. Simultaneously estimating the covariance matrix Λ is difficult due to the fact that its estimate has to be positive definite. We propose to first estimate Λ′ using the moment estimator of Tai and Speed (2006). Specifically, by the weak law of large numbers, S̄ converges in probability to (ν – k – 1)^–1νΛ. Therefore, Λ can be estimated by ${\Lambda }^{\prime }={\widehat{\nu }}^{-1}(\widehat{\nu }-k-1)\stackrel{‒}{\mathbf{S}}$, where $\widehat{\nu }=\text{max}(mean\left({\widehat{\nu }}_j\right),k+6)$, j = 1, · · · , k and ${\widehat{\nu }}_j$ is the estimated prior degrees of freedom based on the jth diagonal elements of the gene-specific sample variance-covariance matrices using the method proposed in Section 6.2 in Smyth (2004). We then fix Λ at its estimate and estimate the other model parameters within the following ICM algorithm (Besag, 1986), which involves the following iterative steps:

• S1. Obtain an initial estimate (Î_g) of the true state (I_g)*, using simple two sample Hotelling's T² test.

• S2. Estimate θ by the value $\widehat{\theta }$ which maximizes the likelihood L_θ(D|(Î_g)) (Equation 5).

• S3. Estimate Φ by the value $\widehat{\Phi }$ which maximizes the following pseudo-likelihood

  $$L_{\Phi }\left(\left({\widehat{I}}_g\right)\right)=\prod _{g=1}^G\frac{\text{exp}\left\{I_{g}F\left(\left({\widehat{I}}_g\right)\right)\right\}}{1+\text{exp}\left\{F\left(\left({\widehat{I}}_g\right)\right)\right\}}.$$
• S4. Carry out a single cycle of ICM based on the current (Î_g), $\widehat{\theta }$ and $\widehat{\Phi }$, to obtain a new (Î_g): for g = 1 to p, update I_g which maximizes

  $$P(I_g\mid \mathbf{D},{\widehat{I}}_{g^{\prime }},g^{\prime }\ne g)\propto P({\mathbf{D}}_g\mid I_g;\widehat{\theta })P(I_g\mid {\widehat{I}}_{g^{\prime }},g^{\prime }\ne g;\widehat{\Phi }).$$

• S5. Go to step 2 until there is convergence in the estimates.

In Step 2, θ = (η, ν) in the HMRF model and they can be estimated using any numerical optimization procedure. After the convergence of the ICM algorithm and obtaining the parameter estimates, we can run the Gibbs sampling to obtain the estimate of the posterior probability of Pr(I_g = 1|data) for each of the gene g. These posterior probabilities can then be used for selecting the DE genes.

4 Simulation Study

We performed simulation studies to evaluate the proposed method and to compare results with other methods for identifying the DE genes. Following Wei and Li (2007), we first obtained 33 human regulatory pathways from the KEGG database (December 2006), where we retained only gene-gene regulatory relations. These 33 regulatory pathways are inter-connected and formed a network of regulatory pathways. We represent such a network as an undirected graph where each node is a gene and two nodes are connected by an edge if there is a regulatory relation between corresponding genes. Loops (nodes connected to themselves) were eliminated. This results in a graph with 1668 nodes and 8011 edges.

To simulate the differential expression states of the genes on this network, we initialized the genes in the K pathways to be DE and the rest genes to be EE, which gives us the initial G₀. We then performed sampling five times based on the current gene differential expression states, according to the Markov random field model with γ₀ = γ₁ = 1 and β = 2 (Wei and Li, 2007). We chose K = 5, 9, 13, 17 to obtain different percentages of genes in DE states. After obtaining the differential expression states for the genes, we simulated the multivariate gene expression levels based on the empirical Bayes models, using the same parameters as Tai and Speed (2006): η = 0.5, ν = 13 and Λ = A × 10^–3, where

$$A=\left(\begin{array}{ccccccc}\hfill 14.69\hfill & \hfill 0.57\hfill & \hfill 0.99\hfill & \hfill 0.40\hfill & \hfill 0.55\hfill & \hfill 0.51\hfill & \hfill -0.23\hfill \\ \hfill 0.57\hfill & \hfill 15.36\hfill & \hfill 1.22\hfill & \hfill 0.84\hfill & \hfill 1.19\hfill & \hfill 0.91\hfill & \hfill 0.86\hfill \\ \hfill 0.99\hfill & \hfill 1.22\hfill & \hfill 14.41\hfill & \hfill 2.47\hfill & \hfill 1.81\hfill & \hfill 1.51\hfill & \hfill 1.07\hfill \\ \hfill 0.40\hfill & \hfill 0.84\hfill & \hfill 2.47\hfill & \hfill 17.05\hfill & \hfill 2.40\hfill & \hfill 2.32\hfill & \hfill 1.33\hfill \\ \hfill 0.55\hfill & \hfill 1.19\hfill & \hfill 1.81\hfill & \hfill 2.40\hfill & \hfill 15.63\hfill & \hfill 3.31\hfill & \hfill 2.75\hfill \\ \hfill 0.51\hfill & \hfill 0.91\hfill & \hfill 1.51\hfill & \hfill 2.32\hfill & \hfill 3.31\hfill & \hfill 13.38\hfill & \hfill 3.15\hfill \\ \hfill -0.23\hfill & \hfill 0.86\hfill & \hfill 1.07\hfill & \hfill 1.33\hfill & \hfill 2.75\hfill & \hfill 3.15\hfill & \hfill 12.90\hfill \end{array}\right).$$

For each condition, we chose the number of independent replications to be 3 for each group and repeated the simulation 100 times.

4.1 Comparison with the method of Tai and Speed

We first examined the parameter estimates of θ = (η, ν) using three different methods: the empirical Bayes (EB) method of Tai and Speed (2006), the ICM algorithm incorporating the network structures and the ICM algorithm assuming that all the nodes are singletons (i.e., no dependency of the differential expression states). The performance results are shown in Table 1. We observed that both ICM algorithms provide better estimates of both η and ν than the EB algorithm.

Table 1.

Comparison of parameter estimates of three different procedures for four sets of simulations with different percentages of DE genes (q).

		Percentage of DE genes (q)
Method	Parameter	0.12 (0.005)	0.19 (0.008)	0.36 (0.009)	0.49 (0.008)
HMRF	$\widehat{\eta }$	0.38 (0.026)	0.40 (0.028)	0.41 (0.018)	0.44 (0.020)
	$\widehat{\nu }$	13.01 (0.061)	13.06 90.061)	13.12 (0.059)	13.18 (0.057)
HMRF-I	$\widehat{\eta }$	0.31 (0.019)	0.34 (0.017)	0.37 (0.013)	0.39 (0.012)
	$\widehat{\nu }$	13.03 (0.060)	13.06 (0.060)	13.15 (0.057)	13.22 (0.056)
EB	$\widehat{\eta }$	0.067 (0.004)	0.053 (0.003)	0.042 (0.002)	0.039 (0.001)
	$\widehat{\nu }$	7.27 (0.21)	7.43 (0.21)	7.86 (0.23)	8.21 (0.25)

HMRF: the proposed HMFR model and the ICM algorithm using the network structures; HMRF-I: the proposed HMFR model and the ICM algorithm without using the network structures; EB: the empirical Bayes method of of Tai and Speed (2006). Parameter estimates are averages over 100 simulations; standard error is shown in parentheses. The true parameters are (η, ν)=(0.5,13).

We then compare the sensitivity, specificity and FDR in identifying the DE genes with the EB method of Tai and Speed (2006). Since the EB method only provides ranks of the genes and does not infer gene states, for the purpose of comparison, we chose a cutoff value to declare genes to be DE using their method so that their approach would have the closest observed FDR levels to our proposed method. We applied the HMRF model to the simulated data sets. The results are summarized in Table 2, clearly showing that our approach obtained significant improvement in sensitivity compared to the other approaches making an independence assumption of genes. The smaller p was, the more improvements we obtained. At the same time, our approach also achieved lower FDRs and comparable specificity. Our proposed algorithm assuming that the genes are independent give very similar results to the EB method of Tai and Speed (2006).

Table 2.

Comparison of performance in terms of sensitivity, specificity and false discovery rate (FDR) of three different procedures based on 100 replications for four different scenarios with different percentages of DE genes (q).

q	Method	Sensitivity	Specificity	FDR
	HMRF	0.80(0.029)	1.00(0.0023)	0.045(0.019)
0.115 (0.005)	HMRF-I	0.70(0.042)	0.99(0.0027)	0.079(0.025)
	EB	0.69(0.054)	0.99(0.0027)	0.079(0.05)
	HMRF	0.87(0.033)	0.99(0.0049)	0.058(0.020)
0.189 (0.008)	HMRF-I	0.76(0.03)	0.99(0.004)	0.074(0.018)
	EB	0.75(0.032)	0.99(0.0041)	0.075(0.018)
	HMRF	0.91(0.016)	0.97(0.0065)	0.054(0.010)
0.357 (0.009)	HMRF-I	0.84(0.020)	0.97(0.0063)	0.066(0.011)
	EB	0.83(0.022)	0.97(0.0064)	0.066(0.011)
	HMRF	0.95(0.012)	0.94(0.012)	0.061(0.012)
0.486 (0.008)	HMRF-I	0.88(0.015)	0.95(0.0086)	0.060(0.0093)
	EB	0.88(0.015)	0.95(0.0087)	0.060(0.0094)

HMRF: the proposed HMFR model using the network structures; HMRF-I: the proposed HMFR model without using the network structures; EB: the empirical Bayes method of Tai and Speed (2006) with FDRs matched to the HMRF algorithm; Summaries are averaged over 100 simulations; standard deviation is shown in parentheses.

4.2 Sensitivity to misspecification of the network structure

Due to the fact that our current knowledge of biological networks is not complete, in practice, it is possible that the network structures that we use for network-based analysis are misspecified. The misspecification can be due to either the true edges of the networks being missed or the wrong edges being included in the network, or both of these scenarios. We performed simulation studies to evaluate how sensitive the results of the HMRF approach are to these three types of misspecifications of the network structures. We used the same data sets of 100 replicates as in the previous section but used different misspecified network structures when we fitted the hidden MRF model.

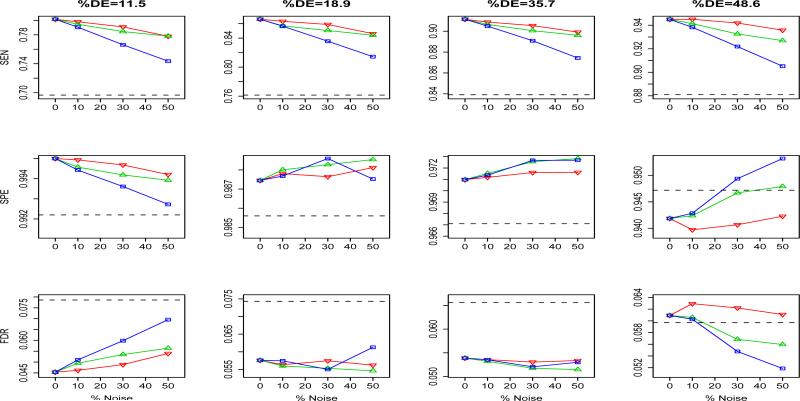
For the first scenario, we randomly removed 801 (10%), 2403 (30%) and 4005 (50%), respectively, from the 8011 true edges from the true KEGG networks when we fit the hidden MRF model. For the second scenario, we randomly added approximately 801, 2403 and 4005 new edges to the KEGG network, respectively. Finally, for the third scenario, we randomly selected 90%, 70% and 50% of the 8011 true edges and also randomly added approximately 801, 2403 and 4005 new edges to the network, respectively, so that the total number of edges remains approximately 8011. The results of the simulations over 100 replications are summarized as Figure 1. First, as expected, since the true number of DE genes is small, the specificities of the HMRF procedure remain very high and are similar when the true network structure is used. Second, we also observed that the FDR rates also remain almost the same as when the true structure is used. However, we observed some decreases in sensitivity in identifying the true DE genes. It is worth pointing out even when the network structure is largely misspecified as in scenario 3, the results from the HMRF model are still comparable to those obtained from the HMRF-I approach where the network structure is not utilized.

Figure 1.

Results in sensitivity, specificity and false discovery rate when the network structure is misspecified for four different sets of simulations corresponding to different proportions of DE genes. ▽: randomly deleting 10%, 30% and 50% of the true edges of the network; △: randomly adding approximately 801 (10%), 2403 (30%) and 4005 (50%) new edges to the network; □: randomly choosing 90%, 70% and 50% of the true edges and randomly adding 10%, 30% and 50% new edges to the network. The dashed line represents results without using the network structures.

Finally, we also applied these simulated data with a randomly created network structure with the same number of nodes and edges. As expected, in this case, the estimate of the β parameter was always zero or very close to zero, and therefore, the results in sensitivity, specificity and FDR are essentially the same as the method that does not utilize the network structure. These simulations seem to indicate that the results of the HMRF model are not too sensitive to the misspecification of the network structure unless the structure is greatly misspecified.

5 Application to Time-Course Gene Expression Study of TrkA- and TrkB-transfected Neuroblastoma Cell Lines

Neuroblastoma is the most common and deadly solid tumor in children, but this tumor also has a very high propensity to undergo spontaneous differentiation or regression. Evidence suggests that the Trk family of neurotrophin receptors plays a critical role in tumor behavior (Broduer, 2003). Neuroblastomas expressing TrkA are biologically favorable and prone to spontaneous differentiation or regression. In contrast, neuroblastomas expressing TrkB usually have MYCN amplification and are among the most aggressive and deadly tumors known. These tumors also express the TrkB ligand, resulting in an autocrine survival pathway. Unlike the TrkA-expressing tumors, exposure to ligand promotes survival under adverse conditions, but does not cause differentiation. In order to explore the biological basis for the very different behavior of neuroblastomas expressing these highly homologous neurotrophin receptors, a microarray time-course gene expression study was conducted by transfecting TrkA and TrkB into SH-SY5Y cells, a neuronal subclone from the NB cell line SK-N-SH. In particular, full length TrkA and TrkB were cloned into the retroviral expression vector pLNCX and transfected into SH-SY5Y cells. Cells were then serum starved overnight and treated with either nerve growth factor (NGF) and brain-derived neurotrophic factor (BDNF) at 37° for 0 to 12 hours. Fifteen micrograms of total RNA were then collected from TrkA- and TrkB-SY5Y cells exposed to 0, 1.5, 4 and 12 hrs of NGF or BDNF and the gene expressions were profiled using the Affymetrix GeneChip 133A. Four and three replicates were performed for the TrkA and TrkB cells, respectively. The robust multi-array (RMA) procedure (Irizarry et al., 2003) was used to obtain the gene expression measures.

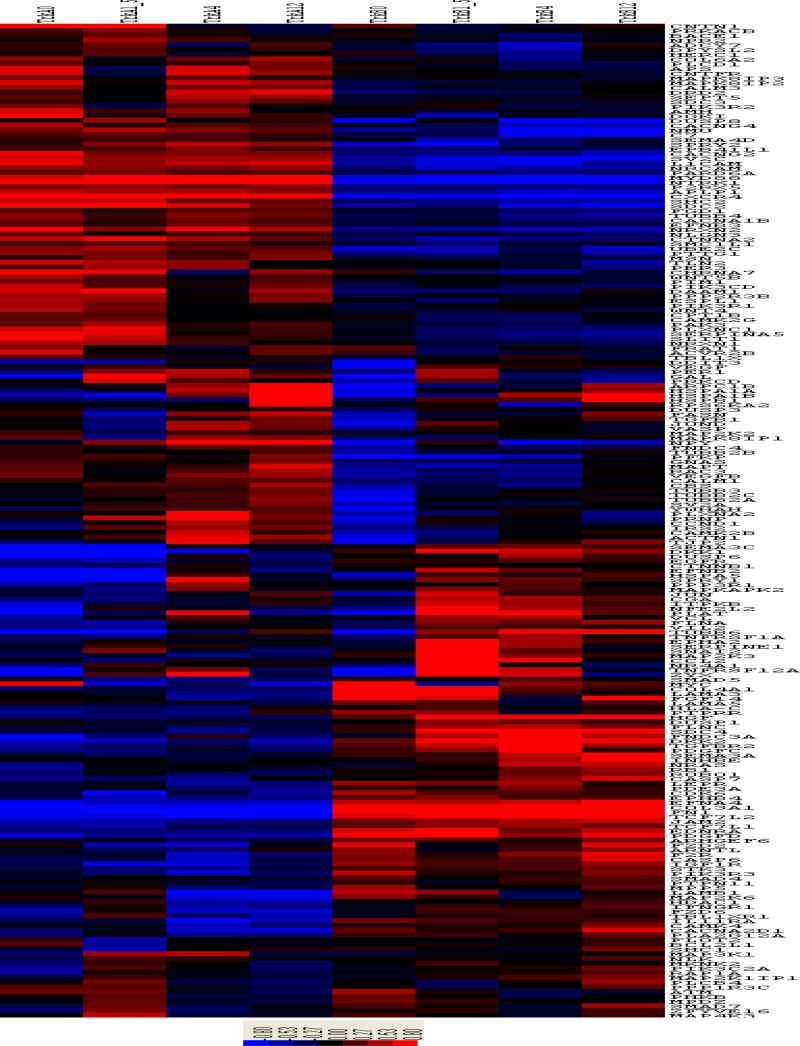
To perform network-based analysis of the data, we merged the gene expression data with the 33 KEGG regulatory pathways and identified 1533 genes on the Hu133A chip that could be found in the 1668-node KEGG network of 33 pathways. Instead of considering all the genes on the Hu133A chip, we only focused our analysis on these 1533 genes and aimed to identify which genes and which subnetworks of the KEGG network of 33 pathways are potentially related to the cell differentiation of TrkA-transfected cell lines. We analyzed the data using the HMRF model and obtained parameter estimates of $\widehat{\alpha }=-1.58$ and $\widehat{\beta }=0.39$, indicating that there are more genes with similar expression patterns than those with different expression patterns. Our method identified 210 DE genes out of the 1533 KEGG genes with posterior probability of being a DE gene greater than 0.5, among these 118 are connected on the KEGG pathways and 92 are isolated, not collecting to other DE genes. There is a large cluster of genes that are largely up-regulated in the Trk A transfected cells but are down-regulated in the Trk B transfected cells. Similarly, there is a cluster of genes that are up-regulated in the Trk B-transfected cells but are down-regulated in the Trk A transfected cells (See Figure 2).

Figure 2.

Heatmap clustering plot of the 210 DE genes on the KEGG pathways, showing different expression patterns between the TrkA and TrkB time-courses. The first four columns correspond to the TrkA time course experiments at times 0, 1.5, 4 and 12 hr, the second four columns correspond to the TrkB time-course experiments at times 0, 1.5, 4 and 12 hr.

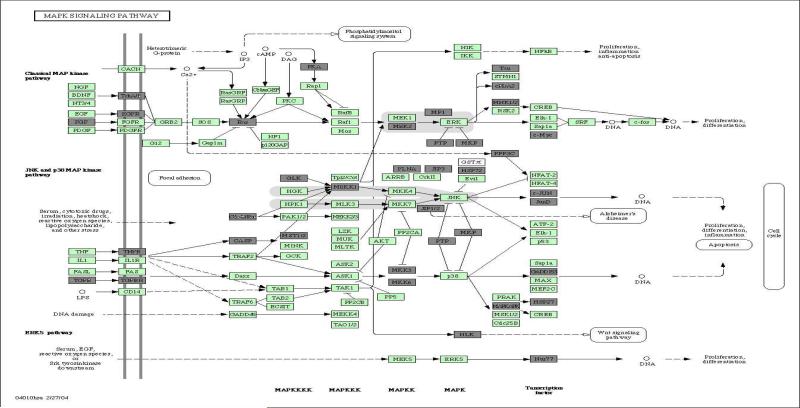
Among the 33 KEGG regulatory pathways, enrichment analysis using DAVID Tools (Dennis et al., 2003) identified that the mitogen-activated protein kinase (MAPK) signaling pathway, focal adhesion pathway and pathway related to prion diseases are enriched with p-values of 0.012, 0.029 and 0.05, respectively, of which the MAPK signaling pathway and the focal adhesion pathway are inter-connected. The MAPK (Erk1/2) signal transduction pathway is expressed and active in both TrkA and TrkB expressing NB cells after specific ligand-mediated Trk receptor phosphorylation. The distinct role that this signaling pathway plays in the biologic heterogeneity of NB is not well known; however, we have shown that the time course of pathway activation by phosphorylation of signal effector proteins is different between TrkA- and TrkB- expressing NB cells, and this may, in part, explain the biological differences between TrkA- vs. TrkB-expressing tumors. To give a detailed comparison of TrkA- and TrkB-mediated genomic responses, we present in Figures 3 and 4 the DE genes on the MAPK signaling pathway and on the KEGG focal adhesion pathway. On the MAPK pathway, it is not surprising that the TrkA/B shows different expression patterns. We also observed that a cluster of genes (or a subnetwork) in the neighborhood of ERK shows different expression patterns, including MEK2, MP1, PTP, MKP, Tau, cPLA2, MNK1/2 and c-Myc (see Figure 3). This subnetwork, leading to cell proliferation and differentiation, may partially explain the difference in cell differentiation between the TrkA- and TrkB-infected NB cells. Another interesting subnetwork in the neighborhood of p38, including MKK3, MKK6, PTP, MKP, MAPKAPK, GADD153 and HSP27, also showed differential expression patterns. This subnetwork also related to cell proliferation and differentiation. Activation of these two subnetworks on the MAPK pathway may explain the different biological behaviors of these two types of NB cells, especially in terms of cell differentiation. MAPK signaling in the nervous system has been shown to promote a broad array of biologic activities including neuronal survival, differentiation, and plasticity. Regulating the duration of MAPK signaling is important in neurogenesis, and likely plays a similar role in the behavior of Trk-expressing neuroblastomas. Prolonged activation of MAPK is correlated with neurotrophin-dependent cell cycle arrest and terminal cellular differentiation in the PC12 pheochromocytoma cell line, whereas short-duration MAPK signaling is correlated with mitogenic and proliferative cell signaling in PC12 cells (Tombes et al., 1998; Kao et al., 2001; Marshall, 1995; Qui and Green, 1992). TrkA-expressing NB cells treated with NGF (which activates MAPK) increase the number and length of extended neurites and decrease cell proliferation resulting in a more mature neuronal appearing cell, while TrkB-expressing NB cells treated with ligand (BDNF) increase cell proliferation without morphologic differentiation.

Figure 3.

Differential expression states for genes on the KEGG MAPK pathway, where genes colored in dark gray are multivariate differentially expressed and those colored in light green are equally expressed.

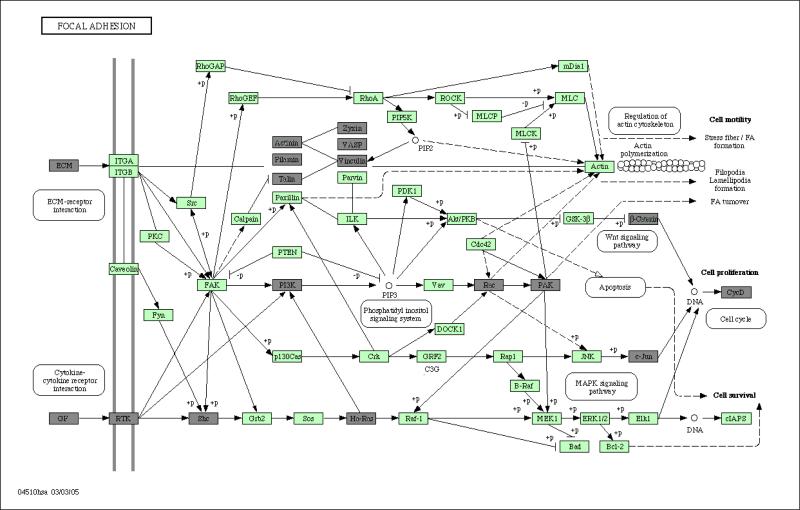
Figure 4.

Differential expression states for genes on the KEGG Focal Adhesion pathway, where genes colored in dark are multivariate differentially expressed and those colored in light green are equally expressed.

Increasing evidence suggests an important role for the focal adhesion kinase (FAK) pathway (See Figure 4) in regulating cancer cell adhesion in response to extracellular forces or mechanical stress. Studies have demonstrated that tumor cells are able to regulate their own adhesion by over-expression or alteration in activity of elements within the FAK signaling pathway, which may have implications in the survival, motility and adhesion of metastatic tumor cells (Basson, 2008). While mechanotransduced stimulation of the FAK signaling pathway appears to be a cell surface receptor independent process, the FAK pathway also acts downstream of receptor tyrosine kinases and has been shown to be phosphorylated in response to external cytokine/ligand stimuli. The insulin-like growth factor-1 receptor (IGF-1R) and FAK physically interact in pancreatic adenocarcinoma cells resulting in activation of a common signal transduction pathway that leads to increased cell proliferation and cell survival (Liu et al., 2008). In neuroblastoma, MYCN regulates FAK expression by directly binding to the FAK promoter, and increasing transcription of FAK mRNA. Beierle et al. (2007) have correlated FAK mRNA abundance with MYCN expression in MYCN-amplified and non-amplified NB cell lines by real time quantitative PCR, and their data suggest that MYCN regulation of FAK expression directly impacts cell survival and apoptosis. On the focal adhesive pathway, we observed that a subnetwork of 6 genes, including Actinin, Filamin, Talin, Zyxin, VASP, Vinculin, that show differential expression patterns (see Figure 4). In addition, PI3K and its neighboring genes GF, RTK, Shc and Ha-Ras show differential expression patterns. We have not yet explored the regulation of FAK pathway activity by TrkA or TrkB expression and activation in our NB cell lines, but the differential expression states for genes on the KEGG FAK pathway suggest differential mediation by TrkA vs. TrkB, that may have downstream biological relevance.

Finally, on the pathway related to prion disease, we observed that Prion Protein (PrPc) and its neighboring genes HSPA5, APLP1, NRF2 and LAMB1 show differential expression patterns.

6 Conclusion and Discussion

In this paper we have proposed a hidden MRF model and an ICM algorithm that utilizes the gene regulatory network information to identify multivariate differentially expressed genes. The method extended the approach of Wei and Li (2007) for univariate to multivariate gene expression data such as time course data. Also different from the approach of Wei and Li (2008) for network-based analysis of microarray time-course gene expression data, this new approach identifies the genes that show different expression patterns over time rather than identifies the differentially expressed genes at each time point. Instead of assuming all genes are independent as in the empirical Bayes approach of Tai and Speed (2006), our method models the dependency of the latent differential expression states based on the prior regulatory network structures. Simulation studies show that our methods outperform the methods that do not utilize network structure information. We applied our method to analyze the MTC data of TrkA- and TrkB-transfected neuroblastoma cell lines and identified the MAPK and focal adhesive pathways from the KEGG that are related to cell differentiation in TrkA-transfected cell lines. Note that the proposed methods can also be applied to other types of genomic data such as proteomic data and protein-protein interaction data.

In this paper, we analyzed the neuroblastoma MTC data using KEGG pathways and aimed to identify the KEGG pathways that may explain the differentiation states of the two different NB cell lines. However, the proposed methods can be applied to any other networks of pathways. If an investigator is only interested in a particular pathway, the proposed method can be applied to that particular pathway. If an investigator is interested in fully exploring his/her data and all available pathways, one should use a large collection of pathways, e.g., the pathways collected by Pathway Commons (http://www.pathwaycommons.org/pc/). It should also be noted that our proposed methods can include all the genes probed on microarray by simply adding isolated nodes to the graphs. A related issue is that our knowledge of pathways is not complete and can potentially include errors or misspecified edges on the networks. Although our simulations demonstrate that our methods are not too sensitive to the misspecification of the network structures, the effects of misspecification of the network on the results deserve further research. One possible solution to this problem is to first check the consistency of the pathway structure using the data available. For example, if the correlation in gene expression levels between two neighboring genes is very small, we may want to remove the edge from the pathway structure. Alternatively, one can build a set of new pathways using various data sources and compare these pathways with those in the pathway databases in order to identify the most plausible pathways for use in the proposed MRF method. For example, we can construct a large molecular network with the nodes being the gene products and the links extracted from the KEGG database, the Biomolecular Interaction Network Database (BIND) and Human Interactome Map (HIMAP) (Alfarano et al., 2005). This will provide more comprehensive description of known biological pathways and networks than using data from only one source.

In summary, generation of high-throughput genomic data together with intensive biomedical research has generated more and more reliable information about regulatory pathways and networks. It is very important to incorporate the network information into the analysis of genomic data in order to obtain more interpretable results in the context of known biological pathways. Such integration of genetic network information with high-throughput genomic data can potentially be useful for identifying the key molecular modules and subnetworks that are related to complex biological processes.