Abstract
Previous research shows that children’s ability to estimate numbers of items using their Approximate Number System (ANS) predicts later math ability. To more closely examine the predictive role of early ANS acuity on later abilities, we assessed the ANS acuity, math ability, and expressive vocabulary of preschoolers twice, six months apart. We also administered attention and memory span tasks to ask whether the previously reported association between ANS acuity and math ability is ANS-specific or attributable to domain-general cognitive skills. We found that early ANS acuity predicted math ability six months later, even when controlling for individual differences in age, expressive vocabulary, and math ability at the initial testing. In addition, ANS acuity was a unique concurrent predictor of math ability above and beyond expressive vocabulary, attention, and memory span. These findings of a predictive relationship between early ANS acuity and later math ability add to the growing evidence for the importance of early numerical estimation skills.
Keywords: Approximate Number System (ANS), math ability, longitudinal, predictive relationship, numerical estimation
1. Is Approximate Number Precision a Stable Predictor of Math Ability?
The percentage of college degrees awarded in the STEM disciplines (science, technology, engineering, and mathematics) in the United States has declined over the past five years while the need for skilled workers in these areas has surged (National Science Board, 2010). Consequently there has been a rise in initiatives to improve education in these fields, and to better understand the factors that lead to children developing interest and ability in math and science. In the domain of mathematics, a wealth of recent research has investigated the relationship between children’s math abilities and environmental factors such as home learning environment (LeFevre et al., 2010; LeFevre et al., 2009; Melhuish et al., 2008), socio-economic status (Jordan & Levine, 2009), culture (Chen & Stevenson, 1995), teacher characteristics (Aunola, Leskinen, & Nurmi, 2006; Beilock, Gunderson, Ramirez, & Levine, 2010; Klibanoff, Levine, Huttenlocher, Vasilyeva, & Hedges, 2006), and instructional style in the classroom (Crosnoe et al., 2010). In addition to these external factors, internal factors such as individual differences in various cognitive skills appear to play a role in explaining differences in math ability (Alloway & Passolunghi, 2011; Cirino, 2011; Geary, Bailey, & Hoard, 2009; LeFevre et al., 2010; Mazzocco & Kover, 2007). Here we investigate one of these internal factors by asking whether differences in children’s basic numerical estimation skills predict their later math ability.
Basic numerical estimation skills are thought to rely on an Approximate Number System (ANS) which represents numerical information using noisy mental magnitudes that are normally distributed around the number to be represented (Dehaene, 1997; Feigenson, Dehaene, & Spelke, 2004; Gallistel & Gelman, 2000). A hallmark of the ANS is that the noise in the numerical representations increases as the numbers get larger (i.e., a representation of ten objects is noisier than a representation of five objects). This feature of the ANS yields estimation performance that adheres to Weber’s Law, whereby success at discriminating two estimated numerosities depends on their ratio rather than their absolute difference. For example, when relying on the ANS it is equally difficult to determine that five objects are less than ten as it is to determine that one hundred objects are less than two hundred. However, it is almost impossible to determine that one hundred objects are less than one hundred-and-five objects without verbally counting each collection. This is because the noisy ANS representations of one hundred and one-hundred-and-five have a large degree of overlap. In contrast, these quantities can be easily differentiated using the system of symbolic integer representations that children acquire when they learn to count (Carey, 2009). This characteristic noisiness of the ANS has been observed across the human lifespan (e.g., Halberda & Feigenson, 2008; Halberda, Ly, Willmer, Naiman, & Germine, 2012; Holloway & Ansari, 2008; Izard, Sann, Spelke, & Streri, 2009; Libertus & Brannon, 2010; Libertus, Pruitt, Woldorff, & Brannon, 2009; Xu & Spelke, 2000), and across a range of non-human animal species (e.g., Agrillo, Dadda, Serena, & Bisazza, 2008; Cantlon & Brannon, 2006; Meck, Church, & Gibbon, 1985) – although the degree of noise in ANS representations differs across people in two important ways. First, ANS acuity has been shown to improve (i.e., become less noisy) across development, until about 30 years of age (Halberda & Feigenson, 2008; Halberda et al., 2012; Libertus & Brannon, 2010; Lipton & Spelke, 2003). Second, even within a single age group there is considerable variation in individual ANS acuity (Halberda, Mazzocco, & Feigenson, 2008; Libertus & Brannon, 2010; Mazzocco, Feigenson, & Halberda, 2011a; Piazza et al., 2010).
Are the primitive representations of the ANS related to the more sophisticated mathematical abilities mastered later in life? On the one hand, the fact that preverbal infants (who are years away from acquiring the exact integer concepts required for formal math) and non-human animals (who will never learn formal math) demonstrate ANS representations may call into question the link between ANS acuity and symbolic math abilities. That these populations show ANS proficiency in the absence of formal math skill shows that having an ANS is not sufficient to generate formal math concepts or abilities. However, recent findings suggest that the ANS and math are in fact linked; these studies found that individual differences in ANS acuity correlate with concurrently measured individual differences in math ability in preschool-aged children (Libertus, Feigenson, & Halberda, 2011), and that this relationship extends through high school (Halberda et al., 2008), into the college years (Libertus, Odic, & Halberda, 2012) and beyond (Halberda et al., 2012). That is, the finer the non-verbal numerical discriminations people are able to make, the better they do on standardized math tests (for review see Feigenson, Libertus, & Halberda, in press).
The above findings suggest a relationship between the ANS and math ability, but do not reveal the causal link between them. One starting point toward filling this gap is to ask whether ANS acuity actually predicts later math abilities, or whether instead the relationship only appears when measured concurrently (e.g., Libertus et al., 2011), or when ANS acuity is used to retrospectively predict math ability (Halberda et al., 2008; Libertus et al., 2012). One finding does suggest that in addition to early counting skills and number knowledge predicting later math abilities (Jordan, Kaplan, Locuniak, & Ramineni, 2007; Jordan, Kaplan, Ramineni, & Locuniak, 2009), early ANS precision also has predictive power. Mazzocco, Feigenson, and Halberda (2011b) measured the ANS acuity of seventeen children when they were in preschool, then measured their math ability as well as IQ and lexical retrieval skills two years later (after the children had entered primary school). Children’s ANS acuity in preschool was found to predict later math ability but not their general IQ or lexical retrieval skills.
Although this finding is consistent with a predictive role of early ANS acuity on later math ability, caution should be taken in its interpretation. Previous research has shown that individual differences in math ability already exist prior to the onset of formal math instruction (e.g., Jordan, Kaplan, Olah, & Locuniak, 2006). As described above, these differences in early math ability are already associated with individual differences in ANS acuity before children enter primary school (Libertus et al., 2011). Therefore, the relationship between ANS acuity and math ability found by Mazzocco and colleagues (2011b) could be due to an early relationship between ANS acuity and math ability where ANS acuity plays no further role in the development of later math skills. Only by controlling for early math abilities can a robust predictive relationship between early ANS acuity and later math ability be demonstrated. Put differently, controlling for early math abilities and then measuring the correlation between early ANS acuity and later math ability allows one to ask whether early ANS acuity predicts growth in math abilities across development. To date, this remains an open question.
Here, we measured the ANS acuity and math ability of 204 preschool-aged children twice, with a 6-month delay, and tested for a predictive relationship between the two. We improved on previous approaches in the following ways: first, we examined the relationship between ANS acuity and later math ability while controlling for individual differences in math ability during the first testing session. Second, we included a larger sample (N = 204 in the present study compared to N = 17 in Mazzocco et al., 2011b). Third, we measured both accuracy and reaction time (RT) in the ANS acuity task. Fourth, we included independent, non-numerical assessments of attention and working memory in order to ask whether accuracy and RT on the ANS acuity task make unique contributions to predicting concurrent math ability even when controlling for domain-general processing speed, attention, and working memory. Previous findings suggest that both RT and accuracy on the ANS acuity task are uniquely linked to math ability (Libertus et al., 2011). However, only by controlling for RT and working memory on nonnumerical tasks can we determine whether these contributions, especially the RT effects, reflect domain-general attention effects, or instead reflect specific links between the ANS and math ability. Taken together, these improvements allow for a more thorough and robust assessment of the relationship between early ANS acuity and later math abilities.
2. Method
2.1. Participants
A sample of 204 children was recruited to participate in a 4-year longitudinal study on the relationship between the Approximate Number System (ANS) and math ability in preschool-aged children. Two hundred of these children completed testing at Time 11 and we attempted to test 201 children at Time 2. Thirty-two of these children could not be re-tested due to family relocation (n = 10), inability to participate at Time 2 (n = 3), declining to remain in the longitudinal study (n = 5), and inability to reach the family by phone, email, or regular mail (n = 14). Testing at Time 2 comprised two experimental sessions. Four children completed only the first session because they were unable to return for the second. Sample sizes and demographic information for each testing time are reported in Table 1. Parents of all children tested provided informed written consent prior to their child’s participation. All children received a small gift (e.g., pencil, stickers) to thank them for their participation.
Table 1.
Demographic information for participants at Time 1 and Time 2
| Time 1 | Time 2 | ||
|---|---|---|---|
| Visit 1 | Visit 2 | ||
| N | 200 | 169 | 165 |
| Mean age (SD) | 4 y 2 m (8.7 m) | 4 y 9 m (8.9 m) | 4 y 10 m (9.0 m) |
| Number of females | 97 | 82 | 79 |
| Tested at preschool | 88 | 82 | 82 |
2.2. Materials and Procedure
At Time 1 and Time 2, we administered an ANS acuity task, the Test of Early Mathematics Ability (TEMA-3; Ginsburg & Baroody, 2003), and an experimenter-designed parent vocabulary questionnaire (Libertus, Odic, Feigenson, & Halberda, under review) to measure ANS acuity, math ability, and expressive vocabulary respectively. At Time 2, we also administered Conners’ Kiddie Continuous Performance Test (K-CPT; Conners, 2006) to measure children’s attention, as well as a forward and backward digit and letter span task to measure children’s memory span. Because of the large literature on the relationship between math ability and memory (e.g., Bull, Espy, & Wiebe, 2008; Swanson & Kim, 2007), we included a memory span assessment for additional empirical questions of interest that are reported in greater detail elsewhere (Libertus, Feigenson, & Halberda, in preparation-b). In the present paper, memory span is only included as a control variable.
2.2.1. ANS acuity task
To measure the acuity of children’s Approximate Number System (ANS), we administered a version of Panamath (the Psychophysical Assessment of Numerical Approximation; Halberda & Ly, in preparation) – a non-symbolic numerical comparison task (Halberda et al., 2008; Libertus et al., 2011) (for a free download of the software visit www.panamath.org). Children were shown arrays of spatially separated blue and yellow dots on a 13-inch Apple MacBook laptop screen, and were asked to indicate whether more of the dots were blue or more of the dots were yellow. The experimenter initiated each trial when the child appeared to be attentive. The blue and yellow dots were visible for 2000 ms followed by a blank screen that remained until the child gave a verbal response (e.g., “yellow”). The experimenter, who was unable to see the computer screen, immediately pressed the corresponding key on an external keyboard (e.g., “y” for “yellow”). This allowed us to record the answer and the response time from the time of image onset until the key press. Two different sounds provided feedback throughout the experiment. A high-pitched tone indicated a correct answer; a low-pitched tone indicated an incorrect answer. Children were familiarized to these sounds on six practice trials during which the experimenter provided additional verbal feedback to ensure that children understood the task and were motivated to participate. Following these practice trials, a total of 60 test trials were presented.
The number of dots in each collection (blue and yellow) ranged from 4 to 15, with these numbers chosen because previous research has shown that numbers in this range successfully tap ANS representations (Halberda & Feigenson, 2008; Halberda et al., 2008; Inglis, Attridge, Batchelor, & Gilmore, 2011). Test trials were randomly drawn from one of four numerical ratio bins: 1:2, 2:3, 3:4, 6:7 (with the absolute number of dots on each trial varying, such that a trial with e.g., 5 yellow versus 10 blue dots would go into the 1:2 ratio bin). On half of the trials the yellow dots were more numerous; on the other half the blue dots were more numerous. On half of the trials the two arrays were equated for individual dot size (i.e., the average size of the dots in each collection was equal). On the other half of the trials, the cumulative surface area of the blue dots and the yellow dots was equated (i.e., the average size of the dots was smaller for the more numerous set). The default radius of the dots was 60 pixels and the maximum variability in size between the dots was +/−35%. The minimum distance between dots was 85 pixels from edge to edge.
Split-half reliability of the performance of children in this sample was 0.65 at Time 1 and 0.72 at Time 2. Previously published data from older children and adults on a similar ANS acuity task showed split-half reliabilities ranging from 0.56 to 0.72 depending on the number of trials (Halberda et al., 2012).
2.2.2. Mathematical ability
At Time 1 and Time 2, we administered Form A of the Test of Early Mathematics Ability (TEMA-3; Ginsburg & Baroody, 2003). The TEMA-3 measures numbering skills (e.g., verbally counting the number of objects on a page), number-comparison facility (e.g., determining which of two spoken number words is larger), numeral literacy (e.g., reading Arabic numerals), mastery of number facts (e.g., retrieving multiplication facts), calculation skills (e.g., solving mental and written addition and subtraction problems), and number concepts (e.g., answering how many tens are in one hundred). The TEMA-3 has been normed for children between the ages of 3 years 0 months and 8 years 11 months, and test-retest reliability for TEMA-3 Form A with a two-week delay between administrations has been found to be high (r = 0.82).
2.2.3. Expressive vocabulary
At Time 1 and Time 2, we measured children’s expressive vocabulary using a parent questionnaire. The questionnaire contained a list of the first 212 words from Form A of the Peabody Picture Vocabulary Test (PPVT-4; Dunn & Dunn, 2007), and parents were asked to indicate which of the listed words they had heard their child say. An independent study found that the number of words that parents reported to have heard their child say from this questionnaire increased significantly with age (R2 = 0.24, p < 0.001) and showed high concurrent (MacArthur-Bates Communicative Development Inventories-III: R2 = 0.63, p < 0.001; PPVT-4: R2 = 0.47, F(1,90) = 79.71, p < 0.001) and predictive validity (R2 = 0.28, p < 0.001) with children’s performance on the PPVT-4 (Libertus et al., under review). We used the questionnaire rather than the experimenter-administered PPVT-4 to shorten the overall testing time, since participants in the current study already were completing several lengthy assessments.
2.2.4. Attention measure
At Time 2 only, we administered Conners’ Kiddie Continuous Performance Test (K-CPT; Conners, 2006) to measure children’s attention and response speed on a simple computerized task that did not involve numbers or numerical comparisons. Children saw images of common objects on a computer screen and were asked to push a button every time they saw a picture other than a ball. Each picture was presented for 500 milliseconds, and in different blocks the inter-stimulus interval (ISI) was either 1.5 or 3 seconds. There were a total of five blocks, with two sub-blocks of 20 trials each for each ISI. The total testing time was 7.5 minutes. The K-CPT is a standardized measure of attention that is normed for children 4–5 years of age. However, since some of the children tested in our study were outside this age range, here we report raw scores instead of standardized scores. Split-half reliability of the K-CPT ranges from 0.72 to 0.88 depending on the measure of interest (Conners, 2006).
2.2.5 Memory span
At Time 2 only, we measured children’s memory span using widely used digit and letter span tasks. The experimenter read sequences of digits or letters out loud at a rate of approximately one item per second, and then the child attempted to repeat the items in the same order (forward span) or the reverse order (backward span). Testing always began with sequences of two items. There were two trials for each sequence length and testing ended when the child erred on both trials of a sequence length for any given condition. Children always completed the digit condition before the letter condition and forward span was always assessed before backward span.
2.2.6. Procedure
Three experienced experimenters conducted all testing sessions, which occurred either in the laboratory or in children’s preschools. At Time 1, testing took place over a single session, and at Time 2 testing was divided into two sessions. The average delay between testing at Time 1 and the first session of Time 2 testing was 6.8 months (SD = 47 days). The average delay between the two testing sessions for assessment Time 2 was 13.01 days (SD = 12.71 days; range = 0 days – 68 days). In a few cases where both testing sessions occurred on the same day, children took a break between the two testing sessions to avoid fatigue.
At Time 1, children completed the Test of Early Mathematics Ability (TEMA-3; Ginsburg & Baroody, 2003) and then the ANS acuity task. Testing lasted about 30–45 minutes. During the first session at Time 2, children completed the TEMA-3 and then Conners’ Kiddie Continuous Performance Test (K-CPT; Conners, 2006). This session lasted about 30–45 minutes. During the second testing session at Time 2, children first completed the ANS acuity task and then the memory span task. The complete results for the latter are reported in a separate paper (Libertus et al., in preparation-b) and performance on this task is only used as a control variable in the present paper. This second session lasted about 20 minutes. Task order was kept constant across participants to reduce between-subject noise variability. Parents of children who were tested in the laboratory completed the expressive vocabulary questionnaire (Libertus et al., under review) before or during children’s testing sessions at Time 1 and Time 2. Parents of children who participated in preschools were sent the questionnaire and asked to return it by email, fax, or regular mail for each testing time.
3. Results
Descriptive results from all tasks are summarized in Table 22. All statistical analyses were performed only on the subsets of our sample that provided data for all measures included in a given analysis (i.e., we did not replace missing data).
Table 2.
Descriptive information for all tasks and dependent measures at Time 1 and Time 2. Note that the attention and memory span tasks were only administered at Time 2. See Libertus, Feigenson and Halberda (2011) for an explanation of each sample size at Time 1 and Footnote 2 for an explanation of each sample size at Time 2.
| Task | Measure | Time 1 N | Time 1 Mean (SD) | Time 2 N | Time 2 Mean (SD) |
|---|---|---|---|---|---|
| ANS acuity task | Accuracy (% correct) | 174 | 65.10 (15.15) | 160 | 76.10 (14.01) |
| RT in ms | 174 | 3205.13 (988.93) | 160 | 2534.10 (615.54) | |
| w | 122 | 0.64 (0.49) | 144 | 0.42 (0.37) | |
| TEMA-3 (math ability task) | Std score | 174 | 107.43 (15.00) | 168 | 109.53 (14.93) |
| Vocabulary questionnaire (expressive vocabulary) | # of words used | 160 | 93.08 (27.81) | 143 | 109.36 (29.85) |
| K-CPT (attention task) | RT | -- | -- | 158 | 687.33 (143.24) |
| d′ | -- | -- | 158 | 0.39 (0.42) | |
| Memory span (forward and backward letter and digit span task) | # of correct sequences | -- | -- | 163 | 4.24 (0.94) |
3.1. ANS Acuity Task
Children’s performance on the Approximate Number System (ANS) acuity task was analyzed in terms of accuracy (percent correct) and response time (RT, see Table 2). As expected, children’s average accuracy increased and RT decreased between Time 1 and Time 2 (for a detailed analysis of the developmental improvement see Libertus, Feigenson, & Halberda, in preparation-a). As predicted by Weber’s Law, children’s accuracy decreased as the numerical ratio increased (i.e., as the ratio of blue to yellow dots approached equality). As in previous studies, we used a psychophysical model to estimate each participant’s Weber fraction w—this served as an index of ANS acuity (i.e., the amount of noise in each participant’s underlying ANS representations; for details see e.g. Halberda & Feigenson, 2008; Halberda et al., 2008; Libertus et al., 2011; Pica, Lemer, Izard, & Dehaene, 2004). Briefly, in this model the numerosities of the two collections are modeled as Gaussian random variables with means n1 and n2 and standard deviations equal to w multiplied by the respective mean. Subtracting the Gaussian for the numerically smaller array from the numerically larger array yields a new Gaussian with a mean of n1-n2 and a standard deviation of . Accuracy is modeled as 1 minus the error rate where the error rate is defined as the area under the tail of the resulting Gaussian: . Using this method, the noise in each participant’s mental ANS representations was estimated by the single free parameter w using maximum likelihood estimation. The model did not settle on a reliable fit for some of our participants (see Table 2). Thus, we performed analyses on w only for participants for whom the model yielded a reliable fit, but also conducted the same analyses using accuracy as an estimate for ANS acuity for all of the children in our sample.
3.2. Mathematical Ability, Vocabulary Size, Attention and Memory Span
Children’s average standardized score on the Test of Early Mathematics Ability (TEMA-3) and their scores on the expressive vocabulary questionnaire are shown in Table 2. We used RT on the Conners’ Kiddie Continuous Performance Test (K-CPT) to control for individual differences in response execution in our ANS acuity task because both tasks involved rapidly responding to briefly-flashed visual stimuli on a computer screen. For the memory span task, scores were obtained by summing the number of correctly reproduced sequences in each condition and then averaging across them. Scores of zero were excluded from further analyses as they probably reflected inattention during task administration or an inability to follow the task instructions (a particular problem for younger children on the backward span tasks). Pearson’s correlation coefficients between all measures can be found in Table 3.
Table 3.
Correlations coefficients between all three ANS acuity measures (Accuracy, RT, w) at T1 and T2, Test of Early Mathematics Ability (TEMA) and expressive vocabulary (Vocab) scores at T1 and T2, and attention (K-CPT) and memory span (MS) measures at T2.
| ANS at T1 | ANS at T2 | TEMA at T1 | TEMA at T2 | Vocab at T1 | Vocab at T2 | K-CPT at T2 | MS at T2 | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Accuracy | RT | w | Accuracy | RT | w | |||||||
| 1 | -- | −0.20* | −0.85** | 0.51** | −0.14 | −0.41** | 0.44** | 0.46** | 0.25** | 0.20* | −0.11 | 0.26** |
| 2 | -- | 0.12 | −0.31** | 0.22** | 0.05 | −0.28** | −0.33** | −0.13 | −0.05 | 0.13 | −0.09 | |
| 3 | -- | −0.36** | −0.03 | 0.34** | −0.26** | −0.25* | −0.20* | −0.13 | 0.05 | −0.21* | ||
| 4 | -- | −0.31** | −0.87** | 0.48** | 0.52** | 0.20* | 0.12 | −0.11 | 0.19* | |||
| 5 | -- | 0.27** | −0.14 | −0.36** | −0.06 | 0.02 | 0.16 | −0.25** | ||||
| 6 | -- | −0.41** | −0.42** | −0.18* | −0.13 | 0.20* | −0.10 | |||||
| 7 | -- | 0.76** | 0.18* | 0.14 | −0.02 | 0.30** | ||||||
| 8 | -- | 0.21* | 0.11 | −0.08 | 0.35** | |||||||
| 9 | -- | 0.73** | −0.06 | 0.17* | ||||||||
| 10 | -- | −0.08 | 0.04 | |||||||||
| 11 | -- | −0.09 | ||||||||||
p < 0.05,
p < 0.01
3.3. Predictive Role of ANS Acuity and Vocabulary Size on Later Math Ability and Expressive Vocabulary
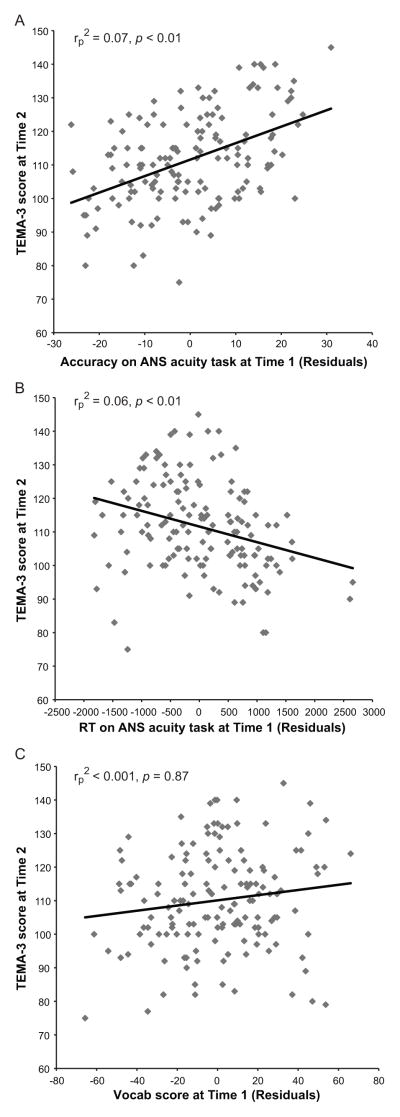
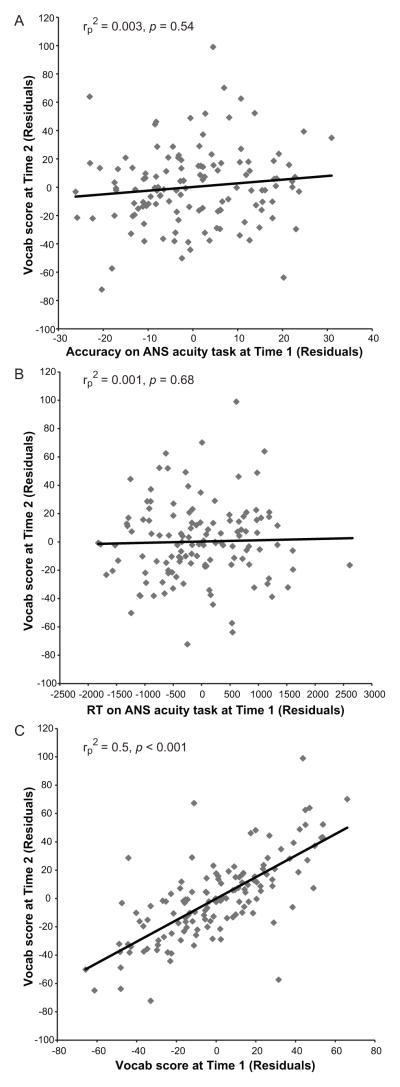
To assess the role of early ANS acuity and vocabulary size on children’s math ability and vocabulary size six months later, we performed two linear regression analyses: ANS acuity (measured via accuracy and RT)3, TEMA-3, and expressive vocabulary scores at Time 1 were all entered as possible predictors for TEMA-3 scores (model 1) and expressive vocabulary scores (model 2) at Time 2. In both analyses, we also controlled for age at the time of testing. As seen in Table 4, the two models predicted a significant amount of variance in children’s math ability and vocabulary size at Time 2. Most importantly, in model 1 accuracy and RT on the ANS acuity task were significant unique predictors of later math ability, even when controlling for initial math ability, age, and expressive vocabulary at Time 1 (see Figure 1). In contrast, in model 2 initial expressive vocabulary scores were the only significant predictor of later expressive vocabulary size (see Figure 2). This demonstrates a specific relationship between early ANS acuity (measured in terms of accuracy and RT on our ANS acuity task) and later math ability, as well as a specific relationship between early and later expressive vocabulary.
Table 4.
Linear regression analyses predicting math ability (TEMA-3, model 1) and expressive vocabulary size (Vocab, model 2) at Time 2 using accuracy and RT on the ANS acuity task, expressive vocabulary scores (Vocab), and TEMA-3 scores at Time 1 as possible predictors
| Model 1 predicting TEMA-3 at Time 2 | Model 2 predicting Vocab at Time 2 | |||||
|---|---|---|---|---|---|---|
| R2 | 0.61 | 0.51 | ||||
| F-statistics | F(4,129) = 50.03 | F(4,119) = 31.25 | ||||
| p-statistics | p < 0.001 | p < 0.001 | ||||
| Predictor | rp2 | p | Predictor | rp2 | p | |
| Vocab | < 0.001 | 0.87 | Vocab | 0.5 | < 0.001 | |
| ANS-RT | 0.06 | 0.004 | ANS-RT | 0.001 | 0.68 | |
| Accuracy | 0.07 | 0.002 | Accuracy | 0.003 | 0.54 | |
| TEMA-3 | 0.45 | < 0.001 | TEMA-3 | < 0.001 | 0.94 | |
Figure 1.
Relationship between math ability (TEMA-3) at Time 2 and accuracy (A) and RT (B) on the ANS acuity task as well as expressive vocabulary score (C) at Time 1 adjusted for age at testing. Statistical results are partial correlations as reported in Table 4.
Figure 2.
Relationship between expressive vocabulary size (Vocab score) at Time 2 and accuracy (A) and RT (B) on the ANS acuity task as well as Vocab score (C) at Time 1 adjusted for age at testing. Statistical results are partial correlations as reported in Table 4.
3.4. The Influences of Expressive Vocabulary, Attention, and Memory Span on the Relationship Between ANS Acuity and Math Ability
To assess the roles of expressive vocabulary, attention, and memory span as possible influences on the concurrent relationship between ANS acuity and math ability, we performed two linear regression analyses using accuracy or w and RT on the ANS acuity task, expressive vocabulary scores, RT on the attention task, and memory span scores as possible concurrent predictors for TEMA-3 scores while controlling for age4. Table 5 reports partial correlations that represent the proportion of variance in math ability scores explained by the listed variable while controlling for the remaining variables. As Table 5 shows, the two models captured a significant amount of variance in children’s math ability. Most importantly, both estimates of ANS acuity in each model (i.e., accuracy and RT, or w and RT) contributed uniquely to the relationship with math ability when controlling for all other variables5. This finding reveals that when observers perform the ANS acuity task, percent correct (as measured in terms of overall accuracy or w) and RT each carry information about the observer’s ANS acuity. Furthermore, the relationship between RT on the ANS acuity task and math ability remained significant even when controlling for RT on the non-numerical attention task.
Table 5.
Linear regression analyses predicting math ability using expressive vocabulary size (Vocab scores), accuracy (model 1), Weber fraction (w, model 2), and RT on the ANS acuity task, RT on the attention task (K-CPT), and memory span scores as possible predictors
| Model 1 incl. accuracy and RT | Model 2 incl. w and RT | |||||
|---|---|---|---|---|---|---|
| R2 | 0.33 | 0.21 | ||||
| F-statistics | F(5,117) = 11.63 | F(5,104) = 5.39 | ||||
| p-statistics | p < 0.001 | p < 0.001 | ||||
| Predictor | rp2 | p | Predictor | rp2 | p | |
| Vocab | 0.01 | 0.28 | Vocab | 0.03 | 0.09 | |
| ANS-RT | 0.05 | 0.01 | ANS-RT | 0.04 | 0.04 | |
| Accuracy | 0.18 | < 0.001 | w | 0.11 | 0.001 | |
| K-CPT-RT | 0.08 | < 0.01 | K-CPT-RT | 0.04 | 0.05 | |
| Memory span | 0.05 | 0.02 | Memory span | 0.05 | 0.02 | |
4. Discussion
Our results replicate the predictive role of early ANS acuity on later math ability recently reported by Mazzocco, Feigenson, and Halberda (2011b), and extend these results in three key ways. First, we show that the relationship between ANS and later math ability holds even when accounting for individual differences in math ability at the initial time of testing. That is, we found that ANS acuity predicted growth in formal math abilities over a six-month period. As shown in Table 4, initial math ability accounted for the largest amount of variability in later math ability (45%), whereas accuracy and RT on the ANS acuity task only contributed 7% and 6% respectively. This suggests that ANS acuity may contribute a small but significant component to gains in school math performance. As previous work has demonstrated, other important contributors likely include external factors such as the home learning environment (LeFevre et al., 2009; Melhuish et al., 2008), socio-economic status (Jordan & Levine, 2009), and preschool teacher characteristics (Klibanoff et al., 2006), as well as internal factors such as linguistic skills (Cirino, 2011; LeFevre et al., 2010), intelligence (Rohde & Thompson, 2007), inhibitory control (Blair & Razza, 2007; Fuhs & McNeil, 2013), and working memory (Passolunghi & Lanfranchi, in press; Passolunghi, Mammarella, & Altoe, 2008). Nevertheless, our results show that ANS acuity contributes uniquely to the variability in future math ability above and beyond initial variations in this math ability – an effect not demonstrated in previous investigations.
Second, our results show that the predictive association between ANS acuity and mathematical ability holds across a much larger sample of children, with greater variability in children’s math ability, than that tested previously (Mazzocco et al., 2011b). Our findings thus suggest that the link between ANS and later math ability is present across a wide range of participants.
Finally, our results demonstrate that RT and accuracy on the ANS acuity task are unique concurrent predictors of math ability, even when controlling for response times on a non-numerical speeded computerized task, expressive vocabulary, and memory span. Accuracy and RT on the ANS acuity task appear to be complementary estimates of ANS acuity that each contribute uniquely to predict individual differences in math ability (see also Halberda et al., 2012). Future studies might disentangle whether these two estimates of ANS acuity play different roles in explaining performance on various types of math tasks, such as timed versus untimed mental arithmetic.
Is it surprising that early estimation abilities predict later mathematics performance? On the one hand, the link we demonstrate here might seem intuitive, in the sense that both the ANS acuity task and the standardized math test focused on quantity-relevant representations and computations. On the other hand, it is far from obvious that the acuity of an evolutionarily ancient mental system, observable in non-human animals and in newborn humans (Cantlon & Brannon, 2006; Izard et al., 2009), would predict performance in the system of symbolic mathematics that only a subset of humans master after years of formal instruction. Most of the published demonstrations of a link between early and later formal math abilities have focused on the link between early symbolic numerical abilities and later math abilities, and have not tested the more basic, non-symbolic numerical approximation abilities assessed here. For example, it has been shown that later math ability can be predicted by early symbolic numerical abilities such as Arabic numeral comparison (Clarke & Shinn, 2004; De Smedt, Verschaffel, & Ghesquiere, 2009; Desoete, Ceulemans, De Weerdt, & Pieters, 2010; Lembke & Foegen, 2009), the placement of Arabic numerals along a spatial number line (Booth & Siegler, 2008), verbal counting ability (Aunola, Leskinen, Lerkkanen, & Nurmi, 2004), ordinal position fluency (i.e., pointing to the picture in nth place), and number recognition fluency (Methe, Hintze, & Floyd, 2008). And while performance on a “number sense” battery in kindergarten has been shown to predict math ability through third grade (Jordan, Glutting, & Ramineni, 2010; Jordan et al., 2007) and growth in math abilities between first and third grade (Jordan et al., 2009), this “number sense” battery also measured symbolically mediated abilities such as verbal counting skill, number knowledge (e.g., comparing numbers), and story problem solving skills (Jordan, Glutting, & Ramineni, 2008). It might be the case that developing a mapping between nonverbal ANS representations and formal number symbols is a crucial link mediating the relationship between ANS acuity and math abilities in older children and adults (Holloway & Ansari, 2009; Lyons & Beilock, 2011). However, such a link is unlikely to be firmly in place for the preschool-aged children we tested here (Le Corre & Carey, 2007). This suggests that ANS acuity may have a role to play in determining early math abilities even before children have firmly mastered the symbolic system of number required for verbal counting, although further work will be needed to better understand this link and to trace its development over time.
However, we also note that alternative accounts for the relationship we observed between ANS acuity and math ability need to be considered. For example, Fuhs and McNeil (2013) recently reported that in a sample of children from low-income homes, ANS acuity and math ability no longer correlated when inhibitory control and receptive vocabulary were taken into account. Inhibitory control abilities may be needed both to perform well on an ANS acuity task where perceptual information may conflict with the numerical information that needs to be extracted, and to solve symbolic math problems. Future work should continue to examine this and other possible contributors to the observed relationship between the ANS and symbolic math performance.
In sum, we found that the acuity of preschool-aged children’s Approximate Number System (ANS) was a significant predictor of their math ability six months later even when controlling for age, initial math ability, and expressive vocabulary. In contrast, only initial vocabulary size was a significant predictor of vocabulary size six months later. Furthermore, ANS acuity was a concurrent predictor of math ability even when controlling for expressive vocabulary, response time on a computerized, non-numerical attention task, and memory span. These findings thereby support the notion of a tight link between a primitive sense of number and growth in more formal math abilities.
Highlights.
Precision in the Approximate Number System (ANS) predicts math ability.
We tested ANS acuity and math ability of preschoolers twice, six months apart.
Early ANS acuity predicted growth in math ability.
The predictive link emphasizes the importance of early estimation skills.
Acknowledgments
We thank XXX for help with testing participants, and all families and children for their participation. We are also thankful to the directors of the local preschools who gave us permission to test in their schools. This research was supported by XXX.
Footnotes
Four children were unavailable for testing at Time 1 because they were out of town during the assigned preschool testing days (n = 2), unwilling to participate (n = 1), or too young (n = 1). Time 1 data from three children with developmental delays were excluded and these children were not followed longitudinally.
Detailed information about sample sizes for each measure at Time 1 can be found in Libertus, Feigenson & Halberda (2011). At Time 2, we were unable to obtain results from the ANS acuity task for nine children due to equipment failure (n = 4), external interference (n = 1) or inability to return for the second testing session (n = 4). Furthermore, we were unable to obtain a usable TEMA score from one child and usable K-CPT scores from five children due to inattentiveness during testing. K-CPT scores were unavailable for six additional children due to equipment failure (n = 5) and external interference during testing (n = 1). Memory span measures were unavailable for six children due to unwillingness to complete the task (n = 2) or inability to return for the second testing session (n = 4). Finally, we were unable to obtain expressive vocabulary scores from twenty-seven children due to parents’ failure to return the forms.
To increase statistical power, we used accuracy as an estimate of ANS acuity at Time 1 and not w because we were unable to obtain reliable estimates of w for many of the participants (see also Libertus et al, 2011).
Two separate models were required because w is derived from accuracy, and therefore including both w and accuracy together in a single model would violate independence.
However, we note that the role of vocabulary size for the development of math ability needs to be examined in more detail. Some previous studies have found a link between children’s performance on the Peabody Picture Vocabulary Test (PPVT), an experimenter-administered measure of receptive vocabulary, and math ability (e.g., Blair & Razza, 2007; Fuhs & McNeil, 2013), but others have not (e.g., Bonny & Lourenco, in press). Our parent report measure of expressive vocabulary correlates highly with the PPVT-4 (Dunn & Dunn, 2007), but we also do not find a consistent link between math ability and vocabulary size (see Table 3) thus hampering its utility as a control variable. More work is needed to unravel the exact contributions of expressive and receptive vocabulary size to math ability.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Agrillo C, Dadda M, Serena G, Bisazza A. Do fish count? Spontaneous discrimination of quantity in female mosquitofish. Anim Cogn. 2008;11(3):495–503. doi: 10.1007/s10071-008-0140-9. [DOI] [PubMed] [Google Scholar]
- Alloway TP, Passolunghi MC. The relationship between working memory, IQ, and mathematical skills in children. Learning and Individual Differences. 2011;21:133–137. [Google Scholar]
- Aunola K, Leskinen E, Lerkkanen MK, Nurmi JE. Developmental Dynamics of Math Performance From Preschool to Grade 2. Journal of Educational Psychology. 2004;96(4):699–713. [Google Scholar]
- Aunola K, Leskinen E, Nurmi JE. Developmental dynamics between mathematical performance, task motivation, and teachers’ goals during the transition to primary school. Br J Educ Psychol. 2006;76(Pt 1):21–40. doi: 10.1348/000709905X51608. [DOI] [PubMed] [Google Scholar]
- Beilock SL, Gunderson EA, Ramirez G, Levine SC. Female teachers’ math anxiety affects girls’ math achievement. Proceedings of the National Academy of Sciences. 2010;107(5):1860–1863. doi: 10.1073/pnas.0910967107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blair C, Razza RP. Relating effortful control, executive function, and false belief understanding to emerging math and literacy ability in kindergarten. Child Dev. 2007;78(2):647–663. doi: 10.1111/j.1467-8624.2007.01019.x. [DOI] [PubMed] [Google Scholar]
- Bonny JW, Lourenco SF. The approximate number system and its relation to early math achievement: Evidence from the preschool years. Journal of Experimental Child Psychology. doi: 10.1016/j.jecp.2012.09.015. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Booth JL, Siegler RS. Numerical magnitude representations influence arithmetic learning. Child Dev. 2008;79(4):1016–1031. doi: 10.1111/j.1467-8624.2008.01173.x. [DOI] [PubMed] [Google Scholar]
- Bull R, Espy KA, Wiebe SA. Short-term memory, working memory, and executive functioning in preschoolers: longitudinal predictors of mathematical achievement at age 7 years. Dev Neuropsychol. 2008;33(3):205–228. doi: 10.1080/87565640801982312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cantlon JF, Brannon EM. Shared system for ordering small and large numbers in monkeys and humans. Psychological Science. 2006;17(5):401–406. doi: 10.1111/j.1467-9280.2006.01719.x. [DOI] [PubMed] [Google Scholar]
- Carey S. The Origin of Concepts. Oxford: Oxford University Press; 2009. [Google Scholar]
- Chen C, Stevenson HW. Motivation and mathematics achievement: a comparative study of Asian-American, Caucasian-American, and east Asian high school students. Child Dev. 1995;66(4):1214–1234. [PubMed] [Google Scholar]
- Cirino PT. The interrelationships of mathematical precursors in kindergarten. J Exp Child Psychol. 2011;108(4):713–733. doi: 10.1016/j.jecp.2010.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clarke B, Shinn MR. A Preliminary Investigation Into the Identification and Development of Early Mathematics Curriculum-Based Measurement. School Psychology Review. 2004;33(2):234–248. [Google Scholar]
- Conners CK. Conners’ Kiddie Continuous Performance Test - Version 5. North Tonawanda, NY: Multi-Health Systems Inc; 2006. [Google Scholar]
- Crosnoe R, Morrison F, Burchinal M, Pianta R, Keating D, Friedman SL, et al. Instruction, Teacher-Student Relations, and Math Achievement Trajectories in Elementary School. J Educ Psychol. 2010;102(2):407–417. doi: 10.1037/a0017762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Smedt B, Verschaffel L, Ghesquiere P. The predictive value of numerical magnitude comparison for individual differences in mathematics achievement. Journal of Experimental Child Psychology. 2009;103(4):469–479. doi: 10.1016/j.jecp.2009.01.010. [DOI] [PubMed] [Google Scholar]
- Dehaene S. The number sense : how the mind creates mathematics. New York: Oxford University Press; 1997. [Google Scholar]
- Desoete A, Ceulemans A, De Weerdt F, Pieters S. Can we predict mathematical learning disabilities from symbolic and non-symbolic comparison tasks in kindergarten? Findings from a longitudinal study. Br J Educ Psychol. 2010 doi: 10.1348/2044-8279.002002. [DOI] [PubMed] [Google Scholar]
- Dunn LM, Dunn DM. Peabody Picture Vocabulary Test. 4. San Antonio, Texas: Pearson; 2007. [Google Scholar]
- Feigenson L, Dehaene S, Spelke E. Core systems of number. Trends in Cognitive Sciences. 2004;8(7):307–314. doi: 10.1016/j.tics.2004.05.002. [DOI] [PubMed] [Google Scholar]
- Feigenson L, Libertus ME, Halberda J. Links between the intuitive sense of number and formal mathematics ability. Child Development Perspectives. doi: 10.1111/cdep.12019. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuhs MW, McNeil NM. ANS acuity and mathematics ability in preschoolers from low-income homes: contributions of inhibitory control. Dev Sci. 2013;16(1):136–148. doi: 10.1111/desc.12013. [DOI] [PubMed] [Google Scholar]
- Gallistel CR, Gelman II. Non-verbal numerical cognition: from reals to integers. Trends in Cognitive Sciences. 2000;4(2):59–65. doi: 10.1016/s1364-6613(99)01424-2. [DOI] [PubMed] [Google Scholar]
- Geary DC, Bailey DH, Hoard MK. Predicting Mathematical Achievement and Mathematical Learning Disability With a Simple Screening Tool: The Number Sets Test. J Psychoeduc Assess. 2009;27(3):265–279. doi: 10.1177/0734282908330592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ginsburg HP, Baroody AJ. Test of Early Mathematics Ability. 3. Austin, Texas: Pro Ed; 2003. [Google Scholar]
- Halberda J, Feigenson L. Developmental change in the acuity of the ‘number sense’: The approximate number system in 3-, 4-, 5-, and 6-year-olds and adults. Developmental Psychology. 2008;44(5):1457–1465. doi: 10.1037/a0012682. [DOI] [PubMed] [Google Scholar]
- Halberda J, Ly R. Panamath: The Psychophysical Assessment of Number-sense Acuity. (in preparation) [Google Scholar]
- Halberda J, Ly R, Willmer J, Naiman D, Germine L. Number sense across the lifespan as revealed by a massive Internet-based sample. Proceedings of the National Academy of Sciences. 2012 doi: 10.1073/pnas.1200196109. http://www.pnas.org/cgi/doi/10.1073/pnas.1200196109. [DOI] [PMC free article] [PubMed]
- Halberda J, Mazzocco MM, Feigenson L. Individual differences in non-verbal number acuity correlate with maths achievement. Nature. 2008;455(7213):665–668. doi: 10.1038/nature07246. [DOI] [PubMed] [Google Scholar]
- Holloway ID, Ansari D. Domain-specific and domain-general changes in children’s development of number comparison. Developmental Science. 2008;11(5):644–649. doi: 10.1111/j.1467-7687.2008.00712.x. [DOI] [PubMed] [Google Scholar]
- Holloway ID, Ansari D. Mapping numerical magnitudes onto symbols: The numerical distance effect and individual differences in children’s mathematics achievement. Journal of Experimental Child Psychology. 2009;103(1):17–29. doi: 10.1016/j.jecp.2008.04.001. [DOI] [PubMed] [Google Scholar]
- Inglis M, Attridge N, Batchelor S, Gilmore C. Non-verbal number acuity correlates with symbolic mathematics achievement: But only in children. Psychonomic Bulletin & Review. 2011 doi: 10.3758/s13423-011-0154-1. [DOI] [PubMed] [Google Scholar]
- Izard V, Sann C, Spelke ES, Streri A. Newborn infants perceive abstract numbers. Proc Natl Acad Sci U S A. 2009;106(25):10382–10385. doi: 10.1073/pnas.0812142106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jordan NC, Glutting J, Ramineni C. A Number Sense Assessment Tool for Identifying Children at Risk For Mathematical Difficulties. In: Dowker A, editor. Mathematical Difficulties: Psychology and Intervention. Oxford: Elsevier; 2008. pp. 45–58. [Google Scholar]
- Jordan NC, Glutting J, Ramineni C. The Importance of Number Sense to Mathematics Achievement in First and Third Grades. Learn Individ Differ. 2010;20(2):82–88. doi: 10.1016/j.lindif.2009.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jordan NC, Kaplan D, Locuniak MN, Ramineni C. Predicting First-Grade Math Achievement from Developmental Number Sense Trajectories. Learning Disabilities Research & Practice. 2007;22(1):36–46. [Google Scholar]
- Jordan NC, Kaplan D, Olah LN, Locuniak MN. Number sense growth in kindergarten: a longitudinal investigation of children at risk for mathematics difficulties. Child Dev. 2006;77(1):153–175. doi: 10.1111/j.1467-8624.2006.00862.x. [DOI] [PubMed] [Google Scholar]
- Jordan NC, Kaplan D, Ramineni C, Locuniak MN. Early math matters: kindergarten number competence and later mathematics outcomes. Dev Psychol. 2009;45(3):850–867. doi: 10.1037/a0014939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jordan NC, Levine SC. Socioeconomic variation, number competence, and mathematics learning difficulties in young children. Dev Disabil Res Rev. 2009;15(1):60–68. doi: 10.1002/ddrr.46. [DOI] [PubMed] [Google Scholar]
- Klibanoff RS, Levine SC, Huttenlocher J, Vasilyeva M, Hedges LV. Preschool children’s mathematical knowledge: The effect of teacher “math talk”. Dev Psychol. 2006;42(1):59–69. doi: 10.1037/0012-1649.42.1.59. [DOI] [PubMed] [Google Scholar]
- Le Corre M, Carey S. One, two, three, four, nothing more: An investigation of the conceptual sources of the verbal counting principles. Cognition. 2007;105(2):395–438. doi: 10.1016/j.cognition.2006.10.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- LeFevre JA, Fast L, Skwarchuk SL, Smith-Chant BL, Bisanz J, Kamawar D, et al. Pathways to mathematics: longitudinal predictors of performance. Child Dev. 2010;81(6):1753–1767. doi: 10.1111/j.1467-8624.2010.01508.x. [DOI] [PubMed] [Google Scholar]
- LeFevre JA, Skwarchuk SL, Smith-Chant BL, Fast L, Kamawar D, Bisanz J. Home numeracy experiences and children’s math performance in the early school years. Canadian Journal of Behavioural Science. 2009;41(2):55–66. [Google Scholar]
- Lembke E, Foegen A. Identifying Early Numeracy Indicators for Kindergarten and First-Grade Students. Learning Disabilities Research & Practice. 2009;24(1):12–20. [Google Scholar]
- Libertus ME, Brannon EM. Stable individual differences in number discrimination in infancy. Developmental Science. 2010;13(6):900–906. doi: 10.1111/j.1467-7687.2009.00948.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Libertus ME, Feigenson L, Halberda J. Preschool Acuity of the Approximate Number System Correlates with School Math Ability. Developmental Science. 2011;14(6):1292–1300. doi: 10.1111/j.1467-7687.2011.01080.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Libertus ME, Feigenson L, Halberda J. The developmental trajectory of approximation skills in preschool-aged children. (in preparation-a) [Google Scholar]
- Libertus ME, Feigenson L, Halberda J. The relationship between working memory and approximation skills and their role in mathematics. (in preparation-b) [Google Scholar]
- Libertus ME, Odic D, Feigenson L, Halberda J. The Developmental Vocabulary Assessment for Parents (DVAP): A Novel Tool to Measure Vocabulary Size in 2- to 7-year-old Children. (under review) [Google Scholar]
- Libertus ME, Odic D, Halberda J. Intuitive sense of number correlates with math scores on college-entrance examination. Acta Psychologica. 2012;141:373–379. doi: 10.1016/j.actpsy.2012.09.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Libertus ME, Pruitt LB, Woldorff MG, Brannon EM. Induced Alpha-band Oscillations Reflect Ratio-dependent Number Discrimination in the Infant Brain. Journal of Cognitive Neuroscience. 2009;21(12):2398–2406. doi: 10.1162/jocn.2008.21162. [DOI] [PubMed] [Google Scholar]
- Lipton JS, Spelke ES. Origins of number sense. Large-number discrimination in human infants. Psychological Science. 2003;14(5):396–401. doi: 10.1111/1467-9280.01453. [DOI] [PubMed] [Google Scholar]
- Lyons IM, Beilock SL. Numerical ordering ability mediates the relation between number-sense and arithmetic competence. Cognition. 2011;121(2):256–261. doi: 10.1016/j.cognition.2011.07.009. [DOI] [PubMed] [Google Scholar]
- Mazzocco MM, Feigenson L, Halberda J. Impaired acuity of the approximate number system underlies mathematical learning disability. Child Development. 2011a;82(4):1224–1237. doi: 10.1111/j.1467-8624.2011.01608.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazzocco MM, Feigenson L, Halberda J. Preschoolers’ precision of the approximate number system predicts later school mathematics performance. PLoS One. 2011b;6(9):e23749. doi: 10.1371/journal.pone.0023749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazzocco MM, Kover ST. A longitudinal assessment of executive function skills and their association with math performance. Child Neuropsychol. 2007;13(1):18–45. doi: 10.1080/09297040600611346. [DOI] [PubMed] [Google Scholar]
- Meck WH, Church RM, Gibbon J. Temporal integration in duration and number discrimination. J Exp Psychol Anim Behav Process. 1985;11(4):591–597. [PubMed] [Google Scholar]
- Melhuish EC, Sylva K, Sammons P, Siraj-Blatchford I, Taggart B, Phan MB, et al. The early years. Preschool influences on mathematics achievement. Science. 2008;321(5893):1161–1162. doi: 10.1126/science.1158808. [DOI] [PubMed] [Google Scholar]
- Methe SA, Hintze JM, Floyd RG. Validation and Decision Accuracy of Early Numeracy Skill Indicators. School Psychology Review. 2008;37(3):359–373. [Google Scholar]
- National Science Board. Science and Engineering Indicators 2010 [Electronic Version] 2010 Retrieved 11/11/11 from http://www.nsf.gov/statistics/seind10/pdfstart.htm.
- Passolunghi MC, Lanfranchi S. Domain-specific and domain-general precursors of mathematical achievement: A longitudinal study from kindergarten to first grade. Br J Educ Psychol. doi: 10.1111/j.2044-8279.2011.02039.x. (in press) [DOI] [PubMed] [Google Scholar]
- Passolunghi MC, Mammarella IC, Altoe G. Cognitive abilities as precursors of the early acquisition of mathematical skills during first through second grades. Dev Neuropsychol. 2008;33(3):229–250. doi: 10.1080/87565640801982320. [DOI] [PubMed] [Google Scholar]
- Piazza M, Facoetti A, Trussardi AN, Berteletti I, Conte S, Lucangeli D, et al. Developmental trajectory of number acuity reveals a severe impairment in developmental dyscalculia. Cognition. 2010;116(1):33–41. doi: 10.1016/j.cognition.2010.03.012. [DOI] [PubMed] [Google Scholar]
- Pica P, Lemer C, Izard V, Dehaene S. Exact and approximate arithmetic in an Amazonian indigene group. Science. 2004;306(5695):499–503. doi: 10.1126/science.1102085. [DOI] [PubMed] [Google Scholar]
- Rohde TE, Thompson LA. Predicting academic achievement with cognitive ability. Intelligence. 2007;35:83–92. [Google Scholar]
- Swanson D, Kim K. Working memory, short-term memory, and naming speed as predictors of children’s mathematical performance. Intelligence. 2007;35:151–168. [Google Scholar]
- Xu F, Spelke ES. Large number discrimination in 6-month-old infants. Cognition. 2000;74(1):B1–B11. doi: 10.1016/s0010-0277(99)00066-9. [DOI] [PubMed] [Google Scholar]