Updated model for dielectric response function of liquid water

Abstract

A modified and updated version of the model of the dielectric response function of liquid water as currently implemented in the PARTRAC code is presented. The updated version takes advantage of the newer experimental information from the Sendai group and implements some improvements in modeling and usability.

1. Introduction

Monte Carlo (MC) radiation transport codes rely on realistic interaction cross sections of charged particles with materials under consideration. MC track structure simulations follow the primary charged particle, as well as all produced secondary electrons, from starting or emission energy, down to total stopping in an event-by-event manner. They therefore require consistent total and differential (energy (E) and momentum (ħK) transfer) cross sections for all primary and secondary particles over a wide energy range. One established method to calculate excitation and ionisation cross sections for charged particles is the plane wave Born approximation (PWBA). Within the PWBA, the double differential cross section factorizes in a kinematic factor and the energy loss function (ELF) η₂(E, K) of the target material. The ELF is a characteristic function of the target material and does not depend on the incoming particle. Once this function is determined, interaction cross sections for all charged particles can be obtained. It should be noted that the PWBA is a first order perturbation theory and based on the assumption that the incoming charged particle is sufficiently fast compared to the orbital electrons. It is common practice to correct the plain PWBA for low-energy charged particle impact, either with semi-empirical correction factors, higher order corrections (see e.g. Emfietzoglou and Nikjoo, 2005; Dingfelder et al., 1998), or by use of semi-empirical or more sophisticated models (see e.g. Dingfelder et al., 2000; ICRU Report 55, 1996; Incerti et al., 2010), depending on the nature of the charged particle. However, cross section calculations are not the scope of this manuscript and will not be discussed further. The following will focus on the modeling of the ELF as basic input to PWBA calculations.

The ELF is related to the dielectric response function (DF) ε(E, K) = ε₁(E, K) + iε₂(E, K) of the material by η₂(E, K) = Im(−1/ε(E, K)), where Im(.) denotes the imaginary part of the argument. The ELF or DF is related to the generalized oscillator strength (GOS) for a single atom (low density limit), and to the optical constants (refraction and absorption index) in the optical limit, i.e., for momentum transfer ħK = 0. These relations are used to obtain experimental information on the materials. In case of liquid water, which serves as a surrogate for soft biological tissue, two measurements are available: the optical reflectance measurement on a liquid water surface by Heller et al. (1974), and the measurement by the Sendai group (Hayashi et al., 2000), measuring the energy loss function of liquid water for high momentum transfer using synchrotron radiation and extrapolating back into the optical limit.

There are three major models of the DF of liquid water available in the literature: the Oak Ridge model (Ritchie et al., 1991) and the PARTRAC model (Dingfelder et al., 1998, 2008) are based on the optical reflectance data by Heller et al. (1974), while the model of Emfietzoglou et al. (2005) is based on the Sendai group data. All models are based on representing the imaginary part of the DF as a superposition of functions representing excitation and ionization levels of water. They differ in details on the representation and the choice of parameter and use different extension algorithms for the momentum dependence of the DF. All models were used to calculate interaction cross sections for charged particles in liquid water, which are implemented in MC track structure codes.

This work describes an updated version of the PARTRAC model, as described in (Dingfelder et al., 1998, 2008), using the newer Sendai-group data Hayashi et al. (2000) instead of the older optical reflectance data from Heller et al. (1974). In order to effectively use the newer data, the model needs to be updated and modified in some details. This is described in the following.

2. The updated model for the dielectric response function of liquid water

The currently used model of the DF of liquid water for cross section calculations in PARTRAC is still based on the old optical reflectance data from Heller et al. (1974). It is described in detail in (Dingfelder et al., 1998) and summarized in (Dingfelder et al., 2008). The DF is modeled as a superposition of Drude-like functions as defined in Appendix Appendix A. Each function represents an excitation or ionization level. Parameter were obtained by physically fitting the DF in the optical limit, i.e, for zero momentum transfer, to existing experimental data and theoretical constraints like sum rules, mean excitation energy, etc. as defined in Eq. 9 – 12. An elaborate extension algorithm is used to add momentum (transfer) dependence to parameter of the Drude functions in the sense of an impulse approximation. Drude functions have the advantage that Kramers-Kronig relations can be performed analytically. Therefore, both the real and the imaginary part are represented as superpositions of these functions and their Kramers-Kronig counterparts, using the same set of parameter. The modified model follows the same approach but makes extensive use of new available experimental information: the inelastic x-ray scattering experiments of the Sendai group (Hayashi et al., 2000) to determine the ELF and their extrapolation of the DF to the optical limit.

2.1. Optical dielectric function

Following the general approach in Dingfelder et al. (1998), the imaginary part of the DF in the optical limit, i.e., for momentum transfer (Ka₀) = 0 is divided in contributions from excitations, outer shell ionizations, and inner shell ionization:

$${\epsilon }_2(E,K=0)=E_p^2\left({\epsilon }_2^{\text{exc}}(E,0)+{\epsilon }_2^{\text{outer}\text{shells}}(E,0)+{\epsilon }_2^{\text{kshell}}(E,0)\right)$$ (1)

The contribution from excitations is modeled as a superposition of derivative Drude functions D^*(E, E_k) (as given in Appendix Appendix A):

$${\epsilon }_2^{\text{exc}}=\sum _{\text{exc}k}{D}^{\ast }(E,E_k),$$ (2)

The contribution from the outer shells (all except the K-shell of oxygen) to ionizations is given by Drude functions, cut at the ionization threshold E_j and smeared out to avoid sharp edges. Above a certain cutoff energy, the Drude function is replaced by a simple power law, E^sj with shell dependent cutoff energies and exponents. The reason for this are twofold. First, Drude functions converge to an asymptotic power law with exponents around −3.0. Theoretical analysis (Inokuti, 1971) show that the generalized oscillator strength should have an asymptotic exponent of −3.5, and therefore the DF or ELF an asymptotic exponent of −4.5. Indeed, ab initio calculations performed for the optical oscillator strength of atomic oxygen with the formalism described in (Segui et al., 2002) yield an exponent −4.5 for outer shells, and an exponent of around −3.8 for the oxygen L-shell. Second, the Sendai group (Hayashi et al., 2000) used a similar method to normalize their data using sum rules: they obtained experimental values for energy transfers up to 100 eV, and used a power law with an exponent of −4.48 for higher energy transfers. Therefore, a similar approach is necessary to fulfill sum rules and to obtain a realistic mean excitation energy. The contribution from the outer shells to the DF is given by

$${\epsilon }_2^{\text{outer}\text{shells}}=\sum _{\text{ion}j}\{\begin{array}{lll}\underset{E_j-{\mathrm{\Delta }}_j}{\overset{E_j+{\mathrm{\Delta }}_j}{\int }}D(E,\mathrm{\Omega })\mathrm{\Theta }(\mathrm{\Omega }-E)G(\mathrm{\Omega },E_j)\text{d}\mathrm{\Omega }\hfill & \text{for}\hfill & E\le E_{\text{cut},j}\hfill \\ t_j{E}^{-s_j}\hfill & \text{for}\hfill & E>E_{\text{cut},j}\hfill \end{array}$$ (3)

D(E, E₀) is the Drude function, Θ(x) the Heavyside Step function, and G(x, x₀) a Gaussian, as defined in Appendix Appendix A. E_cut,j is the cutoff energy, and s_j the exponent of subshell j, and t_j given by

$$t_j=\underset{E_j-{\mathrm{\Delta }}_j}{\overset{E_j+{\mathrm{\Delta }}_j}{\int }}D(E_{\text{cut},j},\mathrm{\Omega })\mathrm{\Theta }(\mathrm{\Omega }-E_{\text{cut},j})G(\mathrm{\Omega },E_j)\text{d}\mathrm{\Omega }\times E_{\text{cut},j}^{s_j}.$$ (4)

The contribution from the oxygen K-shell is modeled using a scaled hydrogen GOS model, as discussed and described in detail in Dingfelder et al. (2000). In the limit of high energy transfers, the imaginary part of the DF becomes small, ε₂ ≪ 1, and the real part of the DF approaches unity, ε₁ ≈ 1. It is therefore assumed, that for the K-shell of oxygen the ELF is approximately the imaginary part of the DF, and that the contribution from the real part of the DF can be neglected, i.e., η₂ ≈ ε₂. Therefore the contribution of the K-shell to ε₂ is given by

$${\epsilon }_2^{\text{kshell}}(E,0)\approx \frac{\pi }{2}\frac{E_p^2}{Z}\frac{1}{E}2\xi \frac{{\text{d}f}^{(H)}(E,0)}{\text{d}E}$$ (5)

where the factor 2 accounts for two electrons in the K–shell. The factor ξ arises from a renormalization. The known value of the total oscillator strength of the oxygen K–shell is 1.79, as stated in Section 4.1 of (Dingfelder et al., 2000). However, the integral of df^(H)(E, 0)/dE over the continuum is 0.88. Therefore, the oscillator strength is renormalized by the factor ξ = 1.79/(2 × 0.88) = 1.017. The GOS for transition from the K-shell to the continuum, for energy transfers $E>\text{Ry}{Z}_{\text{eff}}^2$, Z_eff being the effective charge, then reads

$$\begin{array}{l}\frac{{\text{d}f}^{(H)}(E,K)}{\text{d}E}=2^7\frac{E}{{\text{Ry}}^2{Z}_{\text{eff}}^4}\frac{1}{Z_{\text{eff}}^2}\left({(K{a}_0)}^2+\frac{E}{3\text{Ry}}\right)\\ \times \frac{Z_{\text{eff}}^{12}}{{[{(K{a}_0+\kappa a_0)}^2+Z_{\text{eff}}^2]}^3{[{(K{a}_0-\kappa a_0)}^2+Z_{\text{eff}}^2]}^3}\\ \times exp\left\{-\frac{2Z_{\text{eff}}^2}{\kappa a_0}arctan\left(\frac{2\kappa a_0{Z}_{\text{eff}}}{{(K{a}_0)}^2-{(\kappa a_0)}^2+Z_{\text{eff}}^2}\right)\right\}\\ \times {\left(1-exp\left\{-\frac{2\pi Z_{\text{eff}}}{\kappa a_0}\right\}\right)}^{-1}\end{array}$$ (6)

with $\kappa a_0=\sqrt{E/\text{Ry}-Z_{\text{eff}}^2}$,

and for energies E with $I_{\text{K}-\text{shell}}<E<{\text{Ry}Z}_{\text{eff}}^2$

$$\frac{{df}^{(H)}(E,K)}{dE}=2^7\frac{E}{{\text{Ry}}^2{Z}_{\text{eff}}^4}\frac{1}{Z_{\text{eff}}^2}\left({(K{a}_0)}^2+\frac{E}{3\text{Ry}}\right)\times \frac{Z_{\text{eff}}^{12}}{{\left[{({(K{a}_0)}^2-E/\text{Ry})}^2+4{(K{a}_0)}^2{Z}_{\text{eff}}^2\right]}^3}\times {\left(\frac{1-b}{1+b}\right)}^{Z_{\text{eff}}/\sqrt{Z_{\text{eff}}^2-E/\text{Ry}}}$$ (7)

with

$$b=\frac{2Z_{\text{eff}}\sqrt{Z_{\text{eff}}^2-E/\text{Ry}}}{{(K{a}_0)}^2-E/\text{Ry}+2Z_{\text{eff}}^2}$$ (8)

The real part of the DF ε₁(E, K = 0) is then calculated analytical using the Kramers–Kronig relations for the Drude functions as described in Appendix Appendix C and ignoring the power laws in the imaginary part of the outer shell contributions to the DF for energies above the cutoff energies. At these energies, contribution from the outer shells to ε₁ are almost zero. Once the DF is obtained, the ELF can be calculated.

The model is then fitted to the new experimental data of Hayashi et al. (2000). The fit is done for the imaginary part ε₂ under two constraints: (i) the energy loss function ${\eta }_2={\epsilon }_2(E,0)/({\epsilon }_2^2(E,0)+{\epsilon }_1^2(E,0))$ is reproduced well, because this is the experimentally measured quantity, while ε₂ and ε₁ are derived. The imaginary part of the DF, ε₂, provides detailed information on the excitation and ionization energies (peaks and shoulders at low and higher energies). However, contributions overlap and need to be deconvoluted. On the other hand, the ELF η₂ is not sensitive to the excitation and ionization energies, but to the widths of the ionization levels, which determine the curvature in the maximum of the ELF. Excitations do not contribute there. (ii) all sum rules are fulfilled and a reasonable mean excitation energy is achieved. In particular, the sum rules S1 and S2 and the mean excitation energy I are given by

$$S1(E_{max})=\frac{2}{\pi }\frac{1}{E_p^2}\underset{0}{\overset{E_{max}}{\int }}E{\epsilon }_2(E,0)\text{d}E$$ (9)

and

$$S2(E_{max})=\frac{2}{\pi }\frac{1}{E_p^2}\underset{0}{\overset{E_{max}}{\int }}E{\eta }_2(E,0)\text{d}E$$ (10)

The mean excitation energy I is given by

$$I(E_{max})=exp(S3(E_{max})/S2(E_{max}))$$ (11)

with

$$S3(E_{max})=\frac{2}{\pi }\frac{1}{E_p^2}\underset{0}{\overset{E_{max}}{\int }}Eln(E){\eta }_2(E,0)\text{d}E.$$ (12)

E_max is the maximum energy transfer. The sum rules S1 and S2 yield S1 = 1 and S2 = 1 for E_max → ∞.

The cutoff energies and exponents for the power law part of the outer shells are chosen as E_cut,j = 100 eV and s_j = 4.48 (the actual value, the Sendai group used) for the outer three shells, and as E_cut,j = 500 eV and s_j = 3.80 for the 2a₁ subshell.

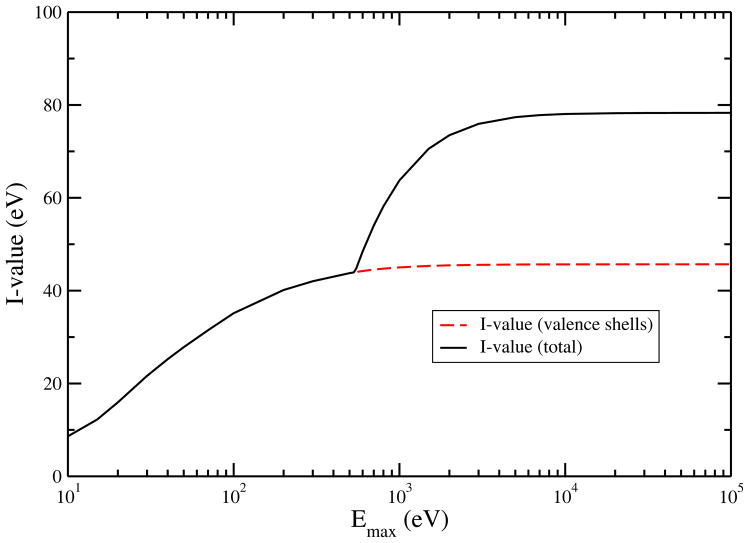
The obtained model parameter from the fit are displayed in Tables 1 and 2. The excitation energies E_k are in general a bit higher than in the old model (Dingfelder et al., 1998), as well as the widths γ_k are larger. The oscillator strength is now more equally distributed within the excitations, except the first electronic excitation, which remains more or less unchanged. The total oscillator strength of the excitations sums up to 10.92 % of the sum rule, about the same value (10.81 %) as for the old model. Contributions of the different subshells to the sum rules are shown in Table 3. The S1 and S2 sum rules are fulfilled within 0.5 %. The mean excitation energy is calculated to be I = 78.30 eV, which is close to the experimental value I = 79.75 eV of Bichsel and Hiraoka (1992) and I = 77.8 eV of other model calculations (Emfietzoglou et al., 2009), but higher than the currently recommended ICRU value I = 75.00 eV (ICRU Report 49, 1993). Total I values for different maximum energy transfers (10 eV to 100 keV) and contributions from the valence shells only (outer shell ionisations and excitations) are shown in Figure 1.

Table 1.

Parameters for the dielectric response function for excitation levels of liquid water.

k	excited state	Ek (eV)	fk	γk (eV)
1	Ã1 B1	8.27	0.0120	2.00
2	B̃1A1	10.55	0.0243	2.70
3	Ryd A+B	12.65	0.0255	3.35
4	Ryd C+D	14.40	0.0240	3.40
5	diffuse bands	16.70	0.0235	3.60

Table 2.

Parameters for the dielectric response function for ionization subshells of liquid water.

j	shells	$E_j^{\text{ion}}(\text{eV})$	Ej (eV)	Δj (eV)	γj (eV)	fj (eV)−1	$E_j^{\text{cut}}(\text{eV})$	sj
1	1b1	10.79	11.89	1.10	27.50	0.1760	100.0	4.48
2	3a1	13.40	14.00	0.60	29.00	0.3150	100.0	4.48
3	1b2	16.85	17.66	0.80	15.00	0.1500	100.0	4.48
4	2a1	30.80	31.80	1.00	120.00	0.0780	500.0	3.80
5	K-shell	539.00	–	–	–	–	–	–

Table 3.

Contribution of the different levels and shells to the sum rules and the mean excitation energy.

k/j	level/shell	S1(∞)	S2(∞)	S3(∞)
1	Ã1B1	0.01200	0.00257	0.00549
2	B̃1A1	0.02430	0.00537	0.01282
3	Ryd A+B	0.02550	0.00637	0.01647
4	Ryd C+D	0.02400	0.00763	0.02073
5	diffuse bands	0.02350	0.01143	0.03263
6	1b1	0.24135	0.25424	0.94490
7	3a1	0.23004	0.25732	0.96202
8	1b2	0.13706	0.16072	0.57203
9	2a1	0.10817	0.11901	0.58447
10	K-shell	0.17900	0.17925	1.22604
	sum:	1.00489	1.00390	4.37760
	I-value (eV)	–	–	78.30

Figure 1.

The calculated mean excitation energy (I-value) as a function of maximum energy transfer. Shown are total values and contributions from valence shells (excitations and outer shell ionisations) only. Asymptotic values are 78.30 eV for the I-value, and 45.7 eV for the valence contributions.

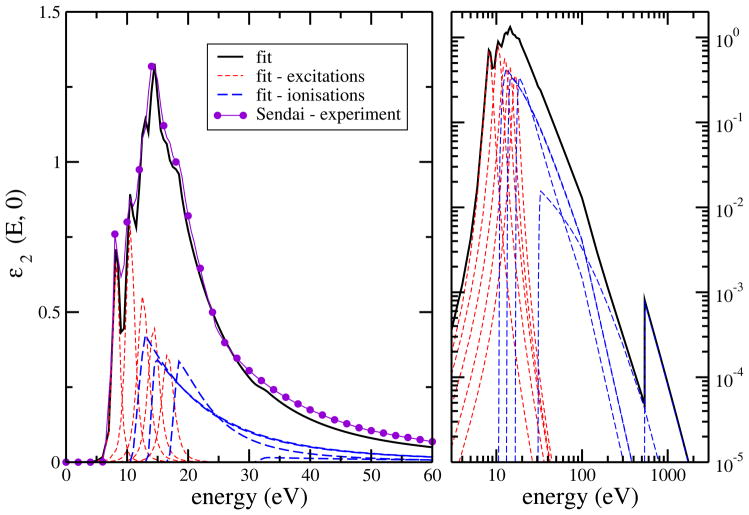
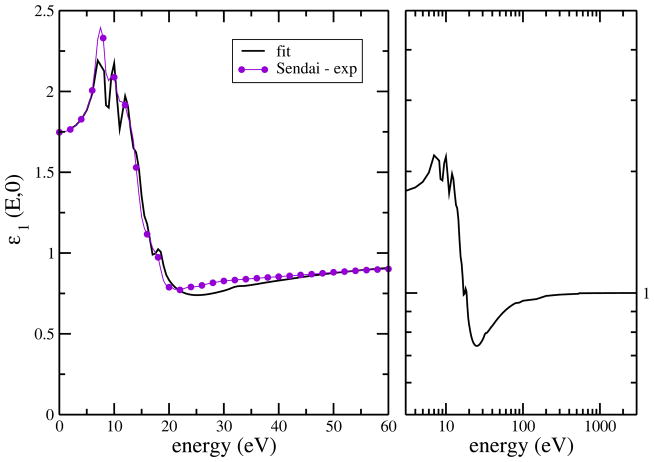
The obtained dielectric response functions ε₂(E, 0) and ε₁(E, 0), as well as the calculated energy loss function η₂(E, 0) are shown in Figures 2–4. Displayed are the total function (solid curves), contributions from different excitation and ionization subshells (dashed/dotted curves) where applicable, and the experimental data obtained by the Sendai group (Hayashi et al., 2000) (symbols).

Figure 2.

New Drude–model with cut high energy tails. Shown are the imaginary part of the dielectric response function ε₂(E, 0) with contributions from excitation levels and ionization shells, compared with experimental data of Hayashi et al. (2000).

Figure 4.

New Drude–model with cut high energy tails. Shown are the energy loss function η₂(E, 0) together with contributions from excitation levels and ionization shells, compared with experimental data of Hayashi et al. (2000).

2.2. Full energy and momentum transfer dependent dielectric function

As mentioned earlier in the text, an extension algorithm is used to add momentum transfer dependence in the sense of an impulse approximation to the DF, as described in detail in Dingfelder et al. (1998, 2008). Strictly speaking, this method is only valid for a pure Drude model, i.e., using Drude functions without cutting them at the ionization threshold and smearing them out, since the full DF and ELF have to fulfill the sum rules S1 and S2 for all momentum transfers ħK. One possible solution is to re-normalize the Drude functions, and do the Kramers–Kronig relations numerically to fulfill the sum rules. However, this is numerically costly and introduces numerical uncertainty. Another approach is modify the existing model slightly, and to calculate these corrections analytically.

The modified model for the full DF then reads:

$${\epsilon }_2(E,K\ne 0)=E_p^2\left({\epsilon }_2^{\text{exc}}(E,K)+{\epsilon }_2^{\text{outer}\text{shells}}(E,K)+{\epsilon }_2^{\text{kshell}}(E,K)\right)$$ (13)

For excitations k the derivative Drude function is replaced by a derivative Drude function, which depends on momentum transfer through the optical oscillator strength f_k → f_k(K),

$${\epsilon }_2^{\text{exc}}(E,K)=\sum _{\text{exc}k}{D}^{\ast }(E,K,E_k)$$ (14)

The momentum dependent derivative Drude function is given by

$$D^{\ast }(E,K,E_k)=E_p^2\frac{f_k(K)}{f_k(0)}{D}^{\ast }(E,E_k),$$ (15)

where D^*(E, E_k) is the derivative Drude function as defined in Appendix Appendix A, f_k(0) = f_k the optical oscillator strength of the excitation k, as given in Table 1, and

$$f_k(K)=f_k\times \{exp(-a_k{(K{a}_0)}^2)+b_k{(K{a}_0)}^{2}exp(-c_k{(K{a}_0)}^2)\}.$$ (16)

The parameter a_k, b_k and c_k are given in Ref. Dingfelder et al. (1998).

For outer ionization shells j we use

$${\epsilon }_2^{\text{outer}\text{shells}}(E,K)=\sum _{\text{ion}j}\{\begin{array}{lll}{E}_p^2\underset{E_j-{\mathrm{\Delta }}_j}{\overset{E_j+{\mathrm{\Delta }}_j}{\int }}D(E,K,\mathrm{\Omega })\mathrm{\Theta }(\mathrm{\Omega }-E)G(\mathrm{\Omega },E_j)\text{d}\mathrm{\Omega }\hfill & \text{for}\hfill & E\le E_{\text{cut},j}\hfill \\ t_j{E}^{-s_j}\times \mathit{FACTOR}(K)\hfill & \text{for}\hfill & E>E_{\text{cut},j}\hfill \end{array}$$ (17)

The momentum dependence of an outer ionization shell j consists of an energy dispersion of

$$E_j\to E_j(K)=E_j+\text{Ry}{(K{a}_0)}^2$$ (18)

in the sense of an impulse approximation, and a momentum dependence of the optical oscillator strength

$$f_j\to {\stackrel{\sim }{f}}_j(K)=f_j\frac{1-{\sum }_k{f}_k(K)}{{\sum }_j{f}_j(K)}$$ (19)

to fulfill the S1 sum rule. The effective (momentum dependent) oscillator strength f_j(K) is given by

$$f_j(K)=\underset{E_j-{\mathrm{\Delta }}_j}{\overset{E_j+{\mathrm{\Delta }}_j}{\int }}{f}_j(K,\mathrm{\Omega })G(\mathrm{\Omega },E_j)\text{d}\mathrm{\Omega },$$ (20)

where f_j(K, E_j) is given by

$$f_j(K,E_j)=\frac{2}{\pi }\int ED(E,K,E_j)\mathrm{\Theta }(E_j-E)\text{d}E.$$ (21)

This integral can be solved analytically. The result is given in Appendix Appendix B. The momentum dependent Drude function is given by

$$D(E,K,E_j)=\frac{f_j{\gamma }_j(K)E}{{(E_j^2(K)-E^2)}^2+{\gamma }_j^2(K)E^2},$$ (22)

with E_j(K) as given above. γ_j(K) reserves the possibility to introduce a momentum dependent width of the Bethe ridge, as already discussed by Ritchie et al. (1991) and by Kuhr and Fitting (1999). It is given by

$${\gamma }_j\to {\gamma }_j(K)={\gamma }_j(1+g_j\text{Ry}{(K{a}_0)}^2).$$ (23)

If it is not explicitly stated we will use g_j ≡ 0 for all ionization shells throughout this study.

Recently, Emfietzoglou and co-workers have published a new version of their model for the dielectric response function in water (Emfietzoglou et al., 2005). Based on Hayashi’s data, they introduced a momentum dependent width considering a constant linear and a quadratic term

$${\gamma }_j\to {\gamma }_j(K)={\gamma }_j+aK+{bK}^2$$ (24)

where they suggest values of a = 10 and b = 6, K in atomic units. In addition to the broadening of the Bethe ridge they introduce a “retarding” term to the energy dispersion,

$$E_j\to E_j(K)=E_j+\text{Ry}{(K{a}_0)}^2(1-exp(-{cK}^d))$$ (25)

where they suggest values of c = 1.5 and d = 0.4, K again in atomic units. They show that their model “reproduces” Hayashi’s experimental data well.

For the K–shell the scaled Hydrogen GOS model is used, which contains already a momentum dependence. In this case the contribution to the sum rule S1 is fixed to f_K-shell = 0.179 through the normalization. For f_K-shell(K) one should use

$$f_{\text{K}-\text{shell}}(K)=\frac{2}{\pi }\frac{1}{E_p^2}\underset{0}{\overset{\infty }{\int }}E{\epsilon }_2^{\text{kshell}}(E,K)\text{d}E.$$ (26)

The real part of the dielectric response function ε₁(E, K) is calculated using the Kramers–Kronig relation. This can be done analytically. The results are given in Appendix Appendix C for the general case K ≠ 0 and for the optical limit K = 0, which agrees with the formulas given in Appendix A of Dingfelder et al. (1998).

Figure 3.

New Drude–model with cut high energy tails. Shown are the real part of the dielectric response function, calculated analytically, compared with experimental data of Hayashi et al. (2000).

Research Highlights.

• Updated model of the dielectric response function and energy loss function of liquid water is presented.

• The new model includes new available experimental information (Sendai data).

• It is an analytical model.

• The mean excitation energy is calculated as 78.3 eV.

Appendix

Appendix A. Definitions and Formulas

In this appendix we sum up definitions of symbols and functions. Most of them can be also found in Refs. Dingfelder et al. (1998) and Dingfelder et al. (2000). The Drude function D(E, E_j) is defined

$$D(E,E_j)=\frac{f_j{\gamma }_{j}E}{{(E_j^2-E^2)}^2+{\gamma }_j^2{E}^2},$$ (A.1)

the derivative Drude function D^*(E, E_k) as

$$D^{\ast }(E,E_k)=\frac{2f_k{\gamma }_k^3{E}^3}{{({(E_k^2-E^2)}^2+{\gamma }_k^2{E}^2)}^2},$$ (A.2)

and the Gaussian function G(E, E_j) as

$$G(E,E_j)=exp\left(-\frac{{(E-E_j)}^2}{2{\mathrm{\Delta }}_j^2}\right)$$ (A.3)

The parameter E_k/j, f_k/j, γ_k/j and Δ_j are given in Tables 1 and 2, respectively.

Appendix B. Effective Oscillator Strength

The integral Eq. (21) (f_j(K, E_j)) can be calculated analytically. We distinguish here between E_j = E_j(0), the ionization energy, coming from the lower integration limit (step function) and E_j(K), the momentum dependent, energy–dispersed parameter, coming from the integrand (Drude function). In the optical limit, K = 0, both coincide.

In the general case (K ≠ 0) we obtain

$$\begin{array}{l}{f}_j(K,E_j)=\frac{2}{\pi }{f}_j\{\frac{1}{2}\left(arctan\left(\frac{-{\gamma }_j(K)E_j}{E_j^2(K)-E_j^2}\right)+\pi \right)\text{for}{\gamma }_j(K)>2E_j(K)\\ +\frac{1}{2}\frac{{\gamma }_j(K)}{\sqrt{{\gamma }_j^2(K)-4E_j^2(K)}}arctan\left(\frac{E_j\sqrt{{\gamma }_j^2(K)-4E^2(K)}}{E_j^2(K)+E_j^2}\right)\}\\ =\frac{2}{3}{f}_j\{\frac{1}{2}\left(arctan\left(\frac{-{\gamma }_j(K)E_j}{E_j^2(K)-E_j^2}\right)+\pi \right)\text{for}{\gamma }_j(K)<2E_j(K)\\ +\frac{1}{4}\frac{{\gamma }_j(K)}{\sqrt{4E_j^2(K)-{\gamma }_j^2(K)}}ln\left(\frac{E_j^2(K)+E_j^2+E_j\sqrt{4E_j^2(K)-{\gamma }_j^2(K)}}{E_j^2(K)+E_j^2-E_j\sqrt{4E_j^2(K)-{\gamma }_j^2(K)}}\right)\}\\ =\frac{2}{\pi }{f}_j\left\{\frac{1}{2}\left(arctan\left(\frac{-{\gamma }_j(K)E_j}{E_j^2(K)-E_j^2}\right)+\pi \right)+\frac{1}{2}\frac{{\gamma }_j(K)E_j}{E_j^2(K)+E_j^2}\right\}\text{for}{\gamma }_j(K)=2E_j(K)\end{array}$$ (B.1)

for the three solutions for γ_j(K) is greater, less or equal to 2E_j(K). In case of the optical limit the formulas reduce to

$$\begin{array}{l}{f}_j(0,E_j)=\frac{2}{\pi }{f}_j\left\{\frac{\pi }{4}+\frac{1}{2}\frac{{\gamma }_j}{\sqrt{{\gamma }_j^2-4E_j^2}}arctan\left(\frac{\sqrt{{\gamma }_j^2-4E^2}}{2E_j}\right)\right\}\text{for}{\gamma }_j>2E_j\\ =\frac{2}{\pi }{f}_j\left\{\frac{\pi }{4}+\frac{1}{4}\frac{{\gamma }_j}{\sqrt{4E_j^2-{\gamma }_j^2}}ln\left(\frac{2E_j+\sqrt{4E_j^2-{\gamma }_j^2}}{2E_j-\sqrt{4E_j^2-{\gamma }_j^2}}\right)\right\}\text{for}{\gamma }_j<(2E_j)\\ =\frac{2}{\pi }{f}_j\left\{\frac{\pi }{4}+\frac{1}{2}\right\}\text{for}{\gamma }_j=2E_j\end{array}$$ (B.2)

and should be used in this form to avoid unexpected “numerical” problems like division by zero.

Appendix C. Kramers–Kronig Relations

Finally, to calculate the Kramers–Kronig relations for a cut Drude function, the following integral is needed:

$$\frac{2}{\pi }{f}_n{\gamma }_{n}I(E)=\frac{2}{\pi }P\int \frac{s}{s^2-e^2}\frac{f_n{\gamma }_{n}s}{Q(s)}\mathrm{\Theta }(s-E_0)\text{d}s$$ (C.1)

with

$$Q(s)={(E_n^2-s^2)}^2+{\gamma }_n^2{s}^2$$ (C.2)

Note: E₀ is the cut off energy (lower integral border), E_n the later momentum dependent binding energy.

This integral can be calculated analytically:

• First case: γ_n > 2E_n. ${\lambda }^2={\gamma }_n^2/4-E_n^2$.

  $$\begin{array}{l}\frac{2}{\pi }{f}_n{\gamma }_{n}I(E)=\frac{1}{Q(E)}\{\frac{1}{2{\gamma }_n}\pi (E_n^2-E^2)-\frac{E}{2}ln\left|\frac{E_n-E}{E_n+E}\right|\\ -\frac{1}{2{\gamma }_n}(E_n^2-E^2)arctan\left(\frac{{\gamma }_n{E}_0}{E_n^2-E_0^2}\right)-\frac{1}{4\lambda }(E_n^2+E^2)arctan\left(\frac{2\lambda E_0}{E_n^2+E_0^2}\right)\}\end{array}$$ (C.3)
  and for the optical limit K = 0

  $$\frac{2}{\pi }{f}_n{\gamma }_{n}I(E)=\frac{1}{Q(E)}\left\{\frac{1}{2{\gamma }_n}\pi (E_n^2-E^2)-\frac{E}{2}ln\left|\frac{E_n-E}{E_n+E}\right|-\frac{1}{4\lambda }(E_n^2+E^2)arctan\left(\frac{\lambda }{E_n}\right)\right\}$$ (C.4)
• Second case: γ_n > 2E_n. ${\mu }^2=E_n^2-{\gamma }_n^2/4$.

  $$\begin{array}{l}\frac{2}{\pi }{f}_n{\gamma }_{n}I(E)=\frac{1}{Q(E)}\{\frac{1}{2{\gamma }_n}\pi (E_n^2-E^2)-\frac{E}{2}ln\left|\frac{E_n-E}{E_n+E}\right|\\ -\frac{E_n^2+E^2}{8\mu }ln\left(\frac{E_n^2+E_0^2+2E_0\mu }{E_n^2+E_0^2-2E_0\mu }\right)-\frac{E_n^2-E^2}{2{\gamma }_n}arctan\left(\frac{{\gamma }_n{E}_0}{2(E_n^2-E_0^2)}\right)\}\end{array}$$ (C.5)
  and for the optical limit K = 0

  $$\frac{2}{\pi }{f}_n{\gamma }_{n}I(E)=\frac{1}{Q(E)}\left\{\frac{1}{2{\gamma }_n}\pi (E_n^2-E^2)-\frac{E}{2}ln\left|\frac{E_n-E}{E_n+E}\right|-\frac{E_n^2+E^2}{8\mu }ln\left(\frac{E_n+\mu }{E_n-\mu }\right)\right\}$$ (C.6)

The integral (E₀, ∞) is calculated as the difference of the integrals (0, ∞) – (0, E₀). The first integral (0, ∞) reflects a pure Drude model, the results are well known.