Partly Conditional Estimation of the Effect of a Time-Dependent Factor in the Presence of Dependent Censoring

Summary

We propose semiparametric methods for estimating the effect of a time-dependent covariate on treatment-free survival. The data structure of interest consists of a longitudinal sequence of measurements and a potentially censored survival time. The factor of interest is time-dependent. Treatment-free survival is of interest and is dependently censored by the receipt of treatment. Patients may be removed from consideration for treatment, temporarily or permanently. The proposed methods combine landmark analysis and partly conditional hazard regression. A set of calendar time cross-sections is specified, and survival time (from cross-section date) is modeled through weighted Cox regression. The assumed model for death is marginal in the sense that time-varying covariates are taken as fixed at each landmark, with the mortality hazard function implicitly averaging across future covariate trajectories. Dependent censoring is overcome by a variant of Inverse Probability of Censoring Weighting (IPCW). The proposed estimators are shown to be consistent and asymptotically normal, with consistent covariance estimators provided. Simulation studies reveal that the proposed estimation procedures are appropriate for practical use. We apply the proposed methods to pre-transplant mortality among End-stage Liver Disease (ESLD) patients.

1. Introduction

Longitudinal and survival data are often observed simultaneously in biomedical studies. For instance, measurements related to patient health may be collected over time as a longitudinal process during the course of a patient’s disease, while time to a failure event (e.g., death) is of chief interest. Information on time-varying covariates is usually collected at multiple follow-up times through the time to the event. For example, the number of CD4-lymphocyte counts is frequently employed as a surrogate marker for HIV; the glomerular filtration rate has been utilized as an indicator of kidney failure; the Model for End-stage Liver Disease (MELD) score (Wiesner et al. 2001) is a very sensitive indicator of liver dysfunction among End-stage Liver Disease (ESLD) patients. In particular, the liver failure setting is the motivation for the methods we propose in this report.

It is often of interest to estimate the effect on survival time of a time-dependent factor hypothesized to be an important indicator for disease progression. In many practical applications, there are actually two important time axes; follow-up time (e.g., time since diagnosis) and calendar time. The latter is important in settings wherein clinical decisions are made in calendar time. For example, in the organ transplant setting, a deceased-donor liver becomes available for allocation on a particular calendar date, and current allocation policy implies that the liver should be offered to the patient predicted to die soonest in the absence of a liver transplant. It makes sense to structure the survival model in accordance with the research question. Hence, the most relevant time scale is time from that calendar date forward, and the cross-section of patients of interest (i.e., those transplant-eligible on that date) have various lengths of prior follow-up time. Covariate information to be used in the model would then include that observed up until the calendar date. Since future covariate information is not known, it is desirable for the model to implicitly average over future covariate paths. Models which condition on only part of the covariate history have been termed ‘partly conditional’; e.g., Pepe and Couper (1997); Zheng and Heagerty (2005).

To jointly model survival and longitudinal data, a regression model for the time dependent covariate process is usually adopted; e.g., Tsiatis, Degruttola and Wulfsohn (1995); Henderson, Diggle and Dobson (1997); Xu and Zeger (2001); Song, Davidian and Tsiatis (2002) and Taylor (2011). In joint modeling of longitudinal/survival data, valid inference on the time-to-event component generally requires that the longitudinal process be modeled accurately, which is difficult to accomplish and may be cumbersome to carry out in many cases (including our motivating example). Moreover, joint modeling approaches typically involve a (‘fully’) conditional model of the death hazard as a function of the covariate at time t. In practice, such an approach may be inconsistent with the investigator’s objectives. For example, in the liver failure setting, it is of interest to determine which of several patients awaiting liver transplantation will die soonest in the absence of a transplant; i.e., based on each patient’s history up until that date, and averaging over the possible scenarios that could subsequently occur without a transplant.

Zheng and Heagerty (2005) proposed a partly conditional model applicable to some settings like that described in the preceding paragraph. Typically in modeling survival data, the event time, D_i, is from study entry (marking the beginning of follow-up) to the occurrence of the failure event. Zheng and Heagerty (2005) modeled survival time from measurement; i.e., (D_i−S_i), with S_i denoting measurement time. The method of Zheng and Heagerty (2005) is referred as partly conditional since the hazard function being modeled (i.e., that of D_i − S_i) only conditions on the covariate history through time S_i, rather than the full covariate history. The time-varying covariate is “frozen” at each measurement time, as opposed to using information on {t : t > S_i}. There would typically be multiple event times for the same subject, each corresponding to a different measurement time. The authors approach this element of the data structure through a multivariate survival analysis framework analogous to Wei, Lin and Weissfeld (1989). The method does not require modeling the longitudinal covariate process and there is no imposed dependence structure between different survival times from the same individual. With respect to related work, Van Houwelingen (2007) proposed a landmark model based on the partly conditional method. In this case, the time clock is not reset to zero every time a measurement is taken.

Existing partly conditional methods require that censoring be independent of death time. However, dependent censoring frequently occurs in observational studies. A particular case is when survival in the absence of treatment (hereafter referred to as treatment-free survival) is of interest and both death and treatment assignment depend on the same time-varying covariates. If the model being fitted had conditioned on the entire history of the time-dependent covariates, then independent censoring could be assumed. However, since landmark methods freeze the time-varying measurement at the landmark time, hence only using part of the covariate history, dependent censoring can result due to the mutual correlation between future treatment assignment date, treatment-free death hazard, and the portion of the covariate process occurring after the landmark time. Naturally, dependent censoring can result in biased estimation.

As stated previously, the data which motivated our current research arise from the liver failure setting. The preferred method of treatment for liver failure is deceased-donor liver transplantation. There are thousands more patients awaiting liver transplantation than there are deceased-donor livers. As a result, patients requiring liver transplantation who are deemed medically suitable are placed on a liver transplant waiting list. Currently in the United States, the guiding principle in prioritizing patients for liver transplantation is that patients who are predicted to die the soonest without a transplant should be given the highest priority for transplantation. Patients with acute liver disease (known as Status 1 patients) have the highest priority for liver transplantation and, hence, are placed at the top of the wait list. They are followed by chronic liver failure patients, who are sequenced in decreasing order of MELD score. Note that MELD scores are updated over time, such that MELD is a time dependent process. In addition, if a patient becomes too sick, then he/she is removed from the transplant waiting list. Or, inactive status can be issued but possibly canceled afterward. During an inactive period, the patient is not eligible for transplantation and will not receive offers of deceased-donor livers. In practice, it is required that an available donor liver be allocated based on information up until (and not beyond) the calendar date of procurement; analogous to the covariate information being frozen. In reality, subsequent liver allocation will be based on updated MELD scores observed after that calendar date. Therefore, although it is clear that liver transplantation censors pre-transplant death, such censoring amounts to dependent censoring in the context of a partly conditional model using landmark methods.

In this report, we propose landmark methods featuring a partly conditional model to estimate the effect of a time-dependent covariate, in the presence of dependent censoring. Inverse Probability of Censoring Weighting (IPCW; Robins and Rotnitzky, 1992; Robins and Finkelstein, 2000) is used to obtain consistent estimators in the presence of dependent censoring. To increase precision, we propose two weight stabilizers that are different than those in the existing IPCW literature. Each landmark is based on a common calendar date, not follow-up time, consistent with the motivating example. At each cross-section (landmark) date, patients who are under observation (alive, uncensored), untreated, and treatment-eligible are included in the cross-section. Survival time, with respect to a cross section, is measured from the landmark date forward; such that the time clock is essentially reset to zero at each cross section date. We assume that the baseline hazards may differ by cross-section, such that a stratified Cox model (1972) is appropriate.

The remainder of this article is organized as follows. In Section 2, we formulate the previously described characteristics of the motivating data structure, then describe the proposed methods. Asymptotic properties of the proposed estimators are given in Section 3. A simulation study is provided in Section 4. Results of applying the proposed method to the afore-described liver failure data are presented in Section 5. In Section 6, we provide some concluding remarks and discussion. Asymptotic derivations are provided in the Web Appendix.

2. Proposed Methods

We begin by setting up the required notation. Let D_i be the treatment-free time to failure for subject i, with i = 1, . . . , n. We assume that D_i may be censored at treatment time, T_i, or independent censoring time, C_i, and therefore we define the treatment-free observation time as X_i = min(D_i, T_i, C_i). We also define the associated indicators, Δ_i = I(X_i = D_i) and ${\mathrm{\Delta }}_i^T=I(X_i=T_i)$, where I(B) = 1 when condition B is true and 0 otherwise. We define Y_i(t) = I(X_i ≥ t). Each patient is characterized by a covariate vector, Z_i(t), of which at least some elements are time-varying. We let A_i(t) take value 1 if patient i is eligible to receive treatment as of follow-up time t, and 0 otherwise. Further, we define the covariate history as Z̃_i(t) = {Z_i(s); s ∈ [0, t]} and the treatment-eligibility history as Ã_i(t) = {A_i(s); s ∈ [0, t]}.

We choose K cross section dates (CS_k, for k = 1, . . . , K), where the cross-section times represent calendar dates. The {CS₁, . . . , CS_K} will typically be equally spaced, and the appropriate number of cross-sections, K, will generally depend on the length of the observation period; issues to which we return in Section 6. Let S_ik denote the follow-up time of the ith subject on the calendar date of the kth cross section, CS_k. As we describe shortly, we will be modeling survival times from the cross-section dates, which essentially amounts to re-setting the time clock to 0 on each cross-section date. Correspondingly, since D_i, T_i and C_i are measured in study time (i.e., time since subject i started follow-up), we then define time since cross-section for death (D_ik = D_i − S_ik), treatment (T_ik = T_i − S_ik) and censoring (C_ik = C_i − S_ik). Thus, D_ik, T_ik and C_ik are each measured from the kth cross section date forward.

With respect to cross-section k, one observes a vector for subject i, ($X_{ik},{\mathrm{\Delta }}_{ik},{\mathrm{\Delta }}_{ik}^T$), where X_ik = min(D_ik, T_ik, C_ik), Δ_ik = I(X_ik = D_ik) and ${\mathrm{\Delta }}_{ik}^T=I(X_{ik}=T_{ik})$. Note that, for a censored subject, ${\mathrm{\Delta }}_{ik}={\mathrm{\Delta }}_{ik}^T=0$. For ease of presentation, define A_ik = A_i(S_ik), an indicator for subject i being treatment-eligible at the time of the kth cross-section. We now set up a modified version of counting process notation. In particular, we let N_ik(t) = I(X_ik ≤ t, Δ_ik = 1) A_ik, and write dN_ik(t) = N_ik(t⁻ + dt) − N_ik(t⁻) for the increment. The at risk process is defined as Y_ik(t) = I(X_ik ≥ t) A_ik; i.e., in addition to subject i being alive and not treated as of time S_ik (i.e., that X_i > S_ik), to be included in the kth cross section, it is also required that the subject is treatment-eligible at time S_ik (i.e., that A_ik = 1). However, if A_ik = 1, subject i is not censored if he/she later becomes inactive at time t > S_ik. Thus, being treatment-eligible at time S_ik is a cross-section inclusion criterion, but subsequently becoming ineligible for treatment is not a censoring criterion. With respect to the treatment process, we define $N_i^T(t)=I(X_i\le t,{\mathrm{\Delta }}_i^T=1)$. Note that $d{N}_i^T(t)=A_i(t)d{N}_i^T(t)$, since treatment assignment can only occur at time t for subject i if subject i is treatment-eligible at time t.

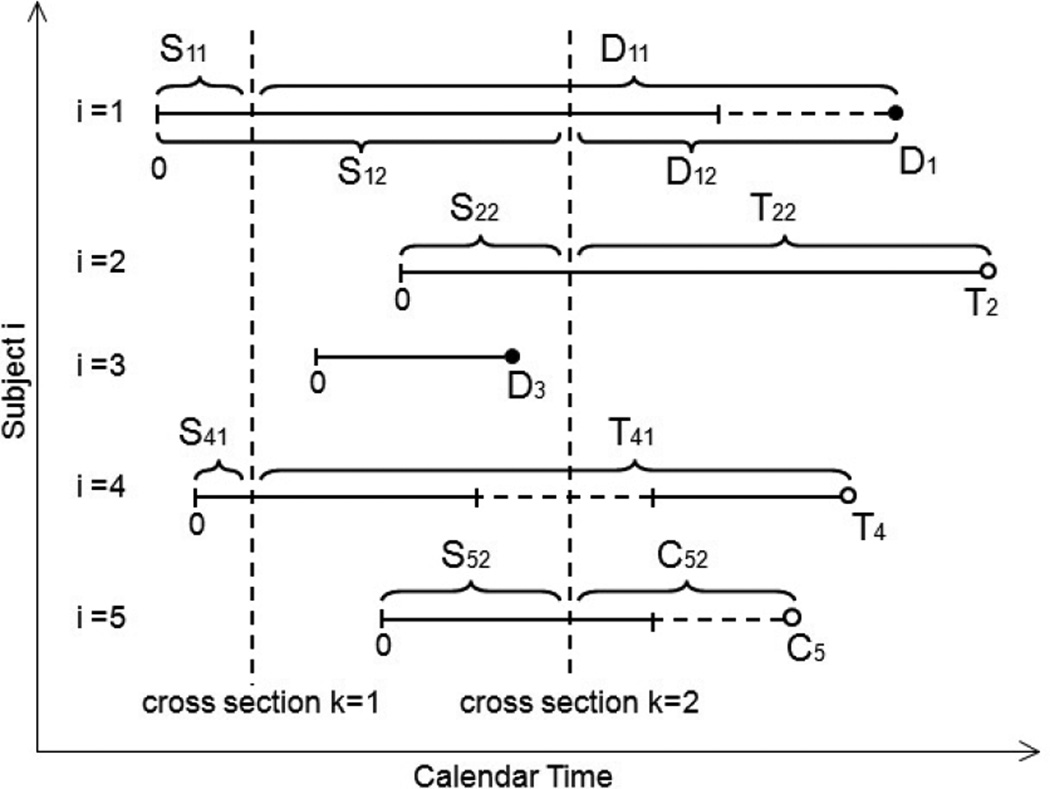
Figure 1 provides a graphical depiction of how each subject’s treatment-free observation time is transformed into a set of time-since-cross-section dates. Five subjects are shown (i = 1, . . . , 5) and two cross sections (k = 1, 2). The five subjects begin follow-up at times which are staggered in calendar time. Subject 1 has failure times D₁₁ corresponding to cross section k = 1 and D₁₂ with respect to cross section k = 2. Note that, even though subject i = 1 is deemed treatment-ineligible after cross section k = 2, the subsequent death is not censored. Subject i = 2 is treated (and therefore censored) at time T₂₂ with respect to cross section k = 2. Subject i = 3 is not included in either cross section since i = 3 starts and then finishes follow-up in between cross-sections. Subject i = 4 is included in cross section k = 1, then becomes treatment-ineligible until after cross section k = 2. Therefore, i = 4 is included only in cross-section k = 1. With respect to cross section k = 1, subject i = 4 is censored at treatment time, T₄₁, as opposed to the time of treatment-ineligibility. Similarly, subject i = 5 is censored at time C₅₂, with respect to cross section k = 2, not at the beginning of the treatment-ineligible period.

Figure 1. Examples of the relationship between cross-section time and follow-up time.

Vertical dashed lines denote cross-section dates (k = 1, 2), while horizontal dashed lines denote treatment-ineligible periods. Subject i = 1 is included in both cross-sections k = 1 and k = 2 and contributes death times D₁₁ and D₁₂ to the analysis. Subject i = 2 is treated at time T₂₂ and, hence, censored (perhaps dependently) at that time. Subject i = 3 is not included in either cross-section. Subject i = 4 is included in cross section k = 1, but not cross section k = 2 due to treatment-ineligibility. Subject i = 5 is censored at time C₅₂ from cross section k = 2. Note that subjects i = 1 and i = 5 are not censored after becoming treatment-ineligible.

The hazard function of interest can be expressed as

$${\lambda }_{ik}(t)=\underset{\delta \downarrow 0}{\text{lim}}\frac{1}{\delta }P[t\le D_{ik}<t+\delta |D_{ik}\ge t,A_{ik}=1,{\tilde{\mathit{Z}}}_i(S_{ik}),{\tilde{A}}_i(S_{ik}),S_{ik}].$$ (1)

We let Z_ik denote the pertinent covariate with respect to the hazard function defined in (1). Essentially, we assume that the derived covariate, Z_ik captures all death hazard predictors from the observed covariate and treatment-eligibility histories; specifically, that

$${\lambda }_{ik}(t|{\mathit{Z}}_{ik},A_{ik}=1,{\tilde{\mathit{Z}}}_i(S_{ik}),{\tilde{A}}_i(S_{ik}),S_{ik})={\lambda }_{ik}(t|{\mathit{Z}}_{ik},A_{ik}=1).$$

Note that the t argument pertains to time after the kth cross-section date, with the covariate “frozen” at its cross-section date value. The objective is to determine the relationship between the covariate (as known on the kth cross-section date) and future treatment-free survival time. Since the underlying goal is to determine what factors are associated with treatment urgency, only subjects who are treatment-eligible at the kth cross-section date are of interest; hence the conditioning on [A_ik = 1].

Death times are modeled using stratified Cox regression,

$${\lambda }_{ik}(t)={\lambda }_{0k}(t)\text{exp}\{{\mathit{\beta }}_0^{\prime }{\mathit{Z}}_{ik}\},$$ (2)

where the baseline hazards are allowed to be cross-section-specific, although covariate effects are assumed to be equal across all cross-sections. We make the standard independent censoring assumption which, in the context of the observed data, is given by:

$${\lambda }_{ik}(t|{\tilde{\mathit{Z}}}_i(S_{ik}+t),{\tilde{A}}_i(S_{ik}+t),A_{ik}=1,T_{ik}>t,C_{ik}>t)={\lambda }_{ik}(t|{\tilde{\mathit{Z}}}_i(S_{ik}+t),{\tilde{A}}_i(S_{ik}+t),A_{ik}=1)$$ (3)

However, a model for D_ik conditioning on only Z_ik does not incorporate {Z_i(r); r ∈ (S_ik, S_ik + t)} or {A_i(r); r ∈ (S_ik, S_ik + t)}. Generally, λ_ik(t|Z_ik, A_ik = 1) ≠ λ_ik(t|Z_ik, A_ik = 1, T_ik > t) due to the correlation between T_ik and D_ik resulting from mutual dependence on {Z_i(r); r > S_ik} and/or {A_i(r); r > S_ik}. In this sense, the assumption listed in (3) does not lead to parameter estimation for model (2) through unweighted methods.

We use a variant of Inverse Probability of Censoring Weighting (IPCW) to overcome the dependent censoring of D_ik by T_ik. The following treatment hazard model is assumed,

$${\lambda }_i^T(t)=A_i(t){\lambda }_0^T(t)\text{exp}\{{\mathit{\theta }}_0^{\prime }{\mathit{Z}}_i(t)\},$$ (4)

where t is the time from study entry. As indicated in equation (1), the treatment hazard is zero at times during which the patient is treatment-ineligible. Therefore, treatment hazards among eligible patients are assumed to be proportional. Similar to the presentation for model (2), the covariate in model (4) is written as Z_i(t) for notational convenience and, more generally, could depend on the covariate and treatment-eligibility histories, Z̃_i(t) and Ã_i(t), respectively. We make a no-unmeasured-confounders type assumption with respect to treatment; i.e, we assume that ${\lambda }_i^T(t|{\mathit{Z}}_i(t),A_i(t),{\tilde{\mathit{Z}}}_i(D_i),{\tilde{A}}_i(D_i),D_i)={\lambda }_i^T(t|{\mathit{Z}}_i(t),A_i(t))$.

The regression coefficient, θ₀, is estimated by θ̂, as the root of the score function,

$$U^T(\mathit{\theta })=\sum _{i=1}^n{\int }_0^{\tau }\{{\mathit{Z}}_i(t)-\overline{\mathit{Z}}(t;\mathit{\theta })\}d{N}_i^T(t),$$

where τ is the largest observation time, $\overline{\mathit{Z}}(t;\mathit{\theta })=R_T^{(1)}(t;\mathit{\theta })/R_T^{(0)}(t;\mathit{\theta })$, and $R_T^{(p)}(t;\mathit{\theta })=n^{-1}{\sum }_{i=1}^n{A}_i(t)Y_i(t){\mathit{Z}}_i{(t)}^{\otimes p}\text{exp}\{\mathit{\theta }\prime {\mathit{Z}}_i(t)\}$ for p = 0, 1, 2, with a, a^⊗0 = 1, a^⊗1 = a, a^⊗2 = aa^T for a vector, a. The Breslow estimator of ${\mathrm{\Lambda }}_0^T(t)$ is given by ${\widehat{\mathrm{\Lambda }}}_0^T(t)=n^{-1}{\sum }_{i=1}^n{\int }_0^t{R}_T^{(0)}{(u;\widehat{\mathit{\theta }})}^{-1}d{N}_i^T(u)$.

The IPCW method allows us to obtain consistent estimators by weighting each subject’s experience by the inverse of (what can be thought of heuristically as) the probability of remaining untreated. In particular, the covariate effect, β₀, can be estimated as the root of the stratified inverse-weighted score function,

$$U(\mathit{\beta },W)=\sum _{k=1}^K\sum _{i=1}^n{\int }_0^{{\tau }_k}{A}_{ik}\{{\mathit{Z}}_{ik}-{\overline{\mathit{Z}}}_k(t;\mathit{\beta },W)\}{W}_{ik}^A(t)d{N}_{ik}(t),$$ (5)

where the weight function is given by $W_{ik}^A(t)=Y_{ik}(t)\text{exp}\{{\mathrm{\Lambda }}_i^T(S_{ik}+t\}-{\mathrm{\Lambda }}_i^T(S_{ik})\}$ and ${\overline{\mathit{Z}}}_k(t;\mathit{\beta },W)=R_k^{(1)}(t;\mathit{\beta },W)/R_k^{(0)}(t;\mathit{\beta },W)$, with $R_k^{(p)}(t;\mathit{\beta },W)=n^{-1}{\sum }_{i=1}^n{A}_{ik}{W}_{ik}^A(t)Y_{ik}(t){\mathit{Z}}_{ik}^{\otimes p}\text{exp}(\mathit{\beta }\prime {\mathit{Z}}_{ik})$ for p = 0, 1, 2. The upper limit, τ_k, satisfies P(X_ik ≥ τ_k) > 0 and in practice would usually be set to max{X_ik}. We refer to $W_{ik}^A(t)$ as the Type A weight. The quantity does not constitute a stabilized weight (Robins and Finkelstein, 2000). However, the quantity can be thought of heuristically as a ratio of two probabilities, P(T_i > S_ik + t|T_i > S_ik)⁻¹. From this angle, large values of ${\mathrm{\Lambda }}_i^T(S_{ik}+t)$ should, to at least some extent, coincide with large values of ${\mathrm{\Lambda }}_i^T(S_{ik})$, such that the Type A weight is less subject to wide variation, unlike the unstabilized weight in more traditional dependent censoring settings. We demonstrate in the Web Appendix that U(β₀, W) from (5) has mean 0. Essentially, the zero mean property arises from $E[W_{ik}^A(t)d{M}_{ik}(t)|{\mathit{Z}}_{ik},A_{ik}=1]=0$, where dM_ik(t) = dN_ik(t) − Y_ik(t) dΛ_ik(t).

Additionally, it can be argued that $E[W_{ik}^A(t)d{M}_{ik}(t)g({\mathit{Z}}_{ik})|{\mathit{Z}}_{ik},A_{ik}=1]=0$, where g(·) ∈ ℛ is a deterministic function of the covariate, Z_ik, used in model (2). Often, g(Z_ik) is chosen to be a probability, since the unstabilized version of the weight is the reciprocal of a probability. Along this train of thought, we define the Type B weight,

$$W_{ik}^B(t)=Y_{ik}(t)\frac{\text{exp}\{{\mathrm{\Lambda }}_i^T(S_{ik}+t)\}}{\text{exp}\{{\mathrm{\Lambda }}_i^T(S_{ik})\}\text{exp}\{{\mathrm{\Lambda }}_{ik}^T(t)\}},$$

where ${\mathrm{\Lambda }}_{ik}^T(t)={\int }_0^t{\lambda }_{ik}^T(u)du$, with

$${\lambda }_{ik}^T(t)=\underset{\delta \downarrow 0}{\text{lim}}\frac{1}{\delta }P[t\le T_{ik}<t+\delta |T_{ik}\ge t,{\mathit{Z}}_{ik},A_{ik}=1].$$ (6)

which we represent through the model,

$${\lambda }_{ik}^T(t)=A_{ik}{\lambda }_{0k}^T(t)\text{exp}\{{\mathit{\theta }}_1^{\prime }{\mathit{Z}}_{ik}\}.$$ (7)

Consistent with the death hazard, ${\lambda }_{ik}^D(t)$, given in (1), the double subscripting in (6) corresponds to the time scale being time from cross-section, and conditionality on [Z_ik, A_ik = 1]. One can interpret ${\lambda }_{ik}^T(t)$ as the hazard function for treatment, with time measured from S_ik onward, among patients alive, untreated and treatment-eligible at time S_ik. We can re-express the Type B weight as $W_{ik}^B(t)=W_{ik}^A(t)\text{exp}\{-{\mathrm{\Lambda }}_{ik}^T(t)\}$, with $\text{exp}\{-{\mathrm{\Lambda }}_{ik}^T(t)\}$ reflecting the conditional probability of remaining untreated t time units after S_ik, given untreated and treatment-eligible at time S_ik. From this perspective, the Type B weight can be viewed as stabilized, since its numerator and denominator are both akin to conditional probabilities. Note that we do not expect (7) to be a correct model; its purpose is to provide a reasonable version of g(Z_ik) to be incorporated into the weight function as a stabilizer. In contrast, consistent estimation of β₀ does require that model (4) be correct.

Another weight which can be used is the Type C weight,

$$W_{ik}^C(t)=Y_{ik}(t)\text{exp}\{{\mathrm{\Lambda }}_i^T(S_{ik}+t)\},$$ (8)

which is reminiscent of the unstabilized weight in more traditional dependent censoring settings. In particular, inverse weighting the data (without a view to the model of interest) would lead to $W_{ik}^C(t)$. However, in our set-up, the Type A weight is actually the ‘raw’ version of the weight; in the sense that the $W_{ik}^A(t)$ function is defined specifically such that $E[W_{ik}^A(t)d{M}_{ik}(t)|{\mathit{Z}}_{ik},A_{ik}=1]=0$, resulting on (5) having mean zero (see the Web Appendix for associated details). Therefore, we could only expect that $E[W_{ik}^C(t)d{M}_{ik}(t)|{\mathit{Z}}_{ik},A_{ik}=1]=0$ if we can express $W_{ik}^C(t)$ as the product of $W_{ik}^A(t)$ and some suitably defined g(Z_ik). From this perspective, setting $g({\mathit{Z}}_{ik})=\text{exp}\{{\mathrm{\Lambda }}_i^T(S_{ik})\}$, and hence $W_{ik}^C(t)=W_{ik}^A(t)\text{exp}\{{\mathrm{\Lambda }}_i^T(S_{ik})\}$, reveals that the Type C weight actually amounts to dividing the ‘raw’ weight function by a probability. Viewed this way, $W_{ik}^C(t)$ should lead, if anything, to increased variance. Our thoughts regarding the Type A, B and C weights are assessed numerically in Section 4.

3. Asymptotic Properties

We assume that the random vectors $\{X_i,{\mathrm{\Delta }}_i,{\mathrm{\Delta }}_i^T,{\tilde{\mathit{Z}}}_i(X_i),{\tilde{A}}_i(X_i)\}$, for i = 1 . . . n, are independent and identically distributed, with Z_i(t) bounded for t ∈ (0, τ], where τ satisfies P(X_i ≥ τ) > 0. We summarize the asymptotic properties of the proposed methods in the following theorem. The regularity conditions are listed in the Web Appendix.

THEOREM 1: Under certain regularity conditions, n^1/2(β̂ − β₀) converges asymptotically to a zero-mean Gaussian process with covariance function $E[{\phi }_i{\phi }_i^{\prime }]$, where {φ₁, . . . , φ_n} are i.i.d. with mean 0 asymptotically, with

$${\phi }_i=\mathrm{\Omega }{({\mathit{\beta }}_0)}^{-1}[\sum _{k=1}^K{A}_{ik}{\int }_0^{{\tau }_k}\{{\mathit{Z}}_{ik}-{\overline{z}}_k(t;{\mathit{\beta }}_0,W)\}{W}_{ik}^A(t)d{M}_{ik}(t)+H\prime (t;{\mathit{\beta }}_0,W){\mathrm{\Omega }}_T{({\mathit{\theta }}_0)}^{-1}{U}_i^T({\mathit{\theta }}_0)+{\int }_{S_{ik}}^{{\tau }_k}G(t,\tau ;{\mathit{\beta }}_0)r_T^{(0)}{(t;{\mathit{\theta }}_0)}^{-1}d{M}_i^T(t)],$$

where

$$\begin{array}{c}d{M}_i^T(t)=d{N}_i^T(t)-A_i(t)Y_i(t)\text{exp}\{\mathit{\theta }\prime {\mathit{Z}}_i(t)\}{\mathrm{\Lambda }}_0^T(t),\hfill \\ {\overline{z}}_k(t;\mathit{\beta },W)=r_k^{(1)}(t;\mathit{\beta },W)/r_k^{(0)}(t;\mathit{\beta },W),\hfill \\ \overline{z}(t;\mathit{\theta })=r_T^{(1)}(t;\mathit{\theta })/r_T^{(0)}(t;\mathit{\theta }),\hfill \\ r_k^{(p)}(t;\mathit{\beta },W)=E[A_{ik}{W}_{ik}^A(t)Y_{ik}(t){\mathit{Z}}_{ik}^{\otimes p}\text{exp}(\mathit{\beta }\prime {\mathit{Z}}_{ik})],p=0,1,2,\hfill \\ r_T^{(p)}(t;\mathit{\theta })=E[A_i(t)Y_i(t){\mathit{Z}}_i{(t)}^{\otimes p}\text{exp}\{\mathit{\theta }\prime {\mathit{Z}}_i(t)\}],p=0,1,2,\hfill \end{array}$$

with Ω(β), H(t; β, W), Ω_T(θ), $U_i^T(\mathit{\theta })$ and G(t₁, t₂; β) defined in the Web Appendix.

The covariance can be estimated consistently by $n^{-1}{\sum }_{i=1}^n{\widehat{\phi }}_i{\widehat{\phi }}_i^{\prime }$, where φ̂_i is obtained by replacing all limiting values in φ_i by their empirical counterparts. A proof of Theorem 1 is provided in the Web Appendix. The proof proceeds by demonstrating that, asymptotically, $n^{1/2}(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0)=n^{-1/2}{\sum }_{i=1}^n{\phi }_i+o_p(1)$ through a sequence of Taylor series expansions.

Note that subjects (i = 1, . . . , n) are assumed to be independent. However, no independence assumption is made regarding the cross-section-specific contributions of a given subject; the dependence structure for the within-subject score function contributions being left unspecified. Since we do not model the within-subject correlation explicitly, our approach is analogous to generalized estimating equations (GEE) with a working independence assumption (Liang and Zeger, 1986). It is well-established in the GEE literature that, so long as the model for the marginal mean is correct, one need not model the within-subject correlation structure accurately in order to obtain a consistent estimator of the regression coefficient for the mean model.

The proof of Theorem 1 is developed in the context of the Type A weight, $W_{ik}^A(t)=Y_{ik}(t)\text{exp}\{{\mathrm{\Lambda }}_i^T(S_{ik}+t)-{\mathrm{\Lambda }}_i^T(S_{ik})\}$. In practice, a stabilized version would usually be preferred. As implied by Theorem 1, the computation of the variance is quite complicated, and is more complicated with the Type B weight. Such considerations motivate a computationally simpler form for the variance estimator. One such simplification involves treating the weight (be it $W_{ik}^A(t),W_{ik}^B(t)\text{or}{W}_{ik}^C(t)$) as fixed; in which case the variance estimator simplifies to $n^{-1}{\sum }_{i=1}^n{\widehat{\phi }}_i^{*}{\widehat{\phi }}_i^{*\prime }$, where

$${\widehat{\phi }}_i^{*}=\widehat{\mathrm{\Omega }}{(\widehat{\mathit{\beta }})}^{-1}\sum _{k=1}^K{A}_{ik}{\int }_0^{{\tau }_k}\{{\mathit{Z}}_{ik}={\overline{\mathit{Z}}}_k(t;\widehat{\mathit{\beta }},\widehat{W})\}{\widehat{W}}_{ik}(t)d{\widehat{M}}_{ik}(t).$$ (9)

This simplified variance estimator can be calculated using Cox regression software that allows weights and a robust variance estimator; e.g., proc phreg in SAS, coxph in R. Pertinent SAS code is available from the first author upon request.

4. Simulations

We modify the algorithm developed by Zheng and Heagerty (2005) to generate data which follow a partly conditional proportional hazards model. We first generate a binary treatment group indicator, Z_ia, taking values 0 and 1 with probability 0.5. A longitudinal marker, Z_i(S_ik), measured at a common set of cross section dates (CS₁, CS₂, . . . , CS_K) is then constructed. To generate data [D_i, Z_ia, Z_ib] where Z_ib = vec{Z_i(S_ik)}, we first create $Z_{ib0}=b_i+{\sum }_{k=1}^K\text{log}(V_{ik})/{\gamma }_2$, where b_i ~ N(μ, σ₂) and the V_ik are independent positive stable variates with index ρ (Samorodnitsky and Taqqu, 1994). A pre-treatment death time D_i, is then generated with hazard ${\lambda }_i(t)=V_{i0}^{1/\rho }{\lambda }_0(t)\text{exp}\{{\gamma }_1{Z}_{ia}+{\gamma }_2{Z}_{ib0}\}$, where V_i0 ~ P(ρ) and is independent of V_ik, with Λ₀(t) = (t/a)^1/ρ2 and a is a constant. Let Z_i(S_ik) = Z_ib0−log(V_ik)/γ₂. The death hazard is then written as

$${\lambda }_i(t)=V_{i0}^{1/\rho }{\lambda }_0(t)\text{exp}\{{\gamma }_1{Z}_{ia}+{\gamma }_2{Z}_i(S_{ik})+\text{log}(V_{ik})\}.$$ (10)

Subject i enters the study on calendar date L_i, where L_i is a Uniform(0, b) variate. Treatment time, T_i, is generated from the proportional hazards model,

$${\lambda }_i^T(t)={\lambda }_0^T(t)\text{exp}\{{\theta }_{01}{Z}_{ia}+{\theta }_{02}I(t>R_i)\},$$ (11)

where ${\lambda }_0^T(t)=d_3$, θ₀ = (θ₀₁, θ₀₂)′, and R_i is time of treatment-ineligibility which is generated with hazard ${\lambda }_i^R(t)={\lambda }_0^R(t)\text{exp}\left\{d_1{V}_{i0}\right\}$, with ${\lambda }_0^R(t)=1/d_2$. Thus, R_i and D_i are positively correlated, which is a reflection of the data which motivated the proposed methods. Note that treatment time and pre-treatment death time, T_i, and D_i, are dependent since both depend on time of treatment ineligibility, R_i.

To see that the prescribed set-up yields proportional hazards, integrating both sides of model (4), gives

$${\mathrm{\Lambda }}_i(t)=V_{i0}^{1/\rho }{\mathrm{\Lambda }}_0(t)\text{exp}\{{\gamma }_1{Z}_{ia}+{\gamma }_2{Z}_i(S_{ik})\}{V}_{ik},$$

such that the pre-treatment survival function is given by

$$\text{exp}\{-{\mathrm{\Lambda }}_i(t)\}=\text{exp}\{-{\mathrm{\Lambda }}_0(t)\text{exp}\{{\gamma }_1{Z}_{ia}+{\gamma }_2{Z}_i(S_{ik})\}{V}_{ik}{V}_{i0}^{1/\rho }\}.$$

Transforming the time scale to reflect time since cross section, define t_k = t − S_ik. Then, take the expectation with respect to V_ik first and using the properties of the positive stable distribution, we have

$$\text{exp}\{-{\mathrm{\Lambda }}_i(t_k|Z_{ia},Z_i(S_{ik}),D_i>S_{ik},V_{i0})\}=\text{exp}\{-{[{\mathrm{\Lambda }}_0(t)\text{exp}\{{\gamma }_1{Z}_{ia}+{\gamma }_2{Z}_i(S_{ik})\}{V}_{i0}^{1/\rho }]}^{\rho }/\text{cos}(\pi \rho /2)\}.$$

Then, taking the expectation with respect to V_i0, we have

$$\text{exp}\{-{\mathrm{\Lambda }}_i(t_k|Z_{ia},Z_i(S_{ik}),D_i>S_{ik})\}=\text{exp}\{-{\mathrm{\Lambda }}_0{(t)}^{{\rho }^2}\text{exp}\{{\rho }^2{\gamma }_1{Z}_{ia}+{\rho }^2{\gamma }_2{Z}_i(S_{ik})\}/\text{cos}{(\pi \rho /2)}^{(\rho +1)}\},$$

which implies the following equation after taking logarithm and negative of both sides

$${\mathrm{\Lambda }}_i(t_k|Z_{ia},Z_i(S_{ik}),D_i>S_{ik})={\mathrm{\Lambda }}_0{(t)}^{{\rho }^2}\text{exp}\{{\rho }^2{\gamma }_1{Z}_{ia}+{\rho }^2{\gamma }_2{Z}_i(S_{ik})\}/\text{cos}{(\pi \rho /2)}^{(\rho +1)}.$$

Differentiating with respect to t_k,

$${\lambda }_i(t_k|Z_{ia},Z_i(S_{ik}),D_i>S_{ik})=\frac{{\lambda }_0(t_k+S_{ik}){\rho }^2{\{{\mathrm{\Lambda }}_0(t_k+S_{ik})\}}^{({\rho }^2-1)}}{\text{cos}{(\pi \rho /2)}^{(\rho +1)}}\text{exp}\{{\rho }^2{\gamma }_1{Z}_{ia}+{\rho }^2{\gamma }_2{Z}_i(S_{ik})\}.$$

Using this construction, the hazard for D_ik = D_i − S_ik will generally depend on S_ik and therefore stratified models similar to those considered by Wei et al. (1989) would be appropriate. With Λ₀(t) = (t/a)^1/ρ2 , λ₀(t_k + S_ik)ρ²{Λ₀(t_k + S_ik)}(^ρ2−1) = 1/a, we obtain

$${\mathrm{\lambda }}_i(t_k|Z_{ia},Z_i(S_{ik}),D_i>S_{ik})=\text{exp}\{{\rho }^2{\gamma }_1{Z}_{ia}+{\rho }^2{\gamma }_2{Z}_i(S_{ik})\}/[a\text{cos}{(\pi \rho /2)}^{(\rho +1)}].$$

If we define λ_ik(t; S_ik) = λ_i(t_k|Z_ia, Z_i(S_ik), D_i > S_ik), λ_{0 k}(t) = [a cos(πρ/2)^(ρ+1)]⁻¹ and β₀ = (β₀₁, β₀₂)′= (ρ²γ₁, ρ²γ₂)′, then the proportional hazard model on treatment-free survival is achieved,

$${\lambda }_{ik}(t;S_{ik})={\lambda }_{0k}(t)\text{exp}\{{\beta }_{01}{Z}_{ia}+{\beta }_{02}{Z}_i(S_{ik})\}.$$ (12)

After generating the data, we only include for analysis those Z_i(S_ik) with Li < S_ik < min(X_i, R_i). Data pertaining to survival time since cross section {X_ik, Δ_ik, Z_ia, Z_i(S_ik)} is used to fit model (6), with time-to-treatment data {$X_i,{\mathrm{\Delta }}_i^T,Z_{ia},{\tilde{Z}}_i(X_i)$} used to fit model (5).

We evaluate samples with n = 1000 subjects and obtain 10%, 20%, and 40% censoring by varying a from 10⁴ to 4 × 10⁷. The value of d₂ varies from 300 to 3000, resulting in ineligibility rates from 10% to 30%. There are K = 10 cross section dates. We set b = 500, [θ₀₁, θ₀₂] = [−1, −1], μ = 18, σ = 1, [γ₁, γ₂] = [−1, −0.5], [−0.5, −0.25], [0, 0], d₁ = d₃ = 0.001, with CS_k = 100 × k. For all our simulated situations, 1000 Monte Carlo data sets are used. We present results using ρ = 0.8, thus [β₀₁, β₀₂] = [−0.64, −0.32] when [γ₁, γ₂] = [−1, −0.5]. With the number of cross sections set to K = 10, the average number of cross sections per subject is 0.7 to 2.4, depending on the censoring level. We apply the simplified variance estimate which treats the estimated weights as fixed; i.e., as given in (9).

Table 1 presents simulation results based on the Type A weight, while Tables 2 and 3 present results for Type B and Type C, respectively. Estimates of β₀ appear to be consistent based on all weights. The variance of the Type B estimator is smaller than that of Type A, which is likely the result of the added stabilizer. Coverage probabilities using the proposed (simplified) variance estimator are close to the nominal 95% level, with those of the Type B estimator being slightly higher than those of Type A. The variance of the Type C estimator appears to be greater than that of Type A, consistent with our comments in Section 2 that the Type C weight can be viewed as the result of dividing a ratio of probabilities (i.e., $W_{ik}^A(t)$, which should be fairly stable) by another probability.

Table 1.

Simulation results for β̂ computed using Type A Weight $W_{ik}^A(t)$; n = 1000.

	β̂01					β̂02
Censored	β01*	Bias	ESE	ASE	CP	β02*	Bias	ESE	ASE	CP
10%	−0.64	−0.009	0.132	0.125	0.93	−0.32	−0.001	0.020	0.020	0.95
20%		−0.004	0.143	0.128	0.92		−0.002	0.020	0.019	0.94
40%		−0.008	0.145	0.129	0.93		0.001	0.018	0.018	0.94
10%	−0.32	0.002	0.146	0.132	0.93	−0.16	0.001	0.013	0.012	0.93
20%		−0.004	0.140	0.129	0.92		−0.001	0.010	0.010	0.94
40%		−0.001	0.144	0.130	0.92		−0.001	0.010	0.009	0.94
10%	0	0.001	0.140	0.130	0.93	−10−4†	−0.003	0.048	0.044	0.94
20%		−0.002	0.136	0.127	0.94		−0.001	0.042	0.041	0.95
40%		−0.007	0.143	0.128	0.93		−0.002	0.038	0.036	0.94

^*β₀ = (β₀₁, β₀₂) = (ρ²γ₁, ρ²γ₂), where ρ = 0.8.

^†The Bias, ESE and ASE shown in this block are in 10⁻⁴ scale.

Table 2.

Simulation results for β̂ computed using Type B Weight given in (4); n = 1000.

	β̂01					β̂02
Censored	β01*	Bias	ESE	ASE	CP	β02*	Bias	ESE	ASE	CP
10%	−0.64	0.004	0.130	0.121	0.94	−0.32	−0.001	0.021	0.020	0.94
20%		−0.008	0.121	0.116	0.94		−0.001	0.018	0.018	0.95
40%		−0.008	0.113	0.112	0.94		−0.001	0.016	0.016	0.95
10%	−0.32	−0.005	0.136	0.130	0.94	−0.16	−0.001	0.012	0.011	0.94
20%		−0.005	0.122	0.117	0.94		−0.001	0.010	0.009	0.94
40%		0.003	0.112	0.109	0.93		−0.001	0.008	0.008	0.94
10%	0	0.005	0.135	0.126	0.93	−10−4†	−0.001	0.044	0.043	0.94
20%		−0.005	0.123	0.118	0.94		−0.002	0.041	0.038	0.94
40%		0.004	0.109	0.109	0.95		−0.002	0.031	0.031	0.95

^*β₀ = (β₀₁, β₀₂) = (ρ²γ₁, ρ²γ₂), where ρ = 0.8.

^†The Bias, ESE and ASE shown in this block are in 10⁻⁴ scale.

Table 3.

Simulation results for β̂ computed using Type C Weight given in (5); n = 1000.

	β̂01					β̂02
Censored	β01*	Bias	ESE	ASE	CP	β02*	Bias	ESE	ASE	CP
10%	−0.64	0.002	0.142	0.129	0.93	−0.32	−0.002	0.022	0.021	0.94
20%		−0.005	0.144	0.136	0.93		−0.001	0.022	0.020	0.92
40%		−0.010	0.159	0.136	0.90		−0.002	0.020	0.019	0.94
10%	−0.32	−0.003	0.146	0.135	0.94	−0.16	−0.001	0.012	0.012	0.94
20%		−0.012	0.154	0.138	0.91		−0.001	0.012	0.011	0.92
40%		−0.003	0.157	0.138	0.91		−0.001	0.011	0.010	0.94
10%	0	−0.008	0.153	0.136	0.92	−10−4†	−0.002	0.047	0.046	0.94
20%		−0.001	0.146	0.134	0.92		−0.002	0.045	0.043	0.94
40%		0.007	0.155	0.137	0.92		−0.002	0.042	0.040	0.93

^*β₀ = (β₀₁, β₀₂) = (ρ²γ₁, ρ²γ₂), where ρ = 0.8.

^†The Bias, ESE and ASE shown in this block are in 10⁻⁴ scale.

5. Data Analysis

We applied the proposed methods in order to compare pre-transplant mortality between acute and chronic End-Stage Liver Disease (ESLD) patients. Data were obtained from the Scientific Registry of Transplant Recipients (SRTR), a national population-based organ transplant registry. The study population included patients initially wait listed for deceased-donor liver transplantation between March 1, 2002 and December 31, 2009 in United States. Only patients age ≥ 18 at listing and not previously transplanted (i.e., not repeat transplant candidates) were included in the study population. Cross-section dates were chosen every 7 days from 03/01/2002 to 12/31/2009, such that there were K = 409 cross sections in all. At any given cross section date, any subject who was still on the wait-list (not inactive and not removed) was included in the cross section since, in practice, patients who got removed or were made inactive were no longer eligible to receive offers for deceased-donor livers. Given the objectives of our analysis, it is appropriate to compare only patients who, in a given cross-section date, are in fact eligible to receive a liver transplant. However, after being included into a given cross-section, such patients are not censored if they are subsequently deactivated or removed from the wait-list. Deactivation and removal (and the associated death that may follow) are potential consequences of not receiving a liver transplant. For the death model, the failure time was defined from the date of cross section to the date of the earliest of death, transplant or censoring.

In order to construct the IPCW weight, ${\mathrm{\Lambda }}_i^T(t)$ was estimated based on a time-dependent Cox model in which transplant was the event. For the time-to-transplant model, time t starts from the beginning of the follow-up (the date of wait listing), as opposed to cross section time. The model was stratified, such that

$${\lambda }_{ir}^T(t)=A_i(t){\lambda }_{0r}^T(t)\text{exp}\{{\mathit{\theta }}_0^{\prime }{\mathit{Z}}_i(t)\},$$

where the subscript r = 1, . . . , 11 stands for region. The presence of the indicator, A_i(t), reflects the fact that a patient’s time while inactive or removed does not contribute to the estimation of θ₀ or ${\mathrm{\Lambda }}_{0r}^T(t)$. The patient level covariate, Z_i(t), included MELD score, Status 1, albumin, age, gender, race, diagnosis of Hepatitis C, body mass index, diabetes, hospitalization, blood type, dialysis within prior week, encephalopathy, ascites and serum creatinine. Among the covariates in this list, MELD score, albumin, dialysis, encephalopathy, ascites and serum creatinine were time-dependent.

We evaluated several different versions of weight, including W_ikr(t) = Y_ikr(t) (unweighted), $W_{ikr}^A(t)=Y_{ikr}(t)\text{exp}\{{\mathrm{\Lambda }}_{ikr}^T(t+S_{ik})-{\mathrm{\Lambda }}_{ikr}^T(S_{ik})\}$, $W_{ikr}^B(t)$ and $W_{ikr}^C(t)$. Some very large values of the weight function occurred, even for $W_{ikr}^B(t)$. Since we found that 99% of weights were less than 10, weights were then capped at 10.

The model of primary interest, the pre-transplant death model, was also stratified

$${\lambda }_{ikr}(t)={\lambda }_{0kr}(t)\text{exp}\{{\mathit{\beta }}_0^{\prime }{Z}_{ik}\},$$

where the subscript r = 1, . . . , 11 stands for region and k = 1, . . . , 409 stands for cross section. The cross-section-specific covariates, Z_ik, included albumin, age, gender, race, diagnosis, body mass index, diabetes, hospitalization status at listing, previous malignancy; as well as the covariate of chief interest, MELD score (21–23, 24–26, 27–29, 30–32, 33–35, 36–40), with each MELD category being compared to Status 1, the reference. Also included in Z_ik were average change in MELD score (pertaining to the time interval between the date of listing and cross-section k date, and estimated using ordinary least squares) and average change in albumin (estimated analogously). Other elements included the percentage of time spent in inactive status, and percent of time receiving dialysis. Since 99% of MELD and albumin slope values before cross sections fell in the [-1,1] interval, the slopes were bounded by −1 and 1. Our final sample consisted of n = 23, 657 patients.

Results based on the death model using the Type B weight are listed in Table 4. Relative to Status 1, pre-transplant mortality is 2.62 times as great for MELD 33–35 (p = 0.001) and 2.58 times as great for MELD 36–40 (p = 0.002).

Table 4.

Analysis of liver wait-list mortality (using Type B Weight)

Group	β̂	$\widehat{SE}(\widehat{\beta })$	eβ̂	p-value
Status 1	0	.	1	.
MELD 21–23	0.05	0.267	1.05	0.87
MELD 24–26	0.18	0.272	1.20	0.50
MELD 27–29	0.52	0.276	1.68	0.06
MELD 30–32	0.25	0.334	1.29	0.45
MELD 33–35	0.96	0.301	2.62	0.001
MELD 36–40	0.95	0.306	2.58	0.002

Both unweighted and weighted results are listed in Table 5. After weighting the model, the parameter estimates of MELD group became larger, in each case. Similar to the findings from simulation studies, the standard errors in Table 5 were the lowest for the Type B weight, while those for Type C were the largest.

Table 5.

Analysis of liver wait-list mortality; Comparison of results using different weights.

	Unweighted		Type C Weight		Type A Weight		Type B Weight
Group	β̂	$\widehat{SE}(\widehat{\beta })$	β̂	$\widehat{SE}(\widehat{\beta })$	β̂	$\widehat{SE}(\widehat{\beta })$	β̂	$\widehat{SE}(\widehat{\beta })$
Status 1	0	.	0	.	0	.	0	.
MELD 21–23	−0.81	0.210	0.01	0.271	0.07	0.270	0.05	0.267
MELD 24–26	−0.75	0.215	−0.002	0.286	0.11	0.281	0.18	0.272
MELD 27–29	−0.29	0.220	0.31	0.287	0.42	0.283	0.52	0.276
MELD 30–32	−0.32	0.256	0.10	0.348	0.11	0.339	0.25	0.334
MELD 33–35	0.26	0.246	0.91	0.345	0.92	0.321	0.96	0.301
MELD 36–40	0.33	0.272	0.79	0.335	0.73	0.324	0.95	0.306

Supplementary analysis revealed that acute patients died very fast in the early stage. The Status 1 Kaplan-Meier curve initially dropped much more quickly than the survival curves for the MELD groups. However, the Status 1 survival curve leveled off eventually, while the survival curves for the MELD groups kept dropping.

6. Discussion

We propose semiparametric methods to estimate the effect of a time dependent covariate on treatment-free survival. Pre-treatment death may be dependently censored by the receipt of treatment, and subjects may experience periods of treatment-ineligibility. The proposed methods estimate the regression parameter of a partly conditional hazard model through landmark analysis and IPCW. The proposed estimators are demonstrated to be consistent and asymptotically normal, with consistent covariance estimators provided.

Zheng and Heagerty (2005) proposed partly conditional Cox regression methods. Van Houwelingen (2007) proposed landmark models based on partly conditional methods. In Zheng and Heagerty (2005), the time clock is re-set at covariate measurement times, unlike our methods, wherein the clock is re-set at cross-section dates. Neither the Zheng and Heagerty (2005) or Van Houwelingen (2007) methods deal with dependent censoring or accommodate treatment ineligibility.

Comparisons of pre-transplant death rates between Status 1 and MELD patients have rarely been conducted; in part, since the assumption that Status 1 patients have the highest death rate is widely accepted by the liver transplant community. However, in a recent study (Sharma et. al, 2011) using a traditional time-dependent model, death rates for patients with MELD ≥ 40 were shown to be significantly higher than those of Status 1. Analysis shown in Section 5 based on the proposed methods show that MELD ≥ 33 is associated with significantly higher pre-transplant mortality than Status 1.

Some discussion regarding the appropriate number of cross-sections, K, is in order. Greater K generally results in a greater amount of information, although returns diminish since information overlaps among different cross-sections. Some guiding principles are as follows. First, it seems reasonable to make the cross-sections equally spaced. Second, it is preferable to select a ‘start’ date (i.e., for cross-section k = 1) that is easy to identify with (e.g., Jan 1, 2000) then fix the time interval between cross-sections thereafter (e.g., every 30 days). Third, the disincentive to choosing a larger number of cross-sections is largely computational burden. Choosing K cross-sections amounts to essentially stacking K data sets together prior to analysis. For a given cross-section k, the covariate used in the death model, Z_ik is defined once per subject. However, each subject will typically contribute multiple records per cross-section since changes in the covariate and eligibility status affect the subject’s inverse weight. In summary, we suggest picking an intuitive cross-section start date for k = 1; making the cross-sections equally spaced; spacing the cross-section dates such that as many cross-sections as computationally feasible are used. One could argue that if an appropriate number of cross-sections is employed, then adding cross-sections will not alter the results for the death model meaningfully.

The proposed methods assume that the death hazards for the subgroups of interest are proportional. It would be useful to develop extensions of the proposed methods to target measures which do not require the proportional hazards assumption.