Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Jun 26;3:2079. doi: 10.1038/srep02079

On the near-wall accumulation of injectable particles in the microcirculation: smaller is not better

Tae-Rin Lee 1,2, Myunghwan Choi 3, Adrian M Kopacz 2, Seok-Hyun Yun 3, Wing Kam Liu 2,4,5,a, Paolo Decuzzi 1,6,b
PMCID: PMC3693098  PMID: 23801070

Abstract

Although most nanofabrication techniques can control nano/micro particle (NMP) size over a wide range, the majority of NMPs for biomedical applications exhibits a diameter of ~100 nm. Here, the vascular distribution of spherical particles, from 10 to 1,000 nm in diameter, is studied using intravital microscopy and computational modeling. Small NMPs (≤100 nm) are observed to move with Red Blood Cells (RBCs), presenting an uniform radial distribution and limited near-wall accumulation. Larger NMPs tend to preferentially accumulate next to the vessel walls, in a size-dependent manner (~70% for 1,000 nm NMPs). RBC-NMP geometrical interference only is responsible for this behavior. In a capillary flow, the effective radial dispersion coefficient of 1,000 nm particles is ~3-fold larger than Brownian diffusion. This suggests that sub-micron particles could deposit within diseased vascular districts more efficiently than conventional nanoparticles.

Over the last 20 years, a plethora of nano/micro particles (NMPs) have been engineered, characterized and developed for the early detection, imaging and treatment of cancer and other diseases1,2. These carriers of therapeutic and imaging agents are sufficiently small to be systemically injected and transported by the blood flow, and can virtually reach any vascular district and tissue within the body. Different NMP sizes, surface properties and shape combinations – the 3S parameters in the design of NMPs – have been tested with the objective of improving the delivery efficiency, that is to say the percentage of injected agents carried at the biological target as compared to the original, total administrated dose. This has led to developing NMPs with a characteristic size ranging from a few nanometers, as in the case of dendrimers3, up to a few micrometers4,5; with a surface charge varying from negative to positive and neutral, as for NMPs decorated with poly(ethylene glycol) (PEG) chains6,7. More recently, the NMP shape has been recognized as a critical determinant in regulating i) the vascular transport8,9; ii) cellular uptake10,11 and iii) differential organ accumulation12. Thus, in addition to the spherical shape, cylindrical, hemispherical and discoidal NMPs are being investigated12,13,14,15. Despite all this, the percentage of injected NMPs accumulating at the biological target is still unsatisfactory low.

Systemically injected particles have to overcome a complex series of biological barriers before reaching their target16,17. From the site of administration, these barriers include i) the transport within the blood vessels where NMPs interact with several circulating cells, including the most abundant red blood cells (RBCs); ii) the sequestration by circulating monocytes and macrophages residing in the liver and spleen; and iii) the diffusion across the intricate tumor matrix while seeking abnormal cells. Each of these barriers reduces the NMP dose eventually reaching the biological target by unspecific sequestration and hijacking18. The use of stealth coatings, such as PEG chains, has increased significantly the average circulation times of NMPs, from minutes up to several hours, by providing a temporary shield against macrophage recognition and uptake6. Sufficiently small NMPs, exhibiting a characteristic size up to a few tens of nanometers (< 50 nm), such as dendrimers and micelles, have been shown to penetrate hundreds of microns deep into the tumor tissue19,20, as well as in organs with highly fenestrated vessels (i.e. liver, spleen, lungs and bone marrow)21. Discoidal particles have demonstrated advantages in navigating and targeting the diseased vasculature, as compared to traditional spherical particles5,15. Although some work has been developed on the interaction between RBCs and micron-sized spherical beads22,23,24, a comprehensive understanding of the interplay between RBCs and NMPs, in the classical size range for intravascular applications, has been so far overlooked.

Blood is a complex fluid comprising an aqueous solution rich in different molecules and proteins – the plasma – and cells – RBCs, white blood cells (WBCs) and platelets. The RBCs are the most abundant accounting for 30 to 50% of the overall blood volume; followed by WBCs with about 1% and platelets at percentages much smaller than 1% of the blood volume. Because of their deformability under flow and biconcave shape, RBCs are confined within the core of the blood vessels and have circulation times of several weeks25,26. On the other hand, WBCs and platelets are required to interact frequently with the blood vessel walls searching for vascular abnormalities. Indeed, these are the features that optimally designed NMPs should also exhibit in order to identify vascular fenestrations and sense for the expression of disease-specific vascular receptors. Interestingly, the RBC confinement in the vessel core regulates and promotes the interaction of WBCs and platelets with the vessel walls. WBCs are twice as big as RBCs and are pushed laterally by the fast moving RBCs so that WBCs can roll and eventually adhere to the vessel walls in the inflamed microcirculation22,23. Differently, platelets are three times smaller than RBCs and, since they cannot penetrate the vessel core densely packed with RBCs, are kept constantly in close proximity of the vessel walls27. Inspired by these two examples, delivery efficiency could be enhanced by designing NMPs that would fully exploit the presence of RBCs in a capillary flow24,28.

This work analyses the transport of NMPs in the microcirculation and their interaction with circulating RBCs. The vascular radial distribution of 200 and 1,000 nm fluorescent beads is studied using intravital video microscopy (IVM)29 in the microcirculation of live mice and the Immersed Finite Element Method (IFEM)30,31,32 to model the transport of NMPs in a capillary flow. Different levels of hematocrit (i.e. the volume percentage of RBCs in blood) are considered ranging from sub-physiological (0 and 15%) to physiologically relevant values (30%). RBCs are treated as biconcave deformable vesicles. The NMPs are spherical in shape and their diameter varies from 10 to 1,000 nm, covering the size range of interest to systemic drug delivery and biomedical imaging systems. Finally, the radial dispersion of the NMPs within the capillary flow is estimated as a function of their size and hematocrit and used as a metric for assessing the likelihood of NMP interaction with the blood vessel walls.

Results

In vivo radial distribution of NMPs in capillary flows

Intravital video microscopy (IVM) was used to monitor the dynamics of 200 and 1,000 nm particles in a live animal. Pegylated fluorescent polystyrene NMPs were injected via tail vein and observed in the microvasculature of the ear of a mouse. The IVM is constituted by a video-rate multiphoton microscopy system that can track flowing NMPs in the bloodstream with a frame rate at 30 Hz (Supplementary Information)15,29. Using the video-rate acquisition, NMPs were tracked with velocity up to ~1 mm/s which covered most capillaries and venules in the ear. To study radial distribution of NMPs, postcapillary venules with lumen diameter ranging from 15–30 μm were considered.

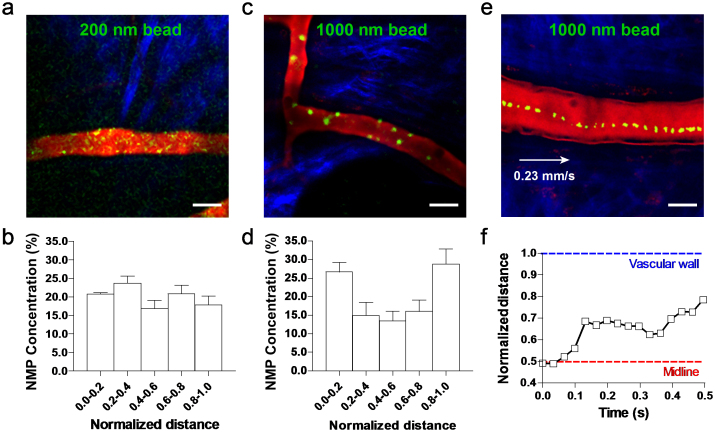
In order to quantify the radial distribution of the circulating NMPs, the longitudinal cross section of the blood vessel was conveniently divided in 5 regions: two outer layers next to the walls and each accounting for 20% of the vessel section (0.0–0.2 and 0.8–1.0); an inner layer whose axis coincides with that of the blood vessel, accounting for 20% of the vessel section (0.4–0.6); and two intermediate layers extending between the outer and inner layers and each accounting for 20% of the vessel section (0.2–0.4 and 0.6–0.8). The number of NMPs moving in each layer divided by the total number of particles counted in the vessel gives the normalized density of NMPs per layer. This parameter was monitored over time for each of the 5 layers and the two different particle sizes. Fig. 1 summarizes the findings from this in vivo analysis. The NMPs appear as yellow dots on a red background identifying the blood vessel of interest. Extravascular tissue showed blue fibrous structure due to second harmonic generation signal from the collagen. The representative IVM image of Fig. 1a shows the 200 nm NMPs distributing quite randomly within the blood vessel without preferential accumulation in any of the 5 layers. This is clearly reflected by the almost uniform normalized density of NMPs over the cross section (Fig. 1b) returning a value close to 0.2 for each layers. It is also demonstrated in the Supplementary Movie S1. Very different is the behavior observed for the 1,000 nm NMPs. These tend to mostly accumulate in the two outer layers, next to the vessel walls (Fig. 1c and Supplementary Movie S2). The bar chart in Fig. 1d quantifies the radial distribution showing that ~60% of the total number of NMPs stays in the two outer layers against a 15% of NMPs residing in the inner most layer and the rest, 30%, in the two intermediate layers (i.e. 15% per each intermediate layer). Thus, the larger NMPs (1,000 nm) are ~3 times more concentrated near the vessel walls than the smaller NMPs (200 nm). Fig. 1e shows a typical trajectory in vivo for the larger 1,000 nm NMP: it drifts laterally from its original position in the vessel core to the periphery moving closer to the wall. The variation in radial position of the NMP with time is plotted in Fig. 1f. This shows that the lateral drift is not a continuous process: the NMP moves laterally away from the vessel midline over the first 0.1 sec with a velocity of ~100 μm/s; then drifts along the flow direction longitudinally with no appreciable radial velocity for about 0.2 sec; and, eventually, turns again towards the vessel wall rapidly moving away from the midline with an average velocity of ~11.7 μm/s. Such a zig-zag motion with rapid changes in direction should be most likely associated with RBC-NMP geometrical interference.

Figure 1. Intravital microscopy analysis of the NMP radial distribution.

Figure 1

Open in a new tab

(a) Representative image of 200 nm spherical polystyrene beads (yellow dots) in the postcapillary venule of a mouse ear. (b) Radial accumulation of the 200 nm beads presented as normalized number density. (c) Representative image of 1,000 nm spherical polystyrene beads (yellow dots) in the postcapillary venule of a mouse ear. (d) Radial accumulation of the 1,000 nm beads presented as normalized number density. (e) Trajectory and (f) radial position of 1,000 nm spherical polystyrene beads (yellow dots) in the postcapillary venule of a mouse ear. (bar = 20 μm).

Predicting the radial transport of NMPs in a capillary flow

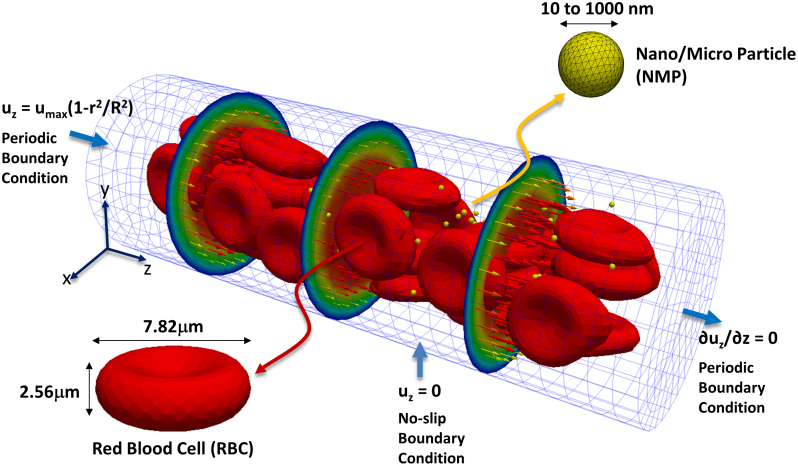
To better elucidate the mechanims regulating the different NMP behaviors observed in the IVM experiments, a computational model is developed within the IFEM30,31,32 to analyze the size-dependent NMP vascular transport. The dynamics of NMPs and RBCs immersed in a blood capillary is followed over time, as schematically shown is Fig. 2. The capillary is a straight tube with a diameter of 20 μm and a parabolic velocity profile imposed at the inlet with a maximum velocity of 100 μm/s. These are typical values for the blood flow in the microcirculation. The vessel is filled with plasma, and RBCs are modeled as vesicles with a hyperelastic membrane containing an aqueous solution similar to plasma. The RBC concentration (hematocrit) varies between 0 and 30%, comparable to physiological values in the microcirculation. NMPs are considered as rigid, spherical beads with a characteristic diameter ranging from 10 to 1,000 nm, having the same density as plasma, to rule out the contribution of the gravitational field. The RBC-RBC and RBC- NMP interactions are accounted for by using interaction potentials with proper coefficients, as described in the Methods and listed in Table 1. Periodic boundary conditions are imposed at the inlet and outlet of the capillary to limit the computational burden, while still considering sufficiently long capillaries. Therefore, RBCs and NMPs are continuously extracted from the outlet of the vessel and re-introduced at the inlet with the same geometric and kinematic conditions. The total number of NMPs in the capillary is fixed for all the simulations and it is equal to 100. The computational model was validated using four different test cases and comparing the numerical results with experimental data provided in the literature (Supplementary Fig. S1). The 4 test cases are i) the analysis of RBC stretching under uniaxial and transversal tensile forces; ii) the computation of the discharge hematocrit out of a tube; iii) the quantification of the apparent blood viscosity as a function of the RBC volumetric concentration; and iv) the thickness of the cell free layer at different hematocrits. A good agreement is observed between the numerical predictions and the experiments, thus supporting the accuracy and validity of the proposed approach.

Figure 2. Computational domain for the capillary flow simulations.

Figure 2

Open in a new tab

Deformable Red Blood Cells (RBCs) and spherical rigid particles are dispersed within an aqueous solution (blood plasma), filling a 20 × 60 μm capillary. Periodic boundary conditions are imposed at the inlet and outlet sections of the capillary. A parabolic velocity profile is assigned at the inlet section with a maximum velocity of 100 μm/s.

Table 1. Parameters used in the IFEM simulation for vascular transport.

Parameter Value
Fluid density 1.0 g/cm3
Fluid viscosity 1.2 g/(m·s)
Cytoplasm viscosity40,41 6.0 g/(m·s)
C1 for RBC hyperelastic material40,41 20.0 Pa
C2 for RBC hyperelastic material 1.0 Pa
De for RBC intracellular interaction 1.0 μJ/m2
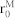Inline graphic for RBC intracellular interaction41 0.49 μm
β for RBC intracellular interaction41 3.84 μm−1
ε for NMP interaction 1.0 × 10−12 J
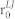Inline graphic for NMP interaction 1.0 nm
Open in a new tab

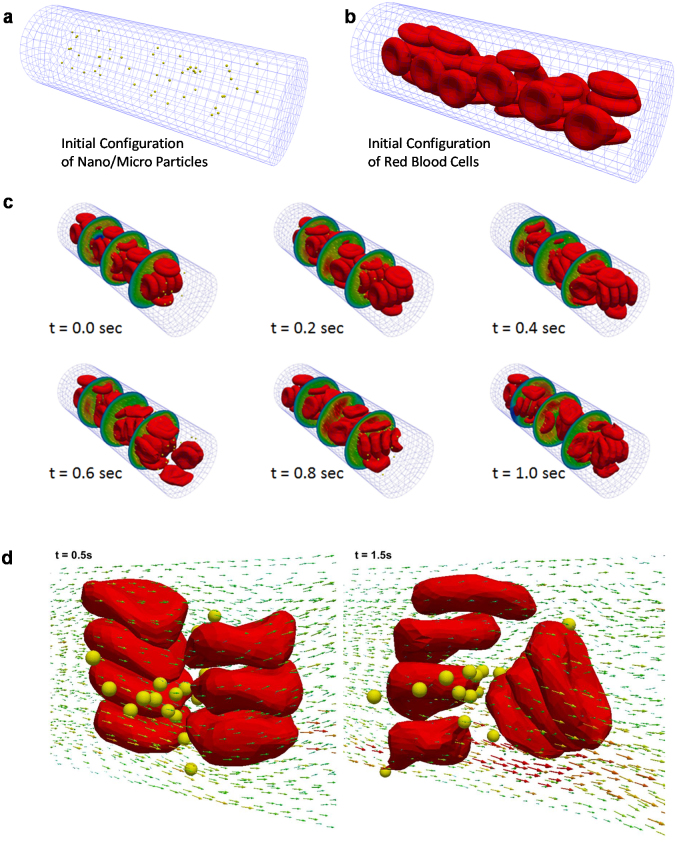
The IFEM model is subsequently used to predict the dynamics of NMPs and RBCs in a capillary flow. Representative snapshots at different time points are presented in Fig. 3 for 100 nm NMPs. As time progresses, RBCs and NMPs are transported downstream by the flowing plasma. Note that the problem is coupled in that the fluid velocity affects the motion of the RBCs and NMPs and vice versa, giving a fairly complicated velocity field in the vicinity of the deformable cells and NMPs. In the initial configuration, the NMPs (yellow dots) are randomly distributed within the capillary together with the RBCs, occupying most of the tube volume (Fig. 3a,b). Under flow, RBCs deform and modify locally the flow field affecting the NMP dynamics (Fig. 3d). This can be readily appreciated in the following insets of Fig. 3 for a characteristic time running from 0.0 to 1.0 sec, and it is also documented in the Supplementary Movies S3 and S4. In the same snapshots the circumferential velocity profile is also provided along the capillary with a velocity growing radially from the periphery to the core of the channel. The RBCs deform under flow, are pushed away from the vessel walls and tend to accumulate within the center of the blood vessel. This leads to the formation of a layer near the vessel wall which is depleted of RBCs (The cell-free-layer). The thickness of the cell-free-layer varies with the hematocrit (HCT), diameter of the capillary and mean blood velocity (Supplementary Fig. S1).

Figure 3. Simulated distribution of RBCs and NMPs within the capillary.

Figure 3

Open in a new tab

(a) RBCs and (b) NMPs are randomly distributed within the capillary in the initial configuration (t = 0 sec). (c) Representative images showing the RBC and NMP distribution within the capillary at different time points during the simulation. The hematocrit is 30% and the number of NMPs is 100. d) The complexity of the flow field around the NMPs, in proximity of the RBCs.

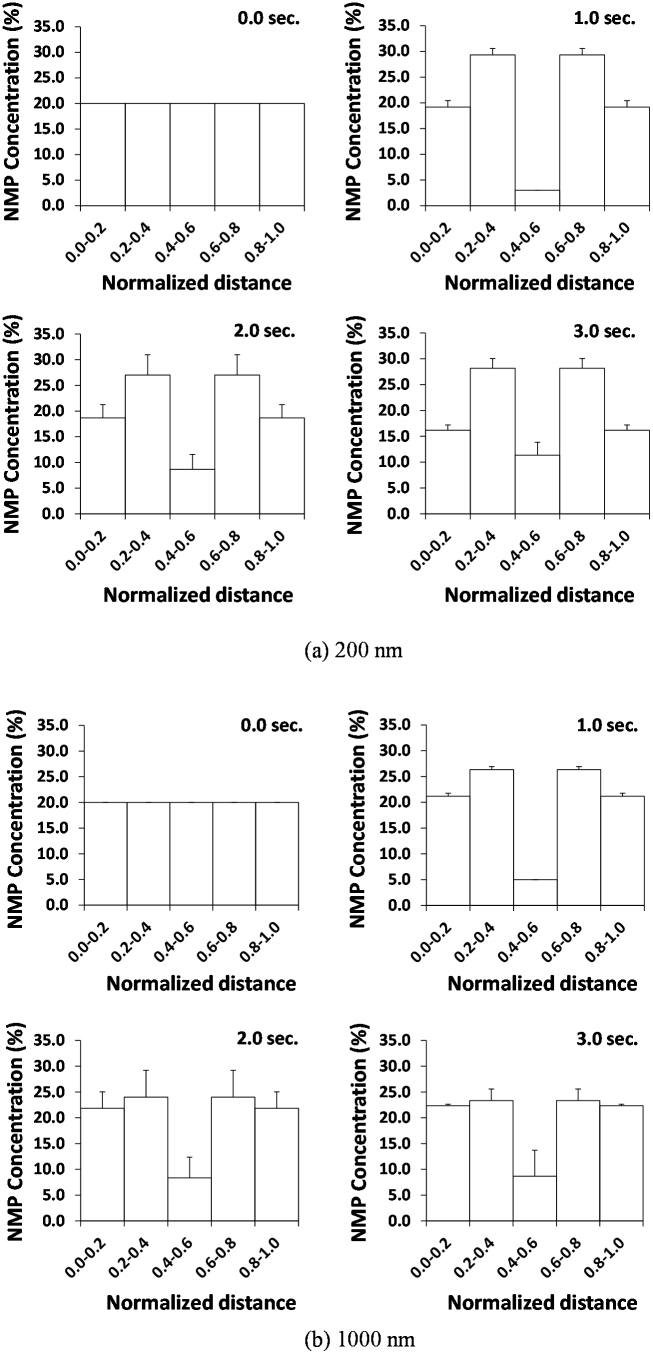
Considering the same vessel partitioning (5 radial layers) introduced for the IVM analysis, the normalized density of 200 and 1,000 nm NMPs is quantified within the 20 μm tube as a function of time, at 30% hematocrit. The corresponding data are presented in the bar charts of Fig. 4 at 0.0, 1.0, 2.0 and 3.0 sec. At time t = 0.0 sec, the NMPs have identical volume concentrations within the 5 layers. As time passes, the NMPs in the inner layers are pushed laterally away from the vessel midline. For the 200 nm particles, the maximum normalized density is achieved in the two intermediate layers where about 27% of the NMPs accumulate, per each layer. In the innermost layer only 12% of the NMPs are left after 3 sec, whereas about 17% of NMPs are found in the two outer layers, per each layer. For the 1,000 nm NMPs, the observed behavior is very different. These NMPs accumulate equally in the outer and intermediate layers reaching a normalized density of 23% per each of the 4 layers and leaving only a normalized density of 8% in the inner-most layer. Although, the normalized density measured in vivo cannot be precisely recapitulated in silico, the IFEM simulations are qualitatively in good agreement with the in vivo data. For the 1,000 nm NMPs, most of the beads are pushed outwards radially; whereas for the 200 nm NMPs, the beads are remixed within the vessel without showing a clear accumulation at the wall. Also, note that the overall behavior shown within the first 1 sec of simulation is confirmed in the following 2 sec, with slightly different values. This would imply that 1 sec of simulation is sufficient to represent the process, and this time period would correspond to a capillary length of ~100 μm, given an inlet blood velocity of 100 μm/s.

Figure 4. Simulated radial distribution of the NMPs.

Figure 4

Open in a new tab

The radial accumulation of (a) 200 nm and (b) 1,000 nm NMPs within the cross section of the capillary over time. Initially, the NMPs are equally distributed within the five considered sectors. The hematocrit is 30% and the number of NMPs is 100.

It is important to emphasize that the interaction between RBCs and NMPs is described by using a Lennard-Jones (LJ) potential (see eq. (5) in the Methods section). Thus the charge of the NMPs is not explicitly considered, but it is rather accounted through the LJ potential strength. As such, this interaction force is proportional to the LJ strength parameter ε, varies with the separation distance r, and is independent of the NMP size. Most importantly, this force is already negligible, as compared to the hydrodynamic forces, for separation distances larger than about r = 10 nm (10 times r0, with r0 = 1 nm). Moreover, Fig. 3d shows the complexity of the flow field around the NMPs, in proximity of the RBCs. The fluid velocity vector has non zero components in the direction normal to the vessel longitudinal axis that are responsible for pushing laterally the NMPs. This would imply that the vascular dynamics of the NMPs is mostly governed by geometrical interference and the resulting local, complex flow dynamics rather than their direct repulsive interaction with the RBCs.

Radial dispersion coefficient as a function of the NMP size

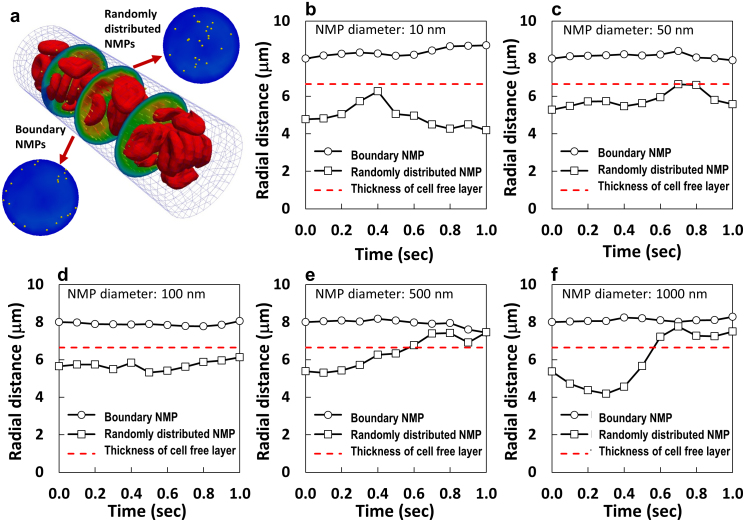
Based on the experimental evidences and the in silico data, the RBC- NMP interaction is size-dependent. Indeed, larger NMP would interfere more with the fast circulating RBCs; whereas small NMPs would more easily find their way within the RBC clusters. It would then be interesting to characterize the lateral transport of spherical beads with varying diameters within whole blood. The dynamics of NMPs with 5 different diameters, namely 10, 50, 100, 500 and 1,000 nm, was studied in whole blood at 30% hematocrit. Note that the vast majority of NMPs developed for systemic drug delivery and imaging have a diameter smaller than or close to 100 nm. The size-dependent NMP behavior is depicted in Fig. 5 which provides the trajectories of individual NMPs with two different initial radial positions: within the cell free layer and the vessel core. The red dashed line in Fig. 5 identifies the cell free layer computed for the current configuration, having a thickness of ~3.35 μm. The smallest NMPs, with a diameter ranging from 10 to 100 nm, originally located within the vessel core, tend to drift laterally moving towards the wall and then drifting back towards the midline without abandoning the core (Fig. 5b–d). Differently, larger NMPs, with a diameter ranging between 500 and 1,000 nm, tend to migrate out of the vessel core and accumulate in the cell-free layer, as they interfere more vigorously with the fast moving RBCs (Fig. 5e,f). On the other hand, NMPs initially located in the cell free layer tend to move within this layer and only the smaller NMPs (< 100 nm) could possibly re-enter the vessel core (Fig. 5b–f, Supplementary Fig. S4). In order to better emphasize the role played by RBCs, the same simulations were performed at different hematocrits, namely 0, 15 and 30%, for the 100 and 1,000 nm NMPs (Supplementary Figs. S2–3). As expected, in the absence of RBCs (0% hematocrit), the NMPs follow a straight trajectory along the streamlines with no lateral drift. Differently, at 15 and 30% hematocrit, a lateral motion is also observed with a trajectory deviating away from and towards the midline. The largest and more rapid fluctuations in lateral dispersion are observed for the smaller NMPs (100 nm), at 15% HCT. Indeed, at lower HCT, the separation distance between adjacent RBCs is larger and NMPs can more easily pass through the circulating cells, thus leading to a more hectic NMP dynamics. Overall, these data demonstrate that larger, submicron to micron-sized NMPs can be more efficiently excluded by the vessel core, pushed laterally by the fast moving RBCs; whereas the smallest NMPs would tend to be confined within the vessel core and circulate for a longer time.

Figure 5. Analysis of the size-dependent vascular behavior of NMPs.

Figure 5

Open in a new tab

(a) Initially, some NMPs are distributed within the cell free layer (boundary NMPs) and other fall within the core of the capillary. Representative trajectories of NMPs with different diameters, namely (b) 10 nm; (c) 50 nm; (d) 100 nm; (e) 500 nm; and (f) 1,000 nm. The red dashed lines identify the cell free layer. The hematocrit is 30% and the number of NMPs is 100.

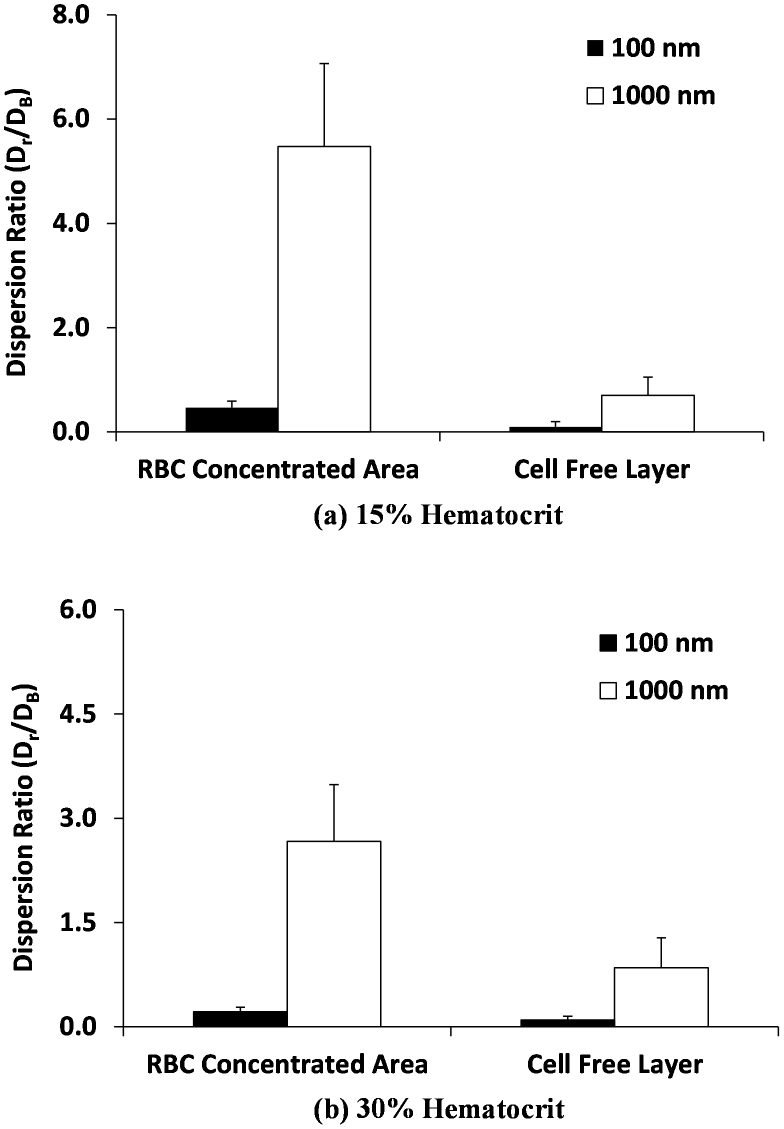
An effective radial dispersion coefficient can be introduced, as defined in the Methods, to account for the radial drift of the NMPs in the presence of RBCs. The actual radial dispersion coefficient Dr of a NMP divided by the corresponding Brownian diffusion DB is plotted in Fig. 6. The radial dispersion coefficient Dr is calculated by equation (7) in the Methods. The NMP Brownian diffusion is given by the Stokes- Einstein relation as DB = kBT/3πμd, where kB is the Boltzmann constant, T is the absolute temperature, μ is the plasma viscosity, and d is the NMP diameter. Two different particle sizes are considered, namely 100 and 1,000 nm, at 15 and 30% HCT. The dispersion ratio Dr/DB is higher for NMPs in the vessel core and reduces for NMPs in the cell free layer. For the 1,000 nm, the dispersion ratio is always larger than for the 100 nm NMPs, confirming that the contribution of the RBCs to the dispersion of small NMPs can be neglected. Also the average dispersion coefficient is significantly larger for the 15% than for 30% HCT, but the standard error is also much larger in the first case. At 15% hematocrit, this has to be related to the larger separation distance among adjacent cells. At 30% hematocrit, the dispersion ratio within the vessel core is about 3 times higher than the Brownian value for the 1,000 nm and it is lower than 1 for the 100 nm. This indicates again that the larger NMPs tend to be more vigorously pushed laterally by the moving RBCs and, thus, have higher chances of identifying vascular abnormalities.

Figure 6. Radial dispersion coefficient Dr of the NMPs.

Figure 6

Open in a new tab

The radial dispersion coefficient is presented for the 100 nm and 1,000 nm NMPs at two different hematocrit values, namely (a) 15% and (b) 30%. Data are presented as absolute dispersion coefficient divided by the corresponding Brownian diffusion coefficient.

Discussion

The present analysis shows that sub-micron NMPs (500–1,000 nm) only are efficiently pushed laterally by the fast moving RBCs towards the vessel walls, so that they can efficiently seek for vascular abnormalities. This is clearly reflected in the intravital microscopy data of Fig. 1, in the computational analysis of Fig. 4, and by the radial dispersion coefficient data of Fig. 6. Conversely, small NMPs (≤100 nm) tend to circulate along with RBCs and interact with the vessel walls only in a small fraction. Incidentally, this less frequent interaction with the vessel walls and the lower surface of adhesion presented by small NMPs could explain the only minimal enhancement in tumor accumulation often observed for biologically targeted NMPs15,33.

Based on the above reasoning and the presented data, sub-micron NMPs should be preferred for vascular targeting in that they would interact more efficiently with the vessel walls seeking for fenestrations and disease-specific vascular markers. On the other hand, NMPs of a few tens of nanometers, and smaller, should be used for the direct, passive targeting of diseased tissues accessible via hyper-permeable blood vessels34,35. Indeed, small NMPs would penetrate deep into the malignant mass overcoming the intricate tumor extracellular matrix and the adverse interstitial fluid pressure19,20, but would also carry a limited payload and are known to be rapidly cleared from the circulation36. Indeed, small NMPs would cross unspecifically the discontinuous endothelium of major organs in the rethiculo endothelial systems (RES), such as the liver, spleen, and bone marrow.

In summary, one could envision the optimal delivery system for vascular targeting as a nanoconstruct characterized by a sub-micrometer size, to maximize the near-wall accumulation within the cell free layer, while still avoiding entrapment in the lungs and in small capillaries5; a spheroidal shape, to enhance the ligand-receptor specific interaction with the vessel walls37 and the lateral drift within the cell free layer towards the vessel walls8; and surface properties supporting specific vascular adhesion and reduced macrophage uptake.

Methods

In vivo intravital microscopy imaging

8-week-old male Balb/c mice (Jackson Laboratory) were used for the in vivo experiments. After anesthesia with intraperitoneal injection of ketamine-xylazine (90 mg/kg and 9 mg/kg respectively), 70 kDa rhodamine dextran (3% w/v, 100 μl in saline) was injected for a clear blood vessel demarcation .Then 200 nm and 1,000 nm spherical beads were injected (50 μl), retro-orbitally, and their dynamics was studied within the microcirculation of the mouse ear. The ear of the mouse was glued on the metal plate and then placed on the stage of the microscope. For imaging, a home-built two-photon microscope with a tunable Ti:Sapphire laser (Mai-Tai DeepSee, Spectra-Physics) was used. The system employed water immersion objective lens (20X, 1.0 NA). The excitation wavelength was set to 810 nm and power was tuned to ~25 mW at the sample. For detection, emissions at 405 ± 10 nm for second harmonic signal from the collagen, 525 ± 25 nm for the microbeads, and 600 ± 50 nm for vascular structure were collected by photomultiplier tubes. All animal experiments were performed in compliance with institutional guidelines and approved by the subcommittee on research animal care at the Massachusetts General Hospital.

Preparation of the spherical beads prior injection

For in vivo circulation studies, PEG (poly-ethylene glycol) coated polystyrene beads were used with two different sizes, 200 nm and 1,000 nm. Amine-modified polystyrene beads were purchased from FluoSpheres, Life Technologies. For surface pegylation, the amine-modified beads were mixed with 20 kDa mPEG-succinimidyl valerate (Laysan Bio) in sodium bicarbonate buffer (pH 8.4) for 3 hours and then buffer was exchanged to phosphate buffered saline before injection.

The computational model

The Immersed Finite Element Method (IFEM)30,31,32 is a computational framework here used to simulate the transport of RBCs and NMPs within a capillary flow. IFEM allows for the efficient analysis of multiple physical interactions within the flow including fluid-structure interaction (FSI) between the plasma and the deformable RBCs and NMPs; cell-cell and cell-NMP adhesive/repulsive interactions arising at the interface between adjacent RBCs and NMPs; Brownian diffusion; pH dependent behavior ; spontaneous self-assembly of molecules and so on30,31,32,38. In this computational framework, the cells and NMPs are treated as Lagrangian solids immersed in an Eulerian fluid domain and the whole transport problem is based on the solution of a Navier-Stokes equation without requiring re-meshing as follows:

graphic file with name srep02079-m1.jpg
graphic file with name srep02079-m2.jpg
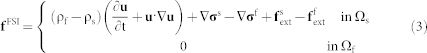graphic file with name srep02079-m3.jpg

where ρf is the fluid density, ρs is the solid density, u is the fluid velocity, σf is the fluid stress, σs is the solid stress, f FSI is the FSI interaction force for IFEM, 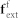Inline graphicis the external force on fluid, 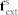Inline graphic is the external force on solid, Ω is the entire domain including fluid and solid domains, Ωs is the solid domain and Ωf is the fluid domain. The fluid in the microvessel is considered as an incompressible viscous liquid with density 1.0 g/cm3, viscosity 1.2 × 10−3 Pa·s. For a detailed description of the computational model, readers are referred to previous work30,31,32,39. Briefly, the FSI forces, represented by the term f FSI in equations (1) and (3) are calculated only on the area of the immersed solid element (individual cell and NMP) then, applied onto the surrounding fluid domain using a direct forcing technique32. The fluid domain, here representing the blood plasma, is directly simulated using a standard fluid solver.

Interactions between immersed solids within the flow field

A Morse type potential31 is incorporated in IFEM scheme for describing the RBC-RBC interaction as

graphic file with name srep02079-m4.jpg

where φM is the Morse potential, De and 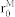Inline graphic are the surface energy and zero force length, β is the scaling factor. Also, to avoid overlapping between solid bodies, a Lennard-Jones potential is used to account for the NMP-NMP and RBC-NMP interactions as follow

graphic file with name srep02079-m5.jpg

where φLJ is the Lennard-Jones potential, ε is the scaling parameter, and 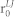Inline graphic is the distance for zero interaction energy. The Morse and Lennard-Jones potentials are converted as an external force term 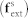Inline graphicand included in equation (3). The values for the parameters used in the present computation are listed in Table 1 and Supplementary Table S1.

RBC constitutive relation

The deformation of RBCs is described by Mooney-Rivlin material description31 as

graphic file with name srep02079-m6.jpg

where W is the elastic energy potential, C1 and C2 are the material constants, and J1 and J2 are functions of the invariants of the Cauchy–Green deformation tensor. σs in equation (3) is calculated by Reproducing Kernel Particle Method39 and incorporated in a part of the f FSI force in equation (1).

Coefficient of radial dispersion (Dr)

For quantifying the radial dispersion of NMPs with a number of particles N, the dispersion coefficient (Dr) is described as27

graphic file with name srep02079-m7.jpg

where ri(t) and ri(0) is the distance of the NMPs from the center of the channel at the time t and the initial distance, respectively.

Author Contributions

T.-R.L. performed all the numerical experiments; M.C. performed all the intravital microscopy experiments; A.M.K. helped in performing the numerical experiments; S.-H.Y. and W.K.L. provided input on the experimental plan; P.D. conceived the idea, designed the experimental plan, and wrote the manuscript. All the authors helped in writing the manuscript, discussed the results and commented on the manuscript.

Supplementary Material

Supplementary Information

Supplementary Movie 1

Download video file (3.6MB, avi)
Supplementary Information

Supplementary Movie 2

Download video file (2.9MB, avi)
Supplementary nformation

Supplementary Movie 3

Download video file (614.9KB, avi)
Supplementary Information

Supplementary Movie 4

Download video file (2MB, avi)
Supplementary Information

Supplementary Information

srep02079-s5.pdf (702.7KB, pdf)

Acknowledgments

PD acknowledges partial support from the Cancer Prevention Research Institute of Texas through (grant CPRIT RP110262); the U.S. National Institutes of Health (grants U54CA143837 and U54CA151668). WKL acknowledges the support of CMMI-0856492 and CMMI-0856333 and this research used resources of the QUEST cluster at Northwestern University and the Argonne Leadership Computing Facility at Argonne National Laboratory, which is supported by the Office of Science of the U.S. Department of Energy under contract DE-AC02-06CH11357. WKL also acknowledges the support of the World Class University Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (R33-10079). SHY acknowledges support from the U.S. National Institutes of Health (grant U54CA143837).

References

  1. Peer D. et al. Nanocarriers as an emerging platform for cancer therapy. Nat Nanotechnol 2, 751–760 (2007). [DOI] [PubMed] [Google Scholar]
  2. Allen T. M. & Cullis P. R. Drug delivery systems: entering the mainstream. Science 303, 1818–1822 (2004). [DOI] [PubMed] [Google Scholar]
  3. Majoros I. J., Williams C. R. & Baker J. R. Jr Current dendrimer applications in cancer diagnosis and therapy. Curr Top Med Chem 8, 1165–1179 (2008). [DOI] [PubMed] [Google Scholar]
  4. Merkel T. J. et al. Using mechanobiological mimicry of red blood cells to extend circulation times of hydrogel microparticles. Proc Natl Acad Sci U S A 108, 586–591 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Decuzzi P. et al. Size and shape effects in the biodistribution of intravascularly injected particles. J Control Release 141, 320–327 (2010). [DOI] [PubMed] [Google Scholar]
  6. Torchilin V. P. Recent advances with liposomes as pharmaceutical carriers. Nat Rev Drug Discov 4, 145–160 (2005). [DOI] [PubMed] [Google Scholar]
  7. Campbell R. B. et al. Cationic charge determines the distribution of liposomes between the vascular and extravascular compartments of tumors. Cancer Res 62, 6831–6836 (2002). [PubMed] [Google Scholar]
  8. Lee S. Y., Ferrari M. & Decuzzi P. Design of bio-mimetic particles with enhanced vascular interaction. J Biomech 42, 1885–1890 (2009). [DOI] [PubMed] [Google Scholar]
  9. Gentile F. et al. The effect of shape on the margination dynamics of non-neutrally buoyant particles in two-dimensional shear flows. J Biomech 41, 2312–2318 (2008). [DOI] [PubMed] [Google Scholar]
  10. Champion J. A. & Mitragotri S. Role of target geometry in phagocytosis. Proc Natl Acad Sci U S A 103, 4930–4934 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Gratton S. E. et al. The effect of particle design on cellular internalization pathways. Proc Natl Acad Sci U S A 105, 11613–11618 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Muro S. et al. Control of endothelial targeting and intracellular delivery of therapeutic enzymes by modulating the size and shape of ICAM-1-targeted carriers. Mol Ther 16, 1450–1458 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Wang J., Byrne J. D., Napier M. E. & DeSimone J. M. More effective nanomedicines through particle design. Small 7, 1919–1931 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Godin B. et al. Discoidal Porous Silicon Particles: Fabrication and Biodistribution in Breast Cancer Bearing Mice. Adv Funct Mater 22, 4225–4235 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. van de Ven A. L. et al. Rapid tumoritropic accumulation of systemically injected plateloid particles and their biodistribution. J Control Release 158, 148–155 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Michor F., Liphardt J., Ferrari M. & Widom J. What does physics have to do with cancer? Nat Rev Cancer 11, 657–670 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Jain R. K. & Stylianopoulos T. Delivering nanomedicine to solid tumors. Nat Rev Clin Oncol 7, 653–664 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Ferrari M. Frontiers in cancer nanomedicine: directing mass transport through biological barriers. Trends Biotechnol 28, 181–188 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Cabral H. et al. Accumulation of sub-100 nm polymeric micelles in poorly permeable tumours depends on size. Nat Nanotechnol 6, 815–823 (2011). [DOI] [PubMed] [Google Scholar]
  20. Perrault S. D., Walkey C., Jennings T., Fischer H. C. & Chan W. C. Mediating tumor targeting efficiency of nanoparticles through design. Nano Lett 9, 1909–1915 (2009). [DOI] [PubMed] [Google Scholar]
  21. Huo S. et al. Superior penetration and retention behavior of 50 nm gold nanoparticles in tumors. Cancer Res 73, 319–330 (2013). [DOI] [PubMed] [Google Scholar]
  22. Hammer D. A. Leukocyte adhesion: what's the catch? Curr Biol 15, R96–99 (2005). [DOI] [PubMed] [Google Scholar]
  23. Sun C., Migliorini C. & Munn L. L. Red blood cells initiate leukocyte rolling in postcapillary expansions: a lattice Boltzmann analysis. Biophys J 85, 208–222 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Charoenphol P., Huang R. B. & Eniola-Adefeso O. Potential role of size and hemodynamics in the efficacy of vascular-targeted spherical drug carriers. Biomaterials 31, 1392–1402 (2010). [DOI] [PubMed] [Google Scholar]
  25. Kim S., Ong P. K., Yalcin O., Intaglietta M. & Johnson P. C. The cell-free layer in microvascular blood flow. Biorheology 46, 181–189 (2009). [DOI] [PubMed] [Google Scholar]
  26. Lipowsky H. H. Microvascular rheology and hemodynamics. Microcirculation 12, 5–15 (2005). [DOI] [PubMed] [Google Scholar]
  27. Yeh C. & Eckstein E. C. Transient lateral transport of platelet-sized particles in flowing blood suspensions. Biophys J 66, 1706–1716 (1994). [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Saadatmand M. et al. Fluid particle diffusion through high-hematocrit blood flow within a capillary tube. J Biomech 44, 170–175 (2011). [DOI] [PubMed] [Google Scholar]
  29. Kim J. K. et al. Fabrication and operation of GRIN probes for in vivo fluorescence cellular imaging of internal organs in small animals. Nature protocols 7, 1456–1469 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Zhang L., Gerstenberger A., Wang X. D. & Liu W. K. Immersed finite element method. Comput Method Appl M 193, 2051–2067 (2004). [Google Scholar]
  31. Liu Y. L. & Liu W. K. Rheology of red blood cell aggregation by computer simulation. J Comput Phys 220, 139–154 (2006). [Google Scholar]
  32. Lee T. R. et al. Immersed finite element method for rigid body motions in the incompressible Navier-Stokes flow. Comput Method Appl M 197, 2305–2316 (2008). [Google Scholar]
  33. Huang X. et al. A reexamination of active and passive tumor targeting by using rod-shaped gold nanocrystals and covalently conjugated peptide ligands. ACS Nano 4, 5887–5896 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Matsumura Y. & Maeda H. A new concept for macromolecular therapeutics in cancer chemotherapy: mechanism of tumoritropic accumulation of proteins and the antitumor agent smancs. Cancer Res 46, 6387–6392 (1986). [PubMed] [Google Scholar]
  35. Maeda H., Wu J., Sawa T., Matsumura Y. & Hori K. Tumor vascular permeability and the EPR effect in macromolecular therapeutics: a review. J Control Release 65, 271–284 (2000). [DOI] [PubMed] [Google Scholar]
  36. Choi H. S. et al. Design considerations for tumour-targeted nanoparticles. Nat Nanotechnol 5, 42–47 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Decuzzi P. & Ferrari M. The adhesive strength of non-spherical particles mediated by specific interactions. Biomaterials 27, 5307–5314 (2006). [DOI] [PubMed] [Google Scholar]
  38. Kopacz A. M., Patankar N. A. & Liu W. K. The immersed molecular finite element method. Computer methods in applied mechanics and engineering 233, 28–39 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Liu W. K., Jun S. & Zhang Y. F. Reproducing Kernel Particle Methods. Int J Numer Meth Fl 20, 1081–1106 (1995). [Google Scholar]
  40. Park Y. et al. Measurement of the nonlinear elasticity of red blood cell membranes. Physical review. E, Statistical, nonlinear, and soft matter physics 83, 051925 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Zhang J., Johnson P. C. & Popel A. S. Red blood cell aggregation and dissociation in shear flows simulated by lattice Boltzmann method. Journal of biomechanics 41, 47–55 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Movie 1

Download video file (3.6MB, avi)
Supplementary Information

Supplementary Movie 2

Download video file (2.9MB, avi)
Supplementary nformation

Supplementary Movie 3

Download video file (614.9KB, avi)
Supplementary Information

Supplementary Movie 4

Download video file (2MB, avi)
Supplementary Information

Supplementary Information

srep02079-s5.pdf (702.7KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES