A Polar Corundum Oxide Displaying Weak Ferromagnetism at Room Temperature

Abstract

Combining long-range magnetic order with polarity in the same structure is a prerequisite for the design of (magnetoelectric) multiferroic materials. There are now several demonstrated strategies to achieve this goal, but retaining magnetic order above room temperature remains a difficult target. Iron oxides in the +3 oxidation state have high magnetic ordering temperatures due to the size of the coupled moments. Here we prepare and characterize ScFeO₃ (SFO), which under pressure and in strain-stabilized thin films adopts a polar variant of the corundum structure, one of the archetypal binary oxide structures. Polar corundum ScFeO₃ has a weak ferromagnetic ground state below 356 K—this is in contrast to the purely antiferromagnetic ground state adopted by the well-studied ferroelectric BiFeO₃.

Introduction

In recent years, multiferroic materials (specifically materials with permanent magnetization and electrical polarization) have attracted great interest, as controlling the magnetic state through the application of an electric field is an enabling feature for novel technologies.¹⁻⁵ However, materials with multiferroic order above room temperature are rare due to the contraindicated nature of magnetism and polar order.^6,7 The most studied systems currently have very small polarizations (structurally undetectable) that are driven by the onset of magnetic order, which lifts the centers of symmetry present in the paramagnetic state.^1,4,5,7 In most of the observed cases, the transitions occur well below room temperature, for room temperature magnetoelectric phenomena, currently the best candidates are the hexaferrites and related phases.^5,8,9 Many ferroelectrics are based on d⁰ structures whereas magnetism clearly requires the presence of open shell cations. BiFeO₃ can be seen as an archetype for an alternative approach where two sublattices are combined where one is ferroelectrically active and the other magnetically, though in this case, at least near room temperature, the system is purely antiferromagnetically ordered.¹⁰ Given the higher ordering temperatures of antiferromagnets, multiferroics with weak ferromagnetism would show promise in this property control.^11,12 A two sublattice approach has proved successful in EuTiO₃¹³ (where lattice strain in a thin film drives a quantum paraelectric to a ferroelectric phase transition) with the magnetic ordering from Eu²⁺ occurring at low temperature. High pressure has been used to convert the layered ilmenite FeTiO₃ into a polar LiNbO₃ polymorph which shows weak ferromagnetism well below room temperature,¹² with AF order up to 270 K found in the partially ordered (In_1–xM_x)MO₃ (M = Fe_1/2Mn_1/2; x = 0.143)^14,15 LiNbO₃ phases.¹⁴⁻¹⁶ Thus, new approaches are needed to increase the temperature of coexistence. We present an alternative approach to generating polarization and magnetization above room temperature by preparing a new polar polymorph of ScFeO₃ (SFO) using high pressure synthesis and biaxial strain based on the corundum structure, which exhibits weak ferromagnetism with an ordering temperature of 356 K. The reported SFO structure is in contrast to the perovskite-derived ScCrO₃¹⁷ and ScVO₃,¹⁸ which are also formed at high pressure for earlier first transition series cations.

Experimental Methods

ScFe_1–xCr_xO₃ (x = 0–1) was prepared from stoichiometric mixtures of Sc₂O₃ (99.999%, Sigma Aldrich), Fe₂O₃ (99.999%, Alpha Aesar), and Cr₂O₃ (99.997%, Alpha Aesar) reacted at 1500 °C (x = 0), 1480 °C (x = 0.03), and 1450 °C (x = 0.10–1) at 6 GPa for 5 min in a Pt-lined Al₂O₃ crucible within a cylindrical graphite furnace in a Walker-type multianvil press and then quenched to room temperature by turning off the voltage supply to the resistance furnace, which reduces the temperature from 1500 to 25 °C in ∼2 s. The pressure is maintained during the temperature quenching.

Thin films were grown using a Neocera pulsed laser deposition (PLD) chamber equipped with Staib RHEED. A stoichiometric ScFeO₃ ceramic target, made by conventional solid state methods, was used in the PLD at a laser energy of 252 mJ over a spot size of approximately 2–3 mm². The films were grown in an oxygen partial pressure of 2 mTorr. The substrate was held at the temperature 850 °C and the distance from the target 47 mm. A 30 kV electron beam was used in the RHEED at a current of 1.55 A. During cooling, the partial oxygen pressure was held at 150 Torr.

Powder X-ray diffraction (XRD) data were recorded on instrument ID31 (for x = 0 over a range of temperatures, λ = 0.3999 Å) at ESRF, Grenoble. Anomalous scattering data were collected on instrument I11 at Diamond Light Source (DLS). The sample was loaded on the external surface of a quartz capillary (diameter 0.5 mm) to minimize absorption.¹⁹ A monochromator scan was used to measure the Fe K edge fluorescence spectrum. High resolution X-ray diffraction patterns were then recorded for 2 h each at six selected energies near the Fe K absorption edge: 7.050, 7.080, 7.112, 7.138, 7.165, and 7.190 keV. The six diffraction patterns were fitted simultaneously using the TOPAS²⁰ software package. The peak shape parameters were constrained to be the same for the six patterns during refinement. Sample absorption was fitted using the Pitschke model²¹⁻²³ for surface roughness in the TOPAS software package.

Neutron powder diffraction (NPD) data were collected on the POLARIS instrument at the ISIS facility, Rutherford Appleton Laboratories. Diffraction data analysis was performed with the GSAS²⁴ suite of Rietveld analysis programs, using the EXPGUI²⁵ interface. Magnetic structures were modeled using a P1 magnetic only phase:²⁶ atomic positions and lattice tensors were fixed/constrained to maintain the nuclear cell and symmetry. The magnetic models were constructed via the representational analysis of the system using SARAh.²⁷ Structural figures were generated using VESTA.²⁸

Convergent beam electron diffraction (CBED) and energy dispersive spectroscopy (EDS) analyses were performed with a JEOL 2000FX electron microscope. High angle annular dark field scanning transmission electron microscopy (HAADF-STEM) images were recorded on a Tecnai G2 microscope operated at 200 kV and on a Titan G3 80-300 microscope equipped with the probe aberration corrector and operated at 300 kV. Calculated HAADF-STEM images were obtained using the QSTEM software.²⁹ Imaging of ceramics used in PFM measurements revealed no change in phase composition at the grain boundaries.

Mössbauer data were obtained using a conventional constant acceleration Mössbauer spectrometer incorporating a ∼25 mCi source of Co⁵⁷ in a Rh matrix. Alternating current and direct current magnetization measurements were carried out with a commercial Quantum Design superconducting quantum interference device (SQUID) magnetometer. We have measured the dielectric and ferroelectric properties of the samples which were sandwiched between Ag paste deposited electrodes, in parallel plate geometry. We used an Agilent E4980A LCR Meter to measure the dielectric properties and a Radiant Precision LC Ferroelectric Tester to measure the P-E loops.

Piezoresponse force microscopy was measured on a 6 × 6 μm² scan area using a DCP-11 diamond coated tip (NT-MDT, Moscow, Russia) while measuring amplitude and phase (R and θ). It was undertaken on a Park XE-100 (Park Systems, Suwon, South Korea) with a SR830 lock in amplifier (Stanford Research, CA, USA) with a bias voltage of 5 V, a time constant of 1 ms, and a sensitivity of 100 μV).

All DFT calculations have been performed using the CRYSTAL09 program.³⁰ We employed the PBE0 hybrid exchange functional that uses 25% Hartree–Fock exchange; reciprocal space sampling has been performed for all structures using a Monkhorst-Pack grid of 8 × 8 × 8 k-points for all structures. Standard all electron basis sets from the CRYSTAL online database (www.crystal.unito.it) have been used for all elements (indicated by the following labels online: Fe_86–411d41G_towler_1992a, Sc_864–11dG*_harrison_2006, O_8–411d11G_valenzano_2006). Full geometry optimizations have been performed for each structure, followed by a series of constant volume optimizations to evaluate the phase diagrams. Enthalpies have been derived from the energy-volume data, by fitting to the second order Birch–Murnaghan equation of state.

Monte Carlo simulations have been performed using an extended Ising model with coupling parameters fitted to a test set of different disordered structures. Sampling has been performed on cells containing 5184 ion pairs. For each temperature, 10000 sampling points, separated by 4 times the correlation length of the simulation, have been used.

Results and Discussion

Reaction of Sc₂O₃ with Fe₂O₃ at 1500 °C for 12 h in air at ambient pressure yields a material adopting the bixbyite structure of Sc₂O₃ (Figure 1a and Supporting Information Figure S1) which shows weak ferromagnetism with a T_c of 39 K³¹⁻³³ (Figure S2). The bixbyite-type ScFeO₃ is an anion vacancy-ordered derivative of fluorite with a disordered distribution of Sc³⁺ and Fe³⁺. This type of structure is a clear candidate for transition to a denser close-packed structure under high pressure by elimination of anion vacancies. Indeed, it has been previously demonstrated that several bixbyite systems convert to corundum type phases at high pressure and temperature.^34,35 Reaction of stoichiometric mixtures of Sc₂O₃ and Fe₂O₃ at 6 GPa and 1500 °C afforded a material (HP SFO) with a unit cell corresponding to the corundum structure (a = 5.198(1) Å, c = 14.003(1) Å) adopted by α-Fe₂O₃ (Figure 1b); this hexagonal close-packed structure has ²/₃ of the octahedral voids filled by metal cations, which can be considered as dimers of face-sharing MO₆ octahedra along the [001] direction of stacking of the close-packed oxide layers, linked by corner-sharing into a three-dimensional framework. Synthesis of the bulk material away from the 1:1 composition in Sc_1–xFe_1+xO₃ (nonstoichiometric Sc_1.024Fe_0.976O₃ (Sc-rich) and Sc_0.976Fe_1.024O₃ (Fe-rich) were prepared under the same conditions as ScFeO₃) does change the unit cell dimensions of the corundum–like phase, but it produces Sc₂O₃ and Fe₂O₃ impurities even at minor deviations from the fully stoichiometric structure (Figure 2a). The absence of an extensive solid solution in SFO, in contrast to In₂O₃–Fe₂O₃ and Ga₂O₃–Fe₂O₃³⁴ is unexpected given the similar size (0.745 and 0.645 Å, respectively³⁶) and identical charge of Sc³⁺ and Fe³⁺, and this indicates the likely presence of short-range ordered structural motifs in SFO (as discussed later).

Figure 1.

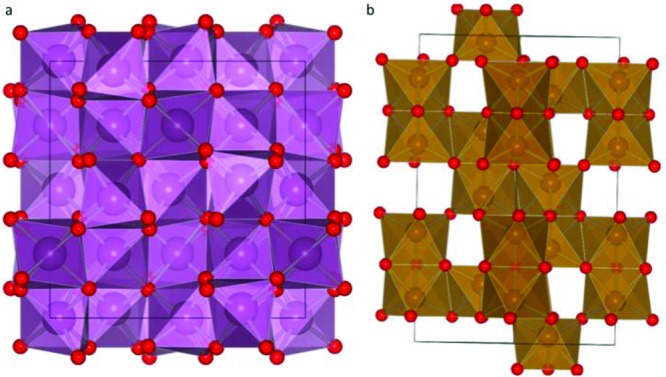
(a) Sc₂O₃ (bixbyite, Ia3̅) viewed along [100]; (b) α-Fe₂O₃ (corundum, R3̅c) structure, viewed along [110].

Figure 2.

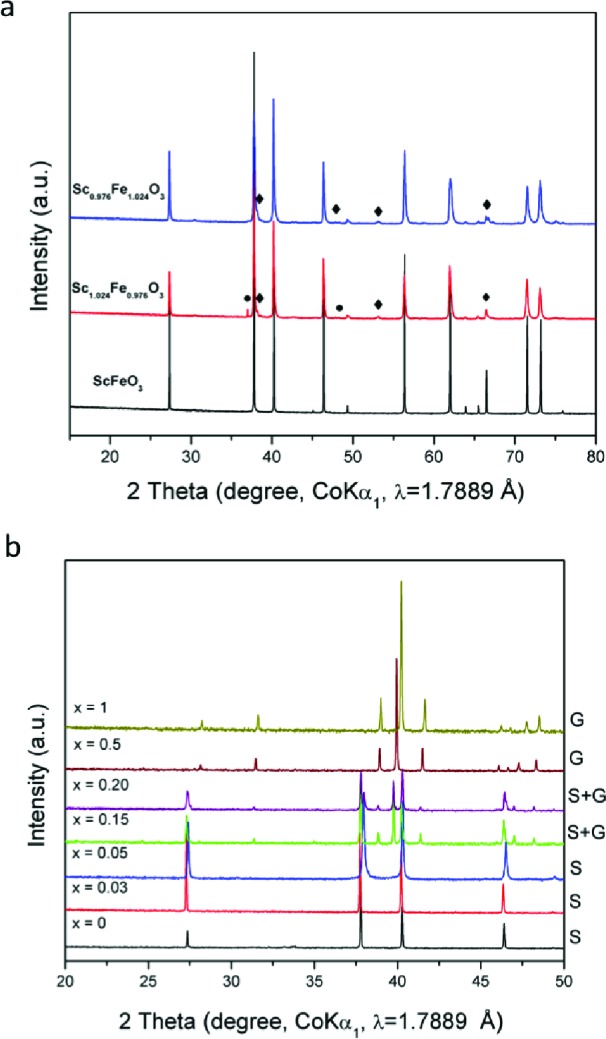
(a) Room temperature XRD patterns for Sc_1–xFe_1+xO₃ (x = 0, ±0.024). Diamonds represent peaks for corundum impurities and dots bixbyite. (b) Room temperature XRD patterns for ScFe_1–xCr_xO₃ (x = 0, 0.03, 0.10, 0.15, 0.20, 0.50, and 1). The resulting phases for each composition are marked on the right side, where S stands for a high pressure ScFeO₃-type phase and G for a GdFeO₃-type phase.

ScFe_1–xCr_xO₃ (x = 0, 0.03, 0.10, 0.15, 0.20, 0.50, 1) solid solutions were also investigated with ScCrO₃, which adopts the distorted perovskite GdFeO₃ structure at high pressure¹⁷ (Figure 2b) The HP SFO corundum-like structure was retained for x ≤ 0.10 (reacted at 1500 °C (x = 0), 1480 °C (x = 0.03), and 1450 °C (x = 0.10)). The HP SFO and GdFeO₃-type structures coexist for x = 0.15 and 0.2. At x ≥ 0.50, only the GdFeO₃-type phase was formed. For x = 0, the material starts to decompose on heating; at about 200 °C, the peaks begin to broaden; and by 500 °C, the material has decomposed into Sc₂O₃ and Fe₂O₃ (Figure S3). Both x = 0.03 (Supporting Information Figure S4) and x = 0.10 (Figure S5) are significantly more robust, not decomposing below 800 °C.

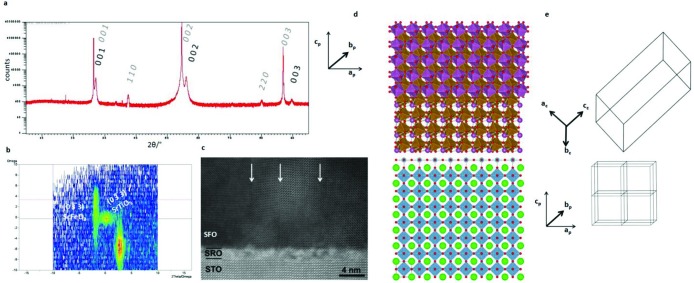
SFO thin films (∼25 nm thick) were grown on SrTiO₃ (001) substrates using pulsed laser deposition (PLD, 850 °C deposition temperature, oxygen partial pressure of 2 mTorr) with an SrRuO₃ buffer layer (typically 3–5 unit cell monolayers) through substrate-imposed strain engineering³⁷ (Figure S6). The lattice mismatch of 2.7% between the pseudocubic perovskite cell of corundum ScFeO₃ (a_p = 3.802 Å, α = 86.2°; Figure 3d and e) and (001) SrTiO₃ is less than that for the ambient pressure bixbyite structure (14.7% in the 45° cube on cube configuration). The observed 3.806 Å out-of-plane lattice parameter (Figure 3a) is consistent with the high-pressure synthesized bulk material.

Figure 3.

Characterization data for thin films of ScFeO₃ grown on SrTiO₃ (100) substrates. The epitaxial relationship of the film to substrate was [2–21]_SFO (cor)||[001]_STO and (012)_SFO (cor)|| (010)_STO. (a) out-of-plane X-ray diffraction scan indexed to the perovskite pseudocubic cell (gray italic indices indicate a reflection from the substrate) with lattice vector relations of [0 0 1]_per ∥ [2 −2 1]_corand (0 1 0)_per ∥(0 1 2)_cor. (b) Reciprocal space map about the (0–33) reflection of the substrate showing coherent alignment of Fe₂O₃ (FO) with ScFeO₃ (0 3 −12)_SFO (cor)∥ (1 3 10)_FO The ScFeO₃ peak is indexed to the perovskite pseudocubic cell. The breadth of the film peak is assigned to strain gradients moving away from the substrate and the domain structure within the film. (c) High resolution HAADF-STEM image of the substrate film interface, the white arrow indicates a boundary between two twin domains. This twinning is due to the rhombohedral distortion having four possible orientations when growing on the cubic SrTiO₃ surface. (d) Schematic indicating the registry of the ScFeO₃ thin films (top) to the SrTiO₃ substrate (bottom). The perovskite pseudocubic cell is indicated and its relationship to the corundum cell. For clarity, the Sc and Fe site are shown disordered with the Sc octahedra removed. Perovskite cell highlighted with respect to the substrate (e) and orientation of the rhombohedral cell with respect to the perovskite cell. In the Figure the out-of-plane lattice parameter is that determined experimentally and the in-plane is set equal to SrTiO₃ with γ = 90° rather than the bulk rhombohedral angle. The experimentally determined γ = 89.2°.

The cell is distorted from the bulk cell due to substrate strain with α determined (Supporting Information p S9) as 89.2° at the substrate film interface. Off-axis reciprocal space maps (RSM) (Figure 3b) reveal Fe₂O₃ coherently aligned with ScFeO₃, consistent with EDX measurement of the film composition as Sc_0.87Fe_1.13O₃, attributed to incomplete stoichiometry transfer from the target and consistent with the restricted compositional variation found in bulk high pressure synthesis. Vertical twin planes separate the film into columnar domains, originating at misfit dislocations that relax the epitaxial strain and are present every 4–10 nm (Figure 3c).

The 1:1 stoichiometric ratio of Sc and Fe observed in HP SFO suggests ordering of these cations within the dimers of face-shared octahedra of the corundum lattice. Density functional theory (DFT) calculations, employing the PBE0 hybrid-exchange functional under periodic boundary conditions, show that structures with only heteronuclear (Sc,Fe) dimers are at least 1.0 eV per dimer more stable than structures with homonuclear (2Fe or 2Sc) pairs. Homonuclear dimers are thus expected only in very low concentration, which explains the lack of solid solutions away from the 1:1 ratio. However, inverting the position of Sc and Fe ions within a heteronuclear dimer has much smaller energetic cost (Supporting Information Table S2) and is likely to occur extensively; we will henceforth refer to this defect as the antisite dimer.

Ordered decoration of the corundum lattice with the energetically favored heteronuclear dimers affords two candidate structures. The ilmenite structure (Figure 4a, left) arises when the two cations form alternate layers perpendicular to c (space group R3̅). If instead the dimers are arranged to avoid octahedral edge-sharing by like cations (Figure 4a, right), we obtain the LiNbO₃ structure with three-dimensional self-connectivity of each cation (space group R3c). DFT calculations (Supporting Information pp S11–12) show an energetic preference of 0.13 eV/formula unit (f.u.) for the R3c variant.

Figure 4.

(a) Polyhedral representation of SFO slabs demonstrating the cation order in ilmenite (left) and LiNbO₃ (right). The black circle indicates an antisite dimer defect in polar corundum SFO. (b) [11̅0] zone axis noncentrosymmetric CBED pattern. A mirror plane and two GjonnesMoodie (GM) lines parallel to it are highlighted which correspond to the c glide plane. (c) The whole [11̅0] zone axis CBED pattern showing a mirror plane. The five CBED patterns shown here and in Supporting Information Figure S5 are all collected from different crystallites. (d) TEM SAED along the [11̅0] zone axis—the spots due to double diffraction are marked by arrows. (e) [241] = ⟨100⟩_p zone axis HAADF-STEM image of ScFeO₃. (f) [121̅] = ⟨110⟩_p zone axis HAADF-STEM image of ScFeO₃. The calculated images for the ordered and disordered structure models are superimposed.

Convergent beam electron diffraction (CBED) allows unique determination of point groups and was thus applied to determine the presence or absence of an inversion center.³⁸ CBED on bulk ScFeO₃ revealed the noncentrosymmetric 3m point group and the presence of c-glide planes in the structure (Figure 4 and Supporting Information Figure S7)—the (006) and (006̅) disks in the [11̅0] zone axis CBED pattern (Figure 4b and c) have different structures, reflected in other differences between (hkl) and (hkl) disks, demonstrating the absence of an inversion center. Together with the selected area electron diffraction data (Figure 4d), the noncentrosymmetric space group R3c was determined. The space group and unit cell correspond to those of ferroelectric LiNbO₃ and multiferroic BiFeO₃. These can be described either as cation ordered corundums (see above) or alternatively as a derivative of perovskite, where a combination of ferroelectric Γ₄^– (x,x,x shift) cation displacement from the AO₃ close-packed layer and R₄ (a^–a^–a^–) octahedral tilting leads to the creation of an octahedral site for the initially 12 coordinate perovskite A cation.^10,39 The polar nature of ScFeO₃ thus suggests some Sc/Fe order in the corundum-like structure. Assuming a completely cation-ordered LiNbO₃-type structure, one would expect the projected Sc and Fe columns to be imaged as dots of different brightness on the high angle annular dark field scanning transmission electron microscopy (HAADF-STEM) images due to a difference in the atomic number of Sc (Z = 21) and Fe (Z = 26). However, no noticeable difference in the brightness of the dots associated with the Sc and Fe columns was observed on the experimental images (Figure 4e and f), indicating that the order of Sc and Fe in ScFeO₃ is incomplete.

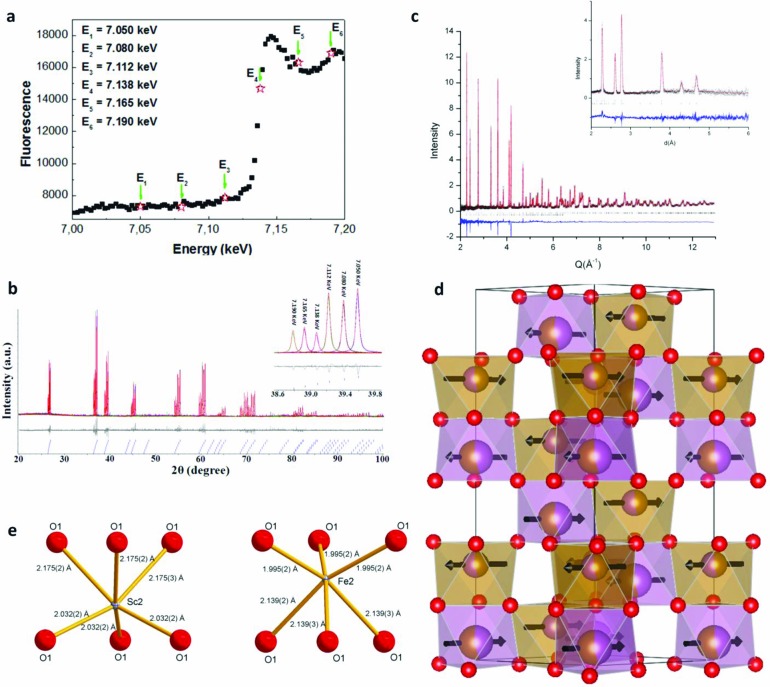
The very similar X-ray and neutron scattering factors of Sc³⁺ and Fe³⁺ prevent unambiguous assignment of the ordering extent, based purely on either neutron or nonresonant X-ray diffraction (qualities of Rietveld fits were insensitive to occupancy). Therefore, anomalous scattering diffraction data at the Fe K edge were collected on the I11 instrument at the Diamond Light Source at six energies near the Fe K absorption edge (Figure 5a). Anomalous scattering experiments exploit the change in the X-ray scattering power of an element as the X-ray wavelength moves through the absorption edge,⁴⁰ and they are used here to increase the contrast between Sc and Fe by working at the Fe K edge. The data were refined to a composition [Sc_0.54(2)Fe_0.46(2)] [Sc_0.46(2)Fe_0.54(2)]O₃(Figure 5b), confirming that only a small degree of order is observed (8(2)% defined as the difference in occupancy), consistent with the polar symmetry observed in CBED, but lack of observable cation order on the HAADF-STEM images due to the negligibly small difference of the scattering power at these positions. These cation site occupancies were then fixed in the refinement of the neutron and nonresonant synchrotron powder diffraction data. The refined structure and coordination environments are shown in Figure 5c–e with refined coordinates, bond lengths, and angles given in Tables 1 and 2 and the cif file provided in the Supporting Information (where the magnetic moments can be found in the gsas .lst file). The Sc³⁺ site is larger (2.104 Å) than the Fe³⁺ site (2.067 Å), as might be expected from simple ionic radii arguments. This is consistent with the DFT-optimized bond lengths (0 K) of 3 × 2.074 Å, 3 × 2.167 Å (Sc–O) and 3 × 1.953 Å, 3 × 2.152 Å (Fe–O) for a fully ordered structure (Supporting Information Tables S3 and S4). The Sc³⁺ site is also more distorted (3.49% vs 3.39%)—the refined bond lengths are thus consistent with the identified polar order. The magnetic structure is that described for α-Fe₂O₃ above the transition Morin transition.⁴¹ The observed reduced moment is consistent with the mean field estimate for T/T_N = 0.84 of 2.8 μ_B/Fe³⁺. The term “polar corundum” is therefore suggested to reflect the combination of partial cation ordering resulting in a noncentrosymmetric corundum-type structure. In polar corundum ScFeO₃, the distinction between oxygen coordination of the two cation sites is less pronounced than in LiNbO₃ and BiFeO₃, favoring incomplete cation order rather than a perovskite-based description.

Figure 5.

(a) Fluorescence intensity versus energy at the Fe K edge for ScFeO₃ on instrument I11 at DLS. The six selected energy levels (En = 7.050, 7.080, 7.112, 7.138, 7.165, and 7.190 keV for n = 1–6, respectively) used for diffraction studies near the Fe K absorption edge were marked by arrows (↓) and stars (☆). (b) Simultaneous Rietveld refinement of X-ray diffraction data for ScFeO₃ collected at six selected energy levels near the Fe K absorption edge, giving a partially ordered composition of [Sc_0.54(2)Fe_0.46(2)] [Sc_0.46(2)Fe_0.54(2)]O₃. The inset (38.6–39.8°) shows the peak evolution and changes in diffraction intensity due to the energy variation of resonant scattering. (c) Rietveld refinement of neutron powder diffraction data (POLARIS 145° bank) for ScFeO₃; black crosses represent observed data, the red line the calculated fit, the blue line the difference, upper black tick marks the allowed nuclear Bragg peaks, and the lower ones the allowed magnetic peaks; the inset shows longer d-spacing data from the 35° bank of POLARIS. (d) Polyhedral representation of the final structure viewed along [110]. Brown polyhedral are 54% Fe, 46% Sc, and purple polyhedra are 54% Sc, 46% Fe. Arrows represent the refined magnetic moment orientations. Local coordination environment of (e) the scandium rich site Sc2 and the iron rich site Fe2 viewed perpendicular to the c axis.

Table 1. Refined Structural Parameters for Polar Corundum ScFeO₃ (R3c, a = 5.202475(4) Å, c = 14.01449(10) Å, V = 328.4944(25) ų, χ² = 1.047, R_wp = 6.1%)^a.

	x	Y	z	100Ui/Ue	M (μB)
Sc1	0	0	0.04769(5)	0.378(5)
Fe1	0	0	0.257903b	0.510(5)	2.72(4)
O1	0.3424(2)	–0.0260 (1)	0.8176(2)	0.482(5)
Fe2	0	0	0.04769(5)	0.378(5)	2.72(4)
Sc2	0	0	0.257903b	0.510(5)

^aFurther details of the refinement can be found in the cif file. Sc1 and Fe2 are 46% occupied whilst Sc2 and Fe1 are 54% occupied as determined from the anomalous scattering experiment.

^bFixed to fix the origin.

Table 2. Refined Bond Lengths for Polar Corundum ScFeO₃.

Fe2|Sc1	O1	3×	1.9948(20) Å
	O1	3×	2.1391(27) Å
Sc2|Fe1	O1	3×	2.0324(17) Å
	O1	3×	2.1752(27) Å

The isolation of polar corundum SFO under high P/T reaction conditions can be understood by DFT calculations of the enthalpies of competing structure types (perovskite, ilmenite, polar corundum, postperovskite (CaIrO₃), and YMnO₃) in comparison with a mixture of the binary oxides at up to 40 GPa (Figure 6). Ferro- (FM) and antiferromagnetic (AFM) phases have been considered for all structures. Taking only 0 K effects into account (upper diagram), the polar corundum structure is predicted not to form a stable phase. Instead, the mixture of AFM binary oxides is stable up to 10.5 GPa, when it transforms into an AFM perovskite, which finally converts into the CaIrO₃ postperovskite structure at pressures above 41 GPa. Temperature effects on the phase stability arise from configurational and magnetic terms. The enthalpy of the paramagnetic phase is approximated as the mean of the AFM and FM enthalpies of each polymorph. Configurational effects are not important for polymorphs where Fe and Sc are in substantially different environments (perovskite, postperovskite, and YMnO₃).

Figure 6.

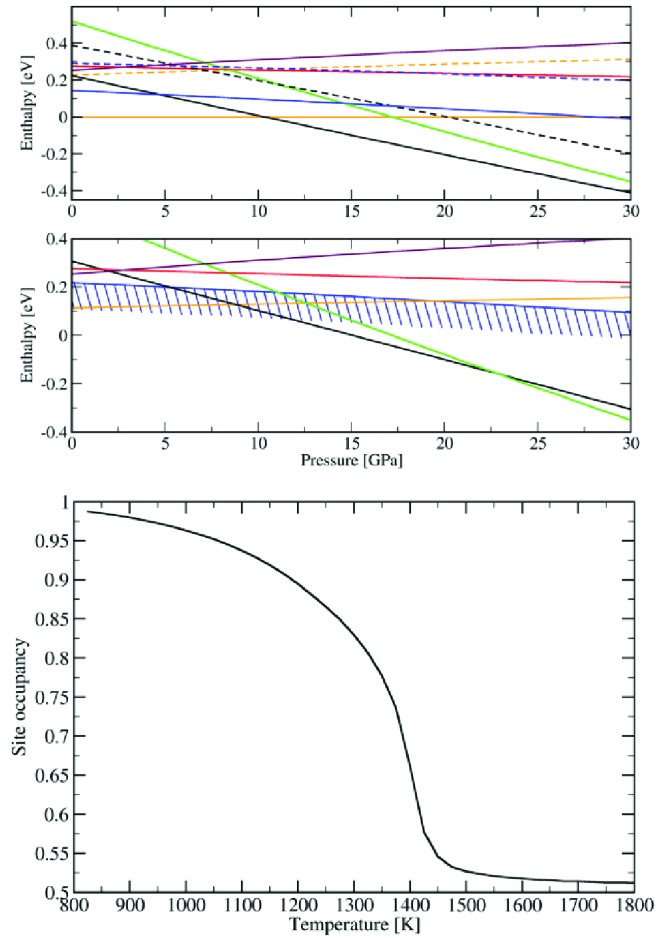
Calculated enthalpies as a function of pressure for ScFeO₃ polymorphs: polar corundum (blue), perovskite (black), YMnO₃ (purple), ilmenite (red), and postperovskite (green) relative to the binary oxides (yellow). Upper plot: 0 K results, for FM (solid lines) and AFM (dashed lined) phases. Mid plot: 1773 K results, for the paramagnetic phase, where the blue area represents the contribution of the configurational entropy to the polar corundum, with the lower bound shown representing the maximum possible stabilizing contribtion. Both magnetic and configurational terms are essential for the polar corundum to become the stable phase between 0 and 12 GPa. Bottom diagram: temperature dependence of cation order in polar corundum SFO from MC simulations, showing a transition from a mainly ordered to a mainly disordered structure between 1300 and 1450 K.

For ilmenite and polar corundum, the results above show that antisite disorder is important. A first order approximation of the entropy can be obtained by describing the material as a solid solution A_xB_(1–x)O₃ of the Fe–Sc dimers, where A and B correspond to the two possible orientations of each dimer. This entropy leads to a stabilization of 0.105 eV/f.u. at 1773 K for ilmenite and polar corundum. Taking configurational and magnetic terms into account stabilizes the polar corundum structure at modest pressures with respect to the binary oxides (Figure 6).

Antisite disorder in the polar corundum structure has been quantified by a series of Monte Carlo (MC) simulations. Interaction parameters are based on an extended Ising model and have been chosen to reproduce the relative energy of different magnetic phases and antisite defects from the DFT calculations (reported in Supporting Information Table S2). The temperature dependence of antisite disorder with respect to the R3c structure (Figure 6) shows a sharp drop in cation order from 0.82 to 0.54 between 1300 and 1450 K. At the synthesis temperature, the MC model predicts the material to be paramagnetic (neither short nor long-range magnetic order remains appreciable in the magnetic RDF) and gives a composition of [Sc_0.515Fe_0.485][Sc_0.485Fe_0.515]O₃, in good agreement with experiment. This indicates that increased cation order can be obtained by annealing the material below 1300 K, but the reduced configurational entropy under these conditions provides insufficient stabilization of the polar corundum structure with respect to the binary oxides.

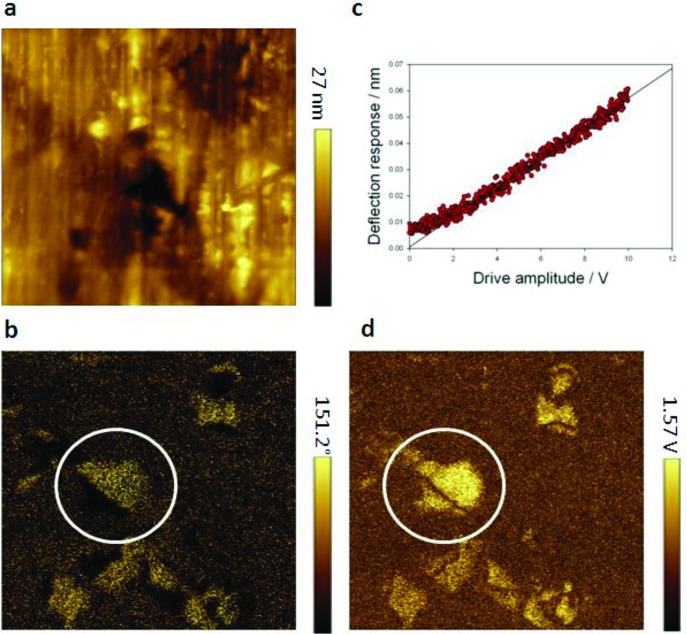
Having ascertained the structural details of SFO as a polar partially disordered phase compatible with ferroic behavior, we measured its functional response to applied electric and magnetic fields. The polarization of the ideal crystal structure was computed using a Wannier function approach. The same inversion mechanism was found as in LiNbO₃⁴² via a migration of an octahedral ion through the face of the octahedron perpendicular to the c-axis (barriers are discussed in Supporting Information Figures S11 and S12). For the fully ordered R3c ScFeO₃ structure, the polarization was computed as 3.3 μC cm^–2. This small value originates from the relative polarity of Fe–O and Sc–O bonds and the difference in the off-center displacements of Sc³⁺ and Fe³⁺, where Fe³⁺ is more able than most magnetic transition metal cations to tolerate irregular environments due to its spherically symmetric d⁵ high spin (HS) configuration. The ionic contribution to the polarization was calculated as 4.0 μC cm^–2 with a formal point charge model at the geometry found in the DFT calculations using the program PSEUDO.⁴³ Experimental measurements made use of piezoresponse force microscopy (PFM).^44,45 The combination of a high level of structural disorder and small polarization even within a fully ordered ScFeO₃ makes PFM observation of polar domains difficult, and in general, no response was observed. In some regions of the ceramic, however, clear 180° domains were seen in the PFM phase image (Figure 7, Figure S11), showing equal amplitude domains separated by a zero amplitude domain wall. The small effective d₃₃ of ∼0.1 pm V^–1 in the ceramic (estimated from a comparison with periodically poled LiNbO₃) reinforces the difficulty of observing the polar domains. PFM spectroscopy was performed on a thin film sample where the PFM amplitude was measured as a function of the ac voltage applied at a single point. The response is ∼5 pm V^–1 and is linear, as would be expected from a piezoelectric material, as opposed to a quadratic response characteristic of electrostriction that occurs in all materials.

Figure 7.

Piezoresponse force microscopy of ScFeO₃. (a) Topography. (b) Vertical PFM phase. (c) Point spectroscopy of the vertical piezoresponse amplitude as a function of ac drive amplitude. (d) Vertical PFM amplitude. PFM images a,b, and d were measured on a ceramic sample; PFM spectroscopy c was measured on a thin film sample. White circles highlight two domains of equal amplitude but opposite phase and are separated by a domain wall of zero amplitude.

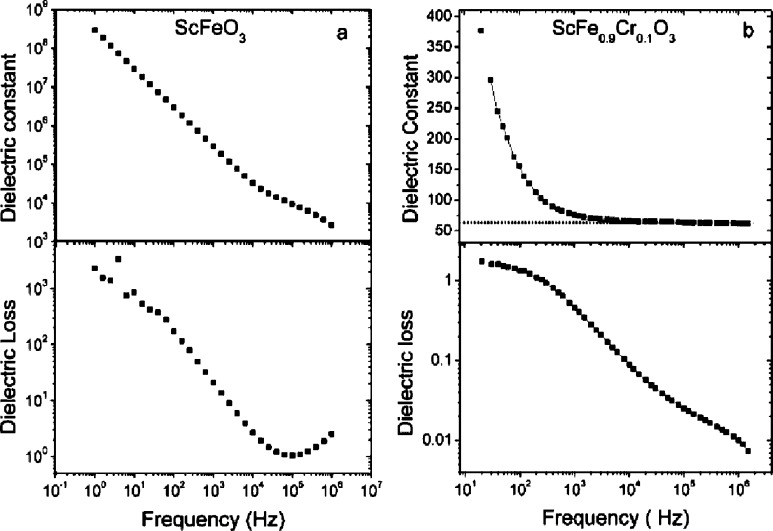
Polar corundum structured ScFeO₃ itself displays poor dielectric characteristics with large and frequency-dependent relative permittivity and loss (Figure S8(a)), together with “dead short” P(E) behavior.⁴⁶ Annealing to reduce the oxygen vacancy content proposed as the origin of the high loss is not possible due to the decomposition of SFO. Substitution of Fe³⁺ by Cr³⁺ in ScFe_1–xCr_xO₃ is possible up to x = 0.1 (Figure 2b) and increases the ambient pressure thermal stability, permitting annealing at 750 °C in oxygen for 6 h (Figure S4). This decreases the dielectric loss significantly (tan δ < 0.1 at 1 kHz), and the (relative) dielectric permittivity attains a frequency-independent high frequency limit of 60 above 1 kHz (Figure 8b), within the range reported for BiFeO₃^10,47,48—this value is suggested to be intrinsic. The divergence of the dielectric constant and dielectric loss at low frequency is ascribed to hopping conductivity,⁴⁹ which is also common for BiFeO₃.^50,51 Cole–Cole plots for ScFe_1–xCr_xO₃ (x = 0 and 0.1) are shown and discussed in the Supporting Information on page S15. P(E) loops close at high frequencies, suggesting removal of the influence of extrinsic charge carriers, but they do not saturate, reaching 1.4 μC/cm² at 50 kV/cm and 100 Hz (Figure S9 is consistent with alignment of the intrinsic polarization without sufficient field being applied to switch it. Nonsaturated P(E) loops are common in polycrystalline BiFeO₃ and explained in terms of high conductivity or large coercive fields due to pinned domain walls.⁵²⁻⁵⁵ Ferroelectricity is not demonstrated by these measurements.)

Figure 8.

Frequency dependent dielectric constant and dielectric loss of (a) ScFeO₃ and (b) ScFe_0.9Cr_0.1O₃.

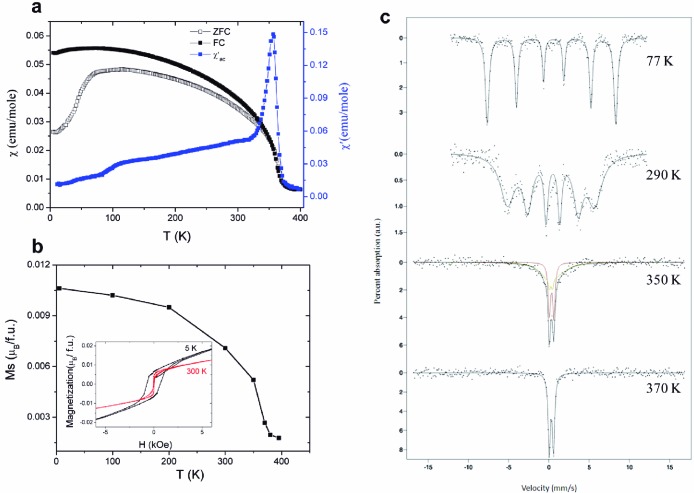
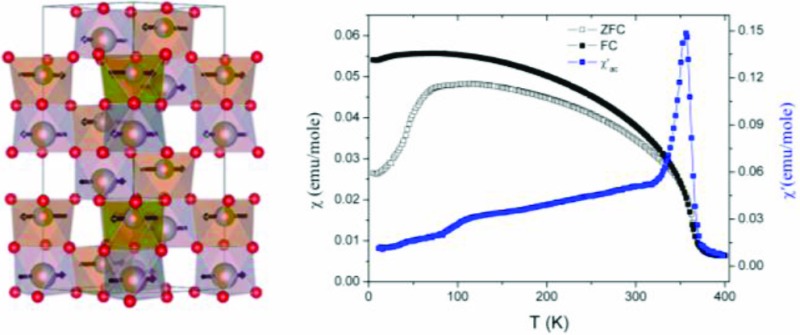
Neutron powder diffraction (NPD) shows that polar corundum ScFeO₃ is magnetically ordered at 300 K, adopting a G-type antiferromagnetic (AFM) structure with antiparallel spins for all nearest neighbors: the observed moment orientation within the close-packed layers is the same as that found in the high temperature phase of α-Fe₂O₃: this orientation permits a weak ferromagnetic (WFM) canting.⁵⁶ Alternating current susceptibility measurements on ScFeO₃ in a 5 Oe magnetic field reveal a cusp at 356 K consistent with the onset of antiferromagnetic order (Figure 9; for Cr doped samples, see Figure 10 and Table 3). Below this temperature, the FC and ZFC DC magnetization data measured at 1000 Oe diverge, and hysteresis is observed in M(H) loops (M_s reaching 0.0106 μ_B/formula unit at 5 K—this small moment canting would not be directly detectable in the NPD measurement), consistent with weak ferromagnetism occurring simultaneously with the antiferromagnetic order. Similar ordering temperatures and magnetization values were obtained in three distinct samples. The bulk nature of the antiferromagnetic order and coupled WFM is proved by Mössbauer spectroscopy (Figure 9c), which reveals T_N = 360 ± 5 K, consistent with the magnetization data. Mössbauer spectroscopy is a local probe of the magnetic field sensed by each iron nucleus and is thus the technique of choice to avoid confusion by small quantities of highly magnetic impurities, which is a potential problem with bulk magnetization measurements used in isolation. The isomer shift indicates Fe³⁺, and the observation of a quadrupole splitting is consistent with the observed distorted octahedral environment. The absence of a center of symmetry on the Fe–O–Fe exchange path allows weak ferromagnetism via the Dzialoshinskii–Moriya interaction. The antisite defects create local FM moments associated with the ilmenite-like environment.

Figure 9.

Magnetic behavior of high pressure ScFeO₃. (a) Temperature dependence of the ZFC and FC dc susceptibility measured at 1000 Oe, and the real part of the ac susceptibility measured at 5 Oe. (b) Temperature dependence of the saturation magnetization, extracted from the M–H curves, by extrapolating the high-field magnetization. The inset shows a magnified version of 5 and 300 K M(H) data; M(H) measurements at other temperatures, used to construct the M_sat vs T plot, are given in Figure S8. (c) Mössbauer spectra recorded at four different temperatures. The green and red subspectra at 350 K represent fits to the ordered and nonordered components, respectively, while the solid lines are guides to the eye.

Figure 10.

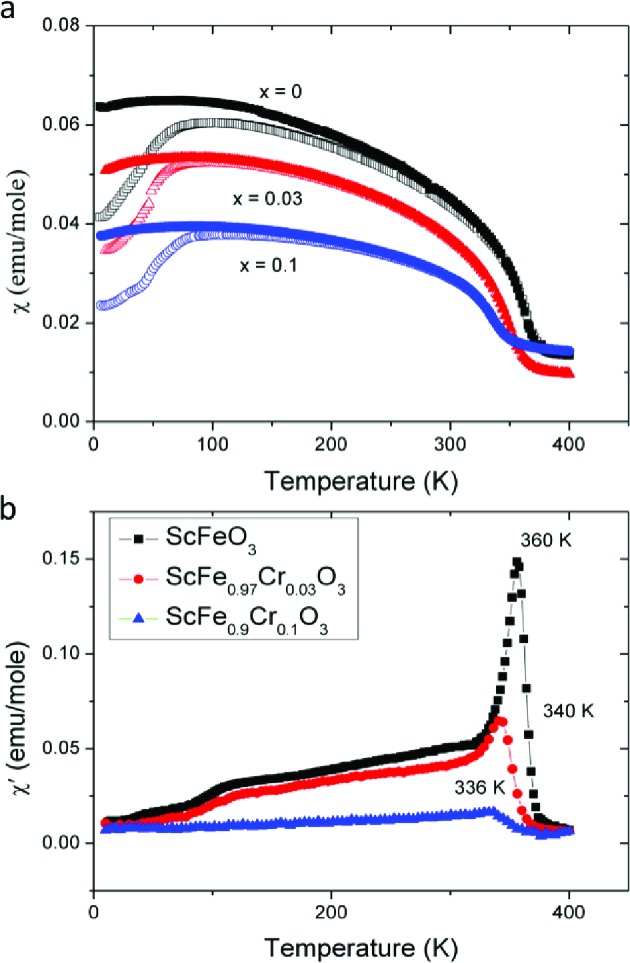
(a) Temperature dependence of the ZFC and FC dc magnetic susceptibility of ScFe_1–xCr_xO₃ (x = 0, 0.03, and 0.10), measured at 1000 Oe. Open and closed symbols represent ZFC and FC data, respectively. (b) Temperature dependence of the real part of the ac susceptibility of ScFe_1–xCr_xO₃ (x = 0, 0.03, and 0.10), measured at 5 Oe.

Table 3. Change of Ordering Temperature in ScFe_1–xCr_xO₃ (x = 0, 0.03, and 0.10).

composition	TN (K)
ScFeO3	356
ScFe0.97Cr0.03O3	340
ScFe0.9Cr0.1O3	336

The simultaneous appearance of WFM with the main AFM order (Figure 9) confirms that WFM is an intrinsic property of SFO. The ordering temperature is an order of magnitude higher than that found in the bixbyite polymorph of ScFeO₃ because of the more favorable Fe–O–Fe angles that allow the extremely strong d⁵–d⁵ AFM superexchange to operate. The dilution of Fe³⁺ with nonmagnetic Sc³⁺ reduces the magnetic ordering temperature from 948 K in the nonpolar R3̅c corundum α-Fe₂O₃ to ∼360 K in ScFeO₃, but the strength of the exchange interaction and retention of the 3D network of Fe³⁺ connectivity in the polar corundum still places the ordering above room temperature. Unlike the case of α-Fe₂O₃ (where canting disappears below the 260 K Morin spin reorientation transition due to changes in the anisotropy aligning the moments along the c-axis), WFM in SFO persists to 5 K. The Cr³⁺-doped compounds on which the permittivity measurements were performed display WFM order above room temperature with coupled T_N and T_c demonstrated by ac and dc magnetization measurements, with both M_s (judged by the low T temperature invariant FC magnetization) and T_N decreasing as the Cr³⁺ content increases (Figure 10, Table 3).

Conclusions

Corundum is an archetypal oxide structure, and the observation of a polar variant in SFO is unexpected. CBED unambiguously demonstrates the polar nature of high pressure ScFeO₃, accounted for by partial Sc/Fe order over the two distinct octahedral cation sites. The extent of the cation site order observed is quantitatively consistent with DFT calculations of antisite dimer defect creation enthalpies. The absence of extensive solid solution in both bulk and thin film is consistent with each dimer containing one Sc and one Fe—the small degree of ordering can then be assigned to disorder in the orientation of these dimers—which agrees with the high energy of homoatomic occupation of the face-sharing octahedral dimers in DFT calculations. The resulting heteroatomic dimers have two possible polar orientations, so the observed antisite disorder entropically stabilizes the polar corundum structure and is intrinsic to its formation. The combination of high pressure (to eliminate vacancies in the bixbyite structure where face-sharing octahedra are absent) and high temperature (to generate sufficient though not complete antisite disorder) is thus required to stabilize the polar corundum structure. In contrast to the high pressure LiNbO₃ polymorph of FeTiO₃¹² and both ordered and corrundum type (In_1–xM_x)MO₃ (M = Fe_1/2Mn_1/2; x = 0.143),^14,15 weak ferromagnetism persists above room temperature and polar distortions are maintained at high levels of disorder. The calculated theoretical electrical polarization value is smaller than that of BiFeO₃ (60 μC/cm²)⁵² while it is 3 orders of magnitude larger than those of multiferroics where a spin spiral breaks the inversion symmetry.^1,4,5 The observed M_s at 5 K (0.01 μ_B/f.u.) is of the same magnitude (0.008 μ_B/f.u) as the M_s measured for high pressure FeTiO₃ at 100 K.¹²

The difference in polarity of the Sc–O and Fe–O bonds, and between Sc³⁺ and Fe³⁺ off-center displacements, thus creates the observed polarization, assigned to the different bonding preferences of d⁰ Sc³⁺ and d⁵ Fe³⁺. The Fe³⁺ 3d⁵ electrons are connected three-dimensionally in the polar corundum, resulting in magnetic order above room temperature. Calculations show antisite defects to have FM nature, and as in α-Fe₂O₃ the absence of an inversion center in the Fe–O–Fe superexchange pathway allows weak ferromagnetism to occur simultaneously with the antiferromagnetic long-range order. Unlike corundum-structured α-Fe₂O₃, weak ferromagnetism in polar corundum ScFeO₃ persists to 5 K, consistent with different local environments of the Fe³⁺ moments in the two materials. Polar corundum is thus a platform for the wide-temperature coexistence of polarity and ferromagnetism, as, in contrast to other mechanisms for combining polarity and permanent magnetization above room temperature,^8,9 it does not rely on symmetry breaking associated with magnetic order, resulting in a polar distortion detectable by both structural and functional (piezoresponse force microscopy) measurements. Further modification of the polar corundum structure based on SFO is required to permit switching of the polarization.

Supporting Information Available

Eleven figures and 4 tables plus gsas list files and powder cif for the final neutron refinement, together with the full author list for ref 13. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.