Intra-day signal instabilities affect decoding performance in an intracortical neural interface system

Abstract

Objective

Motor Neural Interface Systems (NIS) aim to convert neural signals into motor prosthetic or assistive device control, allowing people with paralysis to regain movement or control over their immediate environment. Effector or prosthetic control can degrade if the relationship between recorded neural signals and intended motor behavior changes. Therefore, characterizing both biological and technological sources of signal variability is important for a reliable NIS.

Approach

To address the frequency and causes of neural signal variability in a spike-based NIS, we analyzed within-day fluctuations in spiking activity and action potential amplitude recorded with silicon microelectrode arrays implanted in the motor cortex of three people with tetraplegia (BrainGate pilot clinical trial, IDE).

Main results

Eighty-four percent of the recorded units showed a statistically significant change in apparent firing rate (3.8±8.71Hz or 49% of the mean rate) across several-minute epochs of tasks performed on a single session, and seventy-four percent of the units showed a significant change in spike amplitude (3.7±6.5μV or 5.5% of mean spike amplitude). Forty percent of the recording sessions showed a significant correlation in the occurrence of amplitude changes across electrodes, suggesting array micro-movement. Despite the relatively frequent amplitude changes, only 15% of the observed within-day rate changes originated from recording artifacts such as spike amplitude change or electrical noise, while 85% of the rate changes most likely emerged from physiological mechanisms. Computer simulations confirmed that systematic rate changes of individual neurons could produce a directional “bias” in the decoded neural cursor movements. Instability in apparent neuronal spike rates indeed yielded a directional bias in fifty-six percent of all performance assessments in participant cursor control (n=2 participants, 108 and 20 assessments over two years), resulting in suboptimal performance in these sessions.

Significance

We anticipate that signal acquisition and decoding methods that can adapt to the reported instabilities will further improve the performance of intracortically-based NISs.

1. Introduction

Intracortically-based Neural Interface Systems (NISs) may offer a powerful approach to restore mobility and independence to people with paralysis. Prior studies have demonstrated that information about movement intention can be detected in human motor cortex even after years of paralysis due to stroke, spinal cord injury or ALS (Hochberg et al., 2006, Kim et al., 2008, Chadwick et al., 2011, Simeral et al., 2011a). In turn, extracted movement intention can provide a command signal sufficiently reliable to control a computer cursor on a screen in intact macaques (Ganguly and Carmena, 2009, Carmena et al., 2003, Taylor et al., 2002, Lebedev et al., 2005, Serruya et al., 2002), in people with tetraplegia (Chadwick et al., 2011, Kim et al., 2008, Simeral et al., 2011a, Hochberg et al., 2006), or to perform actions with a robotic limb in macaques (Velliste et al., 2008) or humans (Hochberg et al., 2012, Collinger et al., 2012). Longer term goals include the development of useful, stable, and reliable neurally-controlled assistive devices, such as dexterous robotic assistive devices, communication interfaces, or the restoration of movement of paralyzed limbs by functional electrical stimulation of paralyzed muscles (Donoghue et al., 2007, Pohlmeyer et al., 2009, Cornwell and Kirsch, 2010, Chadwick et al., 2011). To become clinically viable, especially if they require surgical implantation of sensors, these applications must perform reliably over an extended period of time - preferably for a decade or longer.

Technical stability of the recorded neural signals is a desirable design parameter for neuroprosthetic performance. Encouragingly, intracortical recordings using silicon microelectrode platforms demonstrated spiking signals and maintained signal quality over 500 days in monkeys (Suner et al., 2005), point and click cursor control over 1000 days in a person using the same type of sensor (Simeral et al., 2011a), and useful signals for multi-dimensional device control more than five years after implantation in one person (Hochberg et al., 2012). Nevertheless, commonly observed signal instabilities could have arisen from array movement, tissue reaction, array material degradation inside the body, or connector issues externally. Consistent with the contribution of these physical factors, electrode impedance and the number of recorded action potentials have been observed to decrease over months (Parker et al., 2011, Prasad and Sanchez, 2012), and spike amplitudes and root-mean-squared noise show day-to-day and within day changes and an overall signal amplitude decrease on average by ∼2-4%/month (Chestek et al., 2011, Linderman et al., 2006, Santhanam et al., 2007). Whatever the cause, and whether amplitudes increase or decrease, signal changes can be substantial, as 60% of the waveforms recorded with silicon platform arrays in monkey have been reported to change across a 15 day interval (Dickey et al., 2009).

An additional concern for NIS performance is biological stability, i.e. the coding function that relates neuronal activity to behavior. Preferred direction (Stevenson et al., 2011) and its contribution to the decoding model appears to be relatively stable in area M1 (Chestek et al., 2007), as well as decoding performance (Serruya et al., 2003), while somewhat inconsistently, tuning curves (mean rate, preferred direction and modulation depth) in different studies report that coding functions may be unstable, between familiar and novel motor tasks (Rokni et al., 2007, Taylor et al., 2002). Although demonstrations of adaptive filters attempting to mitigate these instabilities exist (Wu and Hatsopoulos, 2008, Eden et al., 2004), the efficacy of these approaches in neuroprosthesis applications has not been established. When designing such an adaptive filter, a principled first step is to understand the source and magnitude of signal variance.

To evaluate the nature and extent of instability in spiking populations recorded in the context of an ongoing pilot clinical trial of people with tetraplegia, we analyzed within-day changes in spike rates, spike amplitudes and their impact upon decoded output, i.e., neural cursor control. We found that systematic rate changes occur commonly; these can cause estimation errors in the decoded kinematic parameters leading to degraded performance that presents itself as a directional bias. These rate changes originated from a combination of recording instabilities (amplitude and noise change) and what appear to be physiological changes. In addition, the majority of the spike amplitude changes we observed were consistent with localized changes at individual electrodes (or recording channels) rather than global motion of the recording array. The present study investigates sources of variance in the recorded neural activity which, if accounted for in real-time neural decoding, would further improve long term neuroprosthetic reliability and performance.

2. Methods

2.1. Participants

We analyzed data from three participants (S3, A1 and T1) in an ongoing pilot clinical trial. S3 (female, age: 56 years) was diagnosed with extensive pontine infraction due to thrombosis of the basilar artery 9 years prior to trial recruitment. A1 and T1 (male and female, ages 37 and 54, respectively) had advanced amyotrophic lateral sclerosis. All participants had tetraplegia and anarthria, A1 and T1 were dependent upon mechanical ventilation. The usual form of communication was through eye movements. This research was conducted with Institutional Review Board (IRB) approval and an FDA IDE. The pilot clinical trial is registered at clinicaltrials.gov/NCT00912041. A detailed description of the BrainGate NIS is presented elsewhere (Simeral et al., 2011a).

2.3. Signal acquisition

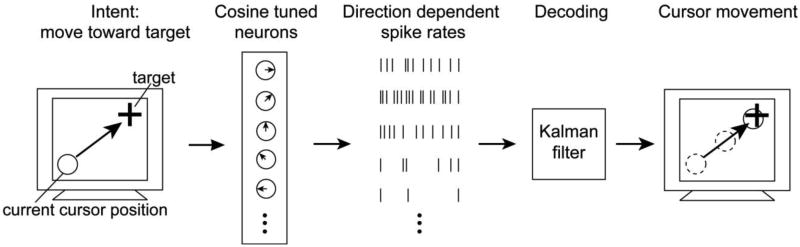
Motor cortical activity was recorded with a 10×10 array of 100 platinum-tipped silicon microelectrodes (1.5 mm length in S3, 1.0 mm in A1 and T1, 400 μm spacing, Blackrock Microsystems) chronically implanted into the motor cortex (M1) arm area (Hochberg et al., 2006, Kim et al., 2008). Recorded electrical signals were passed externally through a titanium percutaneous connector that was secured to the skull. Cabling (94 cm long) attached to the connector and equipped with a unity-gain isolation stage routed signals to an amplifier clamped to the back of the wheelchair, where signals were analog filtered (0.3-7500 Hz), digitized at 30kHz sampling rate and optically transferred to a series of computers for further processing. Sorted spikes were aggregated into 100ms time bins and decoded into cursor positions (Kim et al., 2008) thus controlling the motion of a computer cursor (‘neural cursor’) that the participant viewed on a computer monitor.

2.4. Online spike sorting

Units (single or multi) were manually discriminated by a trained technician at the beginning of each recording session by placing a manually adjusted detection threshold for recorded signals for each of 96 possible recordings channels. Events when the analog voltage signal crossed this threshold triggered the storage of a 1.6-ms long spike waveform. Then one or more manually set time-amplitude windows (window discriminators) were used to detect and sort neural spiking; these events were recorded as a time series of spike counts. Units below 1.5Hz average firing rate were discarded from further analysis. In addition to these manually, on-line, rapidly discriminated units, the broadband recordings of the signal (0.3-7500Hz) were also saved for subsequent offline analysis.

2.5. Offline spike sorting

During offline data processing, we obtained each recorded unit's isolation quality - i.e., its spike waveform signal-to-noise ratio, (SNR) (Suner et al., 2005). Well isolated units above SNR value of 4.5 (n=297 in all sessions and participants) were manually resorted using Offline Sorter (Plexon, Dallas) by manually selecting clusters of the waveforms projected onto a display of their first two principal components (PC). Specifically, the unit's spike waveforms in 2D PC space formed a separate cluster from noise waveforms, the interspike interval distribution exhibited the presence of a clear refractory period (2 ms), and the waveform shapes and peak-to-peak amplitudes showed a characteristic difference when compared with other neuronal waveforms and multiunit activity on the same electrode. The selected units' mean isolation distance (ID) (Harris et al., 2001) was 64. We did not attempt to verify if the same neurons were present each day, thus part of the total unit count likely corresponded to repeated measurement of the same neurons.

2.6. Significance criterion for spike rate change and amplitude change

The neural activity during a daily research session was commonly recorded in a series of short epochs lasting 2-6 minutes during which the subjects performed one or the other of a variety of behavioral tasks (see section 2.9), interleaved by resting periods when no activity was recorded. We used a two-sample Kolmogorov-Smirnov goodness-of-fit hypothesis test (p<0.05) to evaluate whether the firing rates of a unit in a given epoch using one-second bins were significantly different from the rest of the overall mean firing rate (i.e. the rest of the epochs). Correction for multiple testing was employed to control the number of falsely rejected null hypotheses. We used the Benjamini-Hochberg procedure (Benjamini and Hochberg, 1995) with a correction for dependent statistics (Benjamini and Yekutieli, 2001) to set the false discovery rate within a session at the level of 5% for all tests. A neuronal response from a single channel was deemed significant if there was at least one epoch for which the mean firing rate (or amplitude) was significantly different from the rest of the epochs after the correction for multiple testing was made. The same procedure was applied in establishing significance for changes in mean spike amplitude across epochs.

2.7. Significance criterion for synchronous amplitude change across electrodes

As an indication of potential array movement, we addressed whether spike amplitudes on different electrodes change simultaneously. First we calculated mean spike amplitudes within single epochs of 23 sessions (arrays A1, T1 and S3 within the first two months). We included only manually resorted units above 1.5Hz spike rate and SNR >= 4.5 (Suner et al., 2005). Manual resorting was necessary to ensure that the amplitude change was real, and not due to nonstationary electrical noise, change in firing rate of two adjacent units with slightly different spike amplitudes, or other recording artifacts. For each unit, the epoch-to-epoch mean amplitudes were z-scored (i.e. the mean amplitude across all epochs was subtracted from each epoch's mean and normalized to the epoch-to-epoch variance), then the absolute values of these z-scored amplitude fluctuations were averaged across electrodes. Extreme values (see next paragraph) in this overall epoch-to-epoch amplitude change indicated that a substantial fraction of the units had changed synchronously.

Second, a nonparametric bootstrap procedure established the significance criterion by estimating the sampling distribution of the overall amplitude change. In particular, normalized absolute amplitude changes were randomly reshuffled along the session and averaged across electrodes and the most extreme value was stored. This process was repeated 1000 times to generate a bootstrap distribution, to which values of the overall epoch-to-epoch amplitude change was compared. Synchronous change from epoch to epoch was concluded statistically significant if the most extreme value of the overall amplitude change was larger than 99% of the values in the bootstrap distribution (p<0.01).

2.8. Decoder calibration and closed loop control

The first task of each research session was designed to find a linear mapping between volitional neural activity and cursor movements. Specifically, the participant watched a computer-generated sequence of cursor movements (training cursor) while attempting arm motions that would produce such a cursor motion. In this calibration stage the participant received no feedback of how effective his/her movement imagery would have been in controlling the cursor. Neural firing rates recorded during this intended arm/hand movement together with the cursor kinematics (position and velocity) were used to calibrate the Kalman filter's decoding model (Wu et al., 2006, Malik et al., 2011). Once established, this mapping converted subsequently observed neural firing patterns to cursor motion in two dimensions. A second mapping between imagined hand squeeze and the overall firing rate of the same neural cluster was used to create a “click” signal (Kim et al., 2008, Simeral et al., 2011a, Kim et al., 2011).

2.9. Cursor control assessment

Voluntary control over the neural cursor was regularly tested by a radial-4 or radial-8 center-out-back target acquisition task. The goal of this task was to move the neural cursor to one of four (or eight) circularly arranged peripheral targets that were discs on a screen. The cursor was centered on the screen to begin a trial (i.e. cursor movement to a new target), and the participant was asked to direct the cursor to the target (indicated by color change), click on it, then direct the cursor back to the center and click on it to initiate a new trial. Cursor control was assessed by the percent of successfully acquired targets (both peripheral and central) and by testing cursor trajectories for a directional bias, i.e. a systematic tendency to move in a direction other than toward the target.

To measure the direction of a bias during cursor control, for each trial we calculated the cursor's average orthogonal deviation from the straight path between center and target. Note that a jittery cursor with no systematic bias tends to deviate on either side of the straight path, therefore the deviations tend to cancel out. Bias direction was obtained from the vector average of the orthogonal mean deviations over all trials to all targets. Target directions across all epochs were roughly evenly distributed with 12±9 trials/epochs. Occasionally, some of the trials were not executed due to limited cursor control. However, our bias measurement did not require balanced number of target presentations.

Bias significance was estimated by a bootstrap procedure. The sign and length of the orthogonal deviations were randomly reassigned among the trials, i.e. the orthogonal deviation vectors were rotated to be orthogonal to a randomly selected other trial direction, averaged, and the resulting bias vector length was stored. Five thousand repetitions of this shuffling generated a smooth distribution of vector lengths to which the original bias vector length was compared. The assessment was considered significantly biased if the original bias vector length was larger than 99% of the shuffled vector lengths (p<0.01).

In addition to the target acquisition task above, a variety of other tasks were also performed during each clinical trial session and presented elsewhere. These tasks included ‘mFitts’ a sequential tracking paradigm (Simeral et al., 2011a), multi-dimensional control of a robotic or prosthetic arm (Hochberg et al., 2012), the effect of movement imageries on neural responses, or comparisons of decoder types on cursor control. The behavioral results of these tasks fall outside of the scope of this paper.

2.10. Closed- loop simulation

To explore how directional bias could arise from an underlying neuronal spike rate change, we simulated closed-loop cursor control with a virtual subject whose intention was to always move in the direction of the target (Fig. 1). The subject's intention drove direction specific responses of a population of N = 8 neurons with tuning curves f(φ) = (f₁(φ), f₂(φ), … f_N(φ)) describing the mean spike count of each neuron as a function of the movement direction φ. Furthermore, these neurons tiled the space of all directionsuniformly and had unimodal tuning curves following a cosine function. The response for neuron i for movement direction φ was defined as

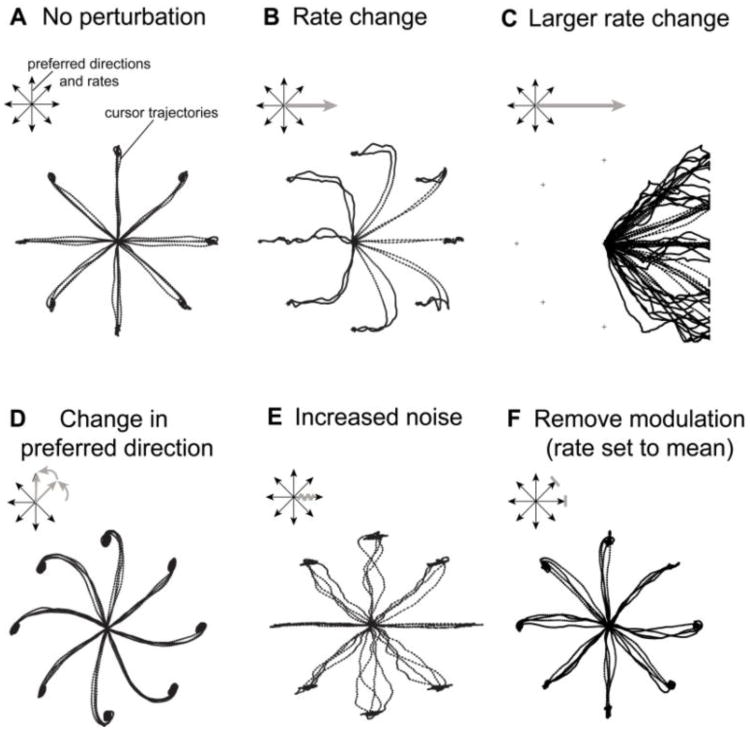
Figure 1.

Computer simulation modeling the effect of neural signal changes on closed-loop neural cursor control.

$$f_i\left(\phi \right)=A+m\ast \mathit{\text{cos}}(\phi -{\phi }_i)+\nu$$ (1)

where A is the baseline firing rate, m (or modulation depth) controls the amplitude of the tuning function, φ_i is the neuron's preferred direction and ν is Gaussian noise.

Decoding the simulated firing rates and generating the cursor trajectories was similar to a typical closed-loop session. First, we generated firing rates based on a training cursor moving toward four cardinal targets, used these rates to calibrate the parameters of the Kalman filter (Malik et al., 2011), and then performed a center out assessment in closed-loop. We simulated closed-loop visual feedback by using the current cursor and target positions to recalculate the intended movement direction (i.e. toward the target) in each successive time step. Firing rates and the subsequent cursor positions were generated iteratively every 100ms. Realistic cursor trajectories were obtained using A=20Hz, m=10Hz and ν =10Hz. Cursor trajectories were stored and are reported in the Results.

3. Results

We analyzed motor cortical neuronal spiking activity recorded from three trial participants during the first two months after electrode implantation (4, 7 and 11 experimental sessions, 8-22 epochs/session, with 352, 668 and 718 manually sorted units for A1, S3 and T1 respectively). We also monitored neural cursor control and the underlying neural activity in center-out-back target acquisition assessments (108 and 20 assessments over 65 and 8 sessions with 32±15 and 88±9 sorted units/assessment for S3 and A1 respectively; see Methods and Table 2). Since cursor control assessments with S3were recorded in a later part of the trial (days 785-1576), her performance data with the corresponding neural data is labeled as ‘S3b’. Participant T1 with advanced ALS did not achieve sufficient 2D cursor control with our decoding and signal selection approach at that time, thus her intra-session performance was not presentable. Below, we describe the signal instabilities, followed by the simulated effect that these could have on actual decoding performance, followed by the cursor control results observed in participant S3b and A1.

3.1. Within-day firing rate changes at the group level

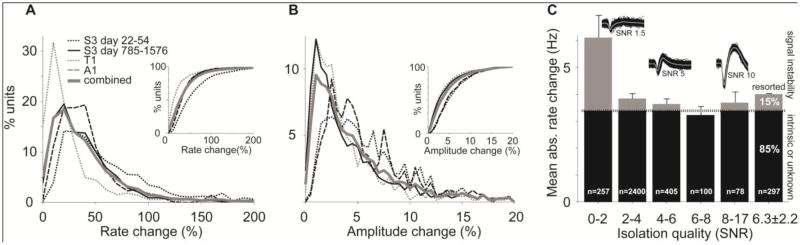
To survey the frequency and magnitude of apparent firing rate changes at the group level, we analyzed data from three participants (A1, T1, S3) during the first two months post-implantation and during a two-year assessment period in S3 (‘S3b’). For each unit in each session, we defined rate change as the largest deviation of an epoch's mean rate from the mean rate over all epochs. The average daily firing rate change was 3.8±8.71Hz or 49% of the mean rate, with a similar magnitude across the three arrays (3.7±4.5, 2.8±5.2, 5.3±6.2 and 3.7±11 Hz for A1, T1, S3 and S3b respectively; see Fig. 2A). Eighty four percent of these changes across epochs within a session were statistically significant (p<0.05 with correction for false discovery rate, see Methods), 5% of the unit recordings showed changes larger than 8.4 Hz (or 113% of the overall mean), and 50% of the significant rate changes were below 1.2 Hz (27% of mean rate).

Figure 2. Spike rate and amplitude instability at the group level.

A. Rate changes show comparable magnitudes across 3 participants over the first two months of implantation and over 5 years in one participant. Inset: cumulative rate change. B. Corresponding magnitude of spike amplitude changes across data sets. C. All but the lowest isolation quality units show similar magnitude of rate change. Only units with statistically significant rate change are included. Insets show representative examples of spike waveforms with different isolation qualities. The gray area indicates the contribution of recording instability estimated by resorting a subset of the units (see text). SNR: signal-to-noise-ratio following Suner et al., 2005.

The generally low apparent firing rates and the relatively small rate changes were both statistically significant and meaningful. The reported mean rates result in part from the inclusion of portions of trials where no intended movement is expected (i.e., rest), and from the largely balanced task where instructed movements in a unit's preferred direction were as common as instructed movements in the opposite (or anti-preferred) direction. The effect (or lack of such effect) that statistically significant group-level mean rate changes might have on closed-loop decoding is not obvious a priori; the actual effect is described below.

One source of apparent rate change would occur if units were not well isolated and hence more or less contaminated with mixtures of spikes. To examine how isolation level influenced rate change, we used the signal-to-noise ratio of the spike waveforms (SNR) (Suner et al., 2005) as an established measure of isolation quality, where low SNR values (0-3) appear to correspond to multi units, and values above ∼4.5 roughly correspond to single units with increased waveform similarity and decreased background noise (Fig. 2C, insets). Units along the SNR spectrum showed comparable rate change (3.2-3.8Hz), except multi unit channels with the lowest level of isolation (SNR: 0-2) which had average rate changes nearly two-fold higher (6.1Hz, Fig. 2C) than cells with >2 SNR. This striking difference likely originated from the fact that amplitude detection thresholds in this lowest SNR group were inevitably close to the background noise, making spike detection more sensitive to subtle changes in recording conditions. In these units, recording instability (discussed below) could play an important role in spike rate instability and ultimately to impaired NIS performance, although these units represented only 8.6% of the significantly changing units (n=257) and 12% of the total rate changes.

3.2. Spike amplitude changes and their possible causes

To survey the extent of within-day spike amplitude changes in the population, we averaged spike valley amplitudes (largest negative excursion of the recorded potential from zero) within each epoch, and then monitored the relative change of the mean amplitudes between subsequent epochs. 74% of the amplitude changes were statistically significant (p<0.01, bootstrapping, see methods). Significant amplitude changes had a slow, meandering time course (1.0±3.4 μV/min), with similar frequency and magnitude across all three electrode arrays (Fig. 2B). The average maximal daily amplitude change was 3.7±6.5μV or 5.5±6.25% of the mean valley amplitude (4.6±6.7, 4.4±6.8, 6±9.4 and 2.3±4.7 μV for A1, T1, S3 and S3b respectively); 5% of the units exhibited a change larger than 8.8 μV, or 13% of the mean amplitude, and in 50% of the units amplitude change was below 1 μV (3%). These instabilities were comparable to within-day amplitude changes observed in monkey motor cortex (Chestek et al., 2011).

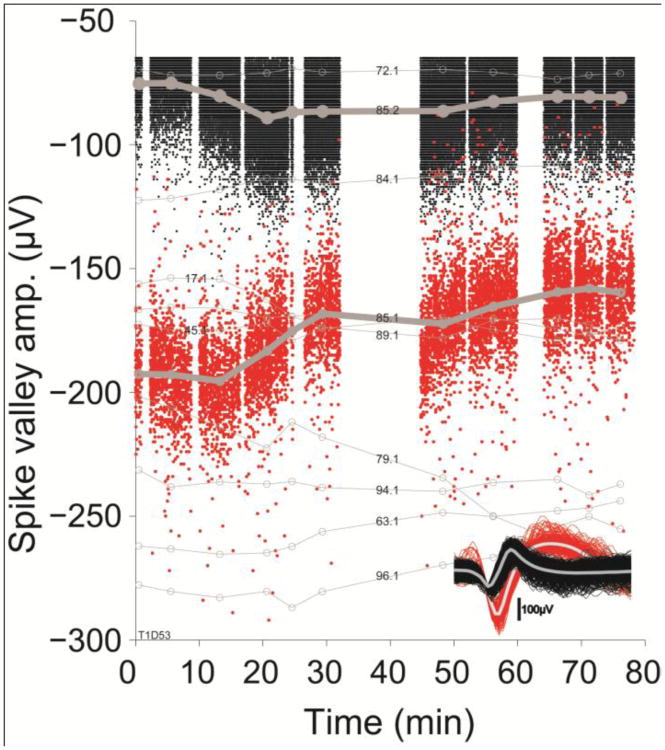
Spike amplitude fluctuations on a time scale of minutes to hours might arise if system parameters (such as electrode impedance, cross-talk between electrodes, or other unknown recording conditions) change. Such instabilities would affect each recorded spike on a given electrode even if the spikes originate from two or more adjacent neurons. An example is useful in highlighting amplitude instabilities in two well-discriminated units recorded simultaneously on the same electrode (Fig. 3). In the first half of the research session (from 0-35 min), the two units' amplitudes changed in opposite directions, while in the second half (from 45-75 min) the amplitudes changed in a similar fashion. These different temporal dynamics argue against more global changes in recording system parameters such as impedance changes or cross-talk (device effects), although micro motion affecting the recording distance between neurons and electrode tip (motion effects) could still explain the different dynamics depending on the geometric arrangement of the units surrounding the electrode tip (Gold et al., 2006, Csicsvari et al., 2003).

Figure 3. Independent spike amplitude dynamics in two units recorded by the same electrode contradict explanations for simple instrumental artifacts.

Small dots indicate the amplitude of individual spikes at the most negative deflection. Clusters of spikes correspond to experimental epochs (with different tasks and instructions) where larger circles and thick line indicate the mean spike amplitude within an epoch. Gaps between spike clusters indicate breaks between epochs, when data collection was paused. Inset: Due to their characteristic shapes and different amplitudes, spikes could be well discriminated into two classes. Over the duration of the experiment, spike amplitudes changed in both units, but with different dynamics. Alterations in electrode impedance, cross-talk, or other system parameters cannot explain these changes, as they would impact both units similarly. Thin gray lines: mean spike amplitude of units on other electrodes show no systematic amplitude change across the array. For clarity, only ten randomly selected amplitude traces are shown. Numbers indicate electrode and unit label.

Global array movement, because it is a rigid monolithic structure, would be expected to influence spike amplitudes on multiple electrodes at the same time. Depending on the units' location relative to the electrode tip, array movement could cause a simultaneous amplitude increase and decrease on different electrodes. In support of this explanation, we found significant synchrony of spike amplitude changes across electrodes and between epochs in 9 out of 23 sessions (39%, p<0.01, see Methods). Following these events firing rate changes doubled; (3.42±4.47Hz) compared to rate changes during randomly selected non-synchronous epoch transitions (1.7±2.5Hz), or between filter calibration and cursor control assessment epochs (1.85±3Hz). Hence, whenever present, micro movements of the array, inferred from synchronous changes in firing rate across the array, could account for up to 50% of the overall rate change in the population. Array movement might cause rate change by physical irritation, although the exact mechanism remains unclear.

However, in the remaining 61% of the sessions (n=23), simultaneous recordings showed uncorrelated changes in temporal dynamics (Fig 3. gray lines), or the amplitude changes were localized to an individual or a few electrodes without any spatial pattern across electrodes. Local changes in tissue geometry (e.g. microvasculature dilatation), hydrostatic changes, relative changes in the regional extracellular milieu or other local change in recording conditions or physiology could account for this observation. In summary, both array movement and local changes in tissue geometry could play a role in amplitude instabilities, although the exact causes remain unexplained.

3.3. Spike amplitude instability can affect apparent firing rates

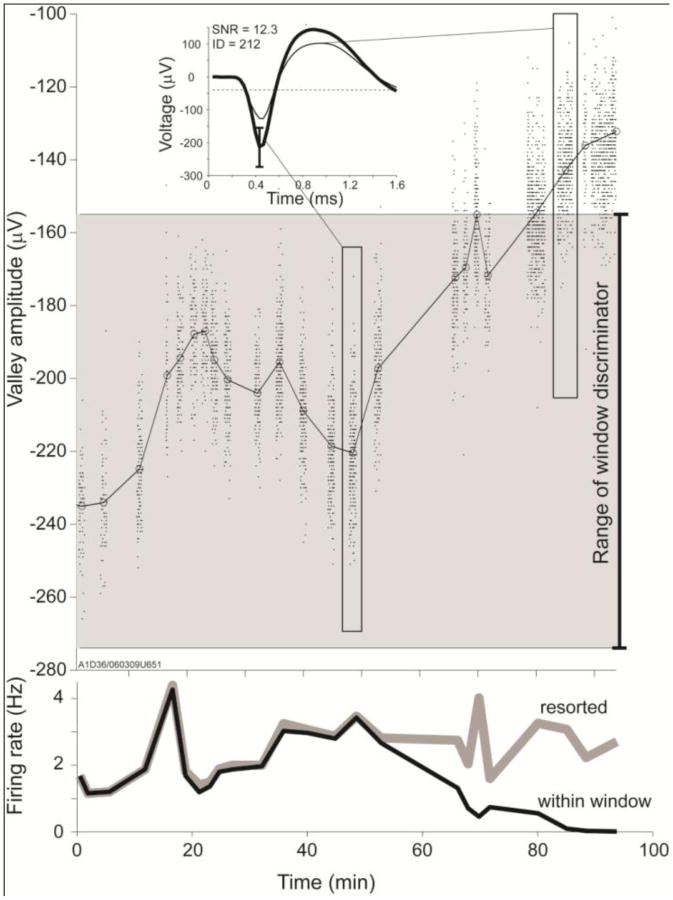
If spike amplitudes change, spikes may fail to fit the discriminator criteria, thus spike detection would suffer. In the example unit presented in Fig. 4A, spike amplitudes decreased by forty-four percent over 1.5 hours (from 235 to 130μV within 1.5 hours). As a result, by the end of the session the majority of spikes for this unit failed to reach the requisite amplitude range required by the time amplitude window discriminator (Fig. 4A, gray area), and thus remained undetected. Comparing the average firing rates between the first and last half of the session, this problem resulted in a 50% decrease in firing rate observed online, even though the actual firing rate as determined by offline resorting showed a modest increase (from 2.15 to 2.8Hz) probably due to the participant's compensatory behavior. In this example, spike detection error occurred by losing/gaining spikes in the time amplitude window discriminator, however similar spike detection error could occur in units with small spike amplitudes by losing/gaining spikes whose amplitude crossed the spike detection threshold.

Figure 4. Spike amplitude instability causes spike detection error.

A. A representative unit demonstrates large spike amplitude instability. The gray shaded area covers the amplitude range between the upper and lower boundaries of the window discriminator as determined manually by the experimenter. Spikes falling outside of these boundaries remained undetected during the online experiment. Inset: average spike waveforms during selected time periods indicated by elongated rectangles. B. Spike rates as determined by online (within window, black) and retrospectively discriminated spikes (resorted, gray). Apparent decline in the online firing rate results from failure of the smaller waveforms to satisfy the discriminator parameters.

To estimate the extent to which amplitude change (or recording instability) contributed to apparent firing rate change at the group level we manually resorted a subset of the units (>4.5 SNR, n=297 units, SNR=6.36±2.2, Methods). If spike amplitude or background noise instabilities changed the detected spike count, this error would be corrected offline by recovering undetected spikes (false negatives) or removing noisy waveforms (false positives). Thus, a reduction in rate change after resorting indicated the amount of change that originated from recording instability (resulting in part from the method of online spike discrimination), while rate change unaffected by resorting was interpreted to reflect intrinsic changes in spike rate due to physiological or unknown factors.

Manual offline resorting reduced firing rate fluctuations by 15% (from 4 to 3.4Hz; across arrays: 30%, 5.6%, 16% and 10% reduction for A1, T1, S3, S3b respectively), suggesting that the contribution of recording instabilities to apparent rate change was small compared to physiological or unknown reasons. Firing rate changes within different groups of isolation quality closely matched the rate change in the resorted neural group, indicating a similar contribution of recording instability to apparent rate change (Fig. 2C). Rate change showed a weak but significant correlation with amplitude change in the lowest isolation group (SNR 0-2, cc=0.11, p=0.05) and in the highest isolation group (SNR 8-17, cc=0.18, p=0.049). We found no significant correlation between rate change and change in baseline noise (i.e. the standard deviation of the first four samples of each spike waveform). In summary, generalizing the sorting results to the entire population, our estimated contribution of intra-day recording instability to rate change at the group level was ∼15%, while the remaining 85% of the changes were likely originating from intrinsic changes in spike generation or other unknown factors.

Spike detection error associated rate change was independent of the type of performed task. To this point, we compared mean rates between epochs of different instructions (see Methods), thus mean firing rates could be modulated in a context dependent manner. However, we also compared rate changes between filter calibration and cursor control assessment, which were expected to be more similar in terms of movement imagery. Comparing similar imagery epochs showed a smaller average rate change (1.85±3Hz), yet resorting a subset of units (n=128 from S3b, SNR=6.3±2) within these epochs also eliminated 14% of the rate changes. Thus while neural activity changed, as expected, during different tasks, the number of spikes lost due to recording instabilities was a constant fraction of the total number of spikes.

3.4. Apparent spike rate changes introduce decoding errors in computer simulation

To investigate the effect of apparent firing rate changes on the decoded neural cursor movements, we performed a computer simulation of a closed-loop cursor control epoch and calculated cursor trajectories. In short, we generated firing rates of eight simulated neurons with evenly distributed preferred directions, cosine-shaped tuning curves and Gaussian noise (see Methods). Each neuron's response was modulated by the movement intention of a ‘virtual’ participant who always attempted to move toward the target in a radial-8 center-out-back target acquisition task (Methods). Based on the generated firing rates we calculated the velocity vector of the neural cursor with a Kalman filter identical to the one used in actual participant experiments.

Cursor trajectories in closed-loop simulation closely resembled those in a balanced center-out assessment performed by clinical trial participants when a good neural decoder had been calibrated (Fig. 5A). However, departure of a single neuron's firing rate from its expected range could disrupt Kalman-filter based neural control. For instance, increasing the mean firing rate of one unit tuned to right movement from 20Hz to 30Hz (50% rate change, i.e. the average proportional rate change in the population) resulted in mild but statistically significant rightward directional bias (p<0.05, Methods). Larger rate changes resulted in increasing magnitudes of rightward directional bias (45Hz: Fig. 5B) to the point where bias magnitude overwhelmed the user's adaptive response, and cursor control failed (extreme example: 60Hz, Fig5C). Changing rates of multiple units also resulted in a directional bias, where the direction and magnitude of the bias was a weighted average of individual unit's rate change, preferred direction and contribution to decoding. As we show below, these simulations faithfully recreated directional bias similar to actual participant research sessions.

Figure 5. Computer simulation demonstrates the impact of neural signal perturbations on decoded cursor kinematics.

A. Simulated closed-loop neural cursor trajectories in a radial-8 center out and back assessment with no perturbation. B and C: Rate change leads to directional bias, i.e. cursor drift in a constant direction, when using a decoder calibrated with neural data in A. D. Change in preferred direction leads to centrifugal distortion of cursor movements. E. Random insertion of spiking events results in jittery trajectories. F. Removing task related modulation of one or more units increases jitter of cursor movements. See text for details.

Closed-loop simulation also enabled us to explore characteristic changes in the Kalman filter-decoded cursor kinematics caused by three additional signal perturbations: preferred direction change, noise change or change in modulation depth. Change in a unit's preferred direction introduced a rotational bias, with a centrifugal distortion of cursor trajectories resembling a pinwheel (Fig. 5D, see supplementary material for additional explanation). In this case, despite of the constant angular error, the simulated visual feedback helped to direct the cursor to the target. The remarkable similarity of this result to actual motor performance in the presence of a curl force field (Li et al., 2001) is consistent with the effect of constant angular error on actual movement trajectories. Although we observed no indication of such a global pinwheel pattern in cursor trajectories during closed-loop participant control, the participant had the ongoing ability to adjust strategy and adapt to small tuning changes. Unless the magnitude of rate change and the decoded velocity overwhelms the user's adaptive response, this bias could be undetectable. Increasing the noise component (see Methods, equation 1) in one or more simulated units resulted in jittery cursor trajectories in all movement directions (Fig. 5E, also frequently observed in cursor control assessments), while reducing modulation depth of two units to zero (i.e., setting firing rate to the mean rate) introduced no systematic distortion, but a slight increase in jittery cursor movements (Fig. 5F).

3.5 Effect of rate change on neuroprosthetic control: participant S3 research sessions

The quality of intra-day neural cursor control with participant S3 was frequently affected by a directional bias, revealed as an apparent drift of the neural cursor in a constant direction (Fig 6B). During assessments of accurate control (Fig. 6A), neural cursor trajectories appeared relatively straight, with any deviations from the axis of target direction remaining small. For example, during the assessment presented in Fig. 6A, the cursor reached the target in 7.14±3.44 seconds (n=47 trials) with high positional accuracy (within 2.7cm from the center of the target) and acquired 100% of the targets within the allotted trial interval (25 sec). In contrast, 56% and 15% of the assessments (n=108 and n=20 for S3 and A1 respectively) showed a statistically significant directional bias in cursor movements (p<0.01, bootstrap procedure, see Methods, Fig. 6B). This bias interfered with the ongoing motion of the cursor towards the target with mild to major effects, occasionally resulting in complete inability to control the cursor. The direction of the bias generally remained stable within a day and appeared to change randomly from day to day, however in one data session we observed a change in bias direction within a single day.

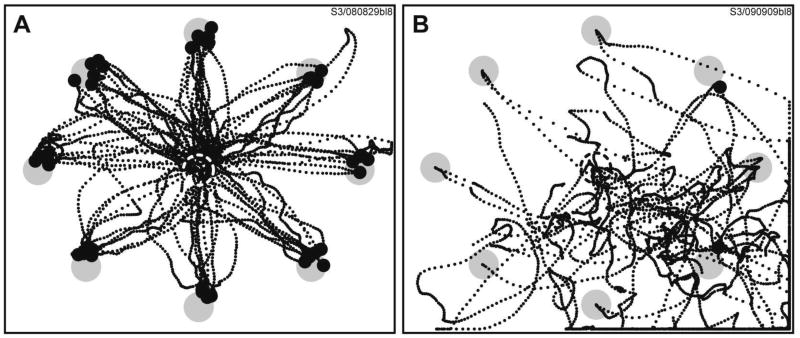
Figure 6. Examples of accurate neural cursor control (A) and cursor control with directional bias (B) during two sessions of a radial-8 center out assessment.

The participant was asked to direct the neural cursor (paths shown as black dots) from the center of the screen (white or black dashed circle) to one of eight peripheral targets (gray discs), click and then return to the center. Black discs: click locations of successfully acquired targets. Cursor trajectories are relatively straight and mark out the eight principal target directions with 100% successful target acquisition rate B. Poor control with 15% correctly acquired targets. Cursor trajectories show frequent direction change and a strong tendency to move towards the bottom right corner of the screen

An example session with significant firing rate changes and the resulting directional bias is presented in Fig. 7. This session started with accurate cursor control (i.e. relatively straight trajectories with 100% success in reaching the instructed target, Fig. 7A, upper left inset). About 30 minutes into this session the cursor repeatedly drifted towards the lower left corner of the screen as the participant attempted to reach any target. Due to this strong directional bias, target acquisition rate diminished to chance level (i.e. no control), but 80 minutes and ∼50 trials later the control gradually returned to near perfect performance without any investigator initiated change in the experimental setup, filter parameters or task instruction (Fig. 7A).

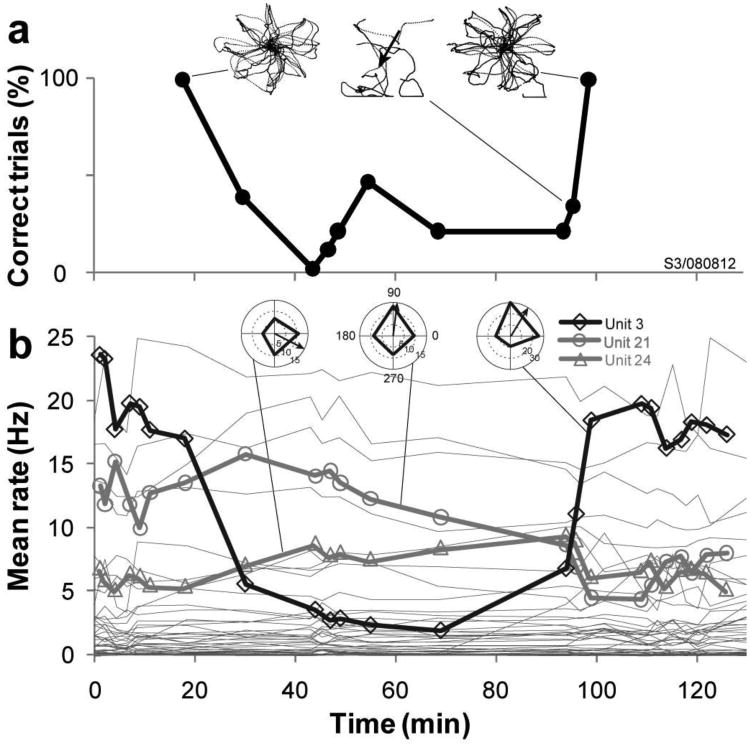
Figure 7. Mean firing rate change of a highly modulated unit correlates with control instability.

A. In a series of radial-8 center-out-and-back assessments, performance decreased from 100% correctly acquired targets to zero percent, but after another forty minutes control recovered spontaneously and reached full performance. This decrease in performance was correlated with a change in one unit's mean firing rate (B). Top insets: cursor trajectories over the session. Arrow indicates bias direction. B. Mean firing rates of twenty-six units used in decoding. Unit 3 (thick black line) decreased its firing rate by 75% over the first ∼70min. The rate change of this unit correlated strongly with decreased performance (Pearson's cc.: 0.87, p≪0.01), and its preferred direction aligned with the axis of directional bias. The reason for these rate changes was unknown. Thicker lines: three units with significant rate change (p<0.01). Insets: direction tuning curves of the three units.

In parallel with this performance degradation, one of the units with significant firing rate change (unit 3, p<0.01, n=26 units contributing to the decoder) showed a 75% reduction in mean firing rate as its spike amplitudes gradually blended into background electrical noise. The rate change of this unit correlated significantly with decaying cursor control (Pearson's cc.: 0.87 p<<0.01) and consistent with its role in creating bias, the preferred direction of the unit matched the axis of directional bias (see Methods for bias measurement). When the firing rate of this unit returned to the original level, cursor control was also restored. Although two other units also showed significant rate changes (unit 21 and 24), their contribution to decoding were small, thus their changing firing rate appeared to have negligible effect on bias direction.

To confirm that the directional bias observed during cursor control assessments indeed originated from changes in firing rate, rather than from other possibilities such as a change in the unit's preferred direction or a latent technical/programming error, we calculated bias direction from the observed rate changes and compared this calculation to the actual bias direction observed in cursor trajectories. Specifically, instead of decoding cursor velocity iteratively from firing rates within short time windows (typically 100ms) we decoded the net cursor velocity (i.e. bias) from the mean firing rates over the entire assessment using the same Kalman filter that we trained prior the analysis. Predicted and measured bias direction correlated significantly (Pearson's cc=0.86; p=7.24*10⁻¹⁹, n = 61 assessments) in center-out assessments with significant directional bias, and the angular error between predicted and observed bias was within 90° in 70% of the assessments, confirming the role of firing rate change in directional bias.

If firing rate changes cause directional bias, one might expect more frequent or larger rate changes in biased assessments than in those assessments where cursor control was good, however we did not observe such dichotomy. Significant rate changes were common (Fig. 2), with both biased and unbiased assessments showing significant rate changes. Only one assessment (∼1%, n=108 assessments, S3b) showed no significant change in the mean rate of any unit (unbiased assessment, Table 1). These indicate that the absolute amount of rate change in the recorded units had little predictive power for forecasting directional bias.

Table 1. Significant rate change and directional bias during performance assessments (S3b).

# of sessions	Bias occurred	Bias did not occur	Total
Any unit with significant rate change	61	46	107
No unit with significant rate change	0	1	1
	61	47	108

Small amplitude units in the SNR group 0-2 showed larger apparent rate changes than well isolated units (Fig. 2C). To address if they were also more likely contributing to directional bias, we analyzed all center-out assessments with significant bias (n = 61 assessments, see Methods) and from each assessment, we selected five units (∼10-20% of all units/assessment) with the strongest contribution to directional bias. We defined a unit's contribution to directional bias as the unit's rate change (between filter calibration and center out assessment) multiplied by the weight of the unit in decoding (Wu et al., 2006). The SNR of these units was slightly higher than the population mean (3.07±1.2 n=310 compared to 2.78±1.08, n=3240), thus units which adversely affected decoding performance were not restricted to the low SNR cohort.

Finally, we investigated time-dependent changes in cursor control during a session. To do so, we analyzed performance metrics of neural cursor control in sessions when cursor control was assessed repeatedly between two to five times (n=28 and n=10 sessions for S3b and A1 respectively) and ∼ 5-180min apart. In both participants, the average performance metrics during the first assessment of the sessions were similar to the following assessments (Table 2). In summary, despite of temporal variation in performance, none of the cursor control metrics showed any systematic tendency to increase or decrease within a session. Further analysis on cursor control assessment using data from A1 and S3 were presented previously (Kim et al., 2008, Simeral et al., 2011a).

Table 2. Summary of cursor control performance metrics for participants S3b and A1.

PC: Percent correct, MT: Movement time, ODC: Orthogonal directional change, MDC: Movement direction change, MV: Movement variability, ME: Movement error, MO: Movement offset, PBE: Percent biased epochs

Epoch #	n (assessment)	PC (%)		MT(sec)		ODC		MDC		MV(mm)		ME(mm)		MO(mm)		PBE(%)
		Mean	SD	Mean	SD	Mean	SD	Mean	SD	Mean	SD	Mean	SD	Mean	SD
Participant S3b, n=108 assessments over 65 sessions, trial days 785-1576
1	65	61.8	33.8	5.3	6	3.7	2.4	4.9	2.5	19.3	9.3	27.7	15.8	24.8	15.5	56.9
2	26	59.3	30.1	6.2	4.9	4.4	2.1	5.6	2.2	21.7	8.9	3I.3	17	28.2	17.5	57.7
3	11	59.5	36.5	4.7	3.5	3.6	1.8	5	1.7	17.8	7	27.5	19.2	24.5	20.3	63.6
4	4	70.4	20.5	4.6	1	4.5	2.7	5.9	2.9	15.4	0.8	21.5	2.4	19.7	3.6	50
5	2	67.8	10.2	4.8	0.1	4	1	5.8	1.6	15.7	2.7	23.7	3.4	22.1	2.2	100
Participant A1, n=20 assessments over 8 sessions, trial days 106-225
1	8	69.3	19	3.4	0.8	6	6.6	7.2	6.8	11.4	4.6	20.9	8	19.6	8	25
2	5	60.5	16.8	3.6	0.6	4.1	4.3	4.6	4.2	12.3	4.8	18.4	7.5	15.9	8.2	0
3	5	69.2	18.8	3	0.3	5	4.6	5.9	4.3	15.5	5.6	24	10.1	21	10.3	17
4	1	70		3.2		5.6		9.4		7.2		9.9		8.4		0
5	1	83.3		3.4		7		8		11.5		15.6		13.4		0

4. Discussion

Our study is the first extensive analysis of apparent firing rate instabilities in a human intracortical neural interface system. As one of the advantages of intracortical recording systems is the ability to harness the information transmitted via modulation in action potential firing rates, characterizing the instabilities is a first step toward reducing them or accounting for them through advances in neural engineering and/or computational approaches.

We showed that firing rate instabilities, if unmodeled, can lead to a directional bias in the decoded kinematic variables and thus to degraded performance. Recording instabilities and subsequent spike detection errors accounted for 15% of the firing rate variability while the majority of rate changes (85%) originated from intrinsic variations in spike generation which may be attributed to actual physiological changes such as task related modulation, attentional changes or plasticity. Whatever the cause, the prevalence of these effects demonstrates that mitigating the contribution of both technical and intrinsic factors is important for optimal system performance and reliability - a key requirement for successful and long-term neuronal ensemble control of assistive devices.

The relatively small contribution of recording instability to neuroprosthetic performance on a short duration (hours) confirms Chestek et al. (2011) who also found variability in amplitude and spike rates on short time scales in monkeys, even though did not see substantial changes in performance due to these fluctuations. However, this level of stability presumably does not generalize over a longer time scale (from days to years), where maintaining a consistent ensemble of neurons appears to remain a challenge. From day to day, neural waveforms change (Dickey et al., 2009), over months electrode impedance can decrease (Parker et al., 2011, Simeral et al., 2011b), amplitudes steadily decline (Chestek et al., 2011) and the number of detected action potentials change, leading to real or apparent spike rate decrease (Chestek et al., 2011, Parker et al., 2011, Suner et al., 2005). Although we have recently demonstrated that an intracortical array can provide useful signals for more than five years (Hochberg et al., 2012), both basic neuroscience and neuroprosthetics will benefit from improvements in recording systems toward providing more consistent and high quality recordings.

Spike amplitude instabilities might originate from a relative motion of the electrode to the recorded neuron by distances < 50 μm (Gold et al., 2006) or due to larger movements and a shifting population of neurons (Suner et al., 2005). Electrode/tissue movements caused by vascular pulsations or changes in global intracerebral pressure linked to ventilation are unlikely explanations of the observed amplitude changes due to the short (∼sec) time course of these repeated physiologic events. Fast head movements or acceleration-induced shifts (Santhanam et al., 2007) could also be excluded since, due to tetraplegia, the participants had no or small and comparatively low angular velocity head movements. Coughing or sneezing could change intracranial pressure and possibly induce array micromotion. While we investigated examples of synchronous amplitude shifts as indicators of array movement, more than half of the sessions showed no sign of coordinated spike amplitude changes, thus the instabilities might reflect local changes in tissue geometry driven by changes in local vessel diameter or by other unknown mechanisms.

Spike amplitude changes might partially originate from intrinsic cellular mechanisms. Bursting related amplitude decrease due to prolonged Na+ channel inactivation (Harris et al., 2001) operates on a short (∼20 seconds) timescale and therefore fails to explain our observed amplitude changes on the time course of minutes to hours. However, changes of afferent activity affecting intrinsic membrane properties might operate on a similar time scale. Physiological states such as sleep/wake cycles (Jackson and Fetz, 2007) or activity dependent attenuations driven by experience can also influence spike amplitude (Quirk et al., 2001).

The majority of the observed rate changes (85%) lacked an immediately apparent technology-related explanation, suggesting a possible biological origin. Part of these changes could be related to changes in experimental task differentially modulating the neural population. However, we observed significant changes in firing rate between epochs of similar instructions, indicating mechanisms that are not directly related to the task. Indeed, the functional connection between M1 neuronal activity and muscle activity, as measured by spike-triggered averaging can show dramatic variability (Rokni et al., 2007, Davidson et al., 2007), and the correlation between firing rate and decoded movement parameters might change with context (Carmena et al., 2005, Jarosiewicz et al., 2008). Cortical waves (Rubino et al, 2006), circadian rhythms (Barnes et al., 1977), and cognitive (such as motivation or attention) or behavioral changes could also strongly influence population activity. Considering that the brain is a complex dynamic system, stationarity would, in fact, be unexpected.

Neuroprosthetic feedback and decoding error might also induce a shift in population activity. For instance, we occasionally observed in neural cursor control that directional bias introduced a compensation strategy by the participant. The underlying shift in population activity might thus be similar to network changes associated with adaptation to an external force field (Li et al., 2001). Adaptation to the decoder could ‘confuse’ the user when using a newly calibrated decoder, thus we might expect to see alternating or decaying session-to-session performance. Instead, participant S3 demonstrated a consistently high performance using a newly calibrated decoder on five consecutive days (Simeral et al., 2011a) – (Fig. 1). Signal instability and the subsequent perturbation in the mapping between motor intention and the executed movement might also introduce compensatory mechanisms that could lead to escalating endpoint errors (Mazzoni and Krakauer, 2006, Taylor and Ivry, 2011). Such a counter-productive error driven adaptive process would manifest in a systematic decay in cursor control within a session, however we found no evidence for such decay (Table 2). In summary, developing a new control strategy might require multi-day training (see Ganguly 2009) rather than a single session.

A possible strategy to improve robustness of neuroprosthetic control might be to minimize signal changes. Improvements in electrode arrays and/or recording technologies (i.e., engineering modifications) may result in the recording of large amplitude spikes consistently over extended periods of time (preferably measured in decades). Increasing the number of electrodes and recorded units would reduce the relative impact of individual instabilities (Carmena et al, 2005). For instance, doubling the number of units in our closed loop simulation diminished bias magnitude and made cursor trajectories smoother by averaging out stochastic neural responses. Furthermore, a different spike detection strategy, such as adaptive spike sorting (Watkins et al., 2004, Linderman et al., 2006) or signal amplitude thresholding alone (Chestek et al., 2011, Fraser et al., 2009, Hochberg et al., 2012) as opposed to thresholding combined with window discriminators could make the decoder less vulnerable to amplitude instabilities (Chestek et al., 2011, Gilja et al., 2011). The feature extraction algorithm could also use complementary signals such as multiunit activity, local field potentials, or surface field potentials that might be more stable over time (Andersen et al., 2004, Bradberry et al., 2010, Stark and Abeles, 2007, Slutzky et al., 2011, Flint et al., 2012a, Flint et al., 2012b).

If neural recordings are relatively stable, the decoding parameters can be optimized by repeated calibration or with an adaptive decoder, and then subsequently fixed using the same units and decoding parameters. Thus signal variability may be compensated for by the user when using a static decoder (Flint et al., 2012c, Gilja et al., 2012, Nuyujukian et al., 2012). This way, learning can take part in consolidating cortical dynamics, leading to a potentially more stable representation and neuroprosthetic performance (Ganguly and Carmena, 2009).

Even if signal variability cannot be fully eliminated, decoding approaches might be able to compensate for its effect. First, the decoding algorithm could identify stable units and use these exclusively for realtime control of the device (Dickey et al., 2009, Wahnoun et al., 2004). Second, an adaptive decoder could monitor changes in the statistical properties of the input signal or environmental noise and adjust the decoding parameters accordingly (Homer et al., 2011, Wu and Hatsopoulos, 2008). Third, recalibration of the model parameters during (Jarosiewicz et al., 2012) and between use could not only compensate for nonstationarities, but further improve the mapping between neural activity and motor parameters. Finally, as this mapping might be task specific, context dependent or inherently variant over time, an improved decoder might operate by switching between several distinct mappings. Thus modeling the observed (Truccolo et al., 2005, Wu and Hatsopoulos, 2008) or hidden sources of variability (Stevenson et al., 2010, Lawhern et al., 2010, Wood et al., 2005, Kulkarni and Paninski, 2007) could provide further improvement in decoding performance.