Estimation of ligand efficacies of metabotropic glutamate receptors from conformational forces obtained from molecular dynamics simulations

Abstract

Group 1 metabotropic glutamate receptors (mGluR) are G-protein coupled receptors with a large bilobate extracellular ligand binding region (LBR) that resembles a Venus fly trap. Closing of this LBR in the presence of a ligand is associated with the activation of the receptor. From conformational sampling of the LBR-ligand complexes using all-atom molecular dynamics (MD) simulations, we characterized the conformational minima related to the hinge like motion associated with the LBR closing/opening in the presence of known agonists and antagonists. By applying a harmonic restraint on the LBR, we also determined the conformational forces generated by the different ligands. The change in the location of the minima and the conformational forces were used to quantify the efficacies of the ligands. This analysis shows that efficacies can be estimated from the forces of a single conformation of the receptor, indicating the potential of MD simulations as an efficient and useful technique to quantify efficacies thereby facilitating the rational design of mGluR agonists and antagonists.

INTRODUCTION

Neuronal excitation in a variety of synapses across the central nervous system is triggered by glutamate.¹ Glutamate receptors are known to play key physiological roles in long-term potentiation, neuronal plasticity, learning, and memory.^{2, 3} They can also mediate pathophysiological responses in the presence of elevated levels of excitatory amino acids, and have been implicated in neuronal cell death associated with both acute neurodegenerative disorders such as stroke and brain trauma ^{4, 5} and chronic neurodegenerative disorders including Alzheimer disease⁶ and Parkinson disease.⁷ Glutamate receptors can be classified into ionotropic glutamate receptors (iGluR) and metabotropic glutamate receptors (mGluR).^{1, 8}

Metabotropic glutamate receptors (mGluR) are family 3 G-protein coupled receptors (GPCRs) that include 8 sub-types, which have been classified into 3 subgroups based on structure and sequence similarity and common ligand selectivity. ⁸ Members of the group 1 mGluR (mGluR1 and mGluR5) are known to modulate neuronal cell death ⁹ and appear to play important roles in response to traumatic brain injury (TBI). TBI causes neuroinflammation associated with the activation of microglia,¹⁰ which contributes to neuronal cell death and irreversible tissue damage. Inflammation after TBI is markedly inhibited by activation of mGluR5 receptors in microglia .¹¹ Although mGluR1 and mGluR5 share high structural and sequence similarity,² they seem to play remarkably different roles in neuronal cell injury.⁹ Activation of mGluR5 inhibits caspase-dependent neuronal apoptosis in cell culture models and provides neuroprotection in limited animal studies.¹² Activation of mGluR1 by selective agonists exacerbates necrotic cell death while selective antagonists are neuroprotective in vitro and in vivo. ¹³

Because of their modulating properties, the mGluR family are considered therapeutic targets. ^{14, 15} Apart from the potential treatment for TBI, activation of mGluR5 has multi-potential neuroprotective actions on inflammation and apoptosis and mechanisms implicated in neurotrauma. Hence, there has been a significant effort to develop selective agonists that have good central activity. Simultaneously, drug design efforts are also directed towards selective antagonists for the mGluR1.

Structurally, the sub-group 1 mGluRs consist of a large extracellular dimeric, bi-lobed ligand binding region (LBR).^{2, 3} The LBR attaches to the seven-transmembrane region through a cysteine-rich-region. The two lobes in the LBR are separated by a large cleft where glutamate binds (Figure 1). Akin to the Venus Fly Trap Module (VFTM) of the mGlu8 receptor, ¹⁶ activation of the receptor is associated with the closing of the LBR to trap the ligand. Interestingly, the glutamate binding region across all eight mGluR sub-type structures^{2, 17–19} reveal a common binding motif for the α-amino and α-carboxylate groups of glutamate.^{14, 20} Thus, competitive agonists of the mGluRs are α-amino acids with various functional groups on the distal end (typically acidic). However, such amino acid analogs typically have poor permeability through the blood brain barrier (BBB) associated with their high polarity, which limits the applicability of such ligands as drug candidates. ¹⁴

Figure 1.

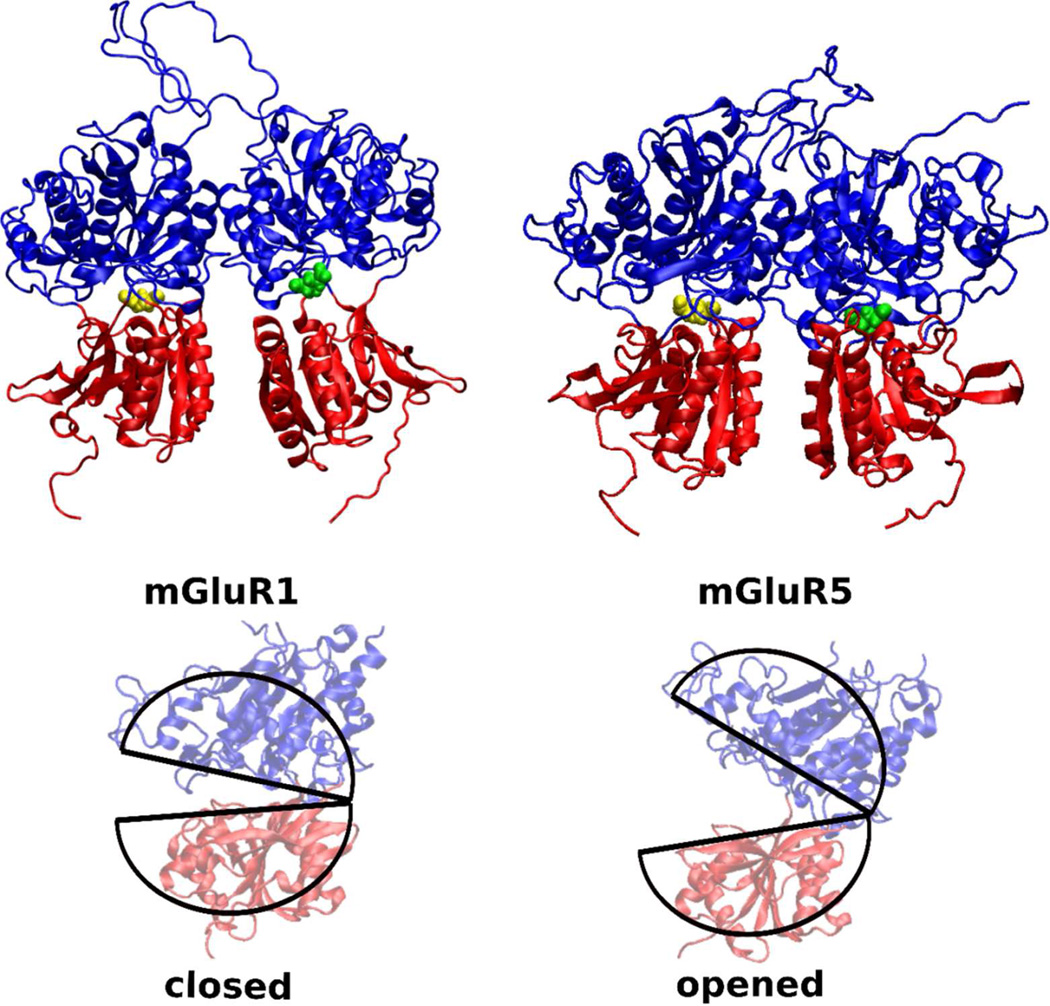
The mGluR1 (PDB:1EWK) and mGluR5 (PDB:3LMK) bi-lobate structures have a strong structural similarity. The glutamate binding region is well preserved across both mGluR1 and mGluR5. Glutamate in the LBR pockets are colored in yellow and green. In mGluR1, LBR with the yellow colored glutamate represents the closed state, while the LBR with the green colored glutamate represents the open state. Both the LBRs of the mGluR5 are in the closed state. Difference in opened and closed conformatiosn of an LBR is highlighted with pie-shaped cartoon traces in the lower panel.

Over the last few years, significant efforts have been directed towards developing novel, potent and selective agonists and antagonists that, while retaining the amino-acid character to bind to the LBR, overcome the problems highlighted above. Towards this direction, a predictive methodology to quantify efficacies quickly would be of great utility. The LBR of the mGluR1 and mGluR5² is thought to participate in a similar open-close mechanism as the VTFM of the mGluR8 based on single conformation crystal structures of mGluR1-glutamate complexes. In this model, ligand efficacies are directly correlated with the amount of cleft closure induced by the bound ligand.^21–23

To understand the VFTM open-close mechanism, in the present study we apply all-atom explicit water molecular dynamics (MD) simulations to investigate the conformational transitions of a closed state dimeric LBR in the presence of both agonists and antagonists for both mGluR1 and mGluR5. Free energy surfaces that represent the conformational sampling of the LBR-ligand complexes support the correlation between the extent of LBR opening and the receptor activation. In addition, we show receptor activation can also be predicted using a computationally economic approach based on a single MD simulation of LBR-ligand complexes with the LBR in the closed state.

METHODS

All simulations were performed using the CHARMM ^{24, NAMD 25} or GROMACS ²⁶ molecular simulations programs, the CHARMM22 protein force field ²⁷ with CMAP backbone correction²⁸ for the proteins, the CHARMM general force field ²⁹ for ligands and the TIP3P water model. ³⁰

PROTEIN PREPARATION

mGluR1: The following residues were missing in both the monomers of the crystal structure (PDB:1EWK) : 33–35 (N terminus), 125–153, and 513–522 (C terminus). We built these residues as loops using MODELLER.³¹ 100 models were generated and ranked using a Discrete Optimized Protein Energy (DOPE) method. ³² The highest ranking model was used as a starting structure. When modeling residues 125–153, we retained the inter-monomer disulphide bridge between C140 ² of each monomer. We also retained the intra-monomer disulphide bridges across residues: 67–109, 289–291, 378–394 and 432–439. Using inputs generated by the CHARMM-GUI ³³, hydrogen atoms were then added (protonation state of the residues are set to reflect a neutral pH); the structure solvated in a box of water of size 125×136X100 A³ and sodium ions were added to neutralize this system.

mGluR5: The following residues were missing in both monomers of the crystal structure (PDB:3LMK) : 14–24 (N terminus), 116–140, 370–377, and 496–505 (c-terminus). We followed the same procedure as with mGluR1, where we built the missing residues as loops using MODELLER.³¹ 100 models were generated and ranked using the DOPE method³² and the highest ranking model was used as the starting structure. When modeling residues 116–140, we retained the inter-monomer disulphide bridge between C129 of each monomer. We also retained the intra-monomer disulphide bridges across residues: 57–99, 276–278, 365–381 and 419–426. Hydrogen atoms were then added (protonation state of the residues are set to reflect a neutral pH); the structure solvated in a box of water of size 125×136X100 A³ and sodium ions were added to neutralize this system.

For both mGluR1 and mGluR5, the solvated LBR+glutamate dimers were minimized for 5000 steps with steepest descent algorithm³⁴ and another 5000 steps of conjugate gradient algorithm³⁵ in the presence of periodic boundary conditions.³⁶ The systems were then heated to 300K at the rate of 5K/ps by periodic reassignment of velocities.³⁷ Following this, the system was equilibrated for 200 ps using velocity reassignment. Through all these steps, a harmonic restraint with a force constant of 2 kcal/mol Ų was applied on the protein backbone atoms. The leap frog version of the Verlet integrator³⁶ with a time step of 1 fs was used for heating and equilibration. Water geometries and bonds involving hydrogen atoms were constrained using the SHAKE algorithm.³⁸ Long range electrostatic interactions were handled with the particle-mesh Ewald method³⁹ with a real space cutoff of 10 Å, a switching function⁴⁰ was applied to the Lennard-Jones interactions at 12 Å, and a long-range isotropic correction³⁶ was applied to the pressure for Lennard-Jones interactions beyond 12 Å cutoff length.

LIGAND PREPARATION

All ligands were initially constructed based on the internal coordinates in CGenFF and assigned physiologically pertinent protonation states consistent with neutral pH. Ligand -NH₃⁽⁺⁾ and −COO⁽⁻⁾ atoms were assigned the same partial charges as that of the glutamate ligand. CGenFF parameters for selected ligands were validated targeting QM vibrational spectra, a dihedral potential energy scan and intramolecular geometries⁴¹ (see Validation of Ligand parameters section in the Supporting Information). It may be noted that CGenFF parameters are assigned based on analogy between the atoms of the ligands and previously optimized parameters of similar atom types.^{42, 43} The accuracy of the prediction is scored with a penalty number. These penalty scores for all the parameters of all the ligands used in the study were low (less than 10) indicating the analogy is satisfactory, requiring little or no further optimization. This was expected as the functionalities in the studied ligands are common to amino acids as well as drug-like molecules and therefore well represented in CGenFF.

The ligands were modeled into the equilibrated LBR such that the α-carbon, COO⁽⁻⁾ and the NH₃⁽⁺⁾ atoms of the ligand superposed with the glutamate ligand in the equilibrated LBR of the pocket. After removing the glutamate, the LBR-ligand complexes were then equilibrated for 200 ps using velocity reassignment to maintain a temperature of 300K. All aspects of the simulation protocol described during the protein preparation were maintained. During this step, we retained the harmonic restraints on the protein backbone atoms.

It may be noted that while both the LBRs of mGluR5 (PDB: 3LMK) are closed, one of the LBRs (chain B in PDB: 1EWK) represents the open state in mGluR1. All of our analyses for mGluR1 are from the LBR that is closed (chain A), although we retain the second LBR and the ligand in its pocket to account for the inter-LBR interactions.

CONFORMATIONAL SAMPLING OF THE LBR-LIGAND COMPLEXES

Following equilibration in the presence of the ligands, the positional restraints on the protein backbone atoms were removed. Each of the dimeric protein-ligand systems were simulated for 32 ns (except for the protein with the ligand 1-aminocyclopentane-1,3,4-tricarboxylic acid, ACPT-II, that was simulated for 64 ns) with a time step of 2 fs, at 300K and 1 atm pressure with a Nose-Hoover thermostat^{44, 45}, and the Langevin piston barostat. ⁴⁶ This final production part of the simulation was run using the NAMD molecular dynamics program. From the conformational sampling of the LBR-ligand complexes through the production runs, after discarding the first 2 ns of the simulation data, we retrieved the inter-lobe α-carbon-pair distances (K409-G293 & S186-D318 for the mGluR1 and K396-G280 & S173-D305 for the mGluR5) every 10 ps. An approximate free energy surface representing the conformational sampling during the simulation was constructed from the two-dimensional histograms of the probabilities of these two reaction coordinates. The statistics from the simulations were collected in the 0.1 Å bins. This approximate free energy surface at every grid point (n) is given by

$$F(n)=-k_{B}Tln(N_n)-{\mathrm{F}}_{\mathrm{o}}$$ (1)

where kB is the Boltzmann constant, T is the temperature (300K), N_n is the number of times the grid point is visited during the length of the simulation and F_o is an arbitrary constant. Over 18 dimeric LBR-ligand systems were studied with a cumulative simulation time of 608 ns. A single 32 ns MD of the dimeric mGluR-ligand system took nearly 10 days on 128 2.4 GHz AMD Magny-Cours processors.

CONFORMATIONAL FORCES

For each of the equilibrated dimeric closed state LBR-ligand complexes, positional restraints on all of the backbone atoms were removed, except for 2 pairs of α-carbons across the upper and lower lobes in each of the LBR. With the harmonic restraints on, each of the dimeric protein-ligand systems were simulated for 12 ns with a 2 fs time step, at 300K and 1 atm pressure with a Nose-Hoover thermostat ^4, , and the Parrinello-Rahman barosta.t This production part of the simulation was run using the GROMACS molecular dynamics program. During the simulation, the 8 α-carbon atoms fluctuate around the center ${\overrightarrow{r}}_0$ of the harmonic potential. Denoting its deviation from ${\overrightarrow{r}}_0$by $\delta {\overrightarrow{r}}_0$, the i -th (i =1,2 or 3) Cartesian component of the force f_i. on the atom at ${\overrightarrow{r}}_0$ is ^{49, 50}

$$f_i\cong \frac{k_{B}T}{\text{var}(\delta r_i)}\langle \delta r_i\rangle +{\sum }_{j\ne i}{F}_{ij}\langle \delta r_j\rangle \text{,}{F}_{ij}\cong -K_{B}T\frac{\text{cov}(\delta r_i,\delta r_j)}{\text{var}(\delta r_i)\text{var}(\delta r_j)}$$ (2)

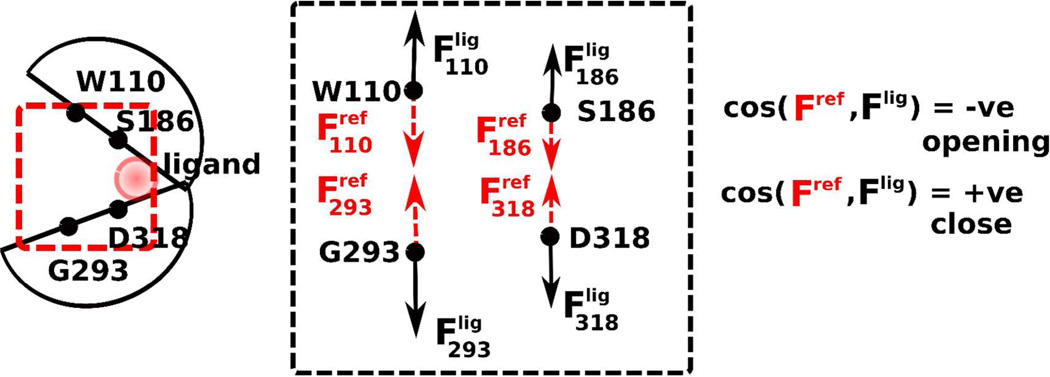
where 〈.〉 denotes the ensemble average over the simulation time, var() and cov() are respectively variance and covariance, and F_ij is the second-order partial derivative of the free energy in the i - and j - directions. As shown in Figure 2, cosine of the force vector $\overrightarrow{f}$ of each of the constrained atoms with the reference vector ${\overrightarrow{f}}^{\text{ref}}$ reveals the direction of the conformational bias.

Figure 2.

Cartoon of the LBR. Forces on the four harmonically constrained pocket atoms reveal the “direction” of the conformational transition. The LBR is likely to open up in the presence of a ligand (and hence deactivate) when the upper- and lower- lobe force vectors point outward, in opposite directions away from the pocket. Similarly, all inward pointing force vectors indicate that pocket is closing. Variable directions of the vector indicate a lack of conformational change in the binding pocket.

The dimeric LBR-glutamate and empty LBR systems, were simulated for 22 ns. Force vectors converged within 12 ns. Hence, all other LBR-ligand systems were simulated over 12 ns. After discarding the first 1 ns of simulation data, coordinates of the harmonically constrained α-carbons were recorded over 10 ps intervals and the forces calculated using Eqn. 2 Over 18 mGluR-ligand systems were studied with a cumulative simulation time of 216 ns. A single 12 ns MD of the dimeric system took approximately 3.7 days on 128 2.4 GHz AMD Magny-Cours processors.

LIGANDS

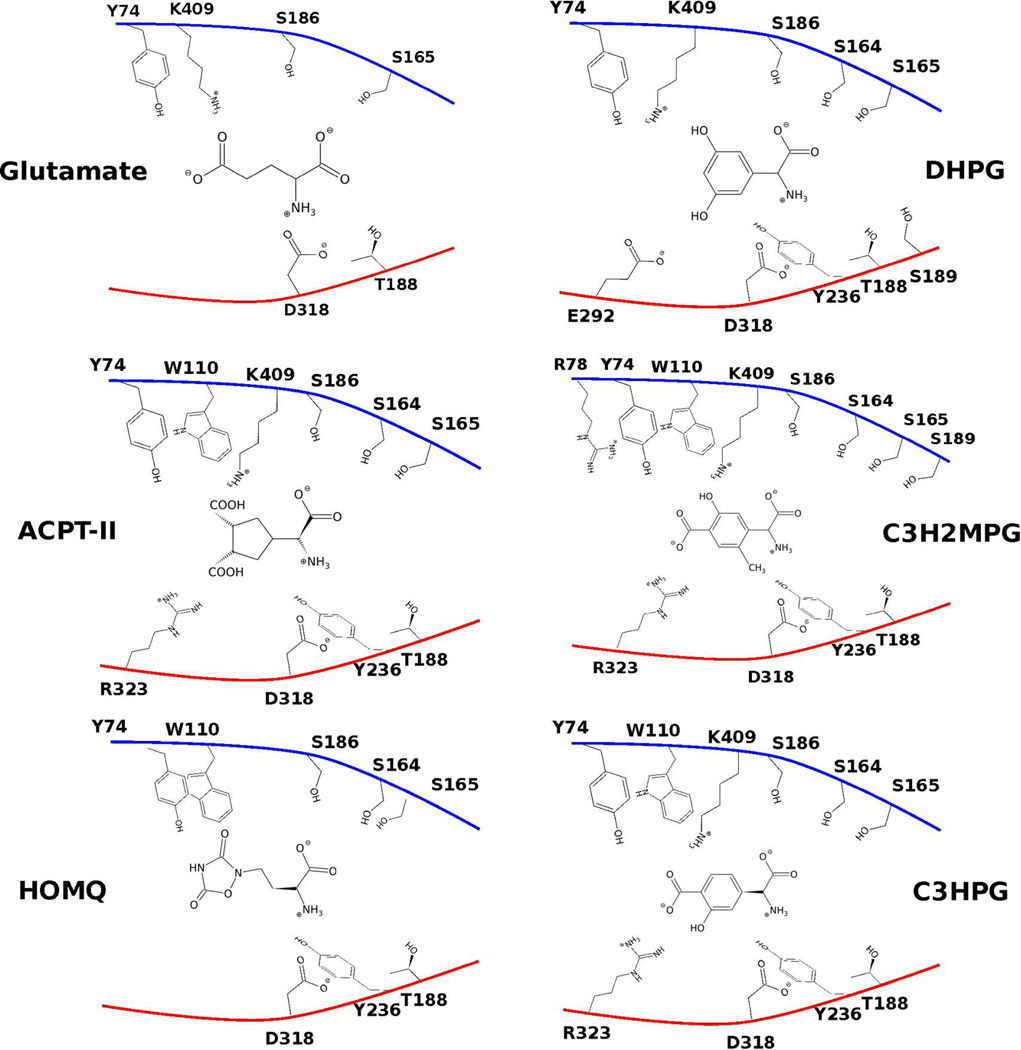
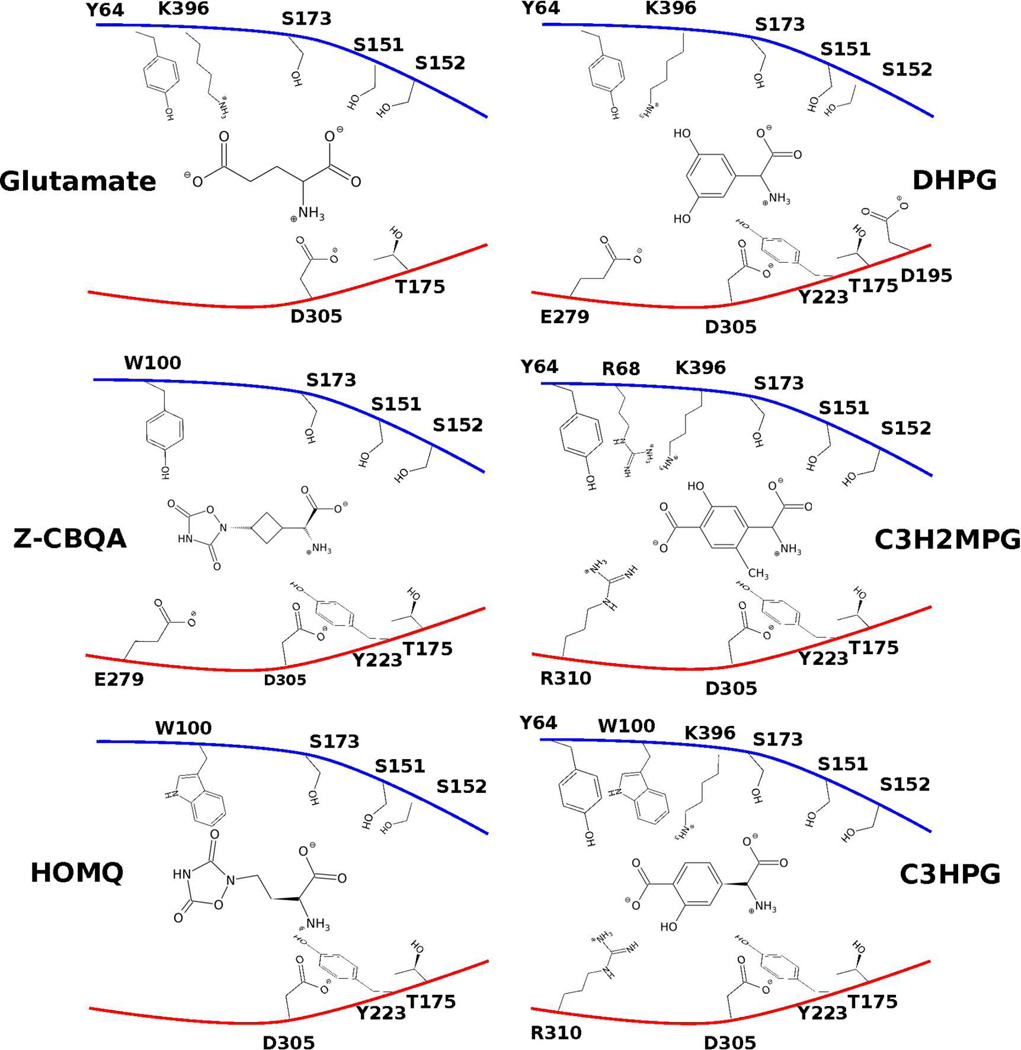
Simulations were performed on the following known agonists and antagonists of mGluR1 and mGluR5. Images of the ligands in the mGluR1 and the mGluR5 pockets are shown in Figure 3 & Figure 4.

Figure 3.

Cartoon of potential contacts between the pocket residues of a closed LBR of the mGluR1 and the ligands considered. Upper and lower lobes are colored blue and red, respectively. Open pocket conformations (2) of C3H2MPG and C3HPG are shown.

Figure 4.

Cartoon of the potential contacts between the pocket residues of a closed LBR of the mGluR5 and the ligands considered. Upper and lower lobes are colored blue and red respectively. Open pocket conformations (2) of C3H2MPG and C3HPG are shown.

DIHYDROXYPHENYLGLYCINE (DHPG)

(S)-3,5-DHPG is one of the early known agonists for the sub-group 1 mGluR with a relatively high potency (EC₅₀ 6.6 µM ).^{8, 14} Further, pharmacological studies revealed that GluRs activated by DHPG are likely to have minimal effects on the cAMP-mGluR second messenger systems. ⁵¹ With its high potency and selectivity to mGluR1 and mGluR5, DHPG was an ideal agonist to test the pocket-closing capability of a ligand.

Z-1-AMINO-3-[2’-(3’,5’-DIOXO-1’,2’,4’-OXADIAZOLIDINYL-CYCLOBUTANE-1-CARBOXYLIC ACID (Z-CBQA)

Quisqualic acid has been recognized as one of the most potent and selective agonists for the group 1 mGluR.⁵² Z-CBQA, while retaining the potency, also had a strong selectivity for mGluR5 (EC₅₀ 11 µM) over mGluR1 (EC₅₀ > 1000 µM) ¹⁴, which is an attractive feature of drug candidates for neurogenerative disorders like TBI. Because of this, there has been a strong interest to develop conformationally constrained analogs of Z-CBQA. ⁵² Thus it would be informative to explore the conformational landscape and the range of contacts Z-CBQA makes with the pocket residues of mGluR5.

(1R,3R,4S)-1-AMINOCYCLOPENTANE-1,3,4-TRICARBOXYLIC ACID (ACPT-II)

This is one of the first specific antagonist for mGluR1 (IC₅₀ 115 µM)¹⁴ and is devoid of activity at the ionotropic glutamate receptors. Hence, there is interest in developing analogs of ACPT-II and to study the properties of the glutamatergic transmission in the total absence of mGluR activation.⁵³

(S)-2-METHYL-4-CARBOXYPHENYLGLYCINE (C3H2MPG)

This is one of the first selective antagonist of mGluR1 with a relatively high potency (IC₅₀ 8.8 µM of mGluR1 vs. > 300 µM for mGluR5).^{14,54, 55} This compound was selected to delineate the range of contacts with the mGluR1 pocket and explore the possibility of ligand selectivity between mGluR1 and mGluR5.

(S)-HOMOQUISQUALIC ACID (HOMQ)

This homologue to (S)- quisqualic acid has been shown to stimulate phosphatidylinositol (PI) hydrolysis in rat brain cortex and rat hippocampus that are mediated by mGluR5 and not by mGluR1.⁵⁶ Thus, it displayed competitive antagonism at mGlu1 (K_B 184 µM) and full agonism at mGlu5 (EC₅₀ 36 µM). Because of this selectivity between mGluR1 and mGluR5, there was an interest to explore the conformational properties of the two receptors in the presence of HOMQ. However, our results below show that the LBRs of both mGluR1 and mGluR5 open up (deactivating the receptor) in the presence of HOMQ. Hence, selectivity must stem from a region outside of the LBR.

(S)-4-CARBOXY-3-HYDROXYPHENYLGLYCINE(C3HPG)

This is another ligand that functions as a weak agonist of mGluR5 and a competitive antagonist of mGluR1 (IC₅₀ 0.3 µM).⁵⁷ Thus, like HOMQ, this compound was chosen to test for effect of this ligand on the conformational properties of the two receptors.

RESULTS

EFFICACIES FROM CONFORMATIONAL SAMPLING OF LBR-LIGAND COMPLEXES

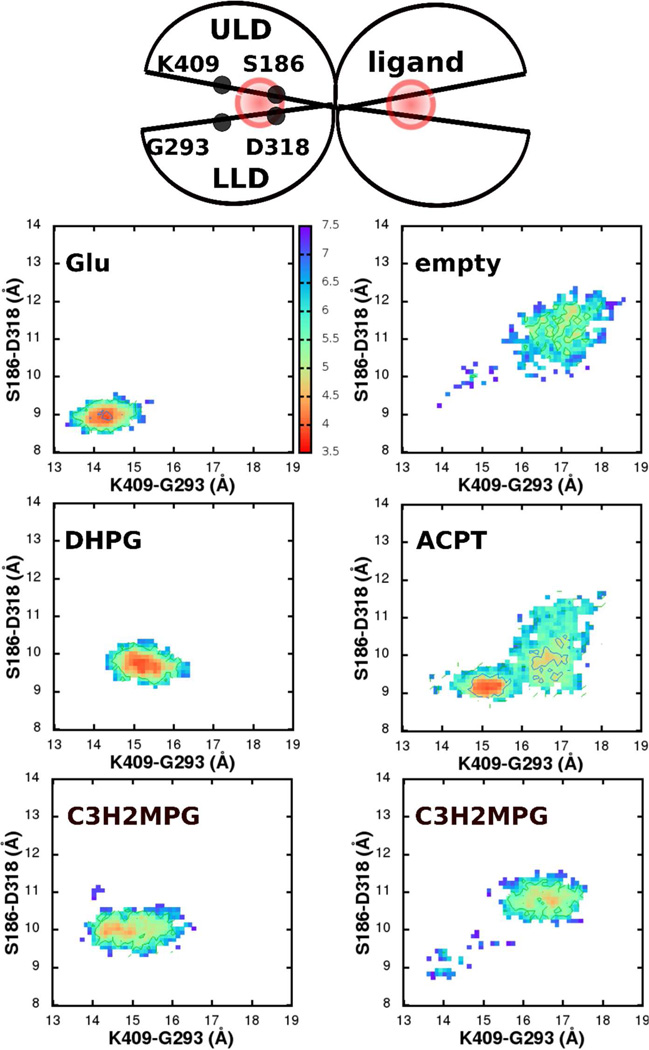
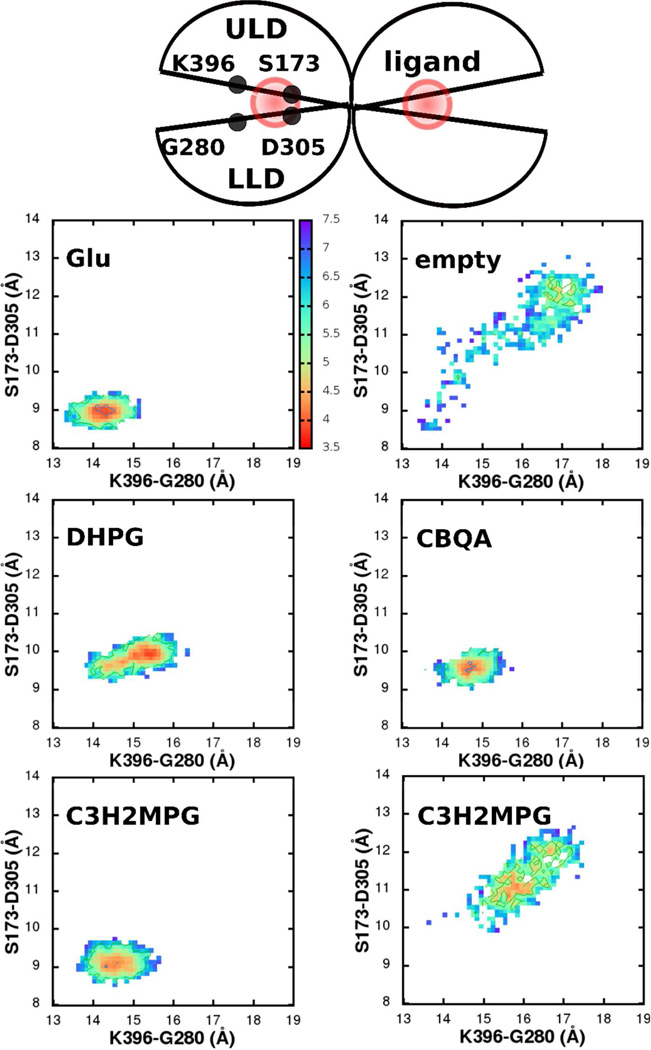
With the closed state LBR-ligand complex as a starting conformation, explicit water unconstrained MD simulations (referred to as “MD” in this section) were performed for a period of 32 ns with each of the ligands in both the mGluR1 and the mGluR5 receptors. Distances across two inter-lobe α-carbon-pairs: S186-D318 & K409-G293 in the mGluR1 and S173-D305 & K396-G280 in the mGluR5 were used as reaction coordinates to extract conformational information from the MD, which is presented as free energies below. Residues S186 and D318 (and the equivalent S175 and D305 in mGluR5) lie in the upper and lower lobes of the LBR, respectively, and interact with the -NH₃⁽⁺⁾ of the ligand. They are close to the inner pocket and the hinge of the LBR, and hence the distance between their α-carbons reveals the inner pocket conformational transitions. Residues K409 and G293 (and the equivalent K396 and G280 in mGluR5) also lie in the upper- and the lower-lobes respectively, but are further outwards from the hinge of the LBR. Distances between these α-carbons hence reveal the outer pocket conformational transitions.

In the dimeric mGluR1 LBR crystal structure (PDB: 1EWK), one of the LBRs (chain A) represents the closed, active conformation, where the α-carbon distances across the S186-D318 and K409-G293 are 9.3 Å and 14.5 Å, respectively. These distances are 11.9 Å and 18.1 Å in the second LBR that represents the open, inactive conformation. MD of the mGluR1 dimer with glutamates in the pockets (Figure 5, upper left) revealed that the closed state LBR retained its closed conformation throughout the length of the simulation (RMSD of the backbone atoms excluding the terminal loops and residues D125-K153 ∼1.2 Å; Supporting Information, Fig. S5), and the second open LBR fluctuated between an open and partially closed conformations. In the least open conformation of the second LBR, S186-D318 and K409-G293 were 10.5 Å and 16.3 Å, respectively. The closed conformation LBR was stabilized by strong interactions between the glutamate and several residues of the pocket.² Among these, the -NH₃⁽⁺⁾ of the glutamate maintained hydrogen bonds with the inner-pocket residues: D318 and T188 in the lower lobe and the S186 in the upper-lobe. Further, -COO⁽⁻⁾ of the glutamate also interacted with S165 of the upper-lobe throughout the simulation. The outer-pocket was kept closed by hydrogen bonds between the Cδ carboxylate and Y74, K409 of the upper lobe (Figure 3).kcal/mol. Glutamate (upper left), DHPG (middle left) and conformation (1) of C3H2MPG keep the LBR closed and active, while ACPT-II (middle right) and conformation (2) of C3H2MPG (lower right) deactivate the pocket, by driving the conformational minimum to be similar to an empty, open pocket (upper right). For fraction of time spent in the closed in the open states, see SI, Table S5.

Figure 5.

Conformational sampling of the mGluR1 in the presence of ligands represented using free energy surfaces. Distances across two pairs of inter-lobe Cα atoms(S186-D318 and K409-G293) are reaction coordinates for the free energies that are measured in k_BT; where 1 k_BT∼0.59

In contrast, in an MD of the mGluR1 dimer, where the glutamates were removed (empty pocket, Figure 5 upper right), the closed LBR opened up such that the S186-D318 and K409-G293 α-carbon distances increased to 9.6 Å and 14.7 Å, respectively, within the first 6 ns of the simulation. The LBR then stayed open throughout the rest of the simulation, with distances of about 11.3 Å and 17.2 Å, respectively, indicating a preference for an open conformation. In this MD, the second open LBR continued to remain open through the length of the simulation. In the free energy surfaces of the first LBR, there is evidence of some sampling of partially closed states. These are located along the diagonal leading to the low energy open conformation implying that opening involves a hinge like motion where both the outer and inner pocket regions open up proportionally.

Along with the hinge-like motion between the upper and the lower lobes, there also exists inter-LBR motion characterized by a 5° shift in the relative orientation of the helices F across the two LBRs in the mGluR1-glutamate MD. This shift increased to ∼12° with the hinge-like motion of the empty pocket LBR. An inter-LBR twist has previously been observed with the iGluR ^{21, 58} and other sub-families of the mGluRs.^59–61

In the dimeric mGluR5 crystal structure (PDB: 3LMK), unlike mGluR1, both the LBRs are in a closed state. Akin to mGluR1, MD of the mGluR5 dimer in the presence of glutamates in the binding pocket retained both the LBRs in a closed conformation (Figure 6, upper left). This closed conformation was stabilized by the same set of contacts between the glutamate and the protein that were observed in mGluR1 (Figure 4: inner pocket: -COO⁽⁻⁾ & -NH₃⁽⁺⁾ of the glutamate with S151, S152, S173, T175 & D305; outer pocket: the Cδ carboxylate and Y64, K396). Also, in the absence of a glutamate, one of the LBRs opened up, characterized by an increase in the S173-D305 & K396-G280 distances to 12.3 Å and 17.1 Å, respectively. We define this as the open, inactive conformation of mGluR5. Also, as with mGluR1, along with the hinge-like motion, the relative orientation of the helices F across the two empty LBRs increased to ∼15°, from around ∼7° in the mGluR5-glutatmate complex. While we use the dimeric LBR system to retain the inter-LBR communication, since the aim of this work is to quantify the effect of a ligand on the conformational opening/closing of an LBR, we do not further discuss the inter-LBR conformational changes, but refer to these earlier studies that discuss this in more detail.^{58, 59, 61} kcal/mol. Glutamate (upper left), DHPG (middle left), Z-CBQA (middle right) and conformation (1) of C3H2MPG keeps the LBR closed and active, while conformation (2) of C3H2MPG (lower right) deactivates the pocket, by driving the conformational minimum to be similar to an empty, open pocket (upper right). For fraction of time spent in the closed in the open states, see SI, Table S6.

Figure 6.

Conformational sampling of the mGluR5 in the presence of ligands represented using free energy surfaces. Distances across two pairs of inter-lobe Cα atoms(S173-D305 and K396-G280) are reaction coordinates for the free energies that are measured in k_BT; 1 k_BT∼0.59

The ideal model system for mGluR ligand optimization would allow for quantitative estimates of ligand efficacy. The results presented above show that without a ligand in the pocket, the LBR prefers an open conformation and an agonist is needed to shift the conformational minimum of the LBR to a closed state. The efficacy of a ligand (Efflig) can then be quantified by measuring the extent of the shift in the conformational minima using equation 3,

$${\text{Eff}}_{\text{lig}}=\left(\frac{{\mathrm{d}}_{\text{emp}}^{\circ }-{\mathrm{d}}_{\text{lig}}^{\circ }}{{\mathrm{d}}_{\text{emp}}^{\circ }-{\mathrm{d}}_{\text{glu}}^{\circ }}\right).\left(\frac{{\mathrm{d}}_{\text{emp}}^{\mathrm{i}}-{\mathrm{d}}_{\text{glu}}^{\mathrm{i}}}{{\mathrm{d}}_{\text{emp}}^{\mathrm{i}}-{\mathrm{d}}_{\text{glu}}^{\mathrm{i}}}\right)$$ (3)

where, d° and dⁱ are the outer and inner pocket distances at the conformational minimum on the free energy surface. Hence, d° is the distance between the α-carbons of K409-G293 in mGluR1 and K396-G280 in mGluR5; dⁱ is distance between the α-carbons of S186-D318 in mGluR1 and S173-D305 in mGluR5. Using this approach, efficacy is 1 for the LBR-glutamate complex (d^x_glu), and 0 for an empty pocket LBR (d^x_emp). Table 1 summarizes the calculated efficacies for the different ligands we considered.

Table 1.

Ligand efficacy scores, Eff_lig, calculated from free energy surfaces that represent the conformational sampling of mGluR1 and mGluR5 with various ligands (Figure 5, Figure 6 & Figure 7) using Eqn 3

Ligand	Efficacy
	mGluR1	mGluR5
Agonists
Glu	1	1
DHPG	0.51	0.46
Z-CBQA		0.61
Antagonists
ACPT-II	0.11	-
C3H2MPG(1)	0.59	0.92
C3H2MPG(2)	0.05	0.16
HOMQ	0.30	0.13
C3HPG(1)	1	0.7
C3HPG(2)	0.25	0.01

Two agonists in addition to glutamate were studied. DHPG, one of the early known and highly potent agonist (EC₅₀ 6.6 µM) ^{8, 14} scored with a moderate efficacy of 0.51 for mGluR1 and 0.46 for mGluR5 (Figure 5 & Figure 6, middle left; Table 1) consistent with experimental data.⁶² Maintenance of the closed conformation was due to strong contacts between the ligand and the pocket residues; along with retaining all of the contacts that glutamate made with the pocket, additional contacts were formed (and maintained throughout the simulation) with E292, Y236, and S189 in mGluR1 and the equivalent, E279, Y223 and S173 in mlGluR5 (Figure 3). Z-CBQA was a more recently developed selective agonist of mGluR5 ⁵² that scored with an efficacy of 0.61 for mGluR5 (Figure 6, middle right; Table 1). Because of its high selectivity towards mGluR5, the mGluR1-Z-CBQA system was not considered. Like, DHPG, the LBR retained its closed conformation due to tight contacts between Z-CBQA and the pocket. Z- CBQA also retained all of the contacts that glutamate made with the pocket, along with making additional contacts with: W100, E279 and Y223 (Figure 4).

Four antagonists were studied, two of which (C3H2MPG and C3HPG) were simulated in two orientations due to asymmetry of the molecules such that they could bind in two possible conformations. ACPT-II is a selective antagonist of mGluR1 that scored a low efficacy of 0.11 for mGluR1 (Figure 5, middle right and Table 1). Because of its strong selectivity for mGluR1 and no activity with mGluR5, the mGluR5-ACPT-II system was not considered. ACPT-II also retained the primary inner contacts that glutamate made with the inner pocket residues: between the -NH₃⁽⁺⁾ and the -COO⁽⁻⁾ of the ligand and the D318, S186 and S165 of the pocket, respectively (Figure 3). However, opening of the pocket occurred, possibly initiated due to repulsion between −COO⁽⁻⁾ of the ligand and the −OH⁽⁻⁾ side-chain moiety of Y74. Unlike the empty-pocket opening, the outer-part of the ligand opened first followed by a gradual influx of water into the LBR pocket that broke the ligand inner pocket interactions. While the outer pocket opening and a partial inner pocket opening was captured within the 32-ns simulation time, an additional 32-ns simulation was run to completely open the up the pocket and allow convergence at the new conformation.

C3H2MPG is another antagonist of the mGluR1 with a moderate selectivity^{14, 54, 55} that scored 0.05, indicating low efficacy, for ligand conformation 2. The two conformations involve a 180° rotation of the phenyl ring about the Cα bond. In the first conformation (C3H2MPG(1)), the methyl group attached to the phenyl group is at a distal position from the -NH₃⁽⁺⁾ in the ligand, while in second conformation (C3H2MPG(2)) it is in a proximal position. Across both the conformations, C3H2MPG retained all of the primary contacts that glutamate made with the inner pocket. In conformation 1, this was further stabilized by additional interactions between the −CH₃ of the ligand and S164-S165 in the upper lobe of the inner pocket and the −OH of the ligand and the R323 in the lower lobe of the outer pocket. Hence, no pocket opening was observed in conformation 1 leading to an efficacy score of 1 (Figure 5, lower left). In conformation 2 the additional interactions between the −OH and −CH₃ of the ligand and the pocket are lost. In addition, the −CH₃ disrupts the -NH₃⁽⁺⁾ to D318 interaction leading to pocket opening and an efficacy score of 0.05. Simulations of the mGluR5-C3H2MPG complex reveal free energy surfaces (Figure 6, lower left and right), efficacy scores (Table 1) and pocket opening mechanism very similar to mGluR1. Conformation 1 again kept the pocket closed due to additional interactions between −CH₃ of the ligand and S173 and the −OH of ligand and R310, while in conformation 2 the pocket opened due to a loss of the hydrogen bond between −NH₃⁽⁺⁾ and D305 due to competition from the proximal position −CH₃, akin to mGluR1. Hence, although the potency of C3H2MPG with mGlurR5 is low (IC₅₀ > 300µM), once the ligand gets into the pocket the conformational mechanism associated with opening or closing appear to be similar to that occurring with mGluR1.

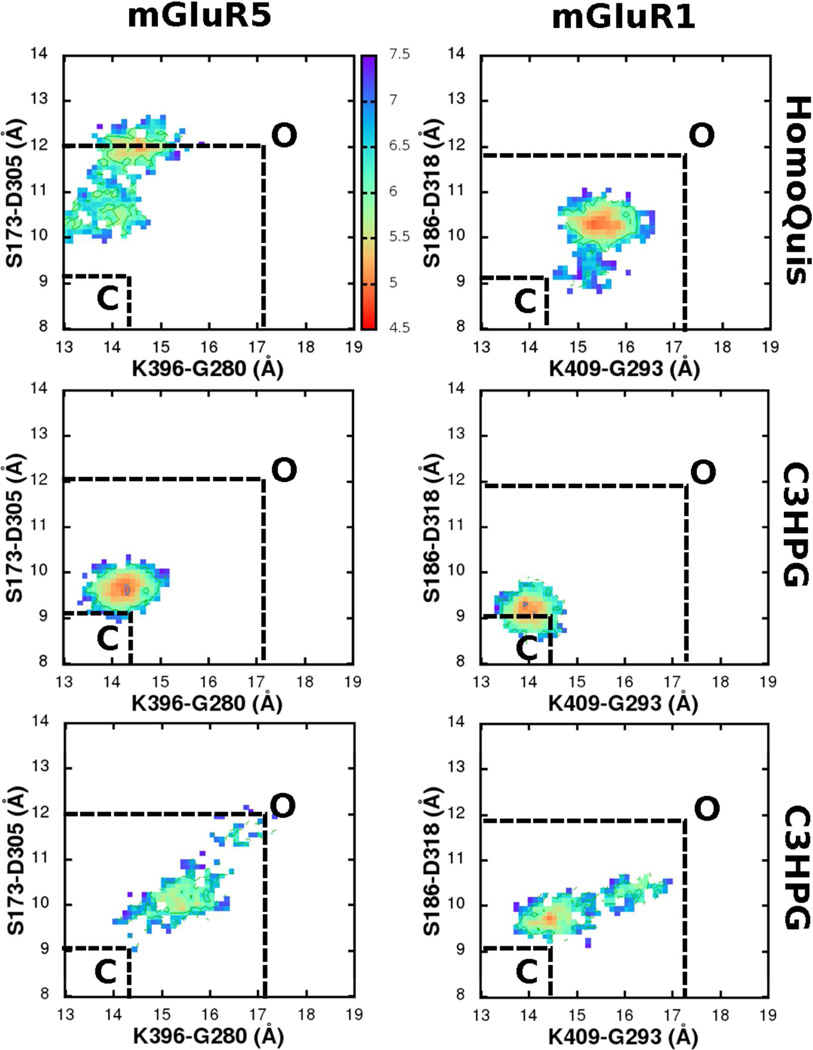
Both HOMQ and C3HPG are agonists with mGluR5 and antagonists with mGluR1 although with extremely low potencies in both cases. ^{56, 57} The free energy surface of mGluR1-HOMQ revealed a partial pocket opening (Figure 7, upper left), thereby scoring an efficacy of 0.30. Like the other ligands, HOMQ also retained the primary contacts that glutamate made with the inner pocket residues: between the -NH₃⁽⁺⁾ and the -COO⁽⁻⁾ moieties of the ligand and D318 and S186/ S165 of the pocket, respectively. However, there were no interactions across the outer part of the pocket and the ligand, thereby driving the pocket into a partially opened conformation. Unlike with ACPT-II, pocket opening of mGluR1 LBR with HOMQ was characterized by conformational densities along the diagonal of the free energy surface. Importantly, the free energy profile of mGluR5 with HOMQ also revealed a pocket opening (Figure 7, upper right). Like in mGluR1, HOMQ retained the primary inner contacts with the pocket residues: between the NH₃⁽⁺⁾ and the -COO⁽⁻⁾ moieties of the ligand and D305 and S173/S151 of the pocket, respectively. However, unlike mGluR1, the inner pocket of mGluR5 opened up more significantly than the outer pocket characterized by off-diagonal conformational densities on the free energy surface.

Figure 7.

Comparison of the conformational free energy surfaces of mGluR1 and mGluR5 with HomQuis (HOMQ) and C3HPG ligands in the LBRs. Distances across two pairs of inter-lobe Cα atoms(S173-D305 and K396-G280) are reaction coordinates for the free energies that are measured in k_BT; 1 k_BT∼0.59 kcal/mol. Closed and open states (C and O) conformational minima are marked based on the free energy profiles from the mGluRx-glutamate and the empty mGluRx (x is 1 or 5) simulations in Figure 5 & Figure 6.

Conformation 2 of C3HPG scored with a low efficacy of 0.25 and 0.1 for mGluR1 and mGluR5, respectively. Like C3H2MPG, two conformations of C3HPG that are separated by a 180° rotation of the phenyl ring about the Cα bond were considered. Conformation 1 of C3HPG (C3HPG(1)), retained all the contacts that glutamate made with the pocket. Additional interactions were found between the −OH group of the ligand and the −NH₃⁽⁺⁾ of K409 of mGluR1 (and the equivalent K396 of mGluR5) which kept the pocket closed throughout the simulation (Figure 7, middle left and right: efficacy of 1 and 0.7 for mGluR1 and mGluR5, respectively). On the other hand, in conformation 2, with the flipping of the phenyl ring, these stabilizing interactions across C3HPG and the outer pocket disappeared, driving pocket opening across both mGluR1 and mGluR5 (Figure 7, lower left and right respectively).

Hence, our simulations reveal that although a ligand may have different affinities for mGluR1 and mGluR5, once it moves into the pocket, the activation/deactivation mechanism of the ligand is the same for both the receptors. Since the pocket residues sequence is completely preserved and the LBR structures are similar between mGluR1 and mGluR5, it is likely that selectivity is driven by do-mains outside of the LBR in the mGluR complexes.

LBR OPENING/CLOSING FROM CONFORMATIONAL FORCES

While the efficacy calculations presented above appear to be robust, they are computationally demanding. Accordingly, a more computationally tractable approach is needed to estimate efficacy. Initial efforts using simulations of the closed conformations of the 20 Å radius LBR-ligand model systems targeted the analysis of interaction energies between the ligand and various binding site residues. However, no consistent metric based on this approach was identified (not shown). Alternatively, the full MD simulations were run with 4 α-carbon atoms of the pocket residues harmonically restrained in both the LBRs for a period of 12 ns. From the thermal fluctuations of the restrained atoms, force vectors were calculated using Eqn. 2 While the magnitude of forces was small, on the order of a few hundred pN, the directions of the force vectors were a metric of the conformational properties of the LBR.

In mGluR1, the restraints were on the α-carbon atoms of residues S186, W110 on the upper lobe and D318 and G293 in the lower lobes. Since S186 and D318 are close to the LBR hinge, force vectors, (F_x; x residue name), developed by these atoms represent the inner pocket conformational transition direction. Likewise, W110 and G293 are further away from the hinge and hence forces vectors of these atoms represent the outer pocket conformational transitions. Reference vectors, F^ref_x(x residue name), were assigned to the restrained atoms that point “into” the pocket (Figure 2). Accordingly, the angle between the force vectors on the restrained atoms and reference vectors F^ref_x yields the direction of any LBR conformational transition, such that a force vector pointing into the pocket, cos(F_x, F_x^ref) > 0 can readily be discerned from a force vector pointing away from the pocket, cos(F_x, F_x^ref) < 0. In this model opening would be indicated by the force vectors all pointing away from the pocket.

Consistent with the unconstrained MD simulations, collectively the force vectors from the restrained MD of the mGluR1 LBR-glutamate complex indicate that the LBR will remain closed (Table 2). While force vector of D318 (F₃₁₈) points inwards, F₁₈₆ points outwards; together (ie. F₃₁₈ and F₁₈₆) they point in the same direction, indicating the both sides of the inner LBR region would shift in the same direction, thereby maintaining a closed, active state. Similarly, in the outer LBR region, F₂₉₃ points inwards, while F₁₁₀ points outwards indicating that both sides of that region are shifting in the same direction and would maintain a closed state. We note that the vectors all pointing in the same direction is associated with the inter-LBR motions observed in the unrestrained full dimer MD simulations. Force vectors from the constrained MD of the empty dimeric LBR all point “outward” (Table 1, efficacy score, Table 2), away from the pocket, indicating an LBR opening. As observed with the free energy surfaces, the force vector results for mGluR5 are similar to mGluR1 (Table 3).

Table 2.

Cosine of the angle between the force and reference vectors at the four constrained α-carbons in the closed LBR of mGluR1 (Figure 2) in the presence of various ligands. Results for the force vector, F_x, for residues x, S186, D318, W110 and G293 with respect to the reference vector (F_x^ref) (see, Figure 2) are presented.

	S186	D318	W110	G293	LBR
Glu	−0.3	0.7	−0.6	1	Close
Empty	−0.5	−0.9	−0.4	−0.6	Open
DHPG	0.6	−0.7	0.4	0.4	Close
ACPT-II	−0.9	0.4	−1	−0.4	Open
C3H2MPG(1)	−0.4	0.5	0	1	Close
C3H2MPG(2)	−0.5	0	−0.8	−1	Open
HOMQ	0.6	−0.5	0.1	−1	Open
C3HPG(1)	0.4	−0.7	0.9	−0.8	Close
4C3HPG(2)	0.1	0.6	−0.6	−0.1	Open

Table 3.

Cosine of the angle between the force and reference vectors at the four constrained α-carbons in the closed LBR of mGluR5 (Figure 2) in the presence of various ligands. Results for the force vectors, F_x, for residues, x, S173, D305, W100 and G280 with respect to the reference vector, F_x^ref,(see Figure 2) are presented.

	S173	D305	W100	G280	LBR
Glu	0.6	−0.1	0.5	−0.6	Close
Empty	−0.1	−0.2	−0.6	−0.4	Open
DHPG	0.6	−0.4	0.4	−0.4	Close
Z-CBQA	0.7	0.9	−0.6	0.1	Close
C3H2MPG(1)	−0.6	0.5	0.5	−0.7	Close
C3H2MPG(2)	−0.5	−0.9	−0.3	0.2	Open
HOMQ	0.9	−0.8	0.7	−0.3	Open
C3HPG(1)	−0.1	0.7	0.3	0.1	Close
C3HPG(2)	−0.4	−0.6	−0.1	−0.6	Open

Table 2 and Table 3 summarize the force vector directions for the 4 restrained atoms of the closed LBR for all the studied ligands in the dimeric mGluR1 and mGluR5, respectively. The force vectors capture the conformational transitions in the LBR due to the presence of the ligands consistent with the unrestrained simulations. For instance, force vectors from the mGluR1-ACPT-II system (Table 2) indicate the outer part of the pocket opening up; while the inner part stays closed. F110 and F293 point outward from the pocket, while the F186 and F318 point along the same direction indicating a “pull” from the other LBR along the inner region of the LBR close to its hinge. On the other hand, with C3H2MPG (conformation 2), as the LBR opens up proportionally, populating conformations along the diagonal of the free energy surface (Figure 5, lower right), the constrained MD simulations reveal all the force vectors pointing away from the pocket, similar to the empty pocket case. As with the glutamate and the empty pocket system, force vectors from the constrained MD of mGluR5-C3H2MPG complex are similar to the mGluR1-C3H2MPG complex. Thus, it is possible to estimate the impact of a ligand on the pocket open/close equilibrium from sampling around a single conformation. This calculation requires less simulation time (the force vectors converge within 12 ns of MD simulation), in comparison to the 32 ns (and 64 ns in the case of mGluR1-ACPT-II) needed for the unrestrained MD simulations, making this more accessible to characterize the effect of a large set of ligands on the LBR. It should be noted that force vectors from a restrained monomeric LBR-ligand system did not capture the pocket-opening/closing capabilities of the ligand, indicating that inclusion of the inter-LBR interactions of the dimeric LBR system is required to faithfully capture the effect of the ligand on the receptor.

DISCUSSION

MD simulations were used to investigate the effect of ligands on the conformational properties of the LBRs of both mGluR1 and mGluR5. Agonists kept the LBR closed through strong interactions with the pocket residues, while antagonists opened up the LBR yielding an inactive conformation. Physiologically, an empty LBR is likely to fluctuate between open and closed conformations due to thermal fluctuations. A ligand binds to the open conformation LBR and, based on the ligand’s interactions with the pocket residues, shifts the conformational equilibrium to the closed, active state or the open, inactive state. The MD simulations with the closed LBR as a starting conformation capture these shifts in equilibrium. Based on how close the ligand retains the conformational minima of the receptors from that calculated with glutamate, allows for an estimation of the ligand’s efficacy. While the model formally allows for a quantitative estimate of the magnitude of efficacy (i.e. agonist, partial agonist, antagonist), most of the available experimental EC₅₀/IC₅₀ data⁶² only classifies the studied compounds as agonists or antagonists. Accordingly, the present model can be considered as a qualitative predictor of efficacy. A recent study by Doumazane and co-workers ²² re-classified some ligands of mGluR2 as partial agonists based on FRET assays to capture the partial cleft opening. Although the FRET methodology is useful, it is limited in that it reports only on distances between two domains across the dimeric LBR. As Rives and co-workers ²³ correctly point out, for the same distance between the two LBRs, multiple conformations (and states) could exist. Conformational sampling using molecular dynamics, hence offers a more comprehensive picture about the various conformational transitions by the LBR in the presence of a ligand.

Because of their opposing physiological effects ^{9, 12, 63}, there is a strong pharmacological interest to find ligands that are selective agonists for the mGluR5 and antagonists for mGluR1. Two ligands, HOMQ ⁵⁶ and C3HPG ⁵⁷ have been shown experimentally to moderately successful in achieving this selectivity. However, conformational sampling of mGluR1 and mGluR5 with these ligands looked remarkably similar, indicating that although a ligand may have different binding affinities between mGluR1 and mGluR5, once it gets into the pocket, the conformational mechanism associated with activation will be the same. Importantly, selectivity is hence likely to be dictated by regions of the protein outside of the LBR in the mGluR structure.

Although unconstrained MD simulations are attractive in understanding the effect of a ligand on the dimeric LBR, they become computationally intractable when scoring efficacies of a large set of ligands. Hence, we explored alternate strategies that are not computationally as expensive as the unconstrained simulations, and yet capture the effect of the ligand on the mGluR. Towards that, MD simulations of the dimeric LBR-ligand system with selected α-carbon pocket atoms harmonically restrained were performed for 12 ns. From these simulations force vectors on the restrained atoms were calculated and shown to be indicative of the conformational preference of the LBR. When the force vectors point inward, into the pocket, the ligand retained the LBR in a closed conformation, and when the force vectors pointed outwards, the ligand pushed the LBR into an inactive conformation. Importantly, these simulations do not have to be as long as the unrestrained MD simulations to directly monitor the conformational shift in the LBR, making this an effective methodology to evaluate efficacies of a large set of ligands. Thus, efficacy calculations from the forces developed on a single conformation may be an attractive methodology to estimate the effect of ligands on other receptors that undergo global conformational transitions on ligand binding.

ABBREVIATIONS

BBB

blood brain barrier

iGluR

ionotropic glutatamate receptor

LBR

ligand binding region

mGluR1

metabotropi glutamate receptor 1

mGluR5

metabotropic glutamate receptor 5

MD

molecular dynamics

PDB

protein data bank

QM

quantum mechanics

TBI

traumatic brain injury

VFTM

venus fly trap module