Automated grading system for evaluation of ocular redness associated with dry eye

Abstract

Background

We have observed that dry eye redness is characterized by a prominence of fine horizontal conjunctival vessels in the exposed ocular surface of the interpalpebral fissure, and have incorporated this feature into the grading of redness in clinical studies of dry eye.

Aim

To develop an automated method of grading dry eye-associated ocular redness in order to expand on the clinical grading system currently used.

Methods

Ninety nine images from 26 dry eye subjects were evaluated by five graders using a 0–4 (in 0.5 increments) dry eye redness (Ora Calibra™ Dry Eye Redness Scale [OCDER]) scale. For the automated method, the Opencv computer vision library was used to develop software for calculating redness and horizontal conjunctival vessels (noted as “horizontality”). From original photograph, the region of interest (ROI) was selected manually using the open source ImageJ software. Total average redness intensity (Com-Red) was calculated as a single channel 8-bit image as R – 0.83G – 0.17B, where R, G and B were the respective intensities of the red, green and blue channels. The location of vessels was detected by normalizing the blue channel and selecting pixels with an intensity of less than 97% of the mean. The horizontal component (Com-Hor) was calculated by the first order Sobel derivative in the vertical direction and the score was calculated as the average blue channel image intensity of this vertical derivative. Pearson correlation coefficients, accuracy and concordance correlation coefficients (CCC) were calculated after regression and standardized regression of the dataset.

Results

The agreement (both Pearson’s and CCC) among investigators using the OCDER scale was 0.67, while the agreement of investigator to computer was 0.76. A multiple regression using both redness and horizontality improved the agreement CCC from 0.66 and 0.69 to 0.76, demonstrating the contribution of vessel geometry to the overall grade. Computer analysis of a given image has 100% repeatability and zero variability from session to session.

Conclusion

This objective means of grading ocular redness in a unified fashion has potential significance as a new clinical endpoint. In comparisons between computer and investigator, computer grading proved to be more reliable than another investigator using the OCDER scale. The best fitting model based on the present sample, and usable for future studies, was $C_4=-12.24+2.12C_2^{HOR}+0.88C_2^{RED}:{\text{C}}_4$ is the predicted investigator grade, and $C_2^{HOR}$ and $C_2^{RED}$ are logarithmic transformations of the computer calculated parameters COM-Hor and COM-Red. Considering the superior repeatability, computer automated grading might be preferable to investigator grading in multicentered dry eye studies in which the subtle differences in redness incurred by treatment have been historically difficult to define.

Introduction

An accurate clinical assessment of redness is essential to the diagnosis and treatment of inflammatory and infectious diseases of the eye. While the presence or absence of redness has long been used as a diagnostic indicator in ophthalmology, little attention has been given to patterns of redness and vasodilation, which can vary greatly according to location, hue or depth of color, and intensity. In the development of clinically significant endpoints to be used across sites in multicentered trials, we have defined redness scales tailored to the disease, be it allergic conjunctivitis,^1,2 dry eye,³ infectious keratitis, immune infiltrates, bacterial conjunctivitis or glaucoma. All these clinical redness scales have been accepted by the FDA for establishing treatment effects in the various diseases. It has been our clinical experience that the hyperemia associated with allergy tends to be mild and diffuse, with no scleral involvement. A circumlimbal hyperemia can be associated with contact lens intolerance or iritis, and conjunctival redness under the lower lids can be a sign of drug-induced allergy. “Fire engine” red or near purple hues are the hallmark of severe ocular infection, corneal ulcer or endophthalmitis, often with deep scleral involvement. We have observed that dry eye-associated ocular hyperemia frequently involves prominent, fine, horizontal vessels in the bulbar conjunctiva, mainly in the interpalpebral fissure, where the ocular surface is exposed.⁴ This has led to the development of a multi-component investigator-grading system for dry eye-associated redness (Ora Calibra™ Dry Eye Redness Scale or OCDER).This 0–4 scale in 0.5 increments uses both reference photographs and descriptive language, defining the degree of redness by intensity, location and prominence of fine horizontal conjunctival vessels (referred to as “horizontality” or FHCV). Horizontal vessels appear to become particularly prominent as the severity of redness increases. For the last 10 years, this scale has been used at our research facility for the grading of redness in dry eye clinical trials.

Analogous work in grading redness has been specifically geared to the complications of contact lens wear, either with artistic renditions^5,6 or photographic standards,^7–11 some validated by comparisons with photometric chromaticity.^12,13

One difficulty in assessing the validity and sensitivity of these redness grading systems is the question of what exactly the grader is measuring: depth of red hue or percent distribution of redness over the visible surface, the contribution and dilation of large versus fine vessels, or increasing visibility of the branching vasculature. Chen et al, in 1987 was one of the first to attempt to objectively quantify the microcirculatory network of the human eye.¹⁴ Papas reported that not only color but the proportion of vessels occupying the scene was an important factor in grading erythema.¹⁵ Schulze et al published a series of studies,^8,11–13 finding that cross-calibration based on subjective grading was not possible. It appears that the questions that arise from using these scales might be better answered by comparisons with objective measures of redness grading.

Image analysis techniques have been investigated over the last 20 years in an attempt to forgo subjective grading scales. Thresholding,^14–19 edge detection,^17,20,21 smoothing,^16,17,20,22 color extraction,^15,16,19,22 morphometry, and densiometry²³ have all been used to measure conjunctival hyperemia. Most are in agreement that vessel prominence increases with redness intensity. Similar reasoning was provided by Fieguth and Simpson, who found that vessel edge detection and hue together predicted the clinical redness grade.¹⁶ Peterson and Wolffsohn also observed in their objective analysis of reference images that clinicians used a combination of overall hue and vessel area when grading redness.²⁴

Agreement between and within graders becomes an issue of greater importance when a multicentered clinical trial is undertaken. The subtlety of dry eye redness patterns has also made it difficult to demonstrate a treatment effect on this endpoint, particularly across multiple sites. This is in contrast to other types of more obvious redness associated with lens complications, acute inflammation, allergy and/or infection.

To improve the sensitivity and agreement of subjective grading, we have developed an automated computer redness grading system (Ora, Inc, Andover, MA, USA, patent pending), which incorporates the two primary components of our already established subjective grading system: redness intensity and FHCVs. This computer-based objective grading system is designed to be used as a tool in clinical trials to grade photographic images from all sites in a unified fashion. This computer based system differs from other objective methods already published, in that it focuses on the geometry of the vessels of the most clinically relevant region in dry eye, the interpalpebral fissure. We chose to focus in both the clinical and computer scale on vessel horizontality, rather than other objective and measurable characteristics of vessels, as this feature commonly becomes more prominent as dry eye severity increases. As with all automated image analysis, advantages of an objective assessment include eliminating the variables of grader fatigue and innate comparative bias that occur when an investigator grades a series of images.

The aim of the present study was to determine the agreement between the new computer-automated system and a panel of investigators using the established clinical scale in use at our research facility, for grading the same set of photographic images of dry eyes.

Methods

Subjects

The study from which the images were collected was conducted in accordance with Institutional Review Board (IRB) regulations and with the ethical principles that originated with the Declaration of Helsinki. The informed consent and study protocol were approved by a properly constituted IRB (Alpha IRB, San Clemente, CA, USA). Prior to a subject’s participation, the study was discussed and subjects wishing to participate gave written informed consent.

Subjects were included if they had a history of use of artificial tear substitutes for symptoms of dry eye within the previous 6 months and a patient- or investigator- reported history of dry eye in both eyes. Subjects were excluded if they had any other ocular inflammation, infection or condition that may have put the subject at risk, confounded study results, or interfered with the subject’s participation in the study. Subjects were also excluded who had a history of laser-assisted in situ keratomileusis or other corneal refractive surgery, or used contact lenses or any prohibited medications within the defined washout period.

Image capture technique

Images of the temporal and nasal conjunctiva were acquired with a 12-megapixel digital camera, the Haag-Streit BX 900 slit lamp system (Haag-Streit International, Koeniz, Switzerland). A diffused fash system was used to avoid refection from the tear layer. The RGB, 8-bit images were captured in a raw format and saved in JPEG format. Other camera parameters, such as aperture size and shutter speed, were kept constant across all subjects. Photographs from 26 dry eye subjects were assessed.

Investigator grading system

Five trained investigators graded a total of 99 photographs each using the clinical grading system developed specifically for dry eye: the OCDER scale. This investigator-based redness scale calibrated to reference photographs has both a redness intensity component and a bulbar conjunctival horizontal vessel component on a scale of 0 to 4 in which 0 = none and 4 = severe vasodilation, with 0.5 increments allowed.

A total of 495 scores (99 × 5) were recorded by the five investigators.

The same 99 photographs were then graded by computer automated image analysis, which provided two separate grades for redness intensity and horizontal vessels.

Computer automated image analysis

The Opencv computer vision library,²⁵ an open source library written in C++, was used to develop software for calculating computer-graded redness intensity (COM-Red) and computer-graded prominence of horizontal vessels (COM-Hor).

Selection of region of interest

From the original photograph (Figure 1A), the region of interest (ROI) was selected manually using the open source ImageJ software (ImageJ, US National Institutes of Health, Bethesda, Maryland). The ROI was defined as a rectangular region centered on the midpoint of the palpebral fissure, and of total height equal to one half the total fissure opening (Figure 1B). While this ROI was proportional in each image, and therefore of slightly differing size, it best represented the area of assessment in clinical grading of dry eye redness. A preliminary comparison of a clinician’s grading of the entire conjunctiva versus the ROI determined that there was no difference in grading just the ROI.

Figure 1.

Automated redness grading system for dry eye. A computer-automated approach for the assessment of conjunctival hyperemia in dry eye subjects. (A) Depicts the original photograph taken of a dry eye subject. (B) Illustrates the region of interest (ROI) in which the redness intensity and horizontality were assessed. (C) Illustrates the vascular structure: prominence of horizontal vessels is graded by image intensity representing regions of large vertical Sobel derivatives (used to calculate computer-graded prominence of horizontal [COM-Hor]).

The calculation of redness intensity

Overall redness

Total average redness intensity was calculated as a single channel 8-bit image as R − 0.83G − 0.17B, where R, G and B were the respective intensities of the red, green and blue channels. This provided an average value over the entire image on the raw scale (COM-Red).

Calculation of horizontal vascular component

We selected blue channel intensity of the vessels in the ROI. We found this method to be simpler and more effective for smaller vessels than edge detection algorithms such as the Canny edge detection algorithm.¹⁶ The location of vessels was detected by normalizing the blue channel of the image and selecting pixels with an intensity less than 97% of the mean. The vertical and horizontal components of the vascular structure were calculated by first order Sobel derivatives in the horizontal direction for vertical vessels and in the vertical direction for horizontal vessels. The computer-graded horizontality score (COM-Hor) is defined as the vertical derivative of the blue channel image intensity averaged over each image (eg, Figure 1C).

The original, raw scale computer grade for both redness and horizontality was effectively a single precision floating point number from 0–1. This was based on information from a single channel of an 8-bit image, with 256 values averaged over all pixels in the image (typically 200,000 pixels). This gave an output in steps of approximately 10⁻⁸ (0.00000001) which was equivalent to a single precision floating point number.

Statistical methods

Agreement was assessed using the concordance correlation coefficient (CCC) proposed by Lin.²⁶ In contrast to the Pearson correlation coefficient (−1 to 1), which measures closeness to any line, the concordance coefficient (−1 to 1) measures closeness to the 45-degree agreement line through the origin. The concordance is less than the correlation unless the two scales share common means and standard deviations, a relationship formalized by the decomposition: concordance = correlation × accuracy, where accuracy (0 to 1) is a function of the two scales’ means and standard deviations. Calculations were based on computations from the REG, CORR, and MEANS procedures of SAS version 9.3 (SAS/STAT® 9.3 User’s Guide, SAS Institute Inc, Cary, NC, USA). Confidence intervals (CI) for the CCC were calculated via Fisher’s Z-transformation Z = 0.5 log([1 + CCC]/[1 − CCC]). As a guide to interpreting agreement magnitudes, Landis and Koch²⁸ suggested: 0–0.2 as slight agreement, 0.2–0.4 as fair agreement, 0.4–0.6 as moderate agreement, 0.6–0.8 as substantial agreement, 0.8–1.0 as almost perfect agreement.

The components of agreement (concordance, correlation, and accuracy) between computer and investigator scores were calculated for redness and horizontality separately, and for redness and horizontality jointly. For each image, the mean clinical grade was taken over the five investigators giving an estimate of the “true” OCDER score for that image. Three successive transformations were applied to the original (0 to 255) computer scores for redness and horizontality (C₁).

First, the original scores were transformed to a logarithmic scale ranging from 0 to 8 (by adding 1 and taking logarithms base 2; C₂ = log(C₁ + 1) in order to enhance the normal linear relationship between computer and investigator scores. Second to obtain computer scores that more closely matched investigator scores, the latter were regressed against log computer scores to obtain predicted scores. This method was applied to redness and horizontality separately using simple regression:

$$C_3=\alpha +\beta C_2,$$

where α and β were estimated by least squares. In addition, it was applied to redness and horizontality jointly using multiple regression:

$$C_3=a+\beta C_2^{HOR}+\gamma C_2^{RED},$$

where α, β and γ were estimated by least squares. Third in order to maximize accuracy, predicted scores were transformed such that means and standard deviations matched those of the investigator score:

$$C_4=a+b{C}_3,$$

where

$$a={\mu }_{INV}-({\sigma }_{INV}/{\sigma }_{COM}){\mu }_{COM}$$

and

$$b=({\sigma }_{INV}/{\sigma }_{COM}).$$

We note that C₄ is also a linear combination of $C_{\text{2}}^{HOR}$ and $C_2^{RED}$.

The last two transformations, corresponding to regression and “standardized” regression methods, provided scores we considered for the purpose of agreement. Regression computer scores maximized the correlation coefficient within the class of all linear combinations of horizontality $(C_2^{HOR})$ and redness $(C_2^{RED})$. Standardized regression computer scores were constructed to give perfect accuracy, thus equalizing concordance and correlation coefficients, and maximizing the concordance coefficient within the class of all linear combinations.

For purposes of comparison, we also calculated how well each investigator graded the images compared to the ‘true grade’ represented by the mean grade of the other 4 graders. The average agreement obtained among these 5 investigators was considered for comparisons of agreement with computer versus investigator grading systems.

Results

Table 1 reports results for comparisons of investigator to computer grade at each level of transformation. The raw computer scores on the original scale, their log transformation, and then, for agreement analyses, the regression, which matched means, and the standardized regression, which matched both means and standard deviations. Unsurprisingly, the testing of agreement with unmatched raw scales (OCDER = 1.98, COM-Hor = 33.47, COM-Red = 14.78) resulted in almost no agreement that redness and horizontality were correlated on the raw scale (r = 0.67), indicating that as redness increased horizontality increased and demonstrating that scale had little effect on correlation.

Table 1.

Mean scores of dry eye redness graded in 99 photographs using the clinical investigator-grading system (Ora Calibra™ Dry Eye Redness Scale [OCDER]) and the computer grading system (COM)

Computer score	OCDER mean	Computer mean	Standard deviation OCDER	Standard deviation computer	Pearson’s correlation coefficient	Accuracy	Concordance correlation coefficient (CCC)	Lower 90% confidence interval CCC	Upper 90% confidence interval CCC
Raw scores (0–255)
COM-Hor	1.98	33.47	0.78	4.51	0.67	0.01	0.00	0.00	0.01
COM-Red	1.98	14.78	0.78	6.36	0.67	0.05	0.03	0.02	0.04
Log base2 scores (0–8)
COM-Hor	1.98	5.09	0.78	0.19	0.66	0.03	0.02	0.01	0.02
COM-Red	1.98	3.88	0.78	0.54	0.69	0.19	0.13	0.09	0.16
Regression scores (0–4 scale)
COM-PredHor	1.98	1.98	0.78	0.52	0.66	0.92	0.61	0.51	0.69
COM-PredRed	1.98	1.98	0.78	0.54	0.69	0.94	0.65	0.55	0.72
COM-PredHR	1.98	1.98	0.78	0.59	0.76	0.96	0.73	0.65	0.79
Standardized regression scores (0–4 scale)
COM-PredHor	1.98	1.98	0.78	0.78	0.66	1.00	0.66	0.56	0.74
COM-PredRed	1.98	1.98	0.78	0.78	0.69	1.00	0.69	0.59	0.77
COM-PredHR	1.98	1.98	0.78	0.78	0.76	1.00	0.76	0.68	0.82

Notes: Computer grades were transformed from the raw scale to a log scale for improved normal distribution and linearity, after which regressions and standardized regressions were calculated on predicted scores to obtain agreement, accuracy and concordance. Note that the OCDER mean is one score, whose mean and standard deviation are repeated in the table for ease of use.

Abbreviations: COM-Hor, computer-graded horizontality; COM-Red, computer-graded redness; COM-PredHor, regression predicted computer grade for horizontality; COM-PredRed, regression predicted computer grade for redness; COM-PredHR, regression predicted computer grade for horizontality and redness combined; OCDER, Ora Calibra™ Dry Eye Redness Scale.

With the initial regression, predicted scores matched computer means to investigator means (1.98). Accuracy increased with matched means to 0.92 for horizontality, 0.94 for redness, and 0.96 for the combination. These corresponded to concordance coefficients of 0.61, 0.65 and 0.73, respectively. The Pearson’s correlation coefficient at for the regression scores was 0.66 for horizontality and 0.69 for redness. When both factors were considered jointly in multiple regression, this correlation increased to 0.76. We note, in passing, that redness and horizontality were correlated on the log scale (r = 0.60).

With the ‘standardized’ regression, predicted scores matched computer means to investigator means, as above (1.98), as well as computer and investigator standard deviations (0.78). With both means and standard deviations matched accuracy was increased to 1, and thus the Pearson’s correlation coefficient and the concordance coefficients were equal: 0.66 for horizontality, 0.69 for redness. The most favorable approach, provided by the linear combination of horizontality and redness (noted previously as $C_3=\alpha +\beta C_2^{HOR}+\gamma C_2^{RED}$ and $C_4=a+b C_3$), gave a CCC of 0.76. Final calculations based on the present sample and usable in future studies

$$C_4=-12.24+2.12C_2^{HOR}+0.88C_2^{RED}.$$

Figures 2–4 illustrate the 99 scores based on the final standardized regression method of transformation for horizontality (Figure 2), redness (Figure 3) and the combination (Figure 4).

Figure 2.

Standardized regression scores for computer-based horizontality against investigator-based OCDER (CCC = 0.66).

Abbreviations: CCC, concordance correlation coefficient; OCDER, Ora Calibra™ Dry Eye Redness Scale.

Figure 4.

Standardized regression scores for computer-based horizontality and redness combined against investigator-based OCDER (CCC = 0.76).

Abbreviations: CCC, concordance correlation coefficient; OCDER, Ora Calibra™ Dry Eye Redness Scale.

Figure 3.

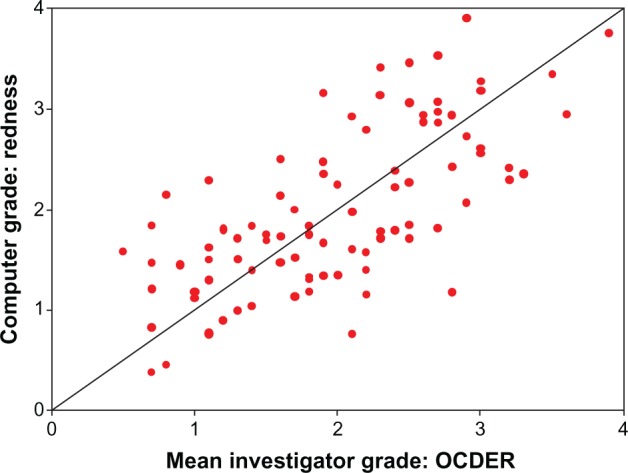
Standardized regression scores for computer-based redness against investigator-based OCDER (CCC = 0.69).

Abbreviations: CCC, concordance correlation coefficient; OCDER, Ora Calibra™ Dry Eye Redness Scale.

Table 2 reports the agreement of each investigator to the mean of the other four investigators (considered the hypothetically ‘true’ grade). The differences in investigator to investigator mean grade ranged from none to 0.86 units (60% difference). These corresponded to Pearson’s correlations of 0.64 to 0.82, accuracy of 0.64 to 0.99 and CCC of 0.47 to 0.82. The average CCC for the five investigators was 0.67.

Table 2.

Mean scores of dry eye redness graded in 99 photographs using the clinical investigator-grading system (Ora Calibra™ Dry Eye Redness Scale [OCDER])

Grader	Mean 4 graders	Mean 1 grader	Standard deviation 4 graders	Standard deviation 1 grader	Pearson’s correlation	Accuracy	CCC	Lower CI CCC	Upper CI CCC
1	1.98	1.98	1.01	0.76	0.83	0.96	0.79	0.73	0.84
2	2.37	1.88	0.91	0.79	0.78	0.66	0.66	0.57	0.73
3	2.25	1.91	0.92	0.80	0.68	0.62	0.62	0.52	0.71
4	1.29	2.15	0.82	0.82	0.73	0.47	0.47	0.38	0.55
5	2.00	1.97	0.90	0.78	0.83	0.82	0.82	0.76	0.87

Notes: Means and standard deviations are presented for each individual grader, as well as the means and standard deviations for the other four investigators, considered as the hypothetical ‘true’ clinical OCDER scores, and used in subsequent agreement analysis for Pearson’s correlation coefficient, accuracy, and concordance correlation coefficients (CCC).

Abbreviations: CCC, concordance correlation coefficient; CI, confidence interval; OCDER, Ora Calibra™ Dry Eye Redness Scale.

Discussion

Hyperemia is an important general sign in ophthalmology, and its presentation differs depending on the underlying disease. With regard to dry eye, one of the inherent problems in assessing new treatment modalities is the lack of one specific sign or symptom that characterizes the disease. A constellation of ocular surface endpoints such as symptom questionnaires, tear film measurements, surface staining patterns and redness must be graded with accurate and sensitive scales to assess the efficacy of treatment. In our clinical experience, we have observed a prominence of fine, horizontal conjunctival vessels in the exposed ocular surface of the interpalpebral fissure in dry eye-associated redness. This redness pattern, specific to exposed regions, might help to differentiate dry eye from other types of inflammation, as well as the subtle changes that occur with treatment.

Our aim was to develop an automated computer system that accurately recorded the same characteristics measured in the clinical OCDER scale, yet could grade images collected in multicentered clinical trials in a unified fashion, minimizing variability between and within sites and thus, minimizing standard deviations and providing a statistically more powerful dataset. To our knowledge, this is the first automated grading system developed specifically for use in dry eye subjects.

We have shown that the combination of computer-graded horizontality and redness increased agreement with the clinical grade from 0.66 and 0.69 to 0.76, which was also a considerable improvement when compared to the average agreement in clinical grading among investigators (0.67). Variability in clinical grading among investigators has been confirmed in the literature by Schultze et al,¹² Fieguth and Simpson,¹⁶ and Peterson and Wolfsson²⁴ among others. While some studies report higher agreement of their objective and subjective scores,^{13,15,16,24,28} our results fell into the high end of the ‘substantial agreement’ range of 0.6 to 0.8 suggested by Landis and Koch.²⁷ Investigators in this study remarked that horizontality of vessels was difficult to grade clinically with the naked eye compared to other properties of redness; this may have contributed to variations from the objective computer assessment. Redness intensity and hue (chromaticity) are known to be easier to grade, both subjectively and objectively, and as such, high agreement can be expected.¹⁸ Furthermore, some studies reported higher agreement based on running the calibrated photographs of a particular clinical scale through their matched objective system rather than on results of a series of images from diseased eyes.^12,13,28 We note that the current study utilized only five investigators compared to as many as 50²⁴ or 72¹⁶ in other studies. High agreement would be expected from these studies since the higher the number of graders, the less variability about the mean. On the other hand, our study involved the grading of almost 100 images, while previous studies graded considerably fewer (16,¹² 25,⁸ 30^6,16).

These results confirm those of previous studies reporting that average subjective grades are best predicted by a combination of vessel characteristics and hue intensity.^16,28 Yoneda et al recently presented their automated hyperemia software, which is similar to ours yet without the geometric component of vessel description.²⁹ In the present study, we have mathematically defined the linear relationship of hue and horizontality provided by our computer grading system of dry eye redness, calculations of which can be applied in future studies. The computer score has better agreement to the OCDER score (CCC = 0.76) than another investigator (CCC = 0.67), while offering the distinct advantages of 100% repeatability and zero variability.

In summary, the objective grading of conjunctival redness here presented provides an advancement in this field with regard to the following: (1) it is specifically tailored to the assessment of dry eye-associated redness, and not to other, more unambiguous forms of redness; (2) it presents a new simple objective measurement of the geometry of vessels that together with hue intensity, provides a global objective assessment; and (3) in conjunction with on-site investigator grading, this system could be of significant value in multicentered studies of dry eye, adding a single unified grading of images across sites without adding operational complexity. This technology might help to identify changes observed in redness brought on by new treatment modalities.