Abstract
It has been suggested that the human mirror neuron system (MNS) plays a critical role in action observation and imitation. However, the transformation of perspective between the observed (allocentric) and the imitated (egocentric) actions has received little attention. We expand a previously proposed biologically plausible MNS model by incorporating general spatial transformation capabilities that are assumed to be encoded by the intraparietal sulcus (IPS) and the superior parietal lobule (SPL) as well as investigating their interactions with the inferior frontal gyrus and the inferior parietal lobule. The results reveal that the IPS/SPL could process the frame of reference and the viewpoint transformations, and provide invariant visual representations for the temporo-parieto-frontal circuit. This allows the imitator to imitate the action performed by a demonstrator under various perspectives while replicating results from the literatures. Our results confirm and extend the importance of perspective transformation processing during action observation and imitation.
I. Introduction
Recent experimental investigations in humans have strongly supported the existence of a large cortical network, called the mirror neuron system (MNS), associated with sensorimotor (mostly visuomotor) integration [1], [2]. In particular, it has been revealed that the inferior frontal gyrus (IFG) and the inferior parietal lobule (IPL) exhibit greater activation in neuroimaging studies of the MNS, and thus they have been named as the frontal and the parietal MNS, respectively [3], [4]. In addition to these MNS components, mirror-like system in the superior temporal sulcus (STS) is also often considered [2]. Further, the similar responses of the temporo-parieto-frontal (TPF) circuit in action observation and execution clearly suggest that this circuit could be a critical network for action imitation, since imitation requires the abilities to observe an action and subsequently replicate through executing the action previously observed [1].
Besides such experimental studies, several conceptual and computational modeling approaches have been proposed to understand the neural mechanisms and functional roles of the MNS [5]–[8]. Specifically, models focusing on a function as a motor control and learning system adopted an internal model framework to implement the MNS. According to the originally proposed model, the STS-IPL-IFG pathway (i.e., an inverse model) would create the motor representation available for imitation from the visual representation of an observed action, whereas the reverse IFG-IPL-STS pathway (i.e., a forward model) could construct the specified visual representation for a self-action from the corresponding motor representation to be imitated [9]. Miall improved this idea by including the cerebellum that carries out other forward and inverse models in parallel with the TPF circuit [6].
Though both experimental and computational approaches examined the neurobehavioral mechanisms for imitation learning, little attention has been given to the problem related to difference of perspective between an observed and an imitated action. For instance, considering a typical imitation task, it is obvious that at least two agents (an imitator and a demonstrator) need to engage in imitative interactions; namely, the imitator reproduces an action performed by the demonstrator. These two agents are generally in different frames of reference (e.g., orientation, position, etc.), thus the imitator needs to transform the action observed in the demonstrator’s allocentric frame to the imitator’s egocentric frame of reference. In addition to frame of reference, two agents could have differences in anthropometry (e.g., upper arm length, forearm length, etc.), the functional range of motion (e.g., shoulder horizontal adduction, elbow horizontal flexion, etc.), and even viewpoint.
A large body of evidence suggests that the intraparietal sulcus (IPS) and the superior parietal lobule (SPL) play a critical role in the transformation between frames of reference, scales, or viewpoints [10]–[12]. Based on such studies, we recently developed an MNS model including an adaptive frontal MNS and limited adaptive parietal components, in which the parietal MNS was known a priori and the IPS/SPL could process only one spatial configuration [13]. Thus, here we expand our earlier model by including an adaptive parietal MNS and, more importantly, an adaptive IPS/SPL with general visuospatial transformation capabilities able to reproduce previous experimental results.
II. Model Overview and Methods
A. Model Overview
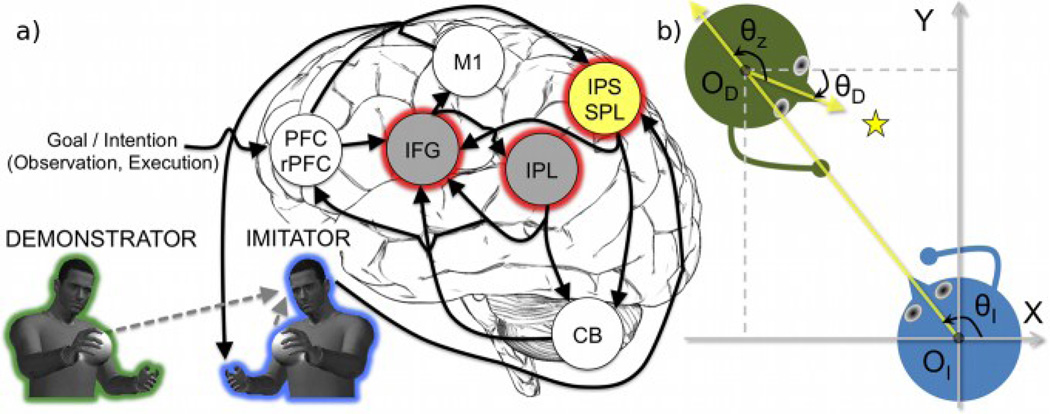
Our model is based on the anatomical and conceptual architecture proposed in our previous work [13] (Fig. 1a). Imitation learning in our MNS model is accomplished through a two-phase process combining action observation and imitation, which is voluntarily triggered by the prefrontal cortex (specifically in the rostral part; PFC/rPFC) [14], [15]. During the observation phase, the kinematic (i.e., visual information) of the demonstrator is sent to the IPS/SPL, which transforms the visual information into the imitator’s egocentric frame of reference, anthropometry, and viewpoint. The transformed observed action updates the IFG by means of mapping from visual to motor representations (i.e., inverse computation), which is then employed to imitate the observed action. Simultaneously, an efference copy of the motor plan is sent to the IPL that would predict the sensory consequences of the corresponding action (i.e., forward computation). Meanwhile, the cerebellum (CB) provides the prediction error for the IFG and the IPL to adjust their internal models.
Fig. 1.
Model overview for the human MNS based on an internal model framework incorporating the IPS/SPL. For the sake of clarity, the STS and its related connections are not shown. (a) The imitator either observes or executes the action based on the current goal/intention. The yellow component (IPS/SPL) generates the neural signal required to process the frame of reference, scaling, and viewpoint transformation. The two gray components (IFG and IPL) indicate the core MNS. Three components with a red halo (IFG, IPL, and IPS/SPL) are currently implemented using artificial neural networks. (b) Each agent has a different frame of reference (e.g., OI and OD) and viewpoint (e.g., yellow line of sights). The imitator (blue) just observes reaching for a star-shaped object (yellow) performed by the demonstrator (green). X and Y represent the coordinate axes of the 2D global (or absolute) coordinate system. θI, θD: angles towards an imitator (I) or a demonstrator’s (D) line of sight from the X-axis; θz: the rotation angle from the demonstrator to the imitator’s viewpoint.
During the ensuing imitation phase, the overall processes of the PFC/rPFC, IFG, IPL, CB, and IPS/SPL are equivalent to those previously described in the observation phase. The only difference is that, in parallel with the IFG to the IPL pathway, neural drive is sent to the musculoskeletal system through the primary motor cortex (M1) to perform the self-action. Afterwards, the imitator egocentrically observes its own actions so that the imitator will apply the identity transformation. Finally, the coincident feedbacks (e.g., somatosensory and visual) are employed to update the TPF network by means of the error between the sensory consequences of the self-action and the observed prior action.
B. Methods
Network Model and Learning Algorithm
The network architecture and the learning procedure for the IPS/SPL, IPL, and IFG were implemented with radial basis function (RBF) networks and the orthogonal least squares learning algorithm, respectively [16], [17]. The RBF network modeled a mapping between the two dimensional vector spaces of real numbers (for further details see [13]).
Adaptive Visuospatial Transformation System
The transformation system was improved to allow a mapping from the allocentric demonstrator’s workspace (D) to the egocentric imitator’s workspace (I) (Fig. 1b). Such a mapping is a process to approximate the composition of the affine transformation functions and can be simply expressed in mathematical form as:
| (1) |
| (2) |
| (3) |
| (4) |
where AI, AD ∈ ℝ2 are the anthropometric data, θI, θD ∈ ℝ are the viewpoint angles, OI, OD ∈ ℝ2 are the position vectors, TS(·) is the scaling matrix, TR(·) is the rotation matrix, TT(·) is the translation matrix, x, y and denotes the components x and y in the XY plane.
In particular, the rotation angle θz is the angular displacement for the mental rotation from the demonstrator to the imitator’s viewpoint:
| (5) |
where the rotation is counterclockwise if 0° < θz ≤ 180° and clockwise if −180° < θz < 0°, respectively. The neural network for the rotation transformation (3) is composed of two subnetworks: one for the clockwise network, and the other for counterclockwise network. The consideration of these dual subnetworks was guided by neurophysiological principles found in humans [18]. They were efficiently trained using only 25 uniformly distributed reference points fully covering the demonstrator’s workspace until reaching an error tolerance threshold (1.0×10−8 m). After training, these subnetworks performed uniform mental rotation with constant angular rate of rotation (±1° per iteration). This network was separately trained before training of the forward and the inverse computations.
Adaptive Forward and Inverse Systems
Similar to the adaptive visuospatial transformation system, the adaptive forward and inverse systems can be respectively described by the mapping and , where and specify the observed action and the motor plan in the visual (V) and the motor (M) domain.
The coordination between learning of the forward and the inverse systems was conducted until both systems reach the error tolerance thresholds (1.0×10−6 m) throughout a behaviorally realistic two-phase learning approach (i.e., sequences of learning by observation and again by execution). As a premiere simulation, a geometrical right upper limb model having 2 degrees of freedom performed horizontal reaching tasks in a two-dimensional plane.
III. Results
The anthropometric data and the functional range of motion of the right upper limb arm as well as the viewpoint for the demonstrator and the imitator are shown in Table I.
TABLE I.
Anthropometric Data, Functional Range of Motion & Viewpoint
| Dimension name | Demonstrator | Imitator |
|---|---|---|
| Right Upper Arm Length | 0.33 m | 0.16 m |
| Right Forearm Length | 0.27 m | 0.12 m |
| Shoulder Horizontal Adduction (θ1)† | 0° to 120° | 0° to 120° |
| Elbow Horizontal Flexion (θ2)† | 0° to 120° | 0° to 120° |
| Viewpoint‡ | −180° to 180° | 0° to 180° |
The 0° start position for establishing the degrees of each motion is 90° shoulder abduction and 90° elbow extension, respectively.
The viewpoint angle is measured from the Cartesian positive X-axis so that the positive and the negative Y-axis have +90° and −90°, respectively.
A. Adaptive Visuospatial Transformation System
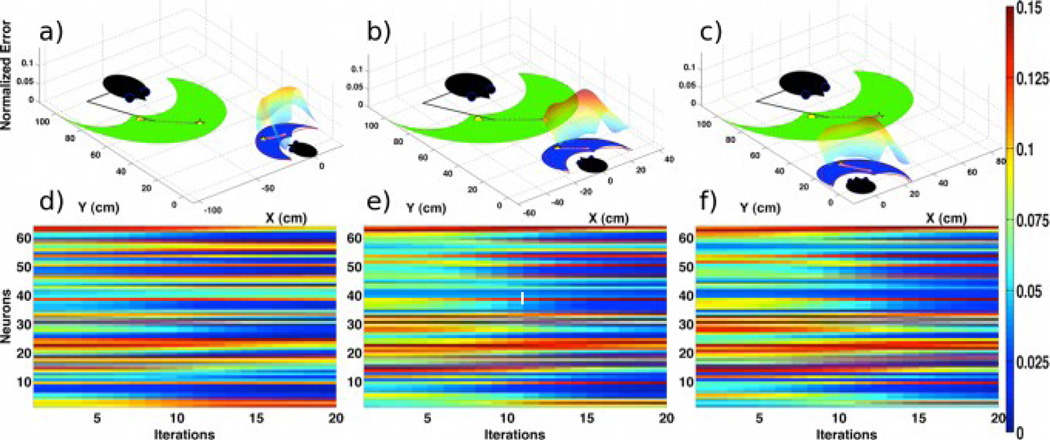
The simulation results revealed that the imitator could successfully transform the demonstrator’s workspace onto its own workspace regardless of mutually different frames of reference and viewpoints (Fig. 2). Our IPS/SPL model was assessed comparing the simulation results with published experimental results in the next two well-known tasks.
Fig. 2.
The demonstrator performs the same reaching action from the imitator’s (a) left side, (b) center, and (c) right side, respectively. The imitator observes the demonstrator’s action while fixing its gaze on the demonstrator. The performance of the visuospatial transformation network is represented as a normalized error surface between the observed and the imitator’s own workspaces, which lies above the imitator’s workspace. (d)–(f) The activation levels over iteration number in a RBF network modeling of the frontal MNS are generally similar across task cases. Currently, the trained neural network contains 64 neurons in its hidden layer, and the reaching action is observed at 20 digitized iteration number (or time).
Frame of Reference and Viewpoint Invariant Frontal MNS
First, the frame of reference and viewpoint invariant frontal MNS were investigated as shown in the literature [3]. The results revealed that the transformation system of the IPS/SPL could induce a similar response of the frontal MNS when the demonstrator performed the same reaching action from the imitator’s center, left, and right sides (Fig. 2). The imitator slightly turned its body towards the demonstrator for the left and right sided cases (here, ±15°). The normalized Euclidean distance between the observed and the imitator’s own workspaces was used to quantify the performance of the IPS/SPL network. Namely, the mean absolute percentage error (or average accuracy) of the transformation network across three task cases was 4.34% ± 1.11%. Besides, the standardized dissimilarity measure (SDM) using procrustes analysis (where values near 0 and 1 indicate a high and low similarity, respectively [19]) revealed a high similarity (only 0.0057 ± 0.0017) between the observed and the transformed spaces. In each case, finally, the normalized activation levels of a RBF network modeling of the frontal MNS were compared to assess its invariant property. An average of correlation coefficients between the activation levels across the cases (0.8544 ± 0.0897) revealed a similar response of the frontal MNS regardless of the demonstrator’s position.
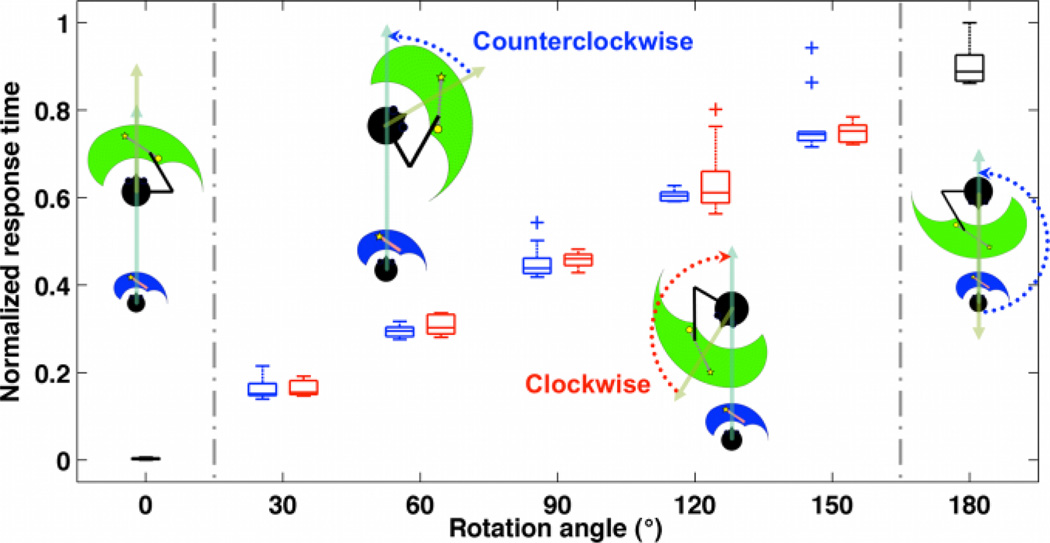
Response Time with respect to the Rotation Angle
In light of previous studies focusing on mental rotation, the relationship between the rotation angle and the response time was examined [20]. Here, the response time was defined as the required time for the IPS/SPL to successfully transform the observed action including rotation, translation, and scaling. Therefore, the response time was not 0 even for a special case of 0° rotation angle (i.e., same viewpoints between the demonstrator and the imitator). In addition, other special case of 180° rotation angle was processed in the counterclockwise network as described in the method section. The results showed that the response time linearly increased with respect to the rotation angle regardless of rotation direction (i.e., counterclockwise or clockwise) (Fig. 3).
Fig. 3.
For a given angle between 30 to 150 degrees, the normalized response time was obtained for both the counterclockwise (blue) and clockwise (red) rotations. The mean and the standard deviation were calculated on 10 trials for each case. The outliers are marked with a plus sign (+).
B. Adaptive Forward and Inverse Systems
The results (not shown here) suggested that the forward and the inverse model could adaptively learn to imitate an action in the imitator’s frame of reference. This suggests that prior knowledge obtained during the observation phase helped the imitator to acquire more rapidly and accurately the action during actual performance. After learning, the imitator was able to imitate sequential reaching actions of a triangular shape with a high similarity SDM 6.25×10−4 as well as a low kinematic error 1.94×10−4 m (for further details see [13]).
IV. Discussion
We amended a previously proposed biologically plausible MNS model for action observation and imitation by including the adaptive parietal MNS and, more importantly, by expanding the IPS/SPL to learn a generalized mapping of the frames of reference and the viewpoints of the demonstrator and the imitator. This resulted in a frame of reference and viewpoint invariant visuospatial representation in the TPF circuit. In particular, as exhibited in humans, the mental rotation network was composed of two subnetworks performing counterclockwise and clockwise rotation to efficiently compute the transformation [21]. For the sake of clarity and conciseness, the discussion will mainly focus on the results related to the IPS/SPL regions.
First, this model could reproduce, to some extent, the neurophysiological findings obtained for the mirror system in monkeys during action observation. Namely, the IPS/SPL of our MNS model could perform transformation for various frames of reference and viewpoints between the demonstrator and the imitator resulting in similar neural activities of the frontal MNS [3]. Thus, we suggest that such a transformation would be performed upstream by the IPS/SPL so that downstream the frontal MNS could process the inverse computation in the egocentric frame of reference independently of the viewpoint from which the action is observed. This would be consistent with the idea that the frontal mirror system in monkeys has neurons that are independent to viewpoint of the observer, and that the activity in the IPS/SPL regions is also related to the viewpoint during action observation [3], [22], [23].
Second, the IPS/SPL of our MNS model was able to reproduce some neurobehavioral findings related to mental rotation tasks evidenced in the literatures. More precisely, in agreement with previous experimental studies, the IPS/SPL simulated similar neural processing times to perform both counterclockwise and clockwise rotation [20]. More importantly, and also consistent with the literature, the neural processing time of the IPS/SPL to perform the mental rotation increased linearly with the magnitude of the rotation angle regardless of the rotation direction [20]. As far as we know, no experimental results investigating both the human MNS and the IPS/SPL regions under various conditions of frames of reference and viewpoints are available in the literature. Therefore, the experimental results mentioned above were obtained during mental rotation of human body parts as well as complex scenes without involving the MNS. However, more recently, it was suggested that, during mental own body rotation, TPF activations and their timing were neuronal correlates of the mental rotation and that the perspective affected also the reaction time [24]. Thus, our MNS model presumes that similar neural processing principles underlying transformation would be commonly recruited during mental rotation, action observation, and imitation when the MNS is engaged. This is in accordance with the neural simulation of action theory which proposes that the motor system is part of a simulation network that is activated during both motor imagery and action observation [25].
Overall, these findings confirm and extend our previous modeling work by suggesting the importance of the visuospatial transformation during action observation and imitation when the MNS is engaged [13]. It must be noted that the current model also contains several limitations. For instance, the implementation of the STS needs to be considered to implement a complete TPF circuit. Another limitation is that the learning of the frontal and parietal MNSs as well as of the IPS/SPL is not combined simultaneously. Thus, future work will incorporate a STS model and examine the concurrent learning of the frontal and parietal MNSs as well as the IPS/SPL regions for action observation and imitation.
Acknowledgments
This work was supported in part by the National Institutes of Health under Grant P01 HD064653.
Contributor Information
Hyuk Oh, Neuroscience and Cognitive Science Program, University of Maryland, College Park, MD 20742 USA.
Rodolphe J. Gentili, Email: rodolphe@umd.edu, Department of Kinesiology, the Maryland Robotics Center, and the Neuroscience and Cognitive Science Program, University of Maryland, College Park, MD 20742 USA.
James A. Reggia, Email: reggia@cs.umd.edu, Department of Computer Science and the University of Maryland Institute for Advanced Computer Studies, University of Maryland, College Park, MD 20742 USA.
José L. Contreras-Vidal, Email: pepe.contreras@ee.uh.edu, Department of Electrical and Computer Engineering, University of Houston, Houston, TX 77004 USA.
References
- 1.Carr L, Iacoboni M, Dubeau MC, Mazziotta JC, Lenzi GL. Neural mechanisms of empathy in humans: A relay from neural systems for imitation to limbic areas. PNAS. 2003;vol. 100:5497–5502. doi: 10.1073/pnas.0935845100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Iacoboni M, Koski LM, Brass M, Bekkering H, Woods RP, et al. Reafferent copies of imitated actions in the right superior temporal cortex. PNAS. 2001;vol. 98:13995–13999. doi: 10.1073/pnas.241474598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Gallese V, Fadiga L, Fogassi L, Rizzolatti G. Action recognition in the premotor cortex. Brain. 1996;vol. 119:593–609. doi: 10.1093/brain/119.2.593. [DOI] [PubMed] [Google Scholar]
- 4.Rizzolatti G, Fogassi L, Gallese V. Neurophysiological mechanisms underlying the understanding and imitation of action. Nat Rev Neurosci. 2001;vol. 2:661–670. doi: 10.1038/35090060. [DOI] [PubMed] [Google Scholar]
- 5.Iacoboni M. Understanding others: imitation, language, and empathy. In: Hurley S, Chater N, editors. Perspectives on Imitation. vol. 1. Cambridge: The MIT Press; 2005. [Google Scholar]
- 6.Miall RC. Connecting mirror neurons and forward models. NeuroReport. 2003;vol. 14:2135–2137. doi: 10.1097/00001756-200312020-00001. [DOI] [PubMed] [Google Scholar]
- 7.Bonaiuto J, Rosta E, Arbib M. Extending the mirror neuron system model, I: Audible actions and invisible grasps. Biol Cybern. 2007;vol. 96:9–38. doi: 10.1007/s00422-006-0110-8. [DOI] [PubMed] [Google Scholar]
- 8.Oztop E, Wolpert D, Kawato M. Mental state inference using visual control parameters. Brain Res Cogn Res. 2005;vol. 22:129–151. doi: 10.1016/j.cogbrainres.2004.08.004. [DOI] [PubMed] [Google Scholar]
- 9.Iacoboni M, Woods RP, Brass M, Bekkering H, Mazziotta JC, Rizzolatti G. Cortical mechanisms of human imitation. Science. 1999;vol. 286:2526–2528. doi: 10.1126/science.286.5449.2526. [DOI] [PubMed] [Google Scholar]
- 10.Buneo CA, Andersen RA. The posterior parietal cortex: sensorimotor interface for the planning and online control of visually guided movements. Neuropsychologia. 2006;vol. 44:2594–2606. doi: 10.1016/j.neuropsychologia.2005.10.011. [DOI] [PubMed] [Google Scholar]
- 11.Culham JC, Kanwisher NG. Neuroimaging of cognitive functions in human parietal cortex. Curr Opin Neurobiol. 2001;vol. 11:157–163. doi: 10.1016/s0959-4388(00)00191-4. [DOI] [PubMed] [Google Scholar]
- 12.Grefkes C, Fink GR. The functional organization of the intraparietal sulcus in humans and monkeys. J Anat. 2005;vol. 207:3–17. doi: 10.1111/j.1469-7580.2005.00426.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Oh H, Gentili RJ, Reggia JA, Contreras-Vidal JL. Learning of Spatial Relationships between Observed and Imitated Actions allows Invariant Inverse Computation in the Frontal Mirror Neuron System; Conf Proc IEEE Eng Med Biol Soc; 2011. pp. 4183–4186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Burgess PW, Dumontheil I, Gilbert SJ. The gateway hypothesis of rostral prefrontal cortex (area 10) function. Trends Cogn Sci. 2007;vol. 11:290–298. doi: 10.1016/j.tics.2007.05.004. [DOI] [PubMed] [Google Scholar]
- 15.Dove A, Pollmann S, Schubert T, Wiggins CJ, von Cramon DY. Prefrontal cortex activation in task switching: an event-related fMRI study. Brain Res Cogn Brain Res. 2000;vol. 9:103–109. doi: 10.1016/s0926-6410(99)00029-4. [DOI] [PubMed] [Google Scholar]
- 16.Chen S, Cowan CFN, Grant PM. Orthogonal least squares learning algorithm for radial basis function networks. IEEE Trans Neural Netw. 1991;vol. 2:302–309. doi: 10.1109/72.80341. [DOI] [PubMed] [Google Scholar]
- 17.Gentili RJ, Oh H, Molina J, Contreras-Vidal JL. Neural network models for reaching and dexterous manipulation in humans and anthropomorphic robot systems. In: Cutsuridis V, Hussain A, Taylor JG, editors. Perception-Action Cycle: Models, Architectures, and Hardware. New York: Springer; 2011. [Google Scholar]
- 18.Cohen MS, Kosslyn SM, Breiter HC, DiGirolamo GJ, Thompson WL, et al. Changes in cortical activity during mental rotation: A mapping study using functional MRI. Brain. 1996;vol. 119:89–100. doi: 10.1093/brain/119.1.89. [DOI] [PubMed] [Google Scholar]
- 19.Seber GAF. Multivariate Observations. Hoboken: John Wiley & Sons; 1984. [Google Scholar]
- 20.Dalecki M, Hoffmann U, Bock O. Mental rotation of letters, body parts and complex scenes: Separate or common mechanisms? Hum Mov Sci. doi: 10.1016/j.humov.2011.12.001. to be published. [DOI] [PubMed] [Google Scholar]
- 21.Burton LA, Wagner N, Lim C, Levy J. Visual field differences for clockwise and counterclockwise mental rotation. Brain Cogn. 1992;vol. 18:192–207. doi: 10.1016/0278-2626(92)90078-z. [DOI] [PubMed] [Google Scholar]
- 22.Caggiano V, Fogassi L, Rizzolatti G, Pomper JK, Their P, et al. View-based encoding of actions in mirror neurons of area f5 in macaque premotor cortex. Curr Biol. 2011;vol. 21:144–148. doi: 10.1016/j.cub.2010.12.022. [DOI] [PubMed] [Google Scholar]
- 23.Shmuelof L, Zohary E. Mirror-image representation of action in the anterior parietal cortex. Nat Neurosci. 2008;vol. 11:1267–1269. doi: 10.1038/nn.2196. [DOI] [PubMed] [Google Scholar]
- 24.Schwabe L, Lenggenhager B, Blanke O. The timing of temporoparietal and frontal activations during mental own body transformations from different visuospatial perspectives. Hum Brain Mapp. 2009;vol. 30:1801–1812. doi: 10.1002/hbm.20764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Jeannerod M. Neural simulation of action: a unifying mechanism for motor cognition. Neuroimage. 2001;vol. 14:S103–S109. doi: 10.1006/nimg.2001.0832. [DOI] [PubMed] [Google Scholar]