Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2013 Jun 26.
Published in final edited form as: Eur J Neurosci. 2009 Dec 18;31(1):42–48. doi: 10.1111/j.1460-9568.2009.07037.x

Lagged cells in the inferior colliculus of the awake ferret

Barak Shechter 1,2, Peter Marvit 3, Didier A Depireux 1,4
Editor: Tomoki Fukai
PMCID: PMC3694174  NIHMSID: NIHMS189686  PMID: 20092554

Abstract

Neurons in primary auditory cortex (AI) encode complex features of the spectral content of sound, such as direction selectivity. Recent findings of temporal symmetry in AI predict a specific organization of the subcortical input into cortex that contributes to the emergence of direction selectivity. We demonstrate two sub-populations of neurons in the central nucleus of the inferior colliculus, which differ in their steady-state temporal response profile: lagged and non-lagged. The lagged cells (23%) are shifted in temporal phase with respect to non-lagged cells and are characterized by an “inhibition first” and delayed excitation in their spectro-temporal receptive fields. Non-lagged cells (77%) have a canonical “excitation first” response. However, we find no difference in the response onset latency to pure tone stimuli between the two sub-populations. Given the homogeneity of tonal response latency, we predict that these lagged cells receive inhibitory input mediated by cortical feedback projections.

Keywords: Auditory, lagged cells, spectro-temporal receptive field, STRF, inferior colliculus, phase, temporal symmetry, direction selectivity

Introduction

Tuning of auditory neurons can be characterized by spectro-temporal receptive fields (STRF), which measure how stimulus history influences neural activity (Aertsen & Johannesma, 1981; Eggermont et al., 1981; Eggermont et al., 1983; Kowalski et al., 1996; deCharms et al., 1998; Depireux et al., 2001; Theunissen et al., 2001; Escabi & Schreiner, 2002; Linden et al., 2003; Shechter & Depireux, 2006; 2007). From the STRF, we extract emergent response properties and stimulus feature selectivity. For instance, cortical cells can respond preferentially to spectral content moving up or down the spectral axis. Such a response is direction selective—a sound attribute encoded in cortex.

Primary auditory cortex (AI) encodes the dynamics of spectral content of sounds (Shechter et al., 2009). How this cortical encoding is constructed from subcortical input is still a subject of debate; however, models derived from cortical data predict a likely organization of fundamental building blocks. It is important to understand how the temporal profile of the neural response depends on input distribution along the spectral axis. Does the cell respond similarly (up to scaling) to all frequencies, or is the temporal response a function of position along the spectral axis? The STRF can be viewed as a series of temporal response profiles arranged along the spectral axis. Direction selectivity requires a precise organization of these profiles along that spectral axis. Their exact arrangement determines the preferred direction for stimulus frequency content. Neurons whose temporal processing is independent of spectral processing (up to scaling) have separable STRFs: they can be expressed as a product of independent spectral and temporal functions (Eggermont et al., 1981; Watson & Ahumada, 1985; Depireux et al., 2001). Spectral and temporal processing are interdependent in direction selective cells; their STRFs are inseparable and cannot be represented simply as the product of spectral and temporal functions.

Simon et al. (2007) found that most AI neurons have inseparable STRFs with temporally symmetric temporal profiles—they shared a common envelope, differing in scale and phase under that envelope. The emergence of temporal symmetry in AI can be accounted for by the existence of two classes of inputs into cortex: lagged and non-lagged. These classes of cells would have separable receptive fields, the distinguishing property between classes being the phase of their temporal response profiles. Given such inputs whose temporal functions can be differentiated by temporal phase, the integrating neuron would have a temporally symmetric response.

Our results parallel a growing body of evidence for similar temporal processing of visual input, where lagged and non-lagged cells underlie direction selectivity in cortex (Mastronarde, 1987b; a). We demonstrate distinct neural classes in the central nucleus of the inferior colliculus (ICC) distinguishable by their response temporal profiles. With ICC an obligatory subcortical convergence of the auditory pathway (Aitkin & Phillips, 1984) and the subcortical-cortical modeling predictions of Simon et. al. (2007), these likely provide the foundation for direction selectivity. The outputs of these cells can be integrated in a thalamo-cortical computational unit to create temporal symmetry and direction selectivity observed in cortex.

Materials and Methods

Surgical preparation

Recordings were from 3 awake adult domestic ferrets (Mustela putorius furo) surgically implanted with chronic multi-electrode arrays containing 8 electrodes each. Electrodes were arranged in a honeycomb pattern (225μm minimal distance between electrodes), as described Dobbins et. al. (2007). All surgical and experimental procedures were approved by the University of Maryland Institutional Animal Care and Use Committee and were in accord with NIH guidelines on the care and use of laboratory animals. Briefly, ferrets were anesthetized with Halothane or Isoflurane (3% induction, then 1.75% maintenance, adjusted to keep heart rate, respiration, and SpO2 within limits), and affixed within a stereotaxic frame. Body temperature was maintained at 37.5°C with a self-regulated heating pad. The skin on the skull was incised along the midline and retracted. After partial bilateral resection of the temporalis muscles, stainless steel screws were inserted around the skull to anchor the subsequent headpost, custom multi-electrode microdrive, and dental cement used to fix the experimental apparatus. A headpost was positioned rostrally over the skull. A small craniotomy was made unilaterally over visual cortex. Visualization of IC was made by evacuating a cylindrical hole 2 mm in diameter within a polyimide tube through cortex. This allowed for an accurate placement of the microdrive, which was slowly lowered into position and affixed to the skull with dental cement. The scalp was then sutured to the cement implant and replaced so the external ears were back in anatomical position. After surgery, the ferrets were given Banamine (1 mg/kg) and Baytril (0.2 mg/kg) for three recovery days before recording began.

Neural recording

Recording sessions took place inside a double-walled sound booth (IAC, Bronx, NY). The ferret was placed in a comfortable holder, with its head fixed using the implanted headpost to ensure the animal stayed within the calibrated sound field and to minimize movement noises. The animal was monitored through a closed-circuit video, and treats (e.g., Ferretone) were given between stimulus presentations to preserve wakefulness as deemed needed from the emergence of monitored slow-wave activity.

Neural activity was recorded with parylene-coated tungsten microelectrodes (initial impedance 3-6 MΩ at 1 kHz, Micro Probe, Inc, Gaithersburg, MD). Electrodes were advanced as an ensemble (in 35μm steps) by manually turning a screw. All recordings were marked with the depth relative to when spikes were first detected upon lowering the electrode bundle. The border of ICC was determined physiologically by the transition of broadly tuned cells to neurons with low CF and comparatively narrower tuning (Moore et al., 1983).

Continuous signals from the electrodes were band-pass filtered from 300 Hz to 6 kHz and saved for offline analysis using the Neuralynx Cheetah data acquisition system (Neuralynx, Tucson, AZ). After a recording session, the neural events were extracted from the continuous record as voltage excursions that exceeded 2.8 times the standard deviation of the signal measured during pre-stimulus silences. Extracted spike waveforms were then sorted using a custom modification of the Autoclass algorithm (http://ic-www.arc.nasa.gov/ic/projects/bayes-group/autoclass/). Spike times were assigned to the peak of the waveform.

Stimulus generation and presentation

All stimuli were generated digitally in MATLAB (Natick, MA), converted to an analog voltage (TDT RX6, Tucker David-Technologies, Alachua, FL) at 100 kHz sampling rate, processed with an analog attenuator (TDT PA5), amplified (Crown DX-70) and presented free field from an overhead speaker (Manger Transducer, Manger, Germany) located 1m at zenith relative to the animal's head in order to minimize spatial/side preferences of the IC neurons under study (Moore, 1982). The sound field was calibrated to obtain a flat response (to within 1.5 dB) from the loudspeaker where the animal's head would be located.

Data analysis

Spectro-temporal receptive fields were computed from the responses to a set of well structured, spectro-temporally rich broadband stimuli known as temporally orthogonal ripple combinations (TORCs). These TORCs are constructed as sums of component auditory gratings—or ripples, each of which have a spectro-temporal profile that is modulated sinusoidally in log-spectrum and in time. The modulation of a grating is characterized in spectrum by its spectral density Ω (cycles/octave), in time by its temporal periodicity w (Hz), and in amplitude by its excursions away from the mean level of the stimulus (modulation depth ΔA, % of mean). The spectro-temporal modulation envelope of a TORC stimulus S(x,t), where x corresponds to frequency f as x = log2(f/f0), f0 the lower edge of the spectrum, and time t, is given as

S(x,t)=L[1+∑iΔA⋅cos(2π(Ωi⋅x+wi⋅t)+ϕi)]

for a linear modulation. L is the average level of the stimulus (measured as the root-mean-square of the stimulus with reference to a 1 kHz sine tone) and ϕi is the starting phase of each component grating. The TORC stimuli were created by modulating 200 logarithmically spaced tones per octave over a bandwidth of 7 octaves; as a result, these stimuli did not elicit the perception of a pitch.

The TORCs were composed of gratings with the same spectral density, but different temporal periodicities, thus sampling a set of points in spectro-temporal space with a single sound. The spectral densities and temporal periodicities spanned by the stimulus set ranged from -2 to 2 cyc/oct and from 4 to 48 Hz, respectively. Each stimulus condition was presented for a duration of 18 seconds at 50 to 75 dB SPL and at 90% modulation.

The derivation of the steady state STRF from TORC stimuli is described in detail in Klein et al. (2000). Briefly, a reverse correlation with the stimulus spectro-temporal envelope is used to obtain the STRF from the spike train elicited by the stimulus. In order to allow the response to reach a steady-state, the spike-triggered analysis was started at 250 msec after stimulus onset, thereby removing the effect of level transients present at the onset of the stimulus. A signal-to-noise ratio (SNR) was computed from the STRF as described in Shechter and Depireux (2007) in order to assess the reliability of the response. Only cells with SNR > 2 were analyzed in this study.

The temporal profile of the STRF was extracted by singular value decomposition (SVD), which decomposes the STRF into the product of spectral and temporal profiles. Since there is an ambiguity in sign of the spectral and temporal functions, we set the temporal profile to be positive at the time point corresponding to the excitatory peak of the STRF. For a linear phase filter (for example, temporal profile of the STRF), its envelope latency and phase under that envelope can be determined from the phases of its Fourier components. The slope and intercept of the unwrapped phases (measured as a linear function of Fourier component) correspond to the envelope latency and phase delay of the profile under that envelope, respectively. The temporal phase of the STRF was determined by the constant term of a linear fit of phase from the Fourier transform of the STRF temporal profile. The latency of the STRF excitatory peak was determined by the point in time corresponding to the STRF temporal profile maximum.

As a basis of comparison for STRF latency, cells were also characterized by their responses to pure tones, presented randomly across 8.5 octaves, from 100 Hz to 36200 Hz (the upper frequency of hearing of the ferret) in 1/3 octave steps. A baseline firing rate and its standard deviation were computed from the spike rate in a 50ms window preceding each stimulus presentation. Response latency to pure tone stimuli was defined as the point in stimulus time where the mean response (averaged across all frequency presentations) deviated in the absolute from the baseline firing rate by 2.5 standard deviations.

Results

Lagged and non-lagged cells in inferior colliculus

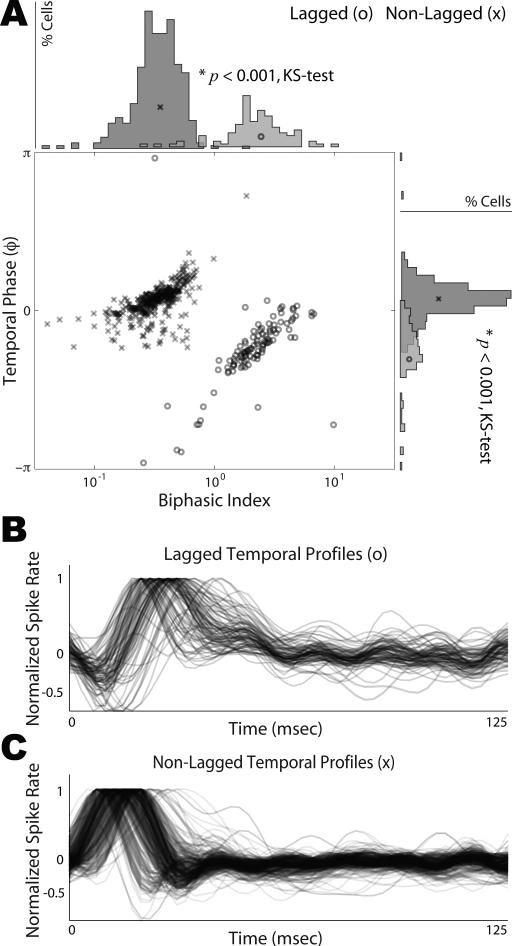
We analyzed neurophysiological data from a population of 436 single unit recordings in the central nucleus of the inferior colliculus of awake ferrets chronically implanted with a custom multi-electrode array device. Each cell was characterized by a spectro-temporal receptive field (STRF) computed from its response to a set of auditory gratings (see Materials and Methods). Our underlying hypothesis was that these STRFs would exhibit a dichotomy in their temporal profiles consistent with the predictions borne out of the temporal symmetry observed in primary cortical STRFs. More specifically, we found that our population of cells could be classified into two sub-populations based on the phase of the temporal profile under its envelope and on the biphasic index (Fig. 1A). This phase determines how the temporal response profile oscillates under its envelope—for example, whether it is inhibition first (lagged) or excitation first (non-lagged). The biphasic index measures the degree to which the response is monophasic or biphasic. It is computed as the absolute magnitude ratio of the second peak to the first peak of the temporal response profile. We found that the STRF for each cell was separable, and could thus be described as having a single temporal profile common across all frequency channels (up to an overall scaling factor). We extracted that temporal profile by SVD, and computed its phase as described above (see Materials and Methods, supplemental Fig. S1).

Figure 1.

Figure 1

Open in a new tab

Distribution of Temporal Phase and Biphasic Index. A, For the population of neurons analyzed in this study, we extracted the temporal profile of the STRF. The temporal profile's phase is plotted as a function of its biphasic index. The marginal distributions of temporal phase and biphasic index are shown. Two sub-populations of responses are readily distinguished, which we call lagged and non-lagged, and are significantly distinct along each marginal (KS test, p < 0.001). Lagged cells are represented by ‘o’ and non-lagged cells are represented by ‘x’. Note that temporal phase is periodic with π = –π. B-C, The STRF temporal profiles from lagged (B) and non-lagged (C) cells were normalized to their absolute maximum and plotted. Lagged profiles have a characteristic inhibition first and delayed excitation, whereas, non-lagged profiles first show excitation followed by a delayed inhibition. The time course of excitation and inhibition are characteristic of each sub-population, and not peak latency, which can vary considerably within each class.

By plotting the phase of the temporal response profile as a function of the biphasic index, we found the responses to be well separated into two classes, which are depicted in Fig. 1A. Based on this analysis, 23% of cells could be classified as lagged cells and 77% of cells as non-lagged cells. While there are specific differences in the temporal profile from cell to cell, the overall differences between the two sub-populations are readily distinguishable. In Fig. 1B-C, we plot an overlay of the normalized temporal profiles for lagged and non-lagged cells, respectively. The lagged profiles have a characteristic inhibition first and delayed excitation. In contrast, the non-lagged profiles show low latency excitation followed by a delayed inhibition. Although there is considerable variability in the absolute latency within these classes, the relevant factor in distinguishing these cells lies in the time course of excitation and inhibition of the temporal profiles, which correspond to the phase distribution of each class. Note that lagged and non-lagged cells were found interspersed, with no clear spatial segregation of the two classes.

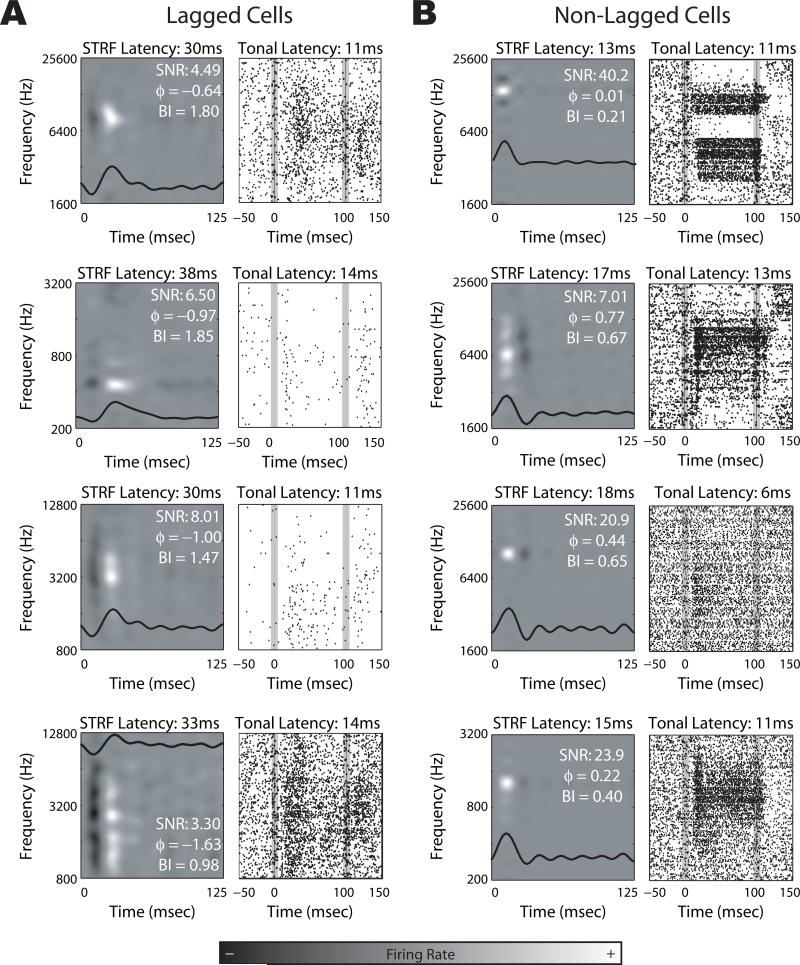
In Fig. 2, we show example STRFs and tonal responses from both lagged and non-lagged cells. The temporal profile of the response is overlaid on the corresponding STRF. The lagged cells all show inhibition first, whereas the opposite is true for non-lagged cells. The non-lagged cells show excitation first, which may or may not be followed by inhibition, thus determining whether a response is monophasic or biphasic. It is important to note that whether a response is lagged or non-lagged does not determine the latency of the cell (as measured by the peak of the STRF); rather, it determines the latency of the STRF peak only with respect to the envelope of the temporal profile: Given the same temporal response profile envelope, a lagged cell will have a longer latency to STRF peak than a non-lagged cell; however, the envelope of the temporal response is not constant across different cells. As such, there is a broad (and overlapping) distribution of latencies within each sub-population, which is readily seen both in the temporal profiles in Fig. 1 and in the example STRFs in Fig. 2. The classification of lagged or non-lagged only corresponds to the timing of excitation and inhibition in the temporal response profile.

Figure 2.

Figure 2

Open in a new tab

Example responses from lagged and non-lagged cells. A-B, STRF and tonal characterizations are displayed for example lagged (A) and non-lagged (B) cells. The temporal response profile of the STRF is overlaid. The onset and offset of the tonal stimuli in the tonal response areas are denoted by the vertical gray bars. SNR: signal-to-noise, ϕ : phase of the temporal profile (in radians), BI: biphasic index.

Latency of Lagged and Non-Lagged Responses

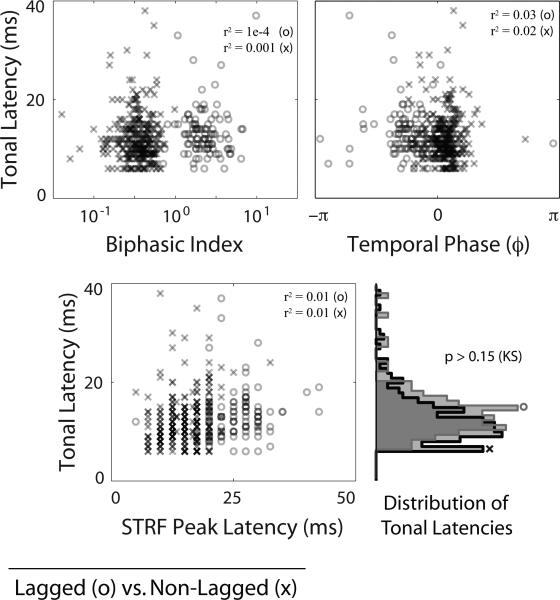
In addition to spectro-temporal receptive field characterization of neural responses in IC, we measured the responses of these cells to pure tone stimuli. If these cells were lagged as an inherent property of feed-forward tuning, we would expect to see a strong correlation between response latency for both types of characterization. We compared the latency of the response to pure tone stimuli (onset response defined as 2.5 standard deviations away from baseline, pre-stimulus firing rate) to the latency of the excitatory peak of the STRF. In Fig. 3, we depict this relationship, in which we found no significant correlation between both measures of latency. We also found no significant correlation between tonal latency and either the biphasic index or the phase of the temporal profile. The distributions of tonal latencies were not significantly different between lagged and non-lagged cells (KS test, p > 0.15).

Figure 3.

Figure 3

Open in a new tab

Comparison to Tonal Response Latency. We plot tonal response latency as a function of biphasic index (top left), phase of the STRF temporal profile (top right), and STRF peak latency (bottom left). Lagged cells are represented by ‘o’ and non-lagged cells are represented by ‘x’. The marginal distributions of tonal response latency for lagged and non-lagged cells are shown (bottom right). There is no significant correlation between tonal response latency and biphasic index, temporal phase, or STRF peak latency (r2 ≤ 0.03, values shown), nor is there any significant difference between tonal response latencies for lagged and non-lagged cells (KS test p > 0.15). This suggests that the lagged profile results from longer latency feedback measured in steady-state, as opposed to being a feed-forward property of the ascending projections. Note that temporal phase is periodic with π = –π.

Discussion

In this study, we characterized the temporal response profiles of neurons in ICC, and found these could be segregated into two distinct classes on the basis of temporal phase and biphasic index. These two classes—lagged and non-lagged—differed in the temporal order of excitation and inhibition. We further found that these cells had statistically equivalent onset response latencies with respect to pure tone stimuli, indicating that lagged and non-lagged response characteristics diverged in the steady state. These two classes of responses likely provide the necessary substrate for temporal symmetry and direction selectivity, which have been well documented in cortical responses.

Temporal symmetry and direction selectivity

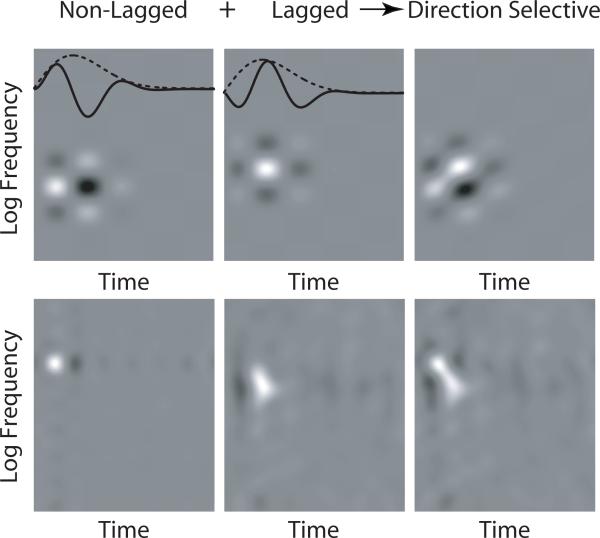
Lagged responses have long been documented in visual responses (Mastronarde, 1987b; a). De Valois et al. (1998; 2000) showed that the temporal response of simple cells in VI could be separated into two classes—monophasic or biphasic—based on the ratio of the magnitudes of the first two extrema (the biphasic index). Saul et al. (2005; 2008) further showed that across cells, responses have a broad distribution of temporal phase. The integration of these classes of inputs—namely, the differences in the temporal characteristics of these lagged cells with respect to their non-lagged counterparts—provides the input needed to create directionally selective responses for visual stimuli. A similar input pattern of lagged and non-lagged subcortical responses into auditory cortex would provide a substrate for creating responses which are selective for the direction of change in frequency content. In Fig. 4, we show simulated examples of direction selective STRFs created by adding lagged and non-lagged STRFs.

Figure 4.

Figure 4

Open in a new tab

Direction selectivity emerges from lagged and non-lagged responses. A direction selective STRF (right) can be created by adding non-lagged (left) and lagged (middle) separable STRFs. Top. Illustrative example using model lagged and non-lagged STRFs. The temporal profiles (overlaid, solid line) of the non-lagged and lagged STRFs share the same envelope (overlaid, dotted line), but are phase shifted with respect to each other. Bottom. Using non-lagged and lagged STRFs shown in Fig. 2, we constructed a direction selective, temporally symmetric STRF typical of cells recorded in AI.

In Simon et al. (2007), the authors found that the responses of neurons in AI were temporally symmetric. The implications of temporal symmetry on the STRF relate the temporal profiles of the response to different spectral inputs. In a temporally symmetric STRF, all temporal cross-sections share the same normalized envelope, but are scaled and phase-shifted under that envelope with respect to each other. A potential input scheme to create such a response pattern might be to have complete spectral support for all phase-shifted temporal cross-sections: in other words, all response phases observed in cortex would already exist in subcortical responses. However, a simpler approach involves having two classes of inputs whose responses are in temporal quadrature. Given two such classes, an integrating neuron could create a response for which the envelope is constant with respect to different spectral inputs, but of arbitrary scaling and phase-shift. The example in Fig. 4 shows temporally symmetric and direction selective STRFs, created from two inputs in temporal quadrature. The results presented in this study demonstrate the existence of two such classes of temporal response phase in the ICC, in support of the latter formulation. The comparatively simpler (separable) receptive fields in IC give rise to the more complex, temporally symmetric receptive fields observed in cortex.

Simon et al. (2007) hypothesized the existence of two classes of cells earlier in the pathway, called lagged and non-lagged. While non-lagged cells have the canonical excitation first temporal response, lagged cells effectively have temporally shifted STRFs with an early inhibition compared to their non-lagged counterparts. In bats, Galazyuk et al. (2005); Sullivan (1982); Voytenko and Galazyuk (2007) refer to “inhibition first” in a sizable proportion of collicular cells as a “paradoxical latency shift.” Whereas they ascribe this to computations that are bat-specific, such computations necessary to extract the spectral profile are quite general and not restricted specifically to hearing specialists.

Corticofugal source of lagged responses

In order to determine the source of the lagged temporal response profile, as measured by the STRF, we measured response latency to pure tone stimuli in both lagged and non-lagged cells. If lagged cells were lagged as an inherent property of feed-forward tuning, we would expect to see a strong correlation between tonal response latency and STRF latency. Consistent with that, we would also expect different tonal latencies for lagged vs. non-lagged cells. When we compared tonal latency with the latency of the excitatory peak of the STRF, we found no significant correlation between both measures of latency, nor was there any significant difference between tonal latency for lagged and non-lagged cells (KS test, p > 0.15). Since the STRF is a steady state measure, it characterizes the response of the neuron to ongoing modulations, once the network has had time to converge. The similarity in tonal latency distributions therefore suggests that the lagged temporal profile of the STRF is resultant of longer latency feedback inhibition. This assertion is strengthened by recent findings by Ma and Suga (2008) in which corticofugal activity modulated the latency of collicular responses, presumably through inhibition. These tonal data suggest that without cortical feedback, the STRFs of lagged cells would revert to the canonical non-lagged profile. Further supporting evidence would be derived from electrophysiological characterization of these lagged cells in IC under reversible inactivation of cortical back-projections.

Given the similarity in tonal latency for both lagged and non-lagged cells, we hypothesize that the lagged profile, being a steady-state response, derives from feedback projections. We predict that the emergence of lagged responses we observe in IC requires inhibitory input resulting from corticofugal feedback projections. Although the cortical output is mainly excitatory, it might preferentially activate local inhibitory circuitry in IC, including the external nucleus of the IC (Jen et al., 2001; Lim & Anderson, 2007). We have not observed lagged responses in anesthetized preparations, nor have they been reported in the auditory literature. This is presumably due to the reduction in overall levels of cortical activity associated with anesthesia—thereby changing the network state of non-evoked activity and reducing feedback inputs. Anatomically, modulating projections have been shown to exist which emanate from auditory cortical regions, and project back to IC cells (Bajo et al., 2007; Lim & Anderson, 2007). The steady-state response we measure and characterize by the STRF already includes contributions from these feedback projections in addition to the feed-forward activation of the pathway.

Supplementary Material

Supp Fig s1
2

Supplemental Figure S1. Extraction of the phase of the STRF temporal profile. (1) For separable STRFs, singular value decomposition (SVD) separates the STRF into the product of a spectral profile rf (x) and a temporal profile ir(τ). (2) In order to compute the phase of the temporal profile, we first compute its Fourier transform (FFT) in order to obtain ĨR(w), a complex valued function which specifies the amplitude A(w) and phase ϕ(w) for each harmonic w component of the temporal profile. (3) A linear regression is then fit to ϕ(w) using the phases of the first six harmonics. The phase of the temporal profile is extracted as the phase intercept along the ordinate.

Acknowledgments

The authors thank Yadong “KK” Ji for extensive help in animal care and data acquisition and Alan Saul for extensive and insightful discussions. This research was funded by NIH/NIDCD RO01 DC005937 awarded to DAD. PM also received support from training grant NIH/NINDS 2T32NS007375-11.

Abbreviations

AI

primary auditory cortex

IC

inferior colliculus

ICC

central nucleus of the inferior colliculus

SNR

signal-to-noise ratio

STRF

spectro-temporal receptive field

SVD

singular value decomposition

TORC

temporally orthogonal ripple combination

References

  1. Aertsen AM, Johannesma PI. The spectro-temporal receptive field. A functional characteristic of auditory neurons. Biol Cybern. 1981;42:133–143. doi: 10.1007/BF00336731. [DOI] [PubMed] [Google Scholar]
  2. Aitkin LM, Phillips SC. Is the inferior colliculus an obligatory relay in the cat auditory system? Neuroscience letters. 1984;44:259–264. doi: 10.1016/0304-3940(84)90032-6. [DOI] [PubMed] [Google Scholar]
  3. Bajo VM, Nodal FR, Bizley JK, Moore DR, King AJ. The ferret auditory cortex: descending projections to the inferior colliculus. Cereb Cortex. 2007;17:475–491. doi: 10.1093/cercor/bhj164. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. De Valois RL, Cottaris NP. Inputs to directionally selective simple cells in macaque striate cortex. Proc Natl Acad Sci U S A. 1998;95:14488–14493. doi: 10.1073/pnas.95.24.14488. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. De Valois RL, Cottaris NP, Mahon LE, Elfar SD, Wilson JA. Spatial and temporal receptive fields of geniculate and cortical cells and directional selectivity. Vision Res. 2000;40:3685–3702. doi: 10.1016/s0042-6989(00)00210-8. [DOI] [PubMed] [Google Scholar]
  6. deCharms RC, Blake DT, Merzenich MM. Optimizing sound features for cortical neurons. Science (New York, N.Y. 1998;280:1439–1443. doi: 10.1126/science.280.5368.1439. [DOI] [PubMed] [Google Scholar]
  7. Depireux DA, Simon JZ, Klein DJ, Shamma SA. Spectro-temporal response field characterization with dynamic ripples in ferret primary auditory cortex. Journal of neurophysiology. 2001;85:1220–1234. doi: 10.1152/jn.2001.85.3.1220. [DOI] [PubMed] [Google Scholar]
  8. Dobbins HD, Marvit P, Ji Y, Depireux DA. Chronically recording with a multi-electrode array device in the auditory cortex of an awake ferret. J Neurosci Methods. 2007;161:101–111. doi: 10.1016/j.jneumeth.2006.10.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Eggermont JJ, Aertsen AM, Hermes DJ, Johannesma PI. Spectro-temporal characterization of auditory neurons: redundant or necessary. Hear Res. 1981;5:109–121. doi: 10.1016/0378-5955(81)90030-7. [DOI] [PubMed] [Google Scholar]
  10. Eggermont JJ, Aertsen AM, Johannesma PI. Quantitative characterisation procedure for auditory neurons based on the spectro-temporal receptive field. Hear Res. 1983;10:167–190. doi: 10.1016/0378-5955(83)90052-7. [DOI] [PubMed] [Google Scholar]
  11. Escabi MA, Schreiner CE. Nonlinear spectrotemporal sound analysis by neurons in the auditory midbrain. J Neurosci. 2002;22:4114–4131. doi: 10.1523/JNEUROSCI.22-10-04114.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Galazyuk AV, Lin W, Llano D, Feng AS. Leading inhibition to neural oscillation is important for time-domain processing in the auditory midbrain. Journal of neurophysiology. 2005;94:314–326. doi: 10.1152/jn.00056.2005. [DOI] [PubMed] [Google Scholar]
  13. Jen PH, Sun X, Chen QC. An electrophysiological study of neural pathways for corticofugally inhibited neurons in the central nucleus of the inferior colliculus of the big brown bat, Eptesicus fuscus. Experimental brain research. Experimentelle Hirnforschung. 2001;137:292–302. doi: 10.1007/s002210000637. [DOI] [PubMed] [Google Scholar]
  14. Klein DJ, Depireux DA, Simon JZ, Shamma SA. Robust spectrotemporal reverse correlation for the auditory system: optimizing stimulus design. Journal of computational neuroscience. 2000;9:85–111. doi: 10.1023/a:1008990412183. [DOI] [PubMed] [Google Scholar]
  15. Kowalski N, Depireux DA, Shamma SA. Analysis of dynamic spectra in ferret primary auditory cortex. I. Characteristics of single-unit responses to moving ripple spectra. Journal of neurophysiology. 1996;76:3503–3523. doi: 10.1152/jn.1996.76.5.3503. [DOI] [PubMed] [Google Scholar]
  16. Lim HH, Anderson DJ. Antidromic activation reveals tonotopically organized projections from primary auditory cortex to the central nucleus of the inferior colliculus in guinea pig. Journal of neurophysiology. 2007;97:1413–1427. doi: 10.1152/jn.00384.2006. [DOI] [PubMed] [Google Scholar]
  17. Linden JF, Liu RC, Sahani M, Schreiner CE, Merzenich MM. Spectrotemporal structure of receptive fields in areas AI and AAF of mouse auditory cortex. Journal of neurophysiology. 2003;90:2660–2675. doi: 10.1152/jn.00751.2002. [DOI] [PubMed] [Google Scholar]
  18. Ma X, Suga N. Corticofugal modulation of the paradoxical latency shifts of inferior collicular neurons. Journal of neurophysiology. 2008;100:1127–1134. doi: 10.1152/jn.90508.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Mastronarde DN. Two classes of single-input X-cells in cat lateral geniculate nucleus. I. Receptive-field properties and classification of cells. Journal of neurophysiology. 1987a;57:357–380. doi: 10.1152/jn.1987.57.2.357. [DOI] [PubMed] [Google Scholar]
  20. Mastronarde DN. Two classes of single-input X-cells in cat lateral geniculate nucleus. II. Retinal inputs and the generation of receptive-field properties. Journal of neurophysiology. 1987b;57:381–413. doi: 10.1152/jn.1987.57.2.381. [DOI] [PubMed] [Google Scholar]
  21. Moore DR. Late onset of hearing in the ferret. Brain research. 1982;253:309–311. doi: 10.1016/0006-8993(82)90698-9. [DOI] [PubMed] [Google Scholar]
  22. Moore DR, Semple MN, Addison PD. Some acoustic properties of neurones in the ferret inferior colliculus. Brain research. 1983;269:69–82. doi: 10.1016/0006-8993(83)90963-0. [DOI] [PubMed] [Google Scholar]
  23. Saul AB. Lagged cells. Neurosignals. 2008;16:209–225. doi: 10.1159/000111564. [DOI] [PubMed] [Google Scholar]
  24. Saul AB, Carras PL, Humphrey AL. Temporal properties of inputs to direction-selective neurons in monkey V1. J Neurophysiol. 2005;94:282–294. doi: 10.1152/jn.00868.2004. [DOI] [PubMed] [Google Scholar]
  25. Shechter B, Depireux DA. Response adaptation to broadband sounds in primary auditory cortex of the awake ferret. Hearing research. 2006;221:91–103. doi: 10.1016/j.heares.2006.08.002. [DOI] [PubMed] [Google Scholar]
  26. Shechter B, Depireux DA. Stability of spectro-temporal tuning over several seconds in primary auditory cortex of the awake ferret. Neuroscience. 2007;148:806–814. doi: 10.1016/j.neuroscience.2007.06.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Shechter B, Dobbins HD, Marvit P, Depireux DA. Dynamics of spectro-temporal tuning in primary auditory cortex of the awake ferret. Hear Res. 2009;256:118–130. doi: 10.1016/j.heares.2009.07.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Simon JZ, Depireux DA, Klein DJ, Fritz JB, Shamma SA. Temporal symmetry in primary auditory cortex: implications for cortical connectivity. Neural Comput. 2007;19:583–638. doi: 10.1162/neco.2007.19.3.583. [DOI] [PubMed] [Google Scholar]
  29. Sullivan WE., 3rd Possible neural mechanisms of target distance coding in auditory system of the echolocating bat Myotis lucifugus. Journal of neurophysiology. 1982;48:1033–1047. doi: 10.1152/jn.1982.48.4.1033. [DOI] [PubMed] [Google Scholar]
  30. Theunissen FE, David SV, Singh NC, Hsu A, Vinje WE, Gallant JL. Estimating spatio-temporal receptive fields of auditory and visual neurons from their responses to natural stimuli. Network (Bristol, England) 2001;12:289–316. [PubMed] [Google Scholar]
  31. Voytenko SV, Galazyuk AV. Intracellular recording reveals temporal integration in inferior colliculus neurons of awake bats. Journal of neurophysiology. 2007;97:1368–1378. doi: 10.1152/jn.00976.2006. [DOI] [PubMed] [Google Scholar]
  32. Watson AB, Ahumada AJ., Jr. Model of human visual-motion sensing. Journal of the Optical Society of America. 1985;2:322–341. doi: 10.1364/josaa.2.000322. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supp Fig s1
NIHMS189686-supplement-Supp_Fig_s1.eps (587.2KB, eps)
2

Supplemental Figure S1. Extraction of the phase of the STRF temporal profile. (1) For separable STRFs, singular value decomposition (SVD) separates the STRF into the product of a spectral profile rf (x) and a temporal profile ir(τ). (2) In order to compute the phase of the temporal profile, we first compute its Fourier transform (FFT) in order to obtain ĨR(w), a complex valued function which specifies the amplitude A(w) and phase ϕ(w) for each harmonic w component of the temporal profile. (3) A linear regression is then fit to ϕ(w) using the phases of the first six harmonics. The phase of the temporal profile is extracted as the phase intercept along the ordinate.

NIHMS189686-supplement-2.pdf (79.1KB, pdf)

RESOURCES