The fine structure of shape tuning in area V4

SUMMARY

Previous studies have shown that neurons in area V4 are involved in the processing of shapes of intermediate complexity and are sensitive to curvature. These studies also suggest that curvature tuned neurons are position-invariant. We sought to examine the mechanisms that endow V4 neurons with these properties. Consistent with previous studies, we found that response rank•order to the most• and least•preferred stimuli were preserved throughout the RF. However, a fine-grained analysis of shape tuning revealed a surprising result: V4 neurons tuned to highly curved shapes exhibit very limited translation invariance. At a fine spatial scale, these neurons exhibit local variation in orientation. In contrast, neurons that prefer straight contours exhibit spatially-invariant orientation tuning, and homogenous fine-scale orientation maps. Both these patterns are consistent with a simple orientation-pooling model, with tuning for straight or curved shapes resulting, respectively, from pooling of homogenous or heterogeneous orientation maps inherited from early visual areas.

INTRODUCTION

Visual shape information is processed in the ventral cortical pathway which progresses from the primary visual cortex (V1), the secondary cortex (V2), intermediate areas (V3/V4) and finally onto the inferotemporal (IT) cortex (Felleman & Essen, 1991). In the earlier stages, shape is encoded primarily through local orientation in V1 (Hubel & Wiesel, 1959; Hubel & Wiesel, 1965; Hubel & Wiesel, 1968) and combinations of orientations in V2 (Anzai et al., 2007; Tao et al., 2012). At the final stages in IT, cells have been shown to be selective for complex objects like faces (Desimone et al., 1984; Tanaka et al., 1991; Tsao et al., 2006). How this transformation is achieved remains largely unknown. In addition, the selectivity to complex features becomes more invariant to simple stimulus transformations such as size or spatial position, as one traverses the ventral cortical hierarchy (Rust & DiCarlo, 2010). To understand how contours of objects are integrated into coherent percepts in the later stages, a detailed understanding of shape processing in intermediate stages like V4 is critical.

Previous studies (Pasupathy & Connor, 1999; Pasupathy & Connor, 2001) suggest that neurons in monkey visual area V4 are involved in the processing of shapes of intermediate complexity and are sensitive to curvature. These studies showed that V4 neurons tend to respond more strongly to a preferred stimulus, as compared to a null stimulus, throughout the receptive field – a form of translation invariance. However, little is known about the mechanisms that underlie shape tuning of neurons in area V4 nor about the degree to which translation invariance depends on stimulus complexity. Using a dense mapping procedure, we sought to understand the detailed structure of shape selectivity within V4 receptive fields.

RESULTS

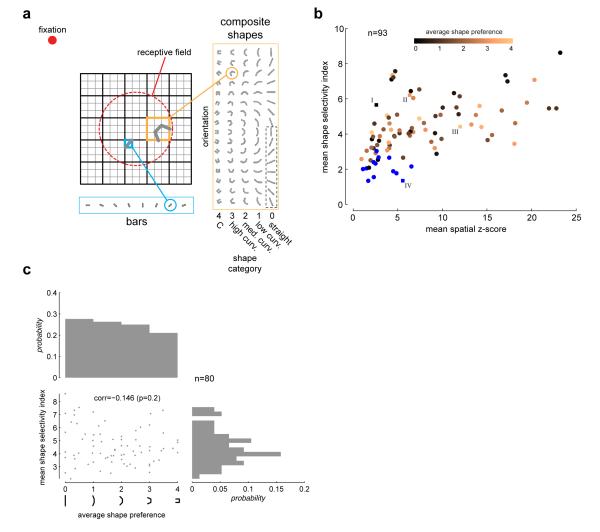
We analyzed responses from 93 isolated neurons in area V4 of two awake behaving male macaques (see Methods). The stimuli consisted of oriented bars presented alone, or linked end to end to form curves or in the most tightly curved conditions, “C” shapes (Fig 1a). Bars were presented at 8 orientations. Composite shapes were composed of 3 bars, linked together to yield 5 categories of shapes: straight, low curvature, medium curvature, high curvature and “C” shape. Stimuli were presented in fast reverse correlation sequences (16 ms duration, exponential distributed delay between stimuli with a mean delay of 16 ms) at various locations within the receptive field (RF) of peripheral V4 neurons (2°-12° eccentricity), while the monkeys maintained fixation for 3s. The composite shapes were presented on a 5×5 location grid centered on the RF, while the oriented bars were presented on a finer 15×15 location grid. The grid of locations and the size of visual stimuli were scaled with RF eccentricity to maintain the same proportions as shown in Fig 1a. A pseudo-random sequence from the combined stimulus sets was presented in each trial.

Fig 1. Stimuli and selectivity.

(a) V4 receptive fields were probed with fast reverse correlation sequences drawn randomly from a set of bars or bar-composite shapes while the animal maintained fixation for 3s. Bars were presented at 8 orientations on a fine 15×15 location grid centered on the neuron’s receptive field (red dashed circle, drawn for illustrative purposes only). The composite stimuli were composed of 3 bars. The end elements were symmetrically linked to the central element at 5 different conjunction angles (0°,22.5°,45°,67.5° an d 90°). These 5 conjunction levels (enumerated as 0=straight, 1=low curvature, 2=medium curvature, 3=high curvature and 4=“C”), together with 16 orientations, yielding a total of 72 unique stimuli (although shown for aesthetic completion, the lower half of the zero curvature shapes [dotted box] is identical to the upper half and was not presented). The composite shapes were presented on a coarser 5×5 location grid that spanned the finer grid. A pseudorandom sequence from the combined stimulus set was shown in each trial. The stimulus duration was 16 ms with an exponentially distributed mean delay of 16 ms between stimuli. (b) Scatter plot of mean shape selectivity index (SSI, see Methods) versus mean spatial z-scores (both means taken across all spatially significant locations) for all candidate neurons (n=93). 13 neurons that were not shape selective are marked in blue. The remaining 80 neurons are color-coded by their average shape preference. Example neurons in Figs 2 and 3 are highlighted. (c) Scatter-plot of mean shape selectivity index (as in b) versus average shape preference for the set of neurons that were significantly shape selective (n=80). There is a non-significant correlation between the two quantities, indicating that shape-selectivity is not significantly different across cells with preference for different shape categories. Also shows are the marginal distributions.

We found that the majority of neurons in our population were significantly selective to the composite contours. Example neurons with significant tuning for composite contours are illustrated in Fig 2 (neurons I, II, and III). The middle panels (labeled b) show the mean firing rate response to each of the composite forms tested (5×16 array) at the most responsive spatial location. The adjacent panels to the right show the z-scores of the responses after subtracting the mean spatial response (see Methods and Supp Fig 1a for details of assessing significance). Example neuron I is preferentially tuned to straight shapes, neuron II to medium curvature shapes, and neuron III to high curvature/”C” shapes. Neuron IV had a significant spatial response, but no significant shape selectivity. The distribution of spatial and shape selective tuning is shown in Fig 1b. Across the population, 80 of 93 neurons showed significant shape selectivity while a smaller subset (n=13, labeled in blue) had spatial tuning without significant shape tuning. We did not analyze this subset further. Furthermore, among neurons with significant shape selectivity, those preferring either straight or more curved stimuli exhibited similar degrees of selectivity (Fig 1c). There was no correlation between the degree of selectivity and shape preference.

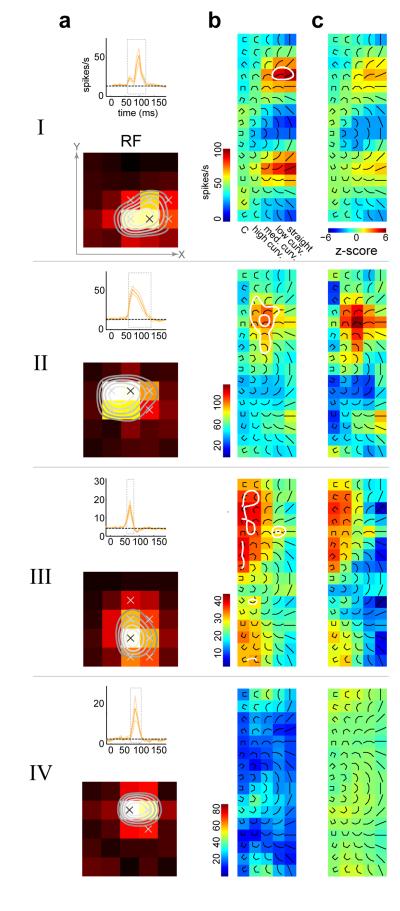
Fig 2. Diversity of shape tuning.

For 4 example neurons: (a) Top panel, average time course to the composite stimuli +/− s.t.d. The average was taken across all stimuli and across all locations on the 5×5 grid. Dotted line is the baseline rate which was determined from a temporal window between 0 and 20 ms after stimulus onset. The dotted gray box marks the temporal window where the average firing rate exceeded the baseline rate by 4 standard deviations. This temporal window was used for all subsequent analysis. Bottom panel, spatial receptive fields obtained by averaging responses across the composite shape stimuli. Significant spatial locations are marked with ‘x’ (see Methods). Contour lines demarcate 90%, 80%, 70% and 60% of maximum response. These were obtained by spatial interpolation of the RF. (b) Location-specific response map at the most responsive spatial location (marked with black ‘x’ in the spatial RF in a). The composite stimuli are overlaid on the maps for ease of reference. (c) Shape z-score maps (see Methods) for the same spatial location in b. Neuron I is significantly selective for straight shapes, neuron II for medium curvature, neuron III for high curvature/square. Neuron IV is not significantly shape selective. Contour lines demarcating z-scores at the 0.05 (outer contour) and the Bonferroni corrected (inner contour) levels are superimposed on the response maps in b. For ease of visualization, all color maps in b and c were smoothed with a Gaussian kernel.

Straight and low-curvature tuned neurons exhibit spatial invariance

We find that neurons that are tuned for straight (zero curvature) or low-curvature contours are spatially invariant in their tuning. That is, they respond preferentially to the same shape in different parts of the receptive field. The response characteristics of an example neuron are shown in Fig 3 (example neuron I). Earlier studies (Pasupathy & Connor, 1999) performed a more restricted examination of spatial invariance, comparing the neuronal responses to the most (black bar) and least (white bar) preferred stimulus across different spatial locations, as seen in the lower right panel of Fig 3a. Our fast mapping procedure allowed us to estimate the selectivity for the full set of composite shapes at different spatial locations. Examination of the location-specific response maps taken from four significant response locations (Fig 3b) reveals the neuron’s full spatial invariance. The local maps show clear tuning for straight shapes, with an orientation preference that is shared across locations. This point is further clarified by plotting the shape (or set of shapes) to which the neuron preferentially responds at different locations of the stimulus grid. This is shown in Fig 3a (bottom-left panel), in which the set of shapes to which the neuron responded (greater than 90% of local peak rate) at each location are spatially superimposed (color indicates firing rate). This spatial invariance to orientation tuning is also reflected in the homogeneity of the fine-scale orientation tuning map obtained from the bar stimuli on the 15×15 grid (Fig 3c). Several other examples of straight and low-curvature tuned neurons exhibiting spatial invariance are shown in Supp Fig 2.

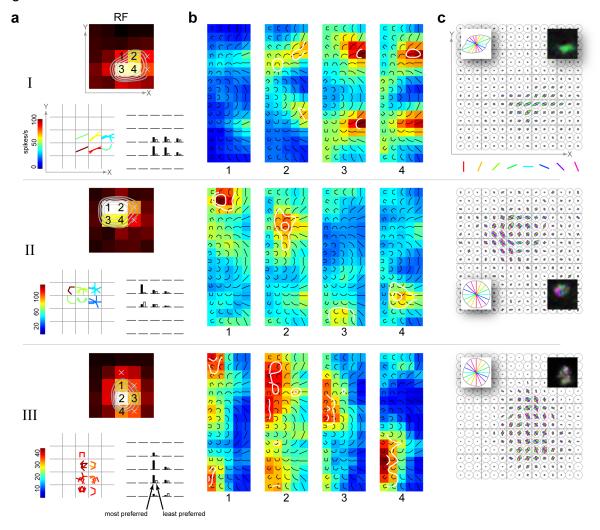
Fig 3. Location specificity of shape tuning.

For example neurons I, II and III in Fig 2: (a) Top panel, spatial receptive fields with significant spatial locations marked with either ‘x’ or numerals. Bottom left panel, location-specific shape or set of shapes to which the neuron responded preferentially (greater than 90% of local peak), at all spatially significant locations. Shapes are spatially superimposed at each grid location with color indicating firing rates. Bottom right panel, Responses to the most- and least- preferred pair of stimuli (determined from each neuron’s most responsive location) at all spatially significant locations. The rank-order is preserved for each neuron. However, this fact does not necessarily imply translation invariance. (b) Location specific response maps at 4 significant locations of the RF. The locations correspond to those marked with numbers in the spatial RFs in a. Neuron I exhibits preferential tuning to straight shapes in a position-invariant manner. In contrast, neurons II and III show spatially varying tuning to medium curvature and high curvature/“C” shapes respectively. Contour lines demarcating shape z-scores (see Methods) at the 0.05 (outer contour) and the Bonferroni corrected (inner contour) levels are superimposed. For ease of visualization, all color maps were smoothed with a Gaussian kernel. (c) Fine-scale orientation tuning maps obtained with the bar stimuli on the 15×15 grid. The color-coded oriented lines represent the bar stimuli; the line lengths are normalized to the maximum across all orientations and locations. Left inset: average orientation response across all locations on the fine grid. Right-inset: smoothed fine-scale orientation map with hue indicating preferred orientation, saturation indicating sharpness of orientation tuning and value indicating average response (see Fig 6 for hue-saturation-value color-coding description). Neuron I has a homogenous fine-scale map. In contrast, neurons II and III have very heterogenous maps – there is local tuning, but the tuning changes across space.

Higher curvature and “C”-shape-tuned neurons are not spatially invariant

In contrast, we found that neurons tuned for curved (medium to high) and “C”-shaped stimuli exhibited a high degree of spatial variation in their shape preference. Two such example neurons are shown in Fig 3 (neurons II and III). In both cases, comparing the relative responses evoked by the most- and least-preferred stimuli across locations (Fig 3a, lower right panels) suggests a degree of spatial invariance, consistent with earlier studies (Pasupathy & Connor, 1999). However, the pattern of selectivity to the full set of stimuli across locations reveals that the preferred stimulus varies considerably across locations. Example neuron II exhibits selectivity for distinct clusters of medium curvature shapes in different parts of its receptive field (Fig 3b). The fine-scale orientation-tuning map for this neuron (Fig 3c) shows that although there is relatively sharp tuning for orientation at each location, there is a systematic variation in tuning across locations, and this variation appears to be correlated with the neuron’s spatially varying curvature preference. Note that the average fine-scale orientation response (Fig 3c, left inset) for this neuron is not tuned, and therefore does not reflect the diversity of orientation tuning at the fine scale. Such a neuron would be mischaracterized as non-orientation selective if mapped at a coarse level.

Example neuron III shows similar spatially varying preference for the “C” stimuli and a heterogeneous fine-scale orientation map. We see evidence for tuning along both dimensions of our stimulus space – orientation (e.g. neuron III, location 4) and shape category (e.g. neuron II, locations 2 and 4). We considered if neurons selective to highly curved shapes might be less tuned to the orientation of the shape. However at the population level we find that orientation tuning, as indexed by circular variance (see Supp Methods), is not correlated with shape preference (Supp Fig 1c). We also considered if these neurons might be less tuned in the shape dimension (Supp Fig 1b). Again we find that at the population level, an index of shape-tuning (see Supp Methods) is not correlated with shape preference (Supp Fig 1d). Other examples of neurons exhibiting spatial variation in shape preference are shown in Supp Fig 3.

Heterogeneity of feature selectivity across RF locations of neurons tuned for higher curvature or “C”-shaped stimuli

To quantify the relationship between curvature preference and spatial invariance at the population level, we examined two complementary aspects of the neuronal data. First, we computed the shape preference and the preferred orientation at each location in the stimulus presentation grid where the neuron responded significantly (see Methods). As one measure of translation invariance, we determined the preferred shape and orientation at the maximally responsive location, and measured how shape and orientation preferences changed relative to those values, at other spatial locations (Fig 4). We find a clear difference in spatial invariance between the population of cells that prefer straight/low curvature (local shape preference values between 0 and 1, n=32, Fig 4a) versus those that either prefer medium curvature (local shape preference values between 1.5 and 2.5, n=16, Fig 4b) or high curvature/“C”-shaped stimuli (local shape preference values between 3 and 4, n=20, Fig 4c). We find that those neurons that preferred straight or low curvature at the most responsive location tend to be tuned for similar orientations at other RF locations, and preserve their shape preference across locations (Fig 4a). In contrast, although neurons that prefer high curvature at their maximally responsive location continue to prefer high curvature at other locations within the RF, the preferred shapes do not generally share the same orientation (Fig 4c). Similarly, neurons with preference for medium curvature at their maximally responsive location tend to prefer medium curvature at other locations, but the preferred shapes are not as sharply aligned with the reference orientation (Fig 4b). The marginal distribution of orientation preference for the straight/low curvature neurons (Figs 4a, right histogram) was significantly different from those of the other two sub-populations (Figs 4b-c, right histograms; p=0.03 and p=0.006 respectively, see Methods).

Fig 4. Heterogeneity of shape tuning across RF locations.

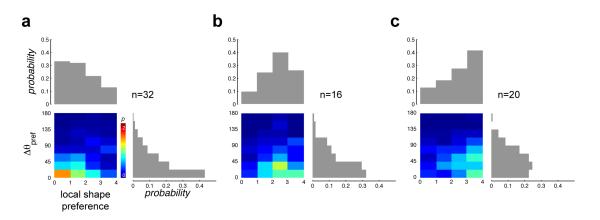
(a) The color map shows the conditional joint distribution of local shape preference and the angular deviation of shape orientation, Δθ_pref, across all neurons (n=32) with local shape preference for straight or low curvatures (shape preference values between 0 and 1) at the maximally responsive location. The joint distribution was computed from all spatially significant locations within the response grid other than the maximally responsive location for each neuron. Δθ_pref was computed as the absolute value of the angular deviation of the local preferred shape orientation from that of the preferred curvature orientation at the maximally responsive location. The histograms at the top and right show the marginal distributions of local shape preference and Δθ_pref respectively. These neurons tend to prefer straight/low curvatures of the same orientation at other locations. (b) Same format as in panel a, but for neurons with local shape preference for medium curvature (n=16, shape preference values between 1.5 and 2.5) at the maximally responsive location. Such neurons tend to prefer medium curvature at other locations, but the preferred shapes are not as sharply tuned to the reference orientation at the maximally responsive location as in a. (c) Same format as in panel a, but for neurons with local shape preference for high curvature/“C” (n=20, shape preference values between 3 and 4) at the maximally responsive location. Such neurons also prefer high curvature/“C” at other locations, but the preferred shapes do not share the same orientation. The marginal distribution of Δθ_pref in a is significantly different from those in b and c.

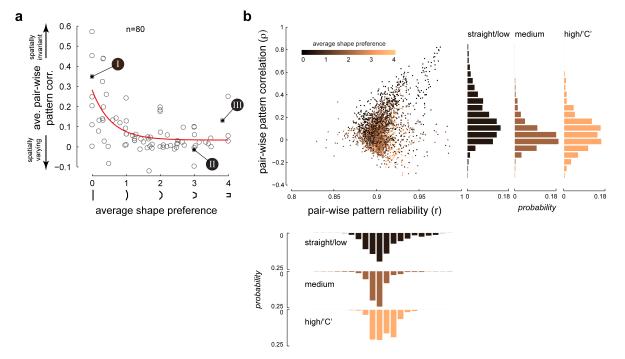
Second, we compared neuronal response patterns across the entire set of curved shapes between pairs of locations within the RF. For any pair of location specific response maps where the neuron responded significantly, we estimated the empirical distribution of correlation coefficients between the response patterns (see Methods, Supp Fig 4). The mean pattern correlation (ρ, expected value of the empirical distribution) provides a measure of tuning similarity or invariance between pairs of locations in the RF, with values closer to 1 corresponding to spatially invariant tuning. The average pattern correlation for each neuron (averaged across all pair-wise ρ values) when plotted against the average shape preference (Fig 5a) shows a power-law decay relationship. This suggests that neurons with preference for medium curvature and higher tend to have little spatial invariance. In contrast, neurons with very low curvature preference tend to have substantial spatial invariance, with few units exhibiting low invariance.

Fig 5. Neurons with preference for curvature have limited spatial invariance.

(a) Average correlation between pairs of response patterns (averaged across all possible pairs of spatially significant response locations for each neuron, see Methods) plotted against the average shape preference for all neurons in our population (n=80) shows an inverse power law relationship (R² = 0.4). Average pattern correlation is high for neurons tuned for straight/low curvature, while the pattern correlation is low for neurons tuned for high curvature/“C”, indicating a tradeoff between curvature and spatial invariance. The three example neurons in Figs 2 and 3 are indicated. (b) Scatter plot of pair-wise pattern correlation versus pair-wise pattern reliability for all possible pairs of significant response locations in our entire neuronal population. The colors indicate the average shape preference of the neuron to which the location pair belongs. Right histograms: Distribution of pattern correlation for pairs that came from three sub-population of neurons: neurons with average shape preference for straight/low curvature (shape preference values between 0 and 1), those that came from neurons with average shape preference for medium curvature (shape preference values between 1.5 and 2.5) and those that came from neurons with average shape preference for high curvature/“C” (shape preference values between 3 and 4). The correlation distribution of the straight/low curvature sub-population is significantly different from those of the other two sub-populations. Bottom histograms: Distribution of pattern reliability for the same three sub-populations as above. The reliability distributions are not significantly different from each other.

For each location pair in our population, we also calculated the reliability of the estimated pattern correlation from the standard deviation of the empirical distribution (see Methods). This controls for the possibility that noisier data gave rise both to greater response heterogeneity and lower pattern correlations. A scatter-plot of pattern correlation (ρ) versus pattern reliability (r) is shown in Fig 5b for all possible location pairs across all neurons in our population. We see no difference in the reliability of our estimates for three sub-populations of location pairs: those that come from neurons with average shape preference for straight/low curvature (shape preference values between 0 and 1), those from neurons with average shape preference for medium curvature (shape preference values between 1.5 and 2.5) and those from neurons with average shape preference for high curvature/“C”-shaped stimuli (shape preference values 3 and 4) (Fig 5b, lower histograms). If those neurons that showed variation in their response pattern across locations did so due to noise in their estimates (i.e. due to low firing rates or fewer trial repeats), then we would expect them to have low reliability values. Thus differences in spatial invariance cannot be attributed to differences in the statistical reliability of estimates. One last point that is worth highlighting is that pairs with lower pattern correlation values come from neurons with preference for higher curvature/“C” shapes, whereas those with higher pattern correlation come from neurons with preference for straight/low curvature shapes. The distribution of pattern correlation of the straight/low curvature sub-population is significantly different from those of the other two sub-populations (Fig 5b, right histograms; p=0.001 and p=0.0001 respectively, see Methods).

We thus find evidence for a tradeoff between shape selectivity and position invariance. This phenomenon is evident in terms of both the peak shape selectivity and the overall firing rate patterns to the entire set of composite shapes.

Spatial layout of fine-scale orientation tuning maps determine shape selectivity

We questioned whether or not we could explain the diversity of shape tuning from the diversity in the fine-scale orientation tuning maps of V4 neurons (Fig 6). Some neurons show high degrees of translation invariance for orientation at this finer scale (Fig 6, bottom row) while others show heterogeneous tuning (Fig 6, top row). As noted above, the spatial layout of the fine-scale orientation tuning maps in our example cells (Fig 3c), seem to reflect the cell’s shape selective properties. It has been proposed, both from experimental observations (Chapman et al., 1991; Jin et al., 2011) and theoretical simulations (Paik & Ringach, 2011), that simple pooling of the spatially segregated afferent connections from the lateral geniculate nucleus (LGN) to the primary visual cortex (V1), might determine both the orientation tuning characteristics of V1 neurons as well as the pin-wheel structure of orientation maps in V1. We hypothesized that this pooling architecture might carry forward to downstream retinotopic extra-striate areas like V4. This hypothesis is also consistent with earlier proposals, in which neuronal responses in V4 to combinations of line elements are weighted averages of the responses evoked by individual elements (Ghose & Maunsell, 2008; Lee & Maunsell, 2010; Reynolds et al., 1999; Reynolds & Heeger, 2009), and related proposals in MT (Heuer & Britten, 2002; Rust et al., 2006) and IT (Zoccolan et al., 2005).

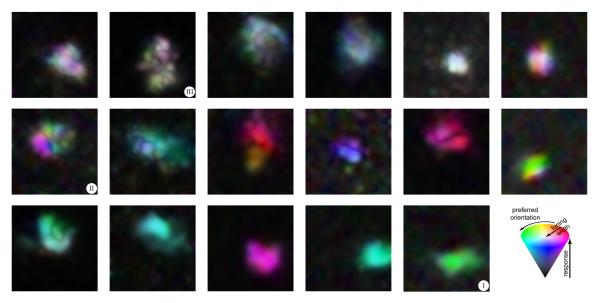
Fig 6. FIne-scale orientation tuning maps illustrate the diversity of tuning in V4 neurons.

Smoothed fine-scale orientation maps are shown for 17 example cells. Smoothing was achieved by linear interpolation of the respective fine-scale maps on the 15×15 grid and color-coding as follows: hue indicates preferred orientation, saturation indicates sharpness of orientation tuning and value indicates normalized average response. The hue-saturation-value color-coding scheme is illustrated by the color cone on the bottom right. The maps are arranged from heterogeneous (top left) to homogenous (bottom right). The three example neurons of Figs 2 and 3 are indicated.

To examine the degree to which the pooling of orientation signals could account for the observed complexity of shape tuning in V4 neurons, we generated location specific response predictions to the composite shapes, derived from a simple weighted average of the component responses obtained from the fine-scale orientation tuning maps (see Methods). We then calculated the correlation coefficient between the observed response pattern and the predicted response pattern. Note that the fine-scale orientation maps contain both a spatial response component and an orientation-tuning component. To investigate the contribution of these components, we also considered two reduced versions of the pooling model (see Methods, Supp Fig 5c). A space-only version was obtained by averaging across orientation at each fine-grid location. This model did not have any local orientation tuning. An orientation-only version was obtained by subtracting the space-only response from the measured data at each fine-grid location, leaving only orientation tuning. Thus this model did not contain any local spatial information.

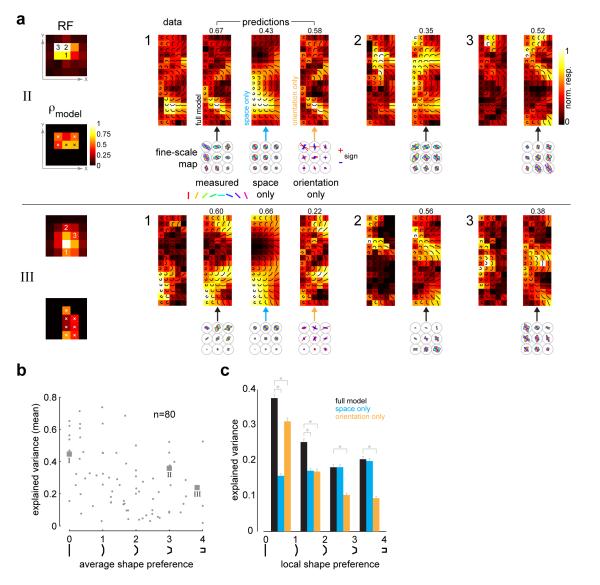
The predicted response maps for two example neurons (neurons II and III in Figs 2-3) are shown in Fig 7a (panels labeled “prediction”). Maps are shown for three different receptive field locations for each neuron. For the RF location marked ‘1’, the left panel shows the empirical data, while the other three panels show the predicted responses from the full model and the two reduced models. Shown below the predicted response maps are the corresponding sections of the fine-scale orientation map which were used to generate the predictions. To take the example for RF location ‘1’ in neuron II, we can see clearly that the selectivity for medium curvature shapes pointing upwards arises from the layout of the fine-scale map: the middle location is tuned to horizontal elements, the upper-left location is tuned to elements tilted 45 degrees counter-clockwise, the upper-right location is tuned to elements tilted 45 degrees clockwise (and also to vertical). There is a close correspondence between the data and the predicted patterns both for the full model and the orientation-only model. The space-only model performed less well, but still explained significant parts of the response (ρ = 0.43 for space-only versus ρ = 0.58 for the orientation-only model). Thus, both spatial and orientation components contribute giving the best correlation (ρ = 0.67) for the full model. Only the predictions of the full model are shown for RF locations ‘2’ and ‘3’. The model correlations (full model only) at each spatially significant location are shown in the lower left panel of Fig 7a.

Fig 7. A weighted average pooling model of local orientation predicts shape tuning.

(a) The pooling model is illustrated for two example neurons (neurons II and III in Figs 2 and 3). For the RF location marked ‘1’, the left panel shows the empirical data, while the other three panels shows the predicted responses for the full model and two reduced models (space-only and orientation-only, see Methods and Supp Fig 5c). Also shown are the corresponding sections of the fine-scale maps used to predict the responses. Indicated above each predicted response map is the pattern correlation between the data and the prediction. Only the predictions of the full model are shown for RF locations ‘2’ and ‘3’. Since our attempt was not to match firing rates, but to quantify the match in the response patterns between the data and prediction, all panels are shown in independently normalized firing rate units. Shown below the RF in the lower left panel are the model correlations (full model only) at each spatially significant location. The spatial locations where the model correlations are significant (compared to spatially shuffled arrangements, see Methods and Supp Fig 5a-b) are demarcated with ‘x’. (b) Scatter-plot of the mean explained variance (averaged across all RF locations for each neuron) for the full model versus average shape preference (n=80). The 3 example neurons in Figs 2 and 3 are highlighted. The marginal distribution of the mean explained variance has a median value of 0.25. (c) Histogram of explained variance for the full and reduce models. The data was aggregated across all spatially significant RF locations for all neurons (n=80) and binned according to local shape preference. The orientation-only model dominates for the straight/low-curvature categories, while the space-only model plays a key role across all shape categories. Paired comparisons between the full and reduced models were tested for statistical significance (t-test) and are indicated with asterisks. Error bars indicate s.e.m.

In the case of example neuron III, the local orientation tuning was highly heterogeneous and most of its curvature selectivity could be explained by local spatial tuning alone. As seen for RF location 1, the largest responses occur for composite shapes whose ends fall in the upper part of the fine-scale grid where the spatial response is higher (i.e., on the RF boundary). The orientation of the end elements is not critical, but only that they fall inside the RF. The space-only model provided a better fit (ρ = 0.66) as compared to the local orientation information (ρ = 0.22), and in fact, the combined orientation and spatial information in the full model slightly worsens the prediction (ρ = 0.60). This neuron may thus be largely non-selective to orientation, but nevertheless exhibits curvature selectivity at the boundaries of the RF due to spatial inhomogeneity. This highlights to what extent texture or non-orientation selective units can exhibit curvature selective responses at their spatial boundaries. Other cells tuned for high curvature shapes exhibited similar orientation heterogeneity (Fig 6, top row), and had selectivity for curved shapes typically at the RF boundary (see examples in Supp Fig 3).

To test the predictive power of the model, we computed a null distribution of the correlation coefficients by repeatedly shuffling the fine-scale orientation maps and then generating response patterns from these shuffled maps (Supp Fig 5a, see Methods). This shuffling procedure perturbed the relative spatial structure of the fine-scale map within a coarse grid location. It thus serves as a comparison against which to test whether contour preferences at a given location depend on the spatial arrangement of the local orientation map. Using this procedure, we calculated whether any of the model correlations (across all spatially significant locations) were significantly different from chance (p=0.05), after correcting for multiple comparisons. The spatial locations where the model correlations are significant are demarcated with ‘x’ for our example neurons (Fig 7a, lower left panels). Across the population, 80% of neurons showed a significant prediction (i.e. at least one RF location with significant p-value; on average 40% of the RF locations had significant p-values).

The linear pooling model accounts for a substantial fraction of the response variance (see Methods) across neurons with varied shape preferences. Fig 7b shows a scatter-plot of the mean explained variance (averaged across RF locations) for the full model versus average shape preference. The marginal distribution of the mean explained variance has a median value of 0.25. Examining the histogram of explained variance for the full and reduced models (Fig 7c), we see that the orientation-only model plays a dominant role for the straight/low-curvature categories (linear Pearson correlation, r=-0.4, p<0.001). We should note that the local orientation significantly improved fits for medium curvature neurons (p<0.001), though not for high curvature neurons. Thus for medium curvature, local orientation plays a significant role. Meanwhile, the space-only model plays a key role across all shape categories (r=0.09, p=0.02). In general, the full model is the best predictor across the population.

We should note that the pooling model explored in our study does not in any way deemphasize the importance of non-linearities in the neuronal response. Previous studies have found that non-linear operations such as divisive normalization help explain the responses of extra-striate neurons to multiple oriented stimuli in their receptive fields (Heuer & Britten, 2002; Lee & Maunsell, 2010; Reynolds et al., 1999). Here we show that the simplest model, linear pooling of local oriented responses, can in fact explain much of the variation in V4 shape tuning across space, but we anticipate that more complete models incorporating non-linearities would perform still better.

Control conditions

To investigate whether some of our results were influenced by the spatial and temporal characteristics of our stimuli, we conducted several control experiments on subsets of cells in our neural population (see Supp Methods). Neurons exhibit virtually identical tuning when stimuli were presented for longer durations (200ms, Supp Fig 6) and when the components of the curved shapes were changed to elongated Gabors (Supp Fig 7a). Neurons did not exhibit tuning to spatially scrambled versions of the stimuli, indicating tuning for spatial structure (Supp Fig 7b). This was consistent with the fact that spatial shuffling of the fine-scale orientation maps yields very poor prediction of shape selectivity, thus lending further support to the importance of local structure.

DISCUSSION

One innovation of the current study is the use of fast reverse correlation procedures to map V4 receptive fields. Such techniques are common in earlier visual areas (Ringach, 2004), but previous studies in V4 have generally used longer duration stimuli, typically with durations ranging from 200-500 ms and correspondingly long inter-stimulus intervals. The primary advantage of the fast mapping technique was that it allowed us to perform a dense mapping of shape selectivity across several locations in the RF, in addition to a fine-grained mapping of the selectivity to individual oriented components of the composite shapes. This provides a more comprehensive description of contour/shape selectivity across the RF than has been possible in previous studies.

The present results reveal considerable heterogeneity in feature selectivity and the translation invariance of neurons in macaque area V4, and force us to reconsider the established notion that neuronal invariance increases as one traverses the ventral visual hierarchy. Consistent with the conclusions of earlier reports, (Pasupathy & Connor, 1999), we find a subpopulation of V4 neurons whose stimulus tuning is maintained throughout the receptive field. Also consistent with earlier studies, the majority of neurons did exhibit a higher firing rate to the most preferred stimulus tested versus the most non-preferred stimulus, across spatial locations. However, a detailed mapping of stimulus tuning reveals many neurons exhibiting considerable variability in tuning across space, and very limited spatial invariance. This diversity can be captured by two underlying organizing principles.

The first is the dichotomy between the heterogeneity of feature selectivity across RF locations in the case of neurons tuned to higher-curvature/”C” shapes and its homogeneity in the case of neurons tuned to straight/low-curvature shapes. The denser sampling of the RF afforded by our method reveals that true translation invariance is largely restricted to neurons preferring straight contours. Neurons with preference for very low curvature tend to exhibit spatial invariance, but curvature/”C” selective neurons often exhibit a high degree of variation in shape preference across their receptive fields. Further, curvature tuned neurons tend to prefer curved over straight elements at different locations in the RF, while varying in the orientation of the preferred shape across locations (Fig 4b-c). These results are echoed by our observations from a separate study where we have observed a trade-off between curvature and invariance using naturalistic images. Thus, we expect that the conclusions of the present study will generalize across different stimulus conditions. This is also supported by the control analyses presented above in which virtually identical tuning was observed when stimuli were presented for longer durations.

There is strong evidence that object recognition is quite rapid as has been demonstrated via rapid serial visual presentation (Potter & Levy, 1969) and rapid object categorizing (Bodelón et al., 2007; Thorpe et al., 1996) paradigms, suggesting a primary involvement of the feed-forward pathway. Our study focused on neuronal selectivity to individual contour fragments and the rapid reverse correlation procedure may have mainly isolated feed-forward contributions to the neuronal response. When we compared the shape selectivity among a sample of neurons with fast mapping procedures and longer duration stimuli we found striking similarities in their selectivity to the individual elements (Supp Fig 6). It is possible that recurrent or feed-back connections, mediated at longer latencies, could refine the selectivity of the initial V4 visual responses, and could contribute to spatial invariance as well as to other object-centered or attention-dependent effects (Connor et al., 1996; Pasupathy & Connor, 2001; Yau et al., 2012). Further studies with dense spatio-temporal mapping are needed to fully understand neuronal selectivity to complex combinations of shape fragments.

The second organizing principle alluded to above is that the diversity of shape tuning in V4 is well accounted for by a simple pooling of local orientation signals. Much of the complexity of V4 tuning in our dataset could be explained by a linear pooling of the local responses to smaller oriented elements used to form our composite stimuli. Both the spatial-response and orientation-tuning components of the local orientation maps play a key role in determining shape selectivity. We find that curvature selectivity could arise either due to systematic variation in fine-scale orientation tuning across RF locations (Fig 6, middle row), or due to purely spatial aspects as in the case of tuning heterogeneity (Fig 6, top row). This latter category presents the interesting possibility that such neurons might respond to closed areas of texture, congruent with the idiosyncratic shape of their receptive fields.

The primary visual cortex is organized into iso-orientation domains punctuated with pinwheel regions that vary in orientation preference over short distances (Blasdel, 1992; Bonhoeffer & Grinvald, 1991; Bosking et al., 1997). Neurons tuned for medium curvature (Fig 6, middle row) may inherit their shape tuning from such domains of heterogeneous orientation tuning. Consistent with this, we found that orientation-tuning maps measured with smaller elements generally varied continuously in their preferred orientations, showing transitions from one orientation to another as one might expect when pooling from neurons near an orientation pinwheel in earlier areas. In contrast, straight-tuned neurons (Fig 6, bottom row) exhibited fine scale orientation maps that were constant in their orientation preference, as would be expected if these neurons inherited their tuning properties from homogenous orientation domains. This hypothesis is also consistent with the conclusion that the RFs of central V4 neurons correspond to a constant-sized sampling of the V1 cortical surface (Motter, 2009). Our control experiments show that these findings are robust against the spatial characteristics of the primitives that made up the curved stimuli.

Previous assessments of spatial invariance were made using the most and least preferred stimuli, either with local curved stimuli (Pasupathy & Connor, 1999) or with larger pattern stimuli (Pasupathy & Connor, 2001), and found consistent selectivity across shifts in position half the receptive field size or more. Models inspired by these earlier findings utilized linear pooling mechanisms to achieve feature selectivity followed by non-linearities such as “soft-max” selection to gain spatial invariance (Cadieu et al., 2007). The “soft-max” operation can be parametrically varied to yield a simple averaging operation at one end (no spatial invariance) to taking the ”max” operation on the other (full spatial invariance). Consistent with the earlier studies, we find that both straight- and curve-preferring neurons do preserve a relative preference for the stimuli that are, on average, most and least preferred (Fig 3a, bottom right panels). However, the more detailed examination in our study leads us to conclude first that shift invariance is much more limited than previously appreciated, at least for local curved elements, and further that much of the response across the receptive field is well explained by linear pooling of local orientation responses.

We note that the variation in curvature tuning that we observe is consistent with previous studies using closed form contour stimuli (Carlson et al., 2011; Pasupathy & Connor, 2001) that show selectivity to different convex and concave curves positioned relative to the center of a closed form. However, the limited spatial invariance that we observe and the success of local orientation pooling in predicting responses, lead us to suggest that spatial invariance to larger pattern stimuli will be much more restricted than previously suggested, falling within one of our coarse grid locations (about 1/3 of the receptive field size). Recent studies at still higher stages of processing such as IT also call into question the spatial extent of invariance in ventral stream representations, suggesting invariance is not intrinsic but a learned attribute of those representations (Cox & DiCarlo, 2008).

It is possible that the 13 neurons excluded from our analyses due to their lack of shape selectivity are purely color selective (see, e.g., Bushnell et al. (2011)). The relationship between the present findings and the recent report of segregated orientation and color domains (Tanigawa et al., 2010) remains to be explored. Since cells selective for higher curvature are not strongly tuned for orientation (Fig 3, example neurons II and III), domain segregation might be somewhat reduced if measured using composite shapes (as in our study). We do not see evidence for the response bias toward acute contour curvature as reported in a recent study (Carlson et al., 2011). This could be due to the fact that in our study we explored the fine structure of the entire RF, whereas the stimuli used in the Carlson et al study were presented at the center of the RF and typically spanned the extent of the RF.

The finding that spatial invariance falls off with preference for more curved contours suggests a possible segregation of function. Spatially invariant neurons selective for orientation may play a role in representing extended regions of uniform texture, where the location of the individual texture elements need not be encoded with great spatial precision. In contrast, neurons selective for curvature are likely activated when an appropriately curved contour falls at a particular location within the receptive field. This form of spatially-selective encoding of curved contours would be useful in localizing contours, particularly at the points of high curvature that often play a critical role in defining shape (ATTNEAVE, 1954; Feldman & Singh, 2005). We note that such a code, although parsimonious, would be ambiguous for downstream neurons, which would likely integrate multiple signals to derive an unambiguous interpretation of a complex contour.

Although the tradeoff between invariance and contour complexity does suggests distinct functions, we also find that V4 responses across this spectrum can be explained using a simple model that pools fine-scale orientation signals. This suggests that differences in invariance and contour complexity depend on differences in the orientation-selective inputs that are pooled to give rise to selectivity in V4. We thus suggest that these different patterns of shape tuning and invariance can be understood as arising from differences in the wiring that links orientation selective inputs to V4, with a simple pooling model serving to integrate these different inputs.

METHODS

Electrophysiology

Neurons were recorded in area V4 in two rhesus macaques. Experimental and surgical procedures have been described previously (Reynolds et al., 1999). See Supp Methods for further details.

Stimulus presentation and eye-movement monitoring

Stimuli were presented on a computer monitor (Sony Trinitron Multiscan, TC, 640×480 pixel resolution, 120 Hz) placed 57 cm from the eye. Eye position was continuously monitored with an infrared eye tracking system (240 Hz, ETL-400; ISCAN, Inc.). Experimental control was handled by NIMH Cortex software (http://www.cortex.salk.edu/). Trials were aborted if eye position deviated more that 1-degree from fixation.

Preliminary RF mapping

At the beginning of each recording session, neuronal RFs were mapped to determine the approximate spatial extent over which stimuli elicited a visual response. Monkeys fixated a central point during which each neuron’s RF was mapped using subspace reverse correlation in which Gabor (eight orientations, 80% luminance contrast, spatial frequency 1.2 cpd, Gaussian half-width 2°) or ring stimuli (80% luminance contrast) appeared at 60 Hz. Each stimulus appeared at a random location selected from a 19 × 15 grid with 1° spacing in the inferior right visua l field. The orientation of the Gabor stimuli and the color of all stimuli (one of six colors or achromatic) were randomly selected. This resulted in an estimate of the spatial RF, orientation, and color preference of each neuron. Recordings were often made from multiple electrodes, and the preferences of units on separate channels did not always match. The stimuli for the main experiment were centered on the estimated spatial RF of the best-isolated units.

Task and stimuli

The monkey began each trial by fixating a central point for 200 ms and then maintained fixation through the trial. Each trial lasted 3s during which neuronal responses to a fast-reverse correlation sequence (16 ms stimulus duration, exponential distributed delay between stimuli with mean delay of 16 ms, i.e. 0 ms delay p=1/2, 16 ms delay p=1/4, 32 ms delay p = 1/8 and so on) were recorded. The stimuli were comprised of oriented bars (8 orientations) or bar-composites (16 orientations × 5 conjunction angles, total of 72 unique stimuli, Fig 1a). These latter stimuli were constructed from the conjunction of 3 bars at conjunction angles of 0°, 22.5 °, 45°, 67.5 ° and 90° between the end elements and the center. The 5 conjunction levels created 5 categories of shapes. These were enumerated as 0 (zero curvature/straight), 1 (low curvature), 2 (medium curvature), 3 (high curvature) and 4 (“C”). A pseudo-random sequence from the combined stimulus sets was presented in each trial. The composite stimuli were presented on a uniform 5×5 location grid (‘coarse grid’) centered on the estimated spatial RF based on the preliminary mapping. The grid locations were separated by one-fourth of the RF eccentricity (for e.g., for a RF centered at 6°, th e grid-spacing was 1.5° and the grid covered a visual extent of 3°-9°). The oriented bar stimuli were presented on a finer 15×15 location grid (‘fine grid’) that spanned the larger 5×5 grid in equal spaced increments. Stimuli were scaled by RF eccentricity, such that each single bar element spanned approximately the diagonal length of the fine grid. The receptive fields of all neurons reported in the study were in the para-foveal region between 2° and 12° in the inferior right visual field.

Inclusion criteria

Only well isolated units were considered as potential candidates (n=251) for the analysis. Among these, only those neurons with robust visual responses were selected. The robustness of the spatio-temporal response to the visual stimuli was determined as follows: a temporal window between 60 and 120 ms after stimulus onset was used to identify a temporal interval of significant visual response. The temporal window was divided into 8.33 ms bins for determining the PSTH. Typical average temporal responses to the composite stimuli are shown in Figure 2a. The temporal window for each neuron, T_sig, was taken as those PSTH bins where the mean firing rate averaged across all stimulus conditions exceeded the baseline rate by 4 standard deviations (significant time points labeled in Fig 2a, dotted gray box). The baseline rate was determined from a temporal window between 0 and 20 ms after stimulus onset. A neuron was considered a potential candidate for further analysis if it had a clear transient response peak that was contained within the larger 60-120 ms interval. 23 single units were eliminated in this process. Of the remaining 228 units, we eliminated a further 135 units since their fine-scale orientation maps (described below) were not fully contained within the stimulus presentation grid i.e. the spatial extent of the receptive fields of these neurons could not be fully characterized.

With the remaining 93 units, we next determined the locations within the coarse 5×5 stimulus grid where the neuron had significant spatial responses. We first performed a jackknife analysis on the data (N_j = 20 jackknifes, each using 95% of trials). For each jackknife, j, we determined the neuronal response, r(x,y,s,j) to a particular composite stimulus, s, at grid location (x,y), as the average firing rate (within T_sig) across stimulus repeats. The mean, $\widehat{r}(x,y,s)$ and s.e.m., η(x,y,s), of the responses across the 20 jackknives were then used to calculate a spatial z-score at each grid location (x,y):

$$Z_{\mathit{space}}(x,y)=\frac{\widehat{r}(x,y{,}^{\ast })-b}{\eta (x,y{,}^{\ast })\times \sqrt{N_j-1}},$$

where b was the baseline firing rate and the * operation indicates that the responses were averaged across stimuli. The grid-location was marked as significant if the spatial z-score exceeded the significance level of 0.05 (corrected for 25 multiple comparisons, see Supp Fig 1a). Spatially significant grid locations for example neurons are marked with ‘x’ or numerals in Figs 2 and 3.

For each spatially significant grid location, we next determined whether the neuron was significantly selective to the composite stimuli at that location. We calculated a z-score for each stimulus:

$$Z_{\mathit{shape}}(x,y,s)=\frac{\widehat{r}(x,y,s)-\widehat{r}(x,y{,}^{\ast })}{\eta (x,y,s)\times \sqrt{N_j-1}}$$

We define a shape selectivity index, SSI(x,y), for that spatial location as the maximum of the shape z-scores:

$$\mathit{SSI}(x,y)=\max \left(Z_{\mathit{shape}}\right(x,y,s\left)\right)$$

A grid location was considered significantly shape selective if the index exceeded the significance level of 0.05 (corrected for 72 × M multiple comparisons, where M was the number of significant spatial locations, see Supp Fig 1a). A neuron was considered significantly shape selective if it had at least one spatially significant grid location that was also significantly shape selective. 13 neurons failed this significance test. These neurons had significant spatial RFs, but were not significantly shape selective (Fig 1b). An example of a non-selective neuron is shown in Fig 2 (example neuron IV). We did not analyze these neurons any further. All subsequent analyses were performed on the remaining 80 neurons.

Data analysis

We used the mean responses $\widehat{r}(x,y,s)$ to generate three basic response maps: (a) location-specific response maps for the composite stimuli at each location in the 5×5 presentation grid (Fig 2b, Fig 3b), (b) average response map, $\widehat{r}(\ast ,\ast ,s)$, for the composite stimuli by averaging across spatially significant grid locations and (c) fine-scale orientation tuning maps using the same procedure as in (a) for the bar stimuli on the 15×15 grid (Fig 3c).

For the population analysis, we determined several metrics from the response maps for each neuron:

Average shape preference: this was calculated by first determining the set of composite shapes, s_i, whose firing rate in the average response map, $\widehat{r}(\ast ,\ast ,s_i)$, exceeded 90% of the maximum firing rate. The shape category, c_i (0: straight, 1: low-curvature, 2: medium-curvature etc.), corresponding to these shapes were weighted and averaged by their firing rates to determine the average shape preference:

$$\sum _i\widehat{r}(\ast ,\ast ,s_i)c_i/\sum _i\widehat{r}(\ast ,\ast ,s_i)$$

Local shape preference: same as above but derived from the location-specific response maps.

Local preferred shape orientation: The orientation (0°, 22.5°, 45° … 337.5°) of th e local preferred shape defined above. We computed the conditional joint distribution of local shape preference and the angular deviation of preferred shape orientation, Δθ_pref (Fig 4). The computation was conditioned on the shape preference and shape orientation at the maximally responsive location for each neuron. For all spatially significant locations other than the maximally responsive location, Δθ_pref was computed as the absolute value of the angular deviation of the local preferred shape orientation from that of the preferred shape orientation at the maximally responsive location. We divided our neuronal population into three sub-populations: those that preferred straight/low curvature (local shape preference values between 0 and 1, Fig 4a, n=32), those that preferred medium curvature (local shape preference values between 1.5 and 2.5, Fig 4b, n=16) and those that preferred high curvature/“C” (local shape preference values between 3 and 4, Fig 4c, n=20) at the maximally responsive location. To test whether the marginal distributions of the orientation deviation, Δθ_pref, between the straight/low curvature preferring units and the high curvature/“C” preferring units (Fig 4a and 4c, right histograms) were significantly different, we calculated the Kullback-Leibler (KL) divergence between the distributions:

$$D_{\mathrm{KL}}(P\Vert Q)=\sum _{i}P\left(i\right)\ln \frac{P\left(i\right)}{Q\left(i\right)}$$

where P is the marginal distribution in Fig 4a and Q is the marginal distribution in Fig 4c. This yielded a value of 0.5685. We then computed a bootstrapped set (Efron & Tibshirani, 1993) (1000 iterations) of divergences D_KL(P ∥ P_null) with respect to the null distribution, P_null, which was obtained from a random sample (with replacement) of the combined data that underlay the two distributions P and Q. Comparing D_KL(P ∥ Q) to this distribution yielded a p-value of 0.006, indicating that the two marginal distributions were significantly different. Similarly, the marginal distributions between the straight/low curvature preferring units and the medium curvature preferring units (Fig 4a and 4b, right histograms) were also significantly different (p=0.03).

Pair-wise pattern correlation (ρ) and pair-wise pattern reliability (r): for any pair of spatially significant coarse grid locations, we estimated the empirical distribution of correlation coefficients between the response patterns (location-specific response maps) at the two locations using a bootstrap procedure (re-sampling with replacement, 1000 iterations) (Efron & Tibshirani, 1993). The pair-wise pattern correlation (ρ) was taken as the expected value of a Gaussian fit to this empirical distribution (Supp Fig 4). The Gaussian fits were in excellent accord with the raw distributions across our data set. The pair-wise pattern reliability, r, was defined as r=1–σ, where σ was the standard deviation of the Gaussian fit to the empirical distribution (Supp Fig 4). The reliability served as a measure of data quality; values closer to 1 indicating that the estimates of pattern correlation were more reliable. A scatter plot of pattern correlation versus pattern reliability for all possible location pairs in our neuronal population is shown in Fig 5b. The marginal distributions of pattern correlation (Fig 5b, right histograms) and pattern reliability (Fig 5b, lower histograms) for three sub-populations -- points that came from neurons with average shape preference for straight/low curvature (average shape preference values between 0 and 1), those that came from neurons with average shape preference for medium curvature (between 1.5 and 2.5) and those that came from neurons with average shape preference for high curvature/“C” (between 3 and 4)) -- were tested for statistical difference (using the same procedure described above using the KL divergence measure). The marginal distribution of pattern correlation for the low/straight neurons was significantly different from those of the high curvature/“C” preferring (p=0.0001) and the medium curvature preferring neurons (p=0.001). The distributions of pattern reliability were not significantly different from each other, indicating that differences in data quality were not an issue.

To examine the idea that local pooling of orientation signals within sub-regions of the RF determine the patterns of selectivity to more complex features, we generated predictions of location-specific response maps. This was done by spatially interpolating the fine-scale orientation tuning map in a three step process: first, the pure spatial information in the fine-scale map, obtained by averaging across orientation at each fine-grid location, was subject to a 2D nearest neighbor interpolation (20 interpolation points) followed by a 2D Gaussian smoothing operator ($\sigma =\frac{2}{3}\times$ the spacing between fine-grid locations); second, the pure orientation information in the map, obtained by subtracting the average orientation response from the measured data at each fine-grid location, was subject to a 2D nearest neighbor interpolation (20 interpolation points) followed by a 2D Gaussian smoothing operator ($\sigma =\frac{4}{3}\times$ the spacing between fine-grid locations); finally, the two components were combined by addition. The composite stimuli (at each coarse grid location) were then projected onto this interpolated space. The response to each component element was read off as the value of the closest orientation match in the interpolated space at the location corresponding to the center of the component element. The predicted response to each composite stimulus was taken as the average of the three component responses. We then calculated the correlation coefficient, ρ_model, between the response patterns in the predicted map and the observed map. Since we were only concerned with pattern selectivity and not with rate matching, the correlation measure was sufficient for our purpose.

To test for the predictive power of the model, we also calculated a null distribution of the correlation coefficients. This was done by spatially shuffling the 9 tuning curves of the fine-scale orientation map within a 3×3 fine grid that underlay a coarse grid location (see Supp Fig 5a), generating the predicted responses from this shuffled map (same procedure as above for the original unshuffled map) and hence the correlation coefficient between the predicted map and the observed map. This shuffling procedure preserved the orientation tuning at the fine scale while perturbing the relative spatial structure of the map within a coarse grid location. This procedure was repeated 1000 times to give an estimate of the null distribution (ρ_null-model, see Supp Fig 5b). The model correlation, ρ_model, was tested against the null distribution for significance (p=0.05, Bonferroni corrected for M multiple comparison, where M is the number of significant spatial locations for each neuron). The model was considered to have significant predictive power for a neuron is there was at least one spatial location that was significant by the above criteria.

We also investigated two reduced versions of the pooling model (Supp Fig 5c). The space-only version was obtained by averaging across orientation at each fine-grid location (Supp Fig 5c, right upper panel). This model did not have any local orientation tuning. The orientation-only version was obtained by subtracting the average orientation response (as in the space-only model) from the measured data at each fine-grid location (Supp Fig 5c, right lower panel). Thus this model did not contain any local spatial information. The model correlations and null distributions for these reduced models were calculated using the same procedure described above for the full model.

The explained variance of our model was estimated by first calculating the model correlation, ρ_model, as above, but on different jackknifed proportions of the data. Specifically, we calculated ρ_model between the predicted response map and the observed response maps from: (i) the full data set, (ii) 95% of trials (iii-v) similarly from each of 90%, 85% and 80% of trials. We then performed a linear regression on the resulting ρ_model values against the reciprocal of the corresponding jackknife fraction values (1, 1/0.95, 1/0.9, 1/0.85, 1/0.8). This procedure is designed to correct for the bias due to finite dataset size (Brenner et al., 2000; Sahani & Linden, 2003; Machens et al., 2004). The square of the y-intercept of the regression line was taken as the explainable variance for that RF location. The explained variances of the reduced space-only and orientation-only models were calculated using the same procedure.