Learning Likelihoods for Labeling (L3): A General Multi-Classifier Segmentation Algorithm

Abstract

PURPOSE

To develop an MRI segmentation method for brain tissues, regions, and substructures that yields improved classification accuracy. Current brain segmentation strategies include two complementary strategies: multi-spectral classification and multi-template label fusion with individual strengths and weaknesses.

METHODS

We propose here a novel multi-classifier fusion algorithm with the advantages of both types of segmentation strategy. We illustrate and validate this algorithm using a group of 14 expertly hand-labeled images.

RESULTS

Our method generated segmentations of cortical and subcortical structures that were more similar to hand-drawn segmentations than majority vote label fusion or a recently published intensity/label fusion method.

CONCLUSIONS

We have presented a novel, general segmentation algorithm with the advantages of both statistical classifiers and label fusion techniques.

1 Background

Vannier introduced multi-spectral classification for brain image segmentation in 1985 [10] and such segmentation strategies have been the standard for years (e.g. [13, 9]). Multi-spectral classification yields segmentations with true fidelity with respect to the image data and the patient, but are unable to label structures where the boundaries are poorly represented by changes in image contrast, such as lobar parcellations and subcortical substructures. With advances in flexible, non-rigid registration technology, multi-atlas approaches have recently become popular (e.g. [7, 1, 8]). These are segmentation-by-registration approaches where registration error is marginalized by fusion of a series of registered template segmentations through some consensus generating process. These methods ultimately have limited ability to resolve structure that cannot be identified through registration alone. Recent work [8] has attempted to address this shortcoming by adding a grayscale image similarity term to the label fusion process. This technique is limited by the simplifying assumption that template image intensities will be similar to subject image intensities, and do not account for the significant differences in image intensity between scanners, pulse sequences, and disease states.

We propose a new method called Learning Likelihoods for Labeling (L3), which unifies label fusion and statistical classification. In our approach, each input template does not define a candidate segmentation to be fused, but instead defines a unique classifier that is used to generate a multi-spectral classification of the target subject. Each of the resulting classifications is then fused, yielding an individualized segmentation true to the underlying data. Our strategy is capable of labeling both types of structures: tissues that are well-defined by the contrast in the images, as well as labels defined by their relative location to other structures. We present below a self-contained learning-by-example strategy for segmentation where the only inputs are a small number of segmented and registered example images and the target MRI to be segmented. We demonstrate this approach on data from a group of 14 subjects for whom gray matter, white matter, ventricles, putamen, caudate, and thalamus have been hand-labeled by an expert.

2 Methodology

2.1 Overview

Our algorithm utilizes a library of template labelmaps {L_n}, n = 1,…,N which have been registered to our target subject. In the present work, we employ a particular non-linear, non-rigid registration approach [2] for aligning the individual library images to the target, but a number of excellent techniques could have been used.

A typical label fusion approach seeks to combine these labels to generate a consensus labelmap or estimated true segmentation T = f(L₁,…,L_n) using some fusion function f, such as majority voting or STAPLE [11]. This approach is limited, however, in its use of intensity information in the images and is therefore only able to segment features well-represented in the template images. By using the template images to guide training of a supervised classifier, we’re able to “learn” about patterns of intensity throughout the image. We also utilize each template individually as a spatial prior, and in so doing retain the benefits of a traditional label fusion strategy where anatomical variation is represented by the distribution of input templates.

We assume that we have aligned, multi-spectral image data from the subject we wish to segment and denote this vector image I. We assume the existence of a supervised classification algorithm C : L × I → S which takes a labelmap for training L, a multi-spectral dataset I and produces a segmentation S. Coupling C with a particular template labelmap L_n yields a new classifier C_n : I → S_n that generates a candidate segmentation S_n. We fuse these classifications to produce the final resulting segmentation T = f(S₁,…, S_n).

2.2 Classification

In order to generate classifications {S_n}, we implement a Bayesian segmentation strategy:

$$p(S_{ni}=s|{\mathbf{I}}_i)=\frac{p({\mathbf{I}}_i|s)p(s)}{{\sum }_{s\prime }p({\mathbf{I}}_i|s\prime )p(s\prime )}$$ (1)

and estimate the likelihood p(I_i|s) of a particular MR intensity value I_i, at voxel i, given a particular tissue class s, using the density estimation strategy due to Cover [4]. Training data for density estimation is generated by sampling each labelmap L_n at a random coordinate i and pairing this label L_ni with the target subject’s image intensity at the same coordinate I_i. A number of such samples, randomly distributed in space, are then employed to estimate the tissue class likelihoods. In the experiments that follow, we used 4000 samples per tissue class and k = 51 for the Cover algorithm.

For the prior in Eq. 1, we use a spatially varying prior derived from an individual template L_n as in [8]. If $D_{ni}^s$ is the signed distance transform of label s in input template L_n, at voxel i, then the prior $p(s)=\frac{1}{Z}\mathit{\text{exp}}(\rho D_{ni}^s)$ where Z is the appropriate normalization constant such that all probabilities sum to 1 and ρ is a parameter which allows us to control the smoothness of the prior. The ideal value of ρ is related to the expected registration error, and for the non-linear registration we used in this work, we chose ρ = −1.4.

Each template labelmap L_n generates a unique segmentation S_n of the target subject that is the product of both a unique prior and likelihood. An alternative strategy might employ a common prior across candidate segmentations S_n, for instance based on the prevalence of a given label across templates. We believe that using each template individually allows us to better marginalize registration error during the fusion process.

2.3 Weighted Fusion

The STAPLE algorithm [11] has previously been used successfully for label fusion in contexts where it is not known how informative each template labelmap is on a label-by-label basis. Indexing voxels by i and individual templates using n, the voxelwise formula for fusion from STAPLE is:

$$p(T_i=s|{\mathbf{S}}_i,\mathbf{\Theta })=\frac{p(T_i=s){\prod }_{n}p(S_{ni}|T_i=s,{\theta }_n)}{{\sum }_{s\prime }p(T_i=s\prime ){\prod }_{n}p(S_{ni}|T_i=s\prime ,{\theta }_n)}$$ (2)

where θ_n is a matrix of performance parameters indicating the probability of mismatch between the individual segmentation S_n and the true, underlying segmentation T for each possible combination of labels s′, s: θ_ns′s ≡ p(S_n = s′|T = s), Θ is the collection of θ₁,…, θ_N, and S is the collection of S₁,…, S_n. This equation is solved using the STAPLE algorithm [11].

The performance parameters Θ in STAPLE depict statistics accumulated across the region of computation. This region may be restricted to a window around each voxel and Θ then depicts a spatially-varying measure of performance. This measure is advantageous for label-fusion applications where true performance may vary across the image, but may lead to undesirable local optima in areas of disagreement. In [3], the authors present a maximum aposteriori (MAP) estimate for Θ. Supplying a prior for Θ stabilizes these estimates in the face of missing structures and avoids undesirable local optima in areas of extreme disagreement.

In the present application, we generated a consensus from each candidate segmentation by running STAPLE MAP locally in a 5 × 5 × 5 voxel window around each voxel. The prior on θ_j is a Beta distribution, as described in [3], with parameters (α = 5, β = 1.5) for the diagonal elements and (α = 1.5, β = 5) for the off-diagonal elements of each θ_j. We utilized a spatially varying prior in STAPLE MAP calculated as the prevalence of each label, at each voxel coordinate, in the registered template images L_n. Finally, a mean-field approximation to a Markov Random Field prior was used as described in [11].

2.4 Improving the Training Data

Given the estimated true segmentation from Equation 2, it is desirable to edit the input training templates {L_n} by removing voxels that are inconsistent with the estimated segmentation [12]. We do this stochastically using the following procedure: for each of our templates L_n, we examine each of the previously sampled training points i, with label L_ni, and remove the training point from further use if p(T_i = L_ni|S, Θ) < rand([0, 1]) where rand([0, 1]) is a random number selected from a uniform distribution between zero and one. For instance, if a particular training point is labeled as “gray matter,” and our estimated true segmentation indicates that the probability of this label at this voxel coordinate is 0.6, then there is a 1 – 0.6 = 0.4 chance that we will remove this point.

Once the training data is edited, we re-estimate the classifications {S_n} and then generate a new weighted consensus using Eq 2. This process continues iteratively until the difference in successive estimates of the final segmentation is small. In [12] we demonstrated that this procedure leads to improved classifications by removing training points which appear inconsistent with the data being segmented. This algorithm serves to detect registration error between the template and the target and removes training data from the boundaries between tissue types where registration errors occur more frequently. This leads to improved classification accuracy.

3 Validation and Experiments

An expert segmented each of 14 normal controls into gray matter, white matter, ventricular cerebrospinal uid (including 3rd, 4th, 5th, and lateral ventricles), caudate, putamen, and thalamus following an established protocol. Segmentations were performed using high-resolution (1mm isotropic) T1-weighted SPGR images acquired at 3T on a GE Signa Imager (General Electric, Wakeusha, WI, USA). For each template, an associated grayscale image was registered to the target subject using an implementation of rigid and affine mutual-information (MI) registration and then using a locally-affine MI-based registration [2]. The resulting registration transform was then used to warp the template segmentation to the target subject. Each of the 14 datasets was segmented using the other 13 as templates in a typical “leave-one-out” fashion.

For comparison to our algorithm, we report values from segmentations obtained with two methods: an implementation of the label/intensity fusion algorithm in [8] and majority voting. Each of the algorithms used the same registered templates and, for compatibility with the other methods, we restricted our tests in these experiments to classification using the T1-weighted intensities alone, although a potential advantage of our method is its ability to perform multispectral classification.

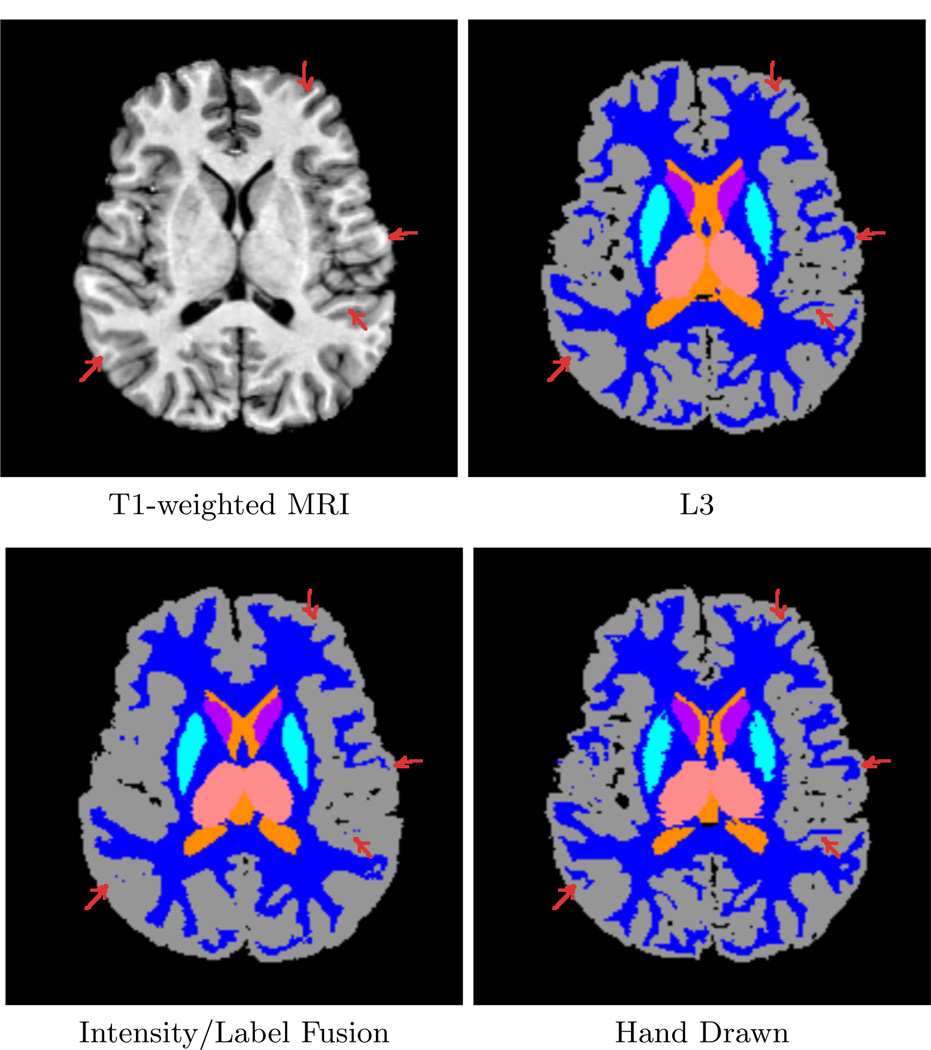
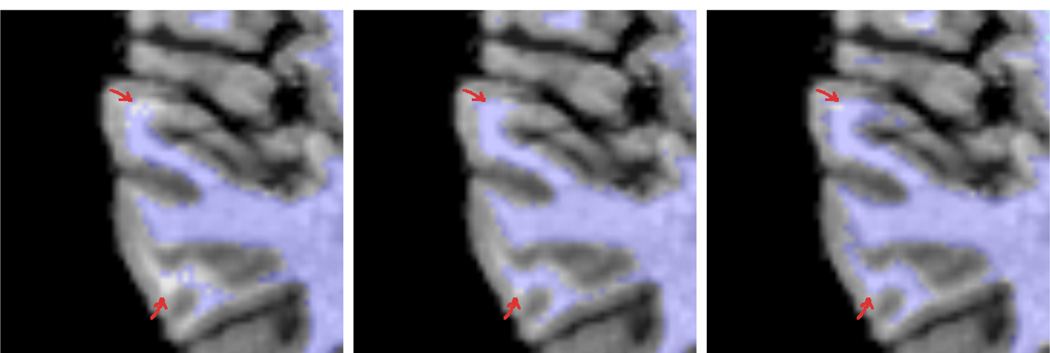
Figure 2 shows a typical T1-weighted image (top left) followed by the result from our algorithm (top right), a label/intensity fusion segmentation (bottom left), and the hand drawn segmentation (bottom right) for Case 1 from our study. The label fusion result appears to routinely oversegment cortical gray matter and misses fine details (arrows). In our algorithm, each individual input template leads to a different set of tissue-class likelihood estimates for the target subject, leading to different classifications which are then fused. We can then iteratively improve these likelihood estimates using the fused classifications. Figure 3 shows a close-up of segmentations overlaid onto the T1 image. On the left is the initial, fused classification using our method (first iteration), with arrows indicating areas where fine white matter details are not well captured. The next image shows the final result of our method, after iteratively improving the class-conditional likelihood estimates. Our new method captures more structure in the white matter as the likelihoods improve with each iteration.

Fig. 2.

Comparison of our method (L3) with a particular intensity/label fusion technique (see text) and hand-drawn segmentations. The intensity/label fusion result (lower left) oversegments gray matter and fails to represent fine sulcal detail in the image. Our method (top right) extracts such detail and better approximates the hand-drawn segmentation (bottom right).

Fig. 3.

The impact of editing the training sets: first iteration of our method (left), final iteration of our method (middle), groundtruth image (right). The method iteratively improves its class-conditional density estimates in order to better capture fine intensity differences within the input. Arrows indicate areas of change.

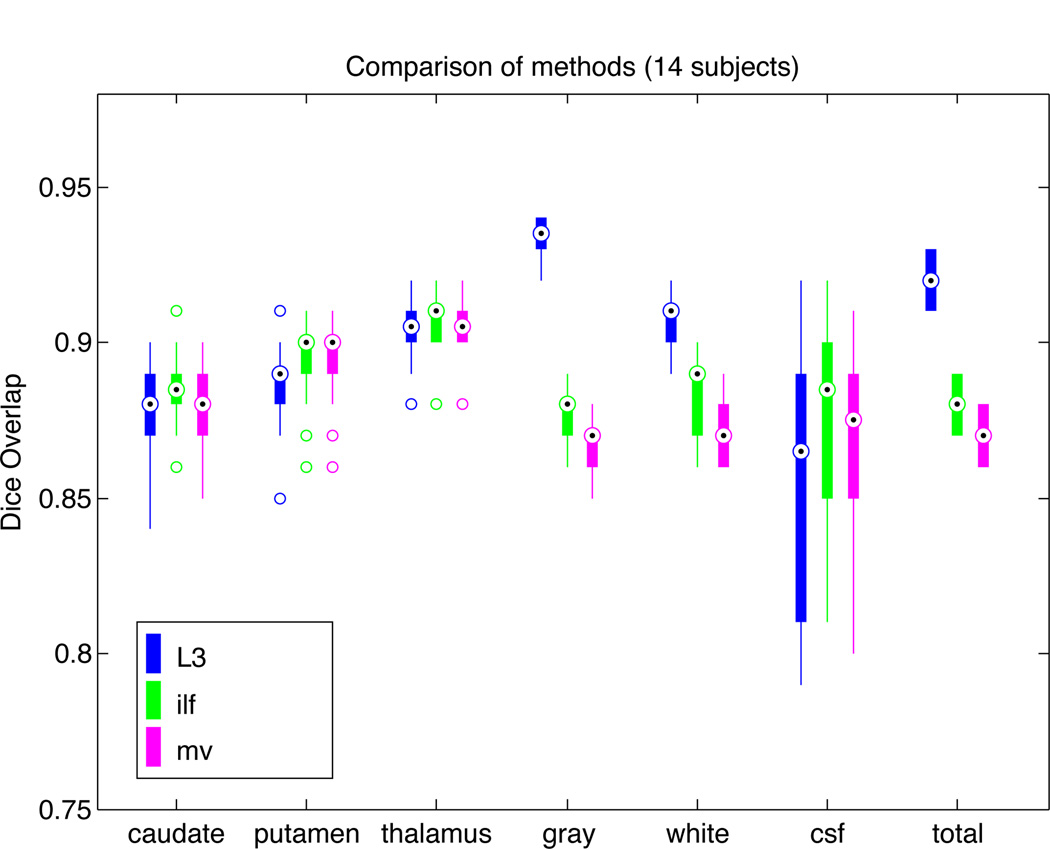
Figure 1 shows a plot of Dice overlap [5] measures for segmentations from our method, as well as majority voting and our implementation of the algorithm in [8], each compared with expert hand-drawn segmentations. Performance of L3 is generally excellent and is consistently highest for gray matter, white matter, and overall. The large variability in CSF segmentation is due to partial volume effects and the difficulty of visualizing CSF on T₁ weighted images. Total Dice measures across labels are computed as $\frac{{\sum }_{s}2|A_s\cap B_s|}{{\sum }_{s}2|A_s|+|B_s|}$

Fig. 1.

Dice overlap comparison between automatic segmentations and hand-drawn images for 14 subjects. Shown are our L3 method (blue), the combined intensity/label fusion method (ilf; green), and majority voting (mv; magenta). L3 performance is similar to other methods for subcortical structures (caudate, putamen, thalamus), but shows superior performance overall due to large improvements in gray matter and white matter segmentation.

4 Discussion and Conclusion

The emergence of very high quality registration technology has led to the emergence of segmentation by registration strategies where grayscale images are aligned and a known segmentation is warped to the target subject. Since the alignment of images from two individuals inevitably contains some registration error, multi-atlas label fusion techniques have been developed in order to marginalize registration error by employing template subjects with a distribution of anatomy. These methods are fundamentally limited in their ability to identify anatomy that cannot be captured through registration alone. Sabuncu[8] attempts to address this issue by incorporating an image intensity similarity term and pairs labelmap templates with intensity templates. This strategy inevitably requires data from the same modality and is incapable of modeling patient or disease specific intensity changes. Lötjönen[6] recognized this shortcoming and added an intensity classification after label fusion, however doing so led to a small Dice overlap improvement of 0.01 – 0.02.

The method we introduce here is a new type of multi-template classifier fusion that exploits the strengths of both label fusion and statistical classification. The anatomical variation in the population is encoded in a library of input templates. By weighting these appropriately, and using them independently, we’re able to employ a learning strategy that identifies areas of mismatch between each template and the target subject. This provides improved classification for diffuse, distributed structures with strong intensity contrast, as well as for structures which are largely isointense, but well defined by their position in the anatomy. Segmentation of the latter is heavily influenced by the template-based prior probabilities, while the former are accurately identified using the learned subject-specific likelihood functions.