Robust Super-resolution Volume Reconstruction from Slice Acquisitions: Application to Fetal Brain MRI

Abstract

Fast magnetic resonance imaging slice acquisition techniques such as single shot fast spin echo are routinely used in the presence of uncontrollable motion. These techniques are widely used for fetal MRI and MRI of moving subjects and organs. Although high-quality slices are frequently acquired by these techniques, inter-slice motion leads to severe motion artifacts that are apparent in out-of-plane views. Slice sequential acquisitions do not enable 3D volume representation. In this study, we have developed a novel technique based on a slice acquisition model, which enables the reconstruction of a volumetric image from multiple-scan slice acquisitions. The super-resolution volume reconstruction is formulated as an inverse problem of finding the underlying structure generating the acquired slices. We have developed a robust M-estimation solution which minimizes a robust error norm function between the model-generated slices and the acquired slices. The accuracy and robustness of this novel technique has been quantitatively assessed through simulations with digital brain phantom images as well as high-resolution newborn images. We also report here successful application of our new technique for the reconstruction of volumetric fetal brain MRI from clinically acquired data.

I. Introduction

In the presence of uncontrolled motion, high-quality and high-resolution slices can be obtained through fast slice acquisition techniques such as half-Fourier acquisition single shot fast spin echo (SSFSE)¹.The slices are acquired as snapshots in fractions of a second, thus freezing the motion of the subject. Important applications include fetal and neonatal magnetic resonance imaging (MRI) [1], [2], [3], [4] and MRI of moving subjects and organs [5], [6].

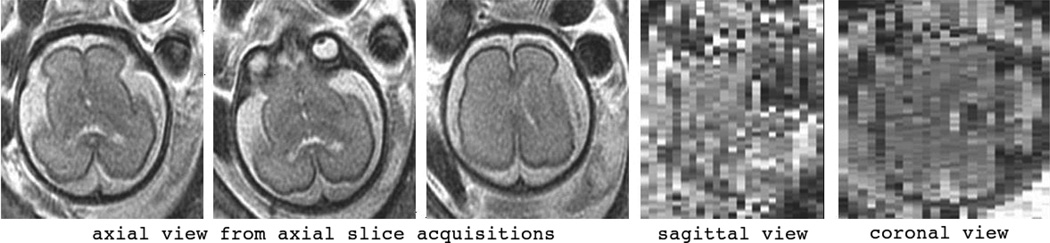
Motion does not normally affect the in-plane slice quality and resolution of SSFSE, but severe inter-slice artifacts frequently appear in out-of-plane views. Therefore the acquisition of appropriate slices is important for effective evaluation. The acquisition of useful slices in fetal MRI can be quite laborious. The imaging session starts with a localizer sequence and oblique acquisitions are planned based on the position and orientation of the fetus to capture fetal axial, coronal, and sagittal planes. The fetus moves during the scanning session and subsequent acquisitions must be planned according to the latest estimated position and orientation of the fetus. Although high-quality images are normally obtained in the slice plane views, due to inter-slice motion and the thick slices necessary to maintain signal-to-noise ratio (SNR) the cross-sectional views only poorly capture the 3D structure of the brain. A sample axial SSFSE scan of a fetus is shown in Fig. 1. The three adjacent axial slices on the left show the high-quality and high in-plane resolution of slice acquisitions, however inter-slice motion is also observed by comparing these slices. The sagittal and coronal views (shown on the right) do not reflect the subject’s anatomy.

Fig. 1.

Sample fetal MRI acquired in the axial plane: the three slices on the left show the high in-plane resolution and quality of the slice acquisitions, however, motion can be seen by comparing these three adjacent slices; on the right: sagittal and coronal views of this scan do not reflect the anatomical details due to the fetal motion and the 4 mm slice thickness needed for sufficient signal-to-noise ratio.

The reconstruction of volumetric fetal brain MRI from slice acquisitions may improve the efficacy of clinical evaluation but also greatly enhances the capacity of image analysis and research on the dynamics of brain maturation [4], brain development [7], [8], and the mechanism of brain injury [9]. There have been recent studies reporting promising results for the reconstruction of volumetric fetal brain MRI from fast slice acquisitions [10], [11]. The slice acquisitions are normally obtained from multiple orthogonal scans to make sure that the image space is sufficiently sampled. These reconstruction techniques utilize iterations of slice-to-volume registration and scattered data interpolation (SDI) and are referred to as SDI approaches here.

The main technical difference between the two previous SDI techniques is that local neighborhood oriented Gaussian kernel scattered data interpolation has been used in [10], while a regular grid of control-points cubic B-Spline scattered data interpolation [12] has been used in [11]. There are also implementation differences between the two techniques for instance in slice-to-volume registration [10], [11], [13]. However, these techniques do not provide a mathematical framework to justify that the reconstructed volume is a minimum error representation of the imaged object given the acquired MRI data. Our main contribution in this article is the formulation of a novel maximum likelihood error norm minimization for super-resolution volume reconstruction from slice acquisitions. For the first time we presented this approach at the MICCAI2009 workshop on image analysis for the developing brain [14]. We have further expanded this novel formulation by robust error norm minimization through M-estimation. A review of the super-resolution image reconstruction literature, given below, provides better understanding of the techniques developed here.

A comprehensive mathematical analysis of the super-resolution image reconstruction problem is initiated through an observation model [15]. The observation model is a forward model which shows how the acquired images are obtained from the imaged scene or object. The super-resolution reconstruction is the inverse problem [16], which involves finding the original scene that generates the acquired images under the imaging conditions. Normally the observation model can be written as a matrix equation such as y = Wx + v where x is a vector of the high-resolution imaged scene or object pixels in the lexicographical order, y is a vector of the acquired image pixels and v is the noise vector. W represents a matrix of the geometric and photometric effects of the imaging device, sensor, and the environment.

Super-resolution image reconstruction takes advantage of different sampling positions of the imaged object using multiple low-resolution image acquisitions. Sub-pixel shifts between low-resolution image frames provide dense sampling of the imaged object, thus super-resolution reconstruction is possible. Sub-pixel shifts between low-resolution image acquisitions can be performed by the imaging device. Alternatively, different sampling positions may be caused by motion. This is particularly useful in imaging moving subjects as well as in super-resolution reconstruction of video sequences. In these cases the motion parameters should be estimated and incorporated in the geometric part of W. This makes the problem nonlinear as both W and x will be unknowns.

Motion estimation and super-resolution reconstruction can be solved separately [17], [15], [18]; so after motion estimation W is considered to be known and super-resolution reconstruction will simplify to a linear inverse problem. The classical solution of this linear inverse problem is analytically obtained through the Moore-Penrose pseudo-inverse of W [16], [19]. From a probabilistic viewpoint the problem can be formulated as a maximum likelihood estimation (MLE). When the noise (v) is Gaussian MLE leads to l₂-norm error minimization, which complies with the classical solution.

In practice W is a large matrix and the computation of the pseudo-inverse is prohibitive [15], [19]. Therefore iterative solutions such as steepest descent or conjugate gradient are normally used [20], [18]. However, the ill-posed nature of the super-resolution reconstruction problem may cause numerical instability when methods such as conjugate gradient are utilized [17]; therefore even in fast super-resolution applications [18] the steepest descent method is normally preferred. When joint estimation of motion parameters and super-resolution reconstruction is performed, nonlinear optimization methods such as expectation maximization may be used [21].

Often the inverse problem of super-resolution image reconstruction is ill-posed due to an insufficient number of acquired image samples. Under these conditions regularization is sought to constrain and stabilize the solution. Regularization is typically interpreted as incorporating image priors in the reconstruction problem, which can be formulated as a maximum a posterior (MAP) estimation [15]. Various image priors may be used, for example Gaussian and Gibbs priors [22], Laplacian priors [23], and total variation (TV) [18]. Care should be taken when using Gaussian and Gibbs image priors to avoid excessive smoothing. A Markov random field model with flexible edge constraints was developed in [24]. Edge-preserving priors have been used in super-resolution image reconstruction [25], [26]. Bilateral total variation is a good example in this category [18]. Also, a few groups have recently developed super-resolution reconstruction techniques that are robust to motion estimation errors [27], [28]. These techniques are particularly useful in video sequence super-resolution and de-interlacing applications where the motion is local and cannot be estimated or corrected accurately.

For the super-resolution volume reconstruction from slice acquisitions two main issues should be addressed, which are considered to be the technical contributions secondary to the main contribution of this work. First, an appropriate slice acquisition model is needed; as compared to a common 2D observation model in the classical super-resolution problem (which is based on planar motion, sensor point-spread-function, and down-sampling) [15], the MRI slice acquisition model is a 3D model based on the physics of MRI which incorporates 3D motion, slice selection and signal averaging (slice profile and signal blur), and sampling. Second, the super-resolution volume reconstruction should be robust to motion-corrupted and mis-registered slices, and noise. This is extremely important as the estimation and correction of 3D inter-slice motion is very challenging, and volume re-construction is quite sensitive to motion correction accuracy. Robustness to noise and outliers was previously investigated in the super-resolution literature through the use of l₁-norm instead of l₂-norm for error minimization and regularization [18]. Robust super-resolution for digital imaging has been recently investigated in several studies [29], [30], [31], [32].

In this work, robust super-resolution has been formulated through the general M-estimation approach [33] that covers a range of techniques between the most accurate estimation in the presence of Gaussian noise (l₂-norm estimation) to the best estimation in the presence of Laplacian noise and outliers (l₁-norm estimation). Nevertheless, in our experiments it was also observed that the M-estimation formulation could not completely compensate the effects of slice outliers. Therefore the technique has further been expanded to use more reliable influence and weight functions. Data-dependent weight functions in the expanded formulation are computed based on slice error metrics in addition to individual voxel error samples. Extensive validation studies and in-vivo experiments show the effectiveness of the developed techniques.

The methodology including the slice acquisition model and the robust super-resolution reconstruction approach is discussed in Section II. Section III involves the algorithm design and implementation. In Section IV the developed technique has been validated through simulations with digital brain phantom and high-resolution newborn images. Also in this section the accuracy of the developed technique has been compared to that of the scattered data interpolation approach and its performance has been evaluated by using different error norm functions in the presence of noise and slice outliers. Section V discusses a volunteer subject experiment. Finally, in Section VI experimental results have been reported for the reconstruction of high-resolution volumetric images from clinically acquired fetal brain MRI data. Section VII contains a brief discussion and the concluding remarks.

II. Robust super-resolution volume reconstruction

A. Slice Acquisition Model

In a trade-off between a realistic model and a feasible solution, the following slice acquisition model is considered in this study:

$${\mathbf{y}}_k={\mathbf{D}}_k{\mathbf{B}}_k{\mathbf{S}}_k{\mathbf{M}}_k\mathbf{x}+{\mathbf{v}}_k;k=1,\dots ,n$$ (1)

where y_k is the vector of the voxels of the k^th 2D slice with slice thickness Δ_skand uniform in-plane spacing of Δρ_k; x is a vector of the desired uniformly-sampled reconstructed image voxels in the lexicographical order with uniform spacing of Δ_ρ; v_k is the residual noise vector, n is the number of slices obtained from N scans, M_k is the matrix of motion parameters, S_k is a matrix representing the slice selection profile, B_k is a blur matrix representing the point spread function of the MRI signal acquisition process, and D_k is a down-sampling matrix.

Slice selection is generated by selective excitation in MRI [34]. To selectively excite spins in a slice, a gradient field and a shaped RF pulse are needed. An RF pulse is only frequency selective therefore a linearly varying gradient field along the slice select direction is augmented with the main magnetic field. In order to get precise localization an appropriate selective excitation is desired to generate a rectangular (boxcar) slice profile with narrow transition regions minimizing slice-to-slice interaction. Spatial selection in the form of a boxcar function translates to a boxcar spectrum of the RF pulse around the Larmor frequency, which in turn, based on the Fourier transform, should be generated by a sinc excitation pulse in the time domain. Nevertheless the sinc function is not physically realizable as it is non-causal and infinite in time.

In practice, a shifted and truncated sinc pulse envelope function is applied. The shift in time results in a linear phase shift in the slice selection profile. This phase shift is compensated by applying a refocusing gradient in the slice select direction in a process called post excitation rephasing. The pulse truncation is modeled by the multiplication of the ideal sinc function with a rectangular window, which according to the Fourier transform is equivalent to the convolution of the ideal boxcar slice profile with a sinc function. Normally the sidelobes of the generated slice profile are small, therefore the slice profile generated by a truncated sinc pulse envelope function can be estimated by a boxcar function. In practice a truncated Gaussian pulse envelope function may be used instead of truncated sinc. In this case the slice profile will be a Gaussian function. For the details of slice selection and spatial localization the reader is referred to chapter five of [34].

In general the slice sampling of a volume in the slice select direction (z) can be written as [35]

$$m_q(z)=[m(z)*q(z)]\sum _j\delta (z-j)$$ (2)

where m(z) is the volume, m_q(z) is the sampled volume, q(z) is the slice profile, and j is slice location. In the case of truncated sinc pulse envelope function, q(z) in Equation (2) can be approximated by a boxcar function. For an arbitrary slice select direction defined by the normal vector of the slice plane equation, the following geometrical equation is obtained for the voxels of slice k (defined by a vector r⃗) in the slice selection process:

$$|{\vec{\mu }}_{sk}·\vec{r}-s_{0k}|<\mathbf{\Delta }{s}_k/2$$ (3)

where Δ_sk is the slice thickness, s_0k is the distance of the slice from the origin, and ${\vec{\mu }}_{sk}$ specifies the slice (or slice-selection) orientation. ${\vec{\mu }}_{sk}$ is interpreted as the normal vector of the slice plane equation. The normal vector can be obtained in the physical coordinate system based on the so-called direction cosines rotation matrix. This matrix is defined by the scanner according to the rotation angles used to generate the requested slice selection gradient field by the gradient coils.

In our formulation slices can be in any direction. This is in reality happening in fetal imaging, as the fetal axial, coronal, and sagittal planes are in arbitrary orientation with respect to the physical coordinates of the scanner. The orientation of fetal images obtained in one scanning session usually vary as the fetus moves and the radiologist prescribes different oblique acquisitions to get the best possible orthogonal views of the fetus. The slice acquisition model can be interpreted as region selection, signal averaging and resampling in the image space. According to Equation (2) in the case of truncated Gaussian pulse envelope function the corresponding Gaussian slice profile results in low pass filtering (smoothing) of the object during slice sampling. The implementation details of generating S_k in Equation (1) from Equation (3) will be discussed in Section III-B.

B. Maximum Likelihood Estimation

Maximum likelihood estimation (MLE) provides an optimum solution to Equation (1) through maximizing the conditional probability density function (PDF) of the acquired slices y_k: given the volume x. The likelihood function is simply defined by the conditional PDF, which in-turn depends on the noise distribution model. If the noise v_k is Gaussian with mean of zero and standard deviation of σ_k, the conditional PDF is written in terms of the estimated error samples having a Gaussian distribution representing the noise residuals:

$$\mathbf{P}\mathbf{r}({\mathbf{y}}_k|\widehat{\mathbf{x}})=\underset{i}{\mathbf{\Pi }}\frac{1}{{\sigma }_k\sqrt{2\pi }}\mathit{\text{exp}}(-\frac{{({\widehat{y}}_k(i)-y_k(i))}^2}{2{\sigma }_k^2})$$ (4)

where y_k(i) are the samples from the acquired slices y_k, ŷ_k(i) are the samples from the estimated slices ŷk = W_kx̂ + v_k, W_k = D_kB_kS_kM_k, and x̂ is an estimate of the reconstructed volume. The error samples are defined by e_k (i) = ŷ_k(i) – y_k(i), and the error vector for the k^th slice is defined as e_k = W_kx̂ – y_k. The log-likelihood function based on the PDF in Equation (4) can be simplified to obtain:

$$ℒ({\mathbf{y}}_k|\widehat{\mathbf{x}})=ℒ({\mathbf{e}}_k)=-\sum _i{({\widehat{y}}_k(i)-y_k(i))}^2=-{\parallel {\mathbf{e}}_k\parallel }_2^2$$ (5)

The right hand side is equal to the l₂-norm of the error between the estimated and acquired values of y_k. Assuming independent slice acquisitions the log-likelihood equals the sum of the l₂-norm of the error vectors over all slices. Consequently the maximization of the likelihood function results in the minimization of the sum of the l₂-norm of the error vectors over the slices:

$${\widehat{\mathbf{x}}}_{\mathrm{M}\mathrm{L}\mathbf{e}}=\text{arg}\underset{\mathbf{x}}{\text{min}}\sum _{k=1}^n{\Vert {\mathbf{W}}_k\widehat{\mathbf{x}}-{\mathbf{y}}_k\Vert }_2^2,$$ (6)

Since the cost function in Equation (6) is positive with a unique minimum at zero, the minimization can be translated to an implicit equation based on error samples. This is obtained by differentiating with respect to the samples of the estimated volume, i.e. x(i):

$$\sum _{k=1}^n\sum _i{e}_k(i)\frac{\partial e_k(i)}{\partial x(i)}=0$$ (7)

The solution to Equation (6) is equivalent to the pseudo-inverse and least-squares solution of Equation (1), and is statistically equal to the computation of the sample mean [20] if all the error samples have the same variance. If the noise v_k has a Laplacian distribution the MLE results in l₁-norm minimization, which is equal to the least absolute deviations, and is statistically equal to the computation of the sample median [18] if the error samples have the same variance. The l₂-norm MLE is not robust to outliers, but the l₁-norm MLE is robust to outliers and heavy-tailed noise [36]. However, the median estimator may lose as much as 40% efficiency over the sample mean when the noise is Gaussian [37].

C. Robust M-estimation

The l₂-norm MLE provides the best solution to the super-resolution reconstruction problem when the noise residuals in Equation (1) are drawn from a Gaussian distribution. In reality, however, noise residuals may not be Gaussian and outliers may also present in the data for various reasons such as inaccurate or failed registration (inaccurate slice motion estimation), motion-induced signal loss, and magnetic field inhomogeneities. In the l₂-norm MLE the influence of the error samples on the output is proportional to their magnitude. Therefore high error values and outliers have significant effects on the estimated output. To reduce the effect of outliers we replace the l₂-norm of the error in Equation (6) with a robust error norm function f(e_k):

$${\widehat{\mathbf{x}}}_{\mathrm{M}\mathbf{e}}=\text{arg}\underset{\mathbf{x}}{\text{min}}\sum _{k=1}^{n}f({\mathbf{W}}_k\widehat{\mathbf{x}}-{\mathbf{y}}_k)$$ (8)

The choice of robust error norm functions is discussed in robust statistics through the M-estimation (ME) framework [33]. Obviously l₁- and l₂-norm MLE super-resolution formulations discussed in section II-B are special cases of the formulation given in Equation (8) by replacing f(e_k) with ${\parallel {\mathbf{e}}_k\parallel }_1^1$ and ${\parallel {\mathbf{e}}_k\parallel }_2^2$ respectively. Note that the error norm function can be defined to be the sum of a function ρ(.) of the error samples:

$$f({\mathbf{e}}_k)=\sum _i\rho (e_k(i))$$ (9)

An appropriate robust error function ρ(.) is symmetric and positive with a unique minimum at zero, thus again similar to Equation (6) the minimization in Equation (8) can be written based on the error samples:

$$\sum _{k=1}^n\sum _i{e}_k(i)\omega (e_k(i))\frac{\partial e_k(i)}{\partial x(i)}=0,$$ (10)

where ω(e) = ψ(e)/e, and ψ(e) = dρ(e)/de is the influence function. This equation can be compared to Equation (7). Within this framework the weight function ω(e) shows the weights given to the error samples in the estimation. For the robust ρ(.) functions, the influence functions saturate and the weights decrease as a function of the error magnitude. For the l₂-norm estimation, ρ(e) = e²/2, ψ(e) = e, and ω(e) = 1 which means that equal weights are given to all error samples. Obviously the l₂-norm is not robust as its influence function is not bounded.

Among different choices for error norm functions, the l_p-norm (power-norm) function with ρ(e) = |e|^p/p, ψ(e) = sign(e)|e|^p−1, and ω(e) = |e|^p−2 can be designed based on the variable p to cover a wide range of estimators. When p changes between 2 to 1 the power-norm estimation changes between the most accurate maximum likelihood estimation in the Gaussian noise environment (l₂-norm estimation) to the most robust estimation (l₁-norm estimation) in a non-Gaussian environment (according to its breakdown point of 50%). The problem with this estimator is the infinite weights given to zero error values, which makes it numerically problematic and inefficient when the error sample distribution is approximately Gaussian.

A convex robust error function that circumvents the problem with the power-norm estimation yet parametrically gives l₂-norm weights to the low error values and l₁-norm weights to the high error values, is the Huber’s error function defined by

$$\rho (e)=\mathbf{\{}\begin{array}{cc}{e}^2/2,\hfill & \left|e\right|<\gamma \hfill \\ \gamma \left|e\right|-{\gamma }^2/2,\hfill & \left|e\right|>\gamma \hfill \end{array}$$ (11)

where γ is a tuning parameter. When γ is large the estimation will be close to the l₂-norm estimation and when γ is small it will be close to the l₁-norm estimation. It is assumed that the error samples are normalized with a scale parameter which can be estimated or approximated based on the data. As a rule of thumb, if the scale parameter is the median absolute deviation of the error samples, an appropriate value of γ is 1.345 [37]. The influence and weight functions associated with Equation (11) are ψ(e) = min(γ, max(−γ, e)) and ω(e) = min (1,γ/|e|) respectively.

Note that there are various choices for robust error functions [33]. Huber’s function is quite popular as it performs well in both Gaussian and non-Gaussian environments as well as in the presence of outliers. Complete rejection of extreme outliers may be preferred, which can be achieved by choosing redescending influence functions. Redescending influence functions are functions that decrease toward zero far from the origin, thus practically give zero weights to extreme outliers. Nevertheless poorly tuned redescending influence functions may result in significant loss in efficiency [33] (page 101).

By replacing Equation (11) in Equation (9) and Equation (8) we obtain a robust error norm minimization scheme for super-resolution volume reconstruction from slice acquisitions; However, since the data-adaptive error weight functions in the formulated M-estimation framework are functions of the individual voxel error samples, this estimation is vulnerable to ill-posedness and inaccuracy when the samples are sparse. Regularization is one way of dealing with ill-posedness and sparse samples, however it may result in over-smoothing. Since the number of samples is limited, a very reliable and accurate data-adaptive scheme is desired to effectively incorporate all the information from the acquired slices while minimizing the effect of outliers.

In super-resolution volume reconstruction from slice acquisitions, noise affects the MRI slices at the voxel level. On the other hand slice mis-registration and motion-induced signal loss artifacts influence an entire slice or a set of voxels within a slice. Consequently error vector norms of the slices, are relatively good indicators for computing robust error norm functions. Therefore we further modify our robust super-resolution volume reconstruction formulation by incorporating error weight functions based on the vector error norms in addition to the individual voxel error samples. The modified error weight function is written as:

$$\varphi (e_k(i),{\mathbf{e}}_k)=\omega (e_k(i))w({\mathbf{e}}_k).$$ (12)

where w(e_k) is a non-negative function of the k^th slice error vector norm. Consequently the modified version of the minimization in Equation (10) is written as

$$\sum _{k=1}^{n}w({\mathbf{e}}_k)\sum _i\omega (e_k(i))e_k(i)\frac{\partial e_k(i)}{\partial x(i)}=0.$$ (13)

This formulation is general and flexible. Appropriate functions may be used for w, for example

$$w({\mathbf{e}}_k)=\text{min}(1,\eta /{\Vert {\mathbf{e}}_k\Vert }_2^2),$$ (14)

where η is a tuning parameter similar to γ in Equation (11). The number of error samples from N scans that contribute to the estimation of each voxel in the high-resolution reconstructed volume space, is relatively small; therefore redescending influence functions may not perform well for robust estimation at the voxel level. On the other hand, the number of slices (n) is typically large, therefore the slice error vector norm can be reliably used as an argument for error weight functions.

In summary we have developed a maximum likelihood formulation in Section II-B which translates to an error minimization framework for super-resolution volume reconstruction from slice acquisitions. This formulation is based on the slice acquisition model discussed in Section II-A. In Section II-C we have made this formulation robust by using robust error norm functions and we have further modified that formulation by incorporating error norm weight functions based on the slice error vector norms. The solutions to the ordinary MLE in Equation (6), robust M-estimation in Equation (8) and Equation (10) and the modified robust M-estimation in Equation (13) along with the algorithm design, parameter assignments, and implementation details will be discussed in the next section.

III. Algorithm design and Implementation

A. Regularization

Before discussing approaches to solve the minimization problems formulated in section II, it is worth noting that sometimes the number of acquired slices is small which results in an under-determined super-resolution volume reconstruction problem. In this case regularization terms can be added to the cost function to enforce a constrained minimal norm solution. An appropriate regularization term penalizes the high-frequency components in the estimated volumetric image, thus it can be defined by a norm function of the high-pass filtered estimated volume. With the l₂-norm regularization a simple term like $\lambda {\parallel \mathbf{C}\mathbf{x}\parallel }_2^2$ is added to the cost functions in Equation (6) and Equation (8), where C is a positive definite matrix and λ is a weighting coefficient. The regularized l₂-norm MLE minimization is written as:

$${\widehat{\mathbf{x}}}_{\mathrm{M}\mathrm{L}\mathbf{e}}=\text{arg}\underset{\mathbf{x}}{\text{min}}\sum _{k=1}^n{\Vert {\mathbf{W}}_k\widehat{\mathbf{x}}-{\mathbf{y}}_k\Vert }_2^2+\lambda {\Vert \mathbf{C}\widehat{\mathbf{x}}\Vert }_2^2$$ (15)

B. Iterative Solution

The augmented matrix of all W_k matrices in Equation (15) is huge and the classical solution through pseudo-inverse is prohibitive. Therefore an iterative solution should be used. In order to avoid possible numerical instabilities caused by conjugate gradient method, we use a steepest descent iterative minimization approach here. The steepest descent iterative solution of Equation (15) is:

$${\widehat{\mathbf{x}}}^{n+1}={\widehat{\mathbf{x}}}^n+\alpha \sum _{k=1}^n{\mathbf{M}}_k^{\mathbf{T}}{\mathbf{S}}_k^{\mathbf{T}}{\mathbf{B}}_k^{\mathbf{T}}{\mathbf{D}}_k^{\mathbf{T}}({\mathbf{y}}_k-{\mathbf{D}}_k{\mathbf{B}}_k{\mathbf{S}}_k{\mathbf{M}}_k{\widehat{\mathbf{x}}}^n)-\lambda {\mathbf{C}}^{\mathbf{T}}\mathbf{C}{\widehat{\mathbf{x}}}^n,$$ (16)

where α is the step size in the direction of the gradient. The matrices D_k, B_k, S_k, and M_k and their transposes are exactly interpreted as corresponding image operators. D_k is defined as a resampling operation. If the desired reconstructed image spacing is considered to be equal to the uniform in-plane spacing (matrix resolution) of the acquired slices then D_k will be an I matrix. B_k is defined as the convolution with a Gaussian kernel resembling the point spread function (PSF) of the MRI signal acquisition process. S_k is defined for each slice based on Equation (3); the slice plane normal vector ${\vec{\mu }}_{sk}$ and the distance s_0k are computed based on the direction cosines matrix and the origin of each slice, respectively. This operation is implemented as rigid 3D rotation with the rotation matrix directly obtained from direction cosines matrix, and its transpose is the inverse (transpose) of the direction cosines matrix. The motion matrix M_k is implemented as a 6-DOF 3D rigid transformation (including three rotations and three translations) and is defined for each slice through slice-to-volume registration, which will be discussed later in this section. C is implemented as a gradient magnitude image operation. The image operations are applied to the reconstructed image and their transposes are applied to the error image exactly as suggested by Equation (16).

An iterative solution to the robust M-estimation problem with the explicit formulation defined in Equation (13) can be obtained by writing the explicit minimization as a weighted least squares problem. This weighted least squares problem along with the regularization term is written as:

$$\widehat{\mathbf{x}}=\text{arg}\underset{\mathbf{x}}{\text{min}}\sum _{k=1}^n{\Vert {\mathbf{\Omega }}_k({\mathbf{e}}_k){\mathbf{e}}_k\Vert }_2^2+\lambda {\Vert \mathbf{C}\widehat{\mathbf{x}}\Vert }_2^2,$$ (17)

where e_k = W_kx̂ − y_k as defined before, and Ω_k(e_k) is a diagonal matrix with its i^th diagonal element defined by ω(e_k(i))w(e_k). The iterative solution involves updating Ω_k(e_k) in each iteration and solving the resulting minimization problem similar to Equation (16). The error vectors e_k and the estimated image x̂ are iteratively computed until the variation in x̂ goes below a threshold. Note that the slice error vector norm $\parallel {\mathbf{e}}_k{\parallel }_2^2$ used for computing w(e_k) in Equation (14) is the mean square intensity differences (MSD) between the voxels of the k^th motion-corrected slice and the reconstructed volume.

Given the above mathematical framework for the super-resolution reconstruction, the entire volume reconstruction algorithm shown in Fig. 2 involves iterations of slice-to-volume registration for motion correction, scattered data interpolation for initial estimation, and super-resolution reconstruction for error minimization between the acquired slices and the estimated volume. Slice-to-volume registration is performed to define M_k. After slice-to-volume registration the acquired image samples will not be on a regular grid, therefore scattered data interpolation is used to define an initial estimate of the reconstructed volume. The estimate of the reconstructed volume in each iteration is used as the target for registration in the next iteration. For the first iteration this target volume is obtained by averaging the resampled acquired thick slice scans. Super-resolution reconstruction is performed based on Equation (16) and Equation (17). The algorithms with the solution to Equation (10) and Equation (13) are referred to as ME and RME respectively.

Fig. 2.

Algorithmic overview: block diagram of the developed super-resolution reconstruction algorithm; TC stands for the termination condition. Note that the previously developed SDI approaches do not involve the super-resolution reconstruction block. This block aims at minimizing an error norm function between the acquired slices and the estimated volume. This is performed through iterative solutions of Equation (10) and Equation (13).

During the iterations the estimated volume which is used as the target volume for registration improves, hence more accurate slice-to-volume registration (slice motion correction) is achieved. The iterative solution of the ME and RME equations are terminated when the associated cost functions or their change per iteration go below a threshold. This threshold is set to be 10⁻⁵ for the norm of the cost function over the norm of the estimated volume in our experiments. The termination condition (TC) for the registration iterations is satisfied when the change per iteration of the root mean square error (RMSE) of the slice-to-volume registration metrics goes below a threshold in two consecutive iterations. The reconstructed volume corresponding to the minimum registration metric is considered as the output. The two remaining blocks in the algorithm include slice-to-volume registration and scattered data interpolation, which will be discussed below.

C. Slice-to-Volume Registration

A robust algorithm has been developed for slice-to-volume registration. The goal is to compute a single 6-DOF rigid transformation (three rotations and three translations) for each slice. The algorithm works in three stages. In each stage, a 6-DOF rigid transformation is computed for a subset of slices. In the first stage, the subset involves slices acquired in one stack of the interleaved acquisition; for example, in a dual interleaved acquisition, two subsets are used: subset of even slices and subset of odd slices. In the second stage of registration, the rigid transformation for each slice is refined based on a subset including that slice and its two interleaved neighbors. For example, in a dual interleaved acquisition the transformation of slice 5 is computed based on registering the set of slices 3, 5, and 7 to the target volume. Finally, in the third stage, only a single slice is used for registration. The algorithm minimizes the mean square intensity differences (MSD) between each subset of slices and the reference volume. Powell optimization [38] with step sizes of 0.05, 0.02, and 0.02 was used in the three stages of registration, respectively.

D. Scattered Data Interpolation

After slice-to-volume registration the image voxels from motion corrected slices are not on a regular grid and are considered as scattered data in the 3D space. Scattered data interpolation (SDI) is needed to obtain a first estimation of the reconstructed volume from this data. As mentioned before, the previous MRI volume reconstruction techniques only utilize iterations of slice-to-volume registration and scattered data interpolation. The two main SDI approaches used for MRI volume reconstruction from slice acquisitions, are the B-Spline SDI [11] and local neighborhood SDI based on oriented Gaussian kernels [10]. In this study we implemented the B-Spline SDI approach (BSP-SDI) as well as a fast local neighborhood Gaussian kernel SDI approach (LNG-SDI) for comparison. The BSP-SDI was implemented as a 3-level cubic B-Spline approximation [11]. The LNG-SDI was used for the initial estimation of the reconstructed volumes in the super-resolution algorithm shown in Fig. 2.

The LNG-SDI involves weighted local intensity injection based on Gaussian kernels: motion correction is performed on the original thick slice acquisitions by applying 6-DOF transformations computed for each slice by slice-to-volume registration. The scattered data points obtained from motion-corrected slices are then mapped to the nearest neighbor grid points in the reconstructed image space and their intensity values are injected into the neighborhood points using Gaussian kernel weights. The SDI volumetric reconstruction approaches implemented in this study (i.e. BSP-SDI and LNG-SDI) only involve iterations of slice-to-volume registration and scattered data interpolation. The performance of these approaches are compared to the super-resolution reconstruction algorithms developed here. The developed algorithms are referred to as ME for M-estimation through Equation (10) and RME for the modified robust M-estimation through Equation (13).

IV. VALIDATION

A. Data for Validation

Prior to the main experiments the algorithm was quantitatively validated using digital brain phantom (DBP) images as well as two cases of high-resolution newborn images. DBP MR images were obtained from the Brainweb database [39] without initial noise and with 1 mm uniform resolution. High-resolution T2-weighted Turbo Spin Echo (TSE) axial images of the newborns were obtained from a database of newborn MRI scans collected at the Children’s Hospital Boston using a Siemens Trio 3T scanner with a 32 channel receiver head coil. The T2-weighted TSE imaging was performed with TR =16 s, TE = 85 ms, matrix size of 192 × 154 pixels, slice thickness of 1.2 mm and in-plane resolution of 0.8 mm.

Slice acquisitions were synthetically generated from the original high-resolution volumes by applying operations based on the slice acquisition model shown in Equation (1). Different parameters were examined based on the requirements for the validation studies. N = 9 was used in most experiments which corresponds to three scans in each of the axial, coronal, and sagittal slice select directions. The in-plane resolution was chosen to be equal to the in-plane resolution of the original high-resolution volumes, and the slice thickness was chosen to be 6 mm for the DBP experiments and 3 to 4 mm for the newborn image experiments. Subject motion was randomly generated for each slice using a uniform random number generator for each of six rigid motion parameters (three rotations and three translations). The range of the uniform random numbers was set to −10 to 10 degrees for rotation parameters and −4 to 4 mm for translation parameters. Slice selection was performed according to Equation (3), and the point spread function was simulated by Gaussian filtering with σ = 0.3. Different noise models were used for noise experiments and outliers were injected by zero filling the slice voxel intensity values when needed.

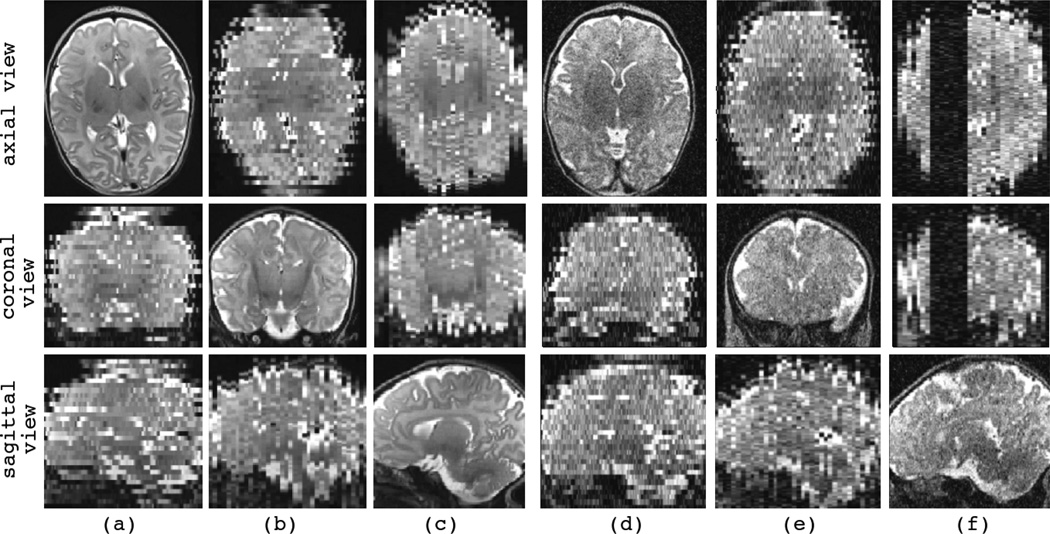
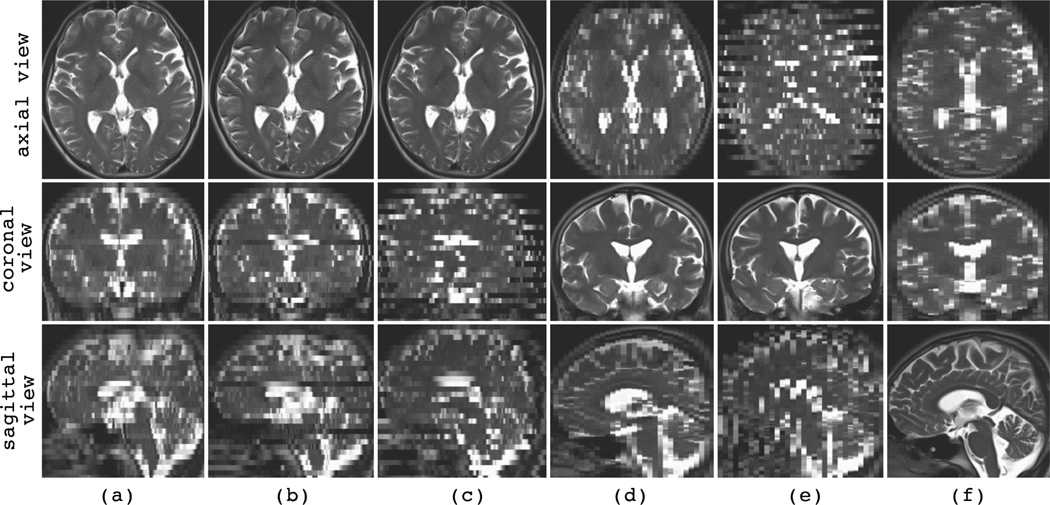
Samples of the synthetic motion-corrupted slice acquisitions are shown in Fig. 3, where the slice select direction in (a) is axial, in (b) is coronal, and in (c) is sagittal. Three slices from orthogonal views (axial, coronal, and sagittal views) are shown for each image, where the views are axial, coronal, and sagittal, respectively from top to bottom. We will consistently use these three views (from top to bottom) to represent an image or volume in the rest of the article. The images shown in (d) to (f) are also synthesized in the axial, coronal, and sagittal slice select directions, respectively, but these images are contaminated with additive Laplacian noise. In addition to noise, the image shown in (f) is corrupted with slice outliers. Sets of multiple images similar to (d), (e), and (f) will be used in Section IV-E to study the effects of noise and outliers on super-resolution volume reconstruction.

Fig. 3.

Sample synthetic motion-corrupted slice acquisitions generated from a high-resolution T2-weighted TSE image of a newborn subject. Three views (axial, coronal, sagittal views) of each synthetic image are shown in a column. The slice select direction in (a) and (d) is axial, in (b) and (e) is coronal, and in (c) and (f) is sagittal. No noise or outlier was added to the images in (a) to (c), while images (d) to (f) were contaminated with additive Laplacian noise (power of noise is σ = 200). Image (f) was also corrupted by synthetic slice outliers. Note that the synthetic images involve high-quality slice plane views but exhibit discontinuous tissue boundaries in the out-of-plane views. For example, the synthetic image in (a) with axial slice select direction exhibits sharp anatomic details in the axial view but not in the coronal and sagittal views.

B. Slice-to-Volume Registration Accuracy

The slice-to-volume registration is very important as the accuracy of super-resolution reconstruction is extremely sensitive to the accuracy of this part for motion correction. In this section we will evaluate the accuracy of slice-to-volume registration, and later in Section IV-C we will discuss about the sensitivity of the volume reconstruction to slice-to-volume registration. The accuracy of the slice-to-volume registration algorithm discussed in section III-C can be evaluated by comparing the known synthetic motion parameters with the estimated motion parameters for each slice. These motion parameters are three translations and three rotations in the 3D space for each slice. Ideally the estimated motion parameters should be equal to the known synthetic motion parameters.

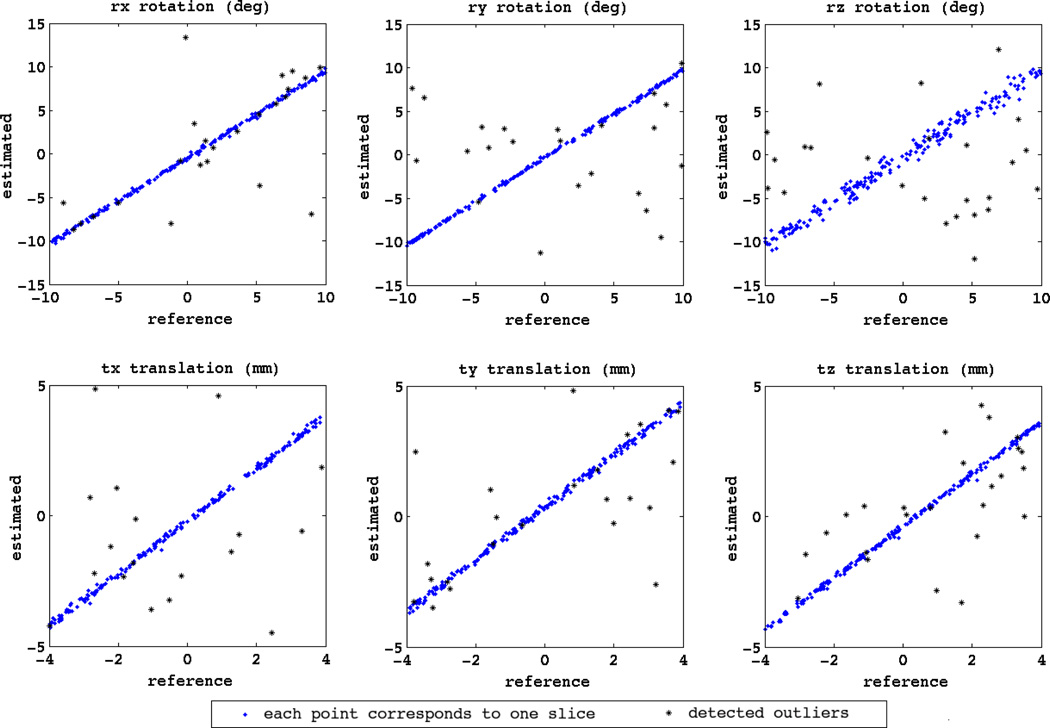
Fig. 4 shows the plots of the estimated motion parameters compared to the known synthetic motion parameters (reference) for the final iteration of a volume reconstruction experiment. Each point on these plots refers to the parameters for one slice. If the motion estimation was perfect, all the points would have been mapped to the diagonal line. This Figure indicates that the slice-to-volume registration was generally successful for estimating the slice motion parameters. However, it also shows that the slice-to-volume registration was prone to inaccuracies in motion estimation, and motion estimation completely failed for a number of slices.

Fig. 4.

The plots of the estimated slice motion parameters (estimated) compared to the actual synthesized slice motion parameters (reference) for the iterative registration and reconstruction of newborn case 2. The six parameters of the randomly generated motion parameters involve three rotations (rx, ry, rz) in degrees and three translations (tx, ty, tz) in millimeters. Each point corresponds to a slice. The points marked by asterisks (*) correspond to the slices detected as moderate and extreme outliers by the box-plot outlier detection method of quartiles based on the MSD of intensity values. Note that the statistical outlier detection method is not perfect and thus a few number of mis-registered slices may not be detected as outliers by MSD, but this analysis indicates that MSD can be used as a relatively reliable measure for assessing the fidelity of slice-to-volume registration.

As discussed before the mis-registered slices should be considered as outliers in the super-resolution volume reconstruction process. In order to examine the usefulness of the slice error vector norm (i.e. the MSD of intensity values) for outlier weighting in robust reconstruction through Equation (12) to Equation (14), we applied the statistical box-plot method of quartiles for slice outlier detection [40]. This statistical method is based on computing the upper (Q₃) and lower (Q₁) quartiles of the set of all slice MSD values, i.e. {MSD_k; k = 1…n}. The slices with MSD_k > 2.5Q₃ − 1.5Q₁ are defined as moderate outliers and the slices with MSD_k > 4Q₃ – 3Q₁ are defined as extreme outliers. The points corresponding to the detected slice outliers (moderate and extreme) are shown by asterisks (*) in Fig. 4. It should be noted that the statistical box-plot method of quartiles based on MSD values (${\parallel {\mathbf{e}}_k\parallel }_2^2$) may not be perfect for slice outlier detection, but this analysis shows that MSD is fairly accurate for the detection of mis-registered slices, hence is appropriate for robust slice error vector norm weighting through Equation (12) to Equation (14).

The accuracy of slice-to-volume registration is quantitatively measured using the root mean square error (RMSE) between the estimated motion parameters and the reference synthetic motion parameters for each slice. Two sets of experiments were performed using the validation datasets. In the first set of experiments, the original ground truth volumes, i.e. the high-resolution DBP volumes and high-resolution TSE volumes of the newborns, were used as the target for registration. These experiments assume a perfect target for registration, thus they evaluate the accuracy of slice-to-volume registration independent of the accuracy of reconstruction. In practice, however, the original high-resolution images are not available and the registration target should be estimated by the super-resolution reconstruction algorithm iteratively. Therefore the second set of experiments with newborn cases are the actual slice-to-volume registration (motion estimation) experiments in a super-resolution volume reconstruction algorithm. In these experiments the reconstructed volume in each iteration was used as the target for registration in the next iteration.

The average RMSE values over all the slices are shown in Table I for the first set of experiments, and in Table II for the second set of experiments. On the basis of the slice outlier detection using the box-plot method of quartiles we recomputed the average RMSE values for all slices excluding the slices detected as outliers. These values are also shown in the Tables. The results reported in Table I and Table II indicate that the developed slice-to-volume registration algorithm is fairly accurate, however it is also evident that the super-resolution volume reconstruction algorithm should be robust to mis-registered slices which are considered to be outliers. The sensitivity of the volume reconstruction algorithm to the slice-to-volume registration accuracy will be considered later in the next section.

TABLE I.

RMSE slice-to-volume registration between the estimated and the actual synthetic motion parameters averaged over the slices for registration to the original high-resolution volumes as the target.

	rx (deg)	ry (deg)	rz (deg)	tx (mm)	ty (mm)	tz (mm)
DBF (all slices)	0.255	0.270	0.666	0.252	0.267	0.198
DBF (excluding detected outliers)	0.186	0.203	0.562	0.217	0.223	0.170
Case 1 (all slices)	0.577	0.598	1.084	0.284	0.202	0.273
Case 1 (excluding detected outliers)	0.068	0.078	0.439	0.063	0.064	0.083
Case 2 (all slices)	0.888	1.214	1.575	0.539	0.430	0.312
Case 2 (excluding detected outliers)	0.131	0.106	0.474	0.096	0.125	0.054

TABLE II.

Rmse slice-to-volume registration between the estimated and the actual synthetic motion parameters averaged over the slices for registration to estimated reconstructed volumes as the target. The parameters are computed for the final iteration of super-resolution reconstruction algorithm.

	rx (deg)	ry (deg)	rz (deg)	tx (mm)	ty (mm)	tz (mm)
DBF (all slices)	0.608	0.653	0.946	0.551	0.516	0.487
DBF (excluding detected outliers)	0.466	0.532	0.922	0.498	0.433	0.442
Case 1 (all slices)	0.748	0.893	1.361	0.419	0.378	0.433
Case 1 (excluding detected outliers)	0.367	0.549	1.014	0.730	0.296	0.422
Case 2 (all slices)	1.054	1.758	1.706	0.898	0.617	0.620
Case 2 (excluding detected outliers)	0.725	0.904	1.032	0.553	0.446	0.475

C. Convergence Criteria and Performance

The super-resolution reconstruction algorithm shown in Fig. 2 iteratively refines the reconstructed volume and the motion correction (slice-to-volume registration). Better reconstructed volumes perform as better targets for registration in the consecutive iterations, and improved registration results in better reconstruction. Within each iteration the robust super-resolution reconstruction formulated in Section II-C is solved using the numerical techniques discussed in Section III-B. The algorithm aims at minimizing a robust error norm function between the reconstructed volume and the slice acquisitions.

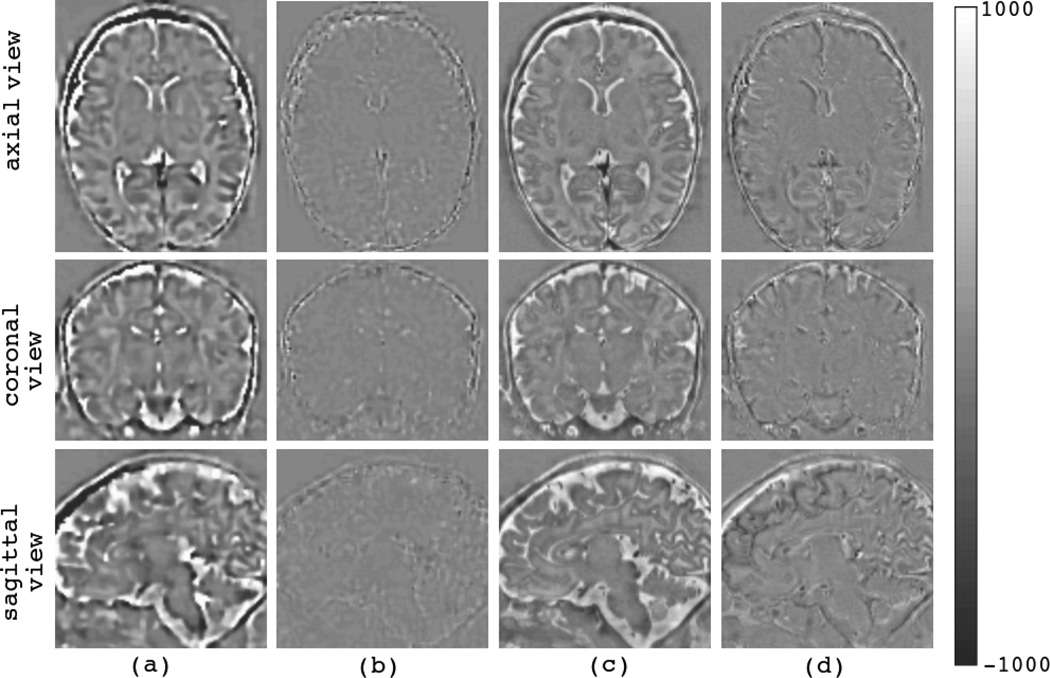
The convergence of the algorithm is evident from the error volumes shown in Fig. 5; the reconstructed error volumes based on the synthesized and estimated slices are shown in (a) and (b) for the first iteration and the last iteration of the algorithm, respectively. Since the ground truth (the original high-resolution volume) was available for the validation datasets, it was also possible to compute the actual error volume between the original high-resolution volume and the estimated volume. These error volumes for the first and the last iterations of the algorithm are shown in (c) and (d), respectively.

Fig. 5.

Error image volumes at the beginning and the end of the super-resolution reconstruction algorithm show the convergence of the algorithm; (a) and (b) show the reconstructed error volumes between the estimated volume and the synthesized slice acquisitions. (c) and (d) show the actual error volumes between the estimated volume and the original high-resolution volumes that are available for the validation datasets. Obviously, the algorithm minimizes the error between the estimated volume and the available slice acquisitions (b), but this may not result in perfect match between the reconstructed volume and the original ground truth volume, thus the actual error volume shown in (d) is not as good as (b).

Obviously the algorithm minimizes the error between the estimated volume and the available slice acquisitions (Fig. 5 (b)), but this may not result in a perfect match between the reconstructed volume and the original ground truth volume, thus the error volume shown in Fig. 5 (d) represents the actual loss in anatomic details due to the entire process of thick-slice image acquisition and super-resolution volume reconstruction. This is expected as some information is lost during the slice acquisition, signal averaging, and resampling processes. Performance limits in super-resolution volume reconstruction from slice acquisitions are mainly induced by thick slice acquisitions causing signal averaging and partial voluming, limited number of slice acquisitions, and limited slice-to-volume registration accuracy.

Since the original high-resolution volumes are available for the validation datasets (i.e. the original DBP and newborn volumes), the accuracy of reconstruction can be measured quantitatively. Two measures are used here: Mean Absolute Error (MAE) and Peak Signal to Noise Ratio (PSNR). MAE is simply defined as the mean absolute differences of the voxel intensity values between the original volume and the reconstructed volume. PSNR is defined in the logarithmic decibel (dB) scale as $20{\text{log}}_{10}(\text{MAX}/\sqrt{\mathrm{M}\mathrm{S}\mathrm{E}})$, where MAX is the maximum possible voxel intensity value (4096 in our experiments) and MSE is the mean square error of the voxel intensity values between the original volume and the reconstructed volume. During six registration iterations of the algorithm for newborn volume reconstruction, MAE was reduced from 155 to 90, and PSNR was increased from 23.9 dB to 28.1 dB. The algorithm was automatically terminated in the 13^th iteration and the volume reconstructed in the 11^th iteration was given as the output.

Various factors affect the accuracy of super-resolution volume reconstruction. The performance limits in super-resolution image reconstruction and the effect of various factors have been addressed in [41] through statistical analysis based on Cramer-Rao bounds. One of the important factors is the number of input scans. Intuitively, better reconstruction is expected when higher number of input scans are available for reconstruction; however in practice the number of scans is limited due to the constraints on total scan time. This is particularly an important constraint in fetal imaging. Using the validation datasets, we carried out experiments with various number of synthetic input scans (between one to seven inputs in each orthogonal slice select direction which translated to total numbers of 3 to 21 input scans). The results indicate that higher PSNR and lower MAE values are obtained with higher number of input scans. According to our analysis the accuracy of volume reconstruction dramatically dropped when less than a total number of 9 input scans were used for reconstruction. The analysis also showed that the accuracy of reconstruction did not significantly improve when the total number of scans went above 15. This analysis basically showed that to effectively reconstruct volumes with uniform resolutions being one-third of the slice thickness, at least three thick-slice scans in each orthogonal direction were needed. However, an effective volume reconstruction technique may provide relatively good reconstructions with lower number of scans.

A very important factor that affects the quality of super-resolution volume reconstruction is the accuracy of slice-to-volume registration. The degradation in performance of super-resolution image reconstruction due to motion estimation has been approximated to be at least 10% to 25% in [41] based on the number of low-resolution observations. In practice this degradation can be much higher in super-resolution volume reconstruction from slice acquisitions. The sensitivity of volume reconstruction to the accuracy of slice-to-volume registration can be quantified by a set of experiments comparing the reconstruction with known slice motion parameters to reconstruction with estimated motion parameters. Inspired by the statistical analysis in [41] we utilize the root mean square differences (RMSD) of voxel intensity values between the reconstructed volumes and the original high-resolution volumes available for the validation datasets. We carried out experiments with known and estimated motion parameters for various number of input scans. The RMSD values and the performance degradation computed as the percentage increase in RMSD due to motion estimation, have been reported in Table III.

TABLE III.

Sensitivity of volume reconstruction accuracy to motion estimation based on the RMSD of intensity values between the original ground truth volumes and the volumes reconstructed with known motion parameters and with unknown (ESTIMATED) motion parameters.

Number of input scans (N)	6	9	12	15
RMSD (MLE with known motion parameters)	113.763	109.669	107.447	106.885
RMSD (MLE with estimated motion parameters)	171.287	147.700	146.65	145.895
Degradation in performance (%)	50.56%	34.68%	36.49%	36.50%

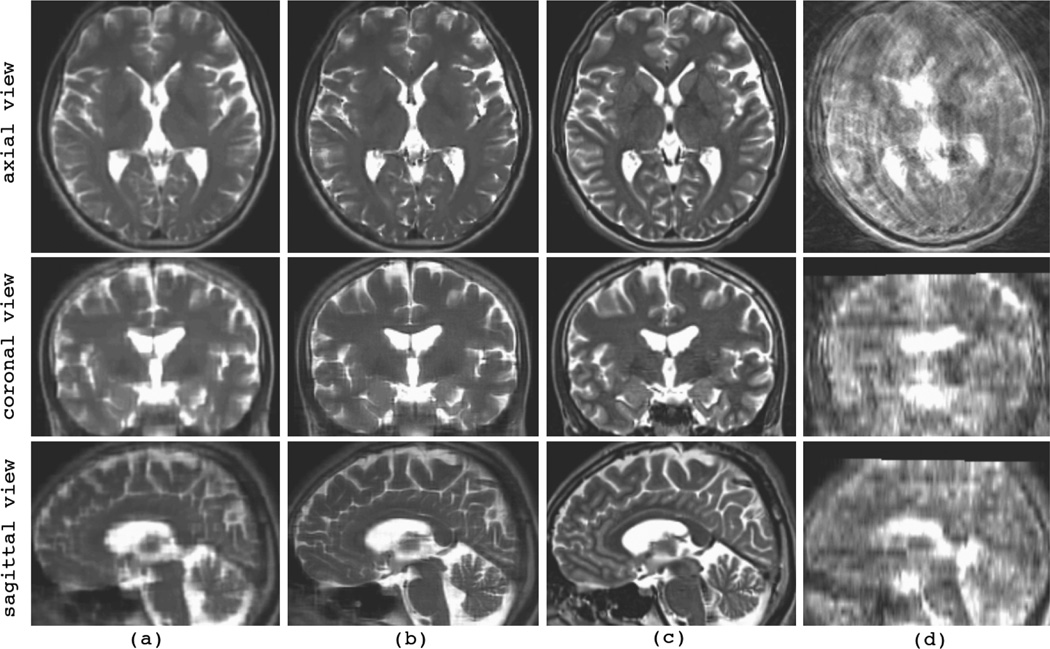
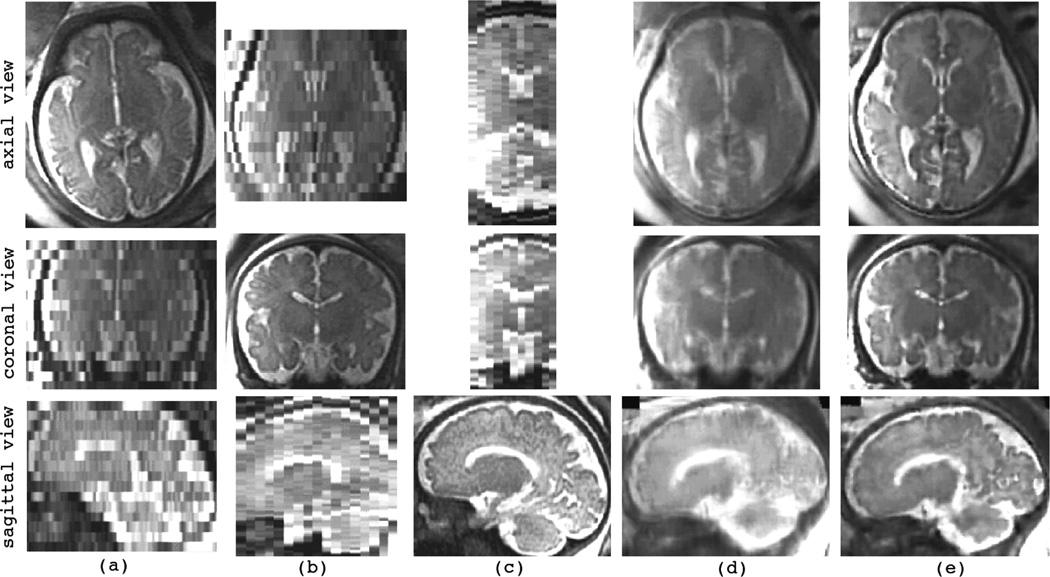
The results of the reconstruction experiments with the newborn database are shown in Fig. 6, where (a) shows the initial estimation of the reconstructed volume obtained by averaging the resampled input scans (AVE), (b) is the reconstructed volume after ten iterations of slice-to-volume registration and super-resolution volume reconstruction (MLE), (c) is the reconstructed volume with known slice motion parameters, (d) is the original high-resolution TSE volume, and (e) is the volume reconstructed with known motion parameters using the B-Spline scattered data interpolation approach (BSP-SDI). The degradation in performance due to motion estimation is observed by comparing (b) and (c). Note that these volumes are reconstructed from thick-slice motion-corrupted input scans similar to those shown in Fig. 3. Simple averaging of these input scans results in the volume shown in (a). Apparently the developed volume reconstruction technique is quite effective in recovering the 3D anatomy and coherent boundaries of structures from motion-corrupted input scans. The comparison between MLE and BSP-SDI reconstructions can be observed from (c) and (e) and will be discussed in the next section.

Fig. 6.

The reconstructed volumes for newborn case 2; (a) shows the initial reconstructed volume based on averaging the resampled input scans (AVE), (b) shows the reconstructed volume after ten iterations of slice-to-volume registration and MLE super-resolution reconstruction algorithm, (c) shows the reconstructed volume obtained from one iteration of MLE with known slice motion parameters, (d) shows the original high-resolution TSE volume (used as the ground truth reference for this validation dataset), and (e) shows the reconstructed volume obtained from BSP-SDI with known slice motion parameters. The comparison between BSP-SDI and MLE is considered in section IV-D.

D. Comparison to Scattered Data Interpolation

It is important to determine if the super-resolution volume reconstruction based on error minimization (i.e. MLE in the simplest form) outperforms the scattered data interpolation (SDI) techniques. Using the newborn datasets without additional noise or outliers, we compared the accuracy of MLE with the initial reconstruction obtained from averaging (AVE) and the reconstructions using B-Spline SDI (BSP-SDI) and local neighborhood Gaussian SDI (LNG-SDI). The difference between the MLE reconstructed volume and the BSP-SDI can be seen by comparing Fig. 6 (c) and (e). It is visually evident that the MLE reconstruction in (c) is much sharper and is a much better approximation to the original volume (d) as compared to the reconstruction by BSP-SDI (e). The volumes reconstructed by LNG-SDI were visually similar to those reconstructed by BSP-SDI. Table IV shows the values of MAE and PSNR for the AVE, BSP-SDI, LNG-SDI, and MLE reconstruction techniques. The best values, shown in bold, are achieved by the MLE reconstruction.

TABLE IV.

Comparing the MAE and PSNR of the original and reconstructed images for the reconstructions by the super-resolution reconstruction technique (MLE), averaging (AVE), and scattered data interpolation based on BSP-SDI and LNG-SDI. The best values in each line are shown in bold text.

	MAE
	AVE	BSP–SDI	LNG–SDI	MLE
Case 1	114.973	56.636	55.606	40.758
Case 2	155.387	69.546	69.535	62.075
	PSNR (dB)
	AVE	BSP–SDI	LNG–SDI	MLE
Case 1	26.909	33.266	32.648	35.358
Case 2	23.866	31.095	30.137	31.462

E. Robustness to Noise and Slice Outliers

Thick slices are normally acquired in SSFSE scans to maintain good SNR. Thinner slices needed to capture the small structures of fetal and neonatal brains are quite noisy. On the other hand, fast impulsive motion may cause partial or complete signal loss during slice acquisitions. Motion-induced and field inhomogeneity artifacts may degrade a number of slices in a dataset. Consequently many of the slices in each SSFSE scanning session may not be perfect or may have significant signal loss artifacts. But the most important source of error in super-resolution volume reconstruction is failed or inaccurate registration. Mis-registered slices result in severe artifacts in the reconstructed volume. Under the circumstances, robustness to noise and outliers is strongly desired for super-resolution volume reconstruction from slice acquisitions.

In order to validate the robustness of the developed robust reconstruction technique (RME) as compared to the developed ME (and MLE) techniques, experiments were carried out with different types of noise and slice outliers. In our experiments nine input scans were used for reconstruction. Gaussian, Laplacian, and mixed (ε-contaminated) noise [36], [33] were added to the synthetic slices obtained from high-resolution DBP and newborn volumes. A block of slice outliers (a region of one-fourth of the slices in one scan) were added to one of the coronal and one of the sagittal scans when needed.

In the first set of experiments, the effect of various noise conditions was considered. The noise conditions are shown by NN for no additive noise, GN for Gaussian noise with mean=0 and σ = 200, LN for Laplacian noise with mean=0 and σ = 200, and MN for mixed ε-contaminated noise with mean=0, σ = 200, and ε = 0.5). MAE and PSNR between the reconstructed volumes and the original ground truth volumes were used for quantitative evaluation. The results for the noise experiments are shown in Table V and Table VI for the DBP and newborn datasets respectively. The M-estimation approach (ME) with different γ values was used for comparison, where γ = 0.001 was used for l₁-norm estimation, γ = 1.345 was used for Huber function estimation, and γ = 1000 was used for l₂-norm estimation. Note that the error values were normalized with respect to their mean absolute deviation.

TABLE V.

Comparing the MAE of intensity values and PSNR (dB) of the M-estimation reconstruction (ME) of the dbp images with various noise conditions using different norm functions. The best values in each row are shown in bold text.

	MAE
	ME (l1–norm)	ME(Huber)	ME (l2–norm)
NN	95.019	68.350	74.210
GN	131.887	128.092	128.816
LN	134.481	149.329	172.777
MN	120.955	117.746	121.834
	PSNR (dB)
	ME (l1–norm)	ME(Huber)	ME (l2–norm)
NN	27.644	30.282	29.681
GN	25.346	25.715	25.393
LN	25.193	24.948	24.185
MN	25.581	25.997	25.760

TABLE VI.

Comparing the MAE of intensity values and PSNR (dB) of the M-estimation reconstruction (ME) of the newborn images with various noise conditions using different norm functions. The best values in each row are shown in bold text.

	MAE
	ME (l1–norm)	ME(Huber)	ME (l2–norm)
NN	64.642	46.673	46.259
GN	75.907	67.968	67.896
LN	78.290	78.884	76.756
MN	72.787	63.070	63.604
	PSNR (dB)
	ME (l1–norm)	ME(Huber)	ME (l2–norm)
NN	30.779	33.673	33.747
GN	30.381	32.218	32.229
LN	30.189	31.176	31.378
MN	30.520	32.585	32.547

Note that the number of scans (N) is typically small and limited number of samples are available for robust statistical noise filtering. Under these conditions the results shown in Table V and Table VI indicate that the Huber’s error norm function generally performed better than the other estimators. The results also indicate that the l₁-norm ME reconstruction may result in significant loss of efficiency when there is little noise or the noise is Gaussian, and the l₂-norm ME reconstruction may result in significant error in the presence of heavy-tailed Laplacian noise. The conclusion from these experiments is that the Huber’s error norm function can be used for robust volume reconstruction under unknown noise conditions.

In the second set of experiments the performance of the RME reconstruction technique was considered under different noise conditions with and without slice outliers. The RME technique was applied with γ = 1.345 for robust voxel-level noise filtering and with various η values. For slice error norm weighting, η was chosen to be 0.001, 1.345, and 1000 for l₁-norm, Huber, and l₂-norm functions, respectively. The slice error vector norms (MSD) values were normalized with respect to their mean absolute deviation. The reconstructed volumes in these experiments are quantitatively compared using the MAE and PSNR measures for both DBP and newborn validation datasets. The results are shown in Table VII and Table VIII. The results for noise experiments without slice outliers are shown by NN for no noise, GN for Gaussian noise, LN for Laplacian noise, and MN for mixed noise. The results with slice outliers are shown by SO. The best values for each experiment are shown in bold text.

TABLE VII.

Comparing the MAE of intensity values and PSNR (dB) of the robust M-estimation reconstruction (RME) of the dbp images with various noise and slice outlier conditions using different slice error norm functions. the best values in each row are shown in bold text.

	MAE
	RME (l1–norm)	RME(Huber)	RME (l2–norm)
NN	87.729	77.919	68.350
GN	131.179	131.174	128.092
LN	151.162	151.162	149.329
MN	120.408	120.362	117.746
SO	80.680	76.175	97.704
SO+GN	149.843	148.176	164.733
SO+LN	175.455	174.429	189.688
SO+MN	135.114	133.506	150.957
	PSNR (dB)
	RME (l1–norm)	RME(Huber)	RME (l2–norm)
NN	28.608	29.250	30.282
GN	25.433	25.433	25.715
LN	24.868	24.868	24.948
MN	25.798	25.800	25.997
SO	26.727	26.888	25.202
SO+GN	24.960	24.991	23.855
SO+LN	23.961	23.979	23.052
SO+MN	25.418	25.442	24.188

TABLE VIII.

Comparing the MAE of intensity values and PSNR (dB) of the robust m-estimation reconstruction (RME) of the newborn images with various noise and slice outlier conditions using different slice error norm functions. The best values in each row are shown in bold text.

	MAE
	RME (l1–norm)	RME(Huber)	RME (l2–norm)
NN	52.687	47.606	46.673
GN	71.616	70.129	67.968
LN	81.368	81.019	79.756
MN	66.979	65.041	63.070
SO	51 .776	46.956	56.011
SO+GN	76.512	73.512	80.434
SO+LN	87.563	85.366	92.453
SO+MN	70.780	67.712	75.057
	PSNR (dB)
	RME (l1–norm)	RME(Huber)	RME (l2–norm)
NN	32.615	33.511	33.673
GN	31.779	31.947	32.218
LN	30.917	30.954	31.078
MN	32.084	32.322	32.585
SO	32.831	33.639	31.963
SO+GN	31.417	31.691	30.612
SO+LN	30.369	30.557	29.211
SO+MN	31.835	32.139	30.937

The results reported in Table VII and Table VIII indicate that when there is no slice outlier, RME (l₂-norm) provides the most accurate results; however, in the presence of slice outliers the performance of this technique dramatically drops. In this case the RME (Huber) which applies robust slice error vector norm weighting, provides the best performance. It is observed that if we use RME (Huber) in all experiments, the loss in accuracy for the experiments without slice outliers is not remarkable; however, if we use RME (l₂-norm) in all cases, there will be a significant loss in accuracy when slice outliers present. Note that slice-to-volume registration in super-resolution volume reconstruction may fail and is not always accurate, therefore the use of robust reconstruction based on slice error vector norm weighting is often helpful.

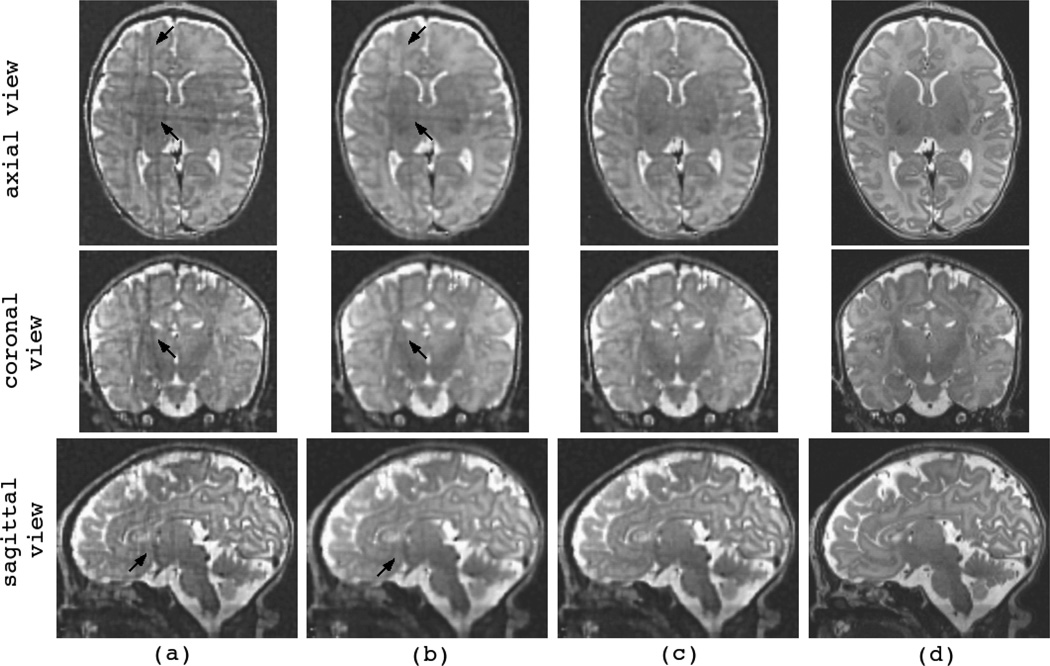
Fig. 7 shows the reconstructed volumes of one of the newborn experiments with additive ε-contaminated noise (mean=0, σ = 200, and ε = 0.5) and slice outliers. Twelve synthetic motion-corrupted scans were used in this experiment. All of the scans were contaminated with noise and one of the coronal and one of the sagittal scans contained a block of slice outliers as shown in Fig. 3 (f). The volumes shown in Fig. 7 involve (a) the reconstructed volume using l₂-norm ME, (b) the reconstructed volume using l₁-norm ME, and (c) the reconstructed volume using RME (Huber). The original high-resolution TSE volume shown in (d) is considered to be the ground truth reference. Severe artifacts are observed in the volume obtained from non-robust l₂-norm ME reconstruction in (a). The robust l₁-norm ME reconstructed volume in (b) is much better but is relatively blurred and yet has some artifacts in the outlier affected regions. On the other hand, the RME reconstructed volume in (c) is sharp and the effect of slice outliers is appropriately eliminated. These observations strongly comply with the quantitative evaluation results discussed above. Finally it should be noted that the volume shown in Fig. 7 (c) was reconstructed from input scans that were strongly affected by ε-contaminated noise and slice outliers. Samples of these input scans were shown in Fig. 3 (d) to (f).

Fig. 7.

The reconstructed volumes for an experiment with mixed noise and slice outliers with the newborn validation dataset; (a) shows the volume reconstructed by ME with l₂-norm error function (i.e. ordinary MLE), (b) shows the volume reconstructed by ME with l₁-norm error function, and (c) shows the volume reconstructed using the RME technique with Huber’s slice error vector norm function. Severe artifacts appear in the non-robust l₂-norm ME volume reconstruction in (a); the black arrows point at some of these artifacts. The volume reconstructed with l₁-norm ME in (b) is blurred and still has some artifacts; finally the volume reconstructed with data-adaptive robust RME in (c) is sharp and the effect of slice outliers is appropriately eliminated.

V. VOLUNTEER SUBJECT EXPERIMENTS

The developed super-resolution volume reconstruction algorithm can be primarily used for the reconstruction of brain volume from fast MRI slice acquisitions. This is particularly useful for T2-weighted imaging of subjects who may move in the scanner, for example newborns or neonates. In this section we report a volunteer subject experiment. Six HASTE scans were acquired for a volunteer subject using a Siemens Trio 3-Tesla scanner. Orthogonal (axial, coronal, and sagittal) views of these scans are shown in Fig. 8 and include three axial, two coronal, and one sagittal acquisitions shown in (a) to (f) respectively. HASTE imaging was performed with TR = 1400 ms, TE = 98 ms, slice thickness of 5.2 mm, and in-plane resolution of 0.86 mm. The subject significantly moved during scans (b), (c), and (e). The imaging session also involved high-resolution T2-weighted axial Turbo Spin Echo (TSE) imaging with TR = 16000 ms, TE = 85 ms, matrix size of 192 × 192 pixels, slice thickness of 1.2 mm, and in-plane resolution of 1.09 mm. The TSE volume was obtained when the volunteer did not move in the scanner. This volume was used as the reference for comparison.

Fig. 8.

Acquired HASTE scans for the volunteer subject experiment; (a)–(c): axial HASTE acquisitions, (d) and (e): coronal HASTE acquisitions, and (f) a sagittal HASTE acquisition. Note that despite the large scale of volunteer motion, the slice quality and resolution is generally preserved in HASTE imaging. However, if the motion is fast, a number of slices may be affected by signal loss and intensity distortion artifacts. A few of these affected slices can be seen in the coronal and sagittal views of the axial acquisition in (b).

Orthogonal slice views of the reconstructed volumes in this experiment are shown in Fig. 9. In this figure (a) is the reconstructed volume based on LNG-SDI, and (b) is the reconstructed volume using the developed RME technique. The reference TSE volume is shown in (c); and (d) shows a TSE volume acquired when the subject was moving. Apparently the TSE volume provides different contrast and better details of the anatomy as compared to the original HASTE scans shown in Fig. 8 and consequently in Fig. 9 (b), but the TSE imaging is not robust to motion. The HASTE scans, on the other hand, are robust to motion, in the sense that the quality and resolution of the fast slice acquisitions is generally preserved despite subject’s movements.

Fig. 9.

The reconstructed volumes for the volunteer subject experiment with six HASTE input scans shown in Fig. 8; (a) is the reconstructed volume using LNG-SDI, (b) is the reconstructed volume using the RME technique, (c) is the reference high-resolution TSE volume, and (d) is a TSE volume acquired when the subject was moving in the scanner.

Due to the differences between the contrast in HASTE and TSE imaging, the TSE volume cannot be considered as a ground truth reference of contrast and intensity values for the reconstructed volumes. However, we expect to see similar anatomical structures in the reconstructed volumes and the TSE volume. Therefore, in addition to visual inspection, we try several measures for quantitative evaluation in this experiment. These measures include (1) similarity to high-resolution TSE volume, (2) RMSE of slice-to-volume registration, and (3) sharpness measures.

First, similarity to a high-resolution volumetric MRI acquisition (reference) is useful in evaluating and comparing the reconstruction techniques. Similar to the validation studies reported in Section IV, MAE and PSNR can be measured between the reconstructed volume and the reference volume. We report these metrics here, however, due to the natural differences in contrast and intensity values of the TSE and HASTE scans, these metrics will not be physically meaningful and cannot be fully trusted. In fact the relationship between the intensity values in the TSE and HASTE volumes is nonlinear and can be better quantified by information-theoretic similarity measures such as mutual information. Here, we compute the normalized mutual information (NMI) similarity measure between the reconstructed volumes and the reference volume. NMI has been widely used in computing the similarity of multi-modal images [42] and is computed based on the marginal and joint entropies of the two volumes [43]. Higher NMI values indicate higher similarity between two volumes.

Second, RMSD of intensity values between the motion-corrected slices and the reconstructed volume was previously used in Section IV-C to assess the sensitivity of volume reconstruction to motion estimation. This measure can be used for performance evaluation of the iterative registration and volume reconstruction. Lower RMSD indicates better convergence of the registration iterations, which in-turn indicates that better reconstructed volumes were used as target (reference) for slice-to-volume registration. Since the same slice-to-volume registration algorithm was used in our experiments, the difference between the RMSD of different reconstruction algorithms is interpreted as the difference between super-resolution reconstruction formulation and the parameters. Therefore lower RMSD indicates better reconstruction technique.

The third set of metrics are from the class of sharpness (focus) measures. The rationale behind using sharpness measures is that when there are uncorrected motion or error residuals between the input slice acquisitions, the average image will be an out-of-focus motion blurred version of the imaged structure. When the motion is more effectively estimated and corrected and the motion-corrected images are more accurately fused in the reconstruction process, sharper structures appear in the reconstructed volume. Two sharpness measures are used in this study: M1 (the intensity variance measure) and M2 (the energy of image gradient measure). Both measures are monotonic and robust to noise [44]. The variance measure is calculated as the sum of square differences (SSD) between each voxel intensity value and the mean image intensity value. M2 is computed by integrating the magnitude of image gradient at all voxels.

Table IX shows the comparison of the above-mentioned measures for volume reconstruction using four techniques: (1) the averaging of three orthogonal scans with the least amount of motion (AVE), (2) scattered data interpolation (SDI), (3) ME with l₂-norm (i.e. MLE) and (4) RME with robust slice error vector norm weighting (RME Huber). The computed measures include MAE, PSNR, and NMI between the reference TSE volume and the reconstructed volumes, RMSE of slice-to-volume registration, and M1 and M2 sharpness measures of the reconstructed volumes. The best value for each measure is shown by bold text. The results suggest that the best volume reconstruction is obtained from RME formulation with Huber’s function for robust slice error norm weighting.

TABLE IX.

Measures used for the evaluation and comparison of reconstructed volumes in the volunteer subiect experiment.

	AVE	SDI	MLE	RME(Huber)
MAE	110.74	100.92	101..317	100.191
PSNR	24.507	25.269	25.272	25.300
NMI	1.137	1.142	1.146	1.150
RMSD	-----	137.397	136.245	136.177
Ml	178531	178051	178377	178972
M2	1.2 × 1011	9.5 × 1010	1.3 × 1011	1.3 × 1011

VI. Experiments: Fetal brain MRI reconstruction

A. Data Acquisition and Visual Assessment of the Reconstruction Quality

Fetal MRI data was obtained from clinical MRI of pregnant patients with diagnosed or suspected cases of fetal anomalies after diagnostic ultrasonography. Clinical fetal MRI was performed using a 1.5-T TwinSpeed Signa system (GE healthcare) and an 8-channel phased-array cardiac coil, without maternal sedation or breath-hold, with the mother supine or in left decubitus position to minimize caval compression. The protocol involved acquisitions in the fetal sagittal, axial and coronal planes using half-Fourier acquisition single-shot fast spin echo (SSFSE) MR imaging with TR varying between 1000 and 4500 ms; TE varying between 80 and 100 ms; variable field of view based on the maternal and fetal body size (between 24–40 cm); variable matrix size between 160 and 512 pixels; and slice thickness between 3 and 6 mm.

Fifteen datasets were used in this study, which were obtained for fetuses in the gestational age (GA) range of 19 weeks and 2 days (19w2d) to 36 weeks and 2 days (36w2d) (mean 28.11, stdev 6.34). A subset of acquired scans in each dataset was pre-selected by visual inspection. The selected scans normally contain high-quality slices, however, occasionally motion-induced intensity distortions and signal loss artifacts present in a number of slices in each dataset. Table X shows the important parameters of the datasets for volumetric MRI reconstruction.

TABLE X.

Some of the parameters of the fetal brain MRI datasets used for volumetric reconstruction.

	GA	N	n	Δsk	Δρk
CI	31w3d	6	93	5 mm	0.78 mm
C2	33w2d	4	96	4 mm	0.70 mm
C3	20w6d	11	161	4–5 mm	0.70 mm
C4	27w6d	9	219	4 mm	0.70 mm
C5	31w5d	8	196	4 mm	0.78 mm
C6	19w2d	5	103	3 mm	0.70 mm
C7	19w2d	5	124	3 mm	0.70 mm
C8	24w0d	3	79	3 mm	0.70 mm
C9	35w3d	6	208	3 mm	0.78 mm
CIO	34w4d	4	276	3 mm	0.70 mm
Cll	29w3d	3	91	5 mm	0.78 mm
C12	36w2d	4	60	6 mm	0.80 mm
C13	19w3d	5	101	3 mm	0.63 mm
C14	27wld	4	112	3 mm	0.63 mm
C15	35w0d	7	134	3–5 mm	0.70 mm
mean	28.1	5.6	140	3.75 mm	0.71 mm
stdev	6.3	2.3	61.8	0.96	0.05

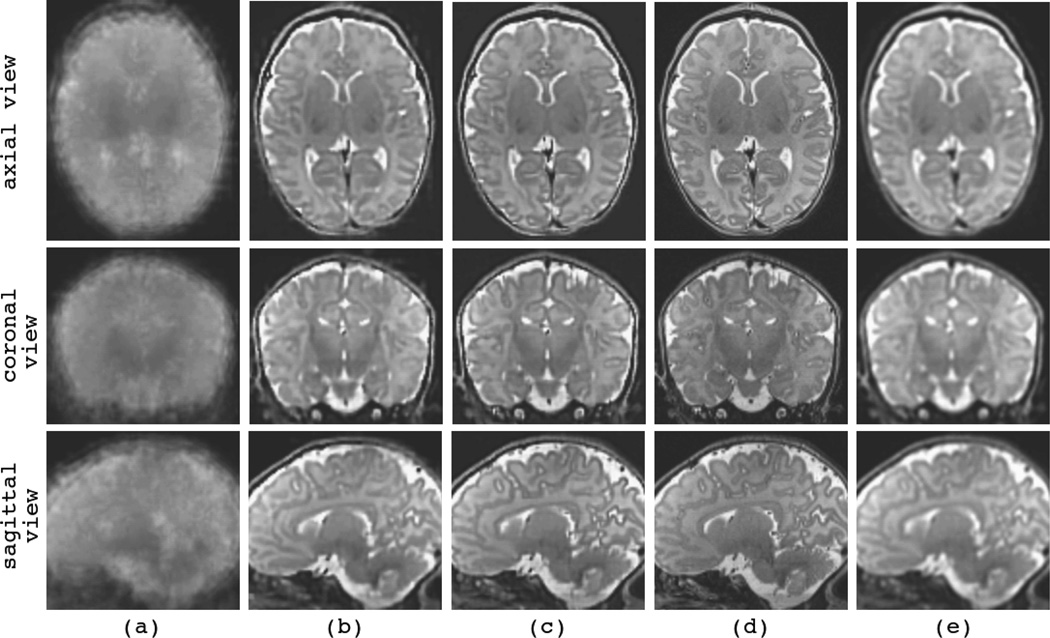
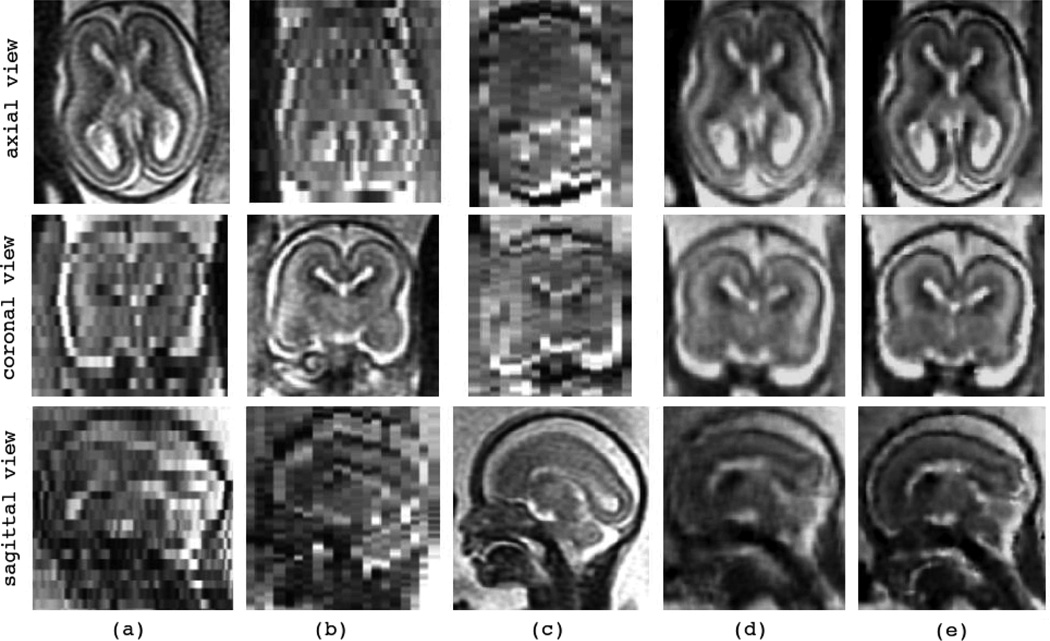
Figure 10 and Figure 11 show the reconstructions of the youngest (C6) and the oldest (C12) fetuses in the database, respectively. The first three columns show three original SSFSE scans acquired in the axial, coronal, and sagittal planes. Fig. 10(d) shows the reconstruction by the SDI (LNG-SDI) technique and (e) shows the reconstruction by the developed l₂-norm ME technique (MLE). Fig. 11(d) shows the initial reconstruction by averaging the resampled input scans (AVE), and (e) shows the reconstruction by the RME technique.

Fig. 10.

The reconstruction of volumetric fetal brain MRI for C6 (GA 19w2d, N = 5); (a)–(c): the acquired SSFSE scans in (a) axial, (b) coronal, and (c) sagittal orthogonal planes, (d) volumetric image reconstructed by LNG-SDI approach, and (e) volumetric image reconstructed by the developed ME technique (with ordinary MLE formulation).

Fig. 11.

The reconstruction of volumetric fetal brain MRI for C12 (GA 36w2d, N = 4); (a)–(c): the acquired SSFSE scans in (a) axial, (b) coronal, and (c) sagittal orthogonal planes, (d) the initial reconstructed volume by averaging (AVE), and (e) the volume reconstructed by the developed RME technique.

The case C12 was quite challenging; only four input scans with a total of 60 slices were available for reconstruction. The slice thickness was relatively large (i.e. 6 mm), and one of the input scans (i.e. the sagittal acquisition shown in Fig. 11(c)) did not cover the full brain region. The volumetric image shown in Fig. 11(e) was generated despite these limitations. The reconstructed volume shown in Fig. 11(e), was generated after 10 iterations of slice-to-volume registration and super-resolution volume reconstruction.

As observed in Figure 10 and Figure 11 the reconstructed volumes clearly reflect the underlying continuity of tissue structure boundaries in all three planes, whereas the original acquisitions exhibit discontinuous tissue boundaries in the out-of-plane views due to the effect of inter-slice motion, thick-slice acquisitions, and partial volume averaging. When coherent structural boundaries appear in all three planes of the reconstructed volumes for an experiment we refer to it as good-quality volume reconstruction. The visual assessment of the quality of reconstructed volumes indicates that good-quality volumetric images were obtained for 14 cases (all cases except C10). Mis-registration artifacts were observed in the reconstructed volumes for C10 (GA 34w4d, N = 4) using all techniques. Artifacts were also observed in the MLE reconstructed volumes for C13 and C14, but good-quality volumes were obtained for these cases by RME. Almost in all cases the volumes reconstructed by MLE and RME were visually much sharper than the volumes reconstructed by SDI These observations are supported by the quantitative evaluation in the next section.

B. Quantitative Evaluation

Two sets of metrics were used to evaluate the relative effectiveness of the RME technique as compared to the initial estimation (AVE), SDI (LNG-SDI), and MLE. The first metric is the root mean square differences (RMSD) of intensity values between the motion-corrected acquired slices and the reconstructed volumes. The average of this metric over the slices for each case was normalized with respect to the RMSD metric of its corresponding initial reconstructed volume (AVE). The results are shown in Table XI for six techniques: AVE, SDI, MLE, and RME reconstructions with η = 1.345 and different values of γ, i.e. γ = 0.001 for RME (l₁-norm), γ = 1000 for RME (l₂-norm), and γ = 1.345 for RME (Huber).

TABLE XI.

Normalized RMSD of intensity values between the reconstructed image and the motion-corrected acquired slices. The lowest values in each row are shown in bold text.

	AVE	SDI	MLE	RME l1–norm	RME Huber	RME l2–norm
CI	1	1.0	0.95	0.99	0.95	0.94
C2	1	0.98	0.92	0.93	0.91	0.92
C3	1	0.97	0.94	0.97	0.94	0.94
C4	1	0.94	0.94	0.85	0.83	0.84
C5	1	0.96	0.90	0.95	0.93	0.92
C6	1	0.82	0.80	0.84	0.81	0.80
C7	1	0.78	0.69	0.75	0.73	0.71
C8	1	0.92	0.80	0.81	0.78	0.75
C9	1	0.92	0.86	0.87	0.83	0.86
CIO	1	0.73	0.67	0.70	0.69	0.66
Cll	1	0.96	0.96	0.91	0.87	0.89
C12	1	0.81	0.77	0.85	0.78	0.77
C13	1	0.87	0.83	0.78	0.78	0.78
C14	1	0.91	0.88	0.91	0.88	0.89
C15	1	0.96	0.91	0.92	0.88	0.90
mean	1	0.89	0.85	0.86	0.83	0.83

Lower RMSD indicates better convergence of registration iterations, which in-turn indicates better reconstructed volumes were used as target (reference) for slice-to-volume registration. The lowest values of RMSD in each row (for each case) are shown in bold text. Obviously in all cases the MLE and RME (with Huber’s and l₂-norm error functions) provided improvements over the initial reconstruction (AVE) and performed better than SDI. It is observed that in many cases the ordinary MLE (l₂-norm ME) generated the best results. However, the mean values over all 15 datasets indicate that RME performed better. In fact for those cases that MLE provided the lowest RMSE, the difference between RME and MLE was not significant. Those cases are considered to be the cases without significant slice outliers or non-Gaussian noise, for which the slice-to-volume registration was also fairly accurate. But significant improvements were observed for cases C4, C8, C11, and C13 by using RME as compared to MLE. These cases are considered to be affected by mis-registered slices, outliers, and/or non-Gaussian noise artifacts.

The second set of metrics are the sharpness measures (M1 and M2) discussed in section V. The results for M1 and M2 sharpness measures are shown in Table XII and Table XIII respectively. Again all the values for each case are normalized with respect to the AVE value for that case. The highest sharpness measures for each case are shown in bold text. The results show that sharper volumetric images are generally obtained by the RME technique as compared to SDI and MLE. In particular these measures suggest that the best performance was obtained from RME with l₂-norm error function. When comparing RME with MLE, significant improvement was seen in M1 for C8, and in M2 for C2, C4, C8, C14, and C15.

TABLE XII.

Normalized Ml sharpness measure for the volumetric fetal brain MRI reconstructed using different techniques. The highest values in each row are shown in bold text.

	AVE	SDI	MLE	RME l1–norm	RME Huber	RME l2–norm
CI	1	1.00	1.03	1.01	1.01	1.02
C2	1	1.03	1.02	1.03	1.04	1.05
C3	1	1.04	1.07	1.06	1.07	1.07
C4	1	1.09	1.06	1.09	1.10	1.10
C5	1	1.09	1.13	1.09	1.10	1.10
C6	1	1.03	1.08	1.06	1.07	1.07
C7	1	1.05	1.08	1.07	1.08	1.09
C8	1	1.26	1.29	1.28	1.47	1.49
C9	1	1.06	1.08	1.05	1.06	1.07
CIO	1	1.11	1.16	1.12	1.13	1.14
Cll	1	1.05	1.09	1.07	1.07	1.09
C12	1	1.08	1.13	1.13	1.12	1.14
C13	1	1.05	1.07	1.08	1.08	1.08
C14	1	1.09	1.11	1.14	1.13	1.14
C15	1	1.09	1.13	1.13	1.15	1.14
mean	1	1.07	1.10	1.09	1.11	1.12

TABLE XIII.

Normalized M2 sharpness measure for the volumetric fetal brain MRI reconstructed using different techniques. The highest values in each row are shown in bold text.

	AVE	SDI	MLE	RME l1–norm	RME Huber	RME l2–norm
CI	1	1.00	1.14	1.23	1.15	1.10
C2	1	1.18	0.95	1.38	1.36	1.37
C3	1	1.10	1.15	1.13	1.14	1.14
C4	1	1.21	1.12	1.17	1.27	1.28
C5	1	1.35	1.56	1.35	1.37	1.42
C6	1	1.08	1.36	1.23	1.31	1.34
C7	1	1.23	1.40	1.33	1.33	1.38
C8	1	1.15	1.31	1.50	1.64	1.66
C9	1	1.28	1.44	1.40	1.43	1.41
CIO	1	1.13	1.60	1.23	1.51	1.55
Cll	1	1.53	1.62	1.60	1.52	1.62
C12	1	1.31	1.73	1.37	1.26	1.73
C13	1	1.10	1.27	1.20	1.23	1.26
C14	1	1.13	1.33	1.55	1.55	1.56
C15	1	1.05	1.25	1.41	1.82	1.66
mean	1	1.19	1.35	1.34	1.39	1.43

VII. Discussion and Conclusion

Novel super-resolution volume reconstruction techniques have been developed in this study based on maximum likelihood and robust M-estimation error minimization for the reconstruction of volumetric MRI from multiple-scan slice acquisitions. The model-based formulation of volume reconstruction is considered as a major development in this area which leads to remarkable improvement in applications that were previously addressed by scattered data interpolation techniques. Both validation studies and experimental results show that the developed model-based technique outperforms the scattered data interpolation techniques. Furthermore, the novel data-adaptive M-estimation approach developed in this study performs well in the presence of slice outliers and appropriately eliminates the effect of mis-registered slices.

The developed formulation is general and the approach can be effectively used for any type of slice acquisitions or any number of input scans. However, in order to guarantee high-resolution reconstruction, multiple orthogonal or overlapped or repeated slice acquisitions are desired. The validation studies carried out here and the fetal brain MRI experiments are based on multiple orthogonal scans, which are normally acquired in clinical imaging. The reconstruction of volumetric images from clinical datasets is quite challenging due to various limitations such as the total scan time, large slice thickness for high SNR, and uncontrolled intermittent motion. Under the circumstances the developed robust reconstruction technique is extremely beneficial. The improved reconstruction capability of volumetric fetal brain MRI enables enhanced clinical evaluation and facilitates further research in automated image analysis, atlas construction, and the research on early brain development, cortical maturation, neuro-developmental disorders, fetal anomalies, and the mechanism of brain injury in newborns and premature infants.