Self-Learning Adaptive Umbrella Sampling Method for the Determination of Free Energy Landscapes in Multiple Dimensions

Abstract

The potential of mean force describing conformational changes of biomolecules is a central quantity that determines the function of biomolecular systems. Calculating an energy landscape of a process that depends on three or more reaction coordinates might require a lot of computational power, making some of multidimensional calculations practically impossible. Here, we present an efficient automatized umbrella sampling strategy for calculating multidimensional potential of mean force. The method progressively learns by itself, through a feedback mechanism, which regions of a multidimensional space are worth exploring and automatically generates a set of umbrella sampling windows that is adapted to the system. The self-learning adaptive umbrella sampling method is first explained with illustrative examples based on simplified reduced model systems, and then applied to two non-trivial situations: the conformational equilibrium of the pentapeptide Met-enkephalin in solution and ion permeation in the KcsA potassium channel. With this method, it is demonstrated that a significant smaller number of umbrella windows needs to be employed to characterize the free energy landscape over the most relevant regions without any loss in accuracy.

INTRODUCTION

Molecular dynamics (MD) simulations of detailed atomic models provide a virtual microscope to examine a wide range of complex molecular processes that can play an important role in chemistry, biochemistry, physics, and material science. While a broad range of system can be investigated computationally, the usefulness of MD is mainly limited by the accuracy of physical approximations used to derive intermolecular forces, and our ability to computationally sample the configurational space adequately.

The most straightforward sampling strategies rely on brute-force simulations, assuming that the evolution of an unbiased trajectory will be sufficient to generate a Boltzmann weighted sample of the configurational space R of interest. To correctly determine the relative statistical weight of different regions of configurational space, it is critical that the unbiased trajectory be sufficiently long in order for the system to return and visit these different regions multiple times. To properly determine the relative statistical weight among different regions of configurational space R, the trajectory must rattles, fluctuates, and travels back-and-forth in that space. Nevertheless, the perception is that such back-and-forth fluctuations of a trajectory evolving freely according to Newton’s classical equation of motions are inefficient and undesirable, because the system spends a large fraction of its time returning to regions that were previously visited. This has motivated a number of special strategies designed to enhance sampling efficiency by trying to prevent excessive return to previously explored regions.

A number of enhanced sampling strategies aim at exploring the configurational space efficiently from the evolution of a trajectory that is propagated, not with the classical equation of motions, but with some effective rules designed to avoid frequent returns toward regions that have been previously visited. One approach that aims at enhancing productive motions and reducing such undesirable and unproductive back-and-forth returns by biasing the momenta forward is Self-Guided Langevin Dynamics (SGLD)^{1, 2}. Because SGLD does not proceed from a modified Hamiltonian, only approximate perturbative expressions are available to recover proper Boltzmann statistics. Another approach designed to flatten the overall energy landscape associated with some degrees of freedom is accelerated MD (aMD)^{3, 4}. As aMD proceeds from a modified Hamiltonian, proper Boltzmann statistics may be recovered by coupling several systems via a replica-exchange algorithm for example⁵.

Both SGLD and aMD can, in principle, be applied to an entire system, although recovering meaningful unbiased statistics often becomes impractical when the number of degrees of freedom is too large. For this reason, applications of these enhanced sampling methods is often limited to a subset of degrees of freedom, e.g., aMD has been used to increase the rate of sidechain rotameric transitions in protein simulations⁶. This effectively brings SGLD and aMD closer in spirit to the family of methods specifically designed to enhance sampling over a chosen subset of coordinates. These methods rely on a pre-identification of a set of so-called collective variables, Z≡{z₁, z₂, …}, which are assumed to capture the most relevant aspects of a system of interest (the z_i are functions of all the Cartesian coordinates R of the system). Such a strategy is advantageous if the remaining degrees of freedom, orthogonal to the subspace Z, relax rapidly and can be sampled efficiently by brute-force simulation without the need of a special enhanced method. Formally, the statistical weight P(Z) within the subspace Z is governed by the free energy landscape or potential of mean force (PMF), i.e., P(Z)∝exp[−βW(Z)].

Among the approaches designed for calculating the PMF over the subspace Z, the most commonly used is perhaps the umbrella sampling (US) method^7–11, which was initially proposed in the 1970’s by Torrie and Valleau to perform accurate Monte Carlo analysis of systems containing large energy barriers. Umbrella sampling introduces the concept of a biased simulation “window”, a theoretical object aimed at producing an enhanced sampling over a focused region of configurational space, which is achieved by introducing an additional potential for each window (called “umbrella potential” or “window potential”). Perhaps the most straightforward implementation of this approach is “stratified” US, in which a collection of simulations with narrowly defined biasing potentials (often of quadratic form) covering the relevant region of Z are carried out. The information from these different biased simulations is converted into local probability histograms, which are then pieced together to produce an unbiased Boltzmann statistical probability. For example, the weighted histogram analysis method (WHAM)^{10, 12–15} can be used to obtain a proper unbiased estimate of the PMF W(Z) from the biased simulation data and to calculate the PMF. Performing stratified US simulations in multiple dimensions is, in principle, straightforward. However, in practical applications, balancing the accuracy and computational cost becomes difficult as the number of reaction coordinates becomes large (N ≥ 3) and/or as the system of interest becomes complicated. Computational resources should be spent on improving the sampling of the energetically significant regions.

A number of approaches to explore a pre-defined subspace Z have been proposed as an alternative to resolve the challenges encountered by stratified US. One approach avoiding biasing window simulations is the temperature accelerated MD (TAMD) method¹⁶. TAMD consists in attaching a high temperature pseudo-particle to the collective variables and let this drag the true system to explore the configurational space associated with a subset of collective variables. TAMD corresponds to a kind of brute-force simulation method, in the sense that the generated trajectory is not guided by any biases but evolves freely on its own. However, under specific assumptions of time-scale separation, it is possible to recover proper Boltzmann statistics from the TAMD trajectory.

A different enhanced sampling strategy consists in introducing an adaptive “on-the-fly” bias that serves to cancel out the variations of the underlying free energy landscape, such that the system is able to efficiently explore the subspace Z. One example of such a strategy is the adaptive biasing force (ABF) method^17–19. However, once the bias is optimal and has succeeded to flatten the effective free energy landscape, proper sampling requires multiple passages and returns over a region that has been previously visited by an ABF trajectory that evolves freely on its own. In the spirit of ABF, metadynamics is also a method that introduces an adaptive time-dependent biasing potential acting over the subset of degrees of freedom Z^20–22. The time-dependent biasing potential is constructed “on-the-fly” from a sum of smooth Gaussian functions to reduce the amount of information required to determine a free energy landscape. According to metadynamics, the system evolves on its own to find the relevant regions within the subspace defined by a set of collective variables Z. Gaussian functions are “dropped” along the way to push the system away from regions that were already visited, yielding effectively the PMF after a sufficiently long metadynamics trajectory. However, achieving proper Boltzmann weights with this strategy is highly sensitive to the rate at which biasing Gaussians of a predetermined width are dropped during a metadynamics trajectory that evolves freely on its own within the subspace Z. Also belonging to the general family of adaptive sampling strategies relying on a pre-identification of a relevant subspace is the order parameter space random walk (OPSRW)^{23, 24}. The OPSRW algorithm seeks to increase sampling efficiency by considering an augmented subspace comprising an order parameter together with the generalized force associated with it.

Lastly, the single-sweep method²⁵ is another approach to rapidly explore through the important regions of a subspace Z and determine the PMF W(Z) using a two-step strategy. First, single-sweep explores the subspace Z via a TAMD trajectory. Then, biased simulations are generated to compute the gradient of the free energy locally at a set of fixed points and a map of the complete free energy landscape is approximated by a linear superposition of basis function (typically Gaussians). Here, the TAMD is used only to cover the most relevant regions of the subspace Z. Then, rather than attempting to accumulate local probability histograms, a limited amount of local information is extracted from a collection of simulations with narrowly defined window biasing potentials (often of quadratic form) to construct an approximate interpolation of the PMF W(Z) from linear superposition of basis functions. By relying on a smoothing and interpolation assumptions, the first-derivative information from the set of points is used to generate a continuous PMF over the entire region represented as a sum of basis set function. Both metadynamics and the single-sweep method rely on a linear superposition of Gaussian functions to represent the underlying free energy surface. While a representation from complete basis set would formally be equivalent to the exact PMF W(Z), both assume that the underlying function W(Z) is smooth and can be represented by a linear superposition of Gaussian functions. This corresponds essentially to a “low-pass” filtering operation, removing rapidly-varying spatial noise and compensating the lack of information by an interpolation procedure. Because it does not attempt to accumulate local probability histograms, a basis set representation of the free energy surface requires less information and may potentially be able to handle situation requiring a set of collective variables Z of higher dimensionality. Nevertheless, the interpolation of the free energy landscape W(Z) from a limited amount of information may lead to problems if the assumption of smoothness is not satisfied.

From a broader perspective, it is clear that many of the goals and advantages of the above enhanced sampling strategies (SGLD, aMD, TAMD, metadynamics, OPSRW) can be integrated within a systematic umbrella sampling procedure. By construction, the biased US simulations are narrowly restrained to a chosen region and unwanted returns to previously visited regions are avoided. While it should be possible to proceed systematically through all the relevant regions of the subspace Z, the main inconvenient of traditional stratified US is that one must choose the set of windows a priori, before any information is available about the free energy landscape of the system in the subspace Z. This means that some time may be wasted with windows located in regions that are essentially unimportant (high free energy), leading to a situation where the number of windows required to cover a multi-dimensional subspace grows extremely rapidly. However, this can be avoided by adding biasing windows progressively only to those regions of Z deemed relevant. Such a decision can be made from a limited knowledge of the PMF, W(Z). Simulating the newly added windows will then provide additional information to generate a more complete estimator of W(Z). This cycle can be repeated until all the relevant regions of the subspace Z have been discovered and sampled. This strategy, which we call “Self-learning Adaptive US” (SLS), makes it possible to systematically explore only the relevant regions of the subspace Z and rigorously generate the proper statistical weight P(Z)∝exp[−βW(Z)], while maintaining all the advantage of enhanced sampling methods such as avoiding wasteful returns to regions previously visited. In this paper, we present a self-learning algorithm that can automatically and adaptively generate umbrella windows where they are necessary. A significantly smaller number of umbrella windows could be employed without loss of accuracy.

The algorithm underlying this automatic self-learning umbrella sampling will be described in the “METHODOLOGY” section, followed by a discussion on its efficiency in comparison to other methods mentioned above. It needs to be pointed out that, when the final targeted state of the system is already known, the string method can be combined with this self-learning algorithm to further improve its efficiency by predefining a free energy pathway connecting the initial and final states. Therefore, a brief description of the string method used in our study will be given in the “METHODOLOGY” section as well. In order to demonstrate the applicability of this approach, it was applied to an analytical potential defined as a Fermat spiral (see Supporting Information), a model system consisted of Lennard-Jones particles, conformational equilibrium of pentapeptide Met-enkephalin, and ion permeation in a potassium channel.

METHODOLOGY

The Self-Learning Adaptive Scheme

The aim of any PMF calculation approach should be to describe the free energy landscape within a subspace of pre-defined reaction coordinates with the greatest accuracy and a minimal sampling effort. Stratified US is arguably the most accurate approach to this task, but it can be computationally expensive in high dimensionality. This limitation can be circumvented if sampling via computationally costly simulations is limited to regions of the subspace of collective variables where the PMF is below a certain maximum threshold. To achieve this, the self-learning adaptive umbrella sampling process progressively builds simulation windows at positions indicated by the ongoing sampling data.

Like for any stratified US approach, an appropriate list of N reaction coordinates z_i with their respective boundaries needs to be determined. A biasing potential, usually defined as w_i(z)= k_i(z_i−z′_i)², and an interval for window creation, Δz_i, are also required for each reaction coordinate. In our current implementation, k_i and Δz_i are fixed, but this is not a requirement of the approach. The sampling could be made even more efficient by adjusting on-the-fly these values to the local features of the free energy landscape. This is made possible by the flexibility of the WHAM algorithm that is used to combine the sampling data provided by the different windows.

The process starts with a system located somewhere within the N-dimensional reaction coordinate space. The creation of a minimal number of simulation windows is required to perform a first assessment of the local free energy landscape. In this first step, 3^N windows are created. The position (z₁, …, z_N) of each initial simulation window is determined by taking the starting state of the system $\left(z_1^A,\dots ,z_N^A\right)$ and changing its reaction coordinates z^A_i by small values Δz_i in both directions, i.e. $(z_1,\dots ,z_N)\in {\displaystyle \prod _i}\left\{z_i^A-\mathrm{\Delta }{z}_i,z_i^A,z_i^A+\mathrm{\Delta }{z}_i\right\}$. The PMF exploration is initialized on the basis of these 3^N windows from which a first PMF is calculated using the WHAM algorithm. The procedure responsible for creating new windows in regions that remain to be explored is based on the current view of the free energy landscape, at the periphery of which new windows are constructed. A parameter W_max is introduced in order to guide the exploration of the subspace Z: no new windows can be created in the areas of the reaction coordinate space where the free energy is higher than W_max. To favor the exploration of lower free energy pathways while allowing exploration of pathways with higher free energy barriers when needed, W_max is initially set to a low value (e.g. 2 kcal/mol) and is incrementally increased up to a predefined limit (e.g. 10 kcal/mol) if the algorithm fails to create new windows at a given cycle.

The procedure can be summarized as follows (see Fig. 1):

Figure 1.

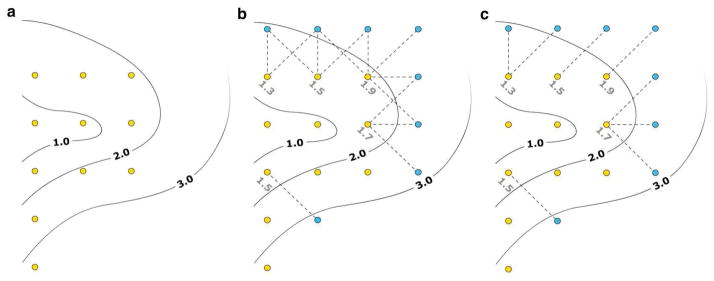
Free energy landscape exploration procedure. (a) The yellow dots correspond to the positions of 11 windows plotted on top of a free energy landscape generated with sampling from these windows. (b) Windows that are located in regions with a free energy below a given level W_max (here W_max= 2.0) attempt to create new windows on free neighboring grid points. (c) When more than one window target a same location, the window associated with the lowest free energy is selected as the source of the system conformation to initiate the new window.

1. The free energy landscape is calculated using the WHAM algorithm once all windows have provided a certain minimal amount of sampling data. (Fig. 1a illustrates such free energy landscape calculated from 11 windows.)

2. Among all existing windows, those with free energy value lower than W_max (initially set to W_max = E₁) are selected as a base for the expansion procedure. (In Fig. 1b, W_max = 2.0 and thus 7 windows could potentially be used for expansion.)

3. Each of the preselected windows attempts to create a new window in 3^N−1 neighboring location. Locations already occupied by windows are omitted. (In Fig. 1b, 5 windows are selected to create 8 new windows.)

4. In the case when two or more windows want to expand to the same location, the window with the lowest free energy is selected as the source of the system conformation to initiate the new simulation window. (See Fig. 1c, for each of the 8 new windows a single window is selected as the source of the initial conformation.)

5. If no window is created in steps 3 and 4, W_max is increased by a small increment (until W_max = E₂) and steps 2 to 4 are repeated.

6. This process cycles until no more windows can be created within the current free energy barrier limit W_max = E₂ (or alternatively when a pathway from the initial state of the system to a predefined target state is found).

The self-learning adaptive US calculation can be initiated from a single state of the system as described above. If the final targeted state of the system is already known, the String method (see below) can be used to predefine a free energy pathway connecting the initial and final states. In this case, a third parameter Δ₁ is employed to restrict the creation of new windows. A window whose distance from its center to the pathway exceeds Δ₁ will not be added.

Efficiency of the Self-Learning Adaptive Umbrella Sampling

For the calculation of PMF in multi-dimension, one key advantage of methods like ABF and metadynamics is the ability to concentrate the sampling effort to regions of the conformational space that correspond to highest probability density. The convergence of these methods is however dependent on stochastic diffusion along the reaction coordinates for accumulating the required sampling data. On the other hand, conventional implementation of stratified US would typically waste time sampling regions of low probability density, but is more systematic in its strategy to accumulate data by using the concept of windows. The algorithm we present here combines the advantage of both approaches, i.e. it concentrates the sampling effort to the region of high interest and accumulates data in a systematic way.

This can be illustrated by the argument brought by van Duijneveldt and Frenkel²⁶ who showed that sampling of narrow windows (steep biasing harmonic window potential) converges more rapidly than that of broad windows (soft biasing potential). This argument also applies to semi brute-force methods like ABF and metadynamics. To flatten a PMF along one dimension using metadynamics or ABF, one needs to sample the length L of this degree of freedom. Diffusion back and forth requires a time t = L²/2D, where D is the diffusion coefficient. Using a stratification procedure, the length L is divided into N windows of width L/N and the time for diffusion within the window is then t_Window = L²/2DN², which goes down like 1/N², much faster than the number of windows. The total theoretical simulation time using a stratified umbrella sampling approach is t_US = Nt_Window = L²/2DN = t/N. The efficiency gain is thus on the order of the number of windows used. For this reason, ABF simulations are also often subdivided into a number of narrower windows.¹⁹ The relaxation time of a diffusing degree of freedom restrained by a harmonic potential goes like k_BT/DK, where K is the force constant of the biasing harmonic potential. By identification with the diffusion time above, the width of the windows would be l² = (L/N)² = 2(k_BT/K). The larger is K, the shorter is the relaxation time and shorter should be the window width. This is however true only up to a point depending on slow motions orthogonal to the chosen set of order parameters.

String Method with Swarms of Trajectories

The string method^27–29 is a computational technique intended to find out the minimum free energy path (MFEP) connecting two stable conformations as well as the free energy along that MFEP in a space defined by a set of collective variables Z≡{z₁, z₂, …}. A path (string) is represented by an ordered set of images Z(α), parametrized by α, where α=0 is the starting image and α=1 is the ending image. Essentially, a path can be viewed as a curve in the collective variable space. A recent variant of the conventional string method, which is named “string method with swarms of trajectories”²⁹, is utilized in our study. It involves the following steps: (1) a string is prepared, (2) each image in the string is equilibrated with restrained MD simulation, (3) a swarm of short unbiased MD trajectories are launched for each image, (4) the average displacement from each swarm of trajectories is calculated and utilized to update the image in collective variable space, and (5) the string is smoothed and re-parametrized to ensure that images are equally distant. The above 5-step procedure is iterated until the MFEP is found. In this paper, the convergence of the string was monitored by the average distance in collective variable space, relative to the initial string. In each string cycle, the distance in collective variable space of each image was calculated. The resulting distances were averaged and used to assess the convergence of the string. A detailed description of the algorithm of the string method with swarms of trajectories is presented in Pan et al²⁹.

COMPUTATIONAL DETAILS

Met-enkephalin in Aqueous Environment

Met-enkephalin is a small penta-peptide with the sequence YGGFM (see Fig. 2). In the present study, Met-enkephalin was solvated in a cubic water box (1202 TIP3P³⁰ water molecules). The dimension of the entire system was 32 × 32 × 32 ų and contained 3687 atoms. All MD simulations concerning Met-enkephalin were performed using version 2.8 of the MD package NAMD³¹. Umbrella sampling calculations were carried out using the Collective Variable module. CHARMM PARAM 27 force field³² was utilized in our simulation of Met-enkephalin. The isobaric-isothermal ensemble was employed for all MD calculations. The pressure and temperature were controlled by Langevin piston method³³ and Langevin dynamics and kept at 1 bar and 300 K, respectively. Periodic boundary conditions were applied to the system. A cutoff of 12 Å was used to truncate the short-range non-bonded interactions, where a switching function was applied beyond 10 Å. Long-range interaction was treated by particle-mesh Ewald algorithm³⁴. Covalent bonds involving a hydrogen atom were constrained to their equilibrium distances and a 2 fs time step was used in all calculations.

Figure 2.

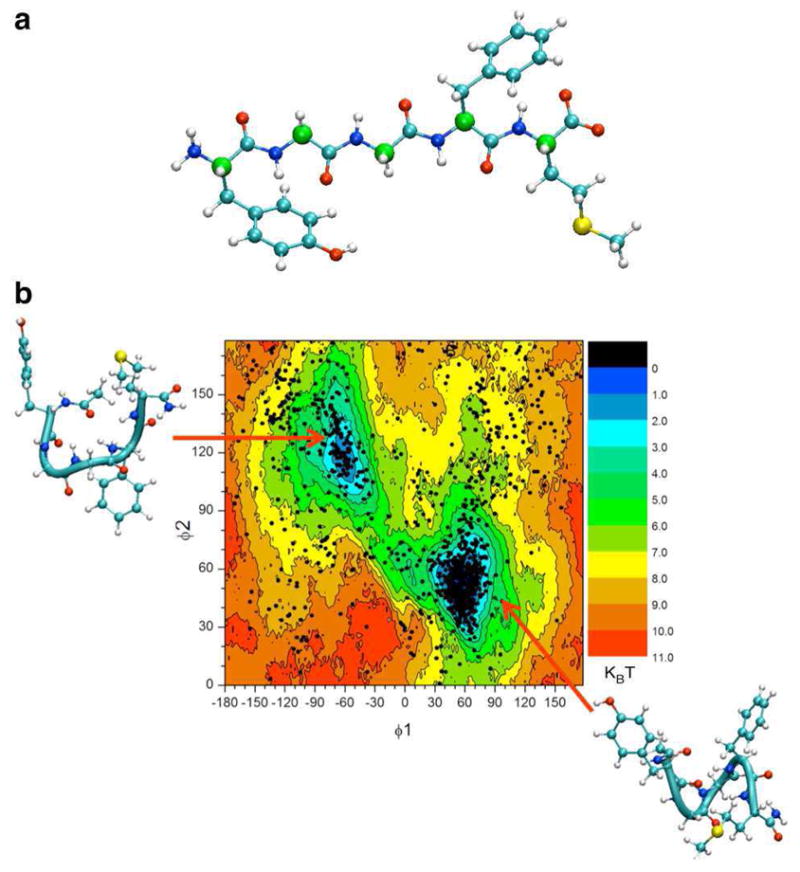
(a) An extended structure of Met-enkephalin. The Cα atoms of Met-enkephalin are marked in green color. The two reaction coordinates used in umbrella sampling are φ1 ≡ CA@Tyr1-CA@Gly2-CA@Gly3-CA@Phe4, and φ2 ≡ CA@Gly2-CA@Gly3-CA@Phe4-CA@Met5. The same two dihedral angles are also used as collective variables in the string method simulations. (b) Reference 2D-PMF overlapped with a scatter plot of (φ1, φ2) generated from 60 ns of brute force MD simulation of Met-enkephalin. The brute force MD simulation validated the existence and location of two stable conformations yielded from umbrella sampling calculations. 2D-PMFs obtained from the self-learning approach will be compared with this reference 2D-PMF. The unit of all Met-enkephalin 2D-PMFs is k_BT, where k_B is the Boltzmann constant and T is at 300 Kelvin.

The system was minimized with steepest decent algorithm for 500 steps and then a 60 ns brute-force MD run was carried out. The purpose of this brute-force MD run was to estimate the number of stable conformations and their locations in the conformational space. Eventually, two dihedral angles, namely φ1 ≡ CA(Tyr1)-CA(Gly2)-CA(Gly3)-CA(Phe4), and φ2 ≡ CA(Gly2)-CA(Gly3)-CA(Phe4)-CA(Met5), were chosen to be the reaction coordinates in our umbrella sampling simulations. φ1 spanned from −180° to 180°, while φ2 covered from 0° to 180°. The umbrella windows were created every 10° in each dimension. Therefore, a total of 648 umbrella windows were utilized in the reference umbrella sampling simulations. Each umbrella window was initially equilibrated for 100 ps and then simulated for another 1 ns. The force constant of the harmonic biasing potential was 0.02 kcal·mol⁻¹·degree⁻².

The self-learning adaptive US algorithm was applied to Met-enkephalin starting with a single conformation or along a pathway predefined using the String method. In either case, the time series needed by WHAM were taken from the reference umbrella sampling calculations. No new simulations were performed. In the first case starting with a single initial conformation, free energy landscape expansion procedure was initialized with the E₁ = E₂ = 3 kcal/mol. In a second set of calculations initiated with a pre-determined pathway (see below), free energy landscape expansion was performed using E₁ = E₂ = 3 kcal/mol, Δ₁ = 30 degree and E₁ = E₂ = 6 kcal/mol, Δ₁ = 60 degree.

Pathways utilized in the second case were generated by the string method with swarms of trajectories calculations. φ1 and φ2 also served as collective variables in the string method calculations. A transition pathway was represented by eleven images (including two endpoints). Structures of the two endpoints in our string method calculation were taken from MD relaxation runs. The initial values of collective variables in non-endpoint images were created by linear interpolation between the endpoints. For each of the 11 images, a swarm of 50 1 ps unbiased MD trajectories was launched with different seed to randomize initial velocity. Then, the trajectories in a swarm were averaged to provide an updated image. Once this averaging was completed for all the images, the string was smoothed, re-parametrized, and relaxed at the updated values for 200 ps before initiating a new cycle.

Ion Permeation in the KcsA Potassium Channel

A molecular system was built based on the canonical structure of the KcsA channel (PDB entry 1K4C)³⁵, which was embedded in a lipid bilayer containing 156 dipalmitoylphosphatidylcholine (DPPC) molecules. This complex was solvated by a 150 mM KCl solution for a total of 59134 atoms. Simulations were performed using the CHARMM molecular simulation program³⁶ and the PARAM27 force field³². The Lennard-Jones parameters for the cation-carbonyl oxygen pair interactions were refined to yield solvation free energies in liquid N-methylacetamide (NMA), similar to those in bulk water³⁷. Periodic boundaries conditions were applied, and long-range electrostatic interactions were treated by the particle mesh Ewald algorithm³⁴. The molecular system was equilibrated for about 300 ps with decreasing harmonic restraints applied to the protein atoms and ions in the pore. All trajectories were generated with a time step of 2 fs at constant normal pressure (1 Atm) controlled by an extended Lagrangian algorithm³³ and constant temperature (323 K) using a Nose-Hoover thermostat³⁸. A restraint of 5 kcal·mol⁻¹·rad⁻² was applied on the psi dihedral angle of Val76 of each subunit in order to prevent reorientation of the Val76/Gly77 amide plane.

PMFs describing the movement of three K⁺ ions in the selectivity filter were calculated using the self-learning adaptive US approach. Since the channel protein naturally constraints the ions to diffuse in single file, the reaction coordinates consist in the positions of the three ions $K_z^i$ along the channel axis (aligned with the Z-axis of the simulation system for convenience), which yields the 3D PMF $W\left[K_z^1,K_z^2,K_z^3\right]$. The problem can be reduced in dimensions by using as a reaction coordinate the center-of-mass of the two ions occupying the selectivity filter in all windows to calculate the 2D PMF $W\left[\mathit{CoM}\left(K_z^1,K_z^2\right),K_z^3\right]$. Beside these two PMFs obtained with the self-learning adaptive US approach, a reference 2D PMF was calculated with windows covering the full conformational space. The center-of-mass of the backbone of the selectivity filter is used as a reference for all reaction coordinates (z_filt=0). Windows were created every 0.5 Å in all dimensions within a box defined by [0,5] × [−10,−3.5] in 2D and [−1,11] × [−7,5] × [−10,1] in 3D. The force constant of the harmonic biasing potential was 20 kcal·mol⁻¹·Å⁻² for all reaction coordinates. Free energy landscape expansion procedure was performed with E₁ = 1.5 kcal/mol and E₂ = 5 kcal/mol. Each simulation window was initially equilibrated for 10 ps and then simulated for another 100 ps before being included in a WHAM analysis. Sampling was extended to 1ns per window in the 2D PMF calculation and to 300 ps per window in the 3D one.

RESULTS AND DISCUSSION

System of Lennard-Jones Particles

To demonstrate the ability of the described window creation procedures to follow complex pathways and to explore high-dimension order parameter space, self-learning adaptive US calculations were carried out on a Lennard-Jones (LJ) particle system in vacuum (see Supporting Information). The free energy landscape of one LJ particle moving inside a lattice of restrained particles was explored using a 3-dimensional (3D) self-learning adaptive US. The Cartesian coordinates of the moving particles were used as reaction coordinates. The calculation required 500 windows, considerably less than the 2057 windows that would have been required to cover the full configurational space with a standard implementation of stratified US. The process of two particles exchanging position in such lattice was described using a combination of the string method and the self-learning adaptive US approach. A MFEP pathway was first defined using the string method in a 6D space (Cartesian coordinates of the two particles). The self-learning adaptive US was afterward used to describe the free energy landscape in the same 6D space in the vicinity of the predefined pathway using 257 windows (10⁵ windows would theoretically be required to cover the 6D space). These examples illustrate that the most relevant conformational space can be successfully sampled with a limited computational cost by employing the self-learning adaptive US approach.

Met-enkephalin in Aqueous Environment

Exploring the folding free energy landscape of a solvated peptide is a realistic task that is often used to demonstrate the efficiency of enhanced sampling approaches^{19, 39–41}. Here we describe the folding of the Met-enkephalin penta-peptide (Figure 2a). Reaction coordinates were defined as the two dihedral angles, φ1 and φ2, connecting the CA of residues 1 to 4 and residues 2 to 5, respectively. A reference potential of mean force W[φ1, φ2] was calculated using 648 umbrella sampling windows covering the whole conformational space. The resulting PMF is presented in Figure 2b together with a scatter plot of (φ1, φ2) from a 60 ns of unbiased MD. The combined plot show that the MD simulation explored the two free energy minima identified by the umbrella sampling calculations. The stable conformations are centered at (φ1, φ2) = (−75°, 120°) and (60°, 60°), corresponding respectively to a U-shaped and a helix-like conformation. On the basis of the reference 2D-PMF, the free energy difference between the two stable conformations (ΔG ≡ G(helix) − G(U-shaped)) is found to be −0.55 kcal/mol with a barrier height (E_h) of 3.0 kcal/mol, in good agreement with previous results obtained from ABF¹⁹.

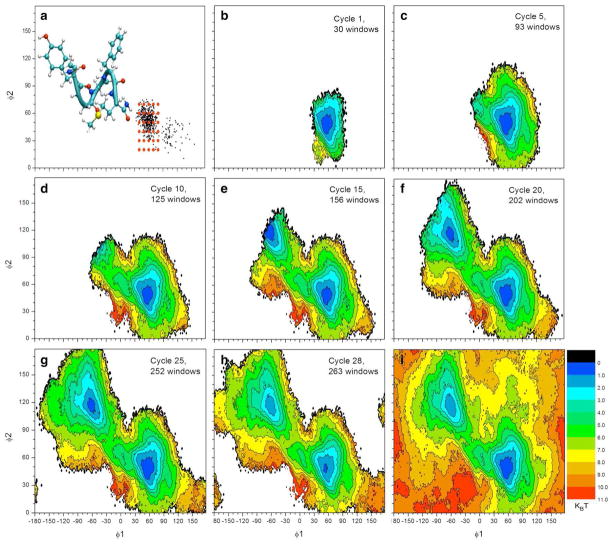
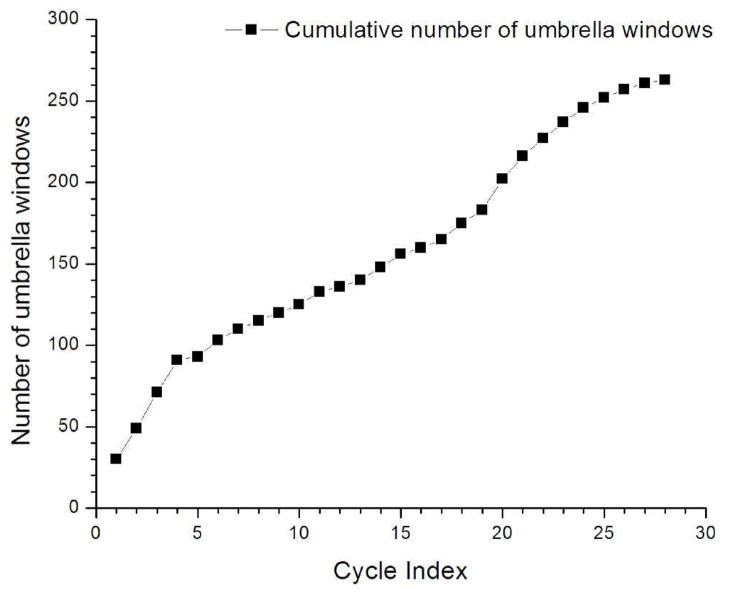
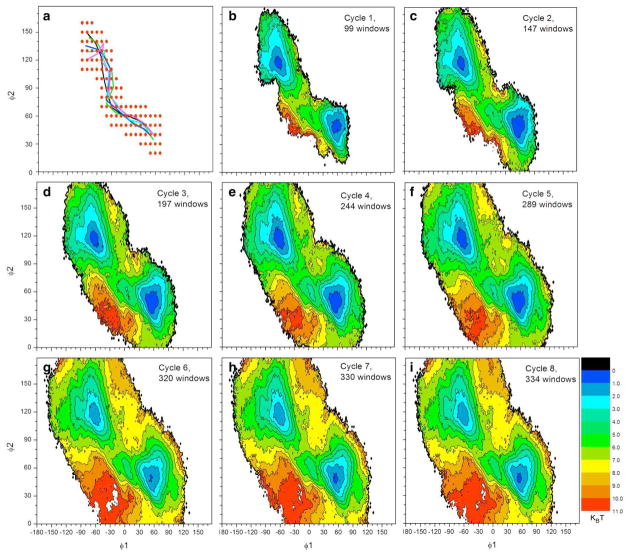
To test the self-learning adaptive US approach, an initial conformation corresponding to the helix-like conformation of Met-enkephalin was selected. Instead of using 9 umbrella windows as defined in the 6-step procedures, the number of initial windows was increased to 30 in order to cover the helix-like conformation. A representative structure of this conformation and the location of the first 30 windows are shown in Figure 3a. The self-learning iteration procedure was applied with E₁ = E₂ = 3 kcal/mol. The MFEP was obtained after 27 cycles with a total of 263 windows, accounting for approximately 41% of the 648 windows in the reference calculation. 2D-PMFs at selected cycles are shown in Figure 3 and the cumulative number of umbrella windows as a function of cycle index is plotted in Figure 4. The ΔG and E_h yielded from self-learning adaptive US was −0.17 and 3.0 kcal/mol, respectively, which were consistent with the reference 2D-PMF. The RMS error in comparison to the reference PMF was 0.45 kcal/mol.

Figure 3.

Evolution of the PMF calculation on Met-enkephalin using self-learning umbrella sampling. (a) The location of the initial umbrella sampling windows and a corresponding structure of Met-enkephalin are shown. (b-h) 2D-PMFs are shown for selected cycles of the self-learning umbrella sampling process, as well as the reference 2D-PMF (i). A free energy value of 3 kcal/mol was used as threshold in the self-learning process.

Figure 4.

Cumulative number of umbrella windows as a function of self-learning umbrella sampling cycles during the Met-enkephalin peptide PMF calculation.

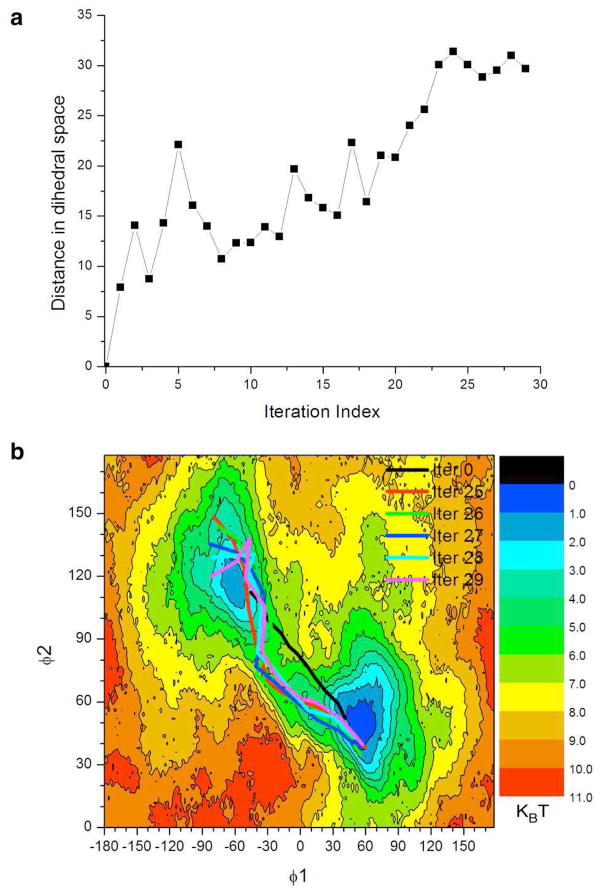
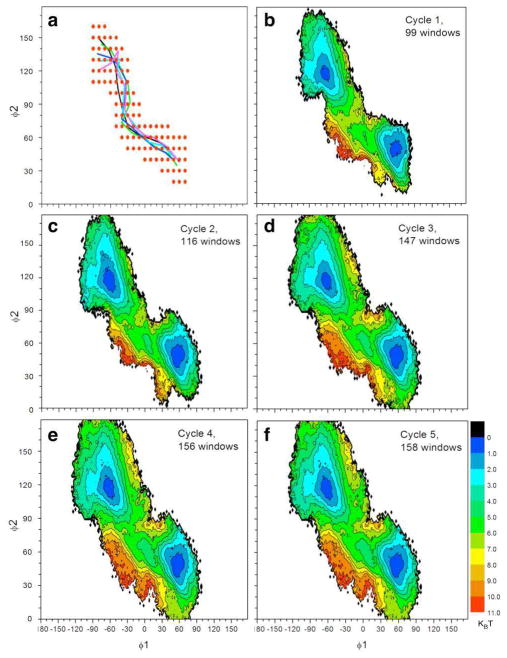
The self-learning adaptive US approach can also be used in combination with the String method. The String method allows to rapidly and efficiently identifies a transition pathway. The self-learning adaptive US approach can be used in a second step to precisely describe the free energy landscape around the transition pathway. The conformational change of Met-enkephalin was this time first determined by 30 cycles of the String algorithm (see Methods). Figure 5a presents the average distance in collective variable space relative to the initial pathway as a function of the iteration index. A plateau is observed starting from iteration 25, indicating that a converged string was obtained. The initial and the last five strings are shown on top of the reference 2D-PMF in Figure 5b. It illustrates that the string method was able to relax the initial string from a high free energy region to a minimal free energy pathway in the collective variable space. A reaction tube consisting of the last five iterations of the string method was used as a source of starting configurations for 99 windows defined for the first round of self-learning adaptive US simulations (the reaction tube and the initial windows are shown in both Figures 6a and 7a). Two sets of parameters were selected to control the iteration of self-learning procedures. In the first set where E₁ = E₂ = 3 kcal/mol and Δ₁ = 30 degree, a total of 5 cycles of the self-learning procedures generated 158 windows, approximately 24% of the windows used to calculate the reference PMF. The 2D-PMF from each cycle is plotted in Figure 6. In the second set where E₁ = E₂ = 6 kcal/mol and Δ₁ = 60 degree, a total of 8 cycles of self-learning procedure generated 334 windows, approximately 52% of the windows used adaptive US calculation. Figure 7 shows the 2D-PMF after each cycle of self-learning adaptive US. The ΔG between the two stable conformations is 0.05, and −0.12 kcal/mol respectively. Umbrella sampling calculation using either set of control parameters yielded an energetic barrier of 3.0 kcal/mol. The RMS errors to the reference PMF were respectively of 0.50 and 0.36 kcal/mol.

Figure 5.

Determination of a transition pathway between the two main conformations of Met-enkephalin using the String method with swarms of trajectories. (a) The average distance to initial string in the collective variable space is plotted as a function of string iteration index. (b) The reference 2D-PMF is overlapped with the initial string and the reaction tube (strings of the last five iterations).

Figure 6.

PMF calculation using the self-learning umbrella sampling approach around a predefined string pathway (a) The reaction tube (colored curves) and the location of the initial umbrella sampling windows (red dots) are shown in collective variable space. (b–f) A 2D-PMF is shown for each self-learning umbrella sampling cycle. A free energy value of 3 kcal/mol and a distance value of 30 degrees were selected as thresholds in the self-learning process.

Figure 7.

PMF calculation using the self-learning umbrella sampling approach around a predefined string pathway (a) The reaction tube (colored curves) and the location of the initial umbrella sampling windows (red dots) are shown in collective variable space. (b–f) A 2D-PMF is shown for each self-learning umbrella sampling cycle. A free energy value of 6 kcal/mol and a distance value of 60 degree were selected as thresholds in the self-learning process.

Note that another advantage of using the self-learning approach in complement to the String method is to identify secondary pathways that would not be found by the String calculation. The self-learning approach would show all free energy valleys originating from the stable states, and not only the one resulting from the String calculation.

Ion translocation in the KcsA Channel

The bacterial KcsA channel was the first K⁺-selective channel for which an atomic-resolution X-ray structure was determined^{35, 42}. Because the permeation pore of KcsA is highly similar to that of eukaryotic K⁺ channels, it has served as a prototypic system to help understand a large class of biologically important channels. The selectivity filter of KcsA, a narrow portion of the pore in which permeating ions are in direct contact with the protein, is illustrated in Figure 8. It is characterized by 5 different binding-sites (S₀ to S₄) to which ions bind in alternation with water molecules. The mechanism of ion permeation in the selectivity filter of the KcsA K⁺ channel has been previously analyzed by multi-dimensional umbrella-sampling^{43, 44} It was found that the predominant pathway is in agreement with the classical knock-on mechanism originally proposed by Hodgkin and Keynes⁴⁵: an ion in the cavity approaches the selectivity filter and pushes the two ions occupying the filter toward the extra-cellular space.

Figure 8.

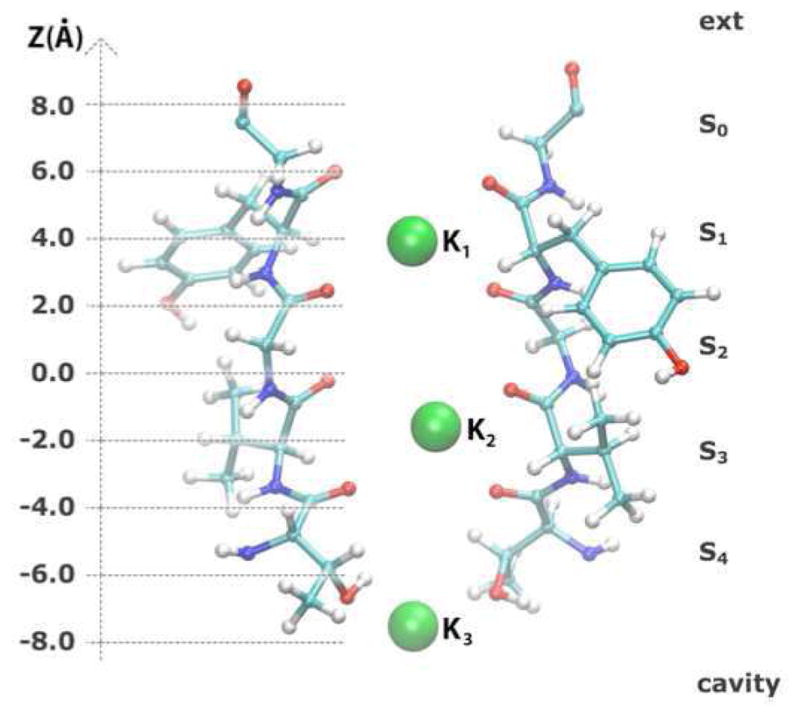
The selectivity filter of the KcsA potassium channel. The filter is shown with its different binding sites labeled S₀ to S₄. This conformation with three ions occupying sites S₁, S₃ and the cavity was used to initiate the self-learning umbrella sampling calculations. The reaction coordinates used for these calculations are the positions of the ions (K¹, K², K³) along the Z axis in reference to the center of mass of the selectivity filer, which corresponds to Z=0.

The question of ion permeation in the KcsA channel constitutes here a realistic test-case of a complex transition pathway ideally described by three reaction coordinates ( $K_Z^1,K_Z^2,K_Z^3$), corresponding to the position of three potassium ions along the axis of the channel, aligned with the Z-axis of the system for convenience (see Figure 8). The number of reaction coordinates can be reduced by considering the center-of-mass of two ions that diffuse in a coordinated manner within the selectivity filter, ( $\mathit{CoM}(K_Z^1,K_Z^2),K_Z^3$)⁴³. While the calculation of the full 3D PMF using explicitly 3 reaction coordinates was considered to be excessively expensive a decade ago, it still remains a complex calculation by today’s standards. The self-learning adaptive US approach presented here should allow for such calculation at a reduced computational cost and without any lost in accuracy.

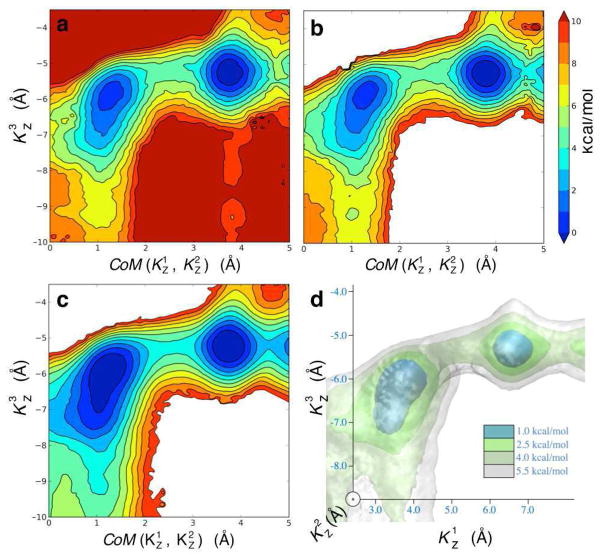
We constructed a system with three potassium ions in the filter region as shown in Figure 8 (i.e. K¹ in S₁, K² in S₃ and K³ in cavity) to initiate PMF calculations in 2D and 3D: $W\left[\mathit{CoM}\left(K_z^1,K_z^2\right),K_z^3\right]$ and $W\left[K_z^1,K_z^2,K_z^3\right]$. Figure 9 presents the progression of the 2D PMF calculation describing the ion translocation pathway from the initial state with an ion in the cavity to the intermediate state in which the three ions are bound to the selectivity filter. The final PMF was obtained with 63 windows, less than half the number of windows that was used in the original calculation, which used 154 windows⁴³. For comparison we calculate a reference PMF with 154 windows covering the full conformational space. This complete PMF is shown in Figure 10 along with the result from the self-leaning adaptive US calculation (panels a and b, respectively). The two PMFs are practically equivalent. Note that the PMF from the self-learning adaptive US is well defined up to a free energy of 10 kcal/mol despite that the E2 parameter, the free energy upper limit, was set to 5 kcal/mol. This is because the selection of the windows in the expansion procedure is based on the free energy at the position of the windows of origin and not at the target point, where the sampling is not optimal until a window is actually added at that point. In practice it means that an extra layer of windows is added to the predefined limit, which assures that the sampling is optimal in all relevant regions.

Figure 9.

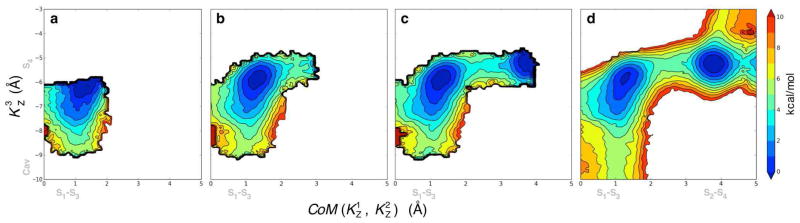
Ion translocation in the KcsA K⁺ channel described by self-learning umbrella sampling. The 2D PMF is shown at different stage of the umbrella sampling calculations: starting with 9 windows (a), moving to 25 (b) and 28 windows (c). The final PMF shown in (d) was calculated from 63 windows. The reaction coordinates are the center-of-mass of ions K¹ and K² along the Z axis, $\mathit{CoM}(K_Z^1,K_Z^2)$, and the position of ion K ³ along the same axis, $K_Z^3$.

Figure 10.

Comparison of the ion translocation PMF obtained through different umbrella sampling approaches: (a) 2D umbrella sampling calculation with 154 windows covering the whole conformational space (regions above 10 kcal/mol are not detailed). (b) Result of the 2D self-learning umbrella sampling calculation using a total of 63 windows. (c–d) 2D projection (c) of a 3D PMF (d) calculated with 385 windows generated by the self-learning approach. The reaction coordinates in panels (a) to (c) are as described in Figure 9. In the 3D PMF presented in (d), each ion is considered separately $W\left[K_z^1,K_z^2,K_z^3\right]$, with $K_Z^2$ sticking out of the plane.

The self-learning adaptive US calculation was repeated in 3D. The permeation pathway was rigorously sampled with 385 windows, which represents 20% of the theoretical number of windows required to cover the full conformational space (see Table 1). A projection of this 3D PMF on the same reaction coordinates as those used for the 2D sampling is presented in Figure 10c, and a full 3D rendering in Figure 10d. Like for the 2D PMFs, the highest energy barrier in the pathway is in the range of 3–4 kcal/mol. The most notable differences between the PMFs obtained from 2D and 3D sampling are at the extremities of the selectivity filter (i.e. extremities of the horizontal axis on the plots), where the reaction coordinate $\mathit{CoM}(K_Z^1,K_Z^2)$ is not well defined as one of the ions escapes the selectivity filter.

Table 1.

Number of windows required to calculate a PMF describing the process of ion permeation in the selectivity filer of the KcsA K⁺ channel.

	2D PMF $W\left[\mathit{CoM}\left(K_z^1,K_z^2\right),K_z^3\right]$	3D PMF $W\left[K_z^1,K_z^2,K_z^3\right]$
Full configuration space	154	1859
Essential configuration space, as delimited by the self-learning procedure	63	385

SUMMARY

The potential of mean force (PMF) is one of the most important quantities to characterize transitions in biomolecular systems. A routinely performed technique to compute a PMF is umbrella sampling. However, one difficulty in performing umbrella sampling with multiple reaction coordinates is balancing the accuracy and computational cost. Computational resources should be spent on improving the sampling of the energetically relevant regions. In this paper, we proposed a strategy to carry out umbrella sampling calculations that can automatically learn about the overall free energy landscape in multiple dimensions, and adaptively generate the simulation windows only where they are most needed. This algorithm was applied to the studies of potassium channel, pentapeptide Met-enkephalin, and a model system consisted of Lennard-Jones particles. Our results suggested that performing calculations in large number of dimensions (such as N = 6) can be achieved with reasonable computational power without losing accuracy.