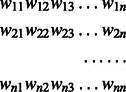Phylogenetic analysis of multiprobe fluorescence in situ hybridization data from tumor cell populations

Abstract

Motivation: Development and progression of solid tumors can be attributed to a process of mutations, which typically includes changes in the number of copies of genes or genomic regions. Although comparisons of cells within single tumors show extensive heterogeneity, recurring features of their evolutionary process may be discerned by comparing multiple regions or cells of a tumor. A useful source of data for studying likely progression of individual tumors is fluorescence in situ hybridization (FISH), which allows one to count copy numbers of several genes in hundreds of single cells. Novel algorithms for interpreting such data phylogenetically are needed, however, to reconstruct likely evolutionary trajectories from states of single cells and facilitate analysis of tumor evolution.

Results: In this article, we develop phylogenetic methods to infer likely models of tumor progression using FISH copy number data and apply them to a study of FISH data from two cancer types. Statistical analyses of topological characteristics of the tree-based model provide insights into likely tumor progression pathways consistent with the prior literature. Furthermore, tree statistics from the resulting phylogenies can be used as features for prediction methods. This results in improved accuracy, relative to unstructured gene copy number data, at predicting tumor state and future metastasis.

Availability: Source code for software that does FISH tree building (FISHtrees) and the data on cervical and breast cancer examined here are available at ftp://ftp.ncbi.nlm.nih.gov/pub/FISHtrees.

Contact: sachowdh@andrew.cmu.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Recent studies of genetic variation in solid tumors have revealed massive intratumor heterogeneity in the spectrum of genomic changes within single tumors (Gerlinger et al., 2012; Heselmeyer-Haddad et al., 2012; Navin et al., 2010, 2011). These observations suggest the importance of understanding cell-to-cell variability, but profiling large numbers of single cells and building coherent models of their evolution remain challenging problems. Fluoresence in situ hybridization (FISH) is a technique that can be used to count the copy number of DNA probes for specific genes or chromosomal regions that has proven useful in studying cancer. Gene gains and losses are common in solid tumors, and FISH provides a practical and reliable method for monitoring such changes in large numbers of individual cells from single tumors (Heselmeyer-Haddad et al., 2002; Janocko et al., 2001). FISH is even more useful when one uses multiple colors to monitor multiple genes simultaneously (Heselmeyer-Haddad et al., 2012; Martins et al., 2012; Wangsa et al., 2009). In this article, we developed new methods to model and analyze the progression of copy number changes, as measured by multi-color FISH. Our methods include analysis of multiple samples from the same patient, typically from different cancer stages.

We applied the new methods to published data on cervical cancer with four gene probes (Wangsa et al., 2009) and breast cancer with eight gene probes (Heselmeyer-Haddad et al., 2012). The data for each sample are presented as a matrix, where each column is one of the probes and each row is a ‘cell count pattern’ of four probe counts, such as 2,3,4,1 (or eight counts for breast cancer), and the number of cells matching that pattern. A normal cell has the count pattern of all 2’s. Both datasets include paired samples from an earlier stage and a later stage in the same patient.

It is of interest to study cervical and breast cancer, as we do, because the number of cases of cervical cancer and breast cancer diagnosed early has increased owing to Pap smears and mammograms, respectively. Early diagnosis is important because lymph node metastasis is one of the best predictors of poor outcome (Buckley et al., 1988; Elledge and McGuire, 1993). Paradoxically, it has been shown statistically that early diagnosis of breast cancer has not led to a substantial decrease in deaths because most of the cancers diagnosed early would not progress to be life-threatening if left untreated (Bleyer and Welch, 2012). These are large-scale studies that do not address the benefits of early detection in individual cases. Therefore, a consistent explanation of these findings is that earlier detection could be of clinical value if there were a better understanding of tumor evolution to help identify the early-stage cancers likely to progress to dangerous forms.

The problem of modeling tumor progression has been studied by a variety of techniques and using different kinds of tumor data (Beerenwinkel et al., 2005; Cheng et al., 2012; Desper et al., 1999; Gerstung et al., 2009; Greenman et al., 2012; Martins et al., 2012; Pennington et al., 2007; Shlush et al., 2012; Subramanian et al., 2012; von Heydebreck et al., 2004; Xu et al., 2012). Several of these methods used techniques from the area of phylogenetics (reviewed by Attolini and Michor, 2009) because of the insight that tumor genomes evolve (Cahill et al., 1999; Nowell et al., 1976). Most prior studies have used either comparative genome hybridization or sequencing of cell populations, which have the advantage that one can do genome-wide analysis, but the disadvantage that the input data are explicitly or implicitly averaged over many cells of the same tumor. Other data types can offer distinct advantages, such as the microsatellite data used by Shlush et al. (2012), which can allow some inference of useful population genetic parameters generally difficult to assess with tumor data.

FISH is the only currently available reliable technique that allows measurements on enough individual cells to model the evolution of substantial intratumor heterogeneity. The disadvantage of FISH is that it uses only a small number of preselected markers. Only two of the previous studies analyzed FISH data (Martins et al., 2012; Pennington et al., 2007). These studies were limited either to two probes (Pennington et al., 2007) or to three probes and coarsely distinguishing only loss (copy number <2), neutral (copy number 2) and gain (copy number >2) (Martins et al., 2012).

We address a need for new methods capable of handling the larger numbers of cells and probes in recent FISH datasets. More specifically, we aim to develop a theoretical foundation for efficient handling of large copy number datasets. Toward this goal, we develop theory and algorithms for a model of tumor progression driven by gains and losses associated with FISH probes. Our methods handle in principle any number of probes and any range of copy numbers 0 through MAX_COPY (default 9). The use of MAX_COPY limits the combinatorial search and hence running time of our methods on inputs where the measured copy numbers exceed this limit. The work is intended to establish a framework capable of giving useful tree inferences on state-of-the-art FISH data, which might be extended in future work to handle even harder problem instances and more realistic models of tumor evolution.

Our contributions include the following:

1. Reducing a model of the problem of modeling progression of FISH probe cell count patterns to the Rectilinear Steiner Minimum Tree (RSMT) problem and thus bringing prior theory on the RSMT problem to bear on the FISH phylogeny problem.

2. Design and implementation of an exponential-time exact method and a polynomial-time heuristic method to construct trees modeling the progression of cell count patterns.

3. Mathematical proof and software implementation of a new inequality that speeds up the RSMT-based computation.

4. Definition and evaluation of new test statistics based on the trees computed by our methods. These test statistics give novel insight into the selective pressures in tumor progression, compared with test statistics derived from the cell count patterns alone.

5. Definition and evaluation of ‘features’ based on the tree structures that can be used with machine learning to classify the tumors. For example, we show improved effectiveness at distinguishing the cervical tumors that metastasize from those that do not.

2 METHODS

In this section, we describe a set of algorithms to identify a most parsimonious tree of copy number changes consistent with a dataset on cell-level tumor copy-number heterogeneity. We first describe an exponential-time exact algorithm. We next propose a set of valid inequalities to reduce the running time of the algorithm. We then propose a heuristic approach that returns an approximate solution in polynomial time. Both the exact and heuristic methods are implemented in the C++ software package FISHtrees (ftp://ftp.ncbi.nlm.nih.gov/pub/FISHtrees).

2.1 Datasets

The cervical cancer (CC) dataset contains genomic copy numbers of the four oncogenes LAMP3 (Kanao et al., 2005), PROX1 (Wigle and Oliver, 1999), PRKAA1 (Huang et al., 2006) and CCND1 (Fu et al., 2004) on samples from 16 lymph node-positive and 15 lymph node-negative patients (Wangsa et al., 2009). For the lymph node-positive patients, this dataset contains a sample from the primary tumor and another from the metastasis, making the total number of samples 47. The number of cells per sample ranges from 223 to 250, after filtering to remove cells that likely had cut nuclei and those in the process of division, as described previously (Heselmeyer-Haddad et al., 2012). The breast cancer (BC) dataset contains copy numbers of five oncogenes, typically, but not always, gained—COX-2 (Howe et al., 2001), MYC (Wolfer and Ramaswamy, 2011), CCND1 (Fu et al., 2004), HER-2 (Tan and Yu, 2007) and ZNF217 (Nonet et al., 2001)—and three tumor suppressor genes, typically lost—DBC2 (Hamaguchi et al., 2002), CDH1 (Birchmeier and Behrens, 1994) and p53 (Vousden and Lane, 2007)—from 26 paired samples, one from the ductal carcinoma in situ (DCIS) and one from an invasive ductal carcinoma (IDC), from 13 patients. The number of interphase cells ranges from 76 to 220. The FISH protocol filters out cells that are in the process of DNA replication using the fact that these cells have recognizable FISH probe doublets (Wangsa et al., 2009).

2.2 RSMT problem

For each patient sample, each cell assayed will have some non-negative integer number of copies of each probe. If we consider measurements on d probes in c cell count patterns for a given patient, then that patient’s information can be represented by a two-dimensional array D with c rows and d + 1 columns where entry D(i, j), for j = 1, d, represents the copy number of gene j in sample pattern i, and column d + 1 has the number of cells with this count pattern. All counts above MAX_COPY are reduced to that value. Each row of D can be treated as a point in R^d. Our goal is to explain the observed data via a phylogenetic tree of single gene duplication and loss events. We use the L₁, or rectilinear distance metric for inferring the Steiner nodes in R^d. If we are given a set S of points in R^d, and we build a Steiner tree T spanning S, then for any particular edge e, joining points x = (x₁, x₂ , … , x_d) and y = (y₁, y₂ , … , y_d), the rectilinear distance w(e) is defined by w(e) = |x₁ − y₁| + |x₂ − y₂| + + |x_d − y_d|. The problem of identifying a minimum weight tree including all the observed points and, as needed, unobserved Steiner nodes with the rectilinear metric is known as the RSMT problem (Hanan, 1966; Snyder, 1992).

The RSMT problem is NP-complete (Garey and Johnson, 1977) and thus does not have an efficient exact algorithm. One potential advantage of reducing to Steiner trees is that there are high-quality implementations of sophisticated branch-and-cut methods that solve large instances to optimality (Koch and Martin, 1998; Polzin and Daneshman, 2001). To keep our implementation free and self-contained, we implemented a simpler domain-specific method for our instances of RSMT. We developed an inefficient exact algorithm and a heuristic algorithm based on the median-joining algorithm for maximum parsimony phylogenetics (Bandelt et al., 1999) adapted for RSMT using theoretical results from Hanan (1966) and Snyder (1992).

2.3 Exact algorithm for the RSMT problem

An exact algorithm for the RSMT problem in two dimensions was first proposed by Hanan (1966). Hanan’s theorem implies that if we draw lines parallel to the two axes through each of the points in S, then there exists an RSMT of S whose Steiner nodes will be located at the intersections of those lines, a two-dimensional grid known as the Hanan grid that identifies a finite set of positions where the Steiner nodes might be found. Snyder (1992) generalized Hanan’s theorem to any dimension d. To formally present Snyder’s theorem, assume S is a set of points in a d dimensional space R^d and that x₁, x₂ , … , x_d are the coordinate axes of R^d. Let P = (p₁, p₂ , … , p_d) be a point belonging to S. There are d hyperplanes orthogonal to the coordinate axes that contain P. Suppose N(P, i) is one of those hyperplanes that is orthogonal to the axis x_i. Hanan’s grid in d dimensional space is formed by taking the union of all N(P, i) for all points P and all dimensions i. Formally, the Hanan grid H(S) in d dimensions is defined as,

For each subset of the form {N(P₁,1), N(P₂,2) , … , N(P_d, d)}, there is a point at which the d hyperplanes intersect. If the set of all of these intersection points are denoted as I_H(S), then the generalized Hanan’s theorem, proposed and proved by Snyder is the following:

Theorem 1 —

(Snyder 1992) For a given set of points S ⊂ R^d, there exists an RSMT T of S, such that if Q is a Steiner point of T, then Q ∈ I_H(S).

According to Theorem 1, the possible Steiner nodes are the intersection points of the Hanan grid H(S). For each possible number of Steiner nodes k, Algorithm 1 enumerates all subsets of k potential Steiner nodes from those allowed by the generalized Hanan’s theorem. For each such subset, the algorithm constructs a minimum spanning tree (MST) using the observed data points and those k specific Steiner nodes. The minimum cost tree over all such subsets and all possible values of k is returned as the optimal tree. This method is guaranteed to find an optimal solution to the RSMT problem. More efficient approaches, such as that proposed in Dreyfus and Wagner (1971), cannot be used in our case, as they assume that all the terminal nodes must be leaf nodes in the Steiner tree, while in tumor progression trees, a terminal node can be a parent node of other terminal nodes. Below, we show that the Algorithm 1 run time is at worst exponential in the number of potential Steiner nodes and the size of the probe set.

Theorem 2 —

The time complexity of Algorithm 1 is exponential in the number of potential Steiner nodes.

Proof —

If MAX_COPY + 1 = m, then, by Theorem 1, the total number of possible Steiner nodes to be considered is s = m^d. To find the exact solution, we consider each possible subset of the inferred Steiner nodes and build a minimum spanning tree on the set of terminals and subset of Steiner nodes under consideration. The total number of subsets of a set with cardinality n is 2ⁿ. We implemented Prim’s algorithm for MST and its complexity is O(nlogn). So, the total running time of Algorithm 1 is O(2^snlogn).

Algorithm 1 Exact algorithm for generating RSMT.

Input: A point set S

Output: Steiner tree including the set of inferred Steiner nodes and weight of the Steiner tree

Infer Steiner node set Q using generalized Hanan’s theorem

Identify MST on S and let min_weight = weight(MST(S))

for k in 1 … |Q| do

  Enumerate all size-k subsets T of Q

  for each element T_k of T do

    Identify MST on {S T_k} and

    Let current_mst_weight = weight(MST({S T_k}))

    if(current_mst_weight < min_weight) then

      min_weight = current_mst_weight

        steiner_tree = MST({S T_k})

Output steiner_tree and min_weight

2.4 Pruning Steiner node subsets

Because the time complexity of Algorithm 1 depends on the number of calls made to the MST routine, we can reduce its runtime by checking beforehand if a call to that procedure cannot lead to a solution of lower cost than current_mst_weight. We propose a lower bound on the weight of the MST, and we add checks in every for loop in Algorithm 1 to test whether the lower bound is higher than the minimum weight MST generated so far. If so, then we do not generate the MST.

Theorem 3 —

Suppose we would like to build an MST on a graph that has n nodes, of which nodes 1 , … , r might have degree 1 in an MST and hence be eligible to be its root, while nodes r + 1 , … , n are required to have degree >1 in the MST and hence are not eligible to be its root. By construction, a Steiner node in the graph must have degree >1 in the MST because otherwise, its inclusion cannot reduce the weight of the MST.

Assume, the weight matrix of the graph is

Then,

(1)

where W(MST(n)) is the total weight of the MST with n nodes and w_i = inf(w_i1, w_i2 , … , w_{i(i − 1)}, w_{i(i + 1)} , … w_in). Here, for a list L, sup(L) and inf(L) denote the lowest upper bound and greatest lower bound of L, respectively.

Proof —

We define the difference on the right hand side of the inequality (claim) as Q(n). For each non-root node v, define p[v] to be the weight of the edge connecting v to its parent in the MST, and define p[root] = 0. We can readily see that p[v] ≥ w_v. p[v] cannot be smaller than w_v as edges do not get split in the MST-building process. For a graph with n nodes, W(MST(n)) = p[1] + p[2] + … + p[n]. If we assume node 1 is the root node, then W(MST(n)) = p[2] + p[3] + + p[n]. We divide into two cases depending on the value of sup(w₁, w₂, w₃ , …… , w_r).

If sup(w₁, w₂, w₃ , …… , w_r) = w₁, then

Q(n) = w₁ + w₂ + w₃ + + w_n − w₁ = w₂ + w₃ + + w_n

Since w_v ≤ p[v] for any node v, we have,

Q(n) = w₂ + w₃ + + w_n ≤ p[2] + p[3] + + p[n] = W(MST(n)).

On the other hand, if w′ = sup(w₁, w₂, w₃ , …… , w_r) > w₁, then,

Q(n) = w₁ + w₂ + w₃ + + w_n − w′ < w₂ + w₃ + + w_n

≤ p[2] + p[3] + + p[n] = W(MST(n))

So, W(MST(n)) ≥ (w₁ + w₂ + + w_n) − sup(w₁, w₂ , … ,w_r).

Distinguishing between the potential Steiner nodes and the non-Steiner nodes in (1) makes the claim more complicated, but leads to a direct simplification of the algorithm. Fewer calls to the MST procedure are made because the lower bound exceeds the current best MST weight more often.

2.5 Heuristic algorithm for the RSMT problem

We also propose a heuristic method that can find a potentially suboptimal solution in polynomial time. Our proposed heuristic method uses the median joining principle of iteratively identifying Steiner nodes (known as median nodes) that allow one to more parsimoniously link some triplet of nodes, using the generalized Hanan theorem to enumerate possible medians. The method, described in Algorithm 2, begins by constructing a minimum spanning network, corresponding to the union of edges in all minimum spanning trees. It then enumerates triplets of nodes (u, v, w) such that at least two pairs of each triplet are connected in the network, followed by enumerating possible median nodes, consisting of combinations of coordinate values of u, v, and w. It then tests whether introducing the given possible median as a Steiner node reduces the cost of the minimum spanning tree. If so, then the median node is added. The process is continued until no additional cost-saving median node can be added.

Theorem 4 —

The time complexity of Algorithm 2 is polynomial in the cardinality of the terminal set.

Proof —

The running time of the heuristic algorithm is dominated by the number of triples that are considered during the Steiner node inference process. The maximum number of triples considered for inferring the Steiner node is . If we are considering d probes, then the maximum number of Steiner nodes is 3^d, where d is the number of probes. So, the total running time of the heuristic approach is O(3^dn⁴logn).

Algorithm 2 Heuristic algorithm for generating RSMT.

Input: A point set S

Output: Steiner tree including the set of inferred Steiner nodes and weight of the Steiner tree

Calculate Minimum Spanning Network (MSN) on S using the approach described in Bandelt et al. (1999)

Identify MST on S and let min_weight = weight(MST(S))

Identify all 3-node subsets of MSN, T, where at least two pairs of nodes out of the 3 nodes are connected

for each element T_i of T do

  Identify candidate Steiner node set L by taking combination of the  values of coordinate axes of the points in T_i

  for each element L_i of L do

    Identify MST on {S L_i} and

    Let current_mst_weight = weight(MST({S L_i}))

    if current_mst_weight < min_weight then

      min_weight = current_mst_weight

      S = S L_i

      steiner_tree = MST({S})

Output steiner_tree and min_weight

2.6 Experimental procedure

We began statistical analysis with a basic test of imbalance in tree topologies to determine whether differential evolutionary pressures in primary/DCIS versus metastatic/IDC environments might be reflected in the trees. To obtain sufficient counts and detect statistically significant trends, we grouped cells into bins by subtrees based on the child of the root from which each cell traces its ancestry. The root node represents a cell type with a copy number count of 2 for each gene probe (i.e., a healthy diploid cell). Direct children of the root are those nodes distinguished by an increase or decrease of one copy in a single probe. For example, for four gene probes in the CC case, the copy number profiles of the eight children of the root are (1, 2, 2, 2), (2, 1, 2, 2), (2, 2, 1, 2), (2, 2, 2, 1), (3, 2, 2, 2), (2, 3, 2, 2), (2, 2, 3, 2) and (2, 2, 2, 3). We refer to all descendants of one second level node as a ‘bin’. We counted the total number of cells in that bin for each of the eight subtrees separately for the 16 pairs of primary and metastasis samples. The resulting eight-dimensional vectors for each primary–metastasis pair were compared by a χ² test to test the null hypothesis of independence between bin counts and primary versus metastasis labels.

To illustrate the difference between the dynamic views of relationships among cell types offered by the trees relative to the static snapshot offered by raw probe counts, we next examined two different measures of the net mutational bias in the CC and BC trees: one based on imbalance of copy numbers in cell counts and one on imbalance in tree edges. These statistics provide two different views of the net evolutionary process of mutation and selection. For the cell count data in CC/BC, we aggregated all 16/13 patients’ primary/DCIS and metastasis/IDC information separately, computing average difference in copy number of individual cells relative to diploid, excluding the contribution of all-diploid cells. For tree-based calculation of gene gain/loss, we measured the net gain or loss of each gene by the number of tree edges showing gain minus those showing loss over all trees generated by FISHtrees.

We also performed a series of experiments on the use of progression tree statistics for classification tasks related to tumor progression and prognosis. In each case, we examined the use of tree statistics as features for prediction methods in comparison with prediction from features derivable solely from raw cell counts. As feature sets, we used:

1. Fractions of cells in the 8/16 subtrees rooted at children of the diploid root: We defined tree-based features consisting of 8/16 features corresponding to the fraction of cells in each of the subtrees corresponding to immediate children of the diploid root.

2. Fractions of edges exhibiting gain or loss of each gene: We used 8/16 features corresponding to the fraction of total tree edges showing gain or loss of each gene.

3. Fractions of cells at each level from one to ten in the trees: We used 10 features corresponding to the fraction of cells at each level in the tree from one to ten. The root (the node representing normal cells) of the tree is assumed to be located at level one.

Fractional rather than absolute counts are used for each measure, so that the sum of the values is normalized to be 1 and the test statistics are not distorted by variability sample-to-sample in the number of cells. These features were compared with four non-tree-based features:

1. Mean gain or loss in each gene individually.

2. Maximum copy number of each gene individually.

3. Shannon index (Park et al., 2010), an information theoretic measure. For each gene G, each distinct combination of gene copy numbers and cellular ploidy represents a species. If p_i denotes the frequency of species i among all tumors, then the Shannon index H for G is given by

   

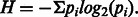
4. Simpson index (Park et al., 2010), D = .

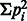We further performed simulation tests to evaluate the correctness of the phylogenetic trees inferred by our algorithm in terms of the underlying tumor progression mechanism. Trees were simulated to approximate true FISH progression trees by expanding from an initial diploid root node by selecting a Poisson number of children of each node (possibly with repetition) and expanding each node selected recursively until the process terminates. To produce trees comparable with the real data, we reject those with <50 or >120 distinct cell types. Individual cells are then chosen uniformly from the nodes in this topology until 250 cells are sampled. Because the true and inferred trees may have different node sets, we evaluate accuracy by a variant of the weighted matching metric of (Lin et al., 2012), seeking a maximum matching of phylogenetic bipartitions between true and inferred trees with each bipartition weighted according to the fraction of nodes it shares with its paired bipartition in the other tree. The total agreement in nodes across all bipartitions provides a fractional accuracy of the inference. Full details of the tree simulation and scoring protocols are provided in the Supplementary Section S2.

3 RESULTS

In this section, we present the results of experiments to evaluate the utility of tumor phylogeny inference for understanding the developmental processes of these tumor types. We also explore the prognostic value of tumor phylogenies by using them to derive features for classification experiments and comparing to features that do not rely on tree inference. For these experiments, we built tumor progression trees of the CC and BC data using the ploidyless heuristic approach to phylogenetic inference described in Methods.

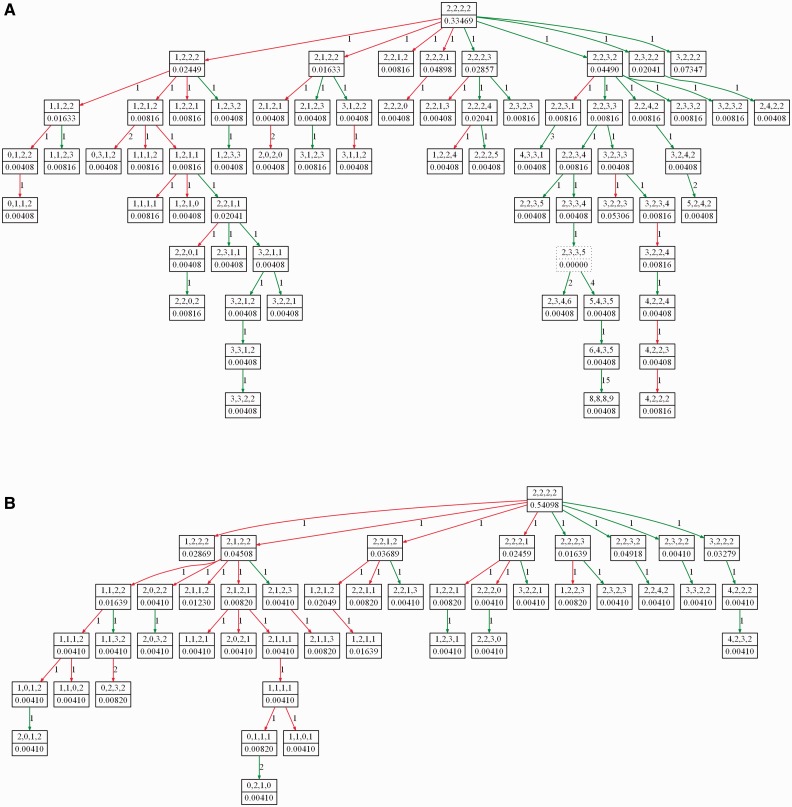
Figure 1 shows representative examples of tumor progression trees from the CC dataset. Figure 1A shows a tree inferred from the primary tumor of patient 1 of the CC dataset. Figure 1B shows the tree for the paired metastatic sample from patient 1. The primary stage tree has more nodes and is more balanced and broader in shape compared with the metastatic stage tree. The distinct topologies of the trees may indicate the fact that cells residing in primary and metastatic sites of the tumor face different selective pressures. Supplementary Figures S4 and S5 show examples of trees inferred from a DCIS sample and an IDC sample of a patient with id 8 of the BC dataset. The complete set of trees from the CC and BC patients is provided in Supplementary Section S6.

Fig. 1.

Phylogenetic trees showing progression of (A) primary and (B) metastasis stage cervical cancer in patient 1. The trees are built from single cell-copy number data using the ploidyless heuristic approach implemented in FISHtrees. Each node in the trees represents a copy number profile of the four gene probes LAMP3, PROX1, PRKAA1 and CCND1, respectively. Nodes with solid borders represent cells present in the collected sample, while nodes with dotted borders represent inferred Steiner nodes. Green and red edges model gene gain and gene loss, respectively. The weight value on each edge connecting two nodes x and y is the rectilinear distance between the states of x and y. The weight on each node describes the fraction of cells in the sample with the particular copy number profile modeled by that node; Steiner nodes are assigned weight 0

3.1 Comparison of exact and heuristic algorithms

To evaluate the quality of the solution generated by the heuristic algorithm, we generated tumor progression trees using both the exact and the heuristic algorithms. We report a comparative study of the two algorithms in Supplementary Table S1. For each example run, we report the number of probes considered, the total number of terminal nodes in the given dataset and a comparison of the weights of the RSMTs generated by the exact and heuristic approach. The heuristic approach returns an optimal solution about 80% of the time. For the cases where the heuristic solution is not optimal, the excess weight is very small. From the runtime comparison of the two approaches, we see that the heuristic approach returns a solution within 1 s every time. The runtime of the exact approach varies from 1 s to 1966 s. When the number of probes is higher than 5, the total running time of the exact approach becomes impractical. The heuristic algorithm can return a solution in <1 min even when using all eight probes in the BC dataset (data not shown).

In Supplementary Table S1, we also report the percentage of total calls to the MST generation routine in Algorithm 1 that are avoided as a result of the inequality we proposed in Theorem 3. For 75% of the examples, the lower bound in Inequality (1) exceeds the current best MST weight >90% of the time. As most of the entries in Inequality (1) are computed just once and used throughout, this results in a huge decrease in the runtime of the exact approach.

3.2 Statistical analyses of tumor phylogenies

3.2.1 Cervical cancer primary versus metastatic samples

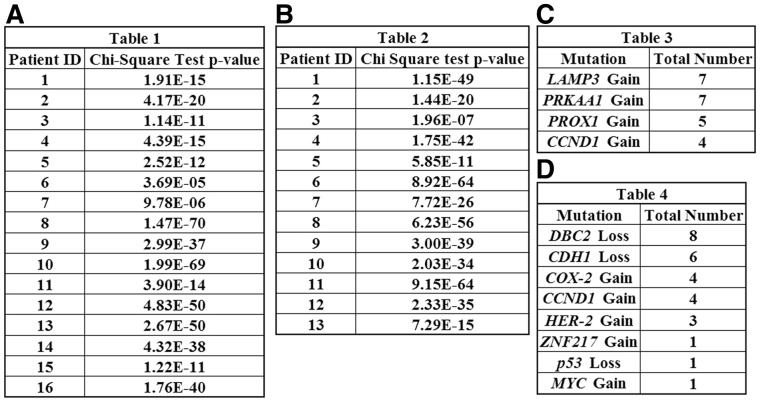
We first examined cervical cancers, looking at paired primary tumor and metastasis samples. Table 1 in Figure 2A reports P-values for χ² tests on all 16 pairs of patients. For each patient, the χ² tests compare two 8-element vectors, one for the primary tumor and one for the metastasis, in which element i is the number of descendants of the ith child of the root. All P-values in this and other tests are corrected for multiple testing. In Figure 2A, all 16 P-values are statistically significant. The same is true for an analogous χ² test of DCIS versus IDC in 13 BC patients in Figure 2B. That these comparisons are significant indicates significant imbalance between tree geometries of the two tumor stages. It may suggest that distinct evolutionary pressures act on growth in the primary tumor versus the metastasis.

Fig. 2.

P-values from χ² tests comparing the number of descendants in the (A) eight children of the root in the primary tumor tree versus the metastasis tree in the same CC patient, (B) 16 children of the root in the DCIS tree versus the IDC tree in the same BC patient. The total number of (C) CC and (D) BC patients for which each bin for gain of oncogenes or loss of tumor suppressor genes shows significance in individual 2 × 2 χ² tests

There is, however, high variability from patient-to-patient in the nature of the imbalance. Supplementary Table S2 shows cell counts for the bins associated with gain of the four genes, with the largest bin of each tree highlighted. The bin accounting for Gain of LAMP3 is the most frequent dominant bin in both primary and metastatic samples. This bin is also the only dominant bin across multiple pairs of primary and metastatic samples. This finding is consistent with the ubiquitous gain of LAMP3 in CC reported in Wangsa et al. (2009). We also performed χ² tests on individual bins in each pair of primary and metastasis samples using 2 × 2 contingency tables. Table 3 in Figure 2C reports the total number of patients for which each bin representing gene gains or losses shows significant association with tumor stage. The results suggest a net trend toward LAMP3 and PRKAA1 gains, with again a significant difference between primary and metastasis. We infer from these results that LAMP3 has a dominant role both in initiation and development of different stages of CC.

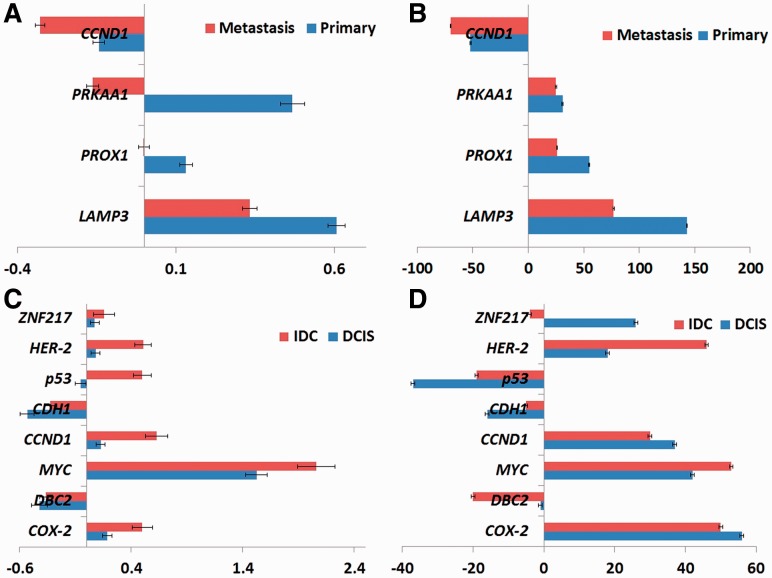
Figure 3 shows the results of cell-count and tree-edge-based analysis of gene gain/loss statistics. Cell counts (Fig. 3A) and edge counts (Fig. 3B) show similar trends in the gain and loss of the marker genes except for two cases. In the first case, cell counts show no net gain or loss of PROX1 in metastasis, while edge counts show a gain. The latter result is supported by the literature (Wangsa et al., 2009) associating gain of PROX1 with metastasis. Likewise, the two measures suggest opposite trends with respect to PRKAA1 in metastasis, with cell counts suggesting net loss but edge counts net gain. Again, net gain has been previously associated with progression to metastasis (Wangsa et al., 2009). These results suggest that quantifying progression via evolutionary events, as enabled by the trees, provides a clearer view of the selective pressure than does quantification by cell counts.

Fig. 3.

Increase and decrease in copy number count of LAMP3, PROX1, PRKAA1 and CCND1 (A and B) across 16 CC patients and COX-2, DBC2, MYC, CCND1, CDH1, p53, HER-2 and ZNF217 (C and D) genes across 13 BC patients. Copy number count is calculated using (A and C) average of cell count data and (B and D) net tree edge changes. The units on the x-axis differ in the two adjacent subfigures due to the different types of data used

3.2.2 Analysis of breast cancer DCIS versus IDC samples

We performed a comparable statistical analysis on the paired BC DCIS and IDC samples to understand how the evolutionary process varies between early stages and late stages of tumor development. The BC dataset includes copy number counts for eight gene probes, yielding 16 potential children of the diploid root node representing single copy number gain and loss of individual gene probes. We again treated the subtrees rooted at each of these 16 children as bins and counted the total number of cells in each bin for each DCIS and IDC tree. We then performed a χ² test using the 16 × 2 contingency table defined by each DCIS/IDC pair. The results of the χ² tests are presented in Table 2 in Figure 2B. As with the CC data, the table consistently shows significant P-values, which again may indicate differences in the evolutionary processes at different stages of tumor development.

We report bin counts for gain of oncogenes and loss of tumor suppressor genes in Supplementary Table S3. Examination of individual bin counts shows that the precise biases tend to differ from patient to patient, with the most frequent dominant bins being loss of the two tumor suppressor genes DBC2 and CDH1.

Table 4 in Figure 2D shows the number of times each of the bins representing gain of oncogenes or loss of tumor suppressor genes shows statistical significance for individual χ² tests on each pair of DCIS and IDC trees. This table again shows bias toward loss of the two tumor suppressor genes DBC2 and CDH1. Loss of DBC2 and CDH1 is part of a dominant imbalance clone reported in Heselmeyer-Haddad et al. (2012) where it is inferred that cells with this imbalance clone have a growth advantage in DCIS and IDC. Our analysis supports this argument.

We next calculated gain/loss statistics based on raw cell count data and based on tree edges, as we did with the CC data. We present the results in Figure panels 3C and D, respectively. The trends are qualitatively generally consistent between cell count and tree-based statistics. With two exceptions, oncogenes are amplified and tumor suppressor genes lost in DCIS and IDC by both measures. One exception is the tumor suppressor gene p53, which shows amplification rather than the expected loss when analyzed by cell count statistics (Fig. 3C) but not with tree statistics (Fig. 3D). The difference may reflect an occasional amplification of p53 concurrent with the rest of chromosome 17 due to aneuploidy. The other exception occurs with respect to the oncogene ZNF217, which shows net gains by both statistics for DCIS, but loss rather than gain in IDC for tree statistic. The discrepancy appears to be due to one case, in which 90% of cells in IDC show ZNF217 deletion. This unusual case might be due to the loss of chromosome 20 (on which ZNF217 resides) in the IDC stage of the tumor for that patient.

3.3 Use of tree statistics for classification

A key question in studying mathematical models of tumor progression is whether an understanding of tumor evolutionary pathways will lead to improved prognostic or diagnostic capabilities. We performed classification experiments on the CC dataset to understand how features derived from progression trees can help differentiate samples from different cancer stages. We used support vector machines (SVM), as implemented in MATLAB, with leave-one-out cross-validation (LOOCV). The performance of each classifier was assessed by two measures: (i) Percentage of samples correctly classified (Accuracy) and (ii) F measure, which is the harmonic mean of precision and recall. We performed 500 rounds of bootstrapping and assessed mean Accuracy and F measure as well as their standard deviations.

3.3.1 Classification of cervical cancer samples

We performed experiments exploring the predictive power added by the three different types of tree-derived features. The three classification experiments on the CC dataset are as follows:

1. Distinguishing primary from metastatic samples using 16 paired primary and metastatic samples,

2. Distinguishing primary from metastatic samples using 16 metastasizing and 15 non-metastasizing primary tumor samples versus 16 metastatic samples, and

3. Distinguishing 16 primary samples that later metastasized from 15 primary samples that did not metastasize.

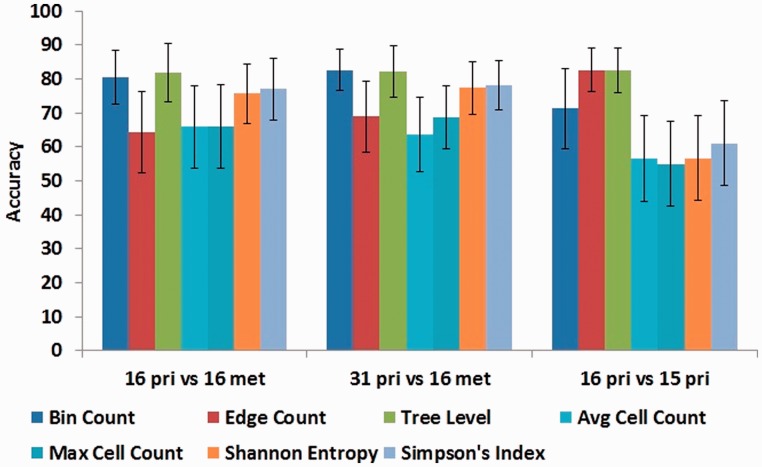
Figure 4 and Supplementary Figure S1 report performance of the two feature sets for the SVM classifier in terms of mean accuracy and mean F measure, along with confidence interval of one standard deviation, respectively. By both measures, tree-based statistics lead to improved classification accuracy in all experiments. The best accuracy on the three tasks is achieved using the tree-based level-count features, at 81.91% accuracy for distinguishing primary tumors from their paired-metastasis samples, 82.26% for distinguishing all primary tumors (metastasizing and non-metastasizing) from the metastasis samples and 82.58% for distinguishing metastasizing versus non-metastasizing primary tumors. This result suggests that the qualitative observation that primary trees appear broader and deeper than metastatic trees (Fig. 1) captures a robust quantitative property of progression trees distinguishing primary from metastatic samples. Among the non-tree based features, Simpson index shows the best classification performance, yielding average accuracies of 76.94, 78.12 and 61.08% on the same tasks. Average and maximum copy number counts show worse performance in all three classification tasks.

Fig. 4.

Accuracy of tree-based versus cell-based features in classification tasks using an SVM classifier. Each chart shows accuracy of three tree-based and four cell-based feature sets on the three defined prediction tasks

Supplementary Figure S1 shows qualitatively similar performance by the F measure. The most striking difference between the two measures is a much worse performance for the edge count and cell count measures at distinguishing primary from metastatic trees when assessed by F-measure. Bin count and tree level features show similarly high performance by both measures.

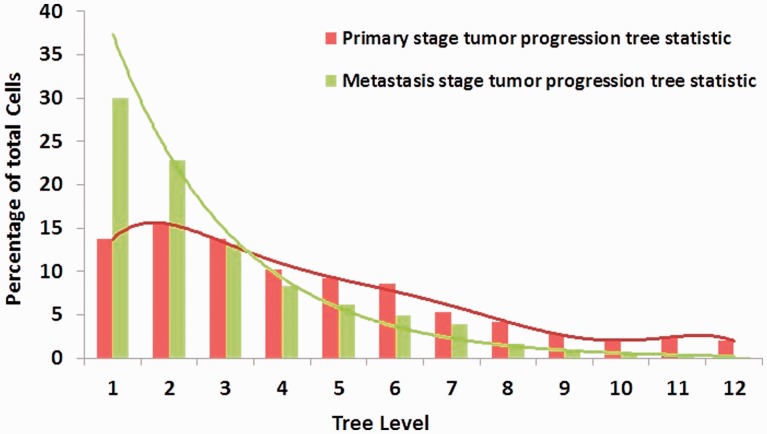
To follow up on the observation that tree topology seems to be the most informative feature type, we examined how this feature varies between primary and metastatic trees. Figure 5 shows the distribution of the aggregated cell counts across different levels of 31 primary stage and 16 metastatic stage tumor progression trees. In the primary stage tumors, ∼70% of the cells are distributed in the first six tree levels, and the cell count decreases gradually when level of the tree is increased. In contrast, for the progression trees of metastatic stage tumors, the total cell count shows an exponential decrease with more than half (53%) of the cells located in the first two tree levels This topological difference could reflect the fact that in the primary stage tumors, the clones have more time to continue diversifying. An alternative hypothesis is that the difference reflects stronger purifying selection for clones that must evolve to be able to migrate to and survive outside their native microenvironment. The BC study was designed to include only patients in whom the diagnosis of IDC and DCIS was concurrent (Heselmeyer-Haddad et al. 2012), which has the effect of making the time of evolution for each sample in a pair comparable, consistent with the hypothesis of increased purifying selection in IDC. The data here, however, are insufficient to reject either hypothesis.

Fig. 5.

Distribution of cells across different levels of tumor progression trees, counted for primary and metastatic trees separately

3.3.2 Informative feature selection

We applied feature selection to identify the most informative features. We exhaustively enumerated subsets of features and tested the cross-validated predictive accuracy of each. Figure 6 shows, for each classification experiment and feature type, the optimal SVM prediction accuracy over all subsets. For the most challenging task, distinguishing metastasizing from non-metastasizing samples based on the primary sample, accuracy peaks at 72% for Bin Counts, 87.1% for Edge Counts and 77.4% for Tree Level topological features. Interestingly, the best performance over all tests at identifying metastasizing tumors (87.1% accuracy) comes from the Edge Count features, despite poorer performance of Edge Count in most tasks. Among the Bin Count features, LAMP3 was an informative feature in all three tasks, reinforcing our statistical result that LAMP3 is an important gene in CC progression.

Fig. 6.

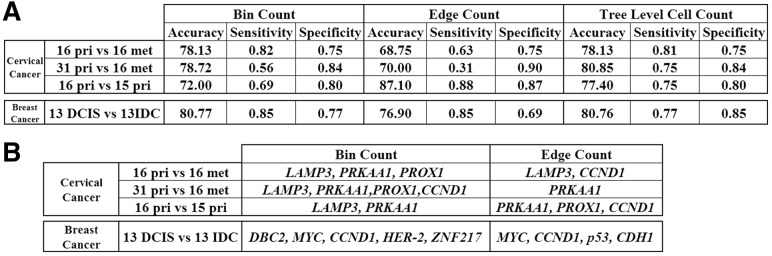
(A) Classification performance for particular subsets of features that show best prediction accuracy among all possible subsets on CC and BC datasets. (B) Sets of gene probes that show best classification accuracy

In previous work on the same classification task, Wangsa et al. reported sensitivity and specificity of 0.75 and 0.87 respectively, with composite FISH markers using percentages of cells with amplified signals for each individual marker, on the CC dataset, but this was done without LOOCV (Wangsa et al., 2009). The optimal feature set identified here improved substantially on the robustness and sensitivity of that result while keeping equal specificity.

We performed similar classification experiments for informative feature selection on the BC data to distinguish DCIS from IDC samples. When we used all the features for classifying the DCIS samples from IDC, Bin Count and Edge Count measures showed 50% accuracy and Tree Level topological features showed 57% accuracy. Figure 6A shows that feature selection improved accuracy to 80.7% for both Bin Count and Tree Level feature subsets. The poor performance while using all features might be owing to the high intra- or inter-tumor heterogeneity (Heselmeyer-Haddad et al., 2012).

When we selected the most informative subsets, the feature sets for BC DCIS versus IDC samples classification (Fig. 6B) differed depending on whether the Bin Count or the Edge Count measure was considered, although both agreed on the selection of MYC. MYC was reported in Heselmeyer-Haddad et al. (2012) to be a prognostic marker in the progression of DCIS to IDC. Deletion of CDH1 was also reported in Heselmeyer-Haddad et al. (2012), and was selected here in the Edge Count case.

3.4 Simulation results

Because we cannot know the ground truth for real data with certainty, we used simulated trees to test accuracy of tree inferences. Comparison over 50 simulated trees shows a mean accuracy of 92% with standard deviation 2.13% in correctly inferring tree topologies. Supplementary Figures S2 and S3 provide more detailed results on the 50 simulated cases individually, showing consistently high accuracy. There is, however, a slight bias toward underestimating the true tree weight, as one would expect for a parsimony measure.

4 CONCLUSIONS

We developed exact and heuristic algorithms for building tumor progression trees using copy number information and applied our methods to two different types of cancer. To reduce the complexity of the exact algorithm, we further developed an inequality that can prune up to 99% of the solution space, resulting in substantial reduction in the runtime of the algorithm. The heuristic approach returns potentially sub-optimal solutions in reasonable time for datasets with large numbers of probes. These algorithms have been implemented in a publicly available C++ software package, FISHtrees. Copy number changes can evolve using additional basic operations such as changing the entire ploidy by 1 or doubling, and FISHtrees includes an implementation of another method that allows these ‘operations’ (Pennington, et al., 2007). Analyses of statistics developed using different features of the tumor progression trees identify some important recurring markers of tumor progression and highlight the different selective pressures at work on different stages of the tumor. Use of tree statistics as features for classification further illustrates the importance of models of the evolutionary process to predicting future progression, a problem of importance to cancer treatment and diagnosis. Further improvements in tree algorithms, analysis of even larger and more complex datasets, and investigation of the resulting trees can be expected to yield further insight into both recurring features of tumor evolution and the ways in which these features vary patient-by-patient.