Short read alignment with populations of genomes

Abstract

Summary: The increasing availability of high-throughput sequencing technologies has led to thousands of human genomes having been sequenced in the past years. Efforts such as the 1000 Genomes Project further add to the availability of human genome variation data. However, to date, there is no method that can map reads of a newly sequenced human genome to a large collection of genomes. Instead, methods rely on aligning reads to a single reference genome. This leads to inherent biases and lower accuracy. To tackle this problem, a new alignment tool BWBBLE is introduced in this article. We (i) introduce a new compressed representation of a collection of genomes, which explicitly tackles the genomic variation observed at every position, and (ii) design a new alignment algorithm based on the Burrows–Wheeler transform that maps short reads from a newly sequenced genome to an arbitrary collection of two or more (up to millions of) genomes with high accuracy and no inherent bias to one specific genome.

Availability: http://viq854.github.com/bwbble.

Contact: serafim@cs.stanford.edu

1 INTRODUCTION

Advancements in next-generation low-cost, high-throughput DNA sequencing technologies have made it possible to sequence a large number of human and other species’ genomes (Cherf et al., 2012; Stein, 2010). Several large-scale sequencing efforts are under way, including the 1000 Genomes Project (The 1000 Genomes Project Consortium, 2010) and the International Cancer Genome Project (International Cancer Genome Consortium, 2013). More than 2000 individuals have already been sequenced by the 1000 Genomes Project. Although the next-generation sequencing technologies provide a vast amount of data samples for advancing genomic research, the ever-increasing volume of genomic data has become a tremendous challenge on multiple fronts (Durbin, 2009; Fritz et al., 2011; Kozanitis et al., 2010). One challenge is the alignment of the short DNA sequences (short reads) produced by these technologies to reference genomes, to discover the variation of a newly sequenced genome with respect to the previously sequenced human genomes. Short read alignment is a common first step during genomic data analysis and plays a critical role in medical and population genetics.

Several efficient short-read alignment programs, such as BWA, SOAP2 and Bowtie (Langmead et al., 2009b; Li and Durbin, 2009; Li et al., 2009), have been developed in the past years (Li and Homer, 2010). These methods use the Burrows–Wheeler transform (BWT) (Burrows and Wheeler, 1994), which facilitates linear-time alignment to a large reference string (Ferragina and Manzini, 2000), such as a genome, and requires only a limited amount of memory (Hon et al., 2007; Nong et al., 2011). These aligners typically precalculate the BWT (and some associated auxiliary structures) of a single reference genome and then map the newly sequenced reads to it using a variant of the BWT backwards search procedure. Any observed differences from the chosen reference genome are treated as novel genomic variants or sequencing errors (e.g. Li and Durbin, 2009). In light of the increasing availability of thousands of sequenced human genomes and databases of human genome variation, the requirement of these methods to use a single human reference genome leads to inherent biases towards the arbitrarily chosen reference. Biased alignment output can be a hindrance to the in-depth and comprehensive understanding of the cancer genome (Lee et al., 2010; Roach et al., 2010), evolutionary history (Kumar et al., 2004), Mendelian diseases (Ng et al., 2010) and numerous other domain applications.

Beyond human, to date, millions of genomic variants have been observed in a wide variety of species and can serve as a valuable resource for alignment. For example, many inbred mouse strains have been sequenced to characterize their genomic variation (Keane et al., 2011). Two such mouse strains can have up to 20 million differences between them. As a result, when they are crossed, their F1 offspring are heterozygous at all loci that differ between the parents. Aligning reads from the F1 offspring to either parent’s genome using current alignment techniques will ignore this known heterozygosity and result in alignment bias towards the chosen reference strain. This can make it difficult to perform an experiment like RNA-seq, which relies on high quality mappings.

The limitations of using conventional references and aligners are even more pronounced when sequencing organisms with a large amount of genomic variation among individuals. For example, the sea squirt, Ciona savignyi, has a polymorphism rate of ∼4.5% (Rumble et al., 2009). With such a high polymorphism rate, the genome of any newly sequenced individual of this species will be very different from a single conventional reference sequence. Current short-read aligners operating on a single reference genome are simply not designed to handle this scenario and will result in poor alignment accuracy.

Although humans have a lower polymorphism rate, the reference bias remains an important problem. Even though individual alignment results may be only slightly biased when aligning with conventional techniques, in a large study involving thousands of individuals, this effect can add up to distort the study’s conclusion.

A vast number of genomic variants in human populations have already been discovered and are maintained in publicly accessible databases, such as dbSNP and SNPedia. The majority of variations between a newly sequenced genome and the reference are likely to already exist in these databases. Moreover, structural variants, such as transpositions, large insertions and deletions and inversions, are difficult to analyse and require split-read alignment techniques (Pang et al., 2010; Snyder et al., 2010). Once a structural variant is detected, it would be desirable to avoid repeating the process of identifying the same variant in other genomes. With this issue in mind, we are facing the challenging problem of how to efficiently incorporate the available genomic variant information during alignment.

The naive solution to this problem is to use the existing fast aligners to map new read samples to all available genomes individually. The state-of-the-art aligners, albeit much faster than their predecessors, still take 3–5 h to map 12.2 million reads to a human genome on a single core processor (Li and Durbin, 2009), so spending 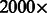more time (roughly a year) to map those reads to all the genomes currently in the 1000 Genomes Project is not a realistic solution, especially as this time will scale linearly with the number of genomes in the collection. Furthermore, even though the space required to store the BWT-related data structures of each genome can be significantly reduced using various compression techniques (Hon et al., 2007), the total amount of space required for storing all the available genome data is considerable. Finally, this solution does not take into account the scenario where the newly sequenced genome has a novel haplotype of several nearby SNPs (i.e. when the newly sequenced genome contains a combination of SNPs that do not occur together in any known genome individually).

An alternative solution is to align the newly sequenced reads to a single reference genome and then query the genomic variation databases to analyze the mismatches. This approach is used in programs such as Crossbow (Langmead et al., 2009a), VarScan (Koboldt et al., 2009), and others (Handsaker et al., 2011; Mokry et al., 2010). However, if the reads are misaligned during the first step (e.g. reads spanning a mutation), incorrect mismatch locations will be propagated to the second step, which can bias the study results and lead to questionable conclusions, especially for a large study involving thousands of genomes (DePristo et al., 2011).

Taking advantage of the high redundancy among sequenced genomes, several techniques have been proposed for compressing genomic data and searching this compressed data directly (Lam et al., 2010; Loh et al., 2012; Makinen et al., 2009; Schneeberger et al., 2009; Siren et al., 2011). Loh et al. (2012) provides the first efficient scheme for compressing genomic libraries and presents compression-accelerated BLAST and BLAT algorithms that search over the compressed data. In particular, their data compression scheme consists of finding fragments (by default, 300 bp long) in the database that are highly similar, keeping only one version of the sequence fragment, and replacing each additional fragment with a link to this sequence and a list of differences.

The first approach for mapping short reads against a collection of genomes simultaneously is presented by Schneeberger et al. (2009). Their algorithm, GenomeMapper, combines the genomes into a joint hash-based graph data structure. More specifically, it builds an index of all available reference genomes that maps sequence k-mers (5–13 bp long) to their positions in the genomes. Identical regions are stored only once, and polymorphic regions are stored separately for each genome (these are represented as branches in the index). During alignment, the hash-based index is first scanned to identify the exact matches, then nearly identical maximal substrings are detected, and finally, bounded dynamic programming is used to extend the partial alignments. Although this technique proved to be successful for aligning with the small Arabidopsis Col-0 genome, its high memory requirement makes its applicability to a human genome still questionable (Li and Homer, 2010).

Siren et al. (2011) proposed a novel index structure for a collection of genomes built by converting the genome multiple alignment into a prefix-sorted finite automaton that can recognize the strings corresponding to all the paths through the multiple alignment. This work generalizes the BWT-based index structure for labelled trees to labelled graphs and uses a modification of the backwards search algorithm to perform read mapping. The technique was demonstrated on the multiple alignment of four assemblies of the human chromosome 18 and is expected to support genomes of up to 100 Mbp using a single workstation. Owing to its high memory consumption during prefix-sorted automaton construction, an external memory implementation is needed to index a collection of human genomes, which is not yet available. Therefore, the applicability of this method to a large collections of human genomes has not yet been demonstrated in practice.

In this article, we present BWBBLE, an aligner that handles genetic variants and thus avoids the inherent bias induced by mapping to a specific genome, while providing reasonable computation time and limited memory consumption for large collections of genomes. The main new contributions of our work are the following: (i) we introduce the concept of a linear reference multi-genome that incorporates the catalogue of all known genomic variants with a reference genome (e.g. SNPs, insertions, deletions and inversions), and (ii) we develop a BWT-based read alignment algorithm, BWBBLE, that accurately maps reads to this multi-genome. We evaluate the effectiveness and efficiency of BWBBLE in Section 4 with a set of experiments using simulated and real read data.

2 BACKGROUND: BURROWS–WHEELER TRANSFORM

The BWT (Burrows and Wheeler, 1994) of a given string is a reversible permutation of the string symbols that enables the search for a pattern P in the original string to take 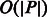time (i.e. linear time with respect to the length of the pattern).

Let 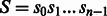be a string of length n defined over some alphabet Σ (e.g. the A/C/G/T nucleotide alphabet if S is a genome) and let $ be a symbol not in Σ that is lexicographically smaller than all the characters of Σ. When constructing the BWT of S, $ is first appended at the end of S, such that 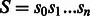, where 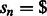(now 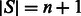). Let SA be the suffix array of S (we have 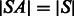), such that 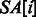stores the position of the i-th lexicographically smallest suffix of S (e.g. 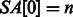since $ is the smallest suffix). A simple technique for constructing the BWT and SA is demonstrated in Figure 1. It can be shown that BWT 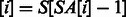when 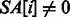(and $ otherwise).

Fig. 1.

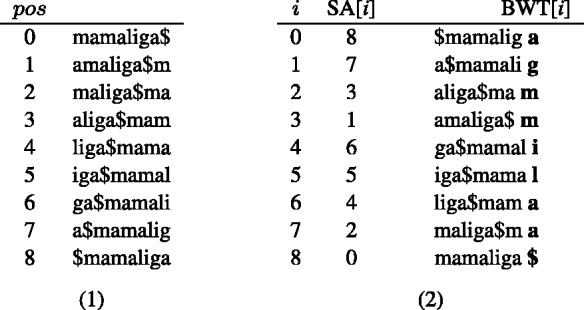
BWT and SA construction for S = mamaliga$. All the rotations of S are first listed (1) and then sorted in lexicographic order (2). The BWT string is assembled from the last character of each sorted rotation (i.e. the right-most column of the sorted rotations matrix) and the suffix array SA is given by the original position in S of the suffix at the start of each sorted rotation (the substring preceding $ in each rotation)

If a pattern P does occur in S, then each of its occurrences will appear at the start of some suffix of S, and these suffixes will be grouped together into a single suffix array interval 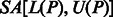, where 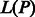and 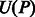represent the indices of the lexicographically smallest and largest suffix starting with P, respectively. Given the SA interval 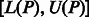, the positions of P in S can be obtained from the corresponding SA values, namely, P will occur in S at all 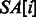, for 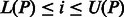. Ferragina and Manzini (2000) showed that if P occurs in S, then:

(1)

(2)

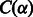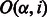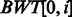where is the number of symbols in S (not counting $) that are lexicographically smaller than α, and is the number of occurrences of in . Therefore, to find the SA interval of P, we can start with the SA interval of an empty string (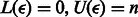) and add a character of P at a time in reverse order (i.e. starting with the last character of P). Assuming that the C and O arrays have been pre-computed, this technique, known as backwards search, enables us to find the interval of all the occurrences of P in S in 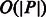time.

3 MULTI-GENOME ALIGNMENT

3.1 Reference multi-genome

In this section, we describe how a single reference genome can be augmented with genomic variant information gathered from an arbitrary collection of genomes. We refer to the augmented reference as the reference multi-genome. We start by handling SNPs and then refine the proposed reference representation with all other possible variations (e.g. insertions, deletions, inversions).

3.1.1 SNPs

To handle SNPs during alignment, we extend the reference genome alphabet from the 4-letter A/C/T/G nucleotide code to the 16-letter IUPAC nucleotide code (Cornish-Bowden, 1985). The IUPAC encoding makes it possible to capture which nucleotides have been observed at a given position across all the available sequenced genomes. For example, if both A and G were discovered at some given position, then the IUPAC character R can be used to represent this variation. For convenience, in our IUPAC alphabet, we have replaced the IUPAC character U by the special character # that represents the absence of the four nucleotides.

As a result, when aligning a read to the reference multi-genome, a given read nucleotide can match more than one character of the reference. For example, read base A can match the IUPAC characters A, D, H, M, N, R, V and W. Therefore, the substrings that a read can map to in the reference might be grouped into multiple separate SA intervals. In particular, if the suffixes are sorted in IUPAC lexicographic order (Fig. 2), then the substrings matching A can fall into up to five separate SA intervals: suffixes starting with A, D, H, [M N R], and [V W] can be separated by suffixes starting with [B C], G, K, and [S T], respectively.

Fig. 2.

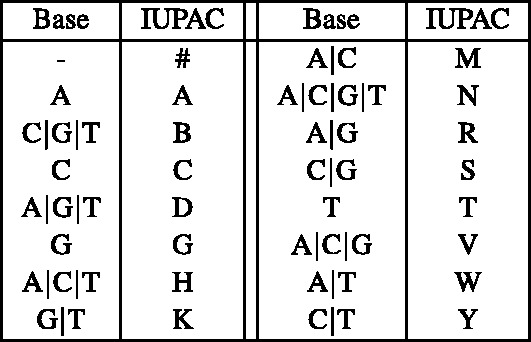
Lexicographic order of the IUPAC code

To minimize the number of separate SA intervals associated with each of the four nucleotides, we propose to use the four-bit Gray code (also known as the reflected binary code) (Gray, 1953) to order the IUPAC characters (instead of ordering them lexicographically). The four-bit Gray code orders four-bit binary values such that two successive values differ by only one bit. For this purpose, we encode each IUPAC character using four bits, such that each bit corresponds to a given nucleotide and is set to 1 if the IUPAC character matches this nucleotide and 0 otherwise. For example, given the nucleotide-to-bit assignment 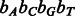, the Gray code value of 1001 corresponds to the IUPAC character W that represents both A and T. Figure 3 shows the IUPAC character order resulting from using this nucleotide-to-bit assignment. We can see that given this new ordering, the IUPAC characters matching A will all fall into a single SA interval (as they are now ordered consecutively). The number of SA intervals per nucleotide will be the following: A 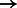1 interval, C 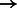1 interval, G 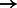2 intervals, T 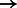4 intervals. Because A and T occur more frequently in the human genome, we expect the nucleotide-to-bit assignment 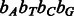to result in better performance. The nucleotide-to-bit assignment can be easily adapted to a specific genome during indexing to prioritize the more frequent nucleotides (e.g. should be used for prokaryotes with a high GC content). It can be theoretically shown that the Gray code order is the optimal order for this problem (see Appendix). Figure 4 shows an example of constructing the BWT and SA of a toy multi-genome using the Gray code order.

Fig. 3.

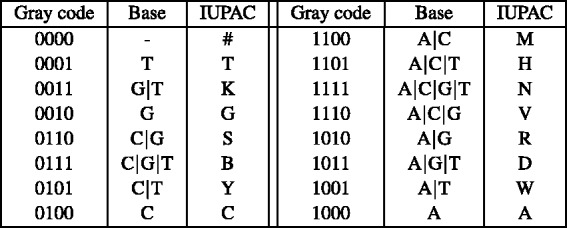
Gray code order of the IUPAC code using the 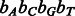nucleotide-to-bit assignment

Fig. 4.

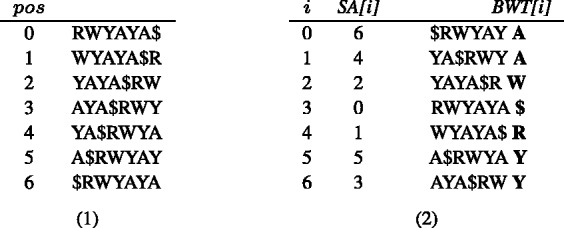
BWT and SA construction of a toy reference multi-genome S = RWYAYA$ (i.e. (AG)(AT)(CT)A(CT)A). All the rotations of S are first listed (1) and then sorted in Gray code order (2)

3.1.2 Extension to other genomic variations

In addition to SNPs, other types of genomic variations are common within and across populations. Such variations include insertions, deletions, inversions and translocations.

If we superimpose the genomes of a given collection, we can collapse the matching nucleotides and encode SNPs with IUPAC characters (as described in Section 3.1.1). The remaining varying-length segments (caused by other types of genomic variations) will visually form a set of bubbles composed of multiple branches, where each branch represents a variant of the genome sequence that was observed at that position in at least one of the genomes in the collection. Figure 5 shows the result of superimposing three sample genomes where the SNPs have been encoded with M and K and the indels form a bubble with three branches.

Fig. 5.

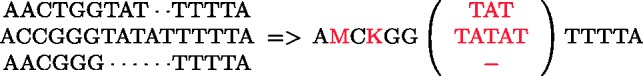
Bubble formed by superimposing three sample genomes

We incorporate the indels into the reference multi-genome as follows. One of the bubble branches is designated as the primary branch and included into the reference at the position at which the bubble occurs. All other bubble branches are appended at the end of the reference genome. Each appended branch is padded at both ends with the bases surrounding the bubble. The length of the padding is a parameter that depends on the expected read length, 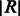, and is set to 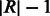. The reference multi-genome augmented with indel information for the example in Figure 5 is shown in Figure 6 for reads of length 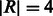(padding of length three). The special character # separates the reference sequence and the bubble branches to prevent reads from being aligned across the sequence and bubble branch boundaries.

Fig. 6.

Reference multi-genome with various variations. Branch padding corresponds to reads of length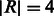

In the case of inversions, translocations and duplications, we can optionally avoid having the bubble branch length increase linearly with the size of the event, 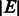, as follows. We create two branches for the two ends of the structural event of length 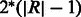centred around the two event boundaries. Reads that span across the original and the variant sequence boundaries will now map to these two branches. We do not include the event sequence interval 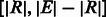, which is already present in either the forward or the reverse complement strand of the reference genome (depending on the type of the structural event). While saving space, the downside of this approach is the fact that reads from the original and the duplicate sequences will be mapped to the original sequence only, which complicates the assessment of the quality of the read mappings (e.g. a read should not be considered confidently mapped if it maps equally well to multiple positions), and other techniques have to be used to detect duplicated regions. These structural events were not included in our experiments, as they are not present in the Integrated Variant Set release (The 1000 Genomes Project Consortium, 2010) we used to construct the reference multi-genome.

Note that although augmenting the reference with indels and other structural variants allows us to easily handle these events during alignment, it does lead to an increase in the size of the reference string due to padding and, therefore, a higher memory overhead. However, by filtering out some rare branches, it is possible to trade-off some accuracy for a lower memory consumption.

3.2 Exact matching

In this section, we present the algorithm for exactly matching a read to the reference multi-genome. This algorithm is an extension of the BWT-based backwards search algorithm presented in Section 2.

Let represent one of the four A/C/T/G read bases and let 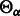be the subset of the IUPAC characters that can match with . We have: 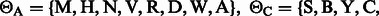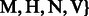, 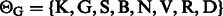and 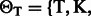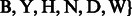. Also, let 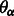represent an element of the set .

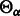Because each read base can match more than one IUPAC character, a given read R can match multiple different substrings in the reference multi-genome (e.g. R = AT will match the substrings AT, RW, AY and others) and, therefore, can align to more than one SA interval. Let 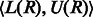represent the set of SA intervals that start with a substring that matches the read R. If R occurs in the reference, then it can be easily shown that:

(3)

where as before,

(4)

(5)

This result enables the iterative backward search for a read in the reference multi-genome. That is, we can start (as before) with the SA interval of an empty string, 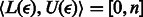, and then iteratively fetch a base from the end of the read re-calculating the SA interval set 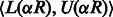using Equations (3)–(5) (here R refers to the partially assembled read). This procedure can be repeated until R equals the entire read. Note that if 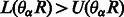, the SA interval is not valid and is discarded.

For clarity, we demonstrate the alignment of the read AT with the reference multi-genome RWYAYA (the SA and BWT for this reference were computed in Fig. 4). We start with the SA interval of the empty string, which is 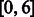. In the first iteration, we consider the last read base T. We calculate 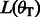and 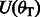for each of the eight characters in 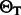. Using Equations (4) and (5), we get 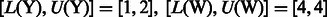and no matches for the remaining characters. Therefore, 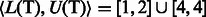. In the next iteration, we add A (the first base of the read) and calculate 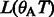and 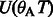for all 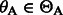. The final result 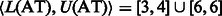can be easily verified.

To achieve reasonable performance, the number of SA intervals has to remain relatively small during alignment. An exponential increase in the number of SA intervals with respect to the length of the read is unacceptable. We have conducted a small experiment to track the number of SA intervals created during exact alignment with a human multi-genome. More specifically, we have created a reference multi-genome by combining the SNPs of 1092 individuals from the 1000 Genomes Project (The 1000 Genomes Project Consortium, 2010) with a popular reference genome (build GRCh37) and then aligned to it 10-K simulated reads of length 100 uniformly sampled from the reference multi-genome. Figure 7 illustrates the average and standard deviation of the number of SA intervals created in each iteration. As we can see, this value reaches its peak within the first 10 iterations and then dramatically drops to a small number. In other words, the majority of SA intervals are created in the first 12–14 iterations of the backwards search. Precalculating the SA intervals for all 12–14-base pair-long substrings can boost the performance. This speedup technique is discussed later in the article.

Fig. 7.

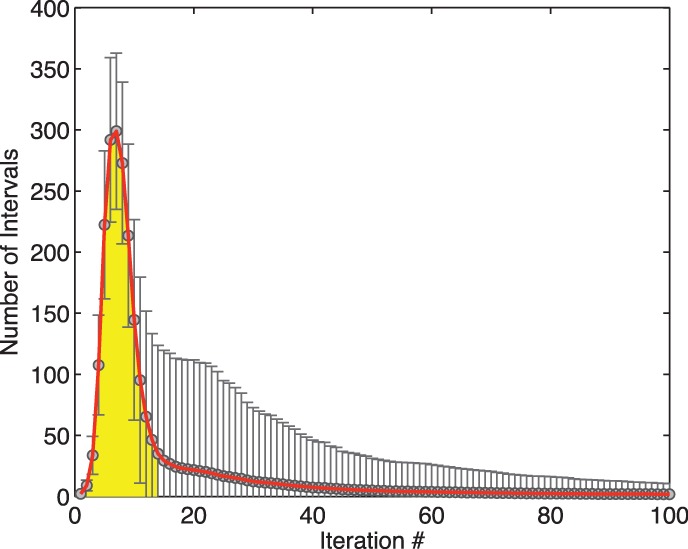
The average and standard deviation of the number of SA intervals generated per iteration during simulated read alignment on the reference multi-genome (averaged over 10K reads)

3.3 Inexact matching

To tolerate sequencing errors and other variations of the reads from the reference multi-genome, we have extended the exact-matching backwards search algorithm to allow mismatches and gaps. Figure 8 shows the high-level pseudo-code of the inexact matching algorithm used for aligning a given read R with the reference multi-genome G with up to n differences (mismatches or gaps). This algorithm is an extension of the inexact search algorithm used by BWA (Li and Durbin, 2009) and is guaranteed to find all the alignments with up to n differences. To handle mismatches and deletions in the read, we consider all the IUPAC characters of the reference multi-genome alphabet (except #) instead of just the set of characters that a given read base matches to exactly. After computing the new SA intervals for each of these characters, we advance the read position for matches/mismatches but not for deletions. To handle insertions, we just skip a given read position without recomputing the SA intervals. We can easily check whether a read base matches a given character by computing the binary AND(&) of the read base and the character Gray code values. The ambiguous base N is considered a mismatch (not shown for simplicity). By skipping #, we are able to avoid mapping across reference sub-sequence boundaries (e.g. chromosome and bubble branch boundaries) since, when the reference multi-genome is assembled into one string, all the subsequences are separated by # (current aligners operate on four-letter A/C/T/G alphabets and need to discard such alignments during post-processing).

Fig. 8.

Inexact matching algorithm. Returns the set of SA intervals of substrings of G matching R with up to n differences. All the auxiliary BWT structures are assumed to have been already pre-computed for G

We have adapted several heuristics from the existing BWA aligner (Li and Durbin, 2009) for reducing the search space and improving the performance of the alignment algorithm. In particular, given a read R, we compute a lower bound array, 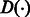, where 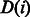is the lower bound on the number of differences of matching the substring 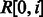with the reference. This lower bound is computed in 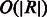time as described in (Li and Durbin, 2009). By replacing the first condition of the InexactMatch procedure with 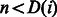, we can terminate the search earlier, if 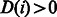. To reduce the search space further, this algorithm has also been modified to prune out alignments that are considered sub-optimal even though they might contain less than the maximum number of allowed differences. Similar to BWA, we use a minimum priority heap-like structure of partial alignments based on alignment score (instead of using recursion) that allows us to process the entries with the best score first. Depending on how many best hits are found and what is the best found difference, the search parameters are dynamically adjusted and the search can be terminated early. In particular, no sub-optimal alignments are explored if the number of best hits exceeds a given threshold. Furthermore, if the number of differences in the best hit, 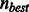, is less than n, then n is reset to 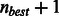. It is also possible to limit how many differences are allowed in the seed sequence (the first k base pairs at the beginning of the read, where k is the seed length and can be adjusted) and disallow insertions and deletions at the ends of the read. Other search parameters available to the users of BWA (e.g. mismatch, gap open and gap extension penalties) have also been incorporated to provide a similar user interface and improve the efficiency of the BWBBLE implementation.

Because the first 12–14 iterations account for a significant share of the computation time (see Fig. 7), we provide an option to precalculate the SA intervals resulting from exactly matching all possible k-length strings (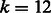 by default) with the given reference multi-genome. The inexact alignment process can then start at position 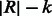of the read by looking up the result of mapping the last k read base pairs. Similar to the construction of the BWT structures, this computation is a one-time effort done prior to the alignment stage. We found the alignment to be six times faster with this setting when given 10-K 125-bp simulated reads and 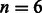. In terms of alignment results, this setting is equivalent to setting the seed length to k and allowing no differences in the seed, which does lead to a considerable decrease in the confidence and accuracy of the results depending on k.

3.4 Memory consumption

To reduce the memory requirement of the BWBBLE program, we compress the BWT string (using four bits to represent each of the 16 IUPAC characters) and only store a sampled subset of the auxiliary O and SA arrays, calculating the intermediate values as needed from the BWT string. More specifically, we only store the values 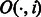and 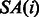where i is a multiple of the predefined interval sizes OCC_INTERVAL (default 128) and SA_INTERVAL (default 32), respectively. To obtain the 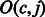value for a j that was not stored, we re-compute the number of times c occurs in the compressed BWT string after the closest available position. To calculate 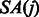that was not stored, we use the following relation between the suffix array SA and the inverse compressed suffix array 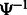(Grossi and Vitter, 2000): 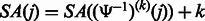, where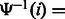 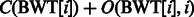and 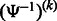means applying 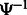k times. Therefore, we can repeatedly apply 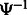until we obtain a position for which the SA value has been stored.

A similar memory reduction technique is also used by other aligners, such as BWA, SOAP2 and Bowtie. However, owing to the larger alphabet size of the reference multi-genome (16 IUPAC characters as opposed to four nucleotides), the memory requirement of the BWBBLE program is higher than that of the existing aligners. Because these aligners only operate on four nucleotides A/C/G/T, they only need two bits to store each character of the BWT string and only need to record the occurrence of four different characters at every position of the 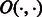array. Therefore, given a genome of size n, they only need 2 n bits to store the BWT string and 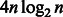bits to store the entire O array (for simplicity, we do not consider the reverse complement reference and the sampling of the O array here). On the other hand, BWBBLE needs 4 n bits to store the BWT string and 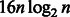bits to store the entire O array. By increasing the interval at which the O values are stored, it is possible to reduce the BWBBLE memory consumption; however, this would increase the time needed to recompute the intermediate O values during the alignment stage. The amount of 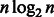bits needed to store the SA array (used in the post-alignment stage) is the same for all the aligners. It is also important to note that the length of the multi-genome reference is expected to be larger than the length of the single reference, as it includes bubbles as described in Section 3.1.2. However, the cost of storing the reference multi-genome index is much smaller than the cost of storing the index for each genome in the population separately.

4 RESULTS

4.1 Implementation

The BWBBLE aligner was implemented in C. The program performs the indexing of and short-read alignment with a reference multi-genome; for convenience, it also provides a separate (faster) mode for aligning to a single genome. Currently the program only supports alignment of single-end reads (paired-end alignment will be supported in the near future). The program accepts the reference genome in the standard FASTA file format and the reads in the FASTQ file format. The alignment results are reported using the SAM file format.

We provide a script to generate the FASTA file for the reference multi-genome. The script accepts a single-genome build (e.g. GRCh37) FASTA file and a set of VCF files with SNPs and indels to be incorporated into the reference multi-genome; it allows users to specify how many genomes to integrate, the minimum number of genomes a variation has to be present in to be integrated, the expected read size and others.

The BWBBLE program supports parallel execution for the alignment process. The code was parallelized using OpenMP by splitting the reads among the parallel threads. Furthermore, the program also uses the 128-bit registers of the Streaming SIMD Extensions to parallelize the character count in the compressed BWT string when retrieving occurrence values for positions at which they were not stored (see Section 3.4). BWBBLE is freely available at http://viq854.github.com/bwbble.

4.2 Experiments

To evaluate the performance of BWBBLE, we have created the reference multi-genome by combining the human genome build GRCh37 with the variants of 1090 individuals obtained from the October 2011 Integrated Variant Set release (The 1000 Genomes Project Consortium, 2010). Only variants occurring in three or more individuals were included. The resulting multi-genome reference incorporates 1 442 639 indels and 25 289 973 SNPs. The size of its FASTA file is 3.2 GB (as opposed to 2.8 GB for the single GRCh37 file).

We compared the performance of BWBBLE with the state-of-the-art BWT-based single-genome aligner, BWA (Li and Durbin, 2009). We evaluated BWBBLE against the multi-genome reference, while BWA was run against the single-genome build GRCh37. We ran BWA with its default parameters and used the same mapping quality threshold (namely, 10) to evaluate the confidence of the alignment results. Reads with a mapping quality score higher than the given threshold were considered confidently aligned. We compiled experimental results on simulated and real reads. The accuracy of the results on simulated read data sets was computed by finding the percentage of the confidently aligned reads that were mapped to their correct position in the reference (note: owing to the presence of bubble branches, more than one multi-genome position can be considered correct).

Furthermore, we also compared BWBBLE with the GCSA program (Siren et al., 2011) that performs indexing and short read alignment with a collection of multiple sequences.

All the experiments were performed on a 2.67 GHz Intel Xeon X5550 processor.

4.2.1 BWT index construction

To compute the suffix array SA, BWBBLE uses the sais library (Mori, 2008), which provides an implementation of the linear-time induced sorting SA construction algorithm (Nong et al., 2011), adapted to support a larger input text size. The BWT string can be easily computed from SA as described in Section 2. The total time taken by the BWBBLE program to construct the BWT string and the auxiliary C, O and SA arrays of the reference multi-genome was 4025 s (1.1 h). The BWA aligner took 4335.1 s (1.2 h) to index the GRCh37 genome.

4.2.2 Simulated read mapping

We have prepared two types of simulated reads using the wgsim program (https://github.com/lh3/wgsim). The first type of simulated reads, simR, was generated using the following standard wgsim parameters: sequencing base error rate = 2%, SNP mutation rate = 0.09% and indel mutation rate = 0.01%. To simulate the fact that in practice, we expect a set of reads to largely contain real known variants (rather than randomly generated SNPs), we have created two additional simulated read sets that incorporate known variants from two human genomes and have the wgsim mutation rate set to 0. In particular, the second type of simulated reads was created by combining the SNPs and indels from two human genome builds, NA18626 (a Han Chinese from Beijing, China) and HG00122 (a British from England and Scotland), with the GRCh37 build and the following wgsim parameters: sequencing base error rate = 2%, SNP mutation rate = 0% and indel mutation rate = 0%. These reads are referred to as simNA and simHG, respectively. The variations from these two human genome builds were not part of the 1090 individuals’ variants included into the reference multi-genome. Table 1 presents the simulated read results.

Table 1.

Evaluation on 100-K simulated reads of length 125 bp with at most differences

Program	Conf (%)	Err (%)	Time (s)
bwa-simR	93.1	0.06	100
bwbble-simR	92.9	0.05	11 295
bwa-simNA	92.7	0.09	110
bwbble-simNA	93.4	0.04	10 896
bwa-simHG	92.6	0.11	107
bwbble-simHG	93.3	0.06	10 892

Note: The percentage of confidently aligned reads (Conf), misaligned confident reads (Err) and sequential execution time of each program are reported.

4.2.3 Real read mapping

We used the two real read sets NA18626 and HG00122 sequenced by Illumina Genome Analyzer II and mapped to build GRCh37. Table 2 presents the real read evaluation results. Because the true mappings are not available for these datasets, only the alignment confidence results are shown.

Table 2.

Evaluation on 100-K real reads of length 108 bp with at most 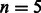differences

Program	Conf (%)	Time (s)
bwa-NA-108	78.3	109
bwbble-NA-108	79.5	9560
bwa-HG-108	90.5	90
bwbble-HG-108	90.4	6672

Note: The percentage of confidently aligned reads (Conf) and sequential execution time of each program are reported.

4.2.4 Comparison with GCSA

We compared BWBBLE with the GCSA program (Siren et al., 2011) that performs short read alignment with a collection of multiple sequences by building a prefix-sorted finite automaton from the multiple alignment of the sequences in the collection. GCSA constructs a generalized BWT-based index from the prefix-sorted automaton. This method has the theoretical advantage of not requiring additional branching due to SNPs during the backwards search, at the expense of the large amount of time and space required to build the index (the construction algorithm has exponential time and space complexity).

Owing to the high memory requirement of the prefix-sorted automaton construction, an external memory implementation is needed for the tool to run on a collection of human genomes, which is currently not ready. For consistency with the GCSA article, we conducted the experiments on the smaller sequence of a single human chromosome 18 and used a set of 1 M reads of length 56 (corresponding to 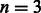differences) simulated using the wgsim program with the same parameters as simR.

The current GCSA implementation accepts as input the multiple alignment of the sequences in the collection; however, for a large number of sequences, the time and space required for creating the multiple sequence alignment using available software can be extremely large. To alleviate this problem, we have created a multiple alignment of the 1092 individuals manually by integrating only known SNPs from each individual, respectively, into chromosome 18 of GRCh37; the optimal multiple alignment is trivial for this scenario. We have also created a reference multi-genome with SNPs only from the 1092 individuals for BWBBLE. The GCSA index construction took 1.87 h, whereas the BWBBLE index construction took 48 s.

Similar to the experiments in the GCSA article, we compared the running time and number of mapped reads for the two programs: GCSA accuracy and confidence cannot be evaluated because the position of mapped reads in the reference sequence is not reported. The following results were obtained for the two tools: GCSA: (find operation only) 8932.93 s/98 307 matches; BWBBLE: 8439.21 s/94 364 matches. GCSA finds more hits, although this does not imply that these matches are biologically plausible. For example, the authors mention that they ‘have no limits on gaps’, which could result in some implausible read mappings. Without being able to evaluate the quality of the reported matches, it is difficult to assess their significance. As expected, the number of exact matches was similar for both tools: GCSA: 15 226 matches; BWBBLE: 15 268 matches.

5 DISCUSSION

Because, in practice, the number of differences (mutations and sequencing errors) between a 125-bp read and a single-genome reference is usually smaller than the BWA default of 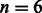differences, the BWA aligner is able to map most of the reads in the dataset, achieving high confidence and accuracy results. However, on most datasets, the BWBBLE aligner does achieve slightly better confidence and accuracy values. Because BWBBLE does not treat as mismatches the deviations from GRCh37 that are known SNPs, it can align reads that have more than n differences from GRCh37 when some of these differences are the SNPs included into the multi-genome reference. Furthermore, because indels are incorporated by appending the bubble branches (with no restrictions on their length), BWBBLE can align reads that span known indels of any length (while BWA with default parameters can only handle indels up to length 6). Therefore, BWBBLE can be expected to perform better on read sets that span a greater number of large indels or regions with a high SNP count (e.g. reads from species that have a higher SNP density than humans; Tenaillon et al., 2001). Zooming in on the evaluation results of the 100-K simNA dataset, we get the following performance counts: BWA (4332 unaligned, 92 735 confident, 92 645 correct); BWBBLE (3330 unaligned, 93 412 confident, 93 375 correct). Out of the 4332 reads unaligned by BWA, 973 are confidently mapped by BWBBLE—out of which 933 are correctly aligned (with 134 reads aligned to appended bubble branches) and 40 are misaligned. Figure 9 shows an example of a read mapped to a long indel and a read mapped to a region with a high concentration of SNPs (both of these reads were unaligned by BWA and correctly aligned by BWBBLE). Note that because appending indels as bubble branches does not (by itself) require a change in the BWT backwards search algorithm, existing aligners (e.g. BWA) could use this technique to handle longer indels without a substantial modification to their code. Furthermore, out of the 406 reads confidently aligned by BWA but not considered confident matches by BWBBLE, 376 were correctly aligned. For 380 of these 406 reads BWBBLE found more than one best match and for the remaining reads it found too many sub-optimal matches. Duplicated regions in the single-genome reference that have a few additional mutations will be likely aligned to with a different score by BWA and not treated as repeats. However, if the mutations occurring in the repeats are only present in the subset of the population, they will be captured as SNPs in the multi-genome reference and can be aligned to with the same score by BWBBLE.

Fig. 9.

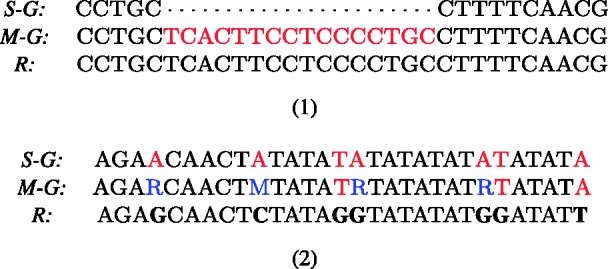
(1) Read R from the simNA dataset unaligned to the single-genome reference S-G by BWA (with default parameters BWA can handle indels up to length 6) and correctly mapped to a bubble branch representing an insertion of 16 bp in the multi-genome reference M-G using BWBBLE. (2) Read R from the simNA dataset unaligned to the single-genome reference S-G by BWA and correctly aligned using BWBBLE. The mismatches between the read and the references are shown in red (for BWA this number exceeds the allowed six differences); the SNPs in the M-G that match the read bases are shown in blue (these SNPs are treated as matches). (Note: only the relevant portions of the read and references are shown.)

The alignment algorithm is entirely memory bound, and its running time is dominated by the random memory access patterns of the sampled occurrence array and the compressed BWT string during the SA interval computation. Owing to the 4-fold increase in the size of the reference multi-genome alphabet, the BWBBLE program performs many more SA interval computations, which causes its running time to be significantly slower. Namely, for each read base, the suffix array interval is computed for 16 (rather than four) different characters while differences (mismatches/gaps) are still allowed and for eight different characters when only exact matching is allowed (an optimization used when the n differences have already been used up). In particular, 188 826 valid SA intervals per read are found on average when aligning to the reference multi-genome during the inexact matching stage only (i.e. while differences are allowed), as opposed to 8825 valid SA intervals for the single-genome reference alignment. For the 100-K read set, this is 18 billion more SA intervals (note: this figure does not include the additional SA interval computations that did not result in a valid interval and the SA intervals computed during the exact matching stage only).

However, although the runtime cost of aligning with a reference multi-genome is very high, it is still significantly lower than the cost of aligning to each genome in the population separately. For example, it would take about 109 200 s to align 100-K reads to 1092 genomes using BWA, and this time will grow linearly with the size of the genome collection. On the other hand, while the BWBBLE running time does depend on the number of SNPs in the reference multi-genome, we expect that the SNP count (and the program performance) will not increase linearly with the number of genomes compiled into the multi-genome reference. This can be seen in Figure 10 that shows how the BWBBLE runtime changes as the number of genomes incorporated into the multi-genome reference grows. Therefore, as the number of available genomes gets significantly larger, the speed-up of aligning with BWBBLE as opposed to each genome individually will also be significantly greater.

Fig. 10.

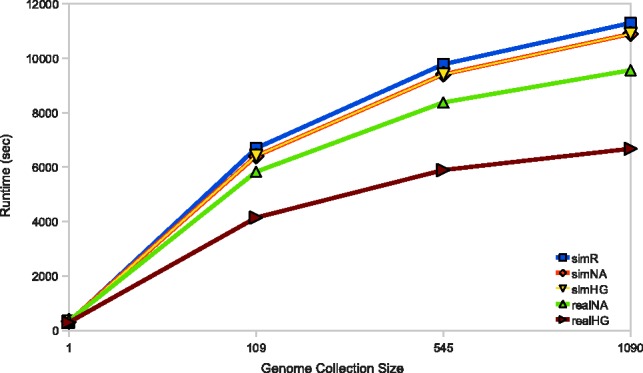
BWBBLE running time vs. genome collection size. The performance is shown for each simulated and real read dataset. The results for the following number of incorporated genomes are shown: 1109 (12 646 424 SNPs), 545 (23 271 932 SNPs) and 1090 (28 929 053 SNPs)

Because BWBBLE runs on a multi-genome almost 100 times slower than BWA on a single genome, it is interesting to compute how many additional reads BWA can align in the same time frame to the genomes in the database (although when aligning to each reference separately, additional effort will have to be spent combining and interpreting the results). To perform this experiment, we have created 99 genomes in addition to GRCh37 (100 genomes total) and aligned the simR, simNA, simHG, NA18626 and HG00122 read sets using BWA with each of these genomes individually. More specifically, each genome was created by adding its known variants on top of build GRCh37. 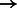The number of reads aligned has increased for each read set as follows: simR: 95 954 95 961; simNA: 95 668 96 655; simHG: 95 619 96 656; NA18626: 81 264 81 594; HG00122: 93 931 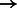94 065. BWBBLE aligned the following number of reads to the original 1090 individuals multi-genome and the 99 individuals multi-genome (note: no rare variant filtering was performed for this reference), respectively: simR: (96 252; 96 283); simNA: (96 670; 96 633); simHG: (96 647; 96 641); NA18626: (81 627; 81 598); HG00122: (93 720; 93 713). As expected, BWA (and BWBBLE on the 99 individuals multi-genome) aligned most of the same reads that BWBBLE aligned to the 1090 multi-genome, as many of the variants can be expected to be present in these 100 genomes.

6 CONCLUSION

In this article, we proposed a compact representation for a collection of genomes (the reference multi-genome) that captures the genomic variations in the collection and presented BWBBLE, a BWT-based short-read aligner that operates on this compiled reference. We demonstrated the performance of BWBBLE on a human reference multi-genome incorporating variants from 1090 individuals. A limitation of our reference multi-genome representation is its use of read length dependent padding to capture structural variants, which to achieve best results necessitates multiple reference indices to be built for each particular read length. In addition, padding can also cause a significant increase in the length of the reference for highly variable species.

Although aligning to the reference multi-genome is much slower than to a single genome, it is considerably more efficient than aligning to each genome in a large collection separately. As the number of sequenced genomes grows, aligning with BWBBLE should become much more time and space efficient. Moreover, because BWBBLE can align reads that span long (known) indels, its utility will increase once large databases of structural variants are available. BWBBLE can also be useful in functional genomics assays of parent/offspring trios, where unbiased peak calling is desired (Goncalves et al., 2012). Finally, BWBBLE can output important information about the SNPs and structural variations that a given read was mapped to (e.g. the number of genomes in the collection that contain this particular variation), which should simplify and improve the current post-alignment processing pipeline.

APPENDIX

Let E = the total expected number of SA intervals; 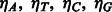= the occurrence percentage of the four nucleotides in the genome; 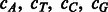= the number of separate SA intervals associated with each of the four nucleotides. We have:

and we need to show that E is minimized with the four-bit Gray code .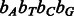

Let’s assume that all 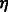’s are equal (this assumption will be lifted later). Without loss of generality, we rename all c’s to be 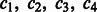and assume 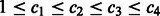. As mentioned in Section 3.1.1, the four-bit Gray code leads to 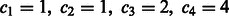. To demonstrate that the Gray code results in the minimized E, we will disproof the existence of the following two cases: (i) 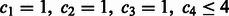and (ii) .

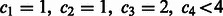Proof: —

We represent an IUPAC symbol with four features, each for an A/C/G/T base. The feature associated with base is denoted by if base can match this IUPAC character, and it is denoted by if base does not match this character. The ‘don’t care’ features are omitted. For instance, the IUPAC symbols that match base but do not match have the features .

Case (i) —

Suppose an order with exists. Define = the smallest IUPAC symbol in this order. Because , the IUPAC symbols with features and the symbols with are consecutive in . Similarly, because we have , the symbols with and those with are also consecutive. With these two constraints, we assign – to the symbols with – to the codes with , and – to the symbols with features , where . To meet the requirement of , we need to assign – to the symbols with and . A value j that meets this demand does not exist and therefore we reach a contradiction.

Case (ii) —

To make , we need to assign – and – to the IUPAC symbols with , where . Without loss of generality, let be 0. Thus, to guarantee that all 16 IUPAC codes represent distinct subsets of four bases, for any k we know that and must have opposite features for base ; that is, one is while the other one must be . The only assignment that makes is assigning – to the symbols with the feature for all . In any order, cannot be smaller than four.

In the context of the human genome, the nucleotides A and T occur more frequently than C and G. In other words, . With the nucleotide-to-bit assignment , we have . The expected SA interval number can be rewritten as:

Switching any two values in the c’s assignment will result in the increment of the E value. Therefore, this assignment is the optimal solution for this problem. □