Skip to main content
PMC home page
Bioinformatics logoLink to Bioinformatics
. 2013 Jun 19;29(13):i9–i17. doi: 10.1093/bioinformatics/btt222

A high-throughput framework to detect synapses in electron microscopy images

Saket Navlakha 1, Joseph Suhan 2, Alison L Barth 2,3, Ziv Bar-Joseph 1,*
PMCID: PMC3694654  PMID: 23813014

Abstract

Motivation: Synaptic connections underlie learning and memory in the brain and are dynamically formed and eliminated during development and in response to stimuli. Quantifying changes in overall density and strength of synapses is an important pre-requisite for studying connectivity and plasticity in these cases or in diseased conditions. Unfortunately, most techniques to detect such changes are either low-throughput (e.g. electrophysiology), prone to error and difficult to automate (e.g. standard electron microscopy) or too coarse (e.g. magnetic resonance imaging) to provide accurate and large-scale measurements.

Results: To facilitate high-throughput analyses, we used a 50-year-old experimental technique to selectively stain for synapses in electron microscopy images, and we developed a machine-learning framework to automatically detect synapses in these images. To validate our method, we experimentally imaged brain tissue of the somatosensory cortex in six mice. We detected thousands of synapses in these images and demonstrate the accuracy of our approach using cross-validation with manually labeled data and by comparing against existing algorithms and against tools that process standard electron microscopy images. We also used a semi-supervised algorithm that leverages unlabeled data to overcome sample heterogeneity and improve performance. Our algorithms are highly efficient and scalable and are freely available for others to use.

Availability: Code is available at http://www.cs.cmu.edu/∼saketn/detect_synapses/

Contact: zivbj@cs.cmu.edu

1 INTRODUCTION

The mammalian brain can contain hundreds of millions of neurons, each with thousands of specialized connections called synapses that enable indirect communication between cells. Estimates for the number of synapses in the mammalian brain ranges into the trillions. Synapses are essential for the transfer of information across neuronal ensembles, and individual synapses can be modulated by patterns of incoming neural activity, a phenomenon thought to underlie learning and memory.

Changes in the relative strength and number of synapses can be regulated by a myriad of factors, including developmental age (Cowan et al., 1984; Huttenlocher and Dabholkar, 1997; Stoneham et al., 2010), sensory experience (Klintsova and Greenough, 1999), drug addiction (Van den Oever et al., 2012), estrus cycle (Cooke and Woolley, 2005) and brain pathology. For example, in a form of autism linked to mutation of the Fragile X gene, spine density in the neocortex is elevated (Hinton et al., 1991; Pfeiffer and Huber, 2009), a feature that has also been observed in mice carrying the same genetic mutation (Nimchinsky et al., 2001). Rett syndrome, another neurodevelopmental disorder, is characterized by smaller brain size caused by deficits in synaptogenesis (Glaze, 2004; Johnston et al., 2005; Na and Monteggia, 2011) that results in fewer spines. Similarly, in Alzheimer’s disease and other dementias, cognitive deficits are associated with reduced synapse density in the hippocampus, a brain structure critical for learning (Clare et al., 2010). Understanding how connectivity across neurons can change is thus an important question that drives contemporary neuroscience research.

Because synapse distribution is a useful and diagnostic criterion to evaluate circuit function in learning and disease, there have been a variety of methods used to estimate synaptic connectivity or overall synapse numbers. Electrophysiological methods to estimate connectivity and the number of inputs per cell can be informative (e.g. Lefort et al., 2009; Yassin et al., 2010), but these approaches are low-throughput and can typically only capture tens or hundreds of connections in reasonable amounts of time (Walz, 2007). MRI-based techniques can be used to study network function at the level of brain regions or voxels, but they do not provide enough spatial resolution to estimate neural connectivity (Sporns, 2010). Anatomically, synapse densities are measured via light-microscopy to identify specialized substructures called spines that stud the dendrites of neurons or using electron microscopy (EM) to identify ultrastructural features that correspond to pre- and post-synaptic elements. Traditional approaches have used cumbersome manual detection to count synapses in these images (e.g. White et al., 1986; Knott et al., 2002; da Costa et al., 2009; Morshedi et al., 2009) and were thus constrained to small-scale measurements or required the use of specialized transgenic animals (Feng et al., 2012; Kim et al., 2012) limiting their usage for studying plasticity and development in wild-type mice.

Since the early 1990s, bioimage informatics has emerged as an important area in the analysis of biological images (Peng, 2008). Imaging datasets are usually much larger than other high-throughput biological datasets (e.g. confocal microscopy data can range in the hundreds of gigabytes for a single imaging session). Accurately identifying elements of interest (molecules, cells, synapses, etc.) within these massive datasets requires the development of sophisticated and efficient computational models. This often involves a classification-based strategy in which a (small) manually labeled training set is used to learn a general model that can be used to analyze a larger collection of images automatically. The key computational challenges involve the reliability and speed at which the analysis is done, as well as dealing with the heterogeneity of biological structures and noise present in each image. Electron microscopy data suffer particularly from these problems and often contain undesired variation in intensity and contrast within and across samples and preparations. This presents a major computational challenge because model parameters learned from one sample may not generalize to other samples. Although reconstruction and segmentation of conventional EM images has helped answer important questions about brain structure and function (Bock et al., 2011; Denk et al., 2012), these approaches have yet to reach the point of full automation (Merchan-Perez et al., 2009; Jain et al., 2010; Cardona et al., 2012), which has limited their scale and accuracy (Kreshuk et al., 2011; Morales et al., 2011).

2 APPROACH

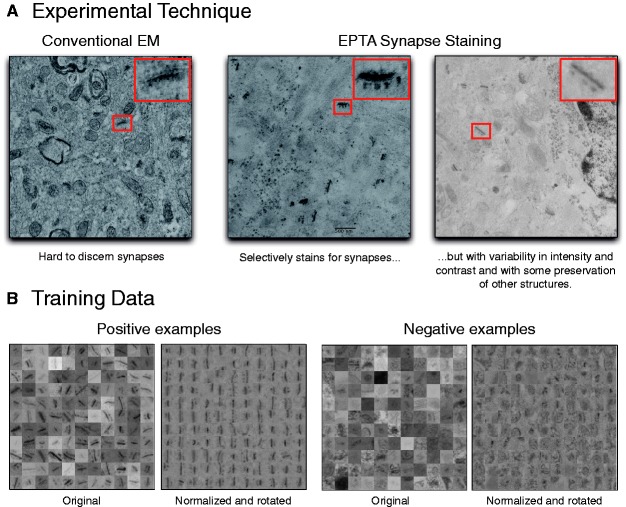
To aid in identifying and quantifying synapses in EM images, we used a 50-year-old experimental technique (Bloom and Aghajanian, 1966, 1968) to selectively stain for synapses in any animal model (Fig. 1A). Unlike conventional EM, this protocol uses ethanolic phosphotungstic acid (EPTA) to pronounce electron opacity at synaptic sites by targeting specific proteins in contact zones. This technique typically leaves non-synaptic membranes (e.g. plasma membranes, neurotubules and vesicles) unstained, though considerable variation can exist from sample to sample. We dissected brain tissue in the mouse somatosensory cortex and performed EM experiments using the EPTA method. We used mice from different ages (P14, P17 and P75) and isolated the same cortical region in each animal to gauge variance in sample quality.

Fig. 1.

Fig. 1.

Open in a new tab

Experimental technique and training data collected. (A) Comparison of conventional and EPTA-stained EM images shows a marked difference in clarity of synaptic structures, albeit high sample-to-sample variability. (B) Subset of positive and negative examples taken from multiple images across all samples. The original examples exhibit high variance and noise; normalization and alignment reduces this heterogeneity

To demonstrate the advantages of this protocol for large-scale synapse identification, we developed a machine-learning framework to detect synapses in these images in a high-throughput and fully-automated manner. We describe a two-step approach. First, we use a highly accurate first-pass filtration step to reduce the search space of possible synapses by 1–2 orders of magnitude, thereby significantly reducing false positives. Second, we train a classifier to recognize synapses using texture- and shape-based features extracted from small image patches around potential objects of interest. We show that our approach is highly accurate and that it outperforms correlation-based (Roseman, 2004) techniques and an automated technique designed to detect synapses in conventional EM images (Morales et al., 2011).

To further improve classification and adjust for varying experimental conditions (different sample, different microscope, different person performing experiments, etc.), we developed a model that classifies synapses in images using both labeled and unlabeled data. This type of approach is known as semi-supervised learning (Zhu, 2005), as it combines ideas from supervised learning (classification) and unsupervised learning (clustering). This technique can be used to build more robust classifiers in cases (such as ours) where large imaging datasets can easily be collected but where it is much harder to manually annotate these images. By integrating unlabeled data in the learning phase, a new sample can help fine-tune parameters of a model built from a previous sample, which can improve accuracy without requiring users to manually annotate images in the new sample. Indeed, we show that a classifier learned only on labeled data from our P14 samples and tested on our P75 samples performs worse than a semi-supervised classifier that also leverages unlabeled data from P75.

3 METHODS

First, we describe the experiments we performed to gather and process mouse brain tissue for EM imaging with EPTA, and then we describe our machine-learning framework to automatically detect synapses in these images.

3.1 Experimental approach and data collected

We gathered tissue from the mouse somatosensory cortex because it is a well-characterized anatomical area in the cortex (Fox, 2008) and thus serves as an important benchmark for the validity of our experimental approach. To prepare the tissue for EM analysis, we extracted, fixed (using 2.5% glutaraldehyde buffered with phosphate buffered saline) and sectioned 50-µm thick tissue from wild-type C57bl6 mice at ages P14, P17 and P75 with two animals per time point. This range of tissue was collected to determine whether our experimental procedure and subsequent computational analysis remained robust to natural variation in tissue samples within and across time points and to variation in the image acquisition process. Each mouse whisker is somatotopically mapped to a single neocortical column. To ensure that the same cortical region was identified in each sample, we applied a mitochondrial stain (cytochrome oxidase) to each section to visually identify layer 4 (called the barrel) of the D1 column/whisker. The barrel was extracted using a dissecting light microscope.

Tissue was prepared for transmission electron microscopy in a series of steps. First, the tissue was washed with three changes (5 min each) of distilled water, followed by an incubation in 0.02% NaOH for 10 min. This latter step was absent from the original procedure of Bloom and Aghajanian (1966, 1968), but we found that it helped increase the contrast of synapses (Fig. 1). Second, the tissue was dehydrated with an ascending series of EtOH (25, 50, 70, 80, 90 and 100%), followed by fixation with 1% phosphotungstic acid (PTA) in 100% EtOH. Third, a small amount, 7 µl, of 95% ethanol, was added to each 1000 µl of PTA stain used, and the PTA was washed from the sample with two changes of 100% ethanol. Fourth, propylene oxide was used as a transitional solvent (the first change of propylene oxide was on ice), and then the specimen was infiltrated with Spurr embedding resin, which was polymerized at 60°C for 48 h. Finally, 100 nm sections were cut using a diamond knife on an ultramicrotome, which were picked up using 50 or 75 mesh copper grids. The specimen was observed using a transmission electron microscope, and images were taken digitally.

We took roughly 130 images per animal (each image is of size 5 µm by 5 µm) covering a total surface area of ∼3000 µm2 per sample and with a total of six samples (see Supplementary Information for additional details about image acquisition). Images were taken from a single plane, and therefore no correction was necessary to account for double-counting synapses across serially sectioned images. There was significant sample-to-sample variability in the images, but synapses were typically dark with most other biological structures washed away (Fig. 1A). In total, we collected >800 images each containing between 0 and 12 synapses. The raw images were provided as input to the machine-learning algorithms described later in the text.

3.2 Strategies for effectively detecting synapses

As described earlier in the text, electron microscopy images are inherently noisy owing to variations in the samples (e.g. different age), in the manual processing steps and in the image acquisition process. To overcome these issues, we developed a pipeline that uses object segmentation, background information, normalization and alignment to obtain a better feature set that can be used for effective classification.

1. Reducing the search space of possible synapses via segmentation

One popular technique to search for objects in an image is the sliding window approach (Szeliski, 2010). In this approach, non-overlapping windows of a pre-defined size are slid across the image, and each window is classified as synapse-containing (positive) or not (negative). One drawback to this technique is that it can double-count synapses that lie in multiple windows or miss synapses that lie adjacent to each other. A more thorough approach is to use overlapping windows, but this greatly increases computational complexity when using large images, and subsequent post-processing steps still need to account for double-counting synapses. Further, this technique creates a large imbalance of negative-to-positive examples (windows), which may lead to many false positive predictions.

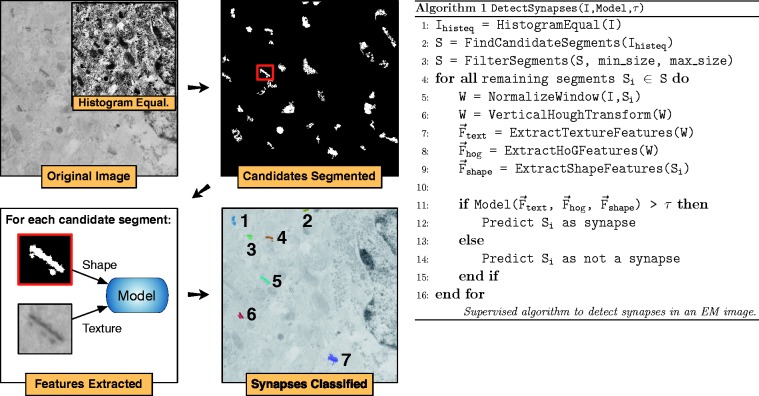
To circumvent these problems, instead of using sliding windows, we apply a filtration step to reduce the number of windows to test by leveraging the fact that the experimental procedure outlined earlier in the text is designed specifically to stain synapses (there may be other biological structures, such as mitochondria and membranes, that also appear in the image, but rarely are there synapses that do not appear as dark). To avoid the challenge of selecting thresholds to segment the image (which may not generalize across samples owing to differences in intensity and enhancement), we adopt the contrast-limiting adaptive histogram equalization algorithm (Zuiderveld, 1994). This method enhances the contrast of each window T in the image to approximately match a flattened histogram by mapping each pixel value 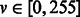Inline graphic to its value in the cumulative distribution f(v) computed in T:

graphic file with name btt222m1.jpg (1)

where Inline graphic represents the original histogram of the image and n is the number of pixels in the window. We also limit the enhancement by clipping the histogram at a scalar value of 0.20 before enhancement. The window is then rescaled to [0,255]. The equalization is performed in each local window of the image, and then the windows are combined using bilinear interpolation to eliminate artificially induced boundaries. By only considering small windows of the image, this technique prevents the overamplification of noise or artifacts that only appear in localized regions of the image.

Next, we binarize the equalized image using a single, sample-independent threshold, which was determined manually to be 10% (i.e. only the top 10% of pixels values are kept). The final segmentation is produced by computing connected components (segments) in the binary image. Compared with a non-overlapping sliding window approach that would produce roughly 300 windows to test per 1016 × 1024-sized pixel image on average, our segmentation produces 25–35 candidate segments per image and an overall ratio of negative-to-positive examples of 9:1. We also allow for optional filtration of segments that are too small or too large to be synapses, as defined by the user. This step is only designed to produce segments and not to normalize the image, which we do separately later in the text.

To validate that the segmentation step preserves synapses, we looked at two samples (P14 and P75) and manually checked what percentage of the first 100 synapses encountered were correctly segmented. We found that only 1% (1 in each sample) of the synapses were lost, and these were always due to two synapses touching each other, which caused them to be merged into a single segment.

2. Using background cues to augment synapse identification

One key indicator to decide whether a candidate segment is a synapse is the physical context in which it lies. We consider a local 75 × 75-pixel window around the centroid of each segment to capture information about the object and the neighborhood surrounding the object. This is important because elongated synapse-like segments may also appear within mitochondria, but such segments are always surrounded by an oval-like contour marking the boundary of the mitochondria, which can be a useful cue for classification. Similarly, dark circular spots in the nucleus may also be stained (see Fig. 1A), but their neighborhoods typically contain other such spots, which also serve as strong discriminators. These are not steadfast rules (synapses can certainly lie adjacent to mitochondria), but local neighborhoods are nonetheless a strong visual cue used by EM experts when annotating images (Arbelaez et al., 2011).

3. Handling experimental variation across samples

The aforementioned technique produces a set of windows (in which each candidate segment is embedded), but the actual pixel values within these windows may vary significantly from sample-to-sample and image-to-image. Figure 1B exemplifies the discrepancy that can exist across both negative and positive examples in the original images. These issues may be caused by a variety of factors (e.g. consistency of chemical reactions during sample preparation, age of the sample, skill of the experimenter, differential illumination in the microscope, etc.) that are extremely difficult to overcome experimentally and thus must be accounted for computationally. To reduce the effect of these differences, we normalize each candidate window W by computing (Arbelaez et al., 2011): 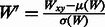Inline graphic, where Wxy is the current value at pixel (x,y) and μ and σ are the mean and standard deviation of the pixel intensities in W. Figure 1B shows that this significantly reduces the variance across windows, which helps features dependent on pixel intensities to be compared in an equal setting.

3. Adjusting for synapse heterogeneity

Synapses in EM images may be angled at any 2D orientation, which may add undesirable variation in training examples. To create a more invariant set of synapses, we applied the generalized Hough transformation (Duda and Hart, 1972) to automatically rotate the segment (within the candidate window) such that its major axis points vertically. Briefly, this is done by computing the Hough transform matrix 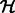Inline graphic, where entry i,j of 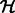Inline graphic corresponds to the number of points in the segment that fall along a line parameterized in polar coordinates as 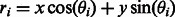Inline graphic. 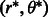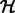We find the element Inline graphic in Inline graphic that corresponds to the (peak) line for which the most segment points lie. The corresponding 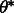Inline graphic is used to compute the angle of rotation. We then cropped the image to 60 × 60 pixels to remove the effects of the interpolation (this size is still large enough to fit almost all synapses). The outcome (Fig. 1B) shows much greater uniformity for both synapses and non-synaptic structures compared with the original images.

3.3 Supervised learning framework and features used to detect synapses

After the processing steps aforementioned, each image is reduced to a set of candidate segments defined by a (normalized and aligned) square window around the centroid of the segment. Next, we build an accurate and robust classifier to discriminate between positive (synapses) and negative candidates using texture- and shape-based features.

Texture is a common cue used by humans when manually segmenting structures from electron micrographs, and its use has become popular in many image processing tasks today (Arbelaez et al., 2011; Varma and Zisserman, 2003). In their seminal article, Leung and Malik (2001) defined texture by convolving an image with a bank of 48 Gaussian filters and used the filter responses at each image location to define a ‘texton’. Textons were clustered and used to represent and classify images in a reduced dimension. Recently, more effective filter banks have been proposed to represent texture based on modeling joint distributions of intensity values over small and compact neighborhoods of the image (as opposed to the entire image), an approach we also adopt here.

The maximum response (MR8) is one such technique that is derived from a set of 38 filters: 6 orientations × 3 scales × 2 oriented filters + 2 isotropic filters. By recording only the maximum response across orientations, the number of responses is reduced to 8 (Varma and Zisserman, 2003). Each pixel is now represented as an 8D vector of responses at its (x, y) location. For each dimension d, we compute a normalized histogram with 17 bins (larger bin sizes yielded marginal gain in performance but increased computational complexity) composed of responses for d over all pixels in the window. Thus, the texture of the window is represented as a 8 × 17-sized vector in 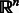Inline graphic. We used the default parameters for MR8 (Varma and Zisserman, 2003).

Synapses also have a characteristic shape (typically long and elongated) that we also attempt to capture by extracting the following 10 shape descriptors for each segment. These features operate on the binary segment only (they ignore the intensity values of the pixels) and therefore contribute different information than texture alone.

  1. Area: the number of pixels in the segment.

  2. Perimeter: the number of pixels in the boundary of the segment.

  3. Major axis: the number of pixels constituting the major axis of the ellipse that has the same normalized second central moments (covariance) as the segment.

  4. Minor axis: same as above but for the minor axis of the ellipse.

  5. Orientation: the angle between the x-axis and the major axis of the ellipse.

  6. Eccentricity: the ratio of the distance between the foci of the ellipse and its major axis length.

  7. Convex area: the number of pixels in the convex hull of the segment.

  8. Solidity: the proportion of pixels in the convex hull that are also in the segment.

  9. Diameter: the diameter of the circle with the same area as the segment.

  10. Extent: the ratio of pixels in the segment to pixels in the smallest bounding box of the segment.

The final feature we use is the histogram of oriented gradients (HoG) descriptor proposed by Dalal and Triggs (2005). We used nine orientation bins, cell and block sizes of 10 × 10 and 6 × 6, respectively, and a value of 0.2 for clipping the L2-norm. Intuitively, this 334D feature describes the appearance of an object by concatenating the distributions of intensity gradients (edge directions) in different subregions of the window. This descriptor has been shown to outperform other popular feature sets (e.g. PCA-SIFT and generalized Haar wavelets) in a variety of object detection tasks (Dalal and Triggs, 2005; Skibbe et al., 2011). In total, each window is represented by a 480D feature vector in 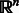Inline graphic. All features are scaled to lie in [0, 1].

These features were then used to build a support vector machine (SVM) classifier (Chang and Lin, 2011) using a radial basis function kernel, and we performed a grid search to optimize parameters of the model. We also learned a Random Forest (Breiman, 2001) classifier and an AdaBoost ensemble model (Freund and Schapire, 1995) using 100 trees/learners, respectively. An overview of the supervised algorithm is shown in Figure 2.

Fig. 2.

Fig. 2.

Open in a new tab

Main steps of the supervised synapse-detection algorithm and corresponding pseudocode. High-contrast objects are automatically segmented using histogram equalization. Shape-based features are extracted from these objects, as well as texture-based features from a small window surrounding the object. A model is learned from these two features types and is used to classify synapses

3.4 Semi-supervised learning

The supervised algorithm described earlier in the text only uses labeled data to train a classifier. We now show how unlabeled data can be used to further improve the classifier using co-training. The co-training algorithm (Blum and Mitchell, 1998) assumes that features can be split into two different and fairly independent sets (in our case, texture and shape). Blum and Mitchell (1998) proved that for a classification problem with two such feature sets, the target concept can be learned based on a few labeled and many unlabeled examples, provided that the views are compatible and uncorrelated. The compatibility condition requires that all examples are identically labeled by the two classifiers (one for each of the feature sets). The uncorrelated condition means that for any pair of features, the two sets of features are independent, given the label. In real applications, these two conditions are rarely satisfied simultaneously. For example, in our task, compatibility may be hindered due to noise and imaging artifacts. Still, co-training has proven useful in several real-world applications (Zhu, 2005).

In a co-training algorithm, two separate classifiers are trained with the labeled data using the two subfeature sets, respectively. Each classifier is applied to the unlabeled examples, and it outputs a list of positive (putative synapses) and negative examples, ranked by confidence of assignments. We consider all the predictions in each list above a given threshold and any example for which both independent classifiers agree on its label is added to the labeled dataset. We iterate this process once and then retrain a final single classifier using all features from the original set of labeled examples and the new (predicted) set of labeled examples obtained during this iterative process.

In addition to our attempts to normalize each image, this approach provides another way to account for variability in never-before-seen samples without requiring explicit annotation, which can be cumbersome to obtain in practice.

3.5 Testing and comparing with other approaches

For experiments using supervised learning, we manually labeled 11% (59) of the 520 images from P14 and P75 distributed equally across each sample. To do so, we performed the first-pass segmentation described earlier in the text and labeled the resulting windows (segments) as positive or negative. A total of 230 synapses were identified (each showing a clear post-synaptic density and elongated shape) along with 2062 negative examples. The MR8, HoG and shape descriptors were extracted from each example and stored as a 480D feature vector. We performed 10-fold cross-validation and report precision, recall and area under the ROC and precision-recall curves. The confidence in each prediction was measured based on the distance from the test vector to the decision boundary in feature space (for SVM) and based on the proportion of tree agreements for the Random Forest classifier. For supervised learning, we did not use any unlabeled data.

For the semi-supervised approach, we selected all the labeled images from one sample (sample A, e.g. P14) and trained two classifiers using texture and shape features, respectively. Each classifier was then applied to the 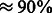Inline graphic of unlabeled images in sample B (P75), and all predictions in either the positive or negative set in which both classifiers agreed (i.e. both predicted the same label with confidence above a given threshold) were added to the training set. A new single classifier 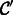Inline graphic was then built using the known labeled examples from sample A as well as the high-confidence examples predicted by the co-trained classifiers. We also learned a baseline classifier Inline graphic that was only trained on the known labels from sample A. Both classifiers were then tested for accuracy on the true labeled examples from sample B.

We compared our supervised approach against a correlation-based technique (Roseman, 2004) that classifies a test window W as synapse-containing with respect to training set T if 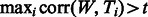Inline graphic; i.e. if the correlation coefficient between W and any positive example in the training set is 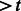Inline graphic, where 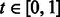Inline graphic. We also compare against Espina (Morales et al., 2011), a tool designed to detect synapses in conventional EM images (see Supplementary Information).

4 RESULTS AND DISCUSSION

4.1 Validating against conventional EM

One potential concern with using the EPTA method is that some synapses may be washed away alongside other non-synaptic structures. To validate the correctness of our experimental procedure, we tested whether EPTA-stained images preserve roughly the same density of synapses that appear in conventional EM images of the same region. First, we isolated tissue corresponding to the D2 barrel of the mouse somatosensory cortex at P75. In one hemisphere, we performed standard EM chemistry and in the other hemisphere, we applied our EPTA stain. We then asked an expert EM biologist (J.S.) and an expert neuroscientist (A.L.B.) to manually annotate 26 conventional EM images for high- and medium-confidence synapses, and we compared density ratios versus our automated algorithm on the EPTA-stained tissue.

EPTA appears to conserve synaptic density compared with conventional EM (Table 1). In particular, the two experts found an average of 3.55 high and medium-confidence synapses per image within the conventional EM data versus 3.25 using the EPTA-stained images (an average difference of only 8%). We can even more closely approximate the number of high-confidence-only synapses by increasing the stringency of the classifier (a difference of <1%). Because synaptic density may slightly vary according to pial depth of the specimen even within D2, some variation may be expected across hemispheres.

Table 1.

EPTA-stained EM images preserve synapse density

Technique Number of images Number of synapses Ratio Time
Expert 1 (Standard EM, manual counting) 0.77 min/image
    High confidence only 26 71 2.73 ± 1.66
    High and medium confidence 26 88 3.38 ± 1.90
Expert 2 (Standard EM, manual counting) 0.58 mins/image
    High confidence only 24 65 2.71 ± 1.55
    High and medium confidence 24 89 3.71 ± 1.85
Algorithm (EPTA EM, automatic counting) 0.06 mins/image
    Threshold = 0.7 275 745 2.71 ± 2.00
    Threshold = 0.5 (default) 275 893 3.25 ± 2.19
Open in a new tab

Note: We manually counted high and medium confidence synapses in 24–26 conventional EM images and used our algorithm to automatically count synapses in 275 EPTA-stained EM images of the same region. Different classifier thresholds allow us to closely approximate the true number of synapses.

If the EPTA stain were selectively staining for only asymmetric (excitatory) synapses and not symmetric (inhibitory) synapses, then we would expect a roughly 20% difference (Micheva and Beaulieu, 1995) between the number of synapses counted using EPTA and conventional EM. However, the close correspondence between the two methods suggests that we may be capturing both. This further demonstrates the validity of the EPTA stain as synapse-preserving (Bloom and Aghajanian, 1966) and provides a way of choosing an appropriate threshold for classification.

4.2 Detecting synapses using supervised and semi-supervised learning

As aforementioned, we used texture- and shape-based features to train several different classifiers (SVM, Random Forest and AdaBoost). We next compared the performance of these classifiers as well as a template-matching algorithm previously suggested for this task (Roseman, 2004) (Fig. 3). The SVM trained on both texture and shape features (MR8, HoG and Shape) performed best with an accuracy ranging from 54.8 to 81.3% on the positive set and 99.6 to 96.8% on the negative set depending on the classifier threshold used. Specifically, the default threshold of 0.5 allowed us to recall 67.8% of the true synapses with a precision of 83.3% (Fig. 3B). This significantly outperformed all other classifiers, as well as the correlation-based template-matching algorithm. These results suggest that the EPTA stain facilitates the high-throughput and automated detection of synapses compared with conventional EM. Such a performance would enable the large-scale use of this method to study experience-dependent plasticity in the brain and to detect abnormal changes in synaptic density owing to neurological disorders.

Fig. 3.

Fig. 3.

Open in a new tab

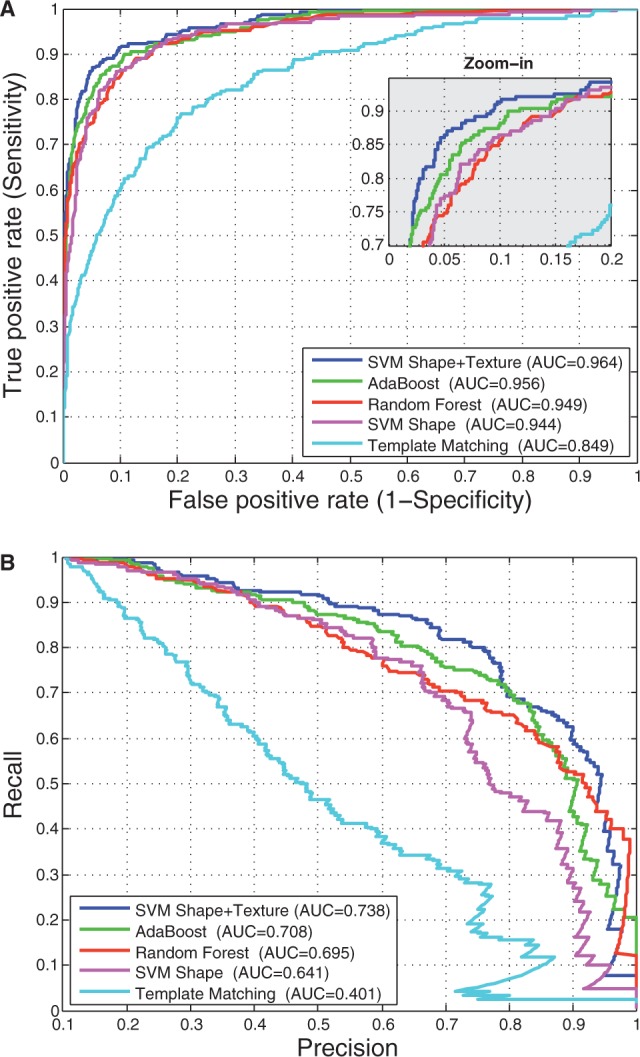
Cross-validation accuracy of all methods. AUC of the ROC curve (top) and precision-recall curve (bottom) show that the SVM trained using both texture and shape descriptors outperforms all other methods

The shape descriptors by themselves worked well for identifying positive examples but predicted many false positives owing to similar contours in, for example, nucleus regions, which are better discriminated using texture. The HoG features especially benefited from the vertical alignment of the synapses (a 7–10% decrease in false negatives with similar false positives comparing classifiers trained with and without alignment).

To further validate our classifier with respect to human annotation, we took 30 unlabeled images from our P14 sample and asked an independent party (a technician in the Barth lab familiar with the EPTA protocol) to manually annotate all high-confidence synapses. We then applied our supervised classifier to these images using the default classifier threshold of 0.5 and obtained an accuracy of 87.25% (89/102) on the set of positive predictions (66.6% recall) and 96.28% (1164/1209) on the negative predictions. These percentages are similar to those obtained using cross-validation.

Next, we applied semi-supervised learning to detect synapses in new samples for which training data is not available (Table 2). Here, we trained a single classifier Inline graphic on one sample (either P14 or P75) and used co-training to learn another classifier Inline graphic using unlabeled examples from the other sample. 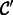We found that the accuracy of Inline graphic increases amongst the positive class by 8–12% and increases the AUC by 1–4% compared with the baseline classifier Inline graphic (see Section 3). We varied the number of unlabeled examples to transfer into Inline graphic and found that using the top 0.5% of positive examples (with a corresponding number of negative examples to maintain the same ratio of positive-to-negative) improved accuracy but that including the top 1.5% led to loss in performance.

Table 2.

Semi-supervised learning boosts cross-sample accuracy

Train/Test Co-training Accuracy
 AUC
Positive (%) Negative (%) Prec-recall (%) ROC (%)
P75/P14 No 66.36 98.20 73.65 96.91
P75/P14 Yes (0.5%) 72.90 98.60 75.75 97.14
P75/P14 Yes (1.5%) 74.77 96.91 73.06 96.65
P14/P75 No 48.78 98.96 60.50 90.38
P14/P75 Yes (0.5%) 60.16 98.21 64.23 92.89
P14/P75 Yes (1.5%) 60.98 97.55 63.80 92.83
Open in a new tab

Note: We trained a classifier using images from one sample and tested it on images from another sample (first column). This was done without co-training as a baseline and with co-training using two thresholds for selecting the number of unlabeled examples to include (second column). The third and fourth columns show accuracy on the positive and negative classes, and the last two columns show the precision-recall and ROC AUCs, respectively. Bold cells indicate best performance.

To explore how semi-supervised learning can account for the variance between mice at the same age, we trained on positive and negative examples from one P75 mouse and used the examples from the other P75 mouse to test (and vice versa). The baseline without semi-supervised learning had an average precision-recall AUC of 68.89% (78.81 and 58.97% individually) and an average ROC AUC of 95.80% (98.48 and 93.12% individually). Then, we used co-training to train a new classifier and improved the average precision-recall AUC to 73.06% (82.45 and 63.66%) and the ROC AUC to 97.15% (98.78 and 95.52%). Both these results demonstrate the power of using semi-supervised learning on unlabeled data, which is often plentiful but ignored in bioimage applications.

Our approach is also scalable and efficient: using unoptimized MATLAB code, we can process a single image in 3.4 s on a standard desktop machine using a single processor.

4.3 Development changes in the mouse barrel cortex

Next, we used our method to study developmental changes in synapse density and size in a defined area of the mouse brain, the representation of a single specified (D1) whisker in layer 4 of somatosensory cortex. We performed additional experiments and imaged the D1 barrel in two P17 mice following the same procedure as outlined in Section 3. We used our classifier to count synapses in images from both time points and, consistent with previous findings (De Felipe et al., 1997), synapse density appeared to rapidly increase from P14 to P17 (2.73 synapses per image at P14 versus 4.25 at P17; Fig. 4A). Further, we found that synapse density decreases in adults to about the same level as P14 (2.78 synapses per image at P75), which is also consistent with prior work on pruning (White et al., 1997). Thus, our pipeline can be used to better understand the rates of developmental processes and can be used to define the precise timelines of their occurrence.

Fig. 4.

Fig. 4.

Open in a new tab

Developmental changes and log-normal distribution of synaptic strength. (A) Histogram of synapse sizes (as measured by length of the perimeter of the synapse) from two P14 (blue), two P17 (red) and two P75 (green) samples. There is significant growth in number of synapses from P14 to P17, followed by pruning by adulthood (P75). Further, all three distributions closely approximate a log-normal curve, which matches electrophysiological data on synaptic connection strengths (Song et al., 2005). (B) Cumulative distribution of synapse sizes suggest a shift in synapse strength over time (Inline graphic, Kolmogorov–Smirnov test)

Finally, to demonstrate the utility of the EPTA stain beyond simply detecting synapses, we used shape features to characterize the strength of each synapse based on its well-established correlation with spine size (Lee et al., 2012). Modulation in synaptic strength is an important facet of neuroplasticity and development (Wen and Barth, 2011) with larger contact areas likely to transmit more current to the post-synaptic neuron. 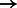We used our classifier-predicted synapses in all samples (P14, P17 and P75) and plotted the distribution of the perimeter of all synapses detected (larger perimeter Inline graphic larger size Inline graphic stronger synapse). Structurally similar synapses may appear to have different sizes when projected onto 2D because the image cross-sections may be taken at any angle. Exactly correcting for this bias would involve 3D reconstruction of synapses from stacks of EM images, which is a separate and interesting problem in its own right (Jain et al., 2010; Kreshuk et al., 2011; Merchan-Perez et al., 2009; Morales et al., 2011).

We found that the distribution of synapse size at all ages fits a log-normal distribution (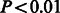Inline graphic by Shapiro–Wilk and Anderson–Darling tests; Fig. 4A), which is consistent with previous electrophysiological data (Song et al., 2005). We also observed that there was a significant shift in the distribution of synapse size toward the emergence of small synapses during the period of rapid increase in synapse density at P17, without a concomitant loss of large synapses within this short developmental time window (Fig. 4B). These data suggest that developmental processes may preferentially enable the addition of new synapses without necessarily augmenting the size of already-existing synapses. The data analysis pipeline that we have established can thus be used to generate and test specific hypotheses about synapse growth and maturation in the developing neocortex in a high-throughput and statistically robust manner.

5 DISCUSSION AND CONCLUSIONS

Synaptic density and strength are dynamically modulated in the brain and are important facets for understanding neural circuitry and function. Experience-dependent plasticity, circuit development and neuropathologies have all been linked to changes in the number and strength of synapses in the brain, and thus their characterization is a useful parameter to facilitate our understanding of network function. Although current experimental techniques for studying these conditions have many advantages [e.g. electrophysiology provides a wealth of data not extractable from images, and conventional EM can be used to resolve synapses to extract pre- and post-synaptic partners and thus potentially allow for reconstruction of microcircuits (Denk et al., 2012)], several interesting questions can also be answered by sampling from brain regions of interest over several conditions or time points and generating high-confidence large-scale statistics of synaptic structures present. But to do so requires both clarity in the data and robust algorithms to explore this data.

We used an old experimental technique for selectively staining synapses in EM images. This technique does not require specialized animal models for enhancing synapses, and we validated it on new tissue of the mouse somatosensory cortex and against conventional EM. We collected >800 images from three time points and developed a fully automated and high-throughput machine-learning framework that detected thousands of synapses in these images. We also used semi-supervised learning to learn models that can adapt to variability in new samples by leveraging unlabeled data. Such an approach is suitable for several other bio-image classification problems that also face issues of sample heterogeneity. Our approach is general and scalable enough to handle large datasets and is freely available for others to use.

For future work, it would be a great interest to perform immunocytochemistry using EPTA against GABA and AMPA receptors to separately classify symmetric and asymmetric synapses. Accuracy could also be improved by detecting synapses in 3D, though this would require many more images and more sophisticated computational techniques that can automatically segment, align and reconstruct synapses across serial sections. The 2D sampling-based strategies (e.g. considering sections separated by 10 µm) may certainly miss synapses, but if the same procedure is applied to each sample at each time point, the relative number of synapses per image or unit area can still be compared in a fair manner. Further, to remove some biases in 2D analysis caused by larger synapses, previous works have proposed formulas to adjust counts based on the average size of synaptic profiles observed in the sample (Coggeshall and Lekan, 1996; Mayhew, 1996; Huttenlocher and Dabholkar, 1997), which we can also use.

ACKNOWLEDGEMENTS

S.N. would like to thank Fernando Amat and Gustavo Rohde for advice on developing the image processing algorithms and Patrick Beukema for manual annotation of EPTA images.

Funding: National Institutes of Health (1RO1 GM085022) and National Science Foundation (DBI-0965316) awards to Z.B.J.

Conflict of Interest: none declared.

REFERENCES

  1. Arbelaez P, et al. Experimental evaluation of support vector machine-based and correlation-based approaches to automatic particle selection. J. Struct. Biol. 2011;175:319–328. doi: 10.1016/j.jsb.2011.05.017. [DOI] [PubMed] [Google Scholar]
  2. Bloom FE, Aghajanian GK. Cytochemistry of synapses: selective staining for electron microscopy. Science. 1966;154:1575–1577. doi: 10.1126/science.154.3756.1575. [DOI] [PubMed] [Google Scholar]
  3. Bloom FE, Aghajanian GK. Fine structural and cytochemical analysis of the staining of synaptic junctions with phosphotungstic acid. J. Ultrastruct. Res. 1968;22:361–375. doi: 10.1016/s0022-5320(68)90027-0. [DOI] [PubMed] [Google Scholar]
  4. Blum A, Mitchell T. 1998. Combining labeled and unlabeled data with co-training. In Proceedings of the 11th Annual Conference on Computational Learning Theory (COLT), COLT’ 98. pp. 92–100, ACM, New York, NY, USA. [Google Scholar]
  5. Bock DD, et al. Network anatomy and in vivo physiology of visual cortical neurons. Nature. 2011;471:177–182. doi: 10.1038/nature09802. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Breiman L. Random forests. Mach. Learn. 2001;45:5–32. [Google Scholar]
  7. Cardona A, et al. TrakEM2 software for neural circuit reconstruction. PLoS One. 2012;7:e38011. doi: 10.1371/journal.pone.0038011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Chang C-C, Lin C-J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011;2 27:1–27:27. [Google Scholar]
  9. Clare R, et al. Synapse loss in dementias. J. Neurosci. Res. 2010;88:2083–2090. doi: 10.1002/jnr.22392. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Coggeshall RE, Lekan HA. Methods for determining numbers of cells and synapses: a case for more uniform standards of review. J. Comp. Neurol. 1996;364:6–15. doi: 10.1002/(SICI)1096-9861(19960101)364:1<6::AID-CNE2>3.0.CO;2-9. [DOI] [PubMed] [Google Scholar]
  11. Cooke BM, Woolley CS. Gonadal hormone modulation of dendrites in the mammalian CNS. J. Neurobiol. 2005;64:34–46. doi: 10.1002/neu.20143. [DOI] [PubMed] [Google Scholar]
  12. Cowan WM, et al. Regressive events in neurogenesis. Science. 1984;225:1258–1265. doi: 10.1126/science.6474175. [DOI] [PubMed] [Google Scholar]
  13. da Costa NM, et al. A systematic random sampling scheme optimized to detect the proportion of rare synapses in the neuropil. J. Neurosci. Methods. 2009;180:77–81. doi: 10.1016/j.jneumeth.2009.03.001. [DOI] [PubMed] [Google Scholar]
  14. Dalal N, Triggs B. 2005. Histograms of oriented gradients for human detection. In: Schmid,C., et al. (eds), Proceedings of the International Conference on Computer Vision and Pattern Recognition (CVPR), Vol. 2, IEEE Computer Society, Washington, DC, USA, pp. 886–893. [Google Scholar]
  15. De Felipe J, et al. Inhibitory synaptogenesis in mouse somatosensory cortex. Cereb. Cortex. 1997;7:619–634. doi: 10.1093/cercor/7.7.619. [DOI] [PubMed] [Google Scholar]
  16. Denk W, et al. Structural neurobiology: missing link to a mechanistic understanding of neural computation. Nat. Rev. Neurosci. 2012;13:351–358. doi: 10.1038/nrn3169. [DOI] [PubMed] [Google Scholar]
  17. Duda RO, Hart PE. Use of the hough transformation to detect lines and curves in pictures. Commun. ACM. 1972;15:11–15. [Google Scholar]
  18. Feng L, et al. Improved synapse detection for mGRASP-assisted brain connectivity mapping. Bioinformatics. 2012;28:25–31. doi: 10.1093/bioinformatics/bts221. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Fox K. Barrel Cortex. Cambridge: Cambridge University Press; 2008. [Google Scholar]
  20. Freund Y, Schapire RE. 1995. A decision-theoretic generalization of on-line learning and an application to boosting. In Proceedings of the Second European Conference on Computational Learning Theory (EuroCOLT). pp. 23–37. Springer-Verlag, London, UK. [Google Scholar]
  21. Glaze DG. Rett syndrome: of girls and mice–lessons for regression in autism. Ment. Retard Dev. Disabil. Res. Rev. 2004;10:154–158. doi: 10.1002/mrdd.20030. [DOI] [PubMed] [Google Scholar]
  22. Hinton VJ, et al. Analysis of neocortex in three males with the fragile X syndrome. Am. J. Med. Genet. 1991;41:289–294. doi: 10.1002/ajmg.1320410306. [DOI] [PubMed] [Google Scholar]
  23. Huttenlocher PR, Dabholkar AS. Regional differences in synaptogenesis in human cerebral cortex. J. Comp. Neurol. 1997;387:167–178. doi: 10.1002/(sici)1096-9861(19971020)387:2<167::aid-cne1>3.0.co;2-z. [DOI] [PubMed] [Google Scholar]
  24. Jain V, et al. Machines that learn to segment images: a crucial technology for connectomics. Curr. Opin. Neurobiol. 2010;20:653–666. doi: 10.1016/j.conb.2010.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Johnston MV, et al. Rett syndrome and neuronal development. J. Child Neurol. 2005;20:759–763. doi: 10.1177/08830738050200091101. [DOI] [PubMed] [Google Scholar]
  26. Kim J, et al. mGRASP enables mapping mammalian synaptic connectivity with light microscopy. Nat. Methods. 2012;9:96–102. doi: 10.1038/nmeth.1784. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Klintsova AY, Greenough WT. Synaptic plasticity in cortical systems. Curr. Opin. Neurobiol. 1999;9:203–208. doi: 10.1016/s0959-4388(99)80028-2. [DOI] [PubMed] [Google Scholar]
  28. Knott GW, et al. Formation of dendritic spines with GABAergic synapses induced by whisker stimulation in adult mice. Neuron. 2002;34:265–273. doi: 10.1016/s0896-6273(02)00663-3. [DOI] [PubMed] [Google Scholar]
  29. Kreshuk A, et al. Automated detection and segmentation of synaptic contacts in nearly isotropic serial electron microscopy images. PLoS One. 2011;6:e24899. doi: 10.1371/journal.pone.0024899. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Lee KF, et al. Examining form and function of dendritic spines. Neural Plast. 2012;2012:704103. doi: 10.1155/2012/704103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Lefort S, et al. The excitatory neuronal network of the c2 barrel column in mouse primary somatosensory cortex. Neuron. 2009;61:301–316. doi: 10.1016/j.neuron.2008.12.020. [DOI] [PubMed] [Google Scholar]
  32. Leung T, Malik J. Representing and recognizing the visual appearance of materials using three-dimensional textons. Int. J. Comput. Vision. 2001;43:29–44. [Google Scholar]
  33. Mayhew TM. How to count synapses unbiasedly and efficiently at the ultrastructural level: proposal for a standard sampling and counting protocol. J. Neurocytol. 1996;25:793–804. doi: 10.1007/BF02284842. [DOI] [PubMed] [Google Scholar]
  34. Merchan-Perez A, et al. Counting synapses using FIB/SEM microscopy: a true revolution for ultrastructural volume reconstruction. Front. Neuroanat. 2009;3:18. doi: 10.3389/neuro.05.018.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Micheva KD, Beaulieu C. An anatomical substrate for experience-dependent plasticity of the rat barrel field cortex. Proc. Natl Acad. Sci. USA. 1995;92:11834–11838. doi: 10.1073/pnas.92.25.11834. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Morales J, et al. Espina: a tool for the automated segmentation and counting of synapses in large stacks of electron microscopy images. Front. Neuroanat. 2011;5:18. doi: 10.3389/fnana.2011.00018. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Morshedi MM, et al. Increased synapses in the medial prefrontal cortex are associated with repeated amphetamine administration. Synapse. 2009;63:126–135. doi: 10.1002/syn.20591. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Na ES, Monteggia LM. The role of MeCP2 in CNS development and function. Horm. Behav. 2011;59:364–368. doi: 10.1016/j.yhbeh.2010.05.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Nimchinsky EA, et al. Abnormal development of dendritic spines in FMR1 knock-out mice. J. Neurosci. 2001;21:5139–5146. doi: 10.1523/JNEUROSCI.21-14-05139.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Peng H. Bioimage informatics: a new area of engineering biology. Bioinformatics. 2008;24:1827–1836. doi: 10.1093/bioinformatics/btn346. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Pfeiffer BE, Huber KM. The state of synapses in fragile X syndrome. Neuroscientist. 2009;15:549–567. doi: 10.1177/1073858409333075. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Roseman AM. FindEM–a fast, efficient program for automatic selection of particles from electron micrographs. J. Struct. Biol. 2004;145:91–99. doi: 10.1016/j.jsb.2003.11.007. [DOI] [PubMed] [Google Scholar]
  43. Skibbe H, et al. 2011. SHOG: spherical hog descriptors for rotation invariant 3d object detection. In Proceedings of the 33rd International Conference on Pattern Recognition, DAGM’11. pp. 142–151. Springer-Verlag, Berlin, Heidelberg. [Google Scholar]
  44. Song S, et al. Highly nonrandom features of synaptic connectivity in local cortical circuits. PLoS Biol. 2005;3:e68. doi: 10.1371/journal.pbio.0030068. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Sporns O. Networks of the Brain. Cambridge: MIT Press; 2010. [Google Scholar]
  46. Stoneham ET, et al. Rules of engagement: factors that regulate activity-dependent synaptic plasticity during neural network development. Biol. Bull. 2010;219:81–99. doi: 10.1086/BBLv219n2p81. [DOI] [PubMed] [Google Scholar]
  47. Szeliski R. Computer Vision: Algorithms and Applications. 1st edn. New York, NY: Springer-Verlag New York, Inc; 2010. [Google Scholar]
  48. Van den Oever MC, et al. The synaptic pathology of drug addiction. Adv. Exp. Med. Biol. 2012;970:469–491. doi: 10.1007/978-3-7091-0932-8_21. [DOI] [PubMed] [Google Scholar]
  49. Varma M, Zisserman A. 2003. Texture classification: are filter banks necessary? In Proceedings of the 2003 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Vol. 2, pages II–691–8 vol. 2. [Google Scholar]
  50. Walz W. Patch-Clamp Analysis: Advanced Techniques. Totowa, New Jersey, USA: Humana Press, Neuromethods Series; 2007. [Google Scholar]
  51. Wen JA, Barth AL. Input-specific critical periods for experience-dependent plasticity in layer 2/3 pyramidal neurons. J. Neurosci. 2011;31:4456–4465. doi: 10.1523/JNEUROSCI.6042-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. White EL, et al. A survey of morphogenesis during the early postnatal period in PMBSF barrels of mouse SmI cortex with emphasis on barrel D4. Somatosens. Mot. Res. 1997;14:34–55. doi: 10.1080/08990229771204. [DOI] [PubMed] [Google Scholar]
  53. White JG, et al. The structure of the nervous system of the nematode Caenorhabditis elegans. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1986;314:1–340. doi: 10.1098/rstb.1986.0056. [DOI] [PubMed] [Google Scholar]
  54. Yassin L, et al. An embedded subnetwork of highly active neurons in the neocortex. Neuron. 2010;68:1043–1050. doi: 10.1016/j.neuron.2010.11.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Zhu X. Technical report. 2005. Semi-supervised learning literature survey. Computer Sciences, University of Wisconsin-Madison, Madison. [Google Scholar]
  56. Zuiderveld K. Graphics Gems IV. Chapter Contrast Limited Adaptive Histogram Equalization. San Diego, CA: Academic Press Professional, Inc; 1994. pp. 474–485. [Google Scholar]

Articles from Bioinformatics are provided here courtesy of Oxford University Press

RESOURCES