Integrating sequence, expression and interaction data to determine condition-specific miRNA regulation

Abstract

Motivation: MicroRNAs (miRNAs) are small non-coding RNAs that regulate gene expression post-transcriptionally. MiRNAs were shown to play an important role in development and disease, and accurately determining the networks regulated by these miRNAs in a specific condition is of great interest. Early work on miRNA target prediction has focused on using static sequence information. More recently, researchers have combined sequence and expression data to identify such targets in various conditions.

Results: We developed the Protein Interaction-based MicroRNA Modules (PIMiM), a regression-based probabilistic method that integrates sequence, expression and interaction data to identify modules of mRNAs controlled by small sets of miRNAs. We formulate an optimization problem and develop a learning framework to determine the module regulation and membership. Applying PIMiM to cancer data, we show that by adding protein interaction data and modeling cooperative regulation of mRNAs by a small number of miRNAs, PIMiM can accurately identify both miRNA and their targets improving on previous methods. We next used PIMiM to jointly analyze a number of different types of cancers and identified both common and cancer-type-specific miRNA regulators.

Contact: zivbj@cs.cmu.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 BACKGROUND

MicroRNAs (miRNAs) are a family of small non-coding RNA molecules that regulate gene expression post-transcriptionally. These single-stranded RNAs, 19–25 nt long, are initially transcribed as longer independent genes or from introns of protein-coding genes. MiRNAs are now known to play a major role in development (Bartel, 2009), various brain functions (Shao et al., 2010) and diseases (Meola et al., 2009). Since their discovery, several 100 miRNAs were identified in each of several different species, including mammals, worms, flies and plants (He and Hannon, 2004). Initial discovery of large sets of miRNAs relied heavily on sequence and conservation analysis (Bartel, 2009), although recent advances in sequencing capacity are now allowing researchers to validate and identify additional miRNAs experimentally (Motameny, 2010). Most miRNAs target the genes they regulate by binding to the 3′-untranslated region of the target mRNAs (using complementary base pairing) and recruiting additional machinery to either degrade these mRNAs or prevent them from being translated. The miRNA regulation is ubiquitous, and a single miRNA can target 100s and even 1000s of genes. As the effect of each miRNA on any single target is often limited, they often work cooperatively with multiple miRNAs targeting the same mRNA in a specific condition (Krek et al., 2005; Krol et al., 2010).

Although the set of active miRNAs can often be determined experimentally (by measuring their expression levels), identifying their targets is much more challenging. Determining such target set is important for fully understanding the role of various miRNAs and to model the networks they regulate in a condition of interest. Initially, computational methods developed to predict such targets primarily relied on sequence information, in some cases, also using conservation information and/or secondary structure predictions. These methods search for base pair complementarity between the mature miRNA and 3′-untranslated regions of all mRNAs, allowing for some mismatches (the penalty for mismatches differs between the methods). Popular methods include TargetScan (Lewis et al., 2005), miRBase (now called MicroCosm) (Griffiths-Jones et al., 2006), miRanda (John et al., 2004) and PicTar (Krek et al., 2005).

Although these predictions are useful, because of the short length of miRNAs, they lead to many false positives and some false negatives (Betel et al., 2010). Conservation analysis has proven especially problematic in this domain, as several real targets are not well conserved and would be ignored if conservation is a requirement (Barakat et al., 2007). In addition, sequence data are static and do not change in different conditions or at different times. Thus, based on sequence data alone, it is impossible to map the set of targets for specific miRNA in a condition of interest (as most genes are not expressed in any specific condition or tissue). Finally, miRNAs often work cooperatively in small groups. As miRNA activation is condition specific, using this cooperative regulation property requires the use of condition-specific data, which of course cannot be inferred from sequence information alone.

Transcription factors (TFs) also play a major role in regulating gene expression, and they have been shown to work combinatorially with miRNAs (Sun et al., 2012). However, a pre-requisite for such combinatorial analysis is a list of targets for individual miRNAs. Unlike TFs, which can serve as activators or repressors and are often post-transcriptionally regulated, miRNAs are only transcriptionally regulated and inhibit their direct targets. This has led to several studies that isolated the miRNA target prediction task by integrating sequence, mRNA and miRNA expression data (Cheng and Li, 2008; Huang et al., 2007a; Joung et al., 2007; Ooi et al., 2011). Unlike sequence data, expression data are dynamic and condition-specific and thus provide useful clues about the set of active miRNAs and mRNAs. A number of methods, mostly based on (anti) correlation or regression analysis using the expression levels of miRNAs and predicted mRNA targets, were suggested for this task (Huang et al., 2011; Wang and Li, 2009). A representative example for this group is GenMiR++ (Huang et al., 2007a), one of the first methods to integrate miRNA and mRNA expression profiles in a unified probabilistic model. Given an expression dataset for both miRNAs and mRNAs and a set of putative miRNA–mRNA interactions (inferred from sequence data), GenMiR++ uses a generative probabilistic regression model to assign targets to miRNAs. It was successfully applied to identify targets of let-7b in retinoblastoma. Another approach is to project mRNA expression data on pathway databases and compute the correlation between miRNAs and average pathway expression levels to identify likely regulators of signaling pathways (Ooi et al., 2011). Although this method does not identify specific targets, it can be used to infer the function of specific miRNAs based on the pathways they regulate. A number of other methods for integrating miRNA and mRNA expression data have been proposed, see (Muniategui et al. 2012) for a recent review.

Finally, there is growing evidence that interacting proteins are more likely to be co-regulated by the same miRNAs (Hsu et al., 2008; Liang and Li, 2007). It has also been shown that some miRNAs coordinately target protein complexes (Sass et al., 2011). Although such complementary information may be important, few previous works have taken advantage of it to predict condition-specific interactions. An exception is a recent work by Zhang et al. (2011), which developed SNMNMF to integrate protein interactions with miRNA and mRNA expression data. The method is based on a non-negative matrix factorization analysis, which factorizes the two expression data matrices such that the two share one common factor, which is assumed to be the module basis matrix . Note, however, that although this method was successfully applied to analyze Ovarian cancer data, it does not use a regression model to explain mRNA expression levels, or requires that miRNAs and mRNAs in the same module be anti-correlated; therefore, the resulting modules do not fully use current knowledge regarding the inhibitory role of miRNAs, which may lead to missing important interactions.

The methods discussed earlier in the text successfully integrated expression and sequence data. However, a major point that is often ignored by these prediction methods is the combinatorial aspect of miRNA regulation. Several studies have shown that individual miRNAs have only limited impact on their targets (Malumbres, 2012) and multiple (different) miRNAs are needed to drastically reduce transcription levels of targets. To allow the use of such group- or module-based regulatory model, we have recently developed GroupMiR (Le and Bar-Joseph, 2011), which uses a non-parametric Bayesian prior based on the Indian Buffet Process (IBP; Griffiths and Ghahramani, 2006) to identify modules of co-regulated miRNAs and their target mRNAs. As we have shown, by using a module-based approach, we can improve on methods that treat miRNAs or mRNAs individually improving the set of correctly recovered miRNA–mRNA interactions (Le and Bar-Joseph, 2011).

Here, we present the Protein Interaction based MicroRNA Modules (PIMiM) method, which extends the regression framework of GroupMiR by using an additional type of data: protein interactions (Fig. 1). As we show, by defining a new target function that encourages interacting proteins to belong to the same module, we can use such data and integrate it with expression and sequence-based data in a probabilistic model. We develop an iterative learning procedure to learn the parameters of our model and show that it converges to a local minima. Comparison of PIMiM with previous methods indicates that by combining a module-based approach with protein interaction data, we can improve on both methods that only rely on modules (GroupMiR) and methods that rely on protein interaction (SNMNMF). We used PIMiM to study miRNA in several types of cancers, allowing us to identify novel regulators that either span multiple cancer types or are unique to specific cancers.

Fig. 1.

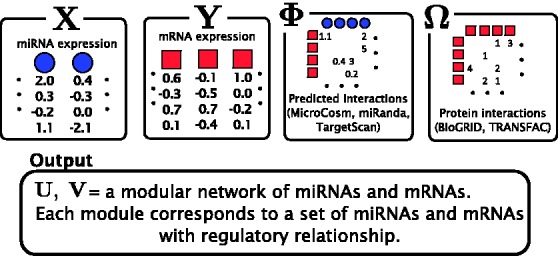
Data used as input for PIMiM. In addition the miRNA and mRNA expression data, PIMiM uses sequence-based predictions of miRNA–mRNA interactions and protein–protein interactions. These datasets are integrated as discussed in Section 2

2 METHODS

2.1 Overview

We developed PIMiM, a module-based method that predicts targets for miRNAs by assigning them, together with the mRNAs they regulate, to one of K modules. Modules may contain several miRNAs and many mRNAs, and both miRNA and mRNAs can be assigned to 0, 1 or multiple modules, and thus modules may overlap.

The input to PIMiM is condition-specific miRNA and mRNA expression data (usually multiple measurements from patients or different time points). In addition, we use sequence-based predictions of miRNA–mRNA interactions (any probabilistic predictions can be used) and static protein interaction data. Using these datasets we learn a regularized probabilistic regression model in which mRNA data are regressed to the expression data of miRNAs assigned to modules regulating it. The downregulation effect of an miRNA on the expression of its target mRNA is aggregated across all modules, allowing information to be shared between modules in the learning process. Our probabilistic model rewards the assignments of predicted miRNA–mRNA pairs to the same module and also rewards assignment of mRNAs of interacting proteins to the same module. Combined, the modules explain the observed mRNA expression data as a function of their regulating miRNAs and the set of proteins they interact with.

2.2 Notations

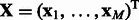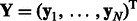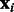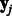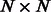We use the following notation in the rest of the article. We assume there are M miRNAs and N mRNAs in each sample. We denote expression profiles of miRNAs by and of mRNAs by , where and are vectors with the expression levels of miRNA i and mRNA j, respectively, in all samples. Both matrices have P columns corresponding to the P-matched samples. In addition, let (sparse matrix) be the weighted adjacency matrix of the protein interactions [obtained from databases, such as BioGRID (Stark et al., 2011) or TRANSFAC (Wingender et al., 2000)] and 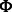(sparse 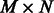matrix) be the list of predicted interactions of miRNAs and mRNAs from sequence data (obtained from prediction databases, such as MicroCosm; Griffiths-Jones et al., 2006). We also define 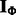and 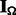as binary matrices indicating whether an entry of 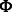and , respectively, is non-zero.

For learning K modules, our goal is to determine (learn) the values of the membership parameters u_ik and v_jk, which represent the propensity that miRNA i or mRNA j belong to module k. Naturally, we restrict these parameters to be non-negative: 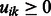and 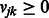, where we interpret that an miRNA or an mRNA is not assigned to a module if the corresponding parameter is zero. We use matrices 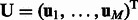and 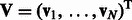to represent this complete set of membership parameters. Finally, we use the following subscript such as 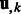or 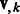to denote the kth column of the matrices.

2.3 Probabilistic regression model

Following previous works (Huang et al., 2007b; Le and Bar-Joseph, 2011), we use a regression-based method to link the expression profiles of miRNAs and mRNAs. Expression values of mRNAs are assumed to be downregulated from a baseline expression level by a linear combination of expression profiles of all their predicted miRNA regulators. For example, mRNA j’s expression values are distributed as: 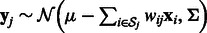, where 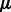is the baseline expression level, 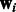are weights associated with miRNAs (which previous methods learn individually for each mRNA) and 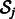is the set of predicted miRNA regulators of mRNA j.

We depart from these previous models in how we specify miRNA regulators and how we learn the weights 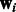. First, each mRNA is assumed to be a target of all miRNAs assigned to the modules it belongs to as long as they are predicted to regulate it (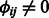). Formally, mRNA j is the target of the set of miRNAs 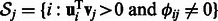. Second, the downregulation weights are aggregated across all modules, such as .

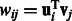Given these assumptions, the likelihood of the observed expression values is

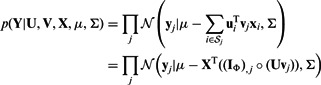(1)

where 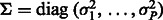is the per-sample variance terms.

2.4 Using protein interactions

So far PIMiM only uses expression values in a regression setting (although we constrain the regulators to come from the sequence-based predicted set, the regression model itself does not directly encourage the assignment of miRNA and predicted mRNA targets to the same module).

To incorporate the input interaction data (predicted miRNA–mRNA pairs 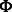and protein interactions ), we use a function that rewards assignments to the same module based on the strength of the predicted edge as follows:

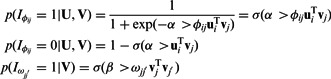(2)

Where α and β are positive tuning parameters that are used to adjust the contributions of the two types of interaction data in our model and 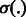is the logistic-sigmoid function. If available (as is the case for the miRNA–mRNA interaction data), we use probabilities for 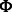and derived directly from the prediction or experimental databases (see Section 4). We deliberately do not include penalty terms for zero entries of because this interaction matrix is extremely sparse (the number of known protein–protein interactions is small compared with the total number of possible interactions). Penalizing zero entries when using such a sparse matrix would lead to small modules and may be less biologically accurate, as not all co-targets of a miRNA interact.

These terms indicates that the higher the probability of interaction (both miRNA–mRNA and protein–protein) the more likely it is that the interacting entities would be assigned to the same set of modules. This is done globally across all modules. For instance, if 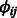is positive, we have previous knowledge that miRNA i and mRNA j interact. To maximize the likelihood 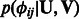, we would need to learn parameters that lead to large values of 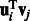, which means that the method is more likely to place them in the same module.

2.5 Overall log-likelihood

To summarize, our target is to minimize the following negative log-likelihood:

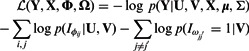(3)

The first term evaluates how well the miRNA expression explains the observed mRNA expression, whereas the second and third terms are rewards for assigning predicted miRNA–mRNA pairs and protein interaction pairs to the same module, respectively. This function is non-convex and thus can have multiple local minima solutions. To constrain the set of solutions, we add a number of regularization terms. First, we add two sets of 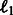norm constraints for the vectors 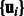and 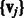. 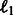norm contraints encourage sparsity leading to smaller and tighter modules. As our goal is to reduce false positives, such constraints are useful, as they reduce the set of predicted miRNA–mRNA pairs. Specifically, we require that

We are using two different regularization parameters C₁ and C₂. This is because the number of miRNAs and mRNAs are different; therefore, a single number does not yield good solutions. Moreover, we choose to use these constraints explicitly instead of adding them to the objective function (using Lagrangian multipliers), as this formulation is simpler to solve in our optimization procedure.

Together, our learning phase solves the following optimization:

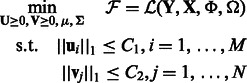(4)

2.6 Learning the parameters of our model

In this section, we discuss how to solve the optimization problem from (4) to determine values for the parameters of our model. As aforementioned, this problem is non-convex, and we cannot analytically compute general solutions. However, we notice that by holding 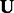and 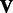fixed, we can solve for 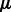and in a closed form using standard linear regression:

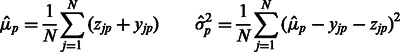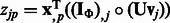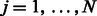where for and .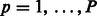

To solve for 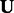and 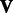for given values of 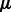and , we use a projected quasi-Newton (PQN) method (Schmidt et al., 2009). Quasi-Newton methods construct an approximation to the Hessian by using the observed gradients at successive iterations. We use the MATLAB implementation min_PQN (http://www.di.ens.fr/mschmidt/Software/PQN.html). There are several reasons why we chose this method instead of directly working with the Hessian. First, our set of constraints is convex, and the projection on this set can be done analytically. Second, although we can compute both the gradients and Hessian of , the memory required to store the Hessian is often too large given the dimensions of the expression data (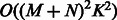). Moreover, because of interactions between miRNAs and mRNAs, the Hessian is not necessary sparse even if both 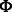and are. During the projection step, to speed-up the convergence of the algorithm, we set the entries of 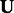, which do not have predicted interactions to zero.

Using the updated values for 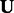and 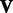, we once again solve for 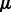and and so on. These two steps lead to an iterative procedure to solve (4) along the lines of coordinate-descent methods. This procedure converges to the local minima because of the fact that the objective function is bounded below, and the sequence of function values is monotonically decreasing, and the gradients at the convergence are zeros. As the problem is non-convex, we perform the learning process several times, randomly initializing the parameters each time. After repeating this process several times (10 iterations in our experiments), we select the parameters from the result that leads to the lowest value for our objective function.

Finally, the regularization and data-type–weighting parameters 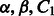and C₂ are chosen based on an external evaluation discussed in Section 4.

3 CONSTRAINT MODULE LEARNING FOR MULTIPLE CONDITION ANALYSIS

So far we have discussed our approach for identifying miRNA-regulated modules using a condition-specific expression dataset. Although the optimization problem in Equation (4) can be used with expression data from multiple conditions (e.g. different types of cancer), the output is one set of modules for all conditions. In some cases, directly identifying similar and divergent modules across conditions is an important goal. Consider, for example, joint analysis of multiple types of cancers. Although some researchers may be interested in regulatory modules that are activated in all different cancer types, others may be interested in unique aspects, or modules, of a specific cancer type when compared with other types of cancer.

In our problem, we would like to learn a set of modules for T different conditions. The interaction input matrices 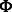and are fixed, whereas for each condition t, we have a set of expression measurements 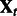and 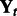. Given this input, we jointly learn T sets of modules 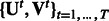. The number of modules is also fixed for all conditions.

This type of learning is called multi-task learning (Caruana, 1997) in the machine-learning community, where many related models are learned simultaneously using the same internal representation. Such learning allows different models (or cancer types) to share some parameters, which improves learning while at the same time it can also identify unique parameters for specific types. In several cases, such framework was shown to lead to better solutions (Caruana, 1997). Many existing methods proposed for multi-task learning focus on multi-output regression problems, where it is often desirable to obtain sparse solutions by performing covariate selection. They rely on regularization technique to jointly select a set of covariates that are relevant to many tasks. One can apply 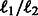penalty of group lasso to select covariates relevant to all tasks (Obozinski et al., 2010).

Here, we adopt the 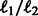penalty of group lasso to regularize the modules over T conditions with the following penalty:

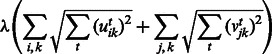This penalty encourages entries 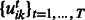and 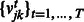to be selected together, which means that miRNAs and mRNAs are assigned to the same modules across conditions. As the penalty is not differentiable at 0, we reformulate the optimization problem by moving the non-differentiable part to the constraints as suggested in (Liu et al., 2009):

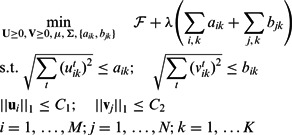(5)

Here, we have introduced new variables 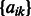and 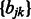into the problem. We update the projection step in Section 2.6 with the projection on the new 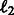norm balls in the constraint set as shown in Liu et al. (2009) (Theorem 4).

4 RESULTS

4.1 MiRNA regulation in ovarian cancer

To test PIMiM and to compare it with previous methods for determining condition-specific miRNA regulation (SNMNMF and GroupMiR), we use the ovarian cancer dataset from Zhang et al. (2011). This dataset contains 385 samples from cancer patients, each measuring the expression of 559 miRNAs and 12 456 mRNAs and was downloaded from the Cancer Genome Atlas data portal (TCGA) (https://tcga-data.nci.nih.gov/tcga/). In addition to expression data, the sequence-based prediction of miRNA–mRNA interactions was downloaded from MicroCosm (Griffiths-Jones et al., 2006), and protein interaction data were downloaded from TRANSFAC (Wingender et al., 2000). We only use MicroCosm here to allow a fair comparison with SNMNMF, which only uses these data. In subsequent analysis, we use other sequence-based prediction methods as well. To evaluate the accuracy of each method, we used a set of 115 cancer miRNAs that were determined to participate in ovarian cancer in a recent review article (Koturbash et al., 2011; Tables 1 and 2). Using this set we compute the precision, recall and F1 score (the harmonic mean of precision and recall) of the set of miRNAs identified by each method.

Table 1.

Evaluation of all methods on the ovarian cancer dataset

F1 score	Cancer miRNAs			Expression correlation	Number of genes/module
	F1	Precision	Recall
PIMiM	0.3768	0.3230	0.4522	−0.0131	67.80
SNMNMF	0.3588	0.3197	0.4087	0.0745	79.26
GroupMiR	0.1227	0.2083	0.0870	−0.0408	54.82

Note: The expression correlation values and number of genes are averaged across modules. Expression correlation: the correlation of expression values of miRNAs and mRNAs. Bold values are the best values for the column (highest or lowest depending on the context).

Table 2.

miRNAs specifically identified for a cancer type

MiRNAs	Predicted type	BRCA	GBM	AML
hsa-miR-663	BRCA	Khoshnaw et al. (2009)	–	–
hsa-miR-433	GBM	–	Hua et al. (2012)	–
hsa-miR-99b	AML	–	–	Garzon et al. (2007)

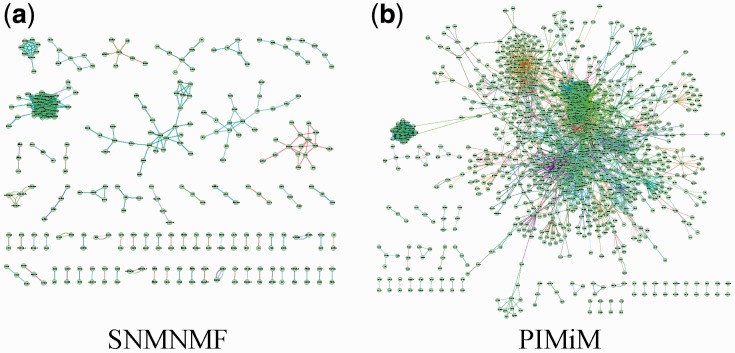
The number of modules K was set to 50 for the non-negative matrix factorization method (SNMNMF) as suggested in Zhang et al. (2011). PIMiM also requires setting regularization and weight parameters 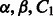and C₂. To set these, we performed an iterative line search (holding three of the four parameters fixed and adjusting the value of the fourth until convergence) to determine the values of these parameters using the F1 score as the target function to optimize. Based on this analysis, we selected K = 40 for PIMiM (see Supplementary Fig. S3 for details). SNMNMF was also run with the optimized set of parameters and input data described in Zhang et al. (2011). Unlike PIMiM and SNMNMF, GroupMiR uses a non-parametric Bayesian prior for the number of modules; therefore, this number cannot be fixed in advance. Thus, for GroupMiR, we report modules and interactions with posterior probability at least 0.3 to get a set of comparable size with other methods. Previously, GroupMiR was shown to outperform several other methods (Le and Bar-Joseph, 2011) including GenMiR++ (Huang et al., 2007b); therefore, we omitted comparison with these methods here. Figure 2 presents a graphical view of the modules identified by PIMiM and SNMNMF. We color interaction edges between genes using different colors for each module. The modules identified by PIMiM are more dense and, hence, are in better agreement with previous findings regarding the regulation of interacting proteins by miRNAs.

Fig. 2.

Interactions between genes of the modules. We show an edge between two genes if they are members of a module and their interaction exists in the database. Each color corresponds to one module. Genes with no edges are omitted to improve visualization

4.1.1 Evaluation: identifying cancer miRNAs

We first looked at the set of miRNAs identified by each method (those belonging to the modules returned by each of the methods). The results in Table 1 demonstrate that using the protein interaction data greatly increases precision, recall and the F1 score. Both methods that use these data (PIMiM and SNMMNF) clearly outperform GroupMiR on this set. In addition, using a regression model also helps as indicated by the increase in F1 score PIMiM obtains over SNMNMF.

4.1.2 Expression coherence

In addition to analyzing the set of identified miRNAs, we also computed the average anti-correlation between miRNAs and mRNAs in the modules identified by each of the methods (Table 1). In this analysis, GroupMiR achieves the highest anti-correlation between miRNAs and the mRNAs they regulate in a module. This is the result of a much smaller module size identified by GroupMiR. As protein interactions are not used, mRNAs in these modules are selected because they are strongly anti-correlated with the miRNAs predicted to regulate the modules. This requirement leads to smaller modules and a better (anti) correlation between miRNAs and mRNAs. Still, PIMiM improves on SNMNMF in identifying anti-correlated miRNA–mRNA pairs. SNMNMF’s objective function does not explicitly include a component for expression anti-correlation between miRNAs and mRNAs, which may explain why it does not capture the inhibitory role of miRNAs. Thus, PIMiM provides a useful compromise between relying strongly on protein interactions, which improves accuracy and using the observed expression values in a regression setting.

4.1.3 MSigDB enrichment analysis

To test the biological function of the modules, we used 880 gene sets of canonical pathways (C2-CP, v.3.0) from MSigDB (Subramanian et al., 2005). We used the hypergeometric distribution to compute enrichment P-values for each of the modules with each of the MSigDB gene sets. To correct for the multiple hypothesis testings, we used the Benjamini–Hochberg procedure implemented in the R function p.adjust, which computes a q-value for each intersection. The results are presented in Figure 3, which depicts the number of modules with at least one enriched set in the MSigDB enrichment analysis and the total number of unique enriched gene sets. PIMiM outperforms SNMNMF, achieving both better enrichment for individual modules and better coverage of different MSigDB sets. MSigDB pathways are biased toward cancer pathways and so may be more relevant for the data we are analyzing here than Gene Ontology analysis. In addition to cancer hits, top hits for MSigDB include signatures for β cells that have been linked to cancer (Pelengaris and Khan, 2001) and several translation-related categories.

Fig. 3.

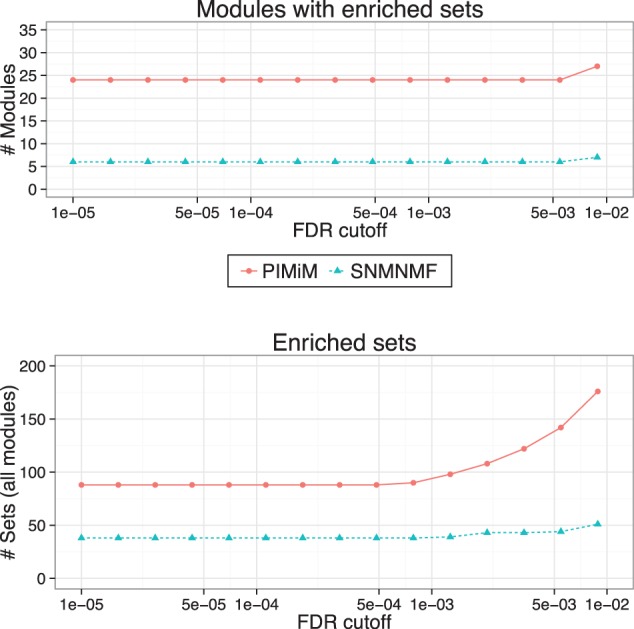
MSigDB enrichment analysis: pathway enrichment analysis was done using 880 gene sets of canonical pathways (C2-CP) from MSigDB (Subramanian et al., 2005). P-values were computed using hypergeometric test (with 10 000 random permutations) on the intersection of the set of genes in each module with MSigDB gene sets. Benjamini–Hochberg procedure was used to control the false discovery rate. Top: Number of modules significantly enriched for at least one MSigDB category for different significance cut-offs. Bottom: Number of MSigDB categories identified as in enriched in at least one of the modules for different significance cut-off

4.1.4 The effect of β on the performance of PIMiM

To test the effects of using the protein interaction data in PIMiM, we re-run PIMiM with different β values. The results are presented in Figure 4. As the figure shows, when decreasing the value of β, the performance of PIMiM on all evaluation metrics decreases indicating the protein protein interactions (PPI) data are useful for identifying coherent modules. On the other hand, increasing β too much leads to high weight for PPI data at the expense of the expression information, which also negatively affects the performance of PIMiM. Thus, balancing the two data types, which is done by setting an intermediate value for β is key to the success of PIMiM.

Fig. 4.

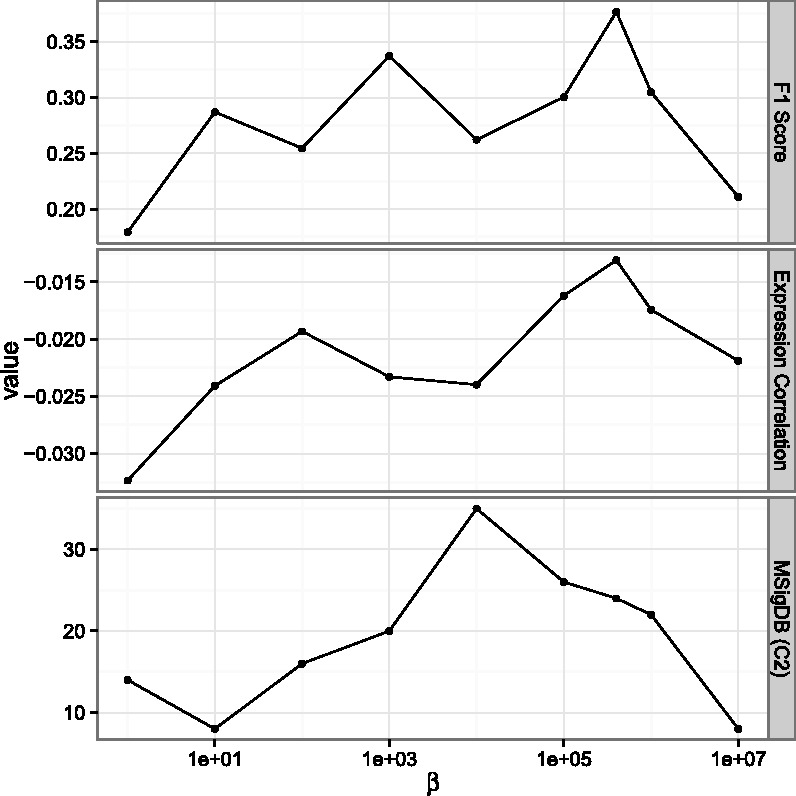
The effect of protein interaction data to the result. We varied the value of β and tested the different metrics discussed in Section 4. As can be seen, both high and low values lead to reduced performance

4.2 Integrating data from multiple types of cancers

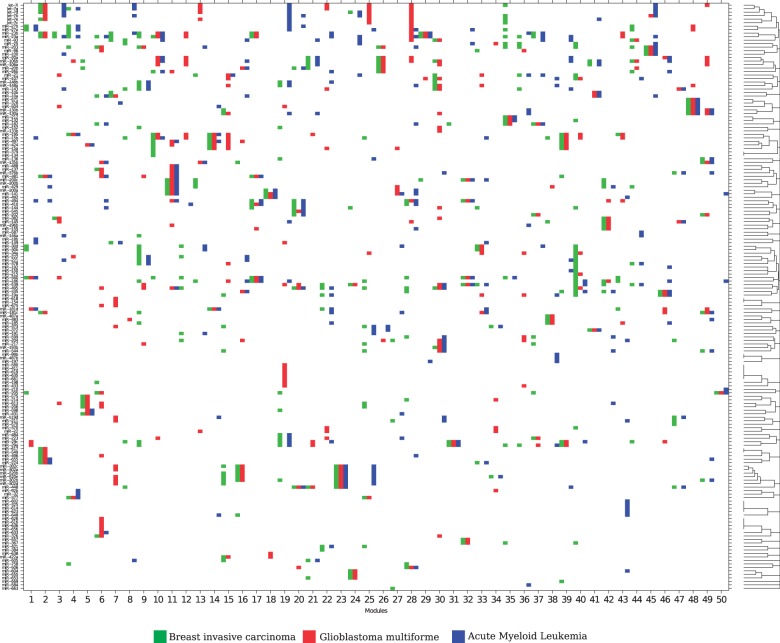
To further investigate miRNA control of different cancers, we applied PIMiM to a dataset of three cancer types using the multi-task learning framework described in Section 3. We learn three sets of modules for three types of cancer: breast invasive carcinoma (BRCA), Glioblastoma multiforme (GBM) and acute myeloid leukemia (AML). The miRNA and gene expression profiles of 89 BRCA, 498 GBM and 173 AML patients were downloaded from the TCGA. This set has 285 miRNAs and 10 922 mRNAs in common. Here, we combine the miRNA–mRNA predicted interactions from three public databases [MicroCosm (Griffiths-Jones et al., 2006), miRanda (John et al., 2004) and TargetScan (Lewis et al., 2005)] and protein interaction data from TRANSFAC (Wingender et al., 2000). For each cancer type, PIMiM learns 1 set of 50 modules. The parameters were set by optimizing for the F1 score of identifying miRNAs relevant to this dataset based on the set of cancer-related miRNAs from Koturbash et al. (2011). Figure 5 displays the miRNA-regulating modules in all three cancer types.

Fig. 5.

Inferred miRNA modules of the three cancer types (BRCA, GBM and AML). The x-axis shows the 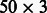modules learned for the three cancer types (each x-axis bar is subdivided into three with the color corresponding to the cancer type). The y-axis shows miRNAs ordered by hierarchical clustering of their module membership vector. In several cases, the same miRNAs are predicted for all or two of the three cancer types

4.2.1 Analysis of identified miRNAs

Several of the modules identified by PIMiM are regulated by known cancer miRNAs. The overall F1 score for cancer miRNAs for the joint analysis was high for all three cancer types: BRCA (0.6167), GBM (0.5789) and AML (0.6111). Well-known cancer miRNAs reported by PIMiM include the let-7b/c/d/e (active in BRCA: Yu et al., 2007, GBM: Lee et al., 2011 and AML: Jongen-Lavrencic et al., 2008), mirR-302a/b/c/d cluster [suppression of the CDK2 and CDK4/6 cell cycle pathways (Lin et al., 2010)] and miR-96 (active in BRCA: Guttilla and White, 2009, AML: Zhao et al., 2010, miR-34a (active in BRCA: O’Day and Lal, 2010, GBM: Li et al., 2009, AML: Zenz et al., 2009, miR-15a/b (active in AML: Calin et al., 2008). Some members of the miR-17-92 cluster (miR-18b, miR-19a, miR-20a/b and miR-93) are also identified by PIMiM (active in BRCA: Mendell, 2008, GBM: Ernst et al., 2010, AML: Mi et al., 2010). Note that some well-known cancer miRNAs, including miR-17 and miR-92, are missing from the modules because their expression is not available for enough of the samples. Several other subsets of miRNAs were assigned to cooperatively regulate modules in multiple types of cancer as shown in Figure 5.

4.2.2 Cancer-specific miRNAs

In addition to finding common cancer regulators, PIMiM can be used to identify cancer-type–specific regulators. These can either be used as biomarkers for a sub-type or can be studied to determine the unique properties of each cancer type. Although it is hard to obtain negative information (i.e. an article that mentions that a certain miRNA does not regulate a specific cancer type) several of the predictions made by PIMiM agree with current literature that, at least so far, only mentions their role in the cancer they were assigned to by PIMiM. Table 2 lists a few of these miRNAs and the cancer type they were predicted to regulate.

4.2.3 Analyzing the miRNAs and mRNAs in an identified module

In addition to identifying important miRNAs for this particular study, PIMiM returns a set of modules providing predictions of cooperative regulation of miRNAs and their mRNAs targets. To demonstrate the informative power of this modular structure, we analyze in more details one of these modules (see also Supplementary Results for detailed discussion of other modules). Figure 6 depicts a network of miRNAs and mRNAs identified as part of Module 11. Across all cancer types, PIMiM identified a set of 14 strongly connected proteins. MiR-200a/b/c, miR-141 and miR-429 are predicted to regulate this set of mRNAs in all types of cancer. These miRNAs have previously been reported to play a role in cancer and cell proliferation (Korpal et al., 2008; Peter, 2009). Interestingly, the miR-200 family is located in two chromosomal regions on 1p36.33 (200b, 200a and 429) and 12p13.31 (200c and 141), respectively (Uhlmann et al., 2010), which may support our prediction of their cooperative regulation. Applying Gene Ontology analysis [using FuncAssociate (Berriz et al., 2009)] and MSigDB enrichment analysis to the set of 14 mRNAs in this module indicates that this set is enriched with members of transcription factor TFTC/STAGA and TFFIID complexes. Recent findings support the link between these complexes and cancer (Kurabe et al., 2007). This module also includes a tumor suppressor gene MSH2 (Wada-Hiraike et al., 2005) and a famous breast cancer susceptibility gene BRCA1 (Miki et al., 1994).

Fig. 6.

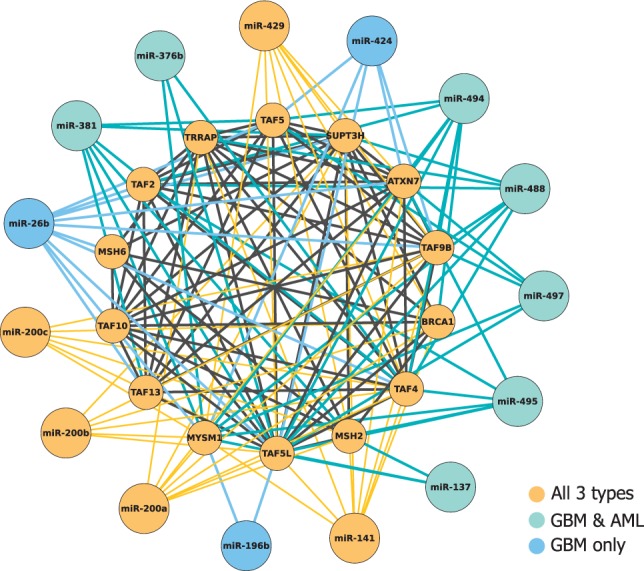
miRNAs and mRNAs assigned to Module 11 in all three cancer types. Color indicates the specific cancer type for which the mRNA or miRNA was selected as part of the module

5 CONCLUSIONS

We presented PIMiM, a new method for inferring condition-specific regulation of miRNAs and for identifying their targets. PIMiM combines sequence, expression and interaction data to discover miRNA-regulated modules of mRNAs. We use a probabilistic model that combines regression with network information to discover these modules. We developed an iterative learning procedure to learn the parameters of our model and a multi-task learning method for combining data from multiple conditions.

We tested PIMiM on ovarian cancer expression data and have shown that it correctly identifies miRNAs regulating this cancer type, and that it is able to group relevant genes together. Comparison with other methods indicates that by using protein interaction data, we can improve accuracy while at the same time PIMiM also maintains expression coherence among mRNAs and anti-correlation between miRNAs and the mRNAs they are predicted to regulate improving on previous methods that have also used protein interaction data. Application of the method to compare and contrast three types of cancer identified both common and unique regulators, which can allow researchers to determine the core cancer regulatory network and the differences in regulation among the various cancers we studied.

Although we believe PIMiM can already be of use to researchers that collect mRNA and miRNA expression data, there are a number of extensions that can further improve it. As aforementioned, we follow several other articles in isolating the miRNA target prediction task from the combinatorial analysis of miRNA–TF regulation. Although such an approach leads to good results as discussed earlier in the text, our longer term goal is to develop a method that can incorporate both types of regulation in a single-modeling framework. For this, we would need to determine the role a specific TF plays (activator or repressor) and its activity level [either based on its expression levels or on the set of its targets (Shi et al., 2009)]. With this information, we can incorporate TFs into our regression model to account for their part in regulating expression, which will hopefully lead to better results regarding the role played by specific miRNAs. The regression component that we considered in PIMiM uses a simple linear model to explain the regulation effect of multiple miRNAs. We could also extend this to incorporate other complex combinatorial analysis (for example, AND, OR logic). However, this requires an extension of the methods derived in the article. We thus leave this for future work. In addition, we would like to incorporate additional types of high-throughput data, for example, epigenetic data to our analysis framework.

Funding: National Institutes of Health (U01 HL108642) and National Science Foundation (DBI-0965316) award (to Z.B.J.).

Conflict of Interest: none declared.