Abstract
Motivation: In silico prediction of drug-target interactions plays an important role toward identifying and developing new uses of existing or abandoned drugs. Network-based approaches have recently become a popular tool for discovering new drug-target interactions (DTIs). Unfortunately, most of these network-based approaches can only predict binary interactions between drugs and targets, and information about different types of interactions has not been well exploited for DTI prediction in previous studies. On the other hand, incorporating additional information about drug-target relationships or drug modes of action can improve prediction of DTIs. Furthermore, the predicted types of DTIs can broaden our understanding about the molecular basis of drug action.
Results: We propose a first machine learning approach to integrate multiple types of DTIs and predict unknown drug-target relationships or drug modes of action. We cast the new DTI prediction problem into a two-layer graphical model, called restricted Boltzmann machine, and apply a practical learning algorithm to train our model and make predictions. Tests on two public databases show that our restricted Boltzmann machine model can effectively capture the latent features of a DTI network and achieve excellent performance on predicting different types of DTIs, with the area under precision-recall curve up to 89.6. In addition, we demonstrate that integrating multiple types of DTIs can significantly outperform other predictions either by simply mixing multiple types of interactions without distinction or using only a single interaction type. Further tests show that our approach can infer a high fraction of novel DTIs that has been validated by known experiments in the literature or other databases. These results indicate that our approach can have highly practical relevance to DTI prediction and drug repositioning, and hence advance the drug discovery process.
Availability: Software and datasets are available on request.
Contact: zengjy321@tsinghua.edu.cn
Supplementary information: Supplementary data are available at Bioinformatics online.
1 INTRODUCTION
Drug development currently remains an expensive and time-consuming process with extremely low success rate: it typically takes 10–15 years and $800 million–1 billion to bring a new drug to market (Dimasi, 2001). In recent decades, the rate of the number of new drugs approved by the US Food and Drug Administration versus the amount of money invested in pharmaceutical research and development has significantly declined (Booth and Zemmel, 2004). This productivity problem has urged drug developers to seek new uses for existing or abandoned drugs (Booth and Zemmel, 2004). Such a new strategy is also called drug repositioning or drug repurposing. A strong support for the possibility of drug repositioning is the increasingly accepted concept of ‘polypharmacology’, i.e. individual drugs can interact with multiple targets rather than a single target (MacDonald et al., 2006; Xie et al., 2012). For example, serotonin and serotonergic drugs can interact with both 5-HT G protein-coupled receptors and  ion channel proteins, even though these two target proteins are not related in sequence or structure (Cheng et al., 2012; Keiser et al., 2007; Kroeze et al., 2002; Roth et al., 2004). This polypharmacological property of a drug enables us to identify more than one target that it can act on and hence develop its new uses.
ion channel proteins, even though these two target proteins are not related in sequence or structure (Cheng et al., 2012; Keiser et al., 2007; Kroeze et al., 2002; Roth et al., 2004). This polypharmacological property of a drug enables us to identify more than one target that it can act on and hence develop its new uses.
In silico prediction of interactions between drugs and target proteins provides an important tool for drug repositioning, as it can significantly reduce wet-laboratory work and lower the cost of the experimental determination of new drug-target interactions (DTIs). Various methods have been proposed for in silico DTI prediction. When 3D structures are available, molecular docking is commonly used to virtually screen a large number of compounds against a target protein (Cheng et al., 2007; Donald, 2011; Morris et al., 2009). When 3D structures of molecules are absent, a number of different approaches have been developed to address the in silico DTI prediction problem. Most of these structure-free methods can be grouped into two classes, namely, ligand-based and network-based approaches. A representative ligand-based approach is the similarity ensemble approach (Keiser et al., 2007, 2009), which predicts new DTIs using 2D structure similarity of ligands. Although ligand-based approaches are able to discover a number of DTIs that have been validated experimentally, they have difficulty in identifying drugs with novel scaffolds that differ from those of reference compounds (Yabuuchi et al., 2011).
Numerous network-based approaches have been proposed to exploit latent features of DTI profiles and have recently become a popular tool for DTI prediction and drug repositioning (Bleakley and Yamanishi, 2009; Chen et al., 2012; Cheng et al., 2012; Mei et al., 2012; van Laarhoven et al., 2011; Xia et al., 2010; Xie et al., 2012; Yamanishi et al., 2008). Although these network-based approaches have achieved promising results, most of them can only predict binary DTIs, that is, they can only determine whether a drug interacts with a target protein, but cannot tell how they interact with each other. However, individual DTIs generally have different meanings. For example, drug-target pairs can be described by different relationships, such as direct and indirect interactions (Günther et al., 2008). A direct interaction is usually caused by protein-ligand binding, whereas an indirect interaction can be induced by the changed expression level of a protein or active metabolites produced by a drug. In addition, DTIs can be annotated with different drug modes of action, e.g. activation and inhibition (Kuhn et al., 2012). Here, ‘drug modes of action’ may be slightly different from the term used in the literature, e.g. (Iorio et al., 2010). In this article, we mainly use this term to represent the following three specific types of interactions: binding, activation and inhibition. Hereinafter, we will use ‘types of DTIs’ to represent both drug-target relationships and drug modes of action. A network in which links are associated with different meanings is called the multidimensional network (Lü and Zhou, 2011). In our context, we call a DTI network where links are annotated with different types of interactions the multidimensional DTI network. On the one hand, types of DTIs provide additional useful information, which can be incorporated into a multidimensional network to improve DTI prediction. On the other hand, the predicted types of DTIs can extend our understanding about the molecular basis of drug action. Despite these positive aspects, current rich information about types of DTIs (Günther et al., 2008; Kuhn et al., 2012) has not been well exploited for DTI prediction, and how to incorporate such information into a multidimensional network to predict different types of DTIs still remains an open question.
In this article, we propose an effective machine-learning approach to accurately predict different types of DTIs on a multidimensional network. Unlike previous network-based approaches (Bleakley and Yamanishi, 2009; Chen et al., 2012; Cheng et al., 2012; Mei et al., 2012; van Laarhoven et al., 2011; Xia et al., 2010; Yamanishi et al., 2008), which only predict binary DTIs, our approach not only identifies new DTIs but also infers their corresponding types of interactions, such as drug-target relationships or drug modes of action. Our approach uses a generalized version of a two-layer undirected graphical model, called restricted Boltzmann machine (RBM) (Hinton and Salakhutdinov, 2006), to represent a multidimensional DTI network, which encodes different types of DTIs. In addition, we apply a practical learning algorithm, called Contrastive Divergence (CD) (Hinton, 2002), to train our RBM model and predict unknown types of DTIs.
To our knowledge, our work is the first approach to predict different types of DTIs on a multidimensional network, which not only describes binary DTIs but also encodes their corresponding types of interactions. We have tested our algorithm on two public databases, namely, MATADOR (Günther et al., 2008) and STITCH (Kuhn et al., 2012), which contain information about drug-target relationships and drug modes of action, respectively. Our tests demonstrate that our RBM model can be used as a highly powerful tool for integrating different types of DTIs into a multidimensional network and predicting different types of interactions with high accuracy. In particular, our results show that integrating different types of DTIs into prediction with distinction can achieve the area under precision-recall curve (AUPR) up to 89.6, which can significantly outperform other predictions either by simply mixing multiple types of interactions without distinction or using only a single interaction type. Further tests show that our approach can predict a high percentage of novel DTIs that has been validated by known experiments in the literature or other databases. These results indicate that our approach can have potential applications in drug repositioning and hence advance the drug discovery process.
1.1 Related work
A number of network-based approaches have been proposed for predicting unknown interactions between drugs and targets. In Yamanishi et al. (2008), a supervised learning framework was developed based on a bipartite graph, which integrates both chemical and genomic spaces by mapping them into a unified space. Cheng et al. (2012) proposed a network-based inference approach to predict new DTIs by exploiting the topology similarity of the underlying interaction network. In Zhao and Li (2010), drug phenotypic, chemical indexes and protein–protein interactions in genomic space were integrated into a computational framework for DTI prediction. Chen et al. (2012) proposed a random walk approach for DTI prediction based on a heterogeneous network, which integrates drug similarity, target similarity and DTI similarity. Bleakley and Yamanishi (2009) presented a new approach, called Bipartite Local Model (BLM), to predict unknown DTIs by combining independent drug-based and target-based prediction results using a supervised learning method. Mei et al. (2012) further extended this BLM approach to incorporate the capacity of learning from neighbors and predict the interactions for new drug or target candidates. In Xia et al. (2010), a manifold regularization semi-supervised learning method was proposed to integrate heterogenous biological data sources for DTI prediction. A regularized least square algorithm was proposed in van Laarhoven et al. (2011) for DTI prediction using a product of kernels derived from DTI profiles. In Gottlieb et al. (2011), He et al. (2010) and Perlman et al. (2011), DTI prediction was formulated into a classification problem after defining multiple groups of drug-related and target-related features, such as drug–drug and gene–gene similarity measures. In addition to chemical and genomic data, phenotypic information, such as side-effect profiles (Campillos et al., 2008; Mizutani et al., 2012), transcriptional response data (Iorio et al., 2010) and public gene expression data (Dudley et al., 2011; Sirota et al., 2011), has also been used for DTI prediction and drug repositioning. Although previous network-based approaches have achieved promising results for DTI prediction and drug repositioning, few of them are specifically designed for integrating and predicting different types of DTIs on a multidimensional network.
RBMs, which are used as important learning modules for constructing deep belief nets (Arel et al., 2010; Bengio, 2009), have been successfully applied in many fields, such as dimensionality reduction (Hinton and Salakhutdinov, 2006), classification (Larochelle and Bengio, 2008), collaborative filtering (Salakhutdinov et al., 2007) and computational biology (Eickholt and Cheng, 2012). Recently, the predictive power of RBMs has also been demonstrated in the Netflix Prize contest (Bell and Koren, 2007; Salakhutdinov et al., 2007), a public competition for developing the best collaborative filtering algorithm to predict user ratings for movies. To our knowledge, our work is the first approach to apply RBMs into large-scale DTI prediction.
2 METHODS
2.1 RBMs for DTI prediction
We use an RBM to formulate the DTI prediction problem on a multidimensional network. An RBM is a two-layer graphical model that can be used to learn a probability distribution over input data (Hinton and Salakhutdinov, 2006). As shown in Figure 1A, an RBM consists of a layer of visible units and a layer of hidden units. Each visible unit is connected to all hidden units, and no intra-layer connection exists between any pair of visible units or any pair of hidden units. In our RBM model, visible units encode observed types of DTIs, such as drug-target relationships and drug modes of action (Fig. 1B), and hidden units represent latent features describing DTIs.
Fig. 1.

An RBM with binary hidden units representing latent features and visible units encoding observed types of DTIs. (A) Overview of an RBM, where m is the number of hidden units and n is the number of visible units. (B) The information encoded in a visible unit
We use a simple example (Fig. 2) to describe how to construct RBMs from a multidimensional DTI network. Figure 2A shows a toy example of a multidimensional DTI network, where each DTI is associated with binary variables, which represent the states of direct and indirect interactions, respectively. As shown in Figure 2B, we build a specific RBM for every single target with the same number of hidden units and the same definitions of visible units. The binary states of visible variables for those missing DTIs are treated as zero in the constructed RBMs. The constructed RBMs for a multidimensional DTI network are associated with the same parameters. In other words, the constructed RBMs for all targets use the same parameters between hidden and visible layers. In Figure 2B, both RBMs for both target 1 and target 2 share the same parameters.
Fig. 2.
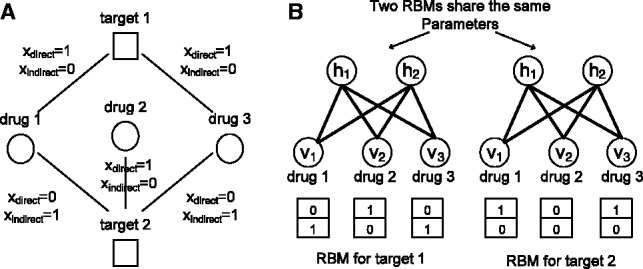
A toy example for constructing RBMs from a multidimensional DTI network. (A) A simple multidimensional DTI network, where indicators xdirect and xindirect are equivalent to 1 if corresponding interaction types are present in visible data and 0 otherwise. (B) Constructed RBMs for corresponding targets. The binary numbers inside rectangles represent the states of visible variables. The RBMs for both target 1 and target 2 share the same parameters
Compared with other prediction approaches, our RBM model can capture not only the correlations of drug-target pairs in a DTI network but also the correlations of different types of DTIs. Here, we use the simple example shown in Figure 2 to illustrate how our RBM model exploits the corrections in a multidimensional network to make prediction. Suppose that we have known different types of DTIs for target 1 in this example. To know which states of hidden units our RBM model should have, we let the three drugs send messages to hidden units and update their corresponding states. Conversely, once we know the states of hidden units for target 1, hidden units then send messages to visible units for the connected drugs and update their corresponding states. As in other collaborative filtering applications (Salakhutdinov et al., 2007), after a number of iterations of the aforementioned updates, our RBM model can effectively capture the underlying features encoded in a multidimensional network. Based on the trained parameters between layers of hidden and visible units, our RBM model can then predict unknown types of DTIs based on input visible data.
In an RBM, suppose that in total there are n visible units, m hidden units and t types of DTI encoded in a visible unit. Let binary indicator vector  , denote state of the i-th visible unit, where visible variables
, denote state of the i-th visible unit, where visible variables
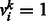 if the k-th type of DTI is observed in input data, and
if the k-th type of DTI is observed in input data, and 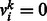 otherwise. Let binary indicator variable hj,
otherwise. Let binary indicator variable hj, 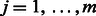 , denote the state of the j-th hidden unit. Let
, denote the state of the j-th hidden unit. Let 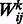 be the weight associated with a connection between visible variable
be the weight associated with a connection between visible variable 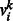 and hidden variable hj. Let
and hidden variable hj. Let 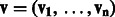 and
and 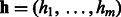 denote the configurations of visible and hidden layers, respectively. Then
denote the configurations of visible and hidden layers, respectively. Then 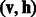 is called a joint configuration of an RBM. As there is no intra-layer connection within both hidden and visible layers in an RBM, the energy of a joint configuration
is called a joint configuration of an RBM. As there is no intra-layer connection within both hidden and visible layers in an RBM, the energy of a joint configuration 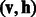 can be defined by
can be defined by
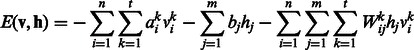 |
(1) |
where n, m and t are the numbers of visible units, hidden units and types of DTI encoded in a visible unit, respectively, 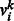 , hj are visible variables and hidden units, respectively, and
, hj are visible variables and hidden units, respectively, and 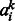 , bj are their corresponding bias weights (offsets), and
, bj are their corresponding bias weights (offsets), and 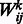 is the corresponding weight for the connection between visible variable
is the corresponding weight for the connection between visible variable 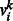 and hidden variable hj. Then, the probability of a joint configuration
and hidden variable hj. Then, the probability of a joint configuration 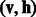 can be defined by
can be defined by
| (2) |
where 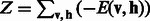 is called the normalizing constant or partition function. Summing over all possible configurations of
is called the normalizing constant or partition function. Summing over all possible configurations of 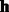 , we obtain the following marginal distribution over visible data
, we obtain the following marginal distribution over visible data  :
:
| (3) |
As there is no intra-layer connection between any pair of visible or hidden units, we can define the following conditional probabilities:
| (4) |
| (5) |
where n, m and t are the numbers of visible units, hidden units and types of DTI encoded in a visible unit, respectively, and 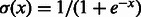 is the logistic function. These conditional probabilities are important for the iterative updates between hidden and visible layers when training an RBM model.
is the logistic function. These conditional probabilities are important for the iterative updates between hidden and visible layers when training an RBM model.
Unlike the conditional probabilities of visible variables in Salakhutdinov et al. (2007), which used a conditional multinomial distribution, here, our conditional probability of visible variables in Equation (4) uses a conditional Bernoulli distribution. This is because in our RBM model, more than one visible variable can be assigned one for a DTI. For example, a DTI can be annotated with ‘direct’, ‘binding’ and ‘inhibition’ simultaneously. Our RBM model is data-driven and respect data as much as possible. As also demonstrated in Salakhutdinov et al. (2007), RBMs can capture the nature distribution of data. As we treat each interaction type as a separate binary variable, it is possible that two inconsistent interaction types (e.g. ‘direct’ and ‘indirect’) can be both yielded by our RBM model. This means that the data implies that these two interaction types are both possible. In addition, by defining each interaction type as a separate variable, our RBM model is general and can be easily extended to include more interaction types from other data sources without much manual inspection on the consistence of different types of DTIs.
2.2 Training
We first use a real example to demonstrate the complexity of parameter training in our RBM model. In the MATADOR-based data that we have tested (Section 3.1), the number of drugs is 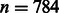 . When only predicting direct and indirect interactions, the number of interaction types that we need to consider is t = 2. In our RBM model, we typically set the number of hidden units
. When only predicting direct and indirect interactions, the number of interaction types that we need to consider is t = 2. In our RBM model, we typically set the number of hidden units 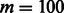 . In such a case, the total number of parameters in our RBM model is
. In such a case, the total number of parameters in our RBM model is 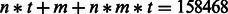 . In general, training an RBM with such a large number of parameters posts a difficult task. Later in the text, we will describe how to perform parameter training in an RBM model.
. In general, training an RBM with such a large number of parameters posts a difficult task. Later in the text, we will describe how to perform parameter training in an RBM model.
To train an RBM and learn its parameter, we need to maximize the likelihood of visible data with respect to the parameters 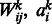 and bj. To achieve this goal, we could perform gradient ascent in the log-likelihood of the training data derived from Equation (3) and incrementally adjust the weights and biases:
and bj. To achieve this goal, we could perform gradient ascent in the log-likelihood of the training data derived from Equation (3) and incrementally adjust the weights and biases:
| (6) |
where ϵ is the learning rate, 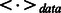 denotes an expectation of the data distribution and
denotes an expectation of the data distribution and 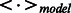 denotes an expectation of the distribution defined by the model.
denotes an expectation of the distribution defined by the model.
In Equation (6), 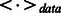 can be computed easily based on the frequency information obtained from visible data. Unfortunately, it is generally difficult to compute
can be computed easily based on the frequency information obtained from visible data. Unfortunately, it is generally difficult to compute 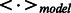 , as it would require exponential time to do so. To avoid this problem, Hinton (2002) proposed a practical learning algorithm, called Contrastive Divergence (CD), which minimizes the Kullback–Leibler divergence. In this work, we use a mean-field version of the CD algorithm (Le Roux and Bengio, 2008; Welling and Hinton, 2002) to train our RBM model. In particular, we use the following procedure in each training pass to incrementally adjust the weights and biases:
, as it would require exponential time to do so. To avoid this problem, Hinton (2002) proposed a practical learning algorithm, called Contrastive Divergence (CD), which minimizes the Kullback–Leibler divergence. In this work, we use a mean-field version of the CD algorithm (Le Roux and Bengio, 2008; Welling and Hinton, 2002) to train our RBM model. In particular, we use the following procedure in each training pass to incrementally adjust the weights and biases:
| (7) |
| (8) |
| (9) |
where ϵ is the learning rate, 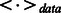 denotes an average value over all input data for each update and
denotes an average value over all input data for each update and 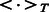 denotes the average value over T mean-field iterations, which is considered a good approximation of
denotes the average value over T mean-field iterations, which is considered a good approximation of 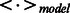 in the log-likelihood function in Equation (6) (Hinton, 2002; Le Roux and Bengio, 2008; Welling and Hinton, 2002).
in the log-likelihood function in Equation (6) (Hinton, 2002; Le Roux and Bengio, 2008; Welling and Hinton, 2002).
2.3 Making predictions
To predict the unknown types of DTIs for a given target with visible data  , we compute the following probability distribution after one iteration of the mean-field updates (Salakhutdinov et al., 2007):
, we compute the following probability distribution after one iteration of the mean-field updates (Salakhutdinov et al., 2007):
| (10) |
| (11) |
where n, m and t are the numbers of visible units, hidden units and types of DTI encoded in a visible unit, respectively, 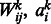 and bj are parameters that have been learned in Section 2.2, and
and bj are parameters that have been learned in Section 2.2, and 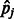 is the conditional probability of hidden variable hj given visible data. After that, we compute the expectation as our final prediction for the query target.
is the conditional probability of hidden variable hj given visible data. After that, we compute the expectation as our final prediction for the query target.
2.4 Conditional RBMs
For a drug-target pair, which does not have a connection on a multidimensional DTI network, it could be considered either a missing interaction or a negative interaction. In general, a set of known DTIs that have been verified experimentally provide more reliable information than those drug-target pairs, which do not have connections on a multidimensional DTI network. To incorporate this additional information, we use a conditional RBM (Salakhutdinov et al., 2007) to further formulate our prediction problem. Let 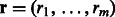 be a binary indicator vector, in which
be a binary indicator vector, in which 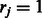 if there exists a known DTI between the input target and the j-th drug, and
if there exists a known DTI between the input target and the j-th drug, and 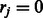 otherwise. The states of rj can be directly obtained based on the visible DTI data from a constructed DTI network. Here, r is a binary indicator vector representing the reliability of observed data. In general, DTIs that have been verified experimentally provide more reliable information than unknown DTIs. A conditional RBM defines a joint distribution over
otherwise. The states of rj can be directly obtained based on the visible DTI data from a constructed DTI network. Here, r is a binary indicator vector representing the reliability of observed data. In general, DTIs that have been verified experimentally provide more reliable information than unknown DTIs. A conditional RBM defines a joint distribution over 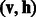 conditioned on r. In a conditional RBM, the conditional probabilities of visible and hidden units can be written as:
conditioned on r. In a conditional RBM, the conditional probabilities of visible and hidden units can be written as:
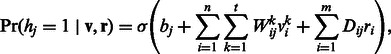 |
(12) |
where Dij is a parameter describing the effect of  on
on 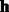 . The parameter Dij can be also learned using the CD algorithm:
. The parameter Dij can be also learned using the CD algorithm:
| (13) |
2.5 Implementation
We chose a conditional RBM to perform DTI prediction on a multidimensional network that encodes different types of DTIs. The algorithm was implemented in Java, using the jaRBM package (http://sourceforge.net/projects/jarbm/). For the value of m, we chose an empirical range according to the literature. Here, we chose 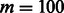 . We set learning rate
. We set learning rate 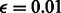 . For other parameters, we chose the default values that were defined in the jaRBM package. The initial values of
. For other parameters, we chose the default values that were defined in the jaRBM package. The initial values of 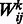 , bj,
, bj, 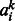 and Dij were sampled from Gaussian distribution with standard derivation 0.1. In the CD learning procedure, we ran the mean-field updates 100 passes over training data. The training of our RBM model runs in several hours on a typical training dataset. For example, the training of our RBM model on the MATADOR-based data (Supplementary Table S1 in Section S1) takes 5.5 h on a PC machine with a 3.3 GHz Intel core i5 processor and 4 GB memory.
and Dij were sampled from Gaussian distribution with standard derivation 0.1. In the CD learning procedure, we ran the mean-field updates 100 passes over training data. The training of our RBM model runs in several hours on a typical training dataset. For example, the training of our RBM model on the MATADOR-based data (Supplementary Table S1 in Section S1) takes 5.5 h on a PC machine with a 3.3 GHz Intel core i5 processor and 4 GB memory.
3 RESULTS AND DISCUSSION
3.1 Datasets and evaluation metrics
We tested our RBM model on two datasets, which were derived from MATADOR (Günther et al., 2008) and STITCH (Kuhn et al., 2012), respectively. MATADOR is a manually curated online database, which mainly describes drug-target relationships, including direct and indirect DTIs. The list of direct and indirect DTIs in MATADOR was first extracted by automated text-mining and then followed by manual annotation (Günther et al., 2008). STITCH provides modes of action for the interactions between proteins and chemicals, which were annotated based on evidence derived from known experiments in the literature (Kuhn et al., 2012). For the MATADOR-based dataset, we only extracted those DTI records in which protein and drug names are present and annotation terms correspond to ‘DIRECT’ or ‘INDIRECT’. For the STITCH-based dataset, we only kept a list of DTI records in which drugs and target proteins overlap those in MATADOR. For the mode of action term in the STITCH-based data, we only considered ‘binding’, ‘activation’ and ‘inhibition’. In summary, the MATADOR-based dataset contains 784 drugs, 2431 protein targets and 13 064 DTIs, in which 7862 interactions are direct and 5202 interactions are indirect. The STITCH-based dataset contains 598 drugs, 671 protein targets and 3296 DTIs, in which 2589, 945 and 1493 interactions are annotated with ‘binding’, ‘activation’ and ‘inhibition’, respectively. Descriptive statistics about these two datasets can be found in Table S1 in Supplementary Material Section S1.
Receiver Operator Characteristic (ROC) and Precision-Recall (PR) curves are commonly used to assess the performance of a prediction model. For highly skewed data, ROC curves can give an overoptimistic picture of an algorithm’s performance (Davis and Goadrich, 2006). In this scenario, PR curves provide a better view of the prediction results than ROC curves. As stated in Bleakley and Yamanishi (2009) and van Laarhoven et al. (2011), when evaluating the DTI prediction results, in which there are usually few positive DTIs, PR curves provide greater biological significance and are considered a better quality measure than ROC curves. Therefore, we mainly used PR curves and the AUPR curve to evaluate the performance of our algorithm, though we also reported the area under the ROC curve (AUC) in our test results.
3.2 Predicting direct and indirect DTIs
In general, drug-target relationships can be classified into two categories, including direct and indirect interactions. Direct interactions are usually caused by protein-ligand binding, whereas indirect interactions can be driven by different mechanisms. For instance, indirect interactions can be induced by metabolites of drugs or changes in gene expressions (Günther et al., 2008). To examine whether our algorithm can accurately predict direct and indirect DTIs on a multidimensional network, we tested it on the MATADOR-based data. In particular, we performed the following three tests: (i) Integrating both direct and indirect DTIs with distinction, which means that the input data of the RBM is a multidimensional vector indicating different types of interactions; (ii) Mixing both direct and indirect DTIs without distinction, which means that the input data is a one-dimensional binary vector indicating whether DTIs are observed; (iii) Using only a single interaction type (i.e. using only direct or indirect DTIs). For each test, we performed a 10-fold cross-validation procedure, as described in Supplementary Material Section S3.
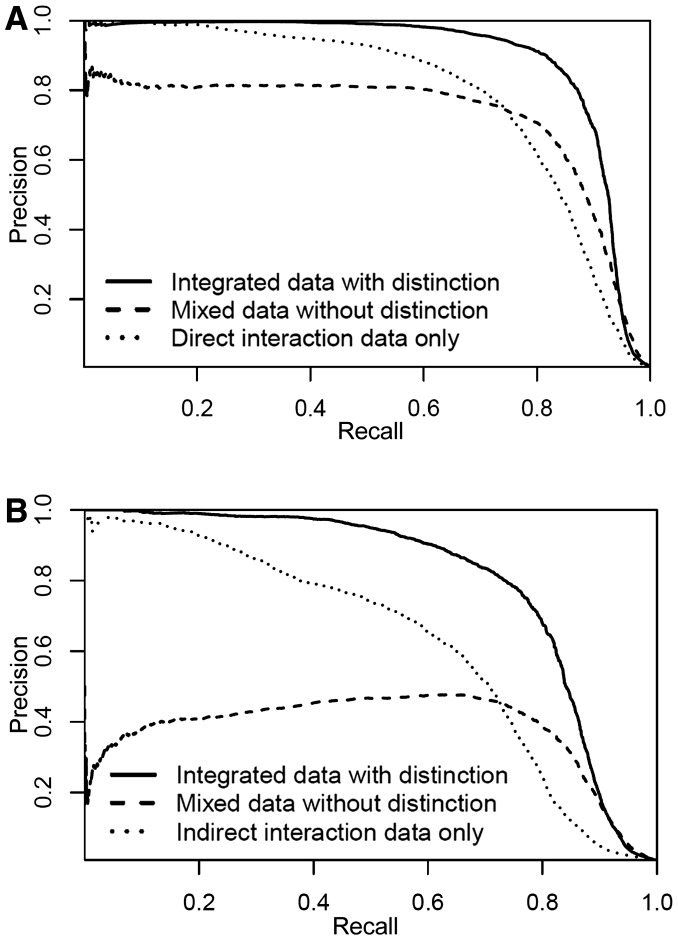
The results of the aforementioned three tests are summarized in Table 1, and their corresponding PR curves are shown in Figure 3. When integrating both direct and indirect interactions with distinction, our algorithm achieved the best performance with an AUPR score up to 89.6 for direct interaction prediction and 80.1 for indirect interaction prediction. These results demonstrated that our RBM model can effectively integrate different drug-target relationships on a multidimensional DTI network to accurately predict direct or indirect interactions. In addition, our results showed that integrating both direct and indirect DTIs with distinction significantly outperformed the other two tests, which only considered a single interaction type or simply mixed direct and indirect interactions without distinction. In particular, the integration of direct and indirect interactions improved the AUPR score by >10% for direct interaction prediction and >17% for indirect interaction prediction (Table 1). In PR curves, compared with the other two tests, integrating both interaction types with distinction achieved a better precision value almost at every recall value (Fig. 3). An interesting result is that mixing both interactions without distinction yielded worse performance than using a single interaction type (Table 1). For example, for direct interaction prediction, the AUPR score was decreased from 78.9 to 72.1. This result implies that incorporating a new data type into DTI prediction is non-trivial and requires careful data integration. In addition, our results show that our RBM model respect the data and can predict a high percentage of consistent DTIs. For example, when we chose 0.5 as the probability threshold to infer the interaction type, >99% of positive DTIs predicted by our algorithm were consistent (i.e. <1% of DTIs were predicted as both direct and indirect interactions).
Table 1.
Results on predicting direct and indirect DTIs
| Drug-target relationship | Test method | AUC | AUPR |
|---|---|---|---|
| Direct interaction | Integrating data with distinction | 98.7 | 89.6 |
| Mixing data without distinction | 98.8 | 72.1 | |
| Using direct interactions only | 98.0 | 78.9 | |
| Indirect interaction | Integrating data with distinction | 97.1 | 80.1 |
| Mixing data without distinction | 97.0 | 37.8 | |
| Using indirect interactions only | 94.8 | 62.4 |
Note: ‘Integrating data with distinction’ corresponds to the test in which our algorithm integrated both direct and indirect interactions with distinction. ‘Mixing data without distinction’ corresponds to the test in which our algorithm mixed both direct and indirect interactions without distinction. ‘Using direct (indirect) interactions only’ corresponds to the test in which our algorithm used only direct (indirect) interactions. The highest AUPR score is shown in bold.
Fig. 3.
PR curves for the direct and indirect DTIs predicted by our RBM model. (A) PR curves for the direct DTIs predicted by our model. (B) PR curves for the indirect DTIs predicted by our model
In our 10-fold cross-validation test (Table 1), the test method ‘using direct (indirect) interaction only’ used less training data than other two test methods. This may create bias when comparing two prediction methods using training data with different sizes. To make a fair comparison, we have made an additional comparison between methods ‘integrating data with distinction’ and ‘using direct (indirect) interaction only’ using training data of the same size (Supplementary Material Section S4). Our new comparison results confirmed that integrating data with distinction outperformed the method that uses a single interaction only.
To check whether our algorithm can have a wider range of applications, we also performed a 5-fold cross-validation test (Supplementary Material Section S3). Compared with the 10-fold cross-validation results, we only found a small decrease in our algorithm’s performance in the 5-fold cross-validation test.
To perform more sanity check on our algorithm’s performance, we also conducted another test that is similar to leave-one-out cross-validation except that we removed homologous proteins from training data. For training data, we only kept those DTIs in which proteins have sequence identity 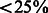 to the target of the validating interaction. This process can significantly reduce the size of dataset. In our test, the training dataset has only ∼300 targets. This test is more rigorous than previous leave-one-out cross-validation (LOOCV) tests performed in (Bleakley and Yamanishi, 2009; van Laarhoven et al., 2011; Yamanishi et al., 2008), in that we have removed similar proteins with high sequence identity from training data and thus reduced impact of protein homology on the network-based prediction of DTIs.
to the target of the validating interaction. This process can significantly reduce the size of dataset. In our test, the training dataset has only ∼300 targets. This test is more rigorous than previous leave-one-out cross-validation (LOOCV) tests performed in (Bleakley and Yamanishi, 2009; van Laarhoven et al., 2011; Yamanishi et al., 2008), in that we have removed similar proteins with high sequence identity from training data and thus reduced impact of protein homology on the network-based prediction of DTIs.
The results of our LOOCV like test show that, our approach still achieved decent prediction accuracy, with AUPR 79.0 for direct interaction prediction, but the AUPR score for indirect interaction prediction dropped to 59.1. We further investigated this problem and found that the average degree of indirect interactions with drugs for targets in training data was reduced to 1.67. With insufficient number of DTIs, it would be difficult to train our RBM model and make accurate prediction.
To mimic the real situation in which DTI network data are available, we also performed an additional test on those DTIs in which the degree of the target is above the average degree of the multidimensional network (i.e. the degree of the target in the validating interaction is 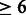 ). The results of this test show that, our approach achieved decent performance, with AUPR 80.4 for direct interaction prediction and 74.5 for indirect interaction prediction. These results indicate that in the real situation, our RBM model can make reasonably accurate prediction even homologous proteins are not present in training data.
). The results of this test show that, our approach achieved decent performance, with AUPR 80.4 for direct interaction prediction and 74.5 for indirect interaction prediction. These results indicate that in the real situation, our RBM model can make reasonably accurate prediction even homologous proteins are not present in training data.
As little work has been developed for predicting unknown types of DTIs in a multidimensional network, it is difficult for us to directly compare our work with other prediction approaches. Instead, we have compared our algorithm with a simple logic-based approach on the MATADOR-based data. This simple logic-based approach follows the basic premise (i.e. similar drugs and targets should have similar interactions) that has been widely used in previous prediction approaches. More details of this simple logic-based algorithm can be found in Supplementary Material Section S5. As summarized in Table 2, the comparison results show that our algorithm outperformed the simple logic based approach. This is expected, as the simple logic based approach simply uses the closest interaction type profiles to predict unknown types of DTIs. Such a strategy only exploits a small proportion of training data and cannot be sufficient enough to capture the deep correlations of different types of DTIs in a multidimensional network. On the other hand, our RBM model uses hidden units to represent the intrinsic correlations of different types of DTIs in the network and can effectively capture the latent feature of drug-target relationships and thus make accurate predictions.
Table 2.
Results on comparing our approach with the simple logic based approach
| Drug-target relationship | Test method | AUC | AUPR |
|---|---|---|---|
| Direct interaction | Our approach | 98.7 | 89.6 |
| Simple logic-based approach | 92.1 | 81.6 | |
| Indirect interaction | Our approach | 97.1 | 80.1 |
| Simple logic-based approach | 88.4 | 74.5 |
Note: The highest AUPR score is shown in bold.
Overall, our approach achieved better performance for direct interaction prediction than for indirect interaction prediction (Table 1). Probably this is because in the MATADOR-based data, indirect interactions describe many different mechanisms of DTIs and thus provide less predictive power than direct interactions. We expect that our method would achieve better performance for indirect interaction prediction if different mechanisms of indirect DTIs in the MATADOR-based data could be further identified.
3.3 Predicting drug modes of action
In addition to direct and indirect interactions, DTIs can be also annotated with different drug modes of action, such as activation or inhibition. To evaluate our algorithm’s performance on predicting different drug modes of action, we tested it mainly on the STITCH-based data. We focused on three drug modes of action, including binding, activation and inhibition. In addition to testing the STITCH-based data, we included two additional tests, which further incorporated the MATADOR-based data, that is, each DTI in the STITCH-based data was also associated with direct or indirect interaction derived from the MATADOR-based data. Overall, we conducted the following five tests: (i) integrating both drug-target relationships from the MATADOR-based data and drug modes of action from the STITCH-based data with distinction; (ii) mixing DTIs from both MATADOR-based and STITCH-based data without distinction (i.e. all DTIs were associated with only binary values); (iii) integrating drug modes of action from the STITCH-based data with distinction; (iv) mixing drug modes of action from the STITCH-based data without distinction; and (v) using a singe mode of action from the STITCH-based data. For every test, we also carried out a 10-fold cross-validation procedure as described in Supplementary Material Section S3.
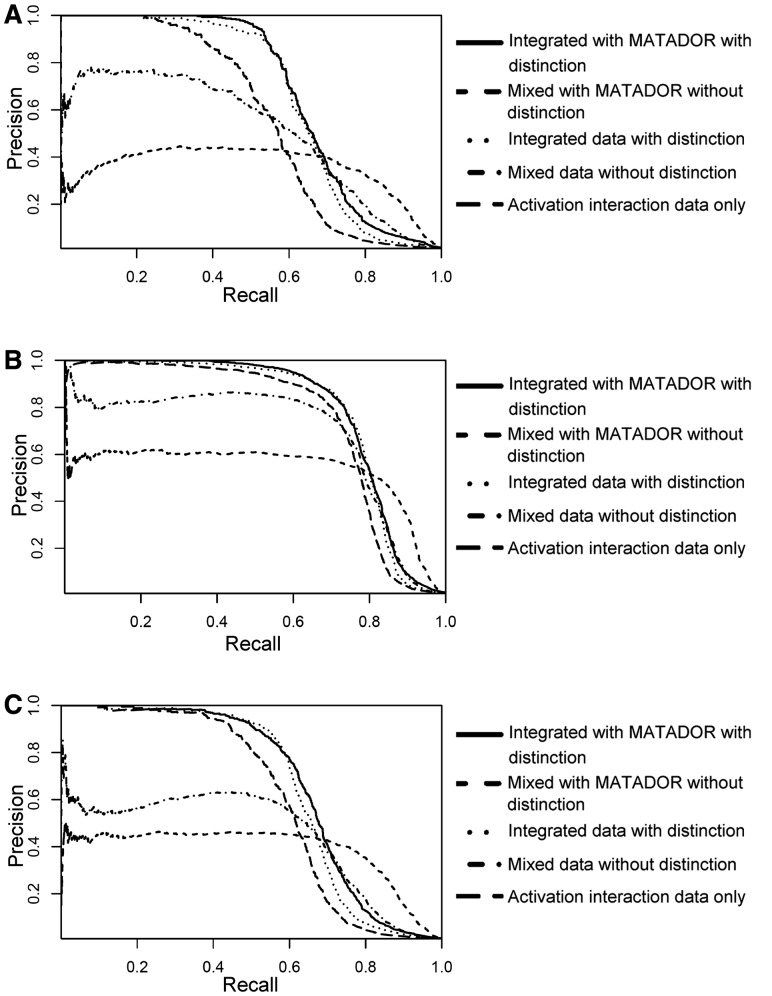
Both AUC and AUPR scores of the aforementioned five tests are reported in Table 3, and their corresponding PR curves are shown in Figure 4. When integrating different types of DTIs with distinction, our algorithm can achieve AUC up to 96.9 and AUPR up to 79.1. The test results showed that our RBM model can effectively exploit different types of interactions encoded in a multidimensional DTI network to predict drug modes of action. Among all five tests, integrating different types of DTIs with distinction produced higher AUPR scores than the other tests, which used only a single interaction type or simply mixed types of interactions without distinction. When differentiating different types of DTIs, integrating direct and indirect interactions from the MATADOR-based data slightly improved the prediction performance. When comparing the results on predicting different modes of action, binding interactions were predicted with higher accuracy than activation and inhibition interactions. This is probably because in the STITCH-based data, binding interactions are more informative in predicting DTIs than other two modes of action.
Table 3.
Results on predicting drug modes of action
| Mode of action | Test method | AUC | AUPR |
|---|---|---|---|
| Binding interaction | Integrating MATADOR and STITCH with distinction | 96.9 | 79.1 |
| Mixing MATADOR and STITCH without distinction | 97.9 | 53.3 | |
| Integrating data with distinction | 95.0 | 78.1 | |
| Mixing data without distinction | 95.6 | 68.0 | |
| Using binding interactions only | 94.1 | 74.4 | |
| Activation interaction | Integrating MATADOR and STITCH with distinction | 94.4 | 67.4 |
| Mixing MATADOR and STITCH without distinction | 96.9 | 35.6 | |
| Integrating data with distinction | 91.2 | 65.2 | |
| Mixing data without distinction | 94.2 | 50.5 | |
| Using activation interactions only | 87.7 | 56.3 | |
| Inhibition interaction | Integrating MATADOR and STITCH with distinction | 94.1 | 67.1 |
| Mixing MATADOR and STITCH without distinction | 96.9 | 38.6 | |
| Integrating data with distinction | 92.5 | 65.2 | |
| Mixing data without distinction | 93.9 | 44.3 | |
| Using inhibition interactions only | 89.5 | 60.2 |
Note: ‘Integrating MATADOR and STITCH with distinction’ corresponds to the test in which our algorithm integrated both drug-target relationships from the MATADOR-based data and drug modes of action from the STITCH-based data with distinction. ‘Mixing MATADOR and STITCH without distinction’ corresponds to the test in which our algorithm mixed DTIs from both MATADOR-based and STITCH-based data without distinction. ‘Integrating data with distinction’ corresponds to the test in which our algorithm integrated drug modes of action from the STITCH-based data with distinction. ‘Mixing data without distinction’ corresponds to the test in which our algorithm mixed drug modes of action from the STITCH-based data without distinction. ‘Using binding (activation or inhibition) interactions only’ corresponds to the test in which our algorithm used only binding (activation or inhibition) interactions from the STITCH-based data. The highest AUPR score is shown in bold.
Fig. 4.
PR curves for the predicted drug modes of action. (A) PR curves for the predicted binding interactions. (B) PR curves for the predicted activation interactions. (C) PR curves for the predicted inhibition interactions
As in Section 3.2, we also performed an additional test using training data of the same size for comparing methods ‘integrating data with distinction’ and ‘using a single data type only’, when predicting different modes of action. Our new comparison results confirmed that integrating different data types with distinction outperformed the method that uses only a single data type (Supplementary Material Section S4).
3.4 New predictions
To examine our algorithm’s ability for predicting novel DTIs that are not present in our data derived from MATADOR, we performed the following test, which is similar to the experiments conducted in (Bleakley and Yamanishi, 2009; van Laarhoven et al., 2011). We predicted unknown direct DTIs using the complete MATADOR-based dataset as training data. For the predicted results, we mainly focused on DTIs involving those proteins that are not listed as drug-metabolizing enzymes or transporter proteins in DrugBank (Knox et al., 2011). We outputted the set of the top 50 scoring predictions that are not present in training data. We then checked whether these new predicted DTIs appear in other databases, including ChEMBL (Gaulton et al., 2011), DrugBank (Knox et al., 2011) and STITCH (Kuhn et al., 2012).
Supplementary Figure S1 in Section S2 visualizes part of the DTI network constructed based on the set of the 50 highest scoring interactions predicted by our approach using the MATADOR-based data. Table 4 shows the list of the top 10 scoring direct DTI predictions. Among these predicted DTIs, a high fraction of the predicted interactions (7 of 10) was found in ChEMBL, DrugBank or STITCH. In the remaining three DTIs that we did not find experimental evidence from the three databases, there might still exist interaction for each drug-target pair. For example, although it is known that mifepristone does not bind to estrogen receptor, it may have some effects on the expression of estrogen receptor (Jiang et al., 2007).
Table 4.
Top 10 scoring direct DTIs predicted by our approach using the MATADOR data
| Rank | Paira | Description | Evidenceb |
|---|---|---|---|
| 1 | DB00812 | Phenylbutazone | C, D, S |
| P23219 | PTGS1: Prostaglandin G/H synthase 1 | ||
| 2 | DB04599 | Aniracetam | S |
| P42261 | GRIA1: Glutamate receptor 1 precursor | ||
| 3 | DB00834 | Mifepristone | |
| P03372 | ESR1: Estrogen receptor | ||
| 4 | DB01392 | Yohimbine | D, S |
| P28222 | HTR1B: 5-hydroxytryptamine 1B receptor | ||
| 5 | DB01297 | Practolol | S |
| P07550 | ADRB2: Beta-2 adrenergic receptor | ||
| 6 | DB01297 | Practolol | |
| P13945 | ADRB3: Beta-3 adrenergic receptor | ||
| 7 | DB00334 | Olanzapine | D, S |
| P08908 | HTR1A: 5-hydroxytryptamine 1 A receptor | ||
| 8 | DB01224 | Quetiapine | D |
| P21918 | DRD5: D(1B) dopamine receptor | ||
| 9 | DB01224 | Quetiapine | D |
| P21728 | DRD1: D(1 A) dopamine receptor | ||
| 10 | DB01233 | Metoclopramide | |
| P21918 | DRD5: D(1B) dopamine receptor |
aDrugs and targets are represented by DrugBank IDs and UniProt ID, respectively.
bDTIs that are observed in ChEMBL, DrugBank and STITCH are marked with ‘C’, ‘D’ and ‘S’, respectively.
In Table 4, some of our new predictions are trivial, as they can also be easily derived based on known interactions of similar proteins or drugs in the dataset. However, our new predictions also provided some interesting results. For example, among the top 50 scoring predictions, our algorithm suggested that there may exist interactions between spironolactone and the membrane progestin receptor gamma protein and between mesalazine (also called 5-aminosalicylic acid) and leukotriene-A4 hydrolase (LTA4H) enzyme. Spironolactone is known as a diuretic or antihypertensive drug and can act on the aldosterone receptor as a competitive antagonist (Macdonald, 1997). Our predicted interaction between spironolactone and membrane progestin receptor gamma protein indicates that spironolactone may have some progestogenic function. Interestingly, this hypothesis can be confirmed from the clinical studies performed in (Nakhjavani et al., 2009). In addition, mesalazine is an anti-inflammatory drug that is primarily used to treat inflammatory bowel disease (Sandborn et al., 2007). LTA4H is an important enzyme that converts leukotriene-A4 to leukotriene-B4 (Rudberg et al., 2004). It has been proposed that leukotriene-B4 may play an important role in a number of different acute and chronic inflammatory diseases, including inflammatory bowel disease (Haeggström, 2000). These studies imply that our predicted interaction between mesalazine and LTA4H is probably true.
These results on new predictions indicated that our RBM model is practically useful in predicting novel DTIs and can have potential applications in drug repositioning.
4 CONCLUSION
In this article, we proposed a first machine-learning approach to predict different types of DTIs on a multidimensional network. Our approach uses an RBM model to effectively encode multiple sources of information about DTIs and accurately predict different types of DTIs, such as drug-target relationships or drug modes of action. Tests on two public databases showed that our algorithm can achieve excellent prediction performance with high AUPR scores. Further tests indicated that our approach can infer a list of novel DTIs, which is practically useful for drug repositioning.
Although our algorithm has been tested only on direct and indirect drug-target relationships, and three drug modes of action, it is general and can be easily extended to integrate other types of DTIs (e.g. phenotypic effects). Current version of our prediction algorithm only considers connections between drugs and targets. In the future, we will extend our approach to exploit the connections within target proteins or drugs. For example, the sequence similarity scores between target proteins, the substructure similarity scores between drugs or drug–drug interactions (Gottlieb et al., 2012; Tatonetti et al., 2012) can be also incorporated into our prediction model. As the conventional version of an RBM does not allow the connections within the same layer, such an extension will require careful thought. Currently, our algorithm has been tested only on two databases (i.e. MATADOR and STITCH). We will test it on more data in the future. For example, it will have more significance if we can predict DTIs based on human proteins and all molecules in PubChem (Kaiser, 2005) or a similar database. Finally, we are also seeking wet-laboratory collaborators to experimentally verify the highest scoring DTIs predicted by our algorithm.
Supplementary Material
ACKNOWLEDGEMENTS
The authors thank Dr L. Wang for the helpful discussions in the early stage of this project. They are grateful to Mr M. Zhou for helping us prepare the drug-target interaction data. They thank the anonymous reviewers for their helpful comments and suggestions.
Funding: This work was supported in part by the National Basic Research Program of China Grant 2011CBA00300, 2011CBA00301, the National Natural Science Foundation of China Grant 61033001, 61061130540, 61073174.
Conflict of Interest: none declared.
REFERENCES
- Arel I, et al. Deep machine learning-a new frontier in artificial intelligence research. IEEE Comput. Intell. Mag. 2010;5:13–18. [Google Scholar]
- Bell R, Koren Y. Lessons from the netflix prize challenge. ACM SIGKDD Explor. Newsl. 2007;9:75–79. [Google Scholar]
- Bengio Y. Learning deep architectures for AI. Found. Trends Mach. Learn. 2009;2:1–127. [Google Scholar]
- Bleakley K, Yamanishi Y. Supervised prediction of drug-target interactions using bipartite local models. Bioinformatics. 2009;25:2397–2403. doi: 10.1093/bioinformatics/btp433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Booth B, Zemmel R. Prospects for productivity. Nat. Rev. Drug. Discov. 2004;3:451–456. doi: 10.1038/nrd1384. [DOI] [PubMed] [Google Scholar]
- Campillos M, et al. Drug target identification using side-effect similarity. Science. 2008;321:263–266. doi: 10.1126/science.1158140. [DOI] [PubMed] [Google Scholar]
- Chen X, et al. Drug-target interaction prediction by random walk on the heterogeneous network. Mol. Biosyst. 2012;8:1970–1978. doi: 10.1039/c2mb00002d. [DOI] [PubMed] [Google Scholar]
- Cheng AC, et al. Structure-based maximal affinity model predicts small-molecule druggability. Nat. Biotechnol. 2007;25:71–75. doi: 10.1038/nbt1273. [DOI] [PubMed] [Google Scholar]
- Cheng F, et al. Prediction of drug-target interactions and drug repositioning via network-based inference. PLoS Comput. Biol. 2012;8:e1002503. doi: 10.1371/journal.pcbi.1002503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis J, Goadrich M. 2006. The relationship between precision-recall and roc curves. In: Proceedings of the 23rd international conference on Machine learning, ICML’06. ACM, New York, NY, USA, pp. 233–240. [Google Scholar]
- Dimasi JA. New drug development in the united states from 1963 to 1999. Clin. Pharmacol. Ther. 2001;69:286–296. doi: 10.1067/mcp.2001.115132. [DOI] [PubMed] [Google Scholar]
- Donald BR. Algorithms in Structural Molecular Biology. Cambridge, MA, USA: MIT Press; 2011. [Google Scholar]
- Dudley JT, et al. Computational repositioning of the anticonvulsant topiramate for inflammatory bowel disease. Sci. Transl. Med. 2011;3:96ra76. doi: 10.1126/scitranslmed.3002648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eickholt J, Cheng J. Predicting protein residue-residue contacts using deep networks and boosting. Bioinformatics. 2012;28:3066–3072. doi: 10.1093/bioinformatics/bts598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gaulton A, et al. ChEMBL: a large-scale bioactivity database for drug discovery. Nucleic Acids Res. 2011;40:D1100–D1107. doi: 10.1093/nar/gkr777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gottlieb A, et al. PREDICT: a method for inferring novel drug indications with application to personalized medicine. Mol. Syst. Biol. 2011;7:496. doi: 10.1038/msb.2011.26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gottlieb A, et al. INDI: a computational framework for inferring drug interactions and their associated recommendations. Mol. Syst. Biol. 2012;8:592. doi: 10.1038/msb.2012.26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Günther S, et al. SuperTarget and Matador: resources for exploring drug-target relationships. Nucleic Acids Res. 2008;36:D919–D922. doi: 10.1093/nar/gkm862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haeggström JZ. Structure, function, and regulation of leukotriene A4 hydrolase. Am. J. Respir. Crit. Care. Med. 2000;161:S25–S31. doi: 10.1164/ajrccm.161.supplement_1.ltta-6. [DOI] [PubMed] [Google Scholar]
- He Z, et al. Predicting drug-target interaction networks based on functional groups and biological features. PLoS One. 2010;5:e9603. doi: 10.1371/journal.pone.0009603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hinton G, Salakhutdinov R. Reducing the dimensionality of data with neural networks. Science. 2006;28:504–507. doi: 10.1126/science.1127647. [DOI] [PubMed] [Google Scholar]
- Hinton GE. Training products of experts by minimizing contrastive divergence. Neural Comput. 2002;14:1771–1800. doi: 10.1162/089976602760128018. [DOI] [PubMed] [Google Scholar]
- Iorio F, et al. Discovery of drug mode of action and drug repositioning from transcriptional responses. Proc. Natl Acad. Sci. USA. 2010;107:14621–14626. doi: 10.1073/pnas.1000138107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang J, et al. Effects of mifepristone on expression of estrogen receptor and progesterone receptor in cultured human eutopic and ectopic endometria. Zhonghua Fu Chan Ke Za Zhi. 2007;36:218–221. [PubMed] [Google Scholar]
- Kaiser J. Science resources. chemists want NIH to curtail database. Science. 2005;308:774. doi: 10.1126/science.308.5723.774a. [DOI] [PubMed] [Google Scholar]
- Keiser MJ, et al. Relating protein pharmacology by ligand chemistry. Nat. Biotechnol. 2007;25:197–206. doi: 10.1038/nbt1284. [DOI] [PubMed] [Google Scholar]
- Keiser MJ, et al. Predicting new molecular targets for known drugs. Nature. 2009;462:175–181. doi: 10.1038/nature08506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knox C, et al. DrugBank 3.0: a comprehensive resource for ‘omics’ research on drugs. Nucleic Acids Res. 2011;39:D1035–D1041. doi: 10.1093/nar/gkq1126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kroeze WK, et al. Molecular biology of serotonin receptors structure and function at the molecular level. Curr. Top. Med. Chem. 2002;2:507–528. doi: 10.2174/1568026023393796. [DOI] [PubMed] [Google Scholar]
- Kuhn M, et al. STITCH 3: zooming in on protein-chemical interactions. Nucleic Acids Res. 2012;40:D876–D880. doi: 10.1093/nar/gkr1011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larochelle H, Bengio Y. 2008. Classification using discriminative restricted boltzmann machines. In: Proceedings of the 25th international conference on Machine learning, ICML’08. ACM, New York, NY, USA, pp. 536–543. [Google Scholar]
- Le Roux N, Bengio Y. Representational power of restricted boltzmann machines and deep belief networks. Neural Comput. 2008;20:1631–1649. doi: 10.1162/neco.2008.04-07-510. [DOI] [PubMed] [Google Scholar]
- Lü L, Zhou T. Link prediction in complex networks: a survey. Physica A Stat. Mech. Appl. 2011;390:1150–1170. [Google Scholar]
- Macdonald F. Dictionary of Pharmacological Agents. Taylor and Francis Group, LLC, Boca Raton, FL, USA: CRC Press; 1997. [Google Scholar]
- MacDonald ML, et al. Identifying off-target effects and hidden phenotypes of drugs in human cells. Nat. Chem. Biol. 2006;2:329–337. doi: 10.1038/nchembio790. [DOI] [PubMed] [Google Scholar]
- Mei JP, et al. Drug-target interaction prediction by learning from local information and neighbors. Bioinformatics. 2012;29:238–245. doi: 10.1093/bioinformatics/bts670. [DOI] [PubMed] [Google Scholar]
- Mizutani S, et al. Relating drug-protein interaction network with drug side effects. Bioinformatics. 2012;28:i522–i528. doi: 10.1093/bioinformatics/bts383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morris GM, et al. AutoDock4 and AutoDockTools4: automated docking with selective receptor flexibility. J. Comput. Chem. 2009;30:2785–2791. doi: 10.1002/jcc.21256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakhjavani M, et al. Short term effects of spironolactone on blood lipid profile: a 3-month study on a cohort of young women with hirsutism. Br. J. Clin. Pharmacol. 2009;68:634–637. doi: 10.1111/j.1365-2125.2009.03483.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perlman L, et al. Combining drug and gene similarity measures for drug-target elucidation. J. Comput. Biol. 2011;18:133–145. doi: 10.1089/cmb.2010.0213. [DOI] [PubMed] [Google Scholar]
- Roth BL, et al. Magic shotguns versus magic bullets: selectively non-selective drugs for mood disorders and schizophrenia. Nat. Rev. Drug Discov. 2004;3:353–359. doi: 10.1038/nrd1346. [DOI] [PubMed] [Google Scholar]
- Rudberg PC, et al. Leukotriene A4 hydrolase: identification of a common carboxylate recognition site for the epoxide hydrolase and aminopeptidase substrates. J. Biol. Chem. 2004;279:27376–27382. doi: 10.1074/jbc.M401031200. [DOI] [PubMed] [Google Scholar]
- Salakhutdinov R, et al. 2007. Restricted boltzmann machines for collaborative filtering. In: Proceedings of the 24th international conference on Machine learning, ICML’07. ACM, New York, NY, USA, pp. 791–798. [Google Scholar]
- Sandborn WJ, et al. Medical management of mild to moderate crohn’s disease: evidence-based treatment algorithms for induction and maintenance of remission. Aliment Pharmacol. Ther. 2007;26:987–1003. doi: 10.1111/j.1365-2036.2007.03455.x. [DOI] [PubMed] [Google Scholar]
- Sirota M, et al. Discovery and preclinical validation of drug indications using compendia of public gene expression data. Sci. Transl. Med. 2011;3:96ra77. doi: 10.1126/scitranslmed.3001318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tatonetti NP, et al. Data-driven prediction of drug effects and interactions. Sci. Transl. Med. 2012;4:125–131. doi: 10.1126/scitranslmed.3003377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Laarhoven T, et al. Gaussian interaction profile kernels for predicting drug-target interaction. Bioinformatics. 2011;27:3036–3043. doi: 10.1093/bioinformatics/btr500. [DOI] [PubMed] [Google Scholar]
- Welling M, Hinton G. A new learning algorithm for mean field boltzmann machines. Artif. Neural Netw. 2002;2415:351–357. [Google Scholar]
- Xia Z, et al. Semi-supervised drug-protein interaction prediction from heterogeneous biological spaces. BMC Syst. Biol. 2010;4 (Suppl. 2):S6. doi: 10.1186/1752-0509-4-S2-S6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie L, et al. Novel computational approaches to polypharmacology as a means to define responses to individual drugs. Annu. Rev. Pharmacol. Toxicol. 2012;52:361–379. doi: 10.1146/annurev-pharmtox-010611-134630. [DOI] [PubMed] [Google Scholar]
- Yabuuchi H, et al. Analysis of multiple compound-protein interactions reveals novel bioactive molecules. Mol. Syst. Biol. 2011;7:472. doi: 10.1038/msb.2011.5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamanishi Y, et al. Prediction of drug-target interaction networks from the integration of chemical and genomic spaces. Bioinformatics. 2008;24:i232–i240. doi: 10.1093/bioinformatics/btn162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao S, Li S. Network-based relating pharmacological and genomic spaces for drug target identification. PLoS One. 2010;5:e11764. doi: 10.1371/journal.pone.0011764. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.