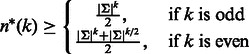Design of shortest double-stranded DNA sequences covering all k-mers with applications to protein-binding microarrays and synthetic enhancers

Abstract

Motivation: Novel technologies can generate large sets of short double-stranded DNA sequences that can be used to measure their regulatory effects. Microarrays can measure in vitro the binding intensity of a protein to thousands of probes. Synthetic enhancer sequences inserted into an organism’s genome allow us to measure in vivo the effect of such sequences on the phenotype. In both applications, by using sequence probes that cover all k-mers, a comprehensive picture of the effect of all possible short sequences on gene regulation is obtained. The value of k that can be used in practice is, however, severely limited by cost and space considerations. A key challenge is, therefore, to cover all k-mers with a minimal number of probes. The standard way to do this uses the de Bruijn sequence of length 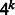. However, as probes are double stranded, when a k-mer is included in a probe, its reverse complement k-mer is accounted for as well.

Results: Here, we show how to efficiently create a shortest possible sequence with the property that it contains each k-mer or its reverse complement, but not necessarily both. The length of the resulting sequence approaches half that of the de Bruijn sequence as k increases resulting in a more efficient array, which allows covering more longer sequences; alternatively, additional sequences with redundant k-mers of interest can be added.

Availability: The software is freely available from our website http://acgt.cs.tau.ac.il/shortcake/.

Contact: rshamir@tau.ac.il

1 INTRODUCTION

Gene regulation is a central focus of biological research. The main factors that regulate gene expression are transcription factors (TFs). These proteins bind to short DNA sequences, either in promoters or enhancers, and by that encourage or impede gene transcription. TFs bind to different DNA sequences with different affinity and specificity. Understanding TF-binding specificity and its effect on gene expression and the final phenotype is a fundamental goal in the study of gene regulation.

Recent technologies measure the binding intensity of a TF to many DNA sequences [e.g. protein-binding microarray (PBM) (Berger et al., 2006) and MITOMI [Fordyce et al., 2010)]. These technologies synthesize a large set of DNA sequences and measure the binding intensity of the TF to each of those sequences. Some technologies use random DNA sequences (Nutiu et al., 2011). Others use sequences that cover all possible DNA k-mers, as they provide a complete picture of the binding spectrum (Berger et al., 2006; Fordyce et al., 2010). A similar approach was also used to test binding in vivo. A recent study used synthesized enhancer oligomers designed to cover all 6mers to test their effect on limb formation in zebrafish (Smith and Ahituv, 2012).

De Bruijn sequences are the most compact sequences that cover all k-mers (Berger et al., 2006; Fordyce et al., 2010). The length of a de Bruijn sequence of order k over alphabet 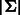is 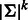, where the DNA alphabet is 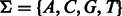. Because of the exponential dependency on k and small space on the experimental device, these technologies are limited to a small value of k. The most popular technology, PBM, was used in hundreds of experiments to date using arrays with k = 10. To create p-long probe sequences, the sequence is split into intervals of length p with k − 1 overlap (p = 36 is used in PBMs).

Despite the universal and high-throughput nature of these technologies, the data produced are still limited. For many TFs, binding depends on >10 DNA positions, usually with six to eight core positions and additional side positions that have a significant contribution (Nutiu et al., 2011; Orenstein et al., 2013). A recent study from the Taipale Laboratory using HT-Selex showed that many TFs have longer motifs that are not covered well by an all 10mer array (Jolma et al., 2013). The RankMotif++ algorithm for PBM data also generates motifs of length 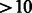in most cases (Chen et al., 2007). Covering all k-mers for a greater value of k will lead to improved understanding of TF binding.

As the probes are double-stranded DNA segments, one can save by using the reverse complementarity of DNA: whenever a k-mer is included, its reverse complement is included as well, and there is no need to cover it again. This brings up the following question: a sequence S is called a reverse complementary complete sequence of order k (RC complete sequence for short) if for each k-mer either the k-mer or its reverse complement are included in S. Can we construct an optimal (minimum length) RC complete sequence? Theoretically, if for each k-mer T the sequence S includes either T or its reverse complement but not both, one could save a factor of nearly 2 compared with the length of a de Bruijn sequence.

Ministeris and Eisen (2006) and Philippakis et al. (2008) proposed the use of (regular) de Bruijn sequences for designing probes for PBMs. Philippakis et al. used linear feedback shift registers to generate a de Bruijn sequence with good coverage of gapped k-mers. This approach was used for constructing two microarrays that are in use today with k = 10 (Berger et al., 2006). The idea of exploiting reverse complementarity was raised by Ministeris and Eisen (2006), who sketched an algorithm for it without proof. In fact, as we shall show, the algorithm of Mintseris and Eisen (2006) does not provide an optimal solution for even values of k. In the context of sequence assembly, Medvedev et al. (Medvedev and Brudno, 2009; Medvedev et al., 2007) solved the problem of constructing a minimum length sequence that covers a given set of k-mers, using reverse complementarity. Although their algorithm can be applied to solve the problem raised in this study, they do not address it directly. When applied to our problem, their algorithm requires 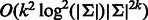time. As we shall see, our algorithm is much faster.

In this study, we address the problem of constructing an optimal RC complete sequence. We first give a lower bound for the length of such a sequence. We prove that for odd k, there exists a sequence that achieves the lower bound and show how to construct it in time complexity that is linear in the output sequence length. For odd k, the algorithm constructs two tours that are reverse complementary to each other and together cover all edges of the de Bruijn graph and is identical to Mintseris and Eisen (2006). Then, we show how to adjust the algorithm to handle the case of even k, achieving a saving factor approaching 2 as k increases. We give two solutions: a simple near-optimal one requiring linear time and a more complex (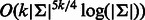 time) solution that guarantees optimality of the resulting sequence. In particular, this implies that the lower bound is not tight for even k. We implemented the algorithm and we demonstrate the saving it achieves. The produced sequences are nearly half the length compared with a regular de Bruijn sequence.

The article is organized as follows. We first provide formal definitions and preliminaries. We then present a lower bound for the length of an optimal sequence based on k-mer counts. Then, we present an algorithm that works in linear time on the de Bruijn graph and prove that it solves the problem for odd k. We conclude by describing the two possible solutions for even k and report on experimental results with all the algorithms.

2 PRELIMINARIES

We start with some basic definitions of graphs and sequences. For more details see, e.g. West et al. (2001).

A directed graph (digraph or simply a graph) 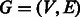is a set of vertices 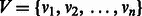and a set of edges 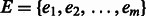. Each edge is an ordered pair of vertices 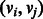, and we say the edge is directed from v_i to v_j. The indegree of vertex v is the number of edges entering v. Similarly, the outdegree is the number of edges outgoing from v. A vertex is balanced if its indegree equals its outdegree. A path in a digraph is a sequence of vertices, 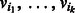, such that for each 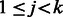there is an edge 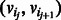. A cycle is a path where 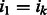. A digraph is strongly connected if for every pair of vertices 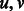there exists a path from u to v and a path from v to u. A strongly connected component in a digraph is a maximal set of vertices that induces a strongly connected subgraph.

An Eulerian tour through a digraph G is a cycle that traverses all edges in G, such that each edge is traversed exactly once. If a digraph contains an Eulerian tour, we call it Eulerian. A digraph is Eulerian if and only if it is strongly connected and all vertices are balanced (West et al., 2001).

A de Bruijn sequence of order k over alphabet Σ is a minimum length sequence that covers each k-mer over Σ exactly once. For convenience, we define the length of the sequence as the number of k-mers in it. Hence, a sequence of length t contains 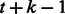characters. A de Bruijn sequence has length 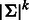, which is the minimum possible for covering all k-mers.

Given sequences 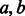over alphabet Σ, the overlap between a and b, denoted 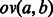, is the largest suffix of a that is also a prefix of b.

A de Bruijn graph of order k is a digraph in which for every possible k-mer 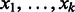there is a vertex denoted by . There is an edge from u to v if and only if 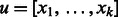and 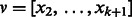, that is, 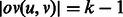. Each edge represents a unique 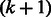-mer. For example, the edge 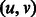above represents 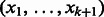. To distinguish vertices from edges, we will use square brackets for vertices. Hence, 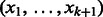is the edge between and 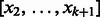. Obviously, for each vertex v the indegree and outdegree are 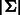, and the graph is strongly connected. Thus, a de Bruijn graph is Eulerian. Any Eulerian tour represents a de Bruijn sequence of order k + 1. Each edge and vertex in the graph is represented by 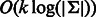bits. Throughout the article, we assume this number of bits is contained in one computer word; hence, we deduce that it takes O(1) time to find an edge or a vertex.

A complementarity relation between characters is a symmetric non-reflexive one-to-one relation. The alphabet of DNA is 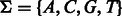with the complementarity relation 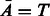and 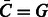. By symmetry also 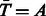and 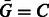. The reverse complement of sequence , denoted 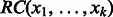, is defined as the sequence obtained by reversing the original sequence and replacing each character by its complement, i.e. 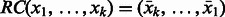. For example, 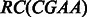= TTCG . A sequence s is called a palindromic reverse complementary sequence or in short a palindrome, if 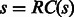. For example, ACGT is a palindrome. We define a reverse complementary complete sequence of order k over alphabet Σ (RC complete sequence for short) as a sequence such that for each k-mer s, at least one of s and RC(s) are in the sequence. Note that unlike a regular de Bruijn sequence, the definition of an RC complete sequence does not require minimality. An RC complete sequence is optimal if it is of minimum length.

3 RESULTS

3.1 A lower bound for the length of an RC complete sequence

First, we derive a lower bound for the length of an RC complete sequence from k-mer counts.

Proposition 1 —

Denote by the length of an optimal RC complete sequence of order k.

(1)

Proof —

We consider separately the cases of odd and even k. For odd k, there are no palindromes, as the middle position in a k-mer differs from its reverse complement. Each k-mer must be represented in the sequence by itself or its reverse complement. Thus, a lower bound for the minimum length is half the number of unique k-mers, which is . For even k, some k-mers are palindromes. For palindromes, the first characters define the last characters. Hence, there are exactly different palindromes. All palindromes must appear at least once in any RC complete sequence, whereas for the non-palindromic k-mers, either they or their reverse complement must appear in the sequence. Thus, for even k, . ▪

We shall show later that is tight for odd k, but not for even k.

3.2 Constructing an optimal RC complete sequence for odd k

In this section, we prove constructively that for odd k there exists an RC complete sequence that achieves the lower bound of Proposition 1 and is thus optimal. The proof modifies the Euler tour algorithm (West et al., 2001). The modified algorithm was presented without proof in Mintseris and Eisen (2006). The algorithm for generating the sequence will work on the de Bruijn graph of order k − 1. Every k-mer is represented in the graph as an edge, the graph is strongly connected and all vertices are balanced. As there are no palindromes of odd length, every edge has a unique reverse complement counterpart that is different from it. This defines a perfect matching M on the edges of the graph.

Given a directed path F in the graph, its reverse complement path is defined as the path R in which each edge 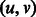in F is replaced by the edge 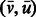. For example, for the path 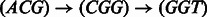, its reverse complement is 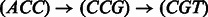(Fig. 1). We will refer to F and R as forward and reverse paths, respectively.

Fig. 1.

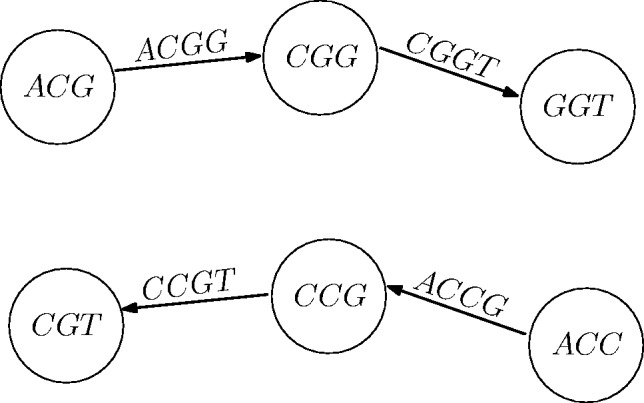
An illustration of forward and reverse paths (top and bottom, respectively). The forward path traverses the edges in their direction. The corresponding reverse path traverses the reverse complementary edges in reverse direction

The following theorem provides a necessary and sufficient condition for the existence of an RC complete sequence that achieves the lower bound.

Theorem 1 —

For odd k, an RC complete sequence s achieves the lower bound (Proposition 1) if there exist two edge-disjoint paths with no repeating edges, corresponding to s and RC(s), that together cover all edges of the de Bruijn graph of order k − 1.

Proof —

Observe that the lower bound assumes one occurrence of either w or RC(w) but not both in the sequence for each k-mer w. Assume an RC complete sequence achieves the lower bound. Then, because of its minimality, it contains no repeating k-mers; therefore, it must correspond to a path F in the de Bruijn graph with no repeating edges. The ordered set of k-mers in corresponds to consecutive edges in F. Note that the reverse complement sequence is also a path R in the graph: the k-mers in R are the reverse complement of those in F; therefore, consecutive edges form a path in the graph traversed in reverse order. As each k-mer or its reverse complement is covered in , it is also true that each k-mer or its reverse complement is covered by , and the two paths F and R, corresponding to the two sequences, together cover all edges.

Suppose there are two edge-disjoint paths F and R with no repeated edges that together cover all edges. As they are reverse complement of each other, and together cover all edges, for each k-mer w, the sequence s (corresponding to path F) must contain either w or RC(w) (otherwise, some edges would have been uncovered). Hence, s is an RC complete sequence. The same argument holds for RC(s) (corresponding to path R). As each contains exactly half the edges, the length of each of them equals the lower bound ▪.

Before presenting the algorithm for finding an optimal RC complete sequence, we remind the reader of the algorithm for finding an Eulerian cycle in a digraph (Fleischner, 1990). The algorithm starts from an arbitrary source vertex. Initially all edges are unmarked. It traverses a path of unmarked edges in arbitrary order. Each traversed edge is marked; therefore, no edge is traversed more than once. The algorithm also maintains a set A of the visited vertices that are still active, i.e. they have outgoing unmarked edges. When the last unmarked edge outgoing from a vertex is traversed, the vertex is removed from A. If the algorithm reaches a dead end, it starts another traversal from another vertex in A. A dead end can only be achieved when closing a cycle (i.e. returning to the source vertex), as in any other vertex there is always a free incoming edge and a free outgoing edge (as for every vertex except the source the unmarked outdegree and the unmarked indegree are equal). If not all edges have been traversed, A is not empty, and the process can start from a new source. In the end, as the graph is strongly connected and all cycles start from visited vertices (except for the initial vertex), the cycles can be joined to form one Eulerian cycle. The running time of the algorithm is linear in the number of vertices and edges.

Algorithm 1 finds an optimal RC complete sequence in a de Bruijn graph of order k − 1 when k is odd. The algorithm imitates the Euler path algorithm but maintains both a forward sequence and a reverse complement sequence simultaneously. The collection of cycles traversed so far is kept in and the corresponding reverse complement cycles set is .

Theorem 2 —

For odd k, Algorithm 1 returns forward and reverse paths that cover together all edges of the graph and represent two optimal RC complete sequences. The algorithm runs in time.

Proof —

We prove the theorem using several lemmas. We first show that if the forward path F reaches a dead end, then so does the reverse path R, and in that case, a cycle is closed (Lemma 1). Note that each pair F, R constructed in Steps 4–7 are reverse complementary paths by the way they are constructed. Then, we show that the cycles in can be merged into one cycle (Lemma 2). Third, we deduce that a strongly connected component is covered by and (Lemma 3). Finally, we conclude that and cover all edges, as there is only one strongly connected component in any de Bruijn graph (Corollary 1). As each edge is traversed once, the paths are of length and, hence, optimal.

Lemma 1 —

If the forward traversal reaches a dead end, then so does the reverse. Both paths close a cycle in this case.

Proof —

Distinguish two cases in which the forward path reaches a dead end:

Case 1 —

F reaches a vertex v and R reaches a vertex , and all outgoing edges from v were already traversed. We prove that in that case, F must close a cycle. Assume to the contrary that F contains no edge outgoing from v. In that case, all outgoing edges were traversed by R. Then, all incoming edges must have been traversed by R as well, as each time R reached v, it must have exited it as well. The only exception is if v is also the first (last added) vertex u in R, contradicting our assumption that . Therefore, all incoming and outgoing edges were covered by R, contradicting the fact that F just entered v. We conclude that F has an edge outgoing from v and thus it closed a cycle.

Denote by the last edge traversed by F. All edges of the form , where , were traversed. Hence, the reverse edges of the form were traversed as well. The last edge traversed by R was , outgoing from the vertex . All incoming edges to this vertex have already been traversed, as they are the reverse complements of the edges outgoing from v, which were traversed by F. Thus, R reaches a dead end as well. R closes a cycle because of a symmetrical argument to that made for F.

Case 2 —

F and R reach the same vertex v simultaneously. Denote the incoming edge used by F . Then, the reverse outgoing edge, which is traversed by R, is . From the fact that both reach the vertex simultaneously, we get that . Hence, in all previous traversals of this vertex F and R also reached the vertex simultaneously. Moreover, the forward and reverse paths reach a dead end together at v. Hence, all incoming and outgoing edges were already traversed, and they are all of the form and , for all . Thus, both paths close a cycle ▪.

Lemma 2 —

The cycles in can be merged into one cycle.

Proof —

According to Lemma 1, when F is added to , it is a cycle in the graph. Thus, is a set of cycles. The first cycle starts from an arbitrary vertex, but all other cycles start from a vertex of another cycle in (denote encompassing cycle). Thus, each inner cycle can be merged into its encompassing cycle, forming one merged cycle. This is true to all cycles, except for the initial cycle ▪.

Lemma 3 —

The merged cycle of and either cover two strongly connected components separately or one strongly connected component together.

Proof —

Cycles are added to and as long as there are unmarked edges. If there are no shared vertices between and , then both sets cover edges of different components. As each set is added edges until all are traversed, they cover two strongly connected components separately. Else, there is at least one shared vertex; thus, they cover the same component. The component is strongly connected, as no edges are left to traverse ▪.

Corollary 1 —

and cover all edges of a de Bruijn graph.

Proof —

Following Lemma 3, as there is only one strongly connected component in a de Bruijn graph, and cover it together ▪.

This completes the proof of Theorem 2 ▪.

Algorithm 1. Find forward and reverse paths that cover all edges in a de Bruijn graph 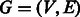of even order k − 1.

1. Initially all edges are unmarke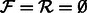d, , and 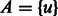, an arbitrary vertex.

2. Although 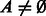do

3.  .

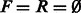4.  Pick any starting vertex from A.

5.  Although there exists an unmarked edge 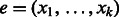outgoing from v do

6.   Append e to F. Prepend RC(e) to R.

7.   Mark e and RC(e).

8.   Set ; .

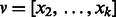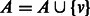9.  Remove v from A.

10. If 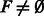, add F to 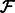; add R to ;

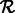11. Merge the cycles in 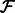to obtain a single forward path.

   Do the same for .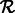

3.3 Two solutions for the case of even k

Algorithm 1 cannot be applied when k is even. A palindrome is represented by one edge in the de Bruijn graph (like any other k-mer). The algorithm must traverse both an edge and its reverse complement edge on the forward and reverse paths; therefore, for a palindromic edge, both paths should use the same edge, which is impossible.

One possible way to rectify the problem is by adding one more copy of each palindromic edge to the de Bruijn graph. Note that in the resulting (multi-) graph, the number of edges is exactly twice the lower bound. Adding the parallel edges would solve the problem discussed earlier in the text, but it will make some vertices unbalanced; therefore, the resulting graph is not Eulerian. Such a graph cannot be represented as a union of two reverse complementary edge-disjoint paths.

A more aggressive augmentation that overcomes this difficulty is adding a cycle for every palindromic edge. This would preserve the balance of all vertices and the strong connectivity as well. If, in addition, the added non-palindromic edges have a perfect matching between reverse complementary edges, the algorithm can be applied.

We present two possible augmentations. One is simple, based on the ideas aforementioned, and near-optimal; the other is optimal but requires a more complex augmentation.

3.3.1 A simple near-optimal augmentation

In this approach, for each palindromic edge, we add to the de Bruijn graph all possible cyclic shifts of it. More formally, let 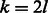. For the palindrome 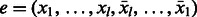, we add k edges corresponding to all possible cyclic shifts of e. Obviously, as these edges form a cycle, all vertices remain balanced. In fact, this cycle contains two edges that are palindromes, 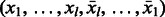and 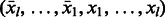; therefore, only one cycle is added for both, and the cycle doubles both palindromic edges. It is easy to see that the remaining 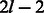edges are in fact l − 1 matching pairs of reverse complementary edges. For each edge that represents the cyclic shift starting at position i, for 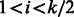, the matching edge starts at 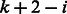. Hence, a perfect matching exists after adding the new cycles. In total, during the edge augmentation process, for each pair of palindromic k-mers, we add k edges. For example, for the palindromes ACGT and GTAC, we add ACGT, CGTA, GTAC and TACG (Fig. 2). The added edges CGTA and TACG match each other. The added palindromes match the original edges in the graph. The resulting augmented graph contains 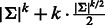edges, where the first term is the number of edges in the original de Bruijn graph, and the second is k for each pair of palindromes.

Fig. 2.

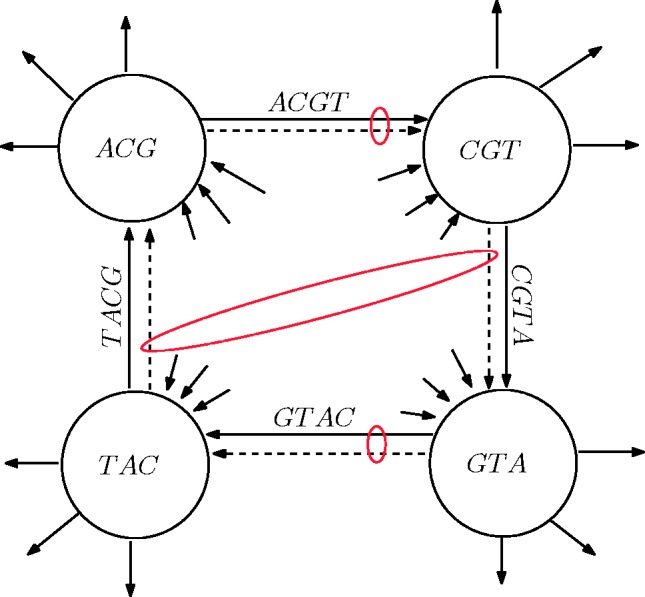
A cycle and edge matching. For the pair of palindromes ACGT and GTAC, all cyclic shifts of these palindromes are added once (dashed edges). In the matching, palindromic edges in the original cycle are paired with their added copies (encircled by small red ovals). Other non-palindromic added edges are paired (encircled by a large red oval)

In some cases, the number of added edges can be reduced. If the palindrome is periodic, then the number of cyclic shifts needed to return to the original k-mer is the length of the period. For example, the period of (ATAT … T) and (TATA … A) is 2. Only two edges suffice in this case, the edges (ATAT … T) and (TATA … A). This also applies to (CGCG … G) and (GCGC … C). Therefore, each two periodic palindromes that are a cyclic shift of each other require an addition of a number of edges equal to the length of their period. Hence, a smaller augmented graph and a shorter RC complete sequence can be obtained by considering the different possible periods, which can only be of even length, as each period is a palindrome.

Denote by 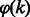the set of even integers that divide k, and by 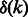the exact number of additional edges.

Theorem 3 —

(2)

Proof —

All k-mer palindromes are divided to pairs, which are cyclic shifts of each other. For each pair, all distinct cyclic shifts are added. The number of shifts is equal to the length of the period of the k-mer. The periods can only be even, as the periodic sequences are palindromes by themselves. The number of i-periodic palindromes is . These contain shorter periods, for which edges have already been counted. Thus, is subtracted, where j is the maximum even integer that divides . The number of edges added for each pair of i-periodic palindromes is i ▪.

Theorem 4 —

Running Algorithm 1 on the augmented graph produces forward and reverse paths that together cover all edges of the graph and represent two RC complete sequences.

Proof —

Algorithm 1 can be run on graphs that satisfy the following properties:

1. The graph is strongly connected.

2. All vertices are balanced.

3. There exists a perfect matching of the edges, such that each pair of edges represent a k-mer and its reverse complement.

The original de Bruijn graph of order k satisfies (1) and (2), and there exists a perfect matching for all non-palindromic k-mers in it. Added edges cannot disturb the connectivity. The addition of cycles preserves the balance. Each added palindromic k-mer matched the edge representing the same k-mer in the original graph. As discussed earlier in the text, the added non-palindromic edges form a perfect matching. Thus, Algorithm 1 can be run on the augmented graph. According to Theorem 2, it produces a forward and reverse path that together covers all edges of the augmented graph.

Each k-mer is represented in the augmented graph as an edge. All edges are covered together by the forward and reverse paths. For each path and for each k-mer, either it or its reverse complement is covered by the path. Thus, the paths represent RC complete sequences ▪.

Algorithm 1 produces two sequences, forward and reverse, each of which is an RC complete sequence (Fig. 3). The length of the produced sequences is the number of edges divided by two. For each pair of palindromic edges, at most k edges were added, and by Theorem 3 exactly 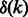edges were added in total. Hence, the length of the sequence is 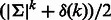, which is bounded by 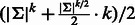. This is an addition of 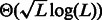characters, where L denotes the lower bound in Proposition 1 for an RC complete sequence of even order k.

Fig. 3.

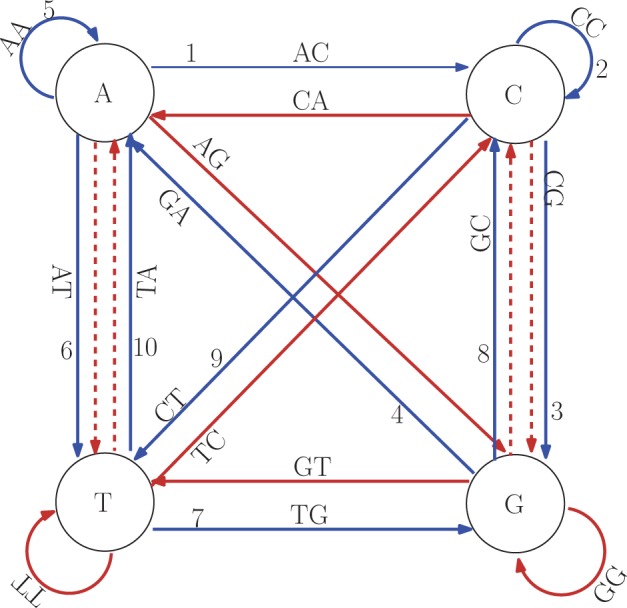
An augmented de Bruijn graph of order 1 and an example of forward and reverse paths in it. The dashed edges are added edges. The blue and brown paths represent the forward and reverse paths, respectively. Numbers on edges are the order of the edges in the forward path. The sequences are ACCGAATGCT and AGCATTCGGT for forward and reverse paths, respectively

3.3.2 An optimal augmentation

We now present another augmentation that has higher time complexity but leads to an optimal RC complete sequence. As before, starting from the de Bruijn graph 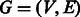, all palindromic edges are doubled, resulting in a graph 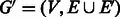. We temporarily disregard the reverse complementarity matching constraints. As a result of the edge doubling, there are unbalanced vertices in 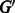. We rectify this by adding short paths between unbalanced vertices. By adding paths of minimum total length, we will obtain a third graph 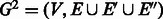in which all degrees are balanced and it has minimum number of edges. Finding an optimal set of edges 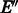can be done by solving a maximum weight-matching problem on a related graph. In fact the problem is equivalent to the Chinese postman problem (Edmonds and Johnson, 1973) [the Chinese postman problem is used in Medvedev and Brudno (2009) and Medvedev et al. (2007) and is also mentioned in Mintseris and Eisen (2006) as a solution on the original de Bruijn graph]. We shall later show that G² can be modified to satisfy the reverse complementarity matching requirement without losing optimality. Hence, applying Algorithm 1 on it will produce an optimal RC complete sequence.

Finding an optimal set of edges 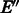is done by solving a maximum weight-matching problem in a bipartite graph, where vertices with greater indegree than outdegree constitute one part, and the vertices with greater outdegree than indegree are the other. The edge weights are k minus the number of characters on the path from one vertex to the other. More formally, let 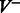(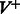) be the set of vertices with indegree greater (smaller) than outdegree in 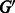. For 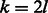, there are 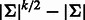vertices in 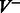of the form 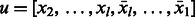and the same number of vertices in 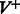of the form 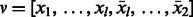[note that 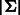palindromes of period 2 are already balanced (e.g. ATA … T)]. We define a complete bipartite graph 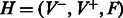, where the weight of edge 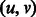is the maximum overlap between the suffix of u and the prefix of v (i.e. 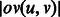). The length of the shortest path 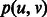between u and v is 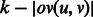(Fig. 4). We are looking for a maximum weight matching in H. The procedure is summarized in Algorithm 2, Steps 1–5.

Algorithm 2. Find an optimal augmentation for a de Bruijn graph 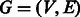of odd order.

1. Add to G the set 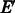of palindromic edges.

 The resulting (multi-)graph is .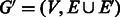

2. Define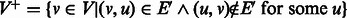

3. Define a complete bipartite graph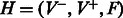

 with edge weights .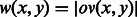

4. Find a maximum weight-matching M in H.

5. Define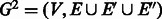

 where .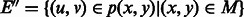

6. Modify M, so that each cycle in the graph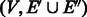

 contains exactly two palindromic edges (Lemma 6).

Fig. 4.

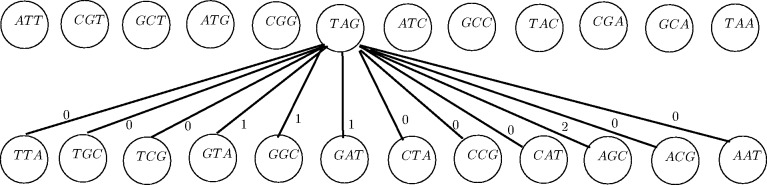
The bipartite graph for matching unbalanced vertices (Algorithm 2). On the top are the vertices with greater indegree, and on the bottom are the vertices with greater outdegree. Weights on the edges are the maximum overlap between the vertices’ sequences. Only the edges out of one vertex are drawn (the graph is a complete bipartite graph). Note that only unbalanced vertices corresponding to 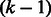-long prefixes and suffixes of palindromes are included

The graph G² produced in Step 5 of Algorithm 2 is strongly connected with all vertices balanced, but it is not guaranteed to satisfy the third property of Theorem 4, i.e. having a perfect matching among reverse complementary edges, which is needed to apply Algorithm 1. We now prove that it can be modified to satisfy this property without losing optimality. In fact, as 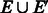has a perfect matching, we only need to prove this property on the added edges 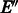. Once this is done, Algorithm 1 can be applied to produce two reverse complementary paths that cover all edges.

To establish Algorithm 2, we prove several lemmas:

Lemma 4 —

The shortest path from palindrome A to the palindrome B is the reverse complementary of the shortest path from B to A.

Proof —

Denote and two palindromes. Let for any be an edge in the shortest path from A to B. Its reverse complement is , which, as are palindromes, which is the same as , an edge in the shortest path from B to A ▪.

Lemma 5 —

No cycle in contains a single palindrome.

Proof —

Suppose there exists a cycle containing only one palindrome. The shortest path to return to the palindrome is t cyclic shifts of the palindrome where t is the length of its period. Let be the palindrome. Its cyclic shift is another palindrome. Thus, the cycle includes more than one palindrome ▪.

Lemma 6 —

Every cycle in can be decomposed into cycles containing exactly two palindromes each, without decreasing the total weight of the matching.

Proof —

The proof is by induction on n, the number of palindromes in the cycle. For the induction base, n = 1 is impossible by Lemma 5, and n = 2 is trivially true. Induction step, for , denote by X, Y, Z and W palindromes in the cycle, where W, X, Y and Z appear in this order in the cycle. Let , , and let w be the sum of overlaps of all palindromes between Z and W (inclusive). In case n = 3, Z = W and w = 0. Without loss of generality, let y be a maximum overlap. The total sum of overlaps is (Fig. 5).

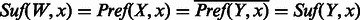
Remove X and Y and form a cycle of these two palindromes. As are palindromes, ; therefore, the contribution of this cycle to the matching is . The total overlap of the remaining cycle is w plus the overlap between W and Z, which is at least . To see this, denote by the i-long prefix of string X, and denote by the i-long suffix of X. If , , where the first, second and fourth equalities follow from the overlap assumptions and the second, third and fourth use the palindrome property. If , similarly . Hence, . The total weight of the two cycles in the new matching is at least . 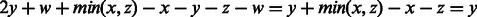Hence, the difference between the new matching and the previous one is at least , where the last inequality follows by the choice of y as a maximum overlap.

The remaining cycle has n − 2 palindromes, and by the induction step, it is breakable to cycles of size two ▪.

Proposition 2 —

There exists a maximum weight matching in which all the added edges form reverse complementary pairs. Any maximum weight matching can be modified to such matching.

Proof —

Consider the graph G² produced in Step 5 of Algorithm 2. If contains cycles of more than two palindromes, by Lemma 6, they can be decomposed into cycles of two palindromes. The new matching is of the same size, and for each cycle with exactly two palindromic edges, the remaining edges match in reverse complementary pairs (Lemma 4) ▪.

The maximum weight-matching problem, also known as the assignment problem (West et al., 2001), can be solved by the Hungarian method in time (Kuhn, 2006). As and , the running time is . An improvement to this algorithm (Kao et al., 1997), when the edge weights are integers, runs in time, where N is the largest edge weight. In our case N = k, which gives running time. The post-processing of the matching (Lemma 6) requires finding two palindromes with maximum overlap. This can be done in total time linear in the number of palindromes, as overlap lengths are integers in the range of 0 to k, and thus can be sorted using count sort. Hence, we conclude

Theorem 5 —

An optimal RC complete sequence for even k can be produced in time .

Summarizing Theorems 2 and 5 we obtain

Theorem 6 —

For every value of k, an optimal RC complete sequence can be obtained in time polynomial in the size of a de Bruijn graph of order k − 1.

Fig. 5.

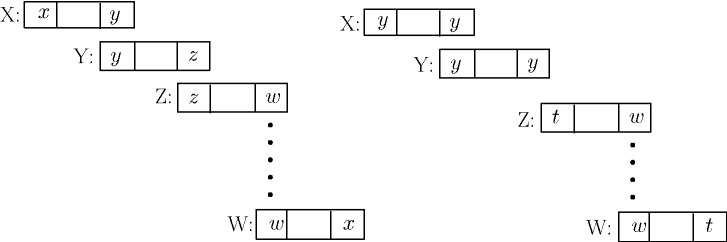
Breaking down cycles with more than two palindromes. Left: Palindrome overlaps in a cycle found by the maximum matching. The rectangles at the ends indicate overlap between contiguous palindromes. Right: Partition into two cycles, one containing only the palindromes X and Y with a maximum overlap y. As 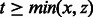, the partition does not decrease the total contribution of the cycles to the weighted matching (Lemma 6)

4 EXPERIMENTAL RESULTS

Table 1 shows the results of the two algorithms for even k. As we can see, the sequence obtained by the algorithm is of length nearly half that of the original de Bruijn sequence. For example, for k = 12, the minimum length is within 0.15 per cent of 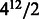and within 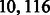characters from the theoretical lower bound.

Table 1.

Length of reverse complementary de Bruijn sequences produced by the two algorithms for even k

k	2	4	6	8	10	12	14
Original	16	256	4096	65 536	1 048 576	16 777 216	268 435 456
Lower bound	10	136	2080	32 896	524 800	8 390 656	134 225 920
Algorithm 1	10	142	2140	33 262	526 840	8 400 808	134 275 060
Optimal	10	142	2140	33 262	526 816	8 400 772	134 274 844
Saving factor	1.6	1.8	1.91	1.97	1.990	1.997	1.999

Note: The top row is the length of a regular de Bruijn sequence that does not exploit complementarity. The next row contains the theoretical lower bound on RC complete sequence length (Proposition 1). The next two rows are the lengths of the sequence computed by the two algorithms of Section 3.3.1 and 3.3.2. The saving factor is the ratio between the original sequence length and length of the optimal RC complete sequence. Note that the lower bound is not tight.

Table 2 lists the number of probes of length p needed to cover all k-mers, by cutting an optimal RC complete sequence to p-long probes with overlaps of k − 1. As we can see, the saved factor in using the RC complete sequence is roughly 2. A comparison to the Table 1 of (Mintseris and Eisen, 2006) shows that the sequence produced in (Mintseris and Eisen, 2006) is sub-optimal.

Table 2.

Number of probes needed to cover all k-mers as a function of probe length and k

k	6	7	8	9	10	11	12	13	14	14-DB
25	107	432	1848	7711	32 926	139 811	600 056	2 581 111	11 189 571	22 369 622
30	86	342	1447	5958	25 087	104 858	442 146	1 864 136	7 898 521	15 790 321
35	72	283	1188	4855	20 263	83 887	350 033	1 458 889	6 103 402	12 201 612
40	62	241	1008	4096	16 995	69 906	289 682	1 198 373	4 973 143	9 942 054
45	54	211	876	3543	14 634	59 919	247 082	1 016 801	4 196 089	8 388 608
50	48	187	774	3121	12 850	52 429	215 405	883 012	3 629 050	7 255 013
55	43	168	693	2789	11 453	46 604	190 927	780 336	3 197 021	6 391 321
60	39	152	628	2521	10 330	41 944	171 445	699 051	2 856 912	5 711 393
65	36	139	574	2300	9408	38 131	155 570	633 103	2 582 209	5 162 221
70	33	128	528	2115	8637	34 953	142 386	578 525	2 355 700	4 709 394

Note: The table contains the number of probes obtained by cutting an optimal RC complete sequence to short segments with overlaps. Left column: probe length; top row: k. Right column: number of probes needed when using a regular de Bruijn sequence for k = 14.

Running times: The simple near-optimal algorithm runs in time roughly linear in 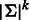. For example, for k = 8, 10 and 12 the running times are 1.5, 26 and 445 s, respectively. The optimal algorithm requires 5, 126 and 2937 s, respectively.

5 SUMMARY AND DISCUSSION

In this article, we studied the problem of constructing a minimum length sequence that covers each k-mer or its reverse complement at least once. The problem has applications in construction of dense double-stranded probe arrays for in vitro measuring of protein–DNA binding (Berger et al., 2006; Fordyce et al., 2010), and for design of synthetic enhancers for in vivo developmental studies (Smith and Ahituv, 2012). For the case of odd k, we provided a proof that a simple modification of the Eulerian tour algorithm applied to the de Bruijn graph of order k − 1 gives an optimal solution. The algorithm requires linear time in the output sequence length, and it cuts the sequence length in half compared with using a regular de Bruijn sequence.

The problem is a bit more involved for even k, and here we provided two algorithms, a linear time near-optimal algorithm and a more complex polynomial algorithm that produces an optimal sequence. The length of the sequence produced by the optimal algorithm is slightly shorter, and both algorithms nearly halve the total length of the sequence.

The following related problem was studied by Medvedev et al. (Medvedev and Brudno, 2009; Medvedev et al., 2007): what is the minimum length sequence that contains a given set of k-mers? Their solution is based on bidirected graphs, which are similar to de Bruijn graphs, with the difference that a k-mer and its reverse complement are represented by the same vertex, and the edges represent the possible ways that double-stranded strings can overlap. These graphs were originally conceived by Kececioglu and Myers (1995) and actually discovered earlier by Edmonds (1967). Medvedev et al. stated, without proof, that an Eulerian path can be found in a bidirected graph in the same way as in a regular de Bruijn graph (Lemma 1), but they did not consider explicitly the problem of covering all k-mers and did not make the distinction between even and odd k. In fact, some vertices in a bidirected graph of odd order (when edges represent k-mers of even length) are unbalanced, and thus an Eulerian tour does not exist. Although their method can be applied to our problem, it is slower than ours: they require 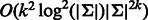, whereas our algorithms requires 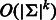for odd k and 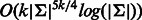for even k.

Beyond the theoretical interest, our results are applicable to current (Berger et al., 2006; Fordyce et al., 2010; Smith and Ahituv, 2012) and future technologies that require complete coverage of double-stranded DNA k-mers. In PBM, although it is desirable to have redundancy in covering k-mers, space on the arrays is limited. By essentially halving the needed sequence length, space is freed on the array to select additional redundant probes with desired properties. Similarly, in designing synthetic enhancer sequences, by using shorter sequences, experiments can be simplified.

In current technologies, the de Bruijn (or RC complete) sequence is cut into probes of length p with overlap k − 1 (Table 2). There is no constraint that forces these probes to come from a single sequence. A variant of the problem we studied is as follows: what is the minimum number of double-stranded DNA probe sequences of length p that together cover all k-mers? As our solution for an RC complete sequence of even k covers, a few k-mers more than once and direct design of probe sequences of length p might reduce the number of probes needed to cover all k-mers.

A heuristic solution to that problem was recently proposed by Riesenfeld and Pollard (Riesenfeld and Pollard, 2012). They studied the following problem: given k and m, design a set of m double-stranded DNA probes (of equal or almost equal length, denoted as 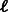) that together cover all k-mers. Their algorithm repeatedly searches for disjoint 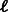-long paths between unbalanced vertices. After removal of all such paths, it finds two reverse-complementary cycles. One cycle is cut into probes (with overlaps of k − 1) of length 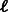or 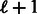. If the program terminates, an optimal set of oligomers is found; however, there is no theoretical guarantee that it will terminate. In our tests, for k = 6, their program terminates in a few seconds, whereas for k = 8, it takes >1 h and for k = 10 > 2 weeks. For some values of m, the produced probes are not of equal length. A modest reduction in the number of oligomers is obtainable compared with our design: for example, for k = 6 and probe length 15, the algorithm of Riesenfeld and Pollard produced 208 oligomers compared with 210 in our design. For greater values of k, the running time was already prohibitive (for k = 12, it kept running for >1 month), and thus we could not test the performance for these values. Our algorithm, on the other hand, produces an output for values of 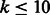in just a few seconds, whereas for k = 12, the linear algorithm takes <10 min and the optimal <1 h. The time is polynomial (or even linear) in the output sequence size, independent of probe length or the number of oligomers.

Our study raises several additional open questions. First, following (Philippakis et al., 2008), can one design an optimal RC complete sequence with improved coverage of gapped k-mers? Second, it is known that the number of distinct de Bruijn sequences is 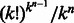. What is the number of different optimal RC complete sequences? Third, can one construct an optimal RC complete sequence for even k in linear time? Fourth, is there a closed formula for the length of an optimal RC complete of even order?

Funding: This study was supported in part by the Israel Science Foundation (grant no. 802/08), and by the I-CORE Program of the Planning and Budgeting Committee and the Israel Science Foundation (grant no. 41/11). Y.O. was supported in part by a fellowship from the Edmond J. Safra Center for Bioinformatics at Tel Aviv University and by a Dan David PhD Fellowship.

Conflict of Interest: none declared.