Changes in Protein Architecture and Sub-Picosecond Protein Dynamics Impact the Reaction Catalyzed by Lactate Dehydrogenase

Abstract

We have previously established the importance of a promoting vibration, a sub-picosecond protein motion that propagates through a specific axis of residues, in the reaction coordinate of lactate dehydrogenase (LDH). To test the effect that perturbation of this motion would have on the enzymatic reaction, we employ transition path sampling to obtain transition path ensembles for four independent LDH enzymatic systems: the wild type enzyme, a version of the enzyme expressing heavy isotopic substitution, and two enzymes with mutations in the promoting vibration axis. We show that even slight changes in the promoting vibration of LDH result in dramatic changes in enzymatic chemistry. In the “heavy” version of the enzyme, we find that the dampening of the sub-picosecond dynamics from heavy isotopic substitution leads to a drastic increase in the time of barrier crossing. Furthermore, we see that mutation of the promoting vibration axis causes a decrease in the variability of transition paths available to the enzymatic reaction. The combined results reveal the importance of the protein architecture of LDH in enzymatic catalysis by establishing how the promoting vibration is finely tuned to facilitate chemistry.

1 Introduction

How enzymes rapidly catalyze chemical reactions is one of the forefront questions of biological physical chemistry. Our understanding of this phenomenon is currently incomplete, and this deficit is best exemplified by our inability to engineer any catalyst with a rate enhancement on the same scale as that of enzymes.^1,2 In comparison to solution chemistry, biological enzymes can accelerate chemical reactions by up to a factor of 10²⁰, whereas artificial catalysts have only been able to achieve rate enhancements on the order of 10⁶.² Traditionally, artificial catalysts have been distinct from biological enzymes (for example, platinum catalyst for hydrogenation reactions³), but even recent biomimetic efforts in the design of artificial catalysts have failed to reproduce the catalytic power of enzymes.⁴

One such attempt to “reverse engineer” biological enzymes is the development of catalytic antibodies.⁵ In this method, antibodies are raised in the presence of transition state analogs until high affinity is achieved. If the main source of an enzyme’s catalytic power is the electrostatic stabilization of the transition state via the active site,^6,7 then the rate enhancement of these catalytic antibodies should approach that of biological enzymes. This, however, is not the case, and these catalysts fall short of this goal by many orders of magnitude.^1,2 In comparison with biological enzymes, catalytic antibodies differ most dramatically in size. A catalytic antibody is a molecule approximately the size of an enzymatic active site,⁵ while enzymes are often bulky structures with a total size much larger than that of their active site alone.

Considering this fact, a new question can be posed: Could the protein bulk of an enzyme somehow be contributing to enzymatic catalysis, and what is the nature of this contribution? Recent work in our group^8–12 as well as others,^13–15 has pointed to a possible answer to this question: sub-picosecond protein dynamics of specific protein architecture. The most robust example of this phenomenon so far has been found in the enzymatic reaction of lactate dehydrogenase (LDH).^10,11,16 LDH catalyzes the interconversion of the substrate pyruvate and the cofactor NADH to the substrate lactate and the cofactor NAD+, a reaction involving a hydride transfer as well as proton transfer (Fig. 1). As with all small particle transfers, donor–acceptor distance is important,¹⁷ and we have shown that a low frequency protein motion which propagates through a specific axis of residues facilitates the enzymatic reaction by dynamically modulating the particle donor–acceptor distances.^10,11 This motion, which we termed a promoting vibration, is a type of density fluctuation with a period on the order of hundreds of femtoseconds (Fig. 2).

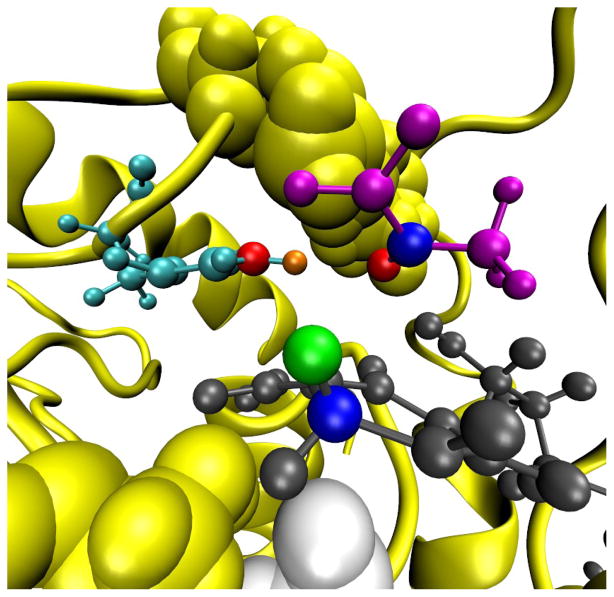
Figure 1.

The active site of LDH shown for the pyruvate side of the enzymatic reaction. The substrate pyruvate is magenta, the active site histidine is cyan, and nicotinamide ring of NADH is dark gray. The hydride and proton donor–acceptor pairs are shown explicitly (the hydride donor and acceptor are blue and the proton donor and acceptor are red) in addition to the particles (the hydride is green and the proton is orange). The atoms of residue 136 are shown as light gray Van der Waals surfaces. The backbone of the rest of the monomer is illustrated as a yellow ribbon and the atoms of the other residues of the promoting vibration are depicted as yellow Van der Waals surfaces.

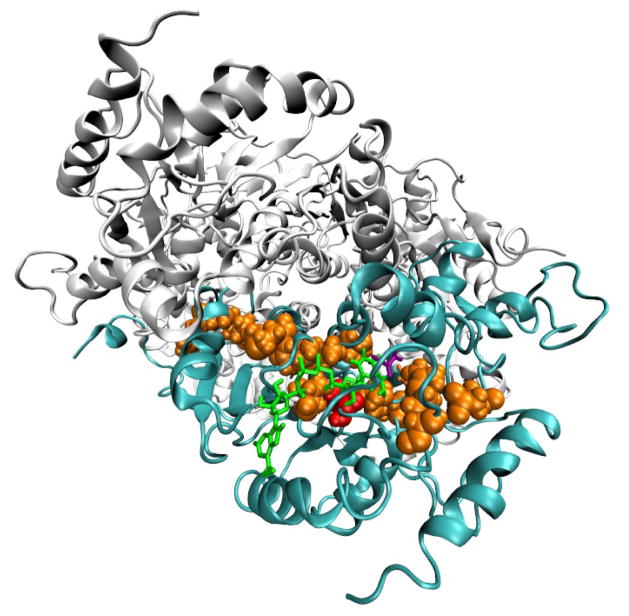
Figure 2.

The residues of the promoting vibration are shown explicitly for one monomer in the LDH tetramer. Residue 136 is red and the other residues of the promoting vibration are orange. The NADH cofactor is green and the pyruvate ligand is purple. The protein backbone of the monomer with the promoting vibration shown is cyan and the backbones of the other monomers in the tetramer are light gray. Each monomer constituting the tetramer contains an independent promoting vibration and active site.

While it is generally accepted that protein dynamics on the time scale of enzymatic turnover (milliseconds to nanoseconds) is necessary for many enzymes to achieve reactive enzyme-substrate complexes,^18–21 the importance of faster protein dynamics, such as the LDH promoting vibration, is still disputed. One issue feeding this controversy has been the lack of suitable experimental methods able to interrogate these fast motions. Recently, Schramm and colleagues have pioneered the development of the “Born-Oppenheimer Enzyme”, an enzyme where all protein carbons, nitrogens, and nonexchangeable hydrogens have been substituted with C¹³, N¹⁵, and H², respectively.^14,15

The term Born-Oppenheimer Enzyme serves to emphasize that, in these “heavy” enzymes, the substitution of heavy nuclei alters the sub-picosecond dynamics of the protein while having no effect on the electronic environment of any part of the active site. Using the model systems HIV-1 protease¹⁴ and purine nucleoside phosphorylase,¹⁵ Schramm and coworkers have experimentally demonstrated that heavy enzymes exhibit a decreased probability of barrier crossing when compared to identical enzymes containing atoms with a natural abundance of isotopes. We have also reported similar findings in a theoretical study of purine nucleoside phosphorylase and have attributed this effect on enzymatic chemistry to the dampening of sub-picosecond protein dynamics.⁸

This theoretical study aims to investigate how alteration of the protein architecture and sub-picosecond protein dynamics of LDH leads to changes in the catalyzed reaction. We employed transition path sampling (TPS), a Monte Carlo technique used to simulate rare events in complex systems,^22,23 to generate ensembles of transition paths for 4 distinct LDH enzymatic systems. One system is the Born-Oppenheimer Enzyme version of LDH (Heavy), while two others are LDH systems expressing a point mutation at a specific location along the promoting vibration axis (V136A and V136F). The residue mutated, residue 136, is a valine in the wild type enzyme, but was mutated to an alanine in V136A and to a phenylalanine in V136F to simulate a local change in mass. To serve as a basis for comparison, we also simulated the tetrameric wild type enzyme with atom masses corresponding to the natural abundance of isotopes (WT). By analyzing the transition path ensembles for these 4 tetrameric LDH systems, we found that even slight changes in the promoting vibration of LDH dramatically affected the enzymatic reaction mechanism, the transition state, and the length of barrier crossing.

2 Methods

2.1 QM/MM Simulation

We performed all molecular dynamics and quantum mechanical/molecular mechanical (QM/MM) calculations using the CHARMM^24,25/MOPAC²⁶ interface and the CHARMM27 all-hydrogen force field. As the source of initial atomic coordinates for simulation of all four LDH systems, we utilized the 2.1 Å-resolution crystal structure of the human heart LDH homotetramer in a ternary complex with the cofactor NADH and the isosteric and isoelectronic substrate mimic oxamate (Brookhaven PDB ID: 1I0Z).²⁷ For each system, we made the following changes to all active sites to create reactive complexes: We substituted the oxamate nitrogen with a carbon to create the pyruvate ligand and protonated the active site histidine (His193). We also generated the missing hydrogens for each system via the CHARMM command HBUILD.^24,25 To create the most physiologically relevant simulations, we solvated each system with a 130 Å-diameter sphere of TIP3P explicit water models²⁸ and neutralized the charged ternary complex with potassium ions. In the Heavy system, we changed the mass parameters of all protein carbons, nitrogens, and nonex-changeable hydrogens to 13.0 amu, 15.0 amu, and 2.0 amu, respectively. The mass of the atoms of the substrate and cofactor were not changed. To create the mutant systems, we replaced Val136 of each monomer with alanine in the V136A system and with phenylalanine in the V136F system. For each ternary complex, we employed DFT calculations to create the parameters for pyruvate.⁹

We treated one active site of each tetrameric LDH system quantum mechanically using the AM1 potential.²⁹ As in previous studies,^10,11,30 the quantum partition of each system consisted of 39 atoms: 17 atoms of NADH, 13 atoms of protonated His193, and 9 atoms of the substrate pyruvate for the pyruvate side of the reaction, and 16 atoms of NAD+, 12 atoms of neutral His193, and 11 atoms of the substrate lactate for the lactate side of the reaction. Using the generalized hybrid orbital (GHO) method,³¹ we linked the quantum mechanical and classical mechanical regions via two boundary atoms; the alpha-carbon of the active site histidine and the NC1’ carbon of the cofactor. During classical dynamics, the hydrogen bonds of the MM region were constrained using the SHAKE algorithm.²⁴ The timestep for integration was 1 femtosecond (fs) for all dynamics performed. We minimized each system using 300 successive steps of steepest descent (SD) followed by 700 steps of adopted basis Newton–Raphson (ABNR). After minimization, we dynamically heated each system from 0 K to 300 K over the course of 300 picoseconds and then equilibrated, via QM/MM dynamics, for 500 picoseconds. The protein backbones of the equilibrated structures of the mutants differed from the WT system by RMSD values of 0.943 Å for the V136A system and 0.981 Å for the V136F system. The protein backbone of the Heavy system deviated from WT by 0.523 Å RMSD.

2.2 Transition Path Sampling

We generated a microcanonical ensemble of reactive trajectories for each enzymatic system utilizing the transition path sampling (TPS) method.^22,23 We have described the use of this method in enzymatic reactions and the implementation of the TPS algorithm in CHARMM,^{8,10–12,30,32} so we will present only a brief overview. The initial step of the TPS algorithm was to designate the reactant and product basins. In all the systems in this study, we considered the reactant basin to be the pyruvate species and the product basin to be the lactate species. We used the reactive bond lengths as the order parameters for each basin and considered a bond formed when the distance between two reactive atoms was ≤ 1.3 Å. Next, we used constrained QM/MM dynamics to generate a 250 fs reactive trajectory connecting the reactant and product basins. Once this was achieved, we selected a random timeslice along the reactive trajectory and perturbed the momenta of all atoms in the system to generate a new set of velocities. This perturbation was taken from a zero mean Gaussian distribution, multiplied by a scaling factor of 0.1, and then rescaled to ensure there was no net angular or linear momentum and that total energy was conserved. After the perturbed momenta was translated into a new set of velocities, we propagated QM/MM dynamics forward and backward in time using these new velocities to create a new trajectory of 500 fs. If this new trajectory connected the reactant and product basins, it was accepted and used as the seed to generate another 500 fs trajectory. If this trajectory did not connect the basins, thus was not reactive, then it was discarded and a new attempt at achieving a reactive trajectory was initiated. In this manner, we were able to achieve an acceptance ratio of ~ 26% (WT system) and generate ensembles of 160 reactive 500 fs trajectories for each system.

2.3 Committor Analysis

To determine the probability of a specific timeslice of a trajectory of going to either reactants or products, we employed committor analysis.^10,16 In this method, QM/MM dynamics is initiated from a specific timeslice a number of times using random velocities until a statistical value for the committor probability can be obtained. We considered 50 randomly initiated trajectories to be sufficient for the analysis of a single timeslice. Initially, we generated trajectories that were 250 fs in length; however, in the case that the trajectory did not reach a basin in that time, it was extended for 750 fs longer. In the event that this trajectory had still not reached a basin, we disregarded this trajectory and did not count it towards the total 50. We used this method to calculate the committor values along reactive trajectories of the transition path ensembles, in addition to timeslices along the constrained trajectories generated for the purpose of committor distribution analysis (see Results and Discussion).

3 Results and Discussion

3.1 Transition Path Ensembles

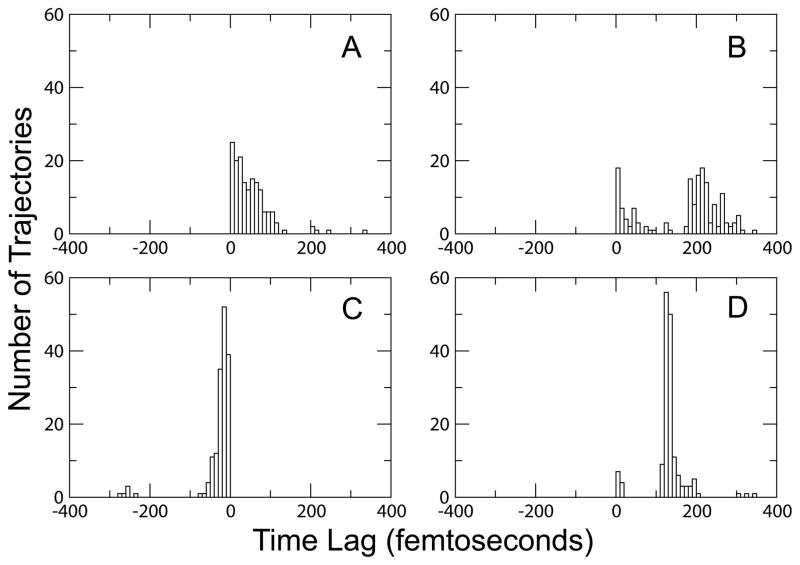
We generated a transition path ensemble (TPE) consisting of 160 reactive trajectories for each enzymatic system. To detect differences in the explored enzymatic reaction mechanisms for each system, we monitored the times of hydride and proton transfers along each trajectory. We considered the moment of particle transfer to be the timeslice where the difference between the distance from the particle to the donor and the distance from the particle to the acceptor was ≤ 0.3 Å. The results of this analysis are shown in Figure 3. All systems displayed the ability to react via a concerted mechanism, where the time lag between the hydride and proton transfers was within the time frame of a single bond vibration (~ 5 fs), in addition to a stepwise mechanism, where the two particle transfers were separated by a time greater than 5 fs. In agreement with previous studies,^10,11 the hydride transfer always preceded the proton transfer when following the reaction in the pyruvate to lactate direction in the WT, Heavy, and V136F systems. In contrast, the hydride transfer always followed the proton transfer in the V136A system.

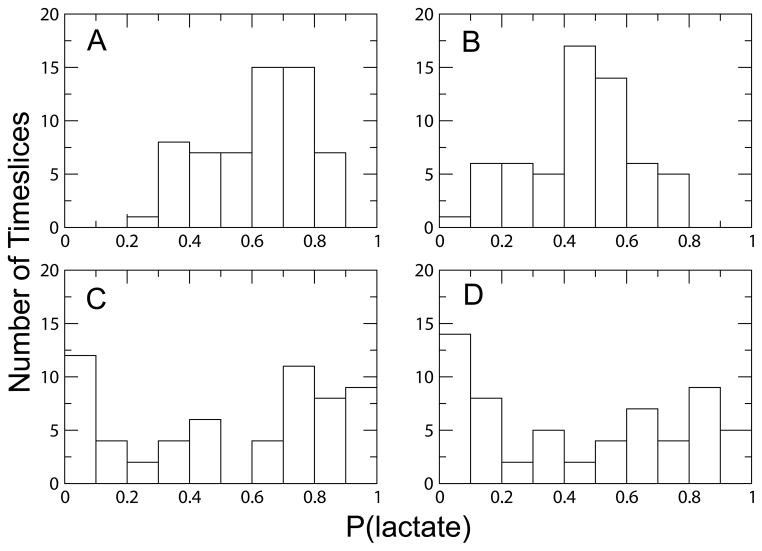
Figure 3.

Distributions of hydride and proton transfer time lags for each TPE. A) WT, B) Heavy, C) V136A, and D) V136F. The mutant systems exhibit a more narrow distribution of transfer time lags over their ensembles. Values for the V136A system are negative since the proton precedes the hydride transfer.

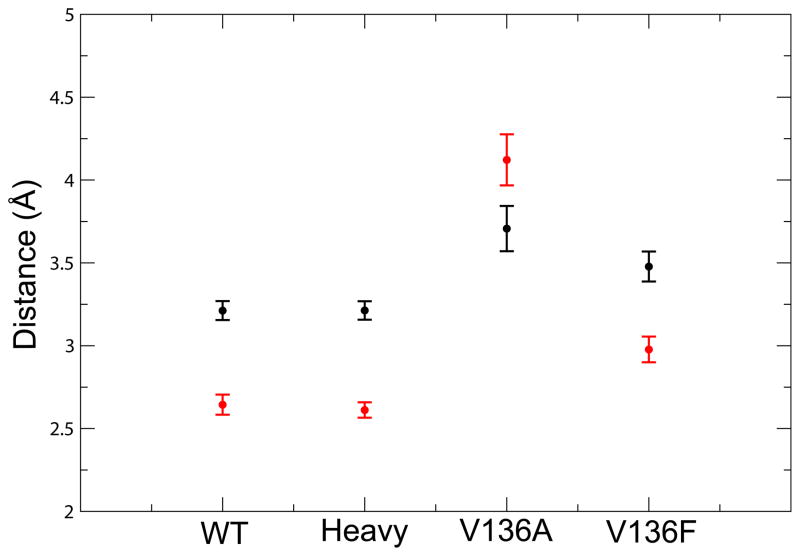
A similar result to that of the V136A system was observed in an earlier TPS study by our laboratory on bacillus lactate dehydrogenase (BsLDH).³⁰ Among the TPE generated for BsLDH, the proton transfer preceded the hydride transfer in 25% of the trajectories. This reversal of particle transfers was attributed to differences in the dynamic donor–acceptor distances for each particle in the bacillus enzymes as compared to the wild type. Similar to the BsLDH results,³⁰ the hydride and proton donor–acceptor distances were larger and exhibited more variability in the V136A system as compared to WT (Fig. 4). We also found that, unlike the other systems in this study, the proton donor–acceptor distance was consistently greater than the hydride donor–acceptor distance. This situation was only occasionally observed in the BsLDH enzyme, but it should also be noted that the mechanism where the order of the two particle transfers was reversed was not the dominant reaction mechanism in this system. It is likely that the reactive conformations of the V136A enzyme which minimize the proton donor–acceptor distance enough to facilitate particle transfer also maximize the hydride donor–acceptor distance, serving as a possible explanation for the reversal of the particle transfers.

Figure 4.

Average particle donor–acceptor distances for each LDH enzymatic system during a 2 picosecond long Molecular Dynamics production run (post-equilibration). The hydride donor–acceptor distances are black, and the proton donor–acceptor distances are red. Error bars represent the standard deviation of the distances sampled. The V136A system exhibits a greater proton donor–acceptor distance as compared to the hydride donor–acceptor distance, in addition to a greater level of variation in both particle donor–acceptor distances when compared to the other systems.

In addition to the order of particle transfers for each system, we also noted differences in the range of hydride–proton transfer time lags observed in each TPE (Fig. 3). As compared to WT, the Heavy system displayed a broader distribution of hydride–proton transfer time lags (Fig. 3). One possible origin for this effect is disruption of the sub-picosecond dynamics of the promoting vibration caused by heavy isotopic substitution. These changes in the promoting vibration are illustrated in Figure 5. The hydride and proton donor–acceptor distances and the distance between Val 31, a promoting vibration residue, and the hydride acceptor all decrease abruptly near the moments of particle transfers in the WT system. In contrast, these distance minimizations occur in a less organized fashion in the Heavy system, possibly allowing for a greater variation in the lifetime of conformations where particle transfer is possible.

Figure 5.

Dynamic distances during example reactive trajectories for the WT (A) and Heavy (B) systems. The distances between the particles and the particle acceptors are solid black for the hydride and solid red for the proton. The hydride donor–acceptor distance is shown as a dashed black line, while the proton donor–acceptor distance is represented by a red dashed line. The blue dashed line depicts the promoting vibration (the distance between the beta carbon of Val 31 and the hydride acceptor). In the WT system, the donor–acceptor distances and the promoting vibration distance reach a minimum at the same moment of the particle transfers, whereas these minimizations are less synchronized with the particle transfers in Heavy LDH.

Conversely, the distributions of hydride–proton transfer time lags in the mutant systems as compared to the WT are notably more narrow. As shown in Figure 3, most trajectories in the V136A ensemble display a transfer time lag in the range of 1–20 fs while the majority of the trajectories in the V136F ensemble exhibit a time lag in the range of 120–140 fs. Since mutation has been shown to generally lead to a decrease in the reactivity of enzymes,³³ the narrowing observed in the distribution of time lags in the mutant systems can be viewed as evidence for a truncation of reactive phase space. The increase in the dynamic donor–acceptor distances for both mutant systems shown in Figure 4 further suggests that the transition paths available to the mutant systems are less than those in the WT system since the reactive conformations of the mutants are likely to be more rare.

3.2 Transition Path Analysis

For each system, we calculated the commitment probabilities for specific timeslices along individual reactive trajectories. We performed this analysis for every 10th trajectory in each TPE to obtain a comprehensive sampling of the distribution of barrier crossings explored. To expedite this analysis, we fit this data to a cumulative Gaussian distribution and considered the time of barrier crossing of an individual trajectory to be the time required for the probability of lactate (P_lac) to go from 0.1 to 0.9. The calculation of at least 2 timeslices with non-integer P_lac values per trajectory was necessary to perform the curve fitting, and the first and last timeslices of each trajectory were assumed to have a P_lac value of 0 and 1, respectively. Figure 6 shows the distributions of barrier crossing times for each system.

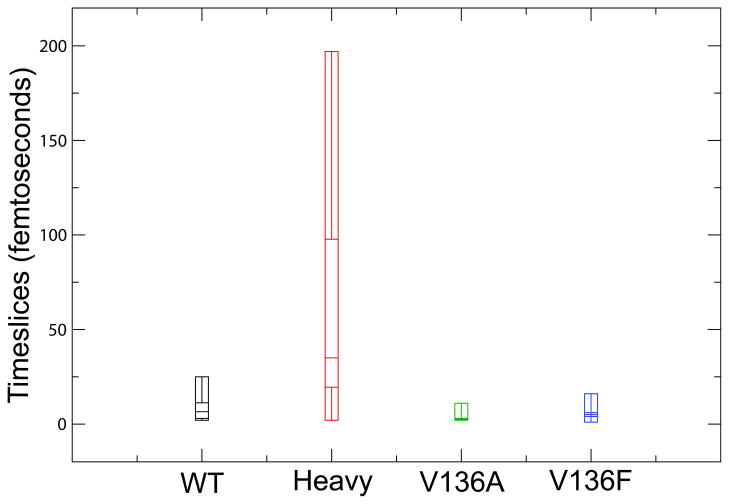
Figure 6.

Box plots showing the differences in time of barrier crossing amongst the TPE’s of each LDH systems. Each box plot describes each distribution of barrier crossing times by displaying the minimum observed time of barrier crossing, the lower quartile, the median, the upper quartile, and the maximum observed barrier crossing time. The time of barrier crossing was defined as the time required for P_lac to go from 0.1 to 0.9. The distribution of barrier crossing times for the Heavy system is significantly different that the distributions for the other systems (p-value less than 0.01).

The range of barrier crossing times and average time of barrier crossing are dramatically increased in the Heavy system as compared to the WT and mutant systems. On average, barrier crossing for the Heavy system took 35 fs, whereas the average barrier crossing of the WT system was 6.5 fs. We attribute this increase in barrier crossing to changes in the sub-picosecond dynamics of the promoting vibration. As shown in Figure 5, heavy isotopic substitution not only alters the timing of the decreases in the hydride and proton donor–acceptor distances and the distance between Val31 and the hydride acceptor (as discussed previously), but it also results in a more gradual decrease in these dynamic distances. This less rapid promoting vibration compression observed in the Heavy system leads to an increase in the time frame needed to achieve the transition state, the enzymatic conformation with a P_lac value of 0.5. Thus, the amount of time the enzyme spends in conformations with non-integer P_lac values is increased.

In contrast with the Heavy system, the average time of barrier crossing in the mutant systems was much closer to that of the WT system (2.5 fs in V136A; 5 fs in V136F). We also saw a slight narrowing of the distribution of barrier crossing times in these mutant systems. Like the narrowing of the distributions of the particle transfer time lags (Fig. 3), this result further suggests that the bottleneck for the transition state region of the mutant systems is more stringent than that of the WT system. Additionally, the RMSD values presented in Table 1 for the protein backbone conformations in the pyruvate, transition, and lactate regions of the TPE’s for each system illustrate that, in general, the structures representative of each region in the mutant systems exhibit less variation than the corresponding WT structures. This further supports the notion that the mutant systems have less reactive paths available to them than the WT system.

Table 1.

Average RMSD (Å) of the protein backbone over each TPE as compared to the last trajectory

	WT	Heavy	V136A	V136F
Pyruvate	0.2000	0.1692	0.2093	0.1703
Transition	0.1446	0.1846	0.1266	0.0837
Lactate	0.2030	0.1766	0.1917	0.1783

3.3 Committor Distribution Analysis

We used committor distribution analysis, a method we have previously applied to the reaction of LDH,^10,16 to interrogate the contribution of specific residues to the enzymatic reaction coordinates of each system. Starting with an enzymatic conformation corresponding to a transition state ( P_lac ~ 0.5), we constrained elements hypothesized to be part of the reaction coordinate. Next, we relaxed the unconstrained degrees of freedom, or those deemed to be superfluous to the enzymatic reaction, via a constrained Molecular Dynamics production run of 1000 fs. We then calculated the commitment probably of every 50th timeslice of the new, constrained trajectory and obtained a distribution of committor values. To ensure the robustness of the committor distribution, we performed the analysis using 3 distinct transition states as starting points to generate 3 constrained trajectories for each analysis performed. If the constraints used for a particular analysis correspond to the true reaction coordinate, all timeslices along these new trajectories would be located along the isocommittor surface of reactive phase space and the committor distribution generated would simply be a spike at 0.5. Selecting the exact reaction coordinate of an enzyme, a system containing many coupled degrees of freedom, is a non-trivial issue, however, so we consider a distribution centered at ~ 0.5 to be indicative of constraints corresponding to the enzymatic reaction coordinate.¹⁰

Figure 7 shows the results for the WT and Heavy systems. Using constraints corresponding to the promoting vibration previously identified in the implicitly solvated monomer of human heart LDH,^10,16 we found that this promoting vibration is maintained in the explicitly solvated, tetrameric WT and Heavy LDH. To see the contribution of residue 136 to the enzymatic reaction coordinate of the WT and Heavy systems, we only constrained this residue for the second set of analyses. As we expected, constraining residue 136 alone was not enough to approximate the enzymatic reaction coordinate, but this analysis did reveal that the relative contribution of this residue to the reaction coordinate was nearly identical in the WT and Heavy systems.

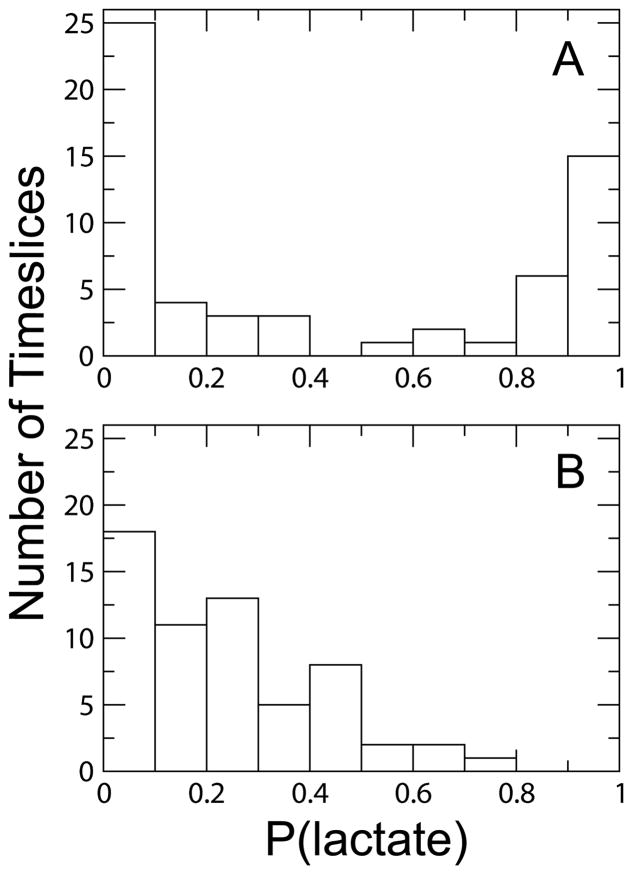
Figure 7.

Committor distributions for the WT and Heavy systems. The top row shows the committor distributions after constraints had been applied to the reactive atoms and the distances of the residues of the promoting vibration from the active site for WT (A) and Heavy (B). Both distributions are centered at approximately 0.5, illustrating that the promoting vibration is the same in the WT and Heavy systems. The bottom row shows the committor distributions where constraints had been applied to the reactive atoms and only the distance of Val136 from the active site (WT is C; Heavy is D). The distributions are generally the same shape for both systems. This indicates that the contribution of Val136 to the promoting vibration of each system is the same.

The results for the mutant systems are illustrated in Figure 8. In this set of analyses, we again applied constraints to only residue 136. We found that, not only does the contribution of this residue to the reaction coordinate of the mutant systems differ from that of WT and Heavy LDH, but the contribution of this residue differs between the mutants. In the V136A system, the participation of residue 136 in the promoting vibration has been nearly abolished, whereas, in V136F, constraining this residue biases reaction towards the side of pyruvate. These results reveal that mutation of a residue in the promoting vibration of LDH alters the enzymatic reaction coordinate.

Figure 8.

Committor distributions for the mutant systems with constraints applied to the reactive atoms and the distance of residue 136 from the active site (V136A is A; V136F is B). Compared to the results for the WT and Heavy systems (Figure 7, graphs C and D, respectively), the contribution of residue 136 to the LDH promoting vibration appears to have been altered in both mutant systems. In V136A, residue 136 displays very little involvement in the enzymatic reaction coordinate since the distribution is no longer centered at 0.5; however, constraining residue 136 in the V136F system shifts the distribution towards the pyruvate basin.

4 Conclusions

This work shows that slight perturbations of protein architecture and dynamics can have dramatic effects on the chemical step of an enzyme. Mutation in the promoting vibration axis of LDH altered the contribution of Residue 136 to the enzymatic reaction coordinate and resulted in a decrease in the transition paths and transition states available to the enzymatic reaction. Disruption of the promoting vibration via heavy isotopic substitution lead to a dramatic increase in the time of the chemical barrier crossing. These combined results reveal that the protein architecture and sub-picosecond protein dynamics are finely tuned in the wild type enzyme to facilitate chemistry, establishing a possible role for the protein bulk of LDH in enzymatic catalysis. The in silico manipulation presented in this work could also be tested in experimental systems, allowing for a facile link between experiment and theory. A deeper understanding of this phenomenon has the potential to impact a large range of areas, such as enzyme engineering.

Abbreviations

LDH

lactate dehydrogenase

TPS

transition path sampling

TPE

transition path ensemble

NADH/NAD+

nicotinamide adenine dinucleotide

DFT

density functional theory

fs

femtosecond

BsLDH

bacillus lactate dehydrogenase