Kinematics, material symmetry, and energy densities for lipid bilayers with spontaneous curvature

Abstract

Continuum mechanical tools are used to describe the deformation, energy density, and material symmetry of a lipid bilayer with spontaneous curvature. In contrast to conventional approaches in which lipid bilayers are modeled by material surfaces, here we rely on a three-dimensional approach in which a lipid bilayer is modeling by a shell-like body with finite thickness. In this setting, the interface between the leaflets of a lipid bilayer is assumed to coincide with the mid-surface of the corresponding shell-like body. The three-dimensional deformation gradient is found to involve the curvature tensors of the mid-surface in the spontaneous and the deformed states, the deformation gradient of the mid-surface, and the transverse deformation. Attention is also given to the coherency of the leaflets and to the area compatibility of closed lipid bilayers (i.e., vesicles). A hyperelastic constitutive theory for lipid bilayers in the liquid phase is developed. In combination, the requirements of frame-indifference and material symmetry yield a representation for the energy density of a lipid bilayer. This representation shows that three scalar invariants suffice to describe the constitutive response of a lipid bilayer exhibiting in-plane fluidity and transverse isotropy. In addition to exploring the geometrical and physical properties of these invariants, fundamental constitutively-associated kinematical quantities are emphasized. On this basis, the effect on the energy density of assuming that the lipid bilayer is incompressible is considered. Lastly, a dimension reduction argument is used to extract an areal energy density per unit area from the three-dimensional energy density. This step explains the origin of spontaneous curvature in the areal energy density. Importantly, along with a standard contribution associated with the natural curvature of lipid bilayer, our analysis indicates that constitutive asymmetry between the leaflets of the lipid bilayer gives rise to a secondary contribution to the spontaneous curvature.

1 Introduction

Biomembranes are essential to the functions of cells, bacteria, and viruses (Harrison and Lunt 1975, Yeagle 2001). Basic to all biological membranes are lipid bilayers, which are thin, sheet-like structural elements composed of two adjacent monomolecular leaflets joined by weak, noncovalent bonds (Bretscher 1973). In the liquid phase, lipid bilayers are very flexible in bending but highly resistant to lateral stretching (Bloom 1991). The architecture of lipid bilayers hinges on the amphiphatic chemical properties of the constituent phospholipid molecules (Tanford 1980). Such molecules consist of hydrophilic head groups and hydrophobic tails. When suspended in aqueous solutions under suitable temperature conditions and at appropriate concentrations, they form various self-assembled complexes with hydrophobic tails facing one another and hydrophilic head groups in contact with the solution (Lasic 1988). These complexes include closed bilayers, known as vesicles or liposomes, which are typically a few nanometers thick and can range between fifty nanometers and tens of micrometers in diameter (Luisi and Walade 2000).

Biomembranes are generally heterogeneous multi-component systems involving hundreds of lipid species along with various proteins and hydrocarbons. The inherent complexity of such systems has driven the development of biomimetic model systems (Chan and Boxer 2007). These model systems include Giant Unilaminar Vesicles (GUVs), which may be composed of as few as two lipid species and a single type of cholesterol. Aside from providing platforms for focused investigations of processes mediated by biomembranes (Lipowsky and Sackmann 1995, Peetla 2009), GUVs are of potential value in various pharmaceutical and technological applications, including biocompatible microcapsules for targeted drug delivery and gene therapy (Allen and Cullis 2004, Attama 2011), adjuvants for immunization (Latif and Bachhawat 1984, Gregoriadis et al. 1996), signal carrying and enhancement in medical diagnostics and analytical biochemistry (Gómez-Hens and Fernández-Romero 2005, Edwards and Baeumner 2006), and biochemical reactors (Tsumoto et al. 2001, Fischer et al. 2002, Michel et al. 2004, Vriezema et al. 2005).

Lipid bilayers readily change shape in response to shifting osmotic and thermal conditions and applied mechanical loads (Lipowsky 1995). Efforts to model such shape changes date back somewhat more than four decades. Canham (1970) emulated the methodology commonly applied in the bending analysis of beams to yield a simplified model capable of predicting the shapes available to a red blood cell. Treating a cell membrane as a surface, Canham (1970) showed that the shapes it manifests in equilibrium emerge as a consequence of bending-energy minimization. Independently, Helfrich (1973) attributed a surface bending-energy to lipid bilayers. In the models of Canham (1970) and Helfrich (1973), energy changes induced by relative molecular misalignment are incorporated through deviations of the principal curvatures (or alternatively, the mean and Gaussian curvatures) of the surface that serves as a proxy for the lipid bilayer. Specifically, according to Canham–Helfrich theory, the bending-energy density (that is, the energy per unit surface area) is given by

$$\psi =\frac{1}{2}\kappa {(H-H_{\circ })}^2+\stackrel{‒}{\kappa }K,$$ (1)

where H and K are the mean and Gaussian curvatures, respectively, and H_o is the spontaneous mean curvature, which embodies the curvature of the bilayer in its natural state. In (1), changes of H and K are respectively penalized by bending moduli κ and $\stackrel{‒}{\kappa }$, known, respectively, as the splay (or ordinary) and saddle-splay (or Gaussian) moduli. As the brothers Cosserat (1909) noted in their work on elastic surfaces, Germain (1821) previously derived a energy density quadratic in the mean and Gaussian curvatures equivalent to (1) and the particular case corresponding to zero spontaneous curvature (H_o = 0) was obtained by Poisson (1812). See also the historical remarks of Nitsche (1993).

The Canham–Helfrich energy is perhaps the simplest model believed suitable to situations where the shape of the lipid bilayer is dominated by bending and the radius of curvature of the lipid bilayer is much larger than its thickness. It can nevertheless be argued that (1) neglects energetic contributions associated with changes of local area or thickness and merely considers the lipid bilayer as a two-dimensional fluid surface that resists curvature deviations. Moreover, the Canham–Helfrich theory does not allow for changes in overall area. This constraint is imposed by adding a term proportional to the area of the surface that models the lipid bilayer to the net bending-energy determined by integrating (1) over that surface. However, as is clear from the discussion of the global and local area preservation provided by Steigmann et al. (2003), this approach does not rule out the local area changes. Importantly, local area or thickness changes can occur in the vicinity of phase interfaces in multi-component lipid bilayers or heterogeneities such as protein molecules (Israelachvili 2011).

In contrast to an elastic shell, a lipid bilayer in the liquid phase does not have the ability to resist in-plane shear forces. This is because the lipid molecules may move freely within a lipid bilayer. Due to the absence of preferred directionality tangent to their surfaces in the liquid phase, lipid bilayers also exhibit in-plane isotropy. Bearing in mind that the general theory of elastic shells allows for a broad range of possible material symmetries, any shell-like model for a lipid bilayer should be consistent with the observed in-plane fluidity and isotropy. Working in the context of modern shell theory, Jenkins (1977) derived the general equations governing the mechanical equilibrium for a shell with material symmetry consistent with that of a lipid bilayer. Steigmann (1999) subsequently reconsidered the mechanical modeling of fluid films with bending elasticity from a fundamental perspective. By treating the lipid bilayer as a two-dimensional (inviscid) fluid and choosing the full set of two-dimensional unimodular transformations as the appropriate material symmetry group, Steigmann (1999) obtained a general energy density depending not only on the mean and Gaussian curvatures H and K but also on the areal stretch J. The areal stretch J represents local expansion/contraction within the tangent plane of the bilayer. Since a lipid bilayer shows no resistance to in-plane shear forces, but rather only to the local area changes, the areal stretch J is the sole kinematical ingredient needed to reckon in-plane deformation of the lipid bilayer. A new free-energy density for biomembranes, based on treating the lipid bilayer as a three-dimensional body rather than a two-dimensional surface, was proposed by Zurlo (2006) and Deseri et al. (2008). An important feature of the formulation of these authors involves the introduction of a symmetry group that describes in-plane fluidity and isotropy at the level of the bulk, three-dimensional, material. However, a proof of the corresponding representation theorem was not provided. Additionally, the analysis of Zurlo (2006) and Deseri et al. (2008) is based on considering a flat reference configuration, which means that spontaneous curvature is tacitly assumed to vanish. Following a dimension reduction from a three-dimensional shell-like structure to a two-dimensional material surface, Zurlo (2006) and Deseri et al. (2008) obtained the superficial energy density per unit area of the reference surface.

Several explanations for the existence of spontaneous curvature have been reported in the literature. Spontaneous curvature is believed to be a measure of the extent to which the upper and lower leaflets of the lipid bilayer are asymmetric (Seifert 1997). Asymmetry may arise due to differences between the molecular compositions of the leaflets, different properties of the aqueous solutions adjacent to the sides of the lipid bilayer (Döbereiner et al. 1999), or interactions with a cytoskeleton (for a review see McMahon and Gallop 2005). For instance, the presence of molecules with different headgroup or tailgroup conformations can lead to spontaneous curvature (McMahon and Gallop 2005). Asymmetry between the upper and lower leaflets of a bilayer can also be caused by helix insertion, scaffolding, transmembrane proteins, and clathrin coating (McMahon and Gallop 2005, Mashi and Bruinsma 1998, Agrawal and Steigmann 2009). Importantly, the presence of different species on a lipid bilayer is not generally sufficient to generate non-zero spontaneous curvature. In fact, spontaneous curvature appears to arise only when the flip-flop diffusion of unlike molecules between two leaflets is very slow compared to other time scales underlying shape changes. Numerical models of vesicles that incorporate spontaneous curvature reveal novel predictions of equilibrium shapes that appear to agree more closely with experimental observations (Luisi and Walade 2000, Wintz et al. 1996, Mutz and Bensimon 1991, Michalet and Bensimon 1995) than otherwise.

In the present paper, continuum mechanical tools are used to study the deformation, material symmetry, and energy density of a lipid bilayer with spontaneous curvature. Attention is restricted to lipid bilayers in the liquid phase. Inspired from Zurlo (2006) and Deseri et al. (2008), these thin structural elements are treated as three-dimensional bodies rather than material surfaces. Specifically, the formulation encompasses bending, in-plane stretching, and thickening/thinning of the bilayer. It also enables characterizations of leaflet coherency and area compatibility; whereas leaflet coherency concerns the local coupling or sliding of upper and lower leaflets, area compatibility concerns the integrity of closed lipid bilayers (i.e., vesicles). After discussing geometry and kinematics, constitutive behavior is considered. Treating the lipid bilayer as a three-dimensional body leads not only to more precise understanding of the deformation of lipid bilayers but also affords insight regarding the material symmetry of lipid bilayers from a bulk material perspective. In particular, stipulating that the lipid bilayer is hyperelastic and invoking suitable material symmetry requirements leads to a representation for the energy density of a lipid bilayer. In addition, the impact of imposing the notion of incompressibility is considered. Finally, dimension reduction is used to derive an areal (two-dimensional) energy density from the three-dimensional energy density. As such, it includes the Canham–Helfrich energy density as a particular case. More broadly, however, it incorporates possible asymmetry and incoherency of the leaflets.

2 Geometry and kinematics

2.1 Basic considerations

Consider a lipid bilayer, either closed or open, represented by a three-dimensional body B (Figure 1). Suppose that the lipid bilayer is in its spontaneous (natural) state. Assume that the thickness of the bilayer in that state is uniform. Allow, however, for the possibility that the upper and lower leaflets may have different, but constant, thicknesses $h_{\circ }^{+}$ and $h_{\circ }^{-}$, respectively, in which case the thickness of the bilayer in its spontaneous state is simply $h_{\circ }^{+}+h_{\circ }^{-}$. It is useful to introduce a reference surface separating the leaflets. This surface is referred to as the mid-surface and is denoted by S_∘. The unit normal vector on S_∘, directed outward from the region enclosed by the vesicle, is denoted by $\mathbb{m}$ (Figure 1). The curvature tensor of the mid-surface S_∘ is denoted by ${\mathbb{L}}_{\circ }$, as defined in (179),¹ and is referred to as the spontaneous curvature tensor. Furthermore, H_∘ and K_∘ denote the corresponding spontaneous mean and Gaussian curvatures, as defined in (180). It is assumed that S_∘ does not intersect itself. Additionally, $h_{\circ }^{+}$ and $h_{\circ }^{-}$ are assumed to be sufficiently small relative to the radius of curvature of S_∘ to ensure that the inner and outer surfaces of lipid bilayer Sⁱ and S^∘ do not fold back on themselves. A generic material point X located on a material surface S_ξ∘ in B can then be uniquely described using its projection $\widehat{\mathbf{X}}$ onto S_∘ and a local coordinate ${\xi }_{\circ }\in [-h_{\circ }^{-},h_{\circ }^{+}]$ that reckons the normal between X and $\widehat{\mathbf{X}}$ specifically,

$$\mathbf{X}=\widehat{X}+{\xi }_{\circ }\mathbb{m}\left(\widehat{X}\right)=\tilde{X}(\widehat{X},{\xi }_{\circ }).$$ (2)

Fig. 1.

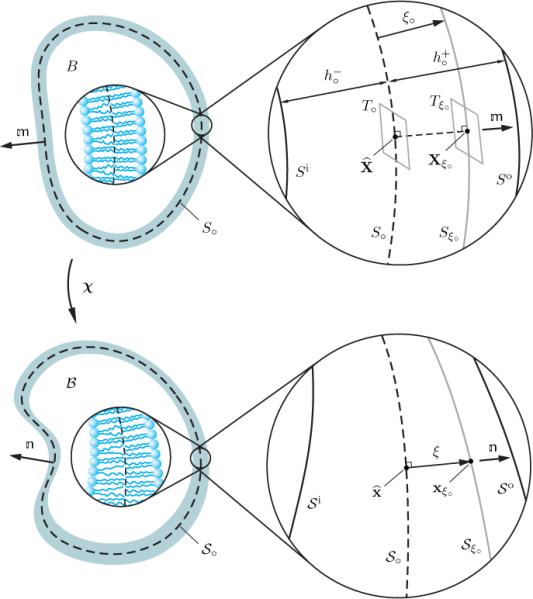
Two-dimensional schematic of a closed lipid bilayer in its spontaneous state and its deformation to a generic spatial configuration.

Consider a deformation χ that maps the lipid bilayer in its spontaneous state into the observed space. Under χ, the reference placement of the body B, midsurface S_∘, and the normal $\mathbb{m}$ to S_∘ map to the observed placement β, mid-surface ${\mathcal{S}}_{\circ }$, and unit normal $\mathbb{n}$ to ${\mathcal{S}}_{\circ }$, respectively (Figure 1). The curvature tensor of the surface ${\mathcal{S}}_{\circ }$ is $\mathbb{L}$, as defined in (179), with corresponding mean and Gaussian curvatures H and K, as defined in (181). In general, the thickness of the deformed bilayer may be nonuniform. As is customary, it is assumed that the deformation χ is such that the images ${\mathcal{S}}_{\circ }$, ${\mathcal{S}}^{\mathrm{i}}$, and ${\mathcal{S}}^{\mathrm{o}}$ of S_∘, Sⁱ, and ${\mathcal{S}}^{\mathrm{o}}$ (see Figure 1) do not fold back on themselves. Hence, there is, for each x in β, a unique X in B such that x = χ(X). In view of (2), the spatial point x can be described as

$$\text{x}=\chi \left(\mathbf{X}\right)=\tilde{\text{x}}(\widehat{X},{\xi }_{\circ }),\widehat{X}\in S_{\circ },{\xi }_{\circ }\in [-h_{\circ }^{-},h_{\circ }^{+}].$$ (3)

The deformation gradient describing the local distortion of B is given by

$$\mathbf{F}=\nabla \chi \left(\mathbf{X}\right),$$ (4)

where ▽ indicates the gradient in the reference space.

Consider a material point X_ξ∘ on S_ξ∘ along with a generic point X located at a normal elevation z from S_ξ∘. Since the tangent planes T_∘ and T_ξ∘ at the points $\widehat{\mathbf{X}}$ and X_ξ∘ are parallel (see Figure 1), the unit normal $\mathbb{m}$ on S_∘ is also normal to S_ξ∘ and, hence, can also be viewed as a function defined on S_ξ∘. Thus, bearing in mind that X coincides with X_ξ∘ for z = 0, X can be expressed as $\mathbf{X}={\mathbf{X}}_{{\xi }_{\circ }}+z\mathbb{m}\left({\mathbf{X}}_{{\xi }_{\circ }}\right)$. The spatial point x corresponding to X, can thus also be described via

$$\text{x}=\chi \left(\mathbf{X}\right)=\stackrel{‒}{x}({\mathbf{X}}_{{\xi }_{\circ }},z),$$ (5)

where X_ξ∘ ∊ S_ε∘ and $z\in \left[\right(-h_{\circ }^{-}-{\xi }_{\circ }),(h_{\circ }^{+}-{\xi }_{\circ }\left)\right]$. In view of (5), the deformation gradient F for a material point located on S_ξ∘ can be expressed as

$$\mathbf{F}=\nabla \mathbf{x}{\mid }_{z=0}={\phantom{\mid }\left({\nabla }_{S_{{\xi }_{\circ }}}\stackrel{‒}{x}+\frac{\partial \stackrel{‒}{x}}{\partial z}\otimes \mathbb{m}\right)\mid }_{z=0},$$ (6)

where ▽_Sξ∘ indicates the surface gradient on S_ξ∘, defined as

$${\nabla }_{S_{{\xi }_{\circ }}}\stackrel{‒}{x}{\mid }_{z=0}=(\nabla \stackrel{‒}{x}{\mid }_{z=0}){\mathbb{P}}_{\mathbb{m}},$$ (7)

where ${\mathbb{P}}_{\mathbb{m}}=1-\mathbb{m}\otimes \mathbb{m}$ is the projection tensor onto the tangent plane T_∘ (or, equivalently T_ξ∘).

Consider a material line element dX_ξ∘ tangent to the surface S_ξ∘ and the corresponding line element dx_ξ∘ tangent to the spatial image ${\mathcal{S}}_{{\xi }_{\circ }}$ of S_ξ∘. According to the description of x in (3),

$$\begin{array}{cc}\hfill {\text{dx}}_{{\xi }_{\circ }}& =\text{d}\tilde{\text{x}}(\widehat{X},{\xi }_{\circ }){\mid }_{{\xi }_{\circ }=\text{constant}}\hfill \\ \hfill & =(\nabla \tilde{\text{x}}(\widehat{X},{\xi }_{\circ }\left){\mid }_{{\xi }_{\circ }=\text{constant}}\right)\text{d}\widehat{X}\hfill \\ \hfill & =(\nabla \tilde{\text{x}}(\widehat{X},{\xi }_{\circ }\left){\mid }_{{\xi }_{\circ }=\text{constant}}\right){\mathbb{P}}_{\mathbb{m}}\text{d}\widehat{X}\hfill \\ \hfill & =\left({\nabla }_{S_{\circ }}\tilde{\text{x}}\right(\widehat{X},{\xi }_{\circ }\left){\mid }_{{\xi }_{\circ }=\text{constant}}\right)\text{d}\widehat{X},\hfill \end{array}$$ (8)

where ▽_S∘ indicates the surface gradient on S_∘, as defined by

$${\nabla }_{S_{\circ }}\tilde{\text{x}}(\widehat{X},{\xi }_{\circ }){\mid }_{{\xi }_{\circ }=\text{constant}}=(\nabla \tilde{\text{x}}(\widehat{X},{\xi }_{\circ }\left){\mid }_{{\xi }_{\circ }=\text{constant}}\right){\mathbb{P}}_{\mathbb{m}}.$$ (9)

Similarly, for the description given in (5) we have

$$\begin{array}{cc}\hfill \text{d}{\mathbf{x}}_{{\xi }_{\circ }}& =(\nabla \stackrel{‒}{x}({\mathbf{X}}_{{\xi }_{\circ }},z\left)\right){\mid }_{z=0}\text{d}{\mathbf{X}}_{{\xi }_{\circ }}\hfill \\ \hfill & =(\nabla \stackrel{‒}{x}({\mathbf{X}}_{{\xi }_{\circ }},z\left)\right){\mid }_{z=0}{\mathbb{P}}_{\text{m}}\text{d}{\mathbf{X}}_{{\xi }_{\circ }}\hfill \\ \hfill & =\left({\nabla }_{S_{{\xi }_{\circ }}}\stackrel{‒}{x}\right({\mathbf{X}}_{{\xi }_{\circ }},z\left){\mid }_{z=0}\right)\text{d}{\mathbf{X}}_{{\xi }_{\circ }}.\hfill \end{array}$$ (10)

Comparing (8) and (10) yields the identity

$$\left({\nabla }_{S_{{\xi }_{\circ }}}\stackrel{‒}{x}{\mid }_{z=0}\right)\text{d}{\mathbf{X}}_{{\xi }_{\circ }}=\left({\nabla }_{S_{\circ }}\tilde{x}{\mid }_{{\xi }_{\circ }=\text{constant}}\right)\text{d}\widehat{X}.$$ (11)

Using (2) and elementary properties of the curvature tensor ${\mathbb{L}}_{\circ }$ (see (179)) it is easy to arrive at the identity

$$\begin{array}{cc}\hfill \text{d}{\mathbf{X}}_{{\xi }_{\circ }}& =d\widehat{X}+{\xi }_{\circ }\text{d}\mathbb{m}\hfill \\ \hfill & =\text{d}\widehat{X}-{\xi }_{\circ }{\mathbb{L}}_{\circ }\text{d}\widehat{X},\hfill \end{array}$$ (12)

which, on introducing

$${\$}_{\circ }={\mathbb{P}}_{\mathbb{m}}-{\xi }_{\circ }{\mathbb{L}}_{\circ },$$ (13)

can alternatively be written as

$$\text{d}{\mathbf{X}}_{{\xi }_{\circ }}={\$}_{\circ }\text{d}\widehat{X}.$$ (14)

Notice that $\mathrm{d}\widehat{\mathbf{X}}$ is a tangent line element on S_∘ at the point $\widehat{\mathbf{X}}$. Since the tangent planes T_∘ and T_ξ∘ are parallel, dX_ξ∘ and $\mathrm{d}\widehat{\mathbf{X}}$ can be viewed as elements of the same tangent space, say T_∘.

The tensor $_∘ defined in (13) is fully tangential (see Appendix A.1 for the definition of such a tensor) and, thus, can be viewed as a mapping from T_∘ to T_∘. By (13), the second principal invariant I₂($_∘) of $_∘ can be expressed as

$$\begin{array}{cc}\hfill I_2\left({\$}_{\circ }\right)& =\frac{1}{2}[{\left(I_1\right({\$}_{\circ }\left)\right)}^2-I_1({\$}_{\circ }^2\left)\right]\hfill \\ \hfill & =1-2{\xi }_{\circ }{H}_{\circ }+{\xi }_{\circ }^2{K}_{\circ }.\hfill \end{array}$$ (15)

Let c_∘1 and c_∘2 denote the principal curvatures of S_∘, so that $H_{\circ }=\frac{1}{2}(c_{\circ 1}+c_{\circ }2)$ and K_∘ = c_∘1c_∘2. Then, by (15),

$$I_2\left({\$}_{\circ }\right)=(1-{\xi }_{\circ }{c}_{\circ 1})(1-{\xi }_{\circ }{c}_{\circ 2}).$$ (16)

Granted the assumption (imposed to ensure avoiding folding back of outer and inner surfaces S^∘ and Sⁱ on themselves) that the thicknesses $h_{\circ }^{+}$ and $h_{\circ }^{-}$ of upper and lower leaflets are very small relative to the radius of curvature of S_∘, ξ_∘ must satisfy

$${\xi }_{\circ }{c}_{\circ \alpha }\ne 1,\alpha =1,2,$$ (17)

and (16) implies that I₂($_∘) ≠ 0. Thus, as described in Appendix A.2, $_∘ has a pseudoinverse ${\mathbb{Q}}_{\circ }$ given by

$${\mathbb{Q}}_{\circ }={\left(I_2\right({\$}_{\circ }\left)\right)}^{-1}\left(I_1\right({\$}_{\circ }){\mathbb{P}}_{\mathbb{m}}-{\$}_{\circ }),$$ (18)

where

$$\begin{array}{cc}\hfill I_1\left({\$}_{\circ }\right)& =\text{tr}({\mathbb{P}}_{\mathbb{m}}-{\xi }_{\circ }{\mathbb{L}}_{\circ })\hfill \\ \hfill & =2(1-{\xi }_{\circ }{H}_{\circ })\hfill \end{array}$$ (19)

is the first principal invariant of $_∘, and, since, as noted above, dX_ξ∘ and $\mathrm{d}\widehat{\mathbf{X}}$ can be viewed as elements of the same tangent space, (14) is equivalent to

$$\text{d}\widehat{X}={\mathbb{Q}}_{\circ }\text{d}{\mathbf{X}}_{{\xi }_{\circ }}.$$ (20)

As regards ${\mathbb{Q}}_{\circ }$, it is convenient to introduce

$${\gamma }_{\circ }\left({\xi }_{\circ }\right)=I_2\left({\$}_{\circ }\right)$$ (21)

and, thus, using (13), (15), and (19) in the representation (18) yields

$${\mathbb{Q}}_{\circ }={\left({\gamma }_{\circ }\right({\xi }_{\circ }\left)\right)}^{-1}({\mathbb{P}}_{\mathbb{m}}-2{\xi }_{\circ }{H}_{\circ }{\mathbb{P}}_{\mathbb{m}}+{\xi }_{\circ }{\mathbb{L}}_{\circ }).$$ (22)

Bearing in mind (14), (11) can be expressed as

$$\left({\nabla }_{S_{{\xi }_{\circ }}}\stackrel{‒}{x}{\mid }_{z=0}\right)\text{d}{\mathbf{X}}_{{\xi }_{\circ }}=\left({\nabla }_{S_{\circ }}\tilde{x}{\mid }_{{\xi }_{\circ }=\text{constant}}\right){\mathbb{Q}}_{\circ }\text{d}{\mathbf{X}}_{{\xi }_{\circ }}.$$ (23)

Since (23) holds for an arbitrary line element dX_ξ∘, we conclude that

$${\nabla }_{S_{{\xi }_{\circ }}}\stackrel{‒}{x}{\mid }_{z=0}=\left({\nabla }_{S_{\circ }}\tilde{x}{\mid }_{{\xi }_{\circ }=\text{constant}}\right){\mathbb{Q}}_{\circ }.$$ (24)

The second term on the far right-hand side of (6) includes the normal derivative $(\nabla \mathrm{x})\mathbb{m}$, as is clear from (176). Notice that, according to the descriptions $\mathrm{x}=\tilde{\mathrm{x}}(\widehat{\mathbf{X}},{\xi }_{\circ })$ and $\mathrm{x}=\tilde{\mathrm{x}}({\widehat{\mathbf{X}}}_{{\xi }_{\circ }},z)$, changes of x in the $\mathbb{m}$ direction are controlled by ξ_∘ and z, respectively. Thus,

$$\begin{array}{cc}\hfill (\nabla \mathbf{x})\mathbb{m}& =\frac{\partial \tilde{x}}{\partial {\xi }_{\circ }}\hfill \\ \hfill & =\frac{\partial \stackrel{‒}{x}}{\partial z},\hfill \end{array}$$ (25)

which, in combination with (6), implies that the deformation gradient F may be written as

$$\mathbf{F}=\left({\nabla }_{S_{\circ }}\tilde{x}\right){\mathbb{Q}}_{\circ }+\frac{\partial \tilde{x}}{\partial {\xi }_{\circ }}\otimes \mathbb{m}.$$ (26)

2.2 Orientation of phospholipid molecules at the mid-surface

Compatible with physical observations of amphiphilic fluid films, we assume that, due to interatomic interactions and packing requirements, the phospholipid molecules comprising the bilayer tend to remain perpendicular to the mid-surface S_∘. This constraint is embodied by the kinematical requirement that: during a deformation, straight line elements perpendicular to S_∘ remain straight and perpendicular to ${\mathcal{S}}_{\circ }$ (Figure 1). This assumption resembles Kirchhoff's (1850) hypothesis in theories of thin plates and shells. However, at variance with that hypothesis, the kinematical constraint imposed here does not restrict the through-thickness deformation of the lipid bilayer.

To provide an analytical characterization of our constraint, it is useful to represent a generic spatial point x in the deformed body in the form $\mathrm{x}=\widehat{\mathrm{x}}+\xi \mathbb{n}\left(\widehat{x}\right)$, where ξ indicates normal distance of x from ${\mathcal{S}}_{\circ }$. Since x is the image of X in the observed space, and also X can be described by $\widehat{\mathbf{X}}$ and ξ_∘ through (2), the out-of-plane coordinate ξ in the body can be expressed in the form

$$\xi =\tilde{\xi }(\widehat{\mathbf{X}},{\xi }_{\circ }).$$ (27)

Moreover, as a result of the constraint, the projection $\widehat{\mathrm{x}}$ of x onto ${\mathcal{S}}_{\circ }$ coincides with the placement of the spatial image of the material point $\widehat{\mathbf{X}}$ on I_∘ (Figure 1). Consequently, bearing in mind (26) and (27), it transpires that

$$\mathbf{F}=\left({\nabla }_{S_{\circ }}\right(\widehat{\mathbf{x}}+\xi \mathbb{n}\left)\right){\mathbb{Q}}_{\circ }+\frac{\partial (\widehat{\mathbf{x}}+\xi \mathbb{n})}{\partial {\xi }_{\circ }}\otimes \mathbb{m},$$ (28)

where $\nabla s_{\circ }(\widehat{\mathrm{x}}+\xi \mathbb{n})$ and $\partial (\widehat{\mathrm{x}}+\xi \mathbb{n})∕\partial {\xi }_{\circ }$ are given by

$${\nabla }_{S_{\circ }}(\widehat{\mathbf{x}}+\xi \mathbb{n})={\nabla }_{S_{\circ }}\widehat{\mathbf{x}}+\xi {\nabla }_{S_{\circ }}\mathbb{n}+\mathbb{n}\otimes {\nabla }_{S_{\circ }}\xi$$ (29)

and

$$\frac{\partial (\widehat{\mathbf{x}}+\xi \mathbb{n})}{\partial {\xi }_{\circ }}=\frac{\partial \xi }{\partial {\xi }_{\circ }}\mathbb{n},$$ (30)

respectively.

It is now convenient to introduce some shorthand notation. Specifically, given a quantity g dependent either explicitly or implicitly on ξ_∘, let

$$g{\mid }_{\circ }≔g{\mid }_{{\xi }_{\circ }}=0$$ (31)

denote its value at the referential mid-surface S_∘. With this convention in mind, and according to the definition of surface gradient of a vector field provided in Appendix A.1, we have

$$\begin{array}{cc}\hfill {\nabla }_{S_{\circ }}\widehat{\mathbf{x}}& =(\nabla \mathbf{x}){\mid }_{\circ }\mathbb{P}\mathbb{m}\hfill \\ \hfill & =\mathbf{F}{\mid }_{\circ }{\mathbb{P}}_{\mathbb{m}}\hfill \\ \hfill & ≕{\mathbb{F}}_{\circ },\hfill \end{array}$$ (32)

where ${\mathbb{F}}_{\circ }$, which designates the superficial deformation gradient on the mid-surface S_∘, maps material line elements on S_∘ to spatial line elements on ${\mathcal{S}}_{\circ }$.

Having introduced ${\mathbb{F}}_{\circ }$, the areal stretch

$$J≔I_2\left({\mathbb{F}}_{\circ }\right)$$ (33)

represents any changes in the area of the mid-surface that may accompany deformation.

In general, $\mathbb{n}$ is a superficial field defined on ${\mathcal{S}}_{\circ }$—that is, $\mathbb{n}$ can be expressed as a function of points $\widehat{\mathrm{x}}$ on ${\mathcal{S}}_{\circ }$. However, $\mathbb{n}$ may be extended to all of β. In particular, consider a normally constant extension ${\mathbb{n}}^e$ of $\mathbb{n}$. Then, in view of developments presented in Appendix A.1,

$$\begin{array}{cc}\hfill {\nabla }_{S_{\circ }}\mathbb{n}& =(\nabla {\mathbb{n}}^e(\chi \left(\mathbf{X}\right)\left)\right){\mid }_{\circ }{\mathbb{P}}_{\mathbb{m}}\hfill \\ \hfill & =\left({\nabla }_{\mathbf{x}}{\mathbb{n}}^e\right(\mathbf{x}\left)\right){\mid }_{\xi =0}\nabla \mathbf{x}{\mid }_{\circ }{\mathbb{P}}_{\mathbb{m}},\hfill \end{array}$$ (34)

where ▽_x indicates the spatial gradient. Next, using properties of the surface gradient (see (175)₁), we have

$${\nabla }_{\mathbf{x}}{\mathbb{n}}^e\left(\mathbf{x}\right)={\nabla }_{{\mathcal{S}}_{{\xi }_{\circ }}}{\mathbb{n}}^e\left(\mathbf{x}\right)+\frac{\partial {\mathbb{n}}^e\left(\mathbf{x}\right)}{\partial \xi }\otimes {\mathbb{n}}^e\left(\mathbf{x}\right),$$ (35)

and, since ${\mathbb{n}}^e$ does not change in the ξ-direction, we arrive at the identification

$$\begin{array}{cc}\hfill \left({\nabla }_{\mathbf{x}}{\mathbb{n}}^e\right(\mathbf{x}\left)\right)\mid \xi =0& =\left({\nabla }_{{\mathcal{S}}_{{\xi }_{\circ }}}{\mathbb{n}}^e\right(\mathbf{x}\left)\right){\mid }_{\xi =0}\hfill \\ \hfill & ={\nabla }_{{\mathcal{S}}_{\circ }}\mathbb{n}\hfill \\ \hfill & =-\mathbb{L}.\hfill \end{array}$$ (36)

In view of (32) and (36), $\nabla s_{\circ }\mathbb{n}$ as defined by (34), can be expressed as

$$\begin{array}{cc}\hfill {\nabla }_{S_{\circ }}\mathbb{n}& =-\mathbb{L}(\nabla \mathbf{x}){\mid }_{\circ }{\mathbb{P}}_{\mathbb{m}}\hfill \\ \hfill & =-\mathbb{L}{\mathbb{F}}_{\circ },\hfill \end{array}$$ (37)

which, in combination with (28), yields a useful alternative representation,

$$\mathbf{F}=({\mathbb{F}}_{\circ }-\xi \mathbb{L}{\mathbb{F}}_{\circ }+\mathbb{n}\otimes {\nabla }_{S_{\circ }}\xi ){\mathbb{Q}}_{\circ }+\frac{\partial \xi }{\partial {\xi }_{\circ }}\mathbb{n}\otimes \mathbb{m},$$ (38)

for the deformation gradient.

Notice that, for a trivial deformation (that is, a deformation for which F = 1 everywhere on B), $\mathbb{n}$, $\mathbb{L}$, ${\mathbb{F}}_{\circ }$, and ξ are given by $\mathbb{n}=\mathbb{m}$, $\mathbb{L}={\mathbb{L}}_{\circ }$, ${\mathbb{F}}_{\circ }={\mathbb{P}}_{\mathbb{m}}$, and ξ = ξ_∘. Under these circumstances, bearing in mind (22), (38) specializes to

$$\begin{array}{cc}\hfill \mathbf{F}& ={\left({\gamma }_{\circ }\right({\xi }_{\circ }\left)\right)}^{-1}({\mathbb{P}}_{\mathbb{m}}-{\xi }_{\circ }{\mathbb{L}}_{\circ })({\mathbb{P}}_{\mathbb{m}}-2{\xi }_{\circ }{H}_{\circ }{\mathbb{P}}_{\mathbb{m}}+{\xi }_{\circ }{\mathbb{L}}_{\circ })+\mathbb{m}\otimes \mathbb{m}\hfill \\ \hfill & ={(1-2{\xi }_{\circ }{H}_{\circ }+{{\xi }_{\circ }}^2{K}_{\circ })}^{-1}\times ({\mathbb{P}}_{\mathbb{m}}-2{\xi }_{\circ }{H}_{\circ }{\mathbb{P}}_{\mathbb{m}}+2{\xi }_{\circ }^2{H}_{\circ }{\mathbb{L}}_{\circ }-{\xi }_{\circ }^2{\mathbb{L}}_{\circ }^2)+\mathbb{m}\otimes \mathbb{m}.\hfill \end{array}$$ (39)

Further, on applying the Cayley–Hamilton theorem (see Appendix A.2) to the spontaneous curvature tensor ${\mathbb{L}}_{\circ }$, (39) becomes

$$\mathbf{F}={\mathbb{P}}_{\mathbb{m}}+\mathbb{m}\otimes \mathbb{m}=1,$$ (40)

which is consistent with what must be true under a trivial deformation. Moreover, it can be immediately checked that (38) reduces to a result of Zurlo (2006) and Deseri et al. (2008) when the spontaneous curvature vanishes (in which case, (18) reduces to ${\mathbb{Q}}_{\circ }={\mathbb{P}}_{\mathbb{m}}$.

2.3 Transformation of normal vectors

If the thickness of the lipid bilayer in the spatial configuration is not uniform, the unit normal vectors of its outer and inner surfaces ${\mathcal{S}}^{\mathrm{o}}$ and ${\mathcal{S}}^{\mathrm{i}}$ may differ, respectively, from the mid-surface unit normal $\mathbb{n}$ and its negative $-\mathbb{n}$. In this case, let the unit normal vectors of inner and outer surfaces of bilayer in the reference and the spatial configuration be denoted by ${\mathbf{m}}^{\mathrm{i}}=-\mathbb{m}$, ${\mathbf{m}}^{\mathrm{o}}=\mathbb{m}$, and nⁱ, n^∘, respectively. Whereas nⁱ and n^∘ must transform according to

$$\mathbf{n}={\phantom{\mid }\frac{{\mathbf{F}}^{-⊺}\mathbf{m}}{\mid {\mathbf{F}}^{-⊺}\mathbf{m}\mid }\mid }_{{\xi }_{\circ }=h_{\circ }^{\pm }},$$ (41)

wherein n and m take the values consistent with

$$(\mathbf{n},\mathbf{m})=({\mathbf{n}}^{\mathbf{i}},{\mathbf{m}}^{\mathbf{i}})\text{or}(\mathbf{n},\mathbf{m})=({\mathbf{n}}^{\circ },{\mathbf{m}}^{\circ }),$$ (42)

$\mathbb{n}$ transforms according to

$$\mathbb{n}=\frac{{\mathbb{F}}_{\circ }{\mathbb{e}}_{\circ }^1\times {\mathbb{F}}_{\circ }{\mathbb{e}}_{\circ }^2}{\mid {\mathbb{F}}_{\circ }{\mathbb{e}}_{\circ }^1\times {\mathbb{F}}_{\circ }{\mathbb{e}}_{\circ }^2\mid },$$ (43)

for any two linearly independent tangent vectors ${\mathbb{e}}_{\circ }^1$ and ${\mathbb{e}}_{\circ }^2$ on the mid-surface S_∘. Substituting (38) into and (41) and invoking (43) shows that n and $\mathbb{n}$ differ unless

$${\nabla }_{S_{\circ }}\xi {\mid }_{{\xi }_{\circ }=h_{\circ }^{\pm }}\to 0,$$ (44)

meaning that any change of bilayer thickness on the spatial mid-surface ${\mathcal{S}}_{\circ }$ must be negligibly small. However, since this need not be the case, it is important to maintain a distinction between $\mathbb{n}$ and n. Existing two-dimensional approaches based on modeling the lipid bilayer as a material surface, as exemplified by the theory of Steigmann (1999), work solely with $\mathbb{n}$.

2.4 Coherency of leaflets

The extent to which the upper and lower leaflets are coherent across the mid-surface S_∘ may influence the mechanical response of of a lipid bilayer (Fischer 1992, Božič et al. 1992, Wiese et al. 1992, Seifert 1997). When lipid molecules of opposite leaflets are interdigitated, their connection is very nearly coherent (Elson et al. 2010). If this is not the case, the leaflets may slide relative to one another. To describe leaflet coherency, consider the Hadamard compatibility condition at S_∘. Let F⁺ and F⁻ denote the respective limiting values of the deformation gradient at S_∘ from the outer and inner sides of the bilayer. To facilitate the calculation, we will introduce some notation. Given a quantity g with potentially different limits on either side of the referential mid-surface S_∘, define its jump $\left[\right[g\left]\right]$ and average 〈g〉 at S_∘ by

$$〚g〛≔g^{+}-g^{-},\langle g\rangle ≔\frac{1}{2}(g^{+}+g^{-}).$$ (45)

In view of (38), the jump $〚\mathbf{F}〛$ of the deformation gradient at the mid-surface (i.e., at ξ_∘ = 0), is given by

$$〚\mathbf{F}〛=〚{\mathbb{F}}_{\circ }〛+{\phantom{\mid }〚\frac{\partial \xi }{\partial {\xi }_{\circ }}〛\mid }_{\circ }\mathbb{n}\otimes \mathbb{m}.$$ (46)

For $〚{\mathbb{F}}_{\circ }=0$, (46) represents the Hadamard condition for a coherent surface. This condition corresponds to the local interdigitation or coupling of the leaflets. However, for $〚{\mathbb{F}}_{\circ }〛\ne 0$, the mid-surface is an incoherent interface across which the leaflets may slide relative to one another. In general, $〚\partial \xi ∕\partial {\xi }_{\circ }〛{\mid }_{\circ }$ need not vanish—as occurs if the lipid bilayer is not symmetric and its constitutive properties are discontinuous across the mid-surface S_∘. As mentioned earlier, a disparity between the molecular compositions of the leaflets is a potential reason for the existence of spontaneous curvature. For lipid bilayers with such induced spontaneous curvature, the jump $〚\partial \xi ∕\partial {\xi }_{\circ }〛{\mid }_{\circ }$ therefore does not generally vanish.

2.5 Area compatibility

For closed lipid bilayers, an additional global compatibility condition becomes important. During the deformation of a vesicle, whether or not the leaflets are coherent, their bounding surfaces at the common interface (what is called here mid-surface) must share the same area. Otherwise, the leaflets may loose their integrity. In view of the definition (33) of the areal stretch, this condition can be codified in the form

$${\int }_{S_{\circ }}〚J〛d{A}_{\circ }=0,$$ (47)

where, bearing in mind (45)₁, $〚J〛$ denotes the jump of the areal stretch at the mid-surface S_∘ and dA_∘ represents the referential area element of S_∘.

3 Energy densities

Any change of energy that accompanies a change in the shape of a lipid bilayer must be due to the displacement of neighboring phospholipid molecules. Various types of lipid molecules with different physical properties can be present in a lipid bilayer. As long as no phase separation occurs and, thus, the chemical energy remains fixed, any energy change can be attributed to purely mechanical phenomena. In this setting, a multi-component biomembrane can be viewed as an effectively homogenous body. For a single-component lipid bilayer, no such assumption is needed.

Molecular displacements are accompanied by changes in the amount of elastic energy stored within the lipid bilayer. This is modeled by introducing an energy density W (per unit referential volume) as a function $\widehat{W}$ of the deformation gradient F, so that the lipid bilayer is modeled as a hyperelastic material:

$$W=\widehat{W}\left(\mathbf{F}\right).$$ (48)

As in the case of a conventional elastic body, we require that the energy density of a lipid bilayer has a local minimum at the spontaneous state:

$$\widehat{W}\left(\mathbf{F}\right)\text{has local minimum at}\mathbf{F}=1.$$ (49)

Also, since the energy density of each material point may be additively scaled (Gurtin et al. 2010), we impose, without loss of generality, the normalization

$$\widehat{W}\left(1\right)=0.$$ (50)

Zurlo (2006) and Deseri et al. (2008) studied the chemo-mechanical coupling of a lipid bilayer undergoing phase separation and elastic deformation. Under these circumstances, $\widehat{W}$ would also be a function of species concentrations and, potentially, also their gradients, which would penalize the formation of phase interfaces on the bilayer.

Requiring the energy density in (48) to be frame-indifferent leads, in conventional fashion, to the conclusion that it may depend on the deformation gradient through at most the right Cauchy–Green tensor C = F^⊺F, whereby (48) is replaced by

$$W=\stackrel{‒}{W}\left(\mathbf{C}\right).$$ (51)

An important point concerning leaflet asymmetry should now be clarified. An asymmetric distribution of lipid molecules with different molecular shapes requires the shape of the lipid bilayer in its natural state to be curved (McMahon and Gallop 2005). This effect might be modeled by allowing for nontrivial spontaneous curvature ${\mathbb{L}}_{\circ }$. There is also considerable evidence pointing to marked differences between the chemical compositions of lipid molecules in the inner and outer leaflets of animal cells (Luckey 2008, Janmey and Kinnunen 2006, and Devaux and Morris 2004). Observed differences in mechanical properties (Janmey and Kinnunen 2006) might therefore be attributed to differences in molecular packing, chemical composition, or both. To encompass differences in the mechanical properties of the leaflets, it might be sufficient to allow the expression determining the energy density function $\stackrel{‒}{W}$ to be distinct in each leaflet.

4 Material symmetry

The constitutive relation (51), which holds for all hyperelastic materials, is very general. To incorporate the properties of a lipid bilayer, the response function $\stackrel{‒}{W}$ must obey certain requirements of material symmetry. Two distinguishing features of biomembranes are in-plane fluidity and in-plane isotropy. Specifically, experimental observations demonstrate unambiguously that phopholipid molecules on the surface of a lipid bilayer in the liquid phase can freely migrate. Additionally, there is no preferred direction in the tangent plane of its mid-surface and therefore the lipid bilayer exhibits in-plane isotropy. In view of these observations, when modeled as three-dimensional, a lipid m bilayer is like a transversely isotropic material with $\mathbb{m}$ being the axis of isotropy and S_ξ∘ being the surface of isotropy, where the range of ξ_∘ covers the thickness of the lipid bilayer. Bearing this in mind, we next derive an appropriate representation theorem for an energy density which correctly incorporates both in-plane fluidity and transverse isotropy. To achieve this, it is necessary to determine a proper unimodular symmetry transformation H of the reference configuration which the leaves response of the body to deformation unchanged. As is customary, the set of all such symmetry transformations is designated by $\mathcal{G}$ and is referred to as the symmetry group.

4.1 Symmetry transformations

Let H be a a symmetry transformation. To encompass the transverse isotropy of the lipid bilayer, H should preserve the direction of any material line element parallel to $\mathbb{m}$. In addition, it is necessary to require that H preserve the length of any material line element parallel to $\mathbb{m}$. If H does not do so, the phospholipid molecules deform along the direction of the tail groups and, consequently, their physical characteristics will generally change. These two requirements simply imply that H should map any normal material line element to itself. Consistent with the in-plane fluidity of lipid bilayers, H should also map any material line element perpendicular to $\mathbb{m}$ to a material line element perpendicular to $\mathbb{m}$. Thus, given a unit normal vector $\mathbb{m}$, H should satisfy

$$\phantom{\{}\begin{array}{c}\mathbf{H}\mathbb{m}=\mathbb{m},\hfill \\ \text{if}\mathbf{e}\cdot \mathbb{m}=0\text{then}\mathbf{He}\cdot \mathbb{m}=0,\hfill \\ \text{det}\mathbf{H}=1.\hfill \end{array}\}$$ (52)

Under a symmetry transformation, the deformation gradient F becomes FH and, hence, the right Cauchy–Green tensor C becomes H^⊺CH, while the energy measured by the response function $\stackrel{‒}{W}$ must be invariant:

$$\stackrel{‒}{W}\left({\mathbf{H}}^{⊺}\mathbf{CH}\right)=\stackrel{‒}{W}\left(\mathbf{C}\right).$$ (53)

As a first step toward determining a representation for the symmetry group $\mathcal{G}$ consistent with (52) and (53), choose two arbitrary linearly independent tangent vectors ${\mathbb{e}}_1$ and ${\mathbb{e}}_2$ satisfying ${\mathbb{e}}_1\cdot \mathbb{m}={\mathbb{e}}_2\mathbb{m}\cdot =0$ and, therefore, belonging to the tangent space T_ξ∘. Without loss of generality, H can be represented as

$$\mathbf{H}={\mathbb{e}}_1\otimes \mathbf{f}+{\mathbb{e}}_2\otimes \mathbf{g}+\mathbb{m}\otimes \mathbf{h},$$ (54)

with f, g, and h being linearly independent. Since $({\mathbb{e}}_1\otimes \mathbf{f}+{\mathbb{e}}_2\otimes \mathbf{g}+\mathbb{m}\otimes \mathbf{h})\mathbb{m}=(\mathbf{f}\cdot \mathbb{m}){\mathbb{e}}_1+(\mathbf{g}\cdot \mathbb{m}){\mathbb{e}}_2+(\mathbf{h}\cdot \mathbb{m})\mathbb{m}$ and ${\mathbb{e}}_1$ and ${\mathbb{e}}_2$ are linearly independent tangent vectors, (52)₁ implies that f and g must obey

$$\mathbf{f}\cdot \mathbb{m}=\mathbf{g}\cdot \mathbb{m}=0$$ (55)

and, hence, must be tangent vectors and that h must obey

$$\mathbf{h}\cdot \mathbb{m}=1.$$ (56)

Next, since $({\mathbb{e}}_1\otimes \mathbf{f}+{\mathbb{e}}_2\otimes \mathbf{g}+\mathbb{m}\otimes \mathbf{h})\mathbf{e}=(\mathbf{f}\cdot \mathbf{e}){\mathbb{e}}_1+(\mathbf{g}\cdot \mathbf{e}){\mathbb{e}}_2+(\mathbf{h}\cdot \mathbf{e})\mathbb{m}$ for any tangent vector e, on defining α₁ = f · e and α₂ = g · e, it follows that

$$\mathbf{He}={\alpha }_1{\mathbb{e}}_1+{\alpha }_2{\mathbb{e}}_2+(\mathbf{h}\cdot \mathbf{e})\mathbb{m}.$$ (57)

However, by (52)₂, h must satisfy

$$\mathbf{h}\cdot \mathbf{e}=0,$$ (58)

which, in combination with (56), yields $\mathbf{h}=\mathbb{m}$. Thus, H must admit a representation of the form

$$\mathbf{H}=\mathbb{H}+\mathbb{m}\otimes \mathbb{m},$$ (59)

where, bearing in mind (55),

$$\mathbb{H}≔{\mathbb{e}}_1\otimes \mathbf{f}+{\mathbb{e}}_2\otimes \mathbf{g}$$ (60)

is a fully tangential tensor and therefore obeys

$$\phantom{\{}\begin{array}{c}\mathbb{Hm}={\mathbb{H}}^{⊺}\mathbb{m}=0,\hfill \\ \mathbb{H}={\mathbb{P}}_{\mathbb{m}}\mathbb{H}={\mathbb{HP}}_{\mathbb{m}}={\mathbb{P}}_{\mathbb{m}}{\mathbb{HP}}_{\mathbb{m}}.\hfill \end{array}\}$$ (61)

Notice that, granted the representation (59) for H, the condition (52)₃ is equivalent to the following condition on $\mathbb{H}$:

$$I_2\left(\mathbb{H}\right)=1.$$ (62)

4.2 Representation theorem for the energy density of a lipid bilayer

Observe that the right Cauchy-Green tensor C can be expressed in the form

$$\mathbf{C}=\mathbb{C}+\mathbb{v}\otimes \mathbb{m}+\mathbb{m}\otimes \mathbb{v}+(\mathbb{m}\cdot \mathbf{C}\mathbb{m})\mathbb{m}\otimes \mathbb{m},$$ (63)

where $\mathbb{C}$ is a fully tangential tensor defined by

$$\mathbb{C}={\left(\mathbf{F}{\mathbb{P}}_{\mathbb{m}}\right)}^{⊺}\left(\mathbf{F}{\mathbb{P}}_m\right)={\mathbb{P}}_m\mathbf{C}{\mathbb{P}}_{\mathbb{m}}$$ (64)

and $\mathbb{v}$ is a tangent vector belonging to T_ξ∘ defined by

$$\mathbb{v}=\mathbf{C}\mathbb{m}-(\mathbb{m}\cdot \mathbf{C}\mathbb{m})\mathbb{m}.$$ (65)

In view of (51) and (63)–(65), the energy density W can be expressed as a function $\tilde{W}$ depending on $\mathbb{C}$, $\mathbb{v}$, and $\mathbb{m}\cdot \mathbf{C}\mathbb{m}$:

$$\begin{array}{cc}\hfill W& =\stackrel{‒}{W}\left(\mathbf{C}\right)\hfill \\ \hfill & =\tilde{W}(\mathbb{C},\mathbb{v},\mathbb{m}\cdot \mathbf{C}\mathbb{m}).\hfill \end{array}$$ (66)

Additionally, by (59) and (63), H^⊺CH can be expressed as

$${\mathbf{H}}^{⊺}\mathbf{CH}={\mathbb{H}}^{⊺}\mathbb{CH}+{\mathbb{H}}^{⊺}\mathbb{v}\otimes \mathbb{m}+\mathbb{m}\otimes {\mathbb{H}}^{⊺}\mathbb{v}+(\mathbb{m}\cdot \mathbf{C}\mathbb{m})\mathbb{m}\otimes \mathbb{m},$$ (67)

and, hence, the symmetry property (53) takes the form

$$\tilde{W}({\mathbb{H}}^{⊺}\mathbb{CH},{\mathbb{H}}^{⊺}\mathbb{v},\mathbb{m}\cdot \mathbf{C}\mathbb{m})=\tilde{W}(\mathbb{C},\mathbb{v},\mathbb{m}\cdot \mathbf{C}\mathbb{m}).$$ (68)

Being fully tangential (see Appendix A.1), $\mathbb{C}$ and $\mathbb{H}$ can be viewed as mappings of the tangent space T_ξ∘ into itself, in which case the transformation rule

$$\mathbb{C}\to {\mathbb{H}}^{⊺}\mathbb{CH}$$ (69)

can be interpreted as one involving tensors that map the tangent space T_ξ∘ into itself. Similarly, since $\mathbb{v}$ belongs to T_ξ∘, the transformation rule

$$\mathbb{v}\to {\mathbb{H}}^{⊺}\mathbb{v}$$ (70)

can be interpreted as one involving two-dimensional referential tangent vectors belonging to T_ξ∘.

Consider the subgroup of the unimodular group comprised by all rotations in the tangent plane with normal vector $\mathbb{m}$. Bearing in mind that, like $\mathbb{C}$ and $\mathbb{H}$, any element of that subgroup can be viewed as a mapping of the space of two-dimensional referential tangent vectors into itself, a representation theorem due to Zheng (1993) can be applied to arrive at the following representation for the energy density:

$$W=\stackrel{\approx }{W}\left(I_1\right(\mathbb{C}),I_2(\mathbb{C}),\mathbb{v}\cdot \mathbb{v},\mathbb{v}\cdot \mathbb{Cv},\mathbb{m}\cdot \mathbf{C}\mathbb{m}).$$ (71)

However, since, by (63),

$$\mathbb{v}\cdot \mathbb{Cv}=\text{det}\mathbf{C}-(\mathbb{m}\cdot \mathbf{C}\mathbb{m})I_2\left(\mathbb{C}\right)+I_1\left(\mathbb{C}\right)[\mathbb{v}\cdot \mathbb{v}-{(\mathbb{m}\cdot \mathbf{C}\mathbb{m})}^2],$$ (72)

(71) can be written as

$$W=\breve{W}\left(I_1\right(\mathbb{C}),I_2(\mathbb{C}),\mathbb{v}\cdot \mathbb{v},\text{det}\mathbf{C},\mathbb{m}\cdot \mathbf{C}\mathbb{m}).$$ (73)

The five arguments of $\breve{W}$ are mutually independent. To see this, first, notice that the tensor C has six independent components and, hence, that the decomposition in (63) defines three independent quantities $\mathbb{C}$, $\mathbb{v}$, and $\mathbb{m}\cdot \mathbf{C}\mathbb{m}$. Since $\mathbb{C}$ is symmetric, it admits a spectral decomposition

$$\mathbb{C}={\omega }_1{\mathbb{t}}_1\otimes {\mathbb{t}}_1+{\omega }_2{\mathbb{t}}_2\otimes {\mathbb{t}}_2$$ (74)

involving eigenvectors ω₁ and ω₂ corresponding, respectively, to eigenvectors ${\mathbb{t}}_1$ and ${\mathbb{t}}_2$ tangent to T_ξ∘ with the property ${\mathbb{t}}_1\times {\mathbb{t}}_2=\mathbb{m}$. Additionally, in terms of the basis $\{{\mathbb{t}}_1,{\mathbb{t}}_2\}$, $\mathbb{v}$ can be expressed in the form

$$\mathbb{v}={\upsilon }_1{\mathbb{t}}_1+{\upsilon }_2{\mathbb{t}}_2,$$ (75)

where υ_α denote the component of $\mathbb{v}$ in the ${\mathbb{t}}_{\alpha }$ direction (α = 1, 2). Also, since $\mathbb{m}\cdot \mathbf{C}\mathbb{m}$ indicates the component of C in the in the direction perpendicular to the tangent space T_ξ∘, it can be chosen independently of the remaining arguments. Put $\tau =\mathbb{m}\cdot \mathbf{C}\mathbb{m}$, bearing in mind that, since C is positive-definite, τ must obey τ > 0. The arguments of (73) can then be expressed as

$$\phantom{\{}\begin{array}{c}{I}_1\left(\mathbb{C}\right)={\omega }_1+{\omega }_2,\hfill \\ I_2\left(\mathbb{C}\right)={\omega }_1{\omega }_2,\hfill \\ \mathbb{v}\cdot \mathbb{v}={\upsilon }_1^2+{\upsilon }_2^2,\hfill \\ \text{det}\mathbf{C}={\omega }_1{\omega }_2\tau -{\omega }_1{\upsilon }_2^2-{\omega }_2{\upsilon }_1^2,\hfill \\ \mathbb{m}\cdot \mathbf{C}\mathbb{m}=\tau .\hfill \end{array}\}$$ (76)

Since ω₁, ω₂, υ₁, υ,₂, and τ are independent, (76) can be used to show that the numbers $I_1\left(\mathbb{C}\right)$, $I_2\left(\mathbb{C}\right)$, det C, and $\mathbb{v}\cdot \mathbb{C}\mathbb{v}$, $\mathbb{m}\cdot \mathbf{C}\mathbb{m}$ can be varied independently.

We next show that, of the five arguments We which upon $\breve{W}$ may depend, as indicated on the right-hand side of (73), only $I_2\left(\mathbb{C}\right)$, det C, and $\mathbb{m}\cdot \mathbf{C}\mathbb{m}$ are invariant under any unimodular symmetry transformation H consistent with (61) and (62). This elucidates the distinction between the symmetry properties of a lipid bilayer with in-plane uidity (that is, a lipid bilayer with symmetry group consisting of all fully tangential unimodular transformations $\mathbb{H}$) with those of a solid transversely isotropic about $\mathbb{m}$. For further insight regarding the symmetry properties of fluid films and transversely isotropic solids due, respectively, to Steigmann (1999) and Green and Adkins (1970) are particularly relevant.

To substantiate the foregoing assertion, choose orthonormal unit tangent vectors ${\mathbb{e}}_1$ and ${\mathbb{e}}_2$ spanning the tangent space T_ξ∘. A generic tangent vector $\mathbb{v}$ in (73) can be represented in the form $\mathbb{v}={\lambda }_1{\mathbb{e}}_1+{\lambda }_2{\mathbb{e}}_2$, with λ₁ and λ₂ being scalars. Without loss of generality, assume that ${\mathbb{e}}_1$ is chosen in the $\mathbb{v}$ direction, so that ${\mathbb{e}}_1=\mathbb{v}∕\mid \mathbb{v}\mid$. To show that $\breve{W}$ can depend at most on $I_2\left(\mathbb{C}\right)$, det C, and $\mathbb{m}\cdot \mathbf{C}\mathbb{m}$, it sufficies to: (i) show that they are invariant under all unimodular symmetry transformations of the kind described in (52), and (ii) find specific tranformations under which $I_1\left(\mathbb{C}\right)$ and $\mathbb{v}\cdot \mathbb{v}$ are not properly invariant. Bearing in mind (52)₃, (59), (61)₁, and (184), it is straightforward to show that, for any H satisfying (52),

$$\phantom{\{}\begin{array}{c}{I}_2\left({\mathbb{H}}^{⊺}\mathbb{CH}\right)=I_2\left(\mathbb{C}\right),\hfill \\ \text{det}\left({\mathbf{H}}^{⊺}\mathbf{CH}\right)=\text{det}\mathbf{C},\hfill \\ \mathbb{m}\cdot {\mathbf{H}}^{⊺}\mathbf{CH}\mathbb{m}=\mathbb{m}\cdot \mathbf{C}\mathbb{m}.\hfill \end{array}\}$$ (77)

Consider, now, the tensor

$${\mathbb{H}}_1={\mathbb{e}}_1\otimes {\mathbb{e}}_1+{\mathbb{e}}_2\otimes {\mathbb{e}}_2+\alpha {\mathbb{e}}_2\otimes {\mathbb{e}}_1,\alpha \in \mathbb{R}$$ (78)

which satisfies (61) and (62) for all choices of the parameter α. Then, since

$$I_1\left({\mathbb{H}}_1^{⊺}{\mathbb{CH}}_1\right)=I_1\left(\mathbb{C}\right)+\phi \left(\alpha \right),$$ (79)

with $\phi \left(\alpha \right)=2\alpha ({\mathbb{e}}_1\cdot \mathbb{C}{\mathbb{e}}_2)+{\alpha }^2({\mathbb{e}}_2\cdot \mathbb{C}{\mathbb{e}}_2)$, and since

$${\mathbb{H}}_1^{⊺}\mathbb{v}\cdot {\mathbb{H}}_1^{⊺}\mathbb{v}=\mathbb{v}\cdot \mathbb{v},$$ (80)

$\breve{W}$ must obey

$$\breve{W}\left(I_1\right(\mathbb{C})+\phi (\alpha ),\cdot ,\mathbb{v}\cdot \mathbb{v},\cdot ,\cdot )=\breve{W}\left(I_1\right(\mathbb{C}),\cdot ,\mathbb{v}\cdot \mathbb{v},\cdot ,\cdot )$$ (81)

for all α. It is possible to choose α in (81) such that $\phi \left(\alpha \right)=\nu I_1\left(\mathbb{C}\right)$ for an arbitrary ν ≥ 0. Also, on defining $x≔I_1\left(\mathbb{C}\right)$ and $y≔(1+\nu )I_1\left(\mathbb{C}\right)$, fixing $I_2\left(\mathbb{C}\right)$, $\mathbb{v}\cdot \mathbb{v}$, det C, and $\mathbb{m}\cdot \mathbf{C}\mathbb{m}$, and defining f via $f\left(x\right)≔\breve{W}(x,I_2(\mathbb{C}),\mathbb{v}\cdot \mathbb{v},\text{det}\mathbf{C},\mathbb{m}\cdot \mathbf{C}\mathbb{m})$, it is evident that f(y) = f(x). Hence, since x and y may be chosen arbitrarily, f must be constant. It follows that $\breve{W}$ must be independent of the argument $I_1\left(\mathbb{C}\right)$. Next, consider the tensor

$${\mathbb{H}}_2=\beta {\mathbb{e}}_1\otimes {\mathbb{e}}_1+\frac{1}{\beta }{\mathbb{e}}_2\otimes {\mathbb{e}}_2,\beta \in \mathbb{R},\beta \ne 0,$$ (82)

which satisfies (61) and (62) for all choices of the parameter β ≠ 0. Then, since

$${\mathbb{H}}_2^{⊺}\mathbb{v}\cdot {\mathbb{H}}_2^{⊺}\mathbb{v}={\beta }^2\mathbb{v}\cdot \mathbb{v},$$ (83)

$\breve{W}$ must obey

$$\breve{W}(\cdot ,{\beta }^2\mathbb{v}\cdot \mathbb{v},\cdot ,\cdot )=\breve{W}(\cdot ,\mathbb{v}\cdot \mathbb{v},\cdot ,\cdot )$$ (84)

for all β ≠ 0. On choosing β in (84) such that ${\beta }^2={(\mathbb{v}\cdot \mathbb{v})}^{-1}$, it follows that $\breve{W}$ must be independent of the argument $\mathbb{v}\cdot \mathbb{v}$. Consequently, we conclude that the energy density W of a lipid bilayer must admit a representation of the form

$$W=\Phi ({\mathcal{I}}_1,{\mathcal{I}}_2,{\mathcal{I}}_3),$$ (85)

with

$${\mathcal{I}}_1={\mathcal{I}}_2\left(\mathbb{C}\right),{\mathcal{I}}_2=\text{det}\mathbf{C},{\mathcal{I}}_3=\mathbb{m}\cdot \mathbf{C}\mathbb{m}.$$ (86)

5 Kinematical discussions

With the representation (38) for the deformation gradient F, the right Cauchy–Green tensor C = F^⊺F can be expressed as

$$\mathbf{C}={\mathbb{Q}}_{\circ }{\mathbb{C}}_{\circ }{\mathbb{Q}}_{\circ }-2\xi {\mathbb{Q}}_{\circ }{\mathbb{F}}_{\circ }^{⊺}{\mathbb{LF}}_{\circ }{\mathbb{Q}}_{\circ }+{\xi }^2{\mathbb{Q}}_{\circ }{\mathbb{F}}_{\circ }^{⊺}{\mathbb{L}}^2{\mathbb{F}}_{\circ }{\mathbb{Q}}_{\circ }+\left({\mathbb{Q}}_{\circ }{\nabla }_{S_{\circ }}\xi \right)\otimes \left({\mathbb{Q}}_{\circ }{\nabla }_{S_{\circ }}\xi \right)+\frac{\partial \xi }{\partial {\xi }_{\circ }}\left(\right({\mathbb{Q}}_{\circ }{\nabla }_{S_{\circ }}\xi )\otimes \mathbb{m}+\mathbb{m}\otimes ({\mathbb{Q}}_{\circ }{\nabla }_{S_{\circ }}\xi \left)\right)+{\left(\frac{\partial \xi }{\partial {\xi }_{\circ }}\right)}^2\mathbb{m}\otimes \mathbb{m},$$ (87)

where we have introduced

$${\mathbb{C}}_{\circ }={\mathbb{F}}_{\circ }^{⊺}{\mathbb{F}}_{\circ }.$$ (88)

In addition, on comparing (64) and (87), it follows that the fully tangential tensor $\mathbb{C}$ can be expressed as

$$\mathbb{C}={\mathbb{Q}}_{\circ }{\mathbb{C}}_{\circ }{\mathbb{Q}}_{\circ }-2\xi {\mathbb{Q}}_{\circ }{\mathbb{F}}_{\circ }^{⊺}{\mathbb{LF}}_{\circ }{\mathbb{Q}}_{\circ }+{\xi }^2{\mathbb{Q}}_{\circ }{\mathbb{F}}_{\circ }^{⊺}{\mathbb{L}}^2{\mathbb{F}}_{\circ }\mathbb{Q}+\left({\mathbb{Q}}_{\circ }{\nabla }_{S_{\circ }}\xi \right)\otimes \left({\mathbb{Q}}_{\circ }{\nabla }_{S_{\circ }}\xi \right).$$ (89)

5.1 The invariants ${\mathcal{I}}_1$, ${\mathcal{I}}_2$, and ${\mathcal{I}}_3$

Prior to formulating specific constitutive relations, it seems necessary to understand the geometric properties of the invariants ${\mathcal{I}}_1$, ${\mathcal{I}}_2$, and ${\mathcal{I}}_3$ entering the representation (85) of the generic energy density for a lipid bilayer.

5.1.1 The invariant ${\mathcal{I}}_1$

We now show that the invariant ${\mathcal{I}}_1=I_2\left(\mathbb{C}\right)$ controls changes in the area of infinitesimal area elements parallel to the mid-surface S_∘ (Figure 2). Toward this goal, choose linearly independent vectors ${\mathbb{e}}_1$ and ${\mathbb{e}}_2$ belonging to the tangent space T_ξ∘ that satisfy ${\mathbb{e}}_1\times {\mathbb{e}}_2=\mathbb{m}$. Further, choose infinitesimal material line elements $\mathrm{d}{\mathbf{X}}_{{\xi }_{\circ }}^1$ and $\mathrm{d}{\mathbf{X}}_{{\xi }_{\circ }}^2$ directed along ${\mathbb{e}}_1$ and ${\mathbb{e}}_2$ such that they span the infinitesimal area element

$$\mathrm{d}{A}_{{\xi }_{\circ }}=\mid {\text{dX}}_{{\xi }_{\circ }}^1\times {\text{dX}}_{{\xi }_{\circ }}^2\mid .$$ (90)

With reference to (20), define elements ${\mathbb{e}}_{\circ }^1$ and ${\mathbb{e}}_{\circ }^2$ of T_∘ by ${\mathbb{e}}_{\circ }^1={\mathbb{Q}}_{\circ }{\mathbb{e}}_1$ and ${\mathbb{e}}_{\circ }^2={\mathbb{Q}}_{\circ }{\mathbb{e}}_2$ and let the infinitesimal line elements $d{\widehat{\mathbf{X}}}_1$ and $d{\widehat{\mathbf{X}}}_2$, as described in (20), denote the images of $d{\mathbf{X}}_{{\xi }_{\circ }}^1$ and $d{\mathbf{X}}_{{\xi }_{\circ }}^2$ directed along ${\mathbb{e}}_{\circ }^1$ and ${\mathbb{e}}_{\circ }^2$ on S_∘. Obviously, $d{\widehat{\mathbf{X}}}_1$ and $d{\widehat{\mathbf{X}}}_2$ span the image

$$\mathrm{d}{A}_{\circ }=\mid \mathrm{d}{\widehat{\mathbf{X}}}_1\times \mathrm{d}{\widehat{\mathbf{X}}}_2\mid$$ (91)

of dA_ξ∘ on S_∘. The area element $d{\mathcal{A}}_{{\xi }_{\circ }}$ corresponding to dA_ξ∘ in the deformed body is

$$\mathrm{d}{\mathcal{A}}_{{\xi }_{\circ }}=\mid \mathbf{F}{\mathbb{e}}_1\times \mathbf{F}{\mathbb{e}}_2\mid \mathrm{d}{A}_{{\xi }_{\circ }}.$$ (92)

Since ${\mathbb{e}}_1$ and ${\mathbb{e}}_2$ are tangent vectors, the deformation gradient F in (92) can be replaced by the superficial deformation gradient

$$\mathbb{F}≔\mathbf{F}{\mathbb{P}}_{\mathbb{m}},$$ (93)

giving

$$\mathrm{d}{\mathcal{A}}_{{\xi }_{\circ }}=\mid {\mathbb{Fe}}_1\times {\mathbb{Fe}}_2\mid \mathrm{d}{A}_{{\xi }_{\circ }},$$ (94)

whereby the area ratio $J_{{\xi }_{\circ }}=\mathrm{d}{\mathcal{A}}_{{\xi }_{\circ }}∕\mathrm{d}{A}_{{\xi }_{\circ }}$ takes the form

$$\begin{array}{cc}\hfill J_{{\xi }_{\circ }}& =\mid {\mathbb{Fe}}_1\times {\mathbb{Fe}}_2\mid \hfill \\ \hfill & =\mid {\mathbb{F}}^c({\mathbb{e}}_1\times {\mathbb{e}}_2)\mid \hfill \\ \hfill & =\mid {\mathbb{F}}^c\mathbb{m}\mid ,\hfill \end{array}$$ (95)

with ${\mathbb{F}}^{\mathrm{c}}$ being the cofactor of $\mathbb{F}$. By (95),

$$\begin{array}{cc}\hfill J_{{\xi }_{\circ }}^2& ={\mid {\mathbb{F}}^c\mathbb{m}\mid }^2\hfill \\ \hfill & ={\mathbb{F}}^c\mathbb{m}\cdot {\mathbb{F}}^c\mathbb{m}\hfill \\ \hfill & =\mathbb{m}\cdot {\left({\mathbb{F}}^c\right)}^{⊺}{\mathbb{F}}^c\mathbb{m}\hfill \\ \hfill & =\mathbb{m}\cdot {\left({\mathbb{F}}^{⊺}\mathbb{F}\right)}^c\mathbb{m}\hfill \\ \hfill & =\mathbb{m}\cdot {\mathbb{C}}^2\mathbb{m}.\hfill \end{array}$$ (96)

By (183), $\mathbb{m}\cdot {\mathbb{C}}^{\mathrm{c}}\mathbb{m}={\mathcal{I}}_1$, which with (96) yields

$${\mathcal{I}}_1=I_2\left(\mathbb{C}\right)=J_{{\xi }_{\circ }}^2={\left(\frac{\mathrm{d}{\mathcal{A}}_{{\xi }_{\circ }}}{\mathrm{d}{A}_{{\xi }_{\circ }}}\right)}^2,$$ (97)

confirming the assertion that ${\mathcal{I}}_1$ controls changes in the area of infinitesimal area elements parallel to S_∘. Evaluating (97) at the mid-surface S_∘ gives

$$J^2={\left(\frac{\mathrm{d}{\mathcal{A}}_{\circ }}{\mathrm{d}{A}_{\circ }}\right)}^2=I_2\left({\mathbb{C}}_{\circ }\right),$$ (98)

where J is defined in (33) and $\mathrm{d}{\mathcal{A}}_{\circ }$ is the image, on ${\mathcal{S}}_{\circ }$, of area element dA_∘.

Fig. 2.

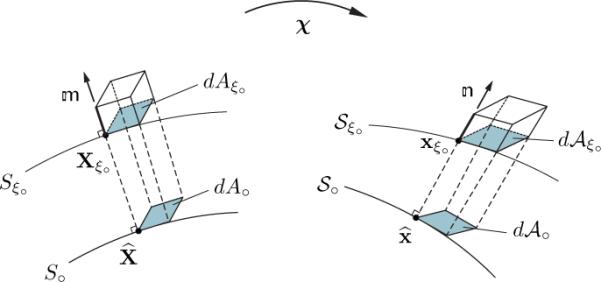
Schematic depiction of changes of volume and tangent area elements.

According to the definition (172) of the surface gradient and the chain rule, ∇_S∘ ξ in (89) can be replaced by ${\mathbb{F}}_{\circ }^{⊺}{\nabla }_{{\mathcal{S}}_{\circ }}\xi$, where ${\nabla }_{{\mathcal{S}}_{\circ }}\xi ={\mathbb{P}}_{\mathbb{n}}{\nabla }_{\mathrm{x}}\xi$ is the surface gradient of ξ on ${\mathcal{S}}_{\circ }$, and

$${\mathbb{P}}_{\mathbb{n}}=1-\mathbb{n}\otimes \mathbb{n}$$ (99)

is the projection tensor onto the tangent plane of ${\mathcal{S}}_{\circ }$. Since ${\mathbb{Q}}_{\circ }$ is symmetric, (89) can be reorganized as

$$\mathbb{C}={\mathbb{Q}}_{\circ }{\mathbb{F}}_{\circ }^{⊺}\mathbb{K}{\mathbb{F}}_{\circ }{\mathbb{Q}}_{\circ },$$ (100)

where we emphasize that

$$\mathbb{K}=\mathbb{P}\mathbb{n}-2\xi \mathbb{L}+{\xi }^2{\mathbb{L}}^2+\left({\nabla }_{{\mathcal{S}}_{\circ }}\xi \right)\otimes \left({\nabla }_{{\mathcal{S}}_{\circ }}\xi \right)$$ (101)

is a fully tangential tensor which can be viewed as a mapping from the tangent space of ${\mathcal{S}}_{\circ }$ to itself. From (184)₂, it follows that

$${\mathcal{I}}_1=I_2\left(\mathbb{C}\right)=I_2^2\left({\mathbb{Q}}_{\circ }\right)I_2\left({\mathbb{C}}_{\circ }\right)I_2\left(\mathbb{K}\right).$$ (102)

The definition (196) of the second principal invariant I₂ and a straightforward calculation lead to

$$I_2\left(\mathbb{K}\right)={\gamma }^2\left(\xi \right)+\mid \left(\right(2H\xi -1){\mathbb{P}}_{\mathbb{n}}-\xi \mathbb{L}){\nabla }_{{\mathcal{S}}_{\circ }}\xi {\mid }^2,$$ (103)

with

$$\gamma \left(\xi \right)≔1-2\xi H+{\xi }^{2}K.$$ (104)

In view of (21), (98) and (184)₂, (102) can be expressed as

$${\mathcal{I}}_1=J^2{\left({\gamma }_{\circ }\right({\xi }_{\circ }\left)\right)}^{-2}\left({\gamma }^2\right(\xi )+\mid ((2H\xi -1){\mathbb{P}}_{\mathbb{n}}-\xi \mathbb{L}\left){\nabla }_{{\mathcal{S}}_{\circ }}\xi {\mid }^2\right).$$ (105)

5.1.2 The invariant ${\mathcal{I}}_2$

It is evident that the invariant ${\mathcal{I}}_2=\text{det}\mathbf{C}={\left(\text{det}\mathbf{F}\right)}^2$ controls volume changes of infinitesimal material regions (Figure 2). However, it is useful to obtain ${\mathcal{I}}_2$ in terms of relavant kinematical quantities. According to the definition of the determinant and upon using (38),

$$\begin{array}{cc}\hfill \text{det}\mathbf{F}& =\left[\right(\mathbf{F}{\mathbb{e}}_1)\times (\mathbf{F}{\mathbb{e}}_2\left)\right]\cdot \mathbf{F}\mathbb{m}.\hfill \\ \hfill & =\frac{\partial \xi }{\partial {\xi }_{\circ }}\left(({\mathbf{g}}_{\circ }^1\times {\mathbf{g}}_{\circ }^2)\cdot \mathbb{n}-\xi \left[\right(\mathbb{L}{\mathbf{g}}_{\circ }^1\times {\mathbf{g}}_{\circ }^2)\cdot \mathbb{n}+({\mathbf{g}}_{\circ }^1\times \mathbb{L}{\mathbf{g}}_{\circ }^2)\cdot \mathbb{n}]+{\xi }^2(\mathbb{L}{\mathbf{g}}_{\circ }^1\times \mathbb{L}{\mathbf{g}}_{\circ }^2)\cdot \mathbb{n}\right),\hfill \end{array}$$ (106)

where ${\mathbf{g}}_{\circ }^1={\mathbb{F}}_{\circ }{\mathbb{e}}_{\circ }^1$ and ${\mathbf{g}}_{\circ }^2={\mathbb{F}}_{\circ }{\mathbb{e}}_{\circ }^2$ are tangent to ${\mathcal{S}}_{\circ }$ and span $\mathrm{d}{\mathcal{A}}_{\circ }$.

In view of (183), (184)₂, and (21)

$$\begin{array}{cc}\hfill {\mathbb{e}}_{\circ }^1\times {\mathbb{e}}_{\circ }^2& ={\mathbb{Q}}_{\circ }{\mathbb{e}}_1\times {\mathbb{Q}}_{\circ }{\mathbb{e}}_2\hfill \\ \hfill & ={\mathbb{Q}}_{\circ }^{\mathrm{c}}({\mathbb{e}}_1\times {\mathbb{e}}_2)\hfill \\ \hfill & ={\mathbb{Q}}_{\circ }^{\mathrm{c}}\mathbb{m}\hfill \\ \hfill & =I_2\left({\mathbb{Q}}_{\circ }\right)\mathbb{m}\hfill \\ \hfill & ={\left(I_2\right({\$}_{\circ }\left)\right)}^{-1}\mathbb{m}\hfill \\ \hfill & ={\left({\gamma }_{\circ }\right({\xi }_{\circ }\left)\right)}^{-1}\mathbb{m}\hfill \end{array}$$ (107)

which, with (96) and (98) implies that

$$\begin{array}{cc}\hfill ({\mathbf{g}}_{\circ }^1\times {\mathbf{g}}_{\circ }^2)\cdot \mathbb{n}& =\mid {\mathbb{F}}_{\circ }{\mathbb{e}}_{\circ }^1\times {\mathbb{F}}_{\circ }{\mathbb{e}}_{\circ }^2\mid \hfill \\ \hfill & ={\left({\gamma }_{\circ }\right({\xi }_{\circ }\left)\right)}^{-1}\mid {\mathbb{F}}_{\circ }^{\mathrm{c}}\mathbb{m}\mid \hfill \\ \hfill & ={\left({\gamma }_{\circ }\right({\xi }_{\circ }\left)\right)}^{-1}J.\hfill \end{array}$$ (108)

By (108), (177), (181)–(183), and elementary properties of the trace and cofactor of $\mathbb{L}$, (106) simplifies to

$$\text{det}\mathbf{F}=J\frac{\partial \xi }{\partial {\xi }_{\circ }}\frac{\gamma \left(\xi \right)}{{\gamma }_{\circ }\left({\xi }_{\circ }\right)},$$ (109)

and, consequently, ${\mathcal{I}}_2$ becomes

$${\mathcal{I}}_2=\text{det}\mathbf{C}=J^2{\left(\frac{\partial \xi }{\partial {\xi }_{\circ }}\right)}^2{\left(\frac{\gamma \left(\xi \right)}{{\gamma }_{\circ }\left({\xi }_{\circ }\right)}\right)}^2.$$ (110)

5.1.3 The invariant ${\mathcal{I}}_3$

Finally, it is evident that the invariant

$$\begin{array}{cc}\hfill {\mathcal{I}}_3& =\mathbb{m}\cdot \mathbf{C}\mathbb{m}\hfill \\ \hfill & ={\left(\frac{\partial \xi }{\partial {\xi }_{\circ }}\right)}^2\hfill \end{array}$$ (111)

controls the stretch of infinitesimal material fibers perpendicular to the mid-surface S_∘.

5.2 Constitutively-associated kinematical variables

In view of (105), (110), (111), we may use (196) in (105) to conclude that the energy density in (85) depends upon the referential variables

$$H_{\circ },K_{\circ },{\xi }_{\circ },$$ (112)

and the spatial variables

$$H,K,\xi ,\frac{\partial \xi }{\partial {\xi }_{\circ }},\mid {\nabla }_{{\mathcal{S}}_{\circ }}\xi {\mid }^2,\left({\nabla }_{{\mathcal{S}}_{\circ }}\xi \right)\cdot \mathbb{L}\left({\nabla }_{{\mathcal{S}}_{\circ }}\xi \right).$$ (113)

Consistent with existing two-dimensional theories, H and K—which are paramount importance in the areal Canham–Helfrich energy density (1)—represent the dependence on the curvature of the spatial mid-surface ${\mathcal{S}}_{\circ }$ and the areal stretch J—which is present in the areal energy density of Steigmann (1999)—embodies localized changes in the area in going from the referential mid-surface S_∘ to the spatial mid-surface ${\mathcal{S}}_{\circ }$ In addition through-thickness dependence via ξ, (85) accounts for the potential influence of transverse normal strain (and, thickness changes) via ∂ξ/∂ξ_∘ as well as both transverse shear strain and thickness nonuniformity via $\mid {\nabla }_{{\mathcal{S}}_{\circ }}\xi {\mid }^2$. Potential coupling between curvature and deviations in thickness is embodied by the quantity $\left({\nabla }_{{\mathcal{S}}_{\circ }}\xi \right)\cdot \mathbb{L}\left({\nabla }_{{\mathcal{S}}_{\circ }}\xi \right)$, which includes information the regarding the orientation of ${\nabla }_{{\mathcal{S}}_{\circ }}\xi$ relative to the principal axes of the curvature tensor $\mathbb{L}$. Notice that, for example, when ${\nabla }_{{\mathcal{S}}_{\circ }}\xi$ coincides with one of the principal axes of $\mathbb{L}$ dependence upon the coupling term $\left({\nabla }_{{\mathcal{S}}_{\circ }}\xi \right)\cdot \mathbb{L}\left({\nabla }_{{\mathcal{S}}_{\circ }}\xi \right)$ is redundant. In particular, this occurs when the spatial mid-surface ${\mathcal{S}}_{\circ }$ is spherical.

5.3 Incompressibility

Various studies suggest that lipid bilayers are very nearly incompressible (Goldstein and Leibler 1989, Lipowsky and Sackmann 1995, Safran 2003). If, to model this observation, the deformation χ is stipulated to be isochoric, then (110) has the elementary consequence

$${\mathcal{I}}_2=1.$$ (114)

Accordingly, the energy density must be independent of ${\mathcal{I}}_2$ and the representation (85) reduces to

$$W=\tilde{\Phi }({\mathcal{I}}_1,{\mathcal{I}}_3).$$ (115)

In addition, using (114) in (110) along with (15), (21), and (104) yields the differential equation

$$\begin{array}{cc}\hfill \frac{\partial \xi }{\partial {\xi }_{\circ }}& =\frac{1}{J}\frac{{\gamma }_{\circ }\left({\xi }_{\circ }\right)}{\gamma \left(\xi \right)}\hfill \\ \hfill & =\frac{1-2{\xi }_{\circ }{H}_{\circ }+{\xi }_{\circ }^2{K}_{\circ }}{(1-2\xi H+{\xi }^{2}K)J},\hfill \end{array}$$ (116)

which with (27) integrates to yield $\xi (1-\xi H+\frac{1}{3}{\xi }^{2}K)J={\xi }_{\circ }(1-{\xi }_{\circ }{H}_{\circ }+\frac{1}{3}{\xi }_{\circ }^2{K}_{\circ })+\varphi \left(\widehat{\mathbf{X}}\right)$. However, on using the condition ξ|_∘ = 0, the integration constant $\varphi \left(\widehat{\mathbf{X}}\right)$ vanishes, giving

$$\xi (1-\xi H+\frac{1}{3}{\xi }^{2}K)J={\xi }_{\circ }(1-{\xi }_{\circ }{H}_{\circ }+\frac{1}{3}{\xi }_{\circ }^2{K}_{\circ }).$$ (117)

The relation (117) reveals that, for an incompressible lipid bilayer, H, K, J, and ξ are not generally independent. For instance, when J, H, and K at any point on the spatial mid-surface ${\mathcal{S}}_{\circ }$ are given, (117) can be solved to determine the distance ξ of a spatial point on ${\mathcal{S}}_{\circ }$ corresponding to the material point at the distance ξ_∘ on S_∘ in the spontaneous state. In addition, the purely geometrical and kinematical result (117) suggests that the thickness of an incompressible lipid bilayer in its spatial configuration will not generally be uniform unless its mid-surface is uniformly bent or stretched and has uniform spontaneous curvature. Zurlo (2006) and Deseri et al. (2008) assume that ξ is linearly proportional to ξ_∘, or, alternatively, that ∂ξ/∂ξ_∘ is the ratio of thickness of the deformed and referential lipid bilayer and refer to this condition as “quasi-incompressibility.” In such a case, the incompressibility condition is only satisfied at the spatial mid-surface ${\mathcal{S}}_{\circ }$ and leads to

$$\frac{\xi }{{\xi }_{\circ }}=\frac{1}{J}.$$ (118)

However, this assumption is valid only if the spontaneous mean and Gaussian curvatures H_∘ and K_∘ and the mean and Gaussian curvatures H and K of the spatial mid-surface are very mild (or, more precisely, if ξH, ξ²K, ξ_∘ H_∘, and ${\xi }_{\circ }^2{K}_{\circ }$ are negligible in comparison with unity).

Notice that (117) can be viewed as a cubic equation for ξ. However, only a unique physically meaningful root of this equation is of interest. First, the root must be real. Also, to guarantee its uniqueness, the root should be an increasing function of ξ_∘. In addition, to satisfy the requirement that ξ|_∘ = 0, the sign of ξ must match that of ξ_∘. These conditions limit the range of the coefficients in (117). In particular, the sign of the discriminant of the cubic equation provides some information about the nature of the roots. A simpler case occurs if the lipid bilayer only has curvature in a two-dimensional space and is uniformly extended in one direction. In this circumstance, K = 0 (for simplicity also assume that K_∘ = 0) in which case (117) reduces to a quadratic equation with the admissible root

$$\xi =\frac{1-\sqrt{1-4{\xi }_{\circ }H(1-{\xi }_{\circ }{H}_{\circ })∕J}}{2H},$$ (119)

which is real if and only if

$$4{\xi }_{\circ }H(1-{\xi }_{\circ }{H}_{\circ })\le J.$$ (120)

For there to exist an admissible root ξ satisfying the incompressibility condition (117), the ratio ξ_∘ H/J of the deformed lipid bilayer must be small enough to satisfy (120) for all ${\xi }_{\circ }\in [-h_{\circ }^{-},h_{\circ }^{+}]$.

To provide a qualitative insight regarding incompressibility-induced changes of thickness, we restrict attention to situations where the spontaneous mean curvature H_∘ vanishes and consider two illustrative examples. Figure 3a shows a lipid bilayer under pure bending (in which case J = 1) with spatial mid-surface ${\mathcal{S}}_{\circ }$ having a sinusoidal shape. It is evident that the thickness of the upper (lower) leaflet decreases (increases) as the curvature H of ${\mathcal{S}}_{\circ }$ increases. Figure 3b shows a lipid bilayer with a flat sptial mid-surface (in which case H = 0) subject to an areal stretch that decreases exponentially toward the left side. Notably, the thicknesses of lipid bilayer leaflets increase symmetrically as the areal stretch decreases from right to left. Thickening phenomena of this kind are well-known to occur in the presence of trans-membrane proteins, in which case hydrophobic mismatch leads to stretching of the lipid molecules in the through-thickness direction (here, the left side of Figure 3b).

Fig. 3.

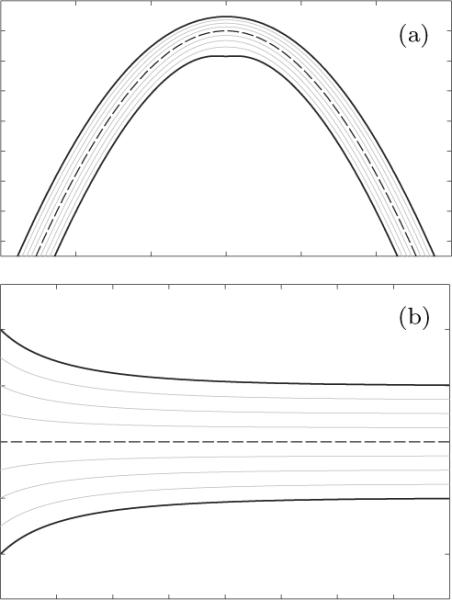
Illustrative isochoric deformations of a lipid bilayer: (a) Thickness change due to pure bending. (b) Thickness change due to pure stretching. While the dashed lines are the sptial mid-surface ${\mathcal{S}}_{\circ }$, the grey lines are spatial placements of few material surfaces with constant ξ_∘ in the reference configuration.

6 Stress relations

Consistent with the procedure pioneered by Coleman and Noll (1963), the elastic Cauchy stress tensor corresponding to an energy density of the form (85) is given by

$$\mathbf{T}=\frac{2}{\sqrt{{\mathcal{I}}_2}}\mathbf{F}\left(\sum _{i=1}^3{\alpha }_i\frac{\partial {\mathcal{I}}_i}{\partial \mathbf{C}}\right){\mathbf{F}}^{⊺},$$ (121)

where ${\alpha }_i=\partial \Phi ∕\partial {\mathcal{I}}_i$ (i = 1, 2, 3). Straightforward calculations based on the definitions (86) lead to

$$\frac{\partial {\mathcal{I}}_1}{\partial \mathbf{C}}=\text{tr}\left(\mathbb{C}\right){\mathbb{P}}_{\mathbb{m}}-\mathbb{C},\frac{\partial {\mathcal{I}}_2}{\partial \mathbf{C}}={\mathcal{I}}_2{\mathbf{C}}^{-1},\frac{\partial {\mathcal{I}}_3}{\partial \mathbf{C}}=\mathbb{m}\otimes \mathbb{m}.$$ (122)

Using (122) in (121) results in

$$\mathbf{T}=\frac{2}{\sqrt{{\mathcal{I}}_2}}\left({\alpha }_1\left(I_1\right(\mathbb{B})\mathbb{B}-{\mathbb{B}}^2)+{\alpha }_2{\mathcal{I}}_{2}1+{\alpha }_3\mathbf{F}\mathbb{m}\otimes \mathbf{F}\mathbb{m}\right),$$ (123)

where $\mathbb{B}=\mathbb{F}{\mathbb{F}}^{\mathrm{T}}$. Notice that, in contrast to $\mathbb{C}$, $\mathbb{B}$ need not be a fully-tangential tensor. When the lipid bilayer is incompressible, (123) should be replaced by

$$\mathbf{T}=-p1+2\left({\tilde{\alpha }}_1\right(I_1\left(\mathbb{B}\right)\mathbb{B}-{\mathbb{B}}^2)+{\tilde{\alpha }}_3\mathbf{F}\mathbb{m}\otimes \mathbf{F}\mathbb{m}),$$ (124)

where ${\tilde{\alpha }}_i=\partial \tilde{\Phi }∕\partial {\mathcal{I}}_i$ (i = 1, 3), and p is an unknown Lagrange multiplier that penalizes the incompressibility.

7 Dimension reduction for an incompressible lipid bilayer

The derivation of two-dimensional models of shell-like structures from three-dimensional elasticity has long been a subject of interest. For a comprehensive review of this subject, see Ciarlet (2005). Simmonds (1985), Stumpf and Makowski (1986), Taber (1987,1988,1989), and Yükseler (2005) have all used the procedure to develop hyperelastic shell theories. However, Zurlo (2006) and Deseri et al. (2008) were the first to apply it to biomembranes. In contrast to the present work, Zurlo (2006) and Deseri et al. (2008) neglected spontaneous curvature.

7.1 General strategy

Granted that a lipid bilayer has thickness considerably smaller than its lateral dimensions, it is very reasonable to attribute to it an energy density, per unit area. The main goal of the dimension reduction described in this section is to obtain an areal energy density ψ_∘ from the volumetric energy density W in accord with the condition

$${\int }_{D_{\circ }}{\psi }_{\circ }\mathrm{d}{A}_{\circ }={\int }_{P}W\mathrm{d}\upsilon ,$$ (125)

where ψ_∘ is measured per unit area on the referential mid-surface S_∘, d_v is the referential volume element, D_∘ ⊂ S_∘ is an arbitrary area on S_∘, and P ⊂ B is the material region associated with D_∘, the lateral faces of which are normal to S_∘ and extended to the inner and outer surfaces Sⁱ and S^∘ (see Figure 4).

Fig. 4.

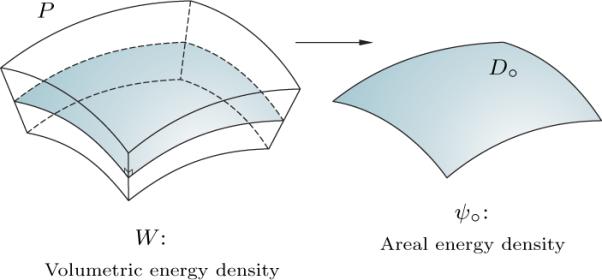
Schematic of the dimension reduction.

In view of (90), (91), and (107), we conclude that

$${\int }_{D_{\circ }}{\psi }_{\circ }\mathrm{d}{A}_{\circ }={\int }_{D_{\circ }}{\int }_{-h_{\circ }^{-}}^{h_{\circ }^{+}}\Phi ({\mathcal{I}}_1,{\mathcal{I}}_2,{\mathcal{I}}_3){\gamma }_{\circ }\left({\xi }_{\circ }\right)\mathrm{d}{\xi }_{\circ }\mathrm{d}{A}_{\circ }.$$ (126)

Since D_∘ is an arbitrary domain, (126) implies that

$${\psi }_{\circ }={\int }_{-h_{\circ }^{-}}^{h_{\circ }^{+}}\Phi ({\mathcal{I}}_1,{\mathcal{I}}_2,{\mathcal{I}}_3){\gamma }_{\circ }\left({\xi }_{\circ }\right)\mathrm{d}{\xi }_{\circ }.$$ (127)

Regarding (105), (110), and (111), and bearing in mind that Φ is an arbitrary function of the invariants ${\mathcal{I}}_1$, ${\mathcal{I}}_2$, and ${\mathcal{I}}_3$, it is evident that the integrand of (127) may, in general, depend on ξ_∘ in a complex manner. This makes integrating (127) difficult. A suitable approximate approach is to expand the integrand in (127) about ξ_∘ = 0 and truncate consistent with some desired degree of accuracy.

7.2 Expansion

Consistent with the consensus regarding the near incompressibility of lipid bilayers, we conduct this expansion only for an energy density of the form (115), in which case (127) is replaced by

$${\psi }_{\circ }={\int }_{-h_{\circ }^{-}}^{h_{\circ }^{+}}\tilde{\Phi }({\mathcal{I}}_1,{\mathcal{I}}_3){\gamma }_{\circ }\left({\xi }_{\circ }\right)\mathrm{d}{\xi }_{\circ }.$$ (128)

Notice that, by (105), (111), and (116), the values of the invariants ${\mathcal{I}}_1$ and ${\mathcal{I}}_3$ at S_∘ are

$${\mathcal{I}}_1{\mid }_{\circ }=J^2$$ (129)

and

$${\mathcal{I}}_3{\mid }_{\circ }=J^{-2}.$$ (130)

In view of (129) and (130), the values of $\tilde{\Phi }$ and any of its partial derivatives at ξ_∘ = 0 may depend at most on the areal stretch J. Anticipating the need to expand $\tilde{\Phi }$ up to second order in ξ_∘, it is therefore convenient to introduce J-dependent quantities f₀, f₁, f₃, f₁₁, f₁₃, and f₃₃ via

$$\phantom{\{}\begin{array}{c}{f}_0=\tilde{\Phi }({\mathcal{I}}_1,{\mathcal{I}}_3){\mid }_{\circ },\hfill \\ f_k={\phantom{\mid }\frac{\partial \tilde{\Phi }({\mathcal{I}}_1,{\mathcal{I}}_3)}{\partial {\mathcal{I}}_k}\mid }_{\circ },k=1,3,\hfill \\ f_{kl}={\phantom{\mid }\frac{{\partial }^2\tilde{\Phi }({\mathcal{I}}_1,{\mathcal{I}}_3)}{\partial {\mathcal{I}}_k\partial {\mathcal{I}}_l}\mid }_{\circ },k,l=1,3.\hfill \end{array}\}$$ (131)

Expanding $\tilde{\Phi }$ to second order in ξ_∘ also requires the values of the first and second derivatives, with respect to ξ_∘, of the invariants ${\mathcal{I}}_1$ and ${\mathcal{I}}_3$ at ξ_∘ = 0. On introducing

$$\tilde{H}=H{J}^{-1}-H_{\circ },\tilde{K}=K{J}^{-2}-K_{\circ },$$ (132)

it follows that

$$\phantom{\{}\begin{array}{c}{\mathcal{I}}_1^{\prime }{\mid }_{\circ }=-4J^2\tilde{H},\hfill \\ {\mathcal{I}}_3^{\prime }{\mid }_{\circ }=4J^{-2}\tilde{H},\hfill \\ {\mathcal{I}}_1^{″}{\mid }_{\circ }=-4J^2(12H_{\circ }\tilde{H}-2\tilde{K}-J^{-4}{\mid \nabla {\mathcal{s}}_{\circ }J\mid }^2),\hfill \\ {\mathcal{I}}_3^{″}{\mid }_{\circ }=4^{-2}(8{\tilde{H}}^2+6H_{\circ }\tilde{H}-\tilde{K}).\hfill \end{array}\}$$ (133)

Expanding $\tilde{\Phi }$ then yields

$${\psi }_{\circ }={\int }_{-h_{\circ }^{-}}^{h_{\circ }^{+}}(f_0+{\alpha }_1{\xi }_0+\frac{1}{2}{\alpha }_2{\xi }_{\circ }^2+\circ ({\xi }_{\circ }^2\left)\right){\gamma }_{\circ }\left({\xi }_{\circ }\right)\mathrm{d}{\xi }_{\circ },$$ (134)

where α₁ and α₂ are given by

$${\alpha }_1=(f_1{\mathcal{I}}_1^{\prime }+f_3{\mathcal{I}}_3^{\prime }){\mid }_{\circ }$$ (135)

and

$${\alpha }_2=(f_1{\mathcal{I}}_1^{″}+f_3{\mathcal{I}}_3^{″}+f_{11}{\left({\mathcal{I}}_1^{\prime }\right)}^2+2f_{13}{\mathcal{I}}_1^{\prime }{\mathcal{I}}_3^{\prime }+f_{33}{\left({\mathcal{I}}_3^{\prime }\right)}^2){\mid }_{\circ },$$ (136)

respectively.

7.3 Restriction to mild areal stretch

Hereafter, we confine our attention to circumstances under which the areal stretch J of the referential mid-surface S_∘ is sufficiently mild to ensure that

$$h_{\circ }{J}^{-1}\mid {\nabla }_{{\mathcal{S}}_{\circ }}J\mid \ll 1.$$ (137)

The gradient term on the right-hand side of (133)₃ is then negligible in comparison to other terms. With this in mind, substituting (131), (135), and (136) in (134), performing the integration, and truncating yields an expression for the areal energy density ψ_∘, measured per unit area of S_∘, yields an expression that depends on H_∘, K_∘, H, K, and J. The dimension reduction therefore provides an areal energy density which includes the effects of spontaneous mean and Gaussian curvatures, deformed mean and Gaussian curvatures, and areal stretch.

In addition, an areal energy density ψ, measured per unit area in the deformed state, has the form

$$\psi =J^{-1}{\psi }_{\circ }$$ (138)

and, thus, depends on the same quantities upon which ψ_∘ depends.

7.4 Specialization to symmetric bilayers

Suppose that the leaflets of the bilayer have identical thickness $h_{\circ }=h_{\circ }^{+}=h_{\circ }^{-}$ and molecular composition, in which case they should be described by a single response function $\tilde{\Phi }$. The areal energy density ψ_∘ determined by the dimension reduction argument then simplifies to

$${\psi }_{\circ }={\psi }_{\mathrm{m}}+\frac{1}{2}\kappa {(H{J}^{-1}-{\stackrel{‒}{H}}_{\circ })}^2+\stackrel{‒}{\kappa }\tilde{K},$$ (139)

where ψ_m, ${\stackrel{‒}{H}}_{\circ }$, κ, and $\stackrel{‒}{\kappa }$ are given by

$$\phantom{\{}\begin{array}{c}{\psi }_{\mathrm{m}}=2h_{\circ }(1+\frac{1}{6}{h}_{\circ }^2{K}_{\circ })f_0+\frac{4}{3}{h}_{\circ }^3{H}_{\circ }^2\left(J^2\right(1-\nu )f_1-J^{-2}(1+7\nu \left)f_3\right),\hfill \\ {\stackrel{‒}{H}}_{\circ }=H_{\circ }(1+\nu ),\hfill \\ \kappa =\frac{32}{3}{h}_{\circ }^3{J}^2\mu ,\stackrel{‒}{\kappa }=\frac{4}{3}{h}_{\circ }^3{J}^2\eta .\hfill \end{array}\}$$ (140)

with

$$\phantom{\{}\begin{array}{c}\nu =\frac{\eta }{4\mu },\eta =(f_1-J^{-4}{f}_3),\hfill \\ \mu =2J^{-4}{f}_3-2J^{-2}{f}_{13}+J^{-6}{f}_{33}+J^2{f}_{11},\hfill \end{array}\}$$ (141)

Notice that the bending moduli κ and $\stackrel{‒}{\kappa }$ given in (140)_3,4 scale with the cube of the leaflet thickness h_∘. Moreover, those moduli differ from those obtained by Zurlo (2006) and Deseri et al. (2008). The difference stems from our use of the exact incompressibility condition (116) in place of their use of the quasi-incompressibitlity condition (118). For instance, the bending moduli in (140) include derivatives of $\tilde{\Phi }$ with respect to ${\mathcal{I}}_3$, derivatives which are absent from the result of Zurlo (2006) and Deseri et al. (2008).

7.5 Alternative interpretations of the splay and saddle-splay moduli

We now provide alternative interpretations of the splay and saddle-splay moduli κ and $\stackrel{‒}{\kappa }$. Consider the state of stress at the spatial mid-surface ${\mathcal{S}}_{\circ }$ of an incompressible lipid bilayer. Since ${\mathbb{F}}_{\circ }$ is a tangential tensor, ${\mathbb{F}}_{\circ }^{⊺}=0$ and ${\mathbb{B}}_{\circ }={\mathbb{F}}_{\circ }{\mathbb{F}}_{\circ }^{⊺}$ is a fully tangential tensor. Using (196), it can be shown that $I_2\left({\mathbb{B}}_{\circ }\right)=I_2\left({\mathbb{C}}_{\circ }\right)=J^2$. As a consequence of these facts, (124) yields

$$\begin{array}{cc}\hfill {\mathbf{T}}_{\circ }:& =\mathbf{T}{\mid }_{\xi =0}\hfill \\ \hfill & =-p1+2(J^2{f}_1{\mathbb{P}}_{\mathbb{n}}+f_3(\mathbf{F}\mathbb{m}\otimes \mathbf{F}\mathbb{m}{\mid }_{\circ }).\hfill \end{array}$$ (142)

Consistent with the kinematical assumption regarding the orientation of the phospholipid molecules, consider a deformation with the property

$$\mathbf{F}{\mid }_{\circ }\mathbb{m}=\varphi \mathbb{n},\varphi >0,$$ (143)

where ϕ is an arbitrary constant. Also, as is customary in the theory of thin shell-like structures, assume that the normal stress $\mathbb{n}\cdot \mathbf{T}\mathbb{n}$ is very small compared to all other erlevant stress components. Then, in view of (143) and the assumption $\mathbb{n}\cdot {\mathbf{T}}_{\circ }\mathbb{n}$, (142) can be written as

$${\mathbf{T}}_{\circ }=2(f_1{J}^2-{\varphi }^2{f}_3){\mathbb{P}}_{\mathbb{n}}.$$ (144)

Moreover, (143) reduces C in (63) to

$$\mathbf{C}{\mid }_{\circ }={\mathbb{C}}_{\circ }+{\varphi }^2\mathbb{m}\otimes \mathbb{m}.$$ (145)

Since the deformation must be isochoric, we find that

$${\varphi }^2={\left(I_2\right({\mathbb{C}}_{\circ }\left)\right)}^{-1}=J^{-2},$$ (146)

which allows us to reduce (144) to

$$\begin{array}{cc}\hfill {\mathbf{T}}_{\circ }& =2J^2(f_1-J^{-4}{f}_3){\mathbb{P}}_{\mathbb{n}},\hfill \\ \hfill & ≕\Sigma {\mathbb{P}}_{\mathbb{n}}.\hfill \end{array}$$ (147)

Notice that T_∘ is an isotropic tensor on the tangent space of ${\mathcal{S}}_{\circ }$. Also, Σ can be considered as the in-plane tension or compression at the spatial mid-surface ${\mathcal{S}}_{\circ }$. Invoking the definitions of Σ in (147) and η provided in (141)₂, we find that

$$\eta =\frac{1}{2}{J}^{-2}\Sigma .$$ (148)

In addition, we may define

$$\Lambda ≔\frac{\partial \Sigma }{\partial J},$$ (149)

as the areal stiffness of the lipid bilayer at ${\mathcal{S}}_{\circ }$, which, with (141) and (147), can be expressed as

$$\Lambda =4J(\mu +\eta ).$$ (150)

Using (148), relation (150) becomes

$$\mu =\frac{J\Lambda -2\Sigma }{4J^2}.$$ (151)

Then, on using (148) and (151), the splay and saddle-splay moduli defined in (140) can be expressed in terms of Σ and Λ as

$$\kappa =\frac{8}{3}{h}_{\circ }^3(J\Lambda -2\Sigma ),\stackrel{‒}{\kappa }=\frac{2}{3}{h}_{\circ }^3\Sigma .$$ (152)

7.6 Canham–Helfrich-type energy density

In many studies, due to high in-plane resistance, the lipid bilayer is stipulated to be inextensible and this constraint is imposed by adding a suitable term to the areal energy density. Necessarily, the introduction of such a constraint is accompanied by the need for a Lagrange multiplier. In this case, the deformation of the lipid bilayer is dominated by bending. To address this limit in our setting, consider the limiting case of J ≈ 1. Regarding the definition of ν in (141)₁, and using (148) and (151), it can be concluded that

$$\nu =\frac{\Sigma }{2(J\Lambda -2\Sigma )}.$$ (153)

In accordance with the high in-plane resistance of the lipid bilayer, the ratio of the areal stress Σ and stiffness Λ should be very small (i.e., $\sum {\Lambda }^{-1}\approx 0$), leading to ν ≈ 0. Thus, the areal energy density is well approximated by

$${\psi }_{\circ }={\psi }_{\mathrm{m}}+\frac{1}{2}\kappa {(H-H_{\circ })}^2+\stackrel{‒}{\kappa }(K-K_{\circ }),$$ (154)

with

$${\psi }_{\mathrm{m}}=2h_{\circ }\left(f_0\right(1+\frac{1}{6}{h}_{\circ }^2{K}_{\circ })+\frac{2}{3}\eta h_{\circ }^2{H}_{\circ }^2),$$ (155)

and

$$\phantom{\{}\begin{array}{c}\kappa =\frac{32}{3}{h}_{\circ }^3(2f_3-2f_{13}+f_{33}+f_{11}),\hfill \\ \stackrel{‒}{\kappa }=\frac{4}{3}{h}_{\circ }^3(f_1-f_3).\hfill \end{array}\}$$ (156)

Also, using the approximations J ≈ 1 and $\sum {\Lambda }^{-1}\approx 0$ in the expression (152)₁ for the splay modulus yields

$$\kappa =\frac{8}{3}{h}_{\circ }^3\Lambda ;$$ (157)

however, the expression (152)₂ for the saddle-splay modulus remains unchanged with these approximations.

Assuming that the lipid bilayer is very thin, the membranal energy given in (155) reduces to ψ_m = 2h_∘f₀. Since f₀ only depends on J, the membranal energy can be represented as ψ_m = φ_∘ (J). Therefore, it is natural to introduce an effective surface tension

$$\sigma ≔\frac{\mathrm{d}{\phi }_{\circ }}{\mathrm{d}J}$$ (158)

and an effective areal stiffness

$$\lambda ≔\frac{{\mathrm{d}}^2{\phi }_{\circ }}{\mathrm{d}{J}^2},$$ (159)

for the lipid bilayer. On using the definitions of η, Σ, and Λ in (141)₂, (147), and (149), respectively, and performing straitforward differentiation, it is possible to verify that

$$\eta =\frac{1}{2}{J}^{-1}\frac{\mathrm{d}{f}_0}{dJ},\Sigma =J\frac{\mathrm{d}{f}_0}{\mathrm{d}J},\Lambda =\Sigma J^{-1}+J\frac{{\mathrm{d}}^2{f}_0}{\mathrm{d}{J}^2},$$ (160)

which, in view of the approximations J ≈ 1 and ΣΛ⁻¹ 0, and (152)₂ and (157), yields

$$\kappa =\frac{4}{3}{h}_{\circ }^2\frac{{\mathrm{d}}^2{\phi }_{\circ }}{\mathrm{d}{J}^2},\stackrel{‒}{\kappa }=\frac{1}{3}{h}_{\circ }^2\frac{\mathrm{d}{\phi }_{\circ }}{\mathrm{d}J};$$ (161)

thus, on referring to (158) and (159), the splay and saddle-splay moduli can be expressed as

$$\kappa =\frac{4}{3}{h}_{\circ }^2\lambda ,\stackrel{‒}{\kappa }=\frac{1}{3}{h}_{\circ }^2\sigma .$$ (162)

From relations (162) it is evident that κ and $\stackrel{‒}{\kappa }$ are directly proportional to the effective areal stiffness and surface tension of the lipid bilayer, respectively.

When the bilayer is in a state of pure bending (i.e., J = 1), ${\mathcal{I}}_1$, and ${\mathcal{I}}_3$ are both equal to unity on the spatial mid-surface ${\mathcal{S}}_{\circ }$, and thus ${\mathcal{S}}_{\circ }$ corresponds to the natural state—that is,

$$\tilde{\Phi }({\mathcal{I}}_1,{\mathcal{I}}_3){\mid }_{{\xi }_{\circ }=0;J=1}=0,$$ (163)

whereby f₀ = 0. Thus, ψ_m = 0, and

$${\psi }_{\circ }=\frac{1}{2}\kappa {(H-H_{\circ })}^2+\stackrel{‒}{\kappa }(K-K_{\circ }).$$ (164)

Since the areal energy density is determinable only up to an arbitrary additive constant, (164) is equivalent to the the Canham–Helfrich energy density (1).

When the lipid bilayer is assumed inextensible, the areal energy density (164) should be considered, while the inextensibility constraint should be penalized by considering a Lagrange multiplier.

7.7 Effect of asymmetric chemistry of the leaflets

Now suppose that, due to possible trans-bilayer asymmetric chemistry of the leaflets (Luckey 2008, Janmey and Kinnunen 2006, and Devaux and Morris 2004, McMahon and Gallop 1998), the response functions ${\tilde{\Phi }}^{+}$ and ${\tilde{\Phi }}^{-}$ in the upper and lower leaflets differ. This situation is very probable when the spontaneous curvature is induced due to asymmetric distribution of lipid molecules with different molecular shapes across the mid-surface of the lipid bilayer (McMahon and Gallop 1998).

The dimension reduction then leads to an energy density of the form

$${\psi }_{\circ }={\psi }_{\mathrm{m}}+\frac{1}{2}\kappa {(H{J}^{-1}-{\widehat{H}}_{\circ })}^2+\stackrel{‒}{\kappa }\tilde{K},$$ (165)

where ψ_m, ${\widehat{H}}_{\circ }$, κ, and $\stackrel{‒}{\kappa }$ are given by

$$\phantom{\{}\begin{array}{c}{\psi }_{\mathrm{m}}=2h_{\circ }(\langle f_0\rangle -\frac{1}{2}〚f_0〛h_{\circ }{H}_{\circ }+\frac{1}{6}{h}_{\circ }^2\langle f_0\rangle K_{\circ })\hfill \\ +\frac{4}{3}{h}_{\circ }^3{H}_{\circ }^2\left(J^2\right(1-\widehat{\nu })\langle f_1\rangle -J^{-2}(1+7\widehat{\nu })\langle f_3\rangle )\hfill \\ -\kappa \widehat{\nu }{H}_{\circ }{H}_c,\hfill \\ {\widehat{H}}_{\circ }=H_{\circ }(1+\widehat{\nu })+H_c,\hfill \\ \kappa =\frac{32}{3}{h}_{\circ }^3\langle \mu \rangle J^2,\stackrel{‒}{\kappa }=\frac{4}{3}{h}_{\circ }^3\langle \eta \rangle J^2,\hfill \end{array}\}$$ (166)

with

$$H_c=2\frac{h_{\circ }^2{J}^2}{\kappa }〚\eta 〛,\widehat{\nu }=\frac{\langle \eta \rangle }{4\langle \eta \rangle },$$ (167)

In addition, for the approximation J ≈ 1, the counterpart of (154) takes the form

$${\psi }_{\circ }={\psi }_{\mathrm{m}}+\frac{1}{2}{\kappa (H-(H_{\circ }+H_c\left)\right)}^2+\stackrel{‒}{\kappa }(K-K_{\circ }),$$ (168)

where ψ_m, H_c, κ, and $\stackrel{‒}{\kappa }$ are given by

$$\phantom{\{}\begin{array}{c}{\psi }_{\mathrm{m}}=2h_{\circ }\langle f_0\rangle ,\hfill \\ H_c=2\frac{h_{\circ }^2}{\kappa }〚f_1-f_3〛,\hfill \\ \kappa =\frac{32}{3}{h}_{\circ }^3\langle 2f_3-2f_{13}+f_{33}+f_{11}\rangle ,\hfill \\ \stackrel{‒}{\kappa }=\frac{4}{3}{h}_{\circ }^3\langle f_1-f_3\rangle .\hfill \end{array}\}$$ (169)

If, moreover, the lipid bilayer is in a state of pure bending then (168) reduces to

$${\psi }_{\circ }=\frac{1}{2}\kappa {(H-(H_{\circ }+H_c\left)\right)}^2+\stackrel{‒}{\kappa }(K-K_{\circ }).$$ (170)

Let H_c denote the constitutively-induced spontaneous mean curvature and introduce the net spontaneous curvatureH_sp = H_∘ + H_c. The net spontaneous mean curvature H_sp for an asymmetric lipid bilayer is then seen to incorporate two contributions: (i) a geometrical contribution H_∘, which stems from the spontaneous geometry of the lipid bilayer, due to asymmetric distribution of phospholipid molecules with different molecular shapes or due to other possible sources (McMahon and Gallop 1998, Döbereiner et al. 1999); (ii) a constitutive contribution H_c, which stems from differences between the constitutive properties of the leaflets.

Also, notice that the alternative representations of κ and $\stackrel{‒}{\kappa }$ in (152), (157), (161), and (162) remain valid under the present circumstances, except that Σ, Λ, and φ_∘ should be replaced by 〈Σ〉, 〈Λ〉, and φ_∘ = 2h_∘〈f₀〉, respectively.

7.8 Effect of the incoherency between the leaflets

The areal energy density obtained by dimension reduction may be generalized to include the effect of incoherency between the leaflets. In such case, the invariants ${\mathcal{I}}_k^{+}$ and ${\mathcal{I}}_k^{-}$ (k = 1, 3) and the areal stretches J⁺ and J⁻ in the upper and lower leaflets differ. The integration in (128) must therefore be performed piecewise. Being very similar to the steps leading to (134), the steps involved are not shown. The final form of the areal energy density depends, as before, on H_∘, K_∘, H, and K; however, instead of J, it includes dependence on both J⁺ and J⁻.

7.9 Remarks

• The Canham–Helfrich energy density is an acceptable areal energy density when (i) the leaflets have identical thickness and the same response function (ii) the ratio of the thickness to the principal radii of curvature is very small, and (iii) the lipid bilayer has pure bending or it is inextensible.

• In contrast to the classical Canham–Helfrich energy density (1), our theory predicts that the spontaneous Gaussian curvature should be included in the areal energy density in a manner analogous to the spontaneous mean curvature. Moreover, in contrast to (1), the energy density (164) vanishes at the spontaneous state. This issue is not important in the case of homogeneous lipid bilayers because the energy density can be additively scaled by any constant. However, for heterogeneous lipid bilayers, such as multi-phase GUVs (e.g., see Baumgart et al. (2005)), where the saddle-splay modulus or the spontaneous curvature are nonuniform, this distinction should be considered.

• As long as the response function $\tilde{\Phi }$ is known, the bending moduli κ and $\stackrel{‒}{\kappa }$ cannot be be arbitrary chosen. Rather, they derive from the response function $\tilde{\Phi }$. This is consistent with the conclusions of Zurlo (2006) and Deseri et al. (2008).

• The bending moduli κ and $\stackrel{‒}{\kappa }$ scale with the cube of the leaflet thickness h_∘. This is in harmony with the deformation of a thin elastic sheet, for example, as described by the classical Föppl–von Kármán theory, where the bending rigidity is proportional to the cube of the sheet thickness. In addition, just as the bending rigidity of an isotropic homogeneous elastic sheet is linearly proportional to its Young modulus, the splay modulus κ is linearly proportional to the in-plane stiffness of the lipid bilayer. In contrast, the saddle-splay modulus $\stackrel{‒}{\kappa }$ is linearly scaled with the surface tension in the lipid bilayer.

• The membranal energy ψ_m includes not only a term proportional to h_∘ but also a secondary term proportional to $h_{\circ }^3$. This term also contains the spontaneous mean and Gaussian curvatures of the lipid bilayer. However, as long as the lipid bilayer is very thin, the contribution of this secondary term is negligible.

• Ostensibly, the areal energy density ψ_∘ obtained from the dimension reduction argument should provide a basis for formulating variational problems to determine minimum energy configurations of lipid bilayers. However, to generate well-posed variational problems, the areal energy density ψ_∘ should at very least satisfy the Legendre–Hadamard condition and thereby guarantee that the second (weak) variation of the underlying functional is positive. For example, based on the established Legendre–Hadamard condition for elastic surfaces of second-grade (see, for instance, Hilgers and Pipkin (1993)), Steigmann (1999) and Agrawal and Steigmann (2008) derived the Legendre–Hadamard condition relevant to a lipid bilayer with an areal energy density depending generically on H, K, and J—which encompasses the result of the dimension reduction obtained here. If, in the present context, the assumption of mild areal stretch embodied by (137) does not hold, then, as is the case in the work of Zurlo (2006) and Deseri et al. (2008), the areal energy density ψ_∘ will include an extra contribution proportional to $\mid {\nabla }_{{\mathcal{S}}_{\circ }}J{\mid }^2$. However, there is no reason to expect that the Legendre–Hadamard conditions for an areal energy density depending on H, K, J, and $\mid {\nabla }_{{\mathcal{S}}_{\circ }}J\mid$ should always be satisfied by the areal energy density arising from the dimensional reduction argument, even if the three-dimensional energy density $\tilde{\Phi }$ leading to ψ_∘ satisfies the appropriate three-dimensional Legendre–Hadamard condition. To see this consider, for example, a flat lipid bilayer, in which the energetic contribution of curvature is absent, so that

  $${\psi }_{\circ }={\phi }_{\circ }\left(J\right)+\frac{2}{3}{h}_{\circ }^3{J}^{-2}{f}_1{\mid \nabla s_{\circ }J\mid }^2.$$ (171)

  The approach of Hilgers and Pipkin (1993) can then be used to show that the Legendre–Hadamard condition is satisfied only if f₁ > 0. A precise understanding of the sign of f₁ depends on the specific structure of the response function $\tilde{\Phi }$ and the value of areal stretch J on the mid-surface. Nevertheless, in view of (147), it can be observed that f₁ may depend on the in-plane stress at the mid-surface of the lipid bilayer. As long as f₁ is positive, the second variation of ψ_∘ is positive and the equilibrium configuration of the lipid bilayer is stable (locally, at least). However, if f₁ is negative, due to a possible contraction in the lipid bilayer, then the Legendre–Hadamard condition is violated, implying that the configuration of the lipid bilayer is unstable. One way to cure this problem is to add a term to ψ_∘, as Hilgers and Pipkin (1996) did in their study of the equilibrium of elastic membranes with strain-gradient energies.

8 Summary

A continuum approach to modeling the deformation of lipid bilayers with spontaneous curvature was provided. In a departure from prevailing tradition, a lipid bilayer was modeled by a three-dimensional body. Apart from a kinematical constraint incorporating natural aspects of the behavior of lipid molecules, no further restrictions were imposed on the deformation. In this context, a general representation for the deformation gradient was derived. That representation involves the curvature tensor of the mid-surface in the spontaneous (or reference) state, the curvature tensor of the mid-surface in the deformed state, the deformation gradient of the mid-surface, and changes in transverse thickness. The coherency of the leaflets that comprise a lipid bilayer, which entails considering local coupling or sliding of those leaflets, was explored, as was the topic of area compatibility.

Geometry and kinematics aside, the material symmetry of lipid bilayers that exhibit in-plane fluidity and transverse isotropy was studied. Moreover, modeling the bilayer as a hyperelastic material, a representation theorem for the energy density was developed. Three invariants were found to be sufficient to describe the constitutive behavior of a lipid bilayer. It was shown that these invariants describe local strecth of area elements parallel to the mid-surface, volume change, and through-thickness stretching. Explicit expressions for these invariants were determined and presented in terms of fundamental kinematical quantities. Among these kinematical quantities are the referential and spatial mid-surface curvatures, the areal stretch of the mid-surface, the transverse normal and shear strains (which, in the present setting, control thickness change and nonuniformity, respectively), and a coupling term between the surface gradient of the transverse deformation and the mid-surface curvature tensor.

The special case of a lipid bilayer that—in accord with experimental observations—is incompressible was considered. Under this constraint, transverse deformation (with respect to the mid-surface) of the lipid bilayer is coupled to mid-surface deformation. This purely geometrical and kinematical consideration suggests that when the mid-surface of an incompressible lipid bilayer has nonuniform bending and/or stretching or when the spontaneous curvature is nonuniform, its thickness in the deformed state is, in general, nonuniform.

Granted that the lipid bilayer is sufficiently thin, a dimension reduction argument was used to extract an areal (two-dimensional) energy density from the volumetric energy density. The conditions under which a Canham–Helfrich-type energy density is derivable were discussed. An energy density for lipid bilayer with asymmetric leaflets was also obtained and it was shown that, for such a medium, the spontaneous curvature can be interpreted as combination of two contributions. The first contribution represents the preferred geometry (i.e., the spontaneous shape) of the lipid bilayer. The second contribution—which may be called the constitutively-induced spontaneous curvature—arises due to differences between the response functions of the leaflets. Lastly, the general form of the areal energy density for a lipid bilayer with incoherent leaflets was considered.

A Appendices

A.1 Superficial fields

A field defined only on a surface is called superficial. For instance, $\mathbb{m}$ is a superficial unit vector field defined on the mid-surface S_∘. The three-dimensional gradient of such a field is undefined. However, a smooth extension of a superficial field to a three-dimensional neighborhood of the surface on which it is defined provides a means for defining its three-dimensional gradient (on the relevant neighborhood). The normally constant extension, in which a superficial field is stipulated to be constant along lines perpendicular to the surface on which it is defined, provides the simplest such extension (Fried and Gurtin 2007). For example, consider a scalar-valued superficial field f defined on S_∘ and let f^e denote a smooth extension of f to a neighborhood of S_∘. This extension can be used to define the surface gradient ▽_S∘ f of f on S_∘ in terms of the three-dimensional gradient ▽f^e of f^e by

$$\nabla s_{\circ }f={\mathbb{P}}_{\mathbb{m}}\nabla f^{\mathrm{e}},$$ (172)

where

$${\mathbb{P}}_{\mathbb{m}}=1-\mathbb{m}\otimes \mathbb{m}$$ (173)

is the projection tensor onto the tangent space T_∘ of S_∘. Notice that ▽f^e in (172) must be evaluated at points on the surface S_∘. It should be mentioned that ▽_S∘ f as determined by (172) is independent of the particular features of the extension f^e. It is easily shown that ▽_S∘ f is tangent to the surface S_∘. Similarly, the surface gradient ${\nabla }_{S_{\circ }}\mathbb{g}$ and surface divergence div ${\text{div}}_{S_{\circ }}\mathbb{g}$ of vector-valued superficial field $\mathbb{g}$ are defined as

$$\phantom{\{}\begin{array}{c}{\nabla }_{s_{\circ }}\mathbb{g}=(\nabla {\mathbb{g}}^{\mathrm{e}}){\mathbb{P}}_{\mathbb{m}},\hfill \\ \mathrm{div}{s}_{\circ }\mathbb{g}=\text{tr}\left({\nabla }_{s_{\circ }}\mathbb{g}\right)={\mathbb{P}}_{\mathbb{m}}\cdot \nabla {\mathbb{g}}^{\mathrm{e}},\hfill \end{array}\}$$ (174)

where ${\mathbb{g}}^{\mathrm{e}}$ is a smooth extension of $\mathbb{g}$. Here, as with ▽f^e in (172), $\nabla {\mathbb{g}}^{\mathrm{e}}$ is evaluated at the point on S_∘. Additionally, in a suitably determined neighborhood of S_∘, the gradient ▽g and divergence div g of a vector field g defined on a three-dimensional region containing S_∘ decomposes according to

$$\phantom{\{}\begin{array}{c}\nabla g={{\nabla }_s}_{\circ }\mathbb{g}+\frac{\partial g}{\partial \mathbb{m}}\otimes \mathbb{m},\hfill \\ \mathrm{div}g=\mathrm{div}{s}_{\circ }\mathbb{g}+\frac{\partial g}{\partial \mathbb{m}}\cdot \mathbb{m},\hfill \end{array}\}$$ (175)

where $\mathbb{g}=\mathbb{g}{\mid }_{S_{\circ }}$ is the restriction of g to S_∘ and

$$\frac{\partial g}{\partial \mathbb{m}}=(\nabla g)\mathbb{m}$$ (176)

is the normal derivative of g.

A superficial tensor field $\mathbb{G}$, besides being defined only on a surface, must satisfy

$$\mathbb{G}\mathbb{m}=0.$$ (177)

For example, the surface gradient ${\nabla }_{S_{\circ }}\mathbb{g}$ of superficial vector field $\mathbb{g}$ is a superficial tensor field. If $\mathbb{G}$ also obeys

$${\mathbb{G}}^{⊺}\mathbb{m}=0,$$ (178)

then $\mathbb{G}$ is said to be a fully tangential tensor field. For example, the projection tensor ${\mathbb{P}}_{\mathbb{m}}$ is fully tangential.

Other examples of fully tangential tensor fields are the curvature tensors ${\mathbb{L}}_{\circ }$ and $\mathbb{L}$ of the surfaces S_∘ and ${\mathcal{S}}_{\circ }$, as defined by

$${\mathbb{L}}_{\circ }=-{\nabla }_{s_{\circ }}\mathbb{m},\mathbb{L}=-{\nabla }_{s_{\circ }}\mathbb{n}.$$ (179)

${\mathbb{L}}_{\circ }$ and $\mathbb{L}$ each possess at most two nontrivial scalar invariants. Convenient choices for these are the mean and Gaussian curvatures. Specifically, while

$$\phantom{\{}\begin{array}{c}{H}_{\circ }=\frac{1}{2}{I}_1\left({\mathbb{L}}_{\circ }\right)=\frac{1}{2}\text{tr}\left({\mathbb{L}}_{\circ }\right),\hfill \\ K_{\circ }=I_2\left({\mathbb{L}}_{\circ }\right)=\frac{1}{2}[{\left(\text{tr}\right({\mathbb{L}}_{\circ }\left)\right)}^2-\text{tr}({\mathbb{L}}_{\circ }^2\left)\right],\hfill \end{array}\}$$ (180)

define the mean and Gaussian curvatures H_∘ and K_∘ of the surface S_∘,

$$\phantom{\{}\begin{array}{c}{H}_{\circ }=\frac{1}{2}{I}_1\left(\mathbb{L}\right)=\frac{1}{2}\text{tr}\left(\mathbb{L}\right),\hfill \\ K_{\circ }=I_2\left(\mathbb{L}\right)=\frac{1}{2}[{\left(\text{tr}\right(\mathbb{L}\left)\right)}^2-\text{tr}({\mathbb{L}}_2\left)\right],\hfill \end{array}\}$$ (181)

define the analogous quantities for ${\mathcal{S}}_{\circ }$.

A useful property of any fully tangential tensor $\mathbb{A}$ is the relation

$${\mathbb{A}}^c={\mathbb{A}}^2-I_1\left(\mathbb{A}\right)\mathbb{A}+I_2\left(\mathbb{A}\right)\mathbb{A}1$$ (182)

determining its cofactor ${\mathbb{A}}^{\mathrm{c}}$, where I₁($\mathbb{A}$) and I₂($\mathbb{A}$) are first two principal invariants of $\mathbb{A}$. A simple, but useful consequence of (182) is that

$${\mathbb{A}}^c\mathbb{m}=I_2\left(\mathbb{A}\right)\mathbb{m}.$$ (183)

Notice that I₂($\mathbb{A}$) can be viewed as the determinant of a two-dimensional matrix representation of $\mathbb{A}$. Having this in mind, other useful identities can be established, including

$$I_2\left({\mathbb{A}}^{⊺}\right)=I_2\left(\mathbb{A}\right),I_2\left(\mathbb{AB}\right)=I_2\left(\mathbb{A}\right)I_2\left(\mathbb{B}\right),$$ (184)

with $\mathbb{B}$ also being a fully tangential tensor.

A.2 Pseudoinverse of a fully tangential tensor

Let $\mathbb{A}$ be a fully tangential tensor. Then

$$\mathbb{Am}={\mathbb{A}}^{⊺}\mathbb{m}=0$$ (185)

and

$$\mathbb{A}={\mathbb{P}}_{\mathbb{m}}\mathbb{A}={\mathbb{AP}}_{\mathbb{m}}.$$ (186)

Since the determinant of ${\mathbb{P}}_{\mathbb{m}}$ vanishes, (186) implies that the determinant of $\mathbb{A}$ must also vanish. Consequently, as a mapping from three-dimensional vector space to itself, $\mathbb{A}$ is not invertible. However, from (186), $\mathbb{A}$ maps any vector from the tangent space T_∘ to a vector in T_∘. If $\mathbb{A}$, considered as a mapping from T_∘ to T_∘, is one-to-one and, thus, invertible, then there exists a tensor ${\mathbb{A}}^{†}$ satisfying

$${\mathbb{AA}}^{†}={\mathbb{A}}^{†}\mathbb{A}={\mathbb{P}}_{\mathbb{m}}.$$ (187)

In view of (187), ${\mathbb{A}}^{†}$ provides an inverse for $\mathbb{A}$ as a mapping from T_∘ to T_∘. However, ${\mathbb{A}}^{†}$ does not provide an inverse of $\mathbb{A}$ considered as a mapping from three-dimensional vector space to itself. Thus, ${\mathbb{A}}^{†}$ may be thought of as a pseudoinverse of $\mathbb{A}$.

To obtain the pseudoinverse ${\mathbb{A}}^{†}$ of a fully tangential tensor $\mathbb{A}$ that is a one-to-one mapping from T_∘ to T_∘, consider the Cayley–Hamilton equation

$${\mathbb{A}}^3-I_1\left(\mathbb{A}\right){\mathbb{A}}^2+I_2\left(\mathbb{A}\right)\mathbb{A}=0,$$ (188)

for $\mathbb{A}$. (Notice that, since $\mathbb{A}$ is fully tangential, its third principal invariant I₃($\mathbb{A}$) obeys $\mathbb{A}$. Hence, a term proportional to I₃($\mathbb{A}$) is absent from (188).) On applying the left-hand side of (188) to an arbitrary vector t and introducing the vector $\mathbb{u}=\mathbb{A}\mathbf{t}$, it follows that

$$({\mathbb{A}}^2-I_1(\mathbb{A})\mathbb{A}+I_2(\mathbb{A}\left){\mathbb{P}}_{\mathbb{m}}\right)\mathbb{u}=0.$$ (189)

Since $\mathbb{u}$ is a tangent vector and, thus, ${\mathbb{P}}_{\mathbb{m}}\mathbb{u}=\mathbb{u}$, keeping 185 and (186) in mind, (189) yields

$$\begin{array}{cc}\hfill \mathbb{u}& =\mathbb{A}\left[{\left(I_2\right(\mathbb{A}\left)\right)}^{-1}\right(I_1\left(\mathbb{A}\right){\mathbb{P}}_{\mathbb{m}}-\mathbb{A}\left)\right]\mathbb{u}\hfill \\ \hfill & =\left[{\left(I_2\right(\mathbb{A}\left)\right)}^{-1}\right(I_1\left(\mathbb{A}\right){\mathbb{P}}_{\mathbb{m}}-\mathbb{A}\left)\right]\mathbb{Au}.\hfill \end{array}$$ (190)

Since, for any invertible tensor T,

$${\mathbf{TT}}^{-1}\mathbb{u}={\mathbf{T}}^{-1}\mathbb{u},$$ (191)

it follows from (190) that

$${\mathbb{A}}^{†}={\left(I_2\right(\mathbb{A}\left)\right)}^{-1}\left(I_1\right(\mathbb{A}){\mathbb{P}}_{\mathbb{m}}-\mathbb{A})$$ (192)

provides a pseudoinverse of the fully tangential tensor $\mathbb{A}$ that is one-to-one as a mapping from T_∘ to T_∘.

In view of (192), a fully tangential tensor $\mathbb{A}$ is pseudoinvertible if and only if

$$I_2\left(\mathbb{A}\right)\ne 0.$$ (193)

Granted that $\mathbb{A}$ is fully tangential, ${\mathbb{A}}^{†}$ defined by (192) is also fully tangential—that is, ${\mathbb{A}}^{†}$ defined by (192) obeys

$${\mathbb{A}}^{†}\mathbb{m}={\left({\mathbb{A}}^{†}\right)}^{⊺}\mathbb{m}=0,$$ (194)

and

$${\mathbb{A}}^{†}={\mathbb{P}}_{\mathbb{m}}{\mathbb{A}}^{†}={\mathbb{A}}^{†}{\mathbb{P}}_{\mathbb{m}}.$$ (195)

Also multiplying (192) by $\mathbb{A}$ and using (187), while invoking (193), yields the relation

$${\mathbb{A}}^2-I_1\left(\mathbb{A}\right)\mathbb{A}+I_2\left(\mathbb{A}\right){\mathbb{P}}_{\mathbb{m}}=0,$$ (196)

which can be viewed as the Cayley–Hamilton equation for a fully tangential tensor (see also Simmonds (1985) for a discussion of the Cayley–Hamilton equation for a linear mapping of two-dimensional vector space into itself). Finally, using (196) in (182) leads to

$${\mathbb{A}}^{\mathrm{c}}=I_2\left(\mathbb{A}\right)\mathbb{m}\otimes \mathbb{m}.$$ (197)