Towards controlling molecular motions in fluorescence microscopy and optical trapping: a spatiotemporal approach

Abstract

This account reviews some recent studies pursued in our group on several control experiments with important applications in (one-photon) confocal and two-photon fluorescence laser-scanning microscopy and optical trapping with laser tweezers. We explore the simultaneous control of internal and external (i.e. centre-of-mass motion) degrees of freedom, which require the coupling of various control parameters to result in the spatiotemporal control. Of particular interest to us is the implementation of such control schemes in living systems. A live cell is a system of a large number of different molecules which combine and interact to generate complex structures and functions. These combinations and interactions of molecules need to be choreographed perfectly in time and space to achieve intended intra-cellular functions. Spatiotemporal control promises to be a versatile tool for dynamical control of spatially manipulated bio-molecules.

1. Introduction

Molecular spectroscopy sheds light on the dynamics of molecules concerning various time-scales while microscopy zooms in the structural detail at various length-scales. There has been a continued effort to combine advanced molecular spectroscopic methods with improved microscopic techniques for simultaneous control over time-scale as well as length-scale. This has been an actively pursued theme of research of various groups. Recently, for example, the Zewail group at Caltech has developed ‘4D electron microscopy’ for studying femtosecond temporal dynamics at angstrom spatial resolution [1]. Such a method furnishes spatially resolved information on dynamics involving internal degrees of freedom while that involving centre-of-mass motion can be obtained by the use of optical tweezers (i.e. photonic force microscopes).

The light based microscopes and tweezers, despite having poorer resolution as compared to the electron microscopes, have proven to be the best choice for experimenting with live specimens. This is because the energy deposited in electron microscopy adversely affects the viability of live specimens. Among various optical microscopy techniques, fluorescence microscopy has gained special consideration because of its improved substrate specificity, local environment sensitivity and time resolution achieved through molecular fluorescence [2,3].

1.1. Advances in fluorescence microscopy and optical trapping

For a century, fluorescence microscopy has come a long way since its inception by Oscar in 1911. Recent developments in novel fluorescent dyes and fluorescent proteins have further boosted the research in fluorescence microscopy. The key parameters that define the quality of a microscope are the resolution, magnification and contrast.¹ The most important of these being the resolution, which is explained as the minimum distance between two bright points in the luminous object that can be distinguished. For any form of far-field fluorescence microscope lateral and axial resolution is limited by diffraction and given by the (modified) Abbe relation² [4-6]:

$$r_{\text{lateral}}\approx 0.61\lambda ∕NA\text{and}{r}_{\text{axial}}\approx 2\eta \lambda ∕N{A}^2,$$

where λ is the wavelength of emitted light, NA the numerical aperture of the collecting objective³ and η the index of refraction. Taking NA ≈ 1.4 and η ≈ 1.45, the lateral resolution turns out to be nearly half of the wavelength, and axial resolution, nearly on the order of the wavelength. One of the most sought after challenges in fluorescence microscopy has been on the advancement of better depth-resolution (also called axial- or z-resolution) in an optically thick specimen (where background fluorescence results in blurring of the image) as evidenced by the development of confocal [7] and multiphoton [8,9] fluorescence laser-scanning microscopic techniques [5,6]. In confocal microscopy, out-of-focus fluorescence is effectively rejected by making use of a pin-hole placed at the conjugate focal-plane of the image-plane (thus the name confocal) while in multiphoton microscopy confocality is inherent due to confined nonlinear fluorescence generation within the focus. A schematic explaining fluorescence generation and detection for these two types of microscopy is given in Figure 1. As shown in the figure, an optically thick specimen can be considered to be composed of several fluorescing layers. The total fluorescence from the specimen is a sum total of fluorescence of each layer. The confocal pin-hole effectively collects fluorescence from the middle layer only (Figure 1(a)) while the multiphoton fluorescence arises only from focal volume, thus, giving rise to a background-free fluorescence detection (Figure 1(b)).⁴

Figure 1.

[Colour online] Confocal (a) and multiphoton (b) fluorescence excitation and detection.

Optical tweezers or single beam gradient optical traps came in 1986 in the hands of Arthur Ashkin (following a lunch-table conversation among Ashkin, Steven Chu and others at the Holmdel Cafeteria in Bell Labs NJ) [10] and today, optical tweezers have far reaching applications like measuring tiny forces exerted by molecular motors that drive vital processes inside a live cell [11]. In Figure 2, we show the ray-optics diagram⁵ of optical tweezing by making use of the gradient force of a tightly focused Gaussian beam (i.e. having transverse Gaussian intensity profile). Using optical tweezers one can manipulate the centre-of-mass motion on a trapped object at will. Also, by changing the light polarisation or changing the beam profile it is possible to exert a torque on a trapped object [12] and thereby control its rotational motion.⁶

Figure 2.

[Colour online] Physics of optical tweezing. The laser beam paths are shown as bent (red) arrows, exerted forces on particle as straight (blue) arrows and the resultant force as dashed (green) arrow and the centre of the propagating beam is shown as dashed (black) line (note that different thickness for lines are used to distinguish relative photon numbers or magnitude of forces.).

1.2. Spatiotemporal control

In going forward with our discussion, by ‘spatial control’ we essentially mean control over the spatial resolution in (fluorescence) microscopy, or a control over spatial manipulation through optical trapping. The first issue is addressed in super-resolution microscopy where fluorophores are selectively turned on/off in a targeted or stochastic fashion.⁴ Spatial manipulation, i.e. controlling the translational motion, becomes important when we consider having control over external degrees of freedom in condensed phase at the single molecule level. This is because one of the crucial criteria in single molecule spectroscopy is to immobilise the molecules under study. Note that although radiation pressure has been found to exert force on single molecules in solution [13], trapping of objects having molecular dimension is still to be explored. Since optical forces are largely dependent on the spatial modes of the laser beam, spatial manipulation demands the optical field to be shaped in space.⁷

Temporal control in fluorescence refers to controlling fluorescence quantum yield of a fluorophore or selective excitation of a particular fluorophore in presence of other fluorophores. Since fluorescence is an optical relaxation of an excited electronic state, (incoherent) control over excited state population dynamics, in turn, imparts control over fluorescence. Studying ultrafast dynamics involving the excited state photo-physics of a fluorophore has been studied in several dynamical techniques with applications in microscopy, e.g. fluorescence up-conversion [14], fluorescence Kerr gating [15] and stimulated emission [16,17]. Alternatively, quantum (coherent) control methods [18-20] with laser pulse shaping [21] have been used for selective excitation of fluorophores to differentiate nearly identical fluorophores in condensed phase [22-24]. Such approaches have also been extended to applications in fluorescence microscopy [25-28] (and also other microscopic techniques, e.g. in coherent anti-Stokes Raman scattering or CARS microscopy [29]).

We may now logically think of combining any type of spatial control schemes to any of temporal control schemes to achieve ‘spatiotemporal control’ as described in Figure 3. For example, Aeschlimann et al. have recently combined photoemission electron microscopy (PEEM) with polarisation pulse shaping to achieve nano-scale ultrafast control [30] and Silberberg group have demonstrated spatiotemporal coherent control where spatial variation of the pulse shape is mapped in nonlinear interactions [31]. The specific strategies for spatiotemporal control pursued in our lab are highlighted in Figure 3 which illustrates the central theme of this account.

Figure 3.

[Colour online] Various approaches of spatiotemporal control: the work presented here is marked within the solid circle.

1.3. Structure of this review

In this review, first we focus on the issue of dynamical control in fluorescence microscopy in Section 2. Section 2.1 presents a comparative discussion on the various pulsed excitation schemes for one-photon excitation. Since this work is aimed at an application in live cell imaging, we devote a separate portion, Section 2.2, which discusses strategies to minimise photo-thermal damage during two-photon excitation. In Section 2.3, we discuss the incoherent (2.3.1) and coherent (2.3.2) control methods, respectively, for selective fluorophore excitation.

In Section 3, we turn our attention from fluorescence microscopy to optical trapping and discuss how to directly trap particles of macromolecular dimension in solution.

Finally, in Section 4, we conclude the review through a discussion on a future extension of the current work that would be capable of complete spatiotemporal control at single molecule level.

In what follows, we review the salient features of spatiotemporal control rendered through fluorescence microscopy and optical trapping based experiments. Certain subtle and further issues are elaborated under ‘Notes’. The details of the major instrumentation (i.e. laser systems, optics lay-out for fluorescence microscope and optical tweezer) as perceived in our lab has been provided in a separate section as Appendix A.

2. Spatiotemporal control in microscopy

We start our discussion on (incoherent) dynamical control in fluorescence with applications in confocal and multiphoton microscopy, i.e. spatially resolved (within the diffraction limit) temporal control. Usually, for confocal microscopy, continuous wave (CW) lasers are used; however, as we continue our discussion, we show that pulsed illumination turns out to be a better choice. On the other hand, the common use of ultrafast pulsed lasers (to facilitate non-linear absorption) for multiphoton microscopy leads to laser induced heating effects, which can be a crucial deterrence for live cell imaging and we present one approach to minimise thermal effects.

The final section focuses on selective fluorophore excitation under two sections: first by (incoherent) stimulated emission and then by quantum (coherent) control using pulse sequences. Note that, unlike quantum (coherent) control, (incoherent) population dynamics is insensitive to the phase coherence of the laser pulse (or the relative phase between pulses). These strategies, however, should not be confused with any time-resolved detection technique e.g. fluorescence life-time imaging (FLIM), which measures fluorescence life-time by time-correlated single photon counting (TCSPC) method [2,3,5,6]. Throughout this review, we investigate (incoherent as well as coherent) dynamical manipulation of the excited state population resulting in modulated time-averaged or steady-state fluorescence; each measurement was done under multiple shots with a definite excitation configuration (e.g. pulse-pair with definite delay and inter-pulse phase). Thus, unlike FILM, although the measurement was time-resolved, the detection itself was not time-resolved.

2.1. Optimal choice of pulsed excitation in one-photon fluorescence

An electronically excited molecule relaxes to the ground state via many pathways, fluorescence being just one of them. Under CW excitation, the steady state is reached where fluorescence competes with various dynamical processes, most importantly, excited state absorption (ESA), intersystem crossing (ISC) and internal conversion (IC). Naturally, to enhance fluorescence we must lessen ESA, ISC and IC rates. One possibility is to engineer novel fluorophores with high quantum yield (i.e. ratio of number of fluorescence photons to the total number of absorbed photons) having intrinsically low ISC or to add triplet state quencher that can arrest triplet-triplet transition. However, since our goal was to maximise fluorescence through optical means from a given fluorophore with fixed quantum yield, our obvious choice was to use pulsed instead of CW illumination so as to avoid attaining steady state.

Pulsed illumination is characterised by two parameters: one is the pulse-width, i.e. the duration of a light pulse and the other is the pulse repetition rate, i.e. inverse of the time lag between two successive pulses. These two pulse parameters dictate how, for a given time-averaged power, the instantaneous pulse intensity (i.e. pulse energy per unit time per unit area) varies. Taking into consideration the photo-physics of an electronically excited molecule, it becomes evident that the optimal excitation pulse should have a pulse-width less than its excited state radiative life-time (≥1 ns) so that the fluorophores can undergo a single photo-physical cycle within the pulse duration (ideally a ‘δ-pulse’ in time). Similarly, the pulse-to-pulse time-lag should be such that the excited molecules relax to the ground state before the next pulse arrives; the slowest of these relaxation processes is the triplet state relaxation (≥1 μs). Thus, excitation pulses with 1 ns pulse-width at a repetition rate ≤1 MHz may be anticipated to be optimal for rhodamine 6 G, which was the bench-mark fluorophore in our studies. In fact, such an excitation scheme has been shown to enhance fluorescence in microscopy named as ‘T-Rex’ excitation scheme in microscopy (that allows complete triplet state relaxation) [32] (as well as at single molecule level [33]). However, this low pulse repetition rate is incompatible with high-speed scanning microscopy as well as for attaining better signal-to-noise ratio. An alternative ‘bunch-pulse’ excitation has been proposed where each pulse-bunch consists of a few pulses (at 25 ns interval), while keeping the separation between consecutive pulse-bunches compatible for near-complete triplet state relaxation [34].

We explored the effect of laser pulse-widths on fluorescence enhancement over a wide range of time-scales, ranging from milli- to nano-seconds [35]. The variable width laser pulses were generated by blanking a 532 nm CW laser output with optical modulators or using a 532 nm nanosecond laser. For sub nano-second pulse effects, an ultrafast oscillator was used. We compared the time-averaged or steady-state fluorescence intensity under the same time-averaged laser power (~10 mW) but with different pulse-width/repetition-rate combinations; the fluorescence intensity values were obtained by integrating the area under each fluorescence spectrum using a fixed base-line while the spectrometer integration time was set to be >100 ms. The laser beam was focused with a 0.5 NA objective producing ~100 μm² spot size. Note that, for confocal microscopy applications the time-averaged laser power is kept much lower (≤1 mW) as one can easily get a diffraction-limited spot size (≤1 μm²) using a high NA objective.

We observed only a little enhancement of fluorescence for milli- and micro-second pulsed illumination in comparison to the CW laser excitation. This fluorescence enhancement was attributed to a reduction in the light-induced sample heating effect (see further discussions under Section 2.2). Thus, pulsed xenon lamps were shown to lessen photo-damage in comparison to continuous illumination due to reduced heating of the sample [2]. Similarly, millisecond pulsed illumination by LEDs have been reported to reduce photo-bleaching (as well as photo-toxicity) [36-38]. However, we observed major fluorescence enhancement for nanosecond (~100 ns) illumination as shown in Figure 4 [35]. At this point, we can generalise: as long as the pulse repetition rate is compatible with triplet-state relaxation time-scale (≤1 MHz), an increase in repetition rate results in an increase in fluorescence, since the peak power is reduced, which results in reduced pulse-saturation (i.e. ground-state depletion) and reduced ESA. It is worthwhile to mention here that this can also explain the reduced photo-bleaching (as well as photo-toxicity) effects in ‘controlled light exposure microscopy’ (CLEM) that exploits a programmable acousto-optic modulator [37].

Figure 4.

[Colour online] R6G fluorescence enhancement with nanosecond pulsed illumination (a) from the Corona laser (120 ns pulses at 1 and 10 kHz) and (b) using the AOD (150 ns pulses at 500 kHz) compared with that under CW illumination at same average power.

Femtosecond excitation generally leads to ‘photo-bleaching’ of the fluorophores (by pulse-saturation and ESA) due to high peak intensity. A ~100 fs pulsed illumination at ~100 MHz repetition rate produces ~1 GW/cm² peak intensity under our experimental condition. We can minimise photo-bleaching if we probe wavelength regions with quite low absorption cross-sections or fluorophores with low quantum yield [39].⁸ For this, we employed ~100 fs excitation at ~100 MHz repetition rate centred on ~400 nm by using second harmonic of a Ti:saph laser. Under these conditions, apart from higher signal-to-noise ratio, an additional advantage is that radiative relaxation (i.e. fluorescence) completes within the ≥10 ns time lag between successive pulses [39-42].⁹

2.2. Understanding photo-thermal effect during two-photon absorption

Two-photon absorption (TPA) [43,44] is a third-order (χ⁽³⁾) nonlinear optical phenomenon where two-photons are absorbed (mediated by ‘virtual states’) by an atom or a molecule. Of special importance to us has been the study of light induced heating or ‘photo-thermal’ effects during TPA, which is one of the demerits of TPA based studies. Down-conversion of absorbed light to heat is common in one-photon absorption and this has been well-studied by ‘thermal lens spectroscopy’ [45]. However, the use of very high instantaneous peak power laser pulses to circumvent low TPA cross-section, leads to heating of the transparent (i.e. with very low linear absorption) solvent, often resulting in adverse effects in experiments with live specimens.

One of the advantages of using femtosecond Ti:saph lasers in TPA studies is that there is negligible linear absorption by water and several organic solvents at ~800 nm. Despite this, due to the gigantic peak power of femtosecond laser pulses, it has been shown that higher order absorption by these solvents at ~800 nm may lead to thermal nonlinearity. This thermal nonlinearity would corrupt the measure of the optical nonlinearity that is being probed, and hence, special care needs to be taken to de-couple the pure optical nonlinear effects from thermal effects [46,47]. Now, since optical nonlinear response is almost instantaneous while thermal nonlinear response is a rather slow process (due to the cumulative effect of myriads of laser pulses rather than being a single pulse effect), pure optical nonlinearity can be retrieved using a high-speed shutter (e.g. by blanking the beam with an optical chopper having ≥50:1 mark-to-space ratio) and following the rise/fall time of the signal. However, using a mechanical chopper with 1:1 mark-to-space ratio (i.e. 50% duty cycle), we can effectively remove this effect as evident from the two-photon absorption and two-photon fluorescence studies discussed below.

2.2.1. Z-scan studies

The probability (or rate) of any nonlinear process that depends on the nth power of intensity (I, expressed in units of photons cm⁻² s⁻¹) can be expressed as

$$P=\frac{{\sigma }_n\left(\lambda \right)}{n}I{\left(\lambda \right)}^n,$$

where σ_n is the n-photon absorption cross-section (which has dimension of area for one photon absorption i.e. n = 1 only). For TPA, the dimension of σ₂ is cm⁻⁴ s⁻¹ (photon)⁻¹ and we take 10⁻⁵⁰ cm⁴ s⁻¹ (photon)⁻¹ as the unit GM (to honor its inventor, of TPA cross-section. This can be measured by the ‘z-scan technique’. In a z-scan measurement [48,49] a single light beam is focused by a lens and the sample is moved across the focus. The total transmitted light is collected by another lens focusing the beam on a photo-detector. From this transmittance measure, we can calculate the nonlinear absorption, which is connected to the imaginary part of the nonlinear refractive index by Kramers–Kronig relationship of the sample.¹⁰ Following Sheikh-Bahae and co-workers [48] for a focused Gaussian beam (i.e. having a Gaussian transverse intensity profile) the transmittance, under ‘thin cell approximation’ (i.e. the sample thickness, L, is at least an order of magnitude smaller than the Rayleigh range), may be expressed in an analytic form. So, by fitting the data points for transmittance values, we can get the TPA cross-section values. In our particular case, we calibrated our set-up by taking the well-accepted TPA cross-section value of R6G as 15.6 GM [50]. Once calibrated as specified, the TPA cross-sections for several novel chromophores were measured [51,52].¹¹ While calibrating, we also experimented with the effective removal of thermal nonlinearity under 1:1 blanking [53,54]. This essentially means minimising the omnipresent thermal effect of cumulative pulses in case of high repetition rate (HRR, typically 10–100 MHz) lasers. When the excitation beam from such a laser is chopped at a few kHz frequencies (depending on the focusing parameters), we found that the z-scan traces become more symmetrical and fit better to the ideal Gaussian beam z-scan model presented above. The resulting TPA cross-section measurements from such experiments using HRR laser (with blanking) tend to asymptotically approach the ideal TPA cross-section measured with low repetition rate (≤1 kHz) laser (without blanking); this is shown in Figure 5(a). This led us to pursue photo-thermal effect in fluorescence experiments as described below.

Figure 5.

[Colour online] Effective removal of photo-thermal effect by blanked-excitation as evidenced from (a) open-aperture z-scan trace of [Ru(bpy)₂]Cl₂ in DCM at 770 nm and (b) fluorescence enhancement of R6G at 780 nm.

2.2.2. Two-photon fluorescence studies

Apart from the built-in depth resolution, TPA induced fluorescence microscopy or two-photon fluorescence (TPF) microscopy is advantageous since the near infra-red wavelengths can penetrate deep inside tissues making subcutaneous fluorescence detection possible [55].¹² Also, the wavelength range (~680–1080 nm) accessed by modern mode-locked Ti:saph lasers nicely matches the TPA spectra of almost all fluorophores.

We investigated the change in time-integrated TPF intensity while blanking the excitation [56] (along with microscopy applications [57]). As discussed before (Section 2.1), we investigated the dependence of time-averaged or steady-state fluorescence intensity on blanking frequency at 300 mW time-averaged laser power (i.e. using a 600 mW laser power with 1:1 blanking); the fluorescence intensity values were obtained by integrating the area under each fluorescence spectrum using a fixed base-line while the spectrometer integration time was set to be >100 ms. The laser beam was focused it with 0.5 NA objective producing ~100 μm² spot size. Three characteristic features were noted from the intensity analysis of the plot shown in the Figure 5(b). First, by blanking the excitation total fluorescence intensity is greatly enhanced (nearly two-fold, which is evident from the square-dependence of absorption on the input intensity [57]) as compared to the un-blanked excitation with same average power (300 mW). Second, the total fluorescence intensity gradually builds up with the blanking frequency with a characteristic time constant before flattening [56]. Third, and the most importantly, the nature of this variation with chopper frequencies neither depends on the solute concentration nor on the average laser power, as long as the power levels are below the pulse-saturation level. Furthermore, similar time scale was observed when we changed the solute (from rhodamine 6 G to rhodamine B) keeping the solvent (methanol) the same. These findings immediately suggest that, as before, solvent heating due to higher order nonlinear absorption is the main source of fluorescence quenching. Thus, due to heating, the solute molecules rapidly lose energy via collision-induced non-radiative relaxation.¹³

It should be noted, however, that 1:1 chopping (i.e. chopping at 50% duty cycle) does not remove photo-thermal effect completely. Theoretical and experimental studies in this direction [46,47] suggest that for a complete removal of photo-thermal effect, the ratio between exposure time to dead time must be roughly 1:50 or more (depending on the experimental condition and the system under study). The rise of fluorescence signal with characteristic time scale and final flattening suggests that 1:1 blanking leads to a new thermal steady-state, where the photo-thermal effect can be considered to be effectively removed although not quite completely.¹⁴ Interestingly, however, for many experimental situations, such an effective removal can suffice the experimental needs as they may as well have reached the experimental signal-to-noise limit.

In a two-photon fluorescence laser-scanning microscopy (TPF-LSM), HRR oscillators are used and the image acquisition is done with point-by-point illumination resulting in pixilated image construction. The high scanning speed (obtained by scanning with a pair of mirrors as in our FV300 microscope system, or with a ‘Nipkow disk’) ensures laser dwell time on each pixel over very small time window (~1–10 μs). Therefore, although the use of HRR lasers suffers from photo-thermal effect, this is not prominent under fast scanning conditions because each pixel is illuminated for a time period not sufficient for building up the photo-thermal effect. Comparing this with a flow cell where the molecules are rapidly swept across the focused laser beam fixed in space, in LSM, a pair of scanning mirrors quickly switches the focused laser beam among ‘spatially frozen’ molecules located at different regions in the sample. Thus, HRR oscillators cause reduced photo-thermal effect in LSM.

2.3. Selective fluorophore excitation

So far we have discussed the optimal choice of illumination in one- and two-photon excitation for maximum fluorescence output with minimal photo-thermal damage. We now start our discussion on selective fluorophore excitation. It should be noted that identical fluorophores can be separated based on the dependence of fluorescence life-time on local environments, which is the working principle for FLIM [2,3,5,6] and this has application in addressing fluorophores localised at different regions of the sample. In contrast, our aim was to distinguish between two (or more) different types of fluorophores by selectively turning on/off of either of them, which is crucial for distinguishing co-localised nearly-identical fluorophores.

For one-photon excitation, selective excitation is not a critical issue as one can use different narrow band laser lines tuned to the sharp one-photon absorption maxima of different fluorophores (as long as the fluorophores do not have nearly identical absorption profiles). Contrary to this, in two-photon excitation the broad overlapping two-photon absorption spectra of commonly employed fluorophores and the large spectral bandwidth of a short pulse (employed to circumvent the low TPA cross-sections of common fluorophores) lead to simultaneous excitation of many fluorophores, which justifies a persistent demand for selective excitation of individual fluorophores. We, therefore, begin our discussion with (incoherent) dynamical control in TPF-LSM to distinguish quite different fluorophore pairs (DAPI/Mito-tracker Red and DAPI/Texas Red) followed by quantum (coherent) control strategies to distinguish similar fluorophores (rhodamine-6G/fluorescein).

2.3.1. Selective fluorescence suppression by one-colour stimulated emission

Literature survey [5] shows that at ~730 nm, certain pairs of dyes from e.g. DAPI (blue fluorophore staining nuclei) and Texas Red-X phalloidin (red fluorophore staining mitochondria) or DAPI and Mito Tracker Red CMXRos (red fluorophore), are simultaneously excited by TPA, which make these fluorophores a perfect choice for our selective excitation experiments. Among these fluorophores, fluorescence from Texas Red extends up to ~750 nm, immediately suggesting the possibility of its fluorescence suppression by stimulated emission; while on the other hand, fluorescence from Mito Tracker Red almost dies out ~750 nm [www.invitrogen.com].

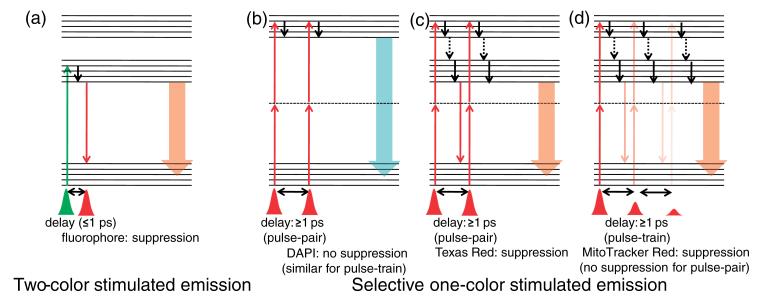
In conventional experiments that utilise stimulated emission [16,17], light pulses of two different colours are used, as shown in Figure 6(a). After excitation by a pump pulse, the population rapidly relaxes to the ground vibrational state of the excited state; a time-delayed dump pulse, wavelength-tuned to the red edge of fluorescence, sends the population back to the ground electronic state by stimulated emission and thus fluorescence is suppressed. Fluorescence, being an incoherent emission, is omni-directional. Stimulated emission, on the other hand, is a coherent process and, as such, photons generated by stimulated emission travel in the direction of the stimulating beam. So, if we collect only the back-scattered fluorescence (epi-fluorescence) there is suppression in fluorescence signal as is with ‘ultrafast dynamical microscopy’ [16]. Note that, in an experiment by Xie group [17], the forward scattered photons were collected and thus, a gain in total measured signal was observed due to stimulated emission turning the weakly fluorescent molecules into suitable candidates for microscopy applications. In contrast to this, we used one colour excitation scheme as shown in Figure 6(b)–(d).

Figure 6.

[Colour online] Excitation scheme for stimulated emission commonly employed (a) in comparison to that used in one-colour pulse-pair and pulse-train methods described here (b)–(d). The excitation and stimulated emission are shown as upward and downward thin arrows, respectively, while fluorescence is shown as broad downward arrow; the colours are chosen to specify the different wavelengths. Little downward black arrows indicate either vibrational relaxation (solid) or internal conversion (broken).

Based on our earlier observation [58,59], we used pulse-pair excitation (Figure 6(b), (c)) employing a Mach-Zehnder type interferometer for selective fluorescence suppression [60,61]. Here, the first pulse causes a TPA for both DAPI and Texas Red; the time-delayed second pulse causes similar TPA as the first pulse does but, in addition, may dump the population by (one-photon) stimulated emission if the red edge of fluorescence coincides with the excitation wavelength. This happens to be the case with Texas Red. We found that interesting control strategies can be implemented even within a time window of 100 fs as shown in the region of 0.9 ps to 1.0 ps at 5 fs step-size as evidenced from the suppression of Texas Red fluorescence in comparison to that of DAPI fluorescence as shown in Figures 7(a) and 8(a) [60,61].

Figure 7.

[Colour online] Relative fluorescence intensity modulation of DAPI/Texas Red (a) and DAPI/Mito-tracker Red (b), (c) under one-colour pulse-pair (a, b) and pulse-train (c) excitation.

Figure 8.

Fluorescence suppression of Texas Red (a) and Mito-tracker Red (b) relative to DAPI as a function of time delay between pulses under one-colour pulse-pair (a) and pulse-train (b) excitation.

Similar excitation scheme does not work for DAPI/Mito-tracker Red pair (Figure 7(b)) which led us to further extend our idea of pulse-pair excitation to pulse-train excitation scheme (Figure 6(d)); this was employed by a Fabry-Perot etalon, where the delay between the successive pulses in a pulse-train was varied from 20 ps (corresponding to the minimum possible delay constrained by the physical separation between two mounts holding a pair of beam-splitters) to 50 ps in steps of 1 ps. The possible explanation for the higher efficiency of pulse-train excitation over pulse-pair excitation may be drawn out as follows [62]: since the intensity of successive pulses in a pulse-train decrease in geometric progression, both two-photon absorption and stimulated emission is decreased but the former decreases much more (due to square dependence on intensity) than the latter (which depends linearly on intensity). An analogy may be drawn with the ‘batch extraction’ process, where a solute is partitioned between from one solution to a new extracting solvent more efficiently when the same amount of solvent is used several times for the extraction than being used just once. Thus, the pulse-train excitation leads to better suppression than pulse-pair excitation. We found noticeable fluorescence suppression of Mito-tracker Red relative to DAPI, as shown in Figures 7(c) and 8(b), which we did not observe in the pulse-pair experiment in 20 ps to 50 ps range (Figure 7(b)) [62].

A crucial point to note in one-colour stimulated emission (Figure 6(c) and (d)) as compared to the conventional two-colour counterpart (Figure 6(a)) is that in the former, TPA excites the red fluorophores to energetically higher electronic states. Thus, population relaxation (to the state from which the stimulated emission occur), involves not only the fast (≤1 ps) vibrational relaxation but also rather slow (≥100 ps) internal conversion. This is precisely the reason for the observed fluorescence suppression at a long pulse-pair delay (up to several tens of picoseconds delay) [60-62].

2.3.2. Fluorophore discrimination by quantum interference

As mentioned in Section 1.2, quantum (coherent) control methods [19-21] using laser pulse shaping [22] has been utilised for selective fluorophore excitation [22-27]. In laser pulse shaping, a grating-spherical/cylindrical lens combination (or a grating-concave mirror combination or just a concave grating to eliminate chromatic aberration) leads to maximum spatial separation of the spectral components in a plane (‘Fourier plane’) and subsequent recombination using another grating-spherical lens combination. Any modulation in the spectral components, spatially arranged in the Fourier plane, translates to the temporal modulation of the pulse owing to the inverse time-frequency Fourier relationship of a mode-locked ultrafast laser pulse [63]. Usually, a spatial light modulator or SLM (or simply a spatial mask [64]¹⁵), kept at the Fourier plane, modulates the phases and/or amplitudes of various frequency components within a pulse and thereby, gives a pulse shaped in time. By using a programmable SLM, one can generate pulses of various shapes and iteratively search for the optimal pulse shape by using learning algorithms where a series of experiments are carried out in a feedback loop until the optimal condition is reached [65].¹⁶ Equivalent to pulse shaping, control over the time delay between a pair of pulses with definite inter-pulse phase relation can manipulate the excited-state population and hence may result in selective fluorescence emission/suppression. This is known as wave-packet interferometry or WPI and was first demonstrated by the Fleming group for vibrational wave-packets [66,67], which is also known as ‘phase-locked spontaneous light emission’ [68].¹⁷

In this specific case, the time delay between pulse-pairs (which corresponds to the time delay between the centres of two pulse envelopes) is directly related to the relative phase between them (with respect to a reference carrier-frequency oscillation). When one pulse is finely delayed with respect to the other pulse precisely in an interferometer, the relative phase between them is periodically modulated; the fluorescence interferogram consists of a rapid interferometric oscillation (known as ‘Ramsey fringe’) with a slow oscillating envelope and these two oscillations can be decoupled by ‘phase-locking’ [66,67].¹⁸ The slow oscillation of the envelope outside the two pulse overlap zone is due to survival of phase coherence over longer time scale.

In condensed phase, decoherence induced by fluctuating environment (as well as dephasing due to ensemble averaging) renders loss of phase coherence outside two pulse overlap zone. Thus, quantum interference between two molecular wave-packets does not survive longer than optical interference (between two light wave-packets i.e. light pulses). However, far away from the ‘zero-delay’ (where optical interference dominate), we can just follow the rapid interferometric oscillation at partial pulse-pulse temporal overlapping zone (where quantum interference takes over) [69], and fluorophores can be discriminated based on this oscillation only sans phase-locking [70]. In Figure 9, fluorescence from rhodamine 6G and fluorescein are shown to oscillate in an anti-correlated fashion, which is a very simple demonstration of fluorophore discrimination based on just tracing the quantum interference signal. One necessary requirement to observe this oscillation in an interferometer is fine delay lines (with resolution on the order of λ/100 or better); this method can be extended to microscopy applications provided that phase stability is maintained over image acquisition time [70]; e.g. using a pulse shaper.¹⁸

Figure 9.

[Colour online] Out-of-phase oscillations of rhodamine 6G (b) and fluorescein (c) fluorescence compared with the interferometric autocorrelation fringe (a) at partial pulse-pulse temporal overlapping region (around −100 fs delay).

3. Spatiotemporal control in optical trapping

In Section 2, we discussed dynamical control strategies that are spatially resolved (within diffraction limit) by fluorescence microscopy. We now turn our attention to optical force microscopy and discuss the issue of spatial manipulation of single molecules. Our discussion is based on harmonic traps created by a Gaussian transverse laser beam profile (Figure 2) although we experimented with flat-top beam as well [71].¹⁹ Force calibrations were done using usual viscous drag and Brownian fluctuation-based methods [11], in addition to a much simpler approach of intensity-modulating the trapping beam [72].²⁰

3.1. Stable trapping of nano-particles

As mentioned in Section 1.1, nano-scale biological manipulation inside a live cell has been rendered through optical trapping. In such experiments, usually a macro-molecule, few nanometers in dimension, is tethered to a micron-sized bead which is trapped and the process can be observed in far-field microscopy. The forces thus measured are never the true forces acting on the single molecules which demands trapping without tethering. Although direct trapping of such objects (dimensionally, nearly similar to macro-molecules) have been demonstrated using CW laser beam, it demands the use of quite high average powers [13]. In the ‘Rayleigh scattering limit’ or the ‘dipole limit’ (when particle dimension is at least an order of magnitude smaller than the wavelength of light), the trapping force is given by

$$F=(\alpha ∕2)\nabla E^2,$$

where α is the polarisability and E is the electric field of trapping light. Since the force depends on the polarisability, earlier efforts [73] revealed that much higher power levels are required to stably trap latex nano-particles; the exertable force was found to be smaller for latex nano-particles than for gold nano-particles, making the former a poor choice for nano-scale applications. Also, as the size of the particle is reduced, the Brownian motion becomes rapid rendering them hard to be held over time.

We found TPF detection was more advantageous than detection based on back-scattering; this is because TPF, being confined only within focus, is background-free and any persistent fluorescence signal corresponds only to the trapped particles that can be observed despite the presence of many other out-of-focus particles within the cone of illumination [74].²¹ Based on the previous theoretical work by Wang and Zhao [75] and experimental work by Amberadkar and Li [76], which discuss the role of instantaneous pulse intensity, we tried to directly trap 100 nm latex (polystyrene) nano-particles with femtosecond pulsed excitation at a low average power [77]. For 100 nm particles, stable trap was observed when the average power was elevated to ~30 mW as shown in Figure 10(a). It was also clearly possible to show trapping of a single particle followed by another one; the relative strength of fluorescence has nearly a 1:2 ratio (after background subtraction), which confirms the number of trapped particles (the spikes with larger heights are due to other particles rapidly diffusing across the focal volume). Since the dimension of the focal volume dimension (nearly diffraction limited focal volume created by ~0.8 μm light) is nearly much larger than the dimension of the particles (0.1 μm), the focus can accommodate many particles at a time (since the volume is nearly three orders of magnitude larger), which is the cause of accumulation of particles in the trapping zone. Similar trapping with CW excitation was observed (by observing back-scattering signal) at much higher average power (≥200 mW). For Q-dots as well, we observed stable trapping as evident from Figure 10(b) [78,79], albeit a low signal-to-noise level.

Figure 10.

[Colour online] Two-photon fluorescence for trapping of (a) 100 nm particles and (b) 10–20 nm Q-dots. The red line in the (a) panel is a guideline for sequential trapping of two particles.

The role of instantaneous pulse power may be explained as follows. Owing to its fleeting temporal existence, a femtosecond laser pulse has gigantic (instantaneous) peak power compared with its time averaged power; the typical ratio between them being 10⁵:1. The high photon flux increases the trap stiffness (or force constant) to such an extent that a stable trap is observed at the same average power level of CW lasers that cannot trap nano-particles. In the ‘Mie scattering limit’ (when particle dimension is at least an order of magnitude larger than the wavelength of light), Brownian motion is sluggish and a shallow potential well (created by a CW or time-averaged pulsed laser) is good enough to trap the nanoparticles. In contrast, a rapidly moving Rayleigh particle cannot be trapped with a shallow force field, but it can be efficiently trapped when the well depth is steep, provided the particle does not diffuse away within the time period of the periodic force field. Thus the pulse repetition rate turns out to be a crucial factor for stably trapping Rayleigh particles. Fortunately, the ~13 ns time lag between two consecutive pulses (inverse of 76 MHz) is too short for the already trapped particle to leave the trapping region [77-79].

To realise the effects of instantaneous forces, we must design an experiment that can sense the difference between CW versus pulsed excitation, and one such experiment is trapping of Rayleigh particles as the random Brownian motion of a tiny Rayleigh particle is sensitive to the instantaneous force field. However, when we measured the trapping forces on micron-sized beads by viscous drag method, we found no difference between trapping efficiencies under CW and pulsed illumination as has also been reported by others [80,81]. This fallacy lies in the fact that both viscous drag as well as the fluctuation based methods involve much slower time scales compared to the interaction time (or pulse-width) of a femtosecond light pulse and hence, the effect of individual pulses are completely washed out. Such experiments, therefore, furnish information only on cumulative force exerted by many pulses, which may be computationally obtained by sampling over many pulses and experimentally, only the average power appears to be the deciding factor [80-82]. This is precisely the reason as to why no effect of pulse chirping on trapping efficiency has been reported [81]. A realistic approach will be to calibrate the instantaneous force exerted by a single pulse, which has been hitherto rendered un-achievable although its effect has been realised experimentally [71,77-79].²²

4. Conclusions and future directions

We have reviewed temporal and spatial control strategies in fluorescence microscopes and optical tweezers. We have shown how pulsed illumination turns out to be a superior choice than the conventional CW illumination in (one-photon) confocal fluorescence microscopy. For two-photon absorption, we have shown how solvent induced photo-thermal effect affects solute absorption and fluorescence, which can be largely removed by blanking the excitation beam (and successfully applied in microscopy). Our experiments on pulse-pair and pulse-train control mediated by stimulated emission have interesting applications in microscopy. The simple quantum control method based on precisely following the fluorescence interferogram has been demonstrated for fluorophore discrimination. Finally, we have demonstrated the role of gigantic instantaneous peak power of an ultrafast pulse excitation (at low average power) to efficiently trap objects of macromolecular dimension.

A schematic of the optical lay-out designed for spatiotemporal control is shown in Figure 11 (see Appendix for detail); although we modified the experimental set-ups from time to time, a generalised lay-out is presented. An ideal experiment will be shaping the pulses both in time/frequency as well as space domains. Thus all degrees of motion of a single molecule can be envisioned to be spatiotemporally controlled at will.

Figure 11.

[Colour online] Schematic of the experimental set-up; the excitation path is shown as red (720–980 nm) or green (532 nm) arrows while the fluorescence (550–650 nm) collection paths are shown as orange arrows.

Appendix A: specific instrumentation

A.1. Laser systems

Overall, five different lasers were used in different experiments. The first one (Verdi5, Coherent) is a diode pumped continuous-wave (CW) Nd:vanadate laser with built-in second harmonic (532 nm) generation (maximum 5 W laser power), which was used for one-photon fluorescence experiments. Optical modulators were used to get desired pulsed output from this laser.

Another Verdi5, pumped (in the ‘side-on pumping’ mode) a Ti:saph (abbreviation for ‘titanium sapphire’) laser oscillator (Mira900-F, Coherent) producing ≥100 fs pulsed near infra-red (NIR) excitation tunable from 720–980 nm and having 76 MHz pulse repetition rate.

The other femtosecond oscillator used is a (home-built) mode-locked Ti:saph laser (TS laser kit, KM Labs) pumped in a similar fashion (by another Verdi5) and producing as short as 20 fs pulses centred at 800 nm (having a spectral bandwidth as high as 50 nm) with 94 MHz repetition rate.

For confocal imaging, the 488 nm CW beam from an argon-ion laser (IMA 10X, Melles Griot, Albuquerque, NM, USA) was used (mostly for alignment purpose within the microscope scan-head).

We also used a Q-switched Nd:YAG laser (Corona, Coherent), producing 120 ns pulses at 532 nm and the pulse repetition rate can be tuned from 1 to 25 kHz.

Figure A1.

[Colour online] Schematic of the microscope system; the excitation path is shown as red (720-980 nm) or blue (488 nm) arrows while the fluorescence (spanning visible wavelength) collection paths are shown as green arrows.

A.2. Microscope system

Our imaging system is a commercial multiphoton-ready confocal microscope (FV300 coupled with IX71, Olympus): a schematic of which unit is shown in Figure A1. All images were taken using an oil-immersion objective (UPlanApoN 40X 1.4 NA, Olympus). The image acquisition and intensity counts were performed using FLUOVIEW software. For (one-photon) confocal microscopy we used the IMA 10X (mostly for alignment purpose within the microscope scan-head) or the second harmonic of MIRA 900 F (at 400 nm) while for two-photon microscopy we used ~730 nm excitation from MIRA 900 F.

A.3. Tweezer system

A schematic of the tweezer set-up is shown in Figure A2. We used the MIRA 900 F laser tuned at 780 nm producing ~120 fs mode-locked pulsed excitation (at 76 MHz pulse repetition rate); the laser was also operated in CW mode. The 780 nm pulsed excitation simultaneously traps and generates backscattered (under both pulsed and CW modes) as well as fluorescence signals (only under a pulsed mode). The expanded laser beam, shown as a solid (red) line, was passed through a telescopic arrangement along with two steering mirrors and sent to the microscope objective (UPLSAPO 1.4 NA 100XO, Olympus) of a completely homemade bench-top inverted microscope. A dichroic mirror, placed just before the objective lens, has ~95% reflectance at 780 nm; at the same wavelength the objective transmits ~65% yielding ~60% of the light at the sample. The two-photon induced fluorescence, shown as a solid (green) line, as well as the backscattered light, shown as a dashed (red) line, was collected by a photomultiplier tube (PMT) using appropriate band-pass filters. The PMT signal was collected by an automotive oscilloscope or picoscope (Pico Technology; or, alternatively, a lock-in amplifier, SR830 DSP, Stanford Research Systems) triggered by the rotating-disk optical chopper. The chopper was introduced for lock-in signal collection; the frequency of chopping was varied and fixed at the optimised position (799 Hz). Thus, our robust setup is capable of measuring the two-photon fluorescence as well as the backscattered light to observe trapping of fluorescent particles in real time. Also a CCD camera (350 K pixels, e-Mark Inc.) was used for video microscopy by bright-field illumination’ shown as wide (gray) line and dark-field (two-photon) fluorescence generation. This illumination scheme (see inset of the schematic in Figure A2), invented by August is used to uniformly illuminate a sample by an extended source; this can alternatively be done by delivering light through an optical fibre where the fibre tip acts like a point source and is known as ‘critical illumination’. Also, the power and area of illumination at the focal plane can be controlled at will.

Figure A2.

[Colour online] Schematic of the tweezer set-up.