An experimental and kinetic investigation of premixed furan/oxygen/argon flames

Abstract

The detailed chemical structures of three low-pressure (35 Torr) premixed laminar furan/oxygen/argon flames with equivalence ratios of 1.4, 1.8 and 2.2 have been investigated by using tunable synchrotron vacuum ultraviolet (VUV) photoionization and molecular-beam mass spectrometry. About 40 combustion species including hydrocarbons and oxygenated intermediates have been identified by measurements of photoionization efficiency spectra. Mole fraction profiles of the flame species including reactants, intermediates and products have been determined by scanning burner position with some selected photon energies near ionization thresholds. Flame temperatures have been measured by a Pt-6%Rh/Pt-30%Rh thermocouple. A new mechanism involving 206 species and 1368 reactions has been proposed whose predictions are in reasonable agreement with measured species profiles for the three investigated flames. Rate-of-production and sensitivity analyses have been performed to track the key reaction paths governing furan consumption for different equivalence ratios. Both experimental and modeling results indicate that few aromatics could be formed in these flames. Furthermore, the current model has been validated against previous pyrolysis results of the literature obtained behind shock waves and the agreement is reasonable as well.

1. Introduction

The interest for studying the gas-phase reactions of biofuels, mainly alcohols, ethers and biodiesels, has increased in recent years because they offer the long-term promise of fuel-source regenerability and reduced climatic impact [1]. In engine tests, Avantium Company demonstrated that furan-based biofuels, or “furanics” were potential biofuels and had significant advantages over first-generation biofuels [2,3]. For example, 2,5-dimethylfuran (DMF) has an energy density 40% greater than ethanol, which is comparable to that of gasoline. Furan and its derivatives have also been identified among the emissions produced from the biomass burning and the combustion of fossil fuels [4-6]. Investigations with pyrolysis of leaf and wood indicate that furan is one of the major degradation products of these compounds [7]. In addition, furan has also been proved to be a significant component of tobacco smoke [8] and is selected as a model oxygenated reburn fuel for NO reduction [9]. Therefore, it is necessary to understand the combustion chemistry of furan.

Previous studies relevant to the gas phase reactions of furan were mainly focused on experiments and modeling of its thermal decomposition [10-18]. In 1972, Cullis and Norris [10] studied the pyrolysis of furan within the temperature range of 1173 – 1323 K at 1 atm. The main products observed were methane (CH₄), acetylene (C₂H₂), ethylene (C₂H₄), and benzene (C₆H₆). With a heated flow reactor and an on-line mass spectrometry (MS), Grela et al. [11] investigated the low-pressure (10⁻³ Torr, 760 Torr = 1 atm) pyrolysis of furan over the temperature range of 1050 – 1270 K and found the presence of C₃H₄ (allene, aC₃H₄/propyne, pC₃H₄) and CO. They also proposed a high-pressure Arrhenius expression k_∞ = 10^15.6exp(−73.5 kcal·mol⁻¹/RT) s⁻¹ as the rate constant for furan decomposition. Later, Bruinsma et al. [13] studied the decomposition of furan within the temperature range of 960 – 1085 K at 1 Torr. CO and C₃H₄ were identified and a very different Arrhenius equation, k = 10^12.9exp(−65.7 kcal·mol⁻¹/RT) s⁻¹, was reported. Three groups [12,14,15] carried out the thermal decomposition of furan behind shock waves. Lifshitz et al. [12] studied the decomposition of furan over the temperature range 1050 – 1460 K at gas densities of 3·10⁻⁵ mol/cm³ (2.6 – 3.6 atm) and proposed that the two main pathways of furan decomposition were due to CO + pC₃H₄ and C₂H₂ + ketene (CH₂CO). By gas chromatography/mass spectrometry (GC/MS) analysis, they identified CO, pC₃H₄, C₂H₂ and indirectly, CH₂CO, as the major products and CH₄, aC₃H₄, C₂H₄, diacetylene (C₄H₂), vinylacetylene (C₄H₄), 1,3-butadiene (C₄H₆) and C₆H₆ as minor products [12]. Based on their measurements, they obtained the rate constant k = 10^15.43±0.45exp[−(78.3±2.0) kcal·mol⁻¹/RT] s⁻¹ for the overall decomposition of furan in the temperature range 1060 – 1260 K [12]. Organ and Mackie [14] extended the temperature range to 1100 – 1700 K (20 atm) and obtained the same conclusion as that of Lifshitz et al. [12] by detecting CO, pC₃H₄, C₂H₂ and CH₂CO directly. The global rate of furan decomposition was given as k = 10^15.3±0.3exp[−(77.9±1.9) kcal·mol⁻¹/RT] s⁻¹ and the initiation was postulated to be the homolytic C-O bond scission leading to a biradical [14]. With laser-schlieren (LS) and time-of-flight (TOF) MS detection techniques, Fulle et al. [15] confirmed the two dominant dissociation channels in the temperature range 1300 – 3000 K (600 Torr) and k = 10^15.3exp[−78.7 kcal·mol⁻¹/RT] s⁻¹ was given. Later, Winkler et al. [16] investigated the continuous flow pyrolysis of furan at 1173 K (1 atm) and up to 22 products were identified by GC-MS. They suggested that aromatics were generated from C₂- and C₃- species and found no tendency for the oxygen containing fragments of furan to form larger molecules. Recently, Hore et al. [17] studied the pyrolysis of furan using a combination of infrared laser powered homogeneous pyrolysis, chemical and physical trapping of radicals and precursors specifically designed to generate selected radicals in the temperature range 950 – 1000 K (~7 Torr) and confirmed the key role of 1,2-H shifts in the theoretical studies (see discussion below). More recently, Vasiliou et al. [18] performed furan decomposition with a high-temperature nozzle as a tubular reactor. They also demonstrated the importance of (CO + pC₃H₄) and (C₂H₂ + CH₂CO) routes; however, furan could also decompose to produce propargyl radical at a temperature higher than 1550 ± 100 K [18].

Despite the numerous experimental investigations of furan thermal decomposition, there were only three theoretical calculations concerning these reactions. Liu et al. [19,20] explored the thermal decomposition of furan with density functional (B3LYP) techniques for geometries and QCISD(T) for energies. They reported the energetics of furan decomposition channels, but gave no information about rate constants. In 2000, Sendt et al. [21] obtained the thermochemistry and rate parameters of several key reactions related to furan at CASSCF, CASPT2 and G2-(MP2) levels. They proposed a detailed kinetic model and validated it against furan pyrolysis data measured by Organ and Mackie [14]; they concluded that the formation of cyclic intermediates and the formation of decomposition products (CO + pC₃H₄) initiated by 1,2-H transfer were the dominant pathways for furan pyrolysis. However, compared to such studies on the thermal decomposition of this molecule, no literature exists on its combustion.

In the present work, low-pressure premixed furan/O₂/Ar flames with three equivalence ratios (Φ) of 1.4 (flame A), 1.8 (flame B) and 2.2 (flame C) have been investigated with the molecular-beam mass spectrometry (MBMS) and tunable VUV synchrotron photoionization techniques [22-24]. Many flame species have been detected and identified by comparing the measured ionization energies (IE) with literature ones; their mole fraction profiles have been determined as well. Moreover, a detailed kinetic model has been developed based on the experimental measurements and reaction pathways were proposed with particular attention to the formation of the major intermediates.

2. Experimental Section

The experiments were performed at National Synchrotron Radiation Laboratory, Hefei, China. The instrument and data analysis procedures have been reported previously [25,26]. Briefly, the apparatus is composed of a flame chamber which contains a movable flat-flame burner (McKenna Burner) with 6 cm diameter, a differentially pumped chamber with a molecular-beam sampling system, and a photoionization chamber installed with a home-made reflectron time-of-flight mass spectrometer (RTOF-MS). Combustion species are sampled by a quartz cone with a 40° included angle and a ~500 μm orifice at the tip. The resulting molecular beam passes into a differentially pumped ionization region through a nickel skimmer, and then crosses with the tunable VUV synchrotron light in the photoionization chamber. The photoions are collected and analyzed by the RTOF-MS with an approximate mass resolution of 1400 [22]. The integrated ion intensities for a specific mass are normalized by the photon flux, and then plotted as a function of the photon energy or distance from the burner surface, which then yields photoionization efficiency (PIE) or mole fraction profiles, respectively. Considering the cooling effect of molecular beam [27], the experimental error for determining IE is within 0.05 eV for stable species and slightly higher for some radicals because of the weak signal-to-noise ratio. The uncertainties of the mole fractions are ±5-10% for the major species, ±25% for intermediates with known photoionization cross sections and a factor of two for those with estimated cross sections.

Three flames from slightly rich (Φ = 1.4, C/O = 0.538) to nearly sooting conditions (Φ = 2.2, C/O = 0.786) were investigated. Flow rates of the gas reagents are controlled separately by MKS mass flow controllers, while the flow rates of liquid fuels into the vaporizer are controlled by a syringe pump (ISCO 1000D, USA). Furan was purchased from Sinopharm Chemical Reagent Limited Co., Shanghai, China with the purity of ≥ 99.5%. No further purification was carried out for this study. The operating conditions are listed in Table 1. For comparison, the pressure was kept at 35 Torr; the flow rate of Ar has a constant value of 1.000 standard liter per minute (SLM) and the cold-gas velocity is 33.49 cm/s for all flames. The temperature profiles have been measured by using a Pt-6%Rh/Pt-30%Rh thermocouple, 0.100 mm in diameter and 15 mm upstream from the sampling cone, with an Y₂O₃-BeO anti-catalytic coating [27]. Radiation heat losses have been considered and calibrated for the temperature profiles [28], the detailed procedures of which were described in [29]. Based on the reproducibility of the measurement, the accuracy of the temperature measurements was estimated to be ± 100 K, within which the modeling results have a 3% uncertainty for the major species and about 10% for intermediates [29].

Table 1.

Flame characteristics

Flame	Φ a	Flowrate (SLM)			C/O	DM b (g/s/cm2)
		Furan	O2	Ar
A	1.4	0.328	1.053	1.000	0.538	2.526E-3
B	1.8	0.395	0.986	1.000	0.667	2.590E-3
C	2.2	0.453	0.928	1.000	0.786	2.646E-3

^aNotes: Φ refers to the equivalence ratio;

^bD_M is the mass flow rate of the gas mixture.

3. Kinetic model

To simulate the species profiles measured in the three furan flames, a new kinetic mechanism has been developed. Table 2 lists the reactions related to furan and derived species. This mechanism was coupled with our recent mechanism which has been developed for the oxidation of toluene [30]. The complete mechanism (206 species and 1368 reactions) is available as supplementary material and only the primary and secondary reaction pathways are described here. Most hermochemical data have been estimated by the software THERGAS based on group additive method [31]. Some intermediate species derived from furan and those involving a missing group in the THERGAS software were estimated by ab initio calculation. The ab initio calculations were performed at the CBS-QB3 level [32] implemented in Gaussian 03 [33]. Enthalpies of formation at 298 K have been obtained from isodesmic reactions, while thermochemical properties as a function of temperature have been calculated using the CHEMRATE software [34] according to statistical mechanical principles. Hindered rotors have been taken into account and relaxed scans have been performed at the B3LYP/6-31G+(2d,p) level to determine the barrier of rotation. Table 3 presents the names, the formulae and the enthalpies of formation (Δ_fH°) of furan and its derived species which were not presented in our previous work [30].

Table 2.

Reactions of furan and derived species

Reaction		A	n	Ea	Footnote	No.
PRIMARY MECHANISM
Reactions of furan
Unimolecular initiations by breaking of a C-O or C-H bond
Furan = FA	(P = 4.7 kPa)	6.0 × 1058	−13.388	94.0	a	(1)
	(P → ∞)	2.3 × 1012	0.416	70.891	a	(1’)
Furan = C2H2 + CH2CO	(P = 4.7 kPa)	3.8 × 1073	−17.412	113.3	a	(2)
	(P → ∞)	1.8 × 1014	0.534	86.591	a	(2’)
Furyl-2 + H = furan		1.0 × 1014	0.0	0.0	b	(3)
Furyl-3 + H = furan		1.0 × 1014	0.0	0.0	b	(4)
Bimolecular initiations
Furan + O2 = furyl-2 + HO2		2.0 × 1013	0.0	70.68	c	(5)
Furan + O2 = furyl-3 + HO2		2.0 × 1013	0.0	70.88	c	(6)
Additions and decompositions
Furan + H = C4H5O-2		2.6 × 1013	0.0	3.2	d	(7)
Furan + H = C4H5O-3		2.6 × 1013	0.0	1.56	d	(8)
Furan + OH = C2H3CHO + CHO		2.7 × 1012	0.0	−1.04	e	(9)
Methylfuran + H = furan + CH3		5.0 × 1014	0.0	8.0	f	(10)
Metatheses
Furan + H = furyl-2 + H2		8.2 × 105	2.5	12.28	e	(11)
Furan + H = furyl-3 + H2		8.2 × 105	2.5	12.28	e	(12)
Furan + O = furyl-2 + OH		1.2 × 1011	0.7	8.96	e	(13)
Furan + O = furyl-3 + OH		1.2 × 1011	0.7	8.96	e	(14)
Furan + OH = furyl-2 + H2O		2.2 × 106	2.0	2.78	e	(15)
Furan + OH = furyl-3 + H2O		2.2 × 106	2.0	2.78	e	(16)
Furan + CH3 = furyl-2 + CH4		1.4 × 100	3.5	12.9	e	(17)
Furan + CH3 = furyl-3 + CH4		1.4 × 100	3.5	12.9	e	(18)
Reactions of furyl radicals (cyclo-C4H3O)
Isomerization
Furyl-3 = furyl-2		1.5 × 1013	0.0	67.8	g	(19)
Decompositions by β-scission
Furyl-2 = CHCHCHCO		1.8 × 1013	0.341	34.511	a	(20)
Furyl-3 = CHCCHCHO		1.1 × 1013	0.306	31.215	a	(21)
Oxidations
Furyl-2 + O2 = CH2CHCO + CO2		4.5 × 1016	−1.39	1.0	h	(22)
Furyl-2 + O2 => CHCHCHO + CO + O		3.3 × 1011	−0.29	10.0	h	(23)
Furyl-3 + O2 = CH2CHCO + CO2		4.5 × 1016	−1.39	1.0	h	(24)
Furyl-3 + O2 => C2H2 + CHO + CO + O		3.3 × 1011	−0.29	10.0	h	(25)
Combinations
Furyl-2 + O = CHCHCHO + CO		3.0 × 1013	0.0	0.0	i	(26)
Furyl-3 + O = CHCHCHO + CO		3.0 × 1013	0.0	0.0	i	(27)
Reactions of cyclo-C4H5O
Isomerization
C4H5O-2 = C4H5O -3		3.3 × 109	1.0	39.1	j	(28)
Decompositions by β-scission
C4H5O-2 = C2H2+CH2CHO		8.1 × 1012	0.246	34.925	a	(29)
C4H5O-3 = CH2CHCHCHO		1.1 × 1013	0.085	22.555	a	(30)
Reactions with O2
C4H5O-2 + O2 = furan + HO2		2.6 × 1011	0.0	2.5	k	(31)
C4H5O-3 + O2 = furan + HO2		1.6 × 1012	0.0	15.2	k	(32)
Combinations
C4H5O-2 + O = C2H3CHO + CHO		5.5 × 1013	0.0	0.0	l	(33)
C4H5O-3 + O = C2H2 + HCHO + CHO		5.5 × 1013	0.0	0.0	l	(34)
C4H5O-2 + H =furan23H		1.0 × 1014	0.0	0.0	b	(35)
C4H5O-3 + H = furan23H		1.0 × 1014	0.0	0.0	b	(36)
C4H5O-3 + H = furan25H		1.0 × 1014	0.0	0.0	b	(37)
Reactions of C4H3O
Decompositions by β-scission
CHCHCHCO = C2H2 + CHCO		5.3 × 1015	−0.234	34.234	a	(38)
CHCHCHCO = CHCCHCO + H		8.7 × 1011	0.706	38.680	a	(39)
CHCCHCHO = CO + C3H3		1.5 × 1012	0.345	48.401	a	(40)
CHCCHCHO = CHCCHCO + H		1.0 × 1012	0.725	51.949	a	(41)
Combinations
CHCCHCHO + H = CHCCH2CHO		1.0 × 1014	0.0	0.0	b	(42)
CHCCHCHO + CH3 = C5H6O		1.5 × 1013	0.0	0.0	m	(43)
Reactions of C4H5O
Isomerization
CH2CHCHCHO = CHCHCHCHOH		2.2 × 1011	0.435	35.127	a	(44)
Decompositions by β-scission
CH2CHCHCHO = CO + C3H5		4.9 × 1012	0.261	47.443	a	(45)
CHCHCHCHOH = C2H2 + CH2CHO		1.2 × 1015	0.102	48.750	a	(46)
Combinations
CH2CHCHCHO + H = CH2CHCH2CHO		1.0 × 1014	0.0	0.0	b	(47)
CH2CHCHCHO + CH3 = C5H8O		1.5 × 1013	0.0	0.0	m	(48)
Reactions of CHCHCHO
Decomposition by β-scission
C2H2 + CHO = CHCHCHO		6.0 × 1011	0.0	7.7	n	(49)
Combination
CHCHCHO + H = C2H3CHO		1.0 × 1014	0.0	0.0	b	(50)
SECONDARY MECHANISM
Reactions of FA (CH2CCHCHO)
Decompositions
FA = C3H3 + CHO	(P = 4.7 kPa)	3.6 × 1014	0.0	69.88	o	(51)
	(P → ∞)	7.9 × 1014	0.0	69.88	o	(51′)
FA = pC3H4 + CO	(P = 4.7 kPa)	8.0 × 1062	−15.352	64.415	a	(52)
	(P → ∞)	6.8 × 1011	0.419	44.231	a	(52′)
Reactions of methylfuran and derived radicals
Unimolecular initiations
Methylfuran = C4H6-2 + CO		2.3 × 1015	0.0	85.1	f	(53)
Methylfuran = 1,3-C4H6 + CO		3.5 × 1015	0.0	79.5	f	(54)
Methylfuran = 1,2-C4H6 + CO		4.5 × 1015	0.0	85.1	f	(55)
Methylfuran = C4H6-1 + CO		2.8 × 1015	0.0	79.5	f	(56)
Methylfuran = pC3H4 + CH2CO		5.8 × 1015	0.0	82.9	f	(57)
Methylfuran = C2H2 + C2H4 + CO		1.7 × 1015	0.0	79.5	f	(58)
Methylfuran = C3H3 + CH3CO		4.0 × 1016	0.0	90.5	f	(59)
Methylfuran = nC4H5 + CHO		4.0 × 1016	0.0	106.0	f	(60)
Bimolecular initiation
Methylfuran + O2 = furylCH2 + HO2		2.2 × 107	2.5	46.045	p	(61)
Metatheses
Methylfuran + H = furylCH2 + H2		3.0 × 1014	0.0	9.0	f	(62)
Methylfuran + O = furylCH2 + OH		6.0 × 1010	0.7	7.632	q	(63)
Methylfuran + OH = furylCH2 + H2O		6.5 × 106	2.0	0.447	r	(64)
Methylfuran + HO2 = furylCH2 + H2O2		7.0 × 102	3.0	12.0	s	(65)
Methylfuran + CH3 = furylCH2 + CH4		1.5 × 1012	0.0	10.0	f	(66)
Methylfuran + C2H3 = furylCH2 + C2H4		2.2 × 100	3.5	4.68	s	(67)
Methylfuran + C3H3 = furylCH2 + pC3H4		8.0 × 1011	0.0	10.0	f	(68)
Methylfuran + C3H5 = furylCH2 + C3H6		8.0 × 1011	0.0	12.0	f	(69)
Methylfuran + iC4H3 = furylCH2 + C4H4		8.0 × 1011	0.0	8.0	f	(70)
Combinations
Methylfuran = furylCH2 + H		1.6 × 1016	0.0	86.0	f	(71)
Decompositions and oxidation of the obtained radicals
FurylCH2 = nC4H5 + CO		2.3 × 1015	0.0	71.0	f	(72)
FurylCH2 = C3H3 + CH2CO		2.3 × 1015	0.0	64.0	f	(73)
FurylCH2 = C4H4 + CHO		2.3 × 1015	0.0	64.0	f	(74)
FurylCH2 = C2H2 + C2H3 + CO		3.3 × 1015	0.0	76.7	f	(75)
FurylCH2 + O2 = furylCH2O + O		6.3 × 1012	0.0	40.0	t	(76)
FurylCH2 + O = furyl-2 + HCHO		1.6 × 1014	0.0	0.0	t	(77)
FurylCH2O = furyl-2 + HCHO		2.0 × 1013	0.0	27.5	u	(78)
Reactions of but-3-ynal (C4H4O)
H-abstractions
CHCCH2CHO + H = C3H3 + H2 + CO		4.0 × 1013	0.0	4.2	v	(79)
CHCCH2CHO + OH = C3H3 + H2O + CO		4.2 × 1012	0.0	0.5	w	(80)
CHCCH2CHO + CH3 = C3H3 + CH4 + CO		2.0 × 10−6	5.6	2.5	x	(81)
Reactions of 3-butenal (C4H6O)
H-abstractions
CH2CHCH2CHO + H = C3H5 + H2 + CO		4.0 × 1013	0.0	4.2	v	(82)
CH2CHCH2CHO + OH = C3H5 + H2O + CO		4.2 × 1012	0.0	0.5	w	(83)
CH2CHCH2CHO + CH3 = C3H5 + CH4 + CO		2.0 × 10−6	5.6	2.5	x	(84)
Reactions of 2-methyl-but-3-ynal (C5H6O)
H-abstractions
C5H6O + H = C4H5-1s + H2 + CO		4.0 × 1013	0.0	4.2	v	(85)
C5H6O + OH = C4H5-1s + H2O + CO		4.2 × 1012	0.0	0.5	w	(86)
C5H6O + CH3 = C4H5-1s + CH4 + CO		2.0 × 10−6	5.6	2.5	x	(87)
Reactions of 2-methyl-3-butenal (C5H8O)
H-abstractions
C5H8O + H = nC4H7 + H2 + CO		4.0 × 1013	0.0	4.2	v	(88)
C5H8O + OH = nC4H7 + H2O + CO		4.2 × 1012	0.0	0.5	w	(89)
C5H8O + CH3 = nC4H7 + CH4 + CO		2.0 × 10−6	5.6	2.5	x	(90)
Reactions of dihydrofuran (C4H6O) and derived radicals
Bimolecular initiation
Furan23H + O2 = C4H5O-2 + HO2		1.4 × 1013	0.0	47.6	c	(91)
furan23H + O2 = C4H5O-3 + HO2		1.4 × 1012	0.0	35.6	c	(92)
furan25H + O2 = C4H5O-3 + HO2		2.8 × 1012	0.0	35.6	c	(93)
Metatheses
Furan23H + H = C4H5O-2 + H2		9.0 × 106	2.0	5.0	e	(94)
Furan23H + H = C4H5O-3 + H2		5.4 × 104	2.5	−1.9	e	(95)
Furan25H + H = C4H5O-3 + H2		1.1 × 105	2.5	−1.9	e	(96)
Furan23H + O = C4H5O-2 + OH		2.6 × 1013	0.0	5.2	e	(97)
Furan23H + O = C4H5O-3 + OH		8.8 × 1010	0.7	3.25	e	(98)
Furan25H + O = C4H5O-2 + OH		1.8 × 1011	0.7	3.25	e	(99)
Furan23H + OH = C4H5O-2 + H2O		2.6× 106	2.0	−0.77	e	(100)
Furan23H + OH = C4H5O-3 + H2O		3.0 × 106	2.0	−1.52	e	(101)
Furan25H + OH = C4H5O-3 + H2O		6.0 × 106	2.0	−1.52	e	(102)
Furan23H + HO2 = C4H5O-2 + H2O2		4.0 × 1011	0.0	15.5	e	(103)
Furan23H + HO2 = C4H5O-3 + H2O2		6.4 × 103	2.6	12.4	e	(104)
Furan25H + HO2 = C4H5O-3 + H2O2		1.3 × 104	2.6	12.4	e	(105)
Furan23H + CH3 = C4H5O-2 + CH4		2.0 × 1011	0.0	9.6	e	(106)
Furan23H + CH3 = C4H5O-3 + CH4		1.0 × 1011	0.0	7.3	e	(107)
Furan25H + CH3 = C4H5O-3 + CH4		2.0 × 1011	0.0	7.3	e	(108)
Additions and decompositions
Furan23H + H = THF-2yl		1.0 × 1014	0.0	3.26	e	(109)
Furan23H + H = THF-3yl		1.0 × 1014	0.0	3.26	e	(110)
Furan25H + H = THF-3yl		1.0 × 1014	0.0	3.26	e	(111)
Furan23H + OH => HCHO + C2H4 + CHO		2.7 × 1012	0.0	−1.1	e	(112)
Furan25H + OH => HCHO + C2H4 + CHO		2.7 × 1012	0.0	−1.1	e	(113)
Decompositions and combinations of the obtained radicals
THF-2yl = C2H4 + CH2CHO		2.0 × 1014	0.005	35.6	y	(114)
THF-3yl = HCHO + C3H5		2.0 × 1014	0.005	35.6	y	(115)
THF-2yl + H = THF		1.0 × 1014	0.0	0.0	b	(116)
THF-3yl + H = THF		1.0 × 1014	0.0	0.0	b	(117)
Reactions of THF (C4H8O)
Bimolecular initiation
THF + O2 = THF-2yl + HO2		2.8 × 1013	0.0	47.6	c	(118)
THF + O2 = THF-3yl + HO2		2.8 × 1013	0.0	47.6	c	(119)
Metatheses
THF + H = THF-2yl + H2		1.8 × 107	2.0	5.0	e	(120)
THF + H = THF-3yl + H2		1.8 × 107	2.0	5.0	e	(121)
THF + O = THF-2yl + OH		5.2 × 1013	0.0	5.2	e	(122)
THF + O = THF-3yl + OH		5.2 × 1013	0.0	5.2	e	(123)
THF + OH = THF-2yl + H2O		5.2× 106	2.0	−0.77	e	(124)
THF + OH = THF-3yl + H2O		5.2× 106	2.0	−0.77	e	(125)
THF + HO2 = THF-2yl + H2O2		8.0 × 1011	0.0	15.5	e	(126)
THF + HO2 = THF-3yl + H2O2		8.0 × 1011	0.0	15.5	e	(127)
THF + CH3 = THF-2yl + CH4		4.0 × 1011	0.0	9.6	e	(128)
THF + CH3 = THF-3yl + CH4		4.0 × 1011	0.0	9.6	e	(129)

Note: the rate constants are given in the form k = A T ⁿ exp(−E_a/RT) where A has units of cm, mol and s, T has units of K, and E_a has units of kcal/mol.

^aRate constant calculated in this work.

^bRate constant taken equal to that of the recombination of H atoms with alkyl radicals as proposed by Allara and Shaw [36].

^cRate constant calculated as proposed by Ingham et al. [37], but E_a corrected with enthalpies of the bimolecular reaction.

^dRate constant estimated by analogy with the values proposed by Gueniche et al. [38] for the similar reaction of 1,3-butadiene.

^eRate constant estimated by using the correlations proposed by Heyberger et al. [39] in the case of alkenes.

^fRate constant taken equal to the values proposed by Lifshitz et al.[40] for methylfuran.

^gRate constant taken equal to that of the isomerization of iC₄H₅ and nC₄H₅ radicals as proposed by Leung and Lindstedt [41].

^hRate constant estimated by analogy with values proposed by Mebel et al. [42] for reactions of O₂ + C₂H₃.

ⁱRate constant estimated by analogy with values proposed by Dagaut et al. [43] for reactions of O + C₂H₃.

^jRate constant taken equal to the values proposed by Gueniche et al. [38] for the similar reaction of lC₄H₇-1 and lC₄H₇Y.

^kRate constant estimated by using the correlations proposed by Touchard et al. [44] in the case of low temperature oxidation of 1-pentene.

^lRate constant estimated by analogy with values proposed by Baulch et al. [45] for the similar reaction of O + C₂H_5.

^mRate constant calculated using the modified collision theory at 1200 K using software KINGAS [56].

ⁿRate constant estimated by analogy with values proposed by Baulch et al. [45] for reaction of C₂H₂ + CH₃ = sC₃H₅.

^oRate constant taken equal to the values proposed by Sendt et al. [21] for formyl allene, with the A-factor divided by 2.2 for flame conditions.

^pRate constant estimated by analogy with values proposed by Oehlschlaeger et al. [46] for reaction of toluene + O₂.

^qRate constant estimated by analogy with values proposed by Pitz et al. [47] for reaction of toluene + O.

^rRate constant estimated by analogy with values proposed by Knispel et al. [48] for reaction of toluene + OH.

^sRate constant estimated by analogy with values proposed by Mehl et al. [49] for reaction of toluene + HO₂.

^tRate constant estimated by using the correlations proposed by Brezinsky et al. [57] in the case of benzyl radical.

^uRate constant estimated by analogy with values proposed by Bounaceur et al. [58] for reaction of C₆H₅CH₂O.

^vRate constant estimated by analogy with values proposed by Warnatz [50] for the similar reaction of CH₃CHO + H.

^wRate constant estimated by analogy with values proposed by Cavanagh et al. [51] for the similar reaction of CH₃CHO + OH.

^xRate constant estimated by analogy with values proposed by Baulch et al. [45] for the similar reaction of CH₃CHO + CH₃.

^yRate constant estimated by analogy with values proposed by Sirjean et al. [52] for the ring opening reaction of C₅H₉#.

Table 3.

Thermochemical data of furan and its derived species.

Species	Structure	ΔfH298k° (kcal/mol)	S298K° (cal/mol/K)	Cp° (T) (cal/mol/K)
				298	400	500	600	800	1000	1500	2000
Furan*		−8.23	65.2	15.5	21.1	25.6	29.2	34.3	37.7	42.7	45.4
Furyl-2*		59.0	66.5	15.1	20.1	23.9	27.0	31.3	34.2	38.2	40.3
Furyl-3*		59.2	66.3	15.0	19.9	23.8	26.9	31.2	34.1	38.1	40.3
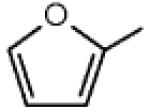
Methylfuran*		−18.9	73.8	21.2	27.8	33.3	37.9	44.8	49.6	56.6	60.5
FurylCH2*		14.4	72.6	21.3	28.0	33.3	37.4	43.3	47.3	53.2	56.4
C4H5O-2		18.1	68.2	21.4	26.1	30.2	33.7	39.1	42.7	43.7	44.7
C4H5O-3		8.45	68.1	21.2	25.8	29.9	33.4	38.9	42.5	43.6	44.7
Furan25H		−14.18	65.1	15.9	23.0	28.9	33.6	40.7	45.7	57.3	61.4
Furan23H		−21.76	67.0	21.7	27.0	31.6	35.7	42.0	46.2	48.2	50.0
THF-2yl		−4.09	71.9	24.9	31.1	36.2	40.6	47.2	51.3	53.2	55.0
THF-3yl		−1.59	71.9	24.9	31.1	36.3	40.6	47.2	51.3	53.2	55.0
THF		−44.08	69.3	25.2	32.0	37.7	42.6	50.0	54.8	57.7	60.2
FurylCH2O		0.25	82.4	26.4	33.4	38.8	43.0	48.8	53.0	67.3	72.7
CHCHCHCO*		66.4	74.5	19.7	23.5	26.4	28.7	32.2	34.7	38.4	40.5
CHCCHCHO		67.0	82.8	19.0	22.3	25.1	27.4	30.9	33.3	37.3	40.3
CH2CHCHCHO		23.9	83.1	20.7	25.1	28.8	31.9	36.7	40.0	45.8	50.1
CHCHCHCHOH		49.3	84.7	22.0	26.3	29.7	32.6	37.1	40.3	45.8	49.9
CHCCHCO*		47.1	70.9	18.9	21.9	24.2	25.9	28.6	30.5	33.5	35.1
CHCHCHO		42.4	72.4	13.9	17.5	20.6	23.4	28.3	32.3	36.7	39.5
CHCCH2CHO		18.7	76.3	20.9	24.4	27.4	30.2	34.5	37.3	38.8	40.7
CH2CHCH2CHO		−18.9	80.4	22.0	26.7	30.9	34.5	40.4	44.3	46.3	49.0
CH2CCHCHO (FA)*		15.6	73.4	19.7	24.0	27.6	30.6	35.2	38.5	43.1	45.5
C5H6O		14.8	83.3	25.8	31.0	35.5	39.4	45.6	49.5	51.4	53.9
C5H8O		−24.5	86.9	26.9	33.3	38.9	43.8	51.5	56.5	58.9	62.2

^*Note: Thermochemical data have been calculated by software THERGAS [31], except for species marked with for which they have been obtained from theoretical calculation (see text).

3.1 Primary mechanism

The primary mechanism contains the reactions of furan and of the radicals directly derived from it. The unimolecular initiations of furan have been considered and Fig. 1 presents the simplified potential energy surface. According to Sendt et al.’s study [21], the most important unimolecular pathways for furan decomposition are the reactions involving 1,2-H migrations, which then lead to the formation of two different cyclic carbenes. These species can decompose to give the major products as CO + pC₃H₄ and C₂H₂ + CH₂CO. For the first route, Sendt et al. [21] showed that two rate-determining steps must be taken into account. The first one corresponds to the initial 1,2-H transfer from furan to form formyl allene (FA, , CH₂CCHCHO, 1,2-butadienal), (reaction 1 (R1) in Table 2), while the second step is related to the decomposition of FA by a concerted reaction (TS2) in which a 1,4-H transfer and a simultaneous C-C bond fission occurs to form CO and pC₃H₄ (R52). It must be noted that the decomposition of FA to propargyl and CHO radical (R51) has been also considered in our mechanism in accordance with the work of Sendt et al. [21].

Fig. 1.

Simplified potential energy surface (PES) for the unimolecular initiation of furan. The energies (in kcal mol⁻¹) are relative to furan and calculated at the CBS-QB3 level of theory at 0 K. (*) This energy has been taken from Sendt et al. [21].

The detailed mechanism for the second unimolecular reaction of furan involves three elementary steps. The first one corresponds to the formation of a cyclic carbene (1,2-H shift) as discussed previously. The second step is related to the ring opening of the cyclic carbene to produce a diradical while the third step involved two successive bond cleavages of this latter species to form C₂H₂ and CH₂CO. It is possible, as mentioned by Sendt et al. [21], to calculate the overall rate constant by considering the last transition state TS3 which corresponds to the highest energy barrier involved in the overall reaction (Fig. 1).

All the calculations have been performed with the CBS-QB3 method [32] and the activation energies found are in a good agreement with those obtained by Sendt et al. [21] at the G2B2 and CASS-SCF level. Frequency analysis makes it possible to point out one imaginary frequency for each transition state (TS). High-pressure limit unimolecular rate constants were calculated using canonical transition state theory. The kinetic parameters were obtained with a modified Arrhenius form (Table 2).

An interesting feature, resulting from previous calculations, is the relatively low barriers involved in the unimolecular initiations. Consequently, these reactions become very important and their rate constants are sensitive parameters. Thus, we performed RRKM calculations in order to take into account pressure effect under flame conditions. Time dependent master equation has been solved with the CHEMRATE program [34] for the two pathways involved in Fig. 1. Calculations have been performed at 4.7 kPa and T = 700-2000 K. A $\Delta {\mathrm{E}}_{\text{down}}^0$ value of 260 cm⁻¹ was used in the master equation analysis, with Ar as third body [35]. Lennard-Jones parameters for furan and other isomers (FA) were estimated as σ = 5.18 Å and $\frac{\epsilon }{k_b}=357$ K in accordance with Joshi and Wang [35]. Rate constants, k(E) have been estimated at 25 cm⁻¹ (0.07 kcal mol⁻¹) increments. The low-pressure rates (4.7 kPa) were used in the simulation of flame results, while the high pressure ones in pyrolysis conditions.

The kinetics of the unimolecular decompositions to give H atoms and furyl radicals (R3 and R4) have been deduced from those of the reverse reactions, k = 1.0×10¹⁴ s⁻¹ according to Allara and Shaw [36]. For the bimolecular initiations with oxygen molecules (R5 and R6), A-factors have been obtained using the correlation proposed by Ingham et al. [37] and the activation energies have been taken equal to the enthalpies of reaction. The rate constants of the additions of H and OH to furan (R7-R9) have been deduced from value proposed for the similar reactions in case of 1,3-butadiene [38] and our previous work on the oxidation of alkenes [39], respectively. The rate for the reaction of furan with CH₃ forming 2-methylfuran () and H (R10) has been taken from the reverse reaction proposed by Lifshitz et al. [40]. The kinetics for the abstractions of vinylic H atoms (R11-R18) were deduced from the correlations proposed by Heyberger et al. [39].

Two furyl radicals, furyl-2 () and furyl-3 () are formed by H-abstractions and two C₄H₅O radicals, dihydrofuryl-2 (, C₄H₅O-2) and dihydrofuryl-3 (, C₄H₅O-3) are produced by H-additions. Isomerization reactions between the two furyl (R19) and the two C₄H₅O radicals (R28) are possible. The rate constants of the isomerizations are deduced from the similar reaction of n-C₄H₅ and i-C₄H₅ radicals for furyl radicals [41], and from that of CH₂=CH-CH₂-CH₂ and CH₂=CH-CH-CH₃ radicals for C₄H₅O radicals [38].

The decomposition reactions of furyl radicals have been also investigated at the CBS-QB3 level of theory [32]. Even if the bond dissociation energy of C-H is very high (about 119 kcal mol⁻¹ according to our calculations), the decomposition of these radicals could play a significant kinetic role under flame conditions where the high temperature and concentration of radicals favor H-abstractions from furan.

Figure 2 shows the major routes of decomposition of furyl radicals. All the activation energies shown in Figs. 2 and 3 have been calculated. For furyl-2, the β-scission of the C-O bond (R20) involves an activation energy of 33.7 kcal mol⁻¹, which is about 26 kcal mol⁻¹ lower than the corresponding C-C bond breaking. Thus, the last reaction was not considered in this study. The radical formed by ring opening can decompose either by C-H bond breaking, yielding ethynylketene (O=C=CH-C≡CH, C₄H₂O) (R39) or by β-scission of the C-C bond to form C₂H₂ and HCCO radical (R38). For furyl-3, only the β-scission of the C-O bond is possible with an activation energy of 31 kcal mol⁻¹ (Fig. 2, R21). Three mesomeric forms exist for the radical obtained by ring opening but only one can decompose by C-H bond breaking to form C₄H₂O (R41) or by isomerization followed by a β-scission yielding CO and propargyl radical (R40) with a very low activation energy (7.6 kcal mol⁻¹).

Fig. 2.

Unimolecular decompositions of furyl radicals considered in this study. Activation energies (in bold) have been calculated at the CBS-QB3 level of theory, at 298 K.

Fig. 3.

Unimolecular decompositions of dihydrofuryl radicals considered in this study. Activation energies (in bold) have been calculated at the CBS-QB3 level of theory, at 298 K.

The high concentration of H atoms formed in flame can contribute to the formation of C₄H₅O radicals by addition of H atoms on the double bond of furan. Figure 3 shows the principal routes of decomposition of C₄H₅O radicals considered in our mechanism, which have been theoretically investigated. The C₄H₅O-2 radical can react by C-C or C-O bond breaking to form a non-cyclic radical. The β-scission of C-O bond (R29) involves an activation energy of 35.3 kcal mol⁻¹ against 43.9 kcal mol⁻¹ for the C-C bond breaking while the β-scission of the linear radicals formed implies, in each case, a lower activation energy. Both routes lead to the formation of C₂H₂ and CH₂CHO radicals. Thus, only the C-O bond breaking has been considered here. The C₄H₅O-3 radical can react by β-scission of the C-O bond (R30), with a low activation energy of 22 kcal mol⁻¹, forming a resonance stabilized radical. The latter can react by 1,5-H transfer (R44) followed by a decomposition to give C₂H₂ and CHCH₂OH (R46). A second pathway involved 1,2-H transfer (R45) followed by the subsequent β-scission to form CO and allyl radical. The two decomposition routes have been considered since in each case, an activation energy of about 47 kcal mol⁻¹ is involved in the rate determining step.

In addition, the furyl radicals could react with oxygen (R22-R25) or O atoms (R26 and R27) with the kinetics estimated by analogy with similar reactions of C₂H₃ radicals [42,43]. Similarly, the C₄H₅O radicals can be consumed by oxygen (R31 and R32) or O atoms (R33 and R34), the rate constants of which have been estimated by using the correlations proposed by Touchard et al. [44] and by analogy with data by Baulch et al. [45], respectively.

Termination steps were written for CHCCHCHO (), CH₂CHCHCHO (), CHCHCHO () and C₄H₅O radicals. For CHCCHCHO and CH₂CHCHCHO, combinations with H atoms can give but-3-ynal (R42) and 3-butenal (R47), and with CH₃ radicals could lead to 2-methyl-but-3-ynal (, R43) and 2-methyl-3-butenal (, R48), while combinations of CHCHCHO and C₄H₅O radicals with H radicals are sources of C₂H₃CHO (R50) and dihydrofuran (, furan23H and , furan25H, R35-R37), respectiviely. The rate constants for these reactions were estimated as proposed by Allara et al. [36].

3.2 Secondary mechanism

The secondary mechanism includes the reactions of the primary products which are not considered in the mechanism of the oxidation of toluene [30], namely FA, methylfuran, but-3-ynal, 3-butenal, 2-methyl-but-3-ynal, 2-methyl-3-butenal, furan23H, furan25H and tetrahydrofuran (, THF). As discussed previously, FA can decompose to pC₃H₄ + CO (R52), the rate constant of which has been determined using quantum calculations with CBS-QB3 method [32]. FA is also a source of C₃H₃ and CHO radicals (R51), the kinetics of which is from Sendt et al. [21] with the A-factor divided by 2.2 to take into account the pressure effect (for R1, the k_∞/k_4.7kPa= 2.2 at 1000 K). In the case of methylfuran, the decomposition by breaking a C-H or C-O bond (R53-R60), bimolecular initiations with oxygen molecules (R61) and H-abstractions (R62-R71) are considered. The rate constants of these reactions were taken from Lifshitz et al. [40], except those of the bimolecular initiation with O₂ [46], and those reactions with O or C₂H₃ [47], with OH [48] and with HO₂ [49] which were obtained by analogy with toluene. For but-3-ynal, 3-butenal, 2-methylbut-3-ynal and 2- methyl3-butenal, the H-abstractions by H, OH and CH₃ radicals followed by decompositions (R79-R90) were taken into account, the kinetics of which were deduced from the similar reactions of acetaldehyde [45,50,51].

For dihydrofuran and THF, the rates for their bimolecular reactions with oxygen (R91-R93, R118 and R119) were estimated from the correlation proposed by Ingham et al. [37] and those of metatheses reactions (R94-R108, R120-R129) were deduced from the correlations proposed by Heyberger et al. [39]. H-additions to dihydrofuran would give THF-2-yl (R109) and THF-3-yl (R110 and R111), respectively, and OH-additions would produce the same products HCHO + C₂H₄ + CHO (R112 and R113), the kinetics of which were from the correlations proposed by Heyberger et al. [39]. By β-scission, THF-2-yl and THF-3-yl could decompose to C₂H₄ + CH₂CHO (R114) and HCHO + C₃H₅ (R115),respectively, with the rates proposed by Sirjean et al. [52]. Terminations of the two tetrahydrofuryl radicals would form THF (R116 and R117), the kinetic data of which were estimated from the work of Allara and Shaw [36].

4. Results and Discussion

4.1 Experimental results

In this study, about 40 combustion intermediates, including hydrocarbons and oxygenated species, were detected and identified in the flames characterized by Φ = 1.4, 1.8 and 2.2. These species are listed in Table 4 along with the literature and measured IEs, peak concentrations and their locations in the flames. The detailed experimental data of mole fractions are available in supplemental material. To illustrate the effect of the equivalence ratio on the flame structure, Figures 4 to 8 present the temperature and concentration profiles. In Fig. 4, the temperature profiles are shown. Due to size of the thermocouple and its perturbation on the flame structure, the temperatures close to the burner (1.0 mm above) were extrapolated to the burner surface. As shown in Fig. 4, the flame temperatures steadily decrease and their peak locations shift downstream with the equivalence ratio increasing. In flame A, the maximum temperature is 1888 K located at 4.4 mm from the burner, while this value is decreased to 1772 K with a location of 6.2 mm in flame B and reaches 1699 K at 7.1 mm in flame C.

Table 4.

Flame species measured with their respective IEs, maximum mole fractions (X_max), and positions (P, mm) in furan/oxygen/argon flames

m/e	Formula	Species	IEs		Mole Fractions
			Literature a	This Work b	Φ = 1.4		Φ = 1.8		Φ = 2.2
					P	Xmax	P	Xmax	P	Xmax
15	CH3	methyl radical	9.84	9.79	3.5	8.9E-04	5.5	9.8E-04	8.5	8.9E-04
16	CH4	methane	12.71	12.71	3.5	2.1E-03	5.0	3.9E-03	8.0	4.3E-03
26	C2H2	acetylene	11.40	11.35	3.5	1.6E-02	5.5	2.8E-02	8.5	3.9E-02
28	C2H4	ethylene	10.52	10.49	3.5	5.8E-03	4.5	7.1E-03	7.5	7.7E-03
30	CH2O	formaldehyde	10.88	10.84	3.0	3.1E-03	4.0	3.3E-03	6.5	3.4E-03
32	CH3OH	methyl alcohol	10.84	10.83	−	−	−	−	−	−
39	C3H3	propargyl radical	8.67	8.67	3.5	6.1E-04	5.5	1.1E-03	8.5	1.5E-03
40	aC3H4	allene	9.83	9.83	3.5	3.6E-04	5.0	5.3E-04	8.0	8.1E-04
	pC3H4	propyne	10.36	10.34	3.0	7.7E-04	5.0	2.4E-03	8.0	4.2E-03
41	C3H5	allyl radical	8.18	8.19	3.0	2.4E-04	5.0	2.6E-04	8.0	1.3E-04
42	CH2CO	ketene	9.62	9.58	2.5	1.4E-03	5.0	1.8E-03	7.0	2.3E-03
44 c	C2H4O	ethenol	9.33	9.30	3.0	4.2E-05	4.0	4.7E-05	6.0	4.8E-05
	C2H4O	acetaldehyde	10.23	10.22
50	C4H2	diacetylene	10.17	10.14	4.0	1.6E-04	5.0	6.7E-04	6.0	7.3E-04
51	C4H3	CH2CCCH	8.06	8.10	−	−	−	−	−	−
52 c	C4H4	1,2,3-butatriene	9.15	9.15	3.5	5.8E-04	5.5	7.4E-04	8.5	1.2E-03
	C4H4	vinylacetylene	9.58	9.56
54	C4H6	1,3-butadiene	9.07	9.04	3.0	1.3E-04	4.5	1.8E-04	8.0	2.6E-04
55	C3H3O	HC=CH-CHO		9.54
56 c	C3H4O	methylketene	8.95	8.91	2.0	1.9E-04	3.5	2.6E-03	6.0	2.9E-03
	C3H4O	propenal	10.11	10.09
58	C3H6O	acetone	9.70	9.70	−	−	−	−	−	−
64 c	C5H4	1,2,3,4-pentatetraene	8.67	8.72	2.5	1.2E-05	5.5	2.5E-05	8.0	6.9E-05
	C5H4	1,3-pentadiyne	9.50	9.48
65	C5H5	cyclopentadienyl radical	8.41	8.41	2.5	1.6E-05	5.5	3.4E-05	8.5	5.8E-05
66 c	C5H6	1,3-cyclopentadiene	8.57	8.54	2.5	2.3E-05	4.5	3.6E-05	8.0	4.6E-05
	C4H2O	ethynylketene	8.77±0.15 d	8.70
68	C4H4O	furan	8.88	8.86	fuel
74	C6H2	1,3,5-hexatriyne	9.50	9.48	2.5	3.3E-05	6.5	4.0E-05	9.0	5.5E-05
76	C6H4	benzyne 3-hexene-1,5-diyne	9.07 9.03	9.06	3.0	1.6E-05	2.5	2.2E-05	8.5	3.9E-05
78 c	C6H6	fulvene	8.36	8.40	3.5	6.0E-05	5.0	8.6E-05	8.0	1.5E-04
	C6H6	benzene	9.26	9.23
80	C6H8	1,3-cyclohexadiene	8.25	8.23	2.5	2.0E-05	4.0	3.0E-05	4.5	4.0E-05
82	C5H6O	2-methyl-furan	8.38	8.36	2.0	1.6E-05	4.0	2.3E-05	7.0	3.8E-05
84	C5H8O	4-pentyn-2-ol	10.24	10.21	−	−	−	−	−	−
92	C7H8	toluene	8.83	8.80	3.5	1.0E-06	4.0	1.5E-06	7.0	3.4E-06
94	C6H6O	phenol	8.49	8.50	3.0	4.0E-06	4.5	3.1E-05	7.5	3.9E-05
102	C8H6	phenylacetylene	8.82	8.79	—	—	—	—	8.5	2.3E-06
104	C8H8	styrene	8.46	8.47	—	—	—	—	7.0	4.9E-06

^aNote: Refers to [59];

^berrors for stable species are ±0.05eV, for radicals are ±0.10eV;

^cthe values are the total mole fraction of a specific mass, for example, the mole fraction of mass 44 includes both ethenol and acetaldehyde;

^drefers to [60].

Fig. 4.

Temperature profiles of the furan/O₂/Ar flames (Φ = 1.4, 1.8 and 2.2).

Fig. 8.

Experimental (symbols) and predicted (lines) concentration profiles of (a) HCHO (formaldehyde), (b) CH₂CO (ketene), (c) C₂H₄O (acetaldehyde), (d) C₃H₄O (methylketene), (e) C₅H₆O (2-methylfuran) and (f) C₆H₅OH (phenol) in the furan/O₂/Ar flames (Φ = 1.4, 1.8 and 2.2).

Mole fraction profiles of the major species including furan, O₂, Ar, H₂, H₂O, CO and CO₂ are displayed as symbols in Fig. 5. The increase of the equivalence ratio in the furan flames causes a noticeable width increase of the reaction zone. In flame A, mole fraction of Ar remains constant after the position of 5.0 mm from the burner surface. This distance where Ar keeps constant shifts downstream to 7.0 mm in flame B and 9.0 mm at flame C. Among the three flames, both furan and O₂ consumed in further distances with the equivalence ratio increasing. The other major species, H₂, H₂O, CO and CO₂ have similar tendencies for the position with equilibrium value as that of Ar. In the post-flame zone, the mole fractions of Ar and CO₂ steadily decrease with the equivalence ratio increasing, while those of H₂ and CO show reverse trends. As evidenced from Fig. 5, the post flame H₂O levels were not sensitive to equivalence ratio. However, equivalence ratio has a significant impact on the X_CO/X_CO2 ratio. In the post-flame zone, the X_CO/X_CO2 ratio is about 1.2 for flame A. This ratio increases to 2.8 in flame B and reaches 8.3 in flame C.

Fig. 5.

Experimental (symbols) and predicted (lines) concentration profiles of Ar, O₂, furan, H₂, H₂O, CO and CO₂ in the furan/O₂/Ar flames (Φ = 1.4, 1.8 and 2.2).

Figures 6 to 8 display the mole fraction profiles of combustion intermediates in the furan flames. Generally, the peak positions of all these species are shifted downstream as Φ increases. Mole fraction profiles of C₁ – C₃ species are shown in Fig. 6. Methyl radical (CH₃) has peak-shaped mole fraction profiles in all investigated flames. Only a little variation is observed for the maximum concentration. As Φ increases from 1.4 to 2.2, the peak concentrations of methane (CH₄), acetylene (C₂H₂), propargyl radical (C₃H₃) and allene (aC₃H₄) are approximately doubled, while that of ethylene (C₂H₄) is multiplied by one and a half, and that of propyne (pC₃H₄) by a factor of 5. For allyl radical (C₃H₅), while, the difference in the maximum mole fraction observed in flame A and B is acceptable, the agreement strongly deteriorates in flame C.

Fig. 6.

Experimental (symbols) and predicted (lines) concentration profiles of (a) CH₃ (methyl radical), (b) CH₄ (methane), (c) C₂H₂ (acetylene), (d) C₂H₄ (ethylene), (e) C₃H₃ (propargyl radical), (f) aC₃H₄ (allene), (g) pC₃H₄ (propyne) and (h) C₃H₅ (allyl radical) in the furan/O₂/Ar flames (Φ = 1.4, 1.8 and 2.2).

The mole fraction profiles for C₄ – C₇ species presented in Fig. 7 also exhibit similar shift trends for the peak positions. With Φ increasing from 1.4 to 2.2, the maximum mole fractions of 1,2,3-butatriene/vinylacetylene (C₄H₄), 1,3-butadiene (C₄H₆), 1,3-cyclopentadiene (C₅H₆), 1,3,5-hexatriyne (C₆H₂) and benzene (C₆H₆) are approximately doubled, while that of diacetylene (C₄H₂) is multiplied by a factor of 5, and those of cyclopentadienyl radical (C₅H₅) and toluene (C₇H₈) are tripled. Thus, the equivalence ratio has the largest effect on the formation of C₄H₂. This can result from the fact that C₂H₂, the major precursor of C₄H₂, is more abundantly formed as Φincreases.

Fig. 7.

Experimental (symbols) and predicted (lines) concentration profiles of (a) C₄H₂ (diacetylene), (b) C₄H₄ (vinylacetylene), (c) C₄H₆ (1,3-butadiene), (d) C₅H₅ (cyclopentadienyl radical), (e) C₅H₆ (1,3-cyclopentadiene), (f) C₆H₂ (1,3,5-hexatriyne), (g) C₆H₆ (benzene) and (h) C₇H₈ (toluene) in the furan/O₂/Ar flames (Φ = 1.4, 1.8 and 2.2).

Figure 8 shows the mole fraction profiles of the oxygenated intermediates. As Φ increases from 1.4 to 2.2, the peak concentration of 2-methylfuran is approximately doubled, while those of CH₂CO and methylketene/2-propenol (C₃H₄O) are multiplied by one and a half, and that of phenol (C₆H₅OH) by a factor of 10. Comparatively, the level of formaldehyde (HCHO) and ethanol/acetaldehyde (C₂H₄O) are not sensitive to equivalence ratio in the flame regime.

4.2 Kinetic modeling results

4.2.1 Simulation of the flame structure

The modeling of the chemical kinetics was performed using the CHEMKIN software [53], with the experimental temperature profiles introduced as input parameters for simulation. To account for the perturbations induced by the quartz probe and the thermocouple [54] and fit the experimental results, the temperature profile was shifted 1.5, 1.7 and 2.2 mm away from the burner surface for the flames with Φ = 1.4, 1.8 and 2.2, respectively. The perturbation effect is known in molecular-beam mass spectroscopic investigations, and a shift equaling 4-5 times the orifice diameter has been reported for premixed low-pressure flames (4.0-5.0 kPa) [29,54,55].

The comparisons between the experimental measurements and predictions for the three flames are presented in Figs. 5-8, in which lines stand for simulated results. There is generally a reasonable agreement between measurements and predictions. For the major species shown in Fig. 5, the current model captures well the experimental values within the error limits. With Φ increasing from 1.4 to 2.2, the model also gives evidence of the increase of the reaction width, which is consistent with the measurements. The present mechanism overpredicts the formation of CO in flames A and B near the burner surface. The flux analysis indicates that CO is mainly formed by the reaction of O₂ with formyl radical (CHO) which is produced by addition of OH radical to the C=C double bond of furan. The too large formation of CO results from the too fast rate of the reaction OH + furan. The rate constant of this reaction needs to be more accurately determined by further experimental or theoretical studies. On the other hand, measurement uncertainties cannot be ruled out especially since the reaction zone is narrower in flames A and B than that in flame C.

Figures 6 and 7 summarize the results for some selected C₁ – C₇ intermediates. Overall, the current model reproduces fairly well the mole fraction profiles of C₂H₂, C₃H₃, pC₃H₄, C₃H₅, C₄H₂, C₄H₄, C₄H₆, C₅H₆, C₆H₂, C₆H₆ and C₇H₈. The predicted peak concentration of CH₃ agrees well with the measurement in flame A. The present mechanism tends to overpredict the contributions from CH₃ in flames B and C. However, the agreement is still within the expected uncertainties (a factor of two for free radicals). In the post-flame zone, CH₃ has a too high predicted concentration, which is produced mainly from the reactions of H atom with pC₃H₄, methanol (CH₃OH) and CH₂CO based on the rate-of-production (ROP) analysis. Compared to the reasonable capture of the CH₄ mole fraction shape for flames A and B, the current model exhibits a longer tail for flame C, which could be due to the reactions of abundant CH₃ with HCHO and CHO radical. With Φ increasing, the maximum mole fraction of C₂H₄ becomes larger and the peak position shifts further. While the simulated mole fraction profiles of C₂H₄ have the same tendencies as the experimental measurements, the peak values are underpredicted in flames A and B. The ROP analysis at the peak positions indicates that C₂H₄ is mainly formed by the reactions of CH₂CO+CH₂ and C₂H₃CHO+H in all three flames. Note that the formation of ethane (C₂H₆) is negligible in all three flames. As revealed by the ROP analysis, C₂H₆ is mainly formed through the combination of CH₃ radicals and most of C₂H₆ converts to C₂H₅ radical and finally to C₂H₄. For aC₃H₄, the current model gives fairly reasonable predictions in flames A and B, but a poor one in flame C. According to the ROP analysis result, most of aC₃H₄ comes from C₃H₅. As seen Fig. 6 (h), the maximum mole fraction of C₃H₅ is somewhat overpredicted in flames B and C, which could then lead to the overprediction of aC₃H₄.

It should be noted that in flame C, the maximum mole fraction of C₄H₂ is about 2.5 times overpredicted. By checking the ROP result, the reaction C₂H₂ + C₂H accounts for more than 80% of C₄H₂ formation. As C₂H₂ is satisfactorily predicted, this disagreement could result from an experimental error. For mass 52 represented in Fig. 7(b), the PIE spectra indicate that it involves the contribution of both 1,2,3-butatriene and vinylacetylene. According to the modeling result, the ratios of their maximum mole fraction X_{vinylacetylene}/X_{1,2,3-butatriene} are 8.8, 8.2 and 4.9 in flames A, B and C, respectively, which demonstrates that vinylacetylene is the dominant species. The ROP result shows that about 70% vinylacetylene comes from the reaction of C₃H₃ with triplet CH₂. As seen in Fig. 7(d), the ratio of the experimental and predicted peak mole fraction for C₅H₅ is within 0.5 ~ 2.0. Considering the experimental and modeling uncertainties, mole fraction profiles of both species are determined accurately enough by the current model. In flame A, the metatheses of 1,3-cyclopentadiene with H and decomposition of phenoxy radical accounts for 45% and 33% C₅H₅ formation, respectively. However, decomposition of phenoxy radical is the major source (81%) of C₅H₅ in flame C. The predicted peak values of the two C₆H₆ isomers, benzene and fulvene (vC₆H₆) reveals that benzene is dominant for mass 78, which is in agreement with experimental observations. An increase after the peak value is observed for the predicted C₇H₈ profile in flame C. This phenomenon is caused by the combination of C₆H₅ radical with CH₃ radical which is abundantly predicted in the post flame zone of flame C.

In Fig. 8, the comparison between the measured and modeled oxygenated combustion intermediates are presented. Contributions from CH₂CO, C₅H₆O and C₆H₅OH are correctly reproduced. Both the measurement and simulation show that HCHO is an abundant oxygenated intermediate in all the three flames. While the predicted shape and maximum mole fraction of HCHO are close to the measurements in flame A, the maximum mole fractions are somewhat overpredicted in flames B and C. For C₂H₄O, the peak positions are predicted correctly. As Φ increases from 1.4 to 2.2, the predicted maximum mole fraction of C₂H₄O decreases. The current model only captures C₂H₄O reasonably in flame C. As revealed from the ROP analysis, an important part of the formation of C₂H₄O in flames A and B comes from the combination of CH₃ and CHO radicals. When CHO radicals are excessively formed through the reaction of OH + furan, a excess of C₂H₄O can be produced. The current model tends to overpredict the C₃H₄O contribution in the three flames, which could result from an inaccurate estimation of the photoionization cross section of C₃H₄O. The ROP result indicates that C₃H₄O is mainly formed by the addition of OH to furan in both flame A (81%) and C (82%).

It is obvious that there are some discrepancies between the predictions of the present model and the experimental measurements, especially for intermediates such as CH₃, CH₄, C₂H₄, C₄H₂ and benzene in flame C. The uncertain rate constants of some reactions, for instance, furan + OH = C₂H₃CHO + CHO (correlated with similar reaction) and CH₂CCHCHO = C₃H₃ + CHO (considered the pressure effect) could cast influence on the predictions. Moreover, the estimation of photoionization cross section for some intermediates can be another issue of the disagreement. As the current model is the first attempt to simulate the furan oxidation under flame conditions, further flame data are desirable for the validation of the present mechanism.

4.2.2 Rate-of-production and sensitivity analysis for furan consumption in flames

To illustrate the major reaction channels of furan, flux analysis has been performed for two equivalence ratios 1.4 (flame A, at 3.7 mm from the burner, T = 1470 K, 88.9% furan conversion) and 2.2 (flame C, at 7.9 mm from the burner, T = 1609 K, 85.0% furan conversion). As presented in Fig. 9, the major routes are quite different between the two flames. Metatheses by H, O and OH to produce furyl-2 and furyl-3 radicals account for about 26.8% of furan consumption in flame C, while this value is as high as 47.2% in flame A. Both furyl-2 and furyl-3 radicals are consumed mainly by decomposition via β-scission, giving CH=CH-CH=C=O and CH≡C-CH=CH-O radicals, respectively. By β-scission, CH=CH-CH=C=O radicals are completely converted to C₂H₂ and HCCO radicals, which is an important source of C₂H₂. In both flames A and C, most of the CH≡C-CH=CH-O radicals decompose to give C₃H₃ + CO (1,2-H transfer followed by a fast C-O bond dissociation) and CH≡C-CH=C=O + H, as displayed in Fig. 2.

Fig. 9.

Rate-of-production analysis for the consumption of furan at two equivalence ratios, (a) Φ = 1.4 (flame A, at 3.7 mm from the burner, T = 1470 K, 88.9% furan conversion) and (b) Φ = 2.2 (flame C, at 7.9 mm from the burner, T = 1609 K, 85.0% furan conversion).

While the reaction furan = FA accounts for 35.7% of furan conversion in flame C, it plays a less significant role (only 3.5%) in flame A. This results from the characteristics of flame C being closer to pyrolysis conditions under which thermal decomposition reactions have more important influence on the furan consumption than that in flame A. FA is consumed dominantly by decomposition to C₃H₃ and HCO radicals and only about one-third goes to CO + pC₃H₄ in flame C, while it is the reverse case in flame A. It should be noted that the addition of OH to the C=C bond forming C₃H₄O + HCO is also important for furan consumption. More than 15% furan in flame A and about 6% furan in flame C decompose via this pathway.

In general, H-additions of furan forming C₄H₅O radicals account for about 20% of furan consumption in both flame A and C. The C₄H₅O-2 and C₄H₅O-3 radicals are finally converted to C₂H₂ + CH₂CHO and CO + C₃H₅. In addition, unimolecular decomposition of furan to C₂H₂ + CH₂CO accounts for 7.1% of furan consumption in flame C. However, this reaction has a less important effect on furan consumption (1%) than the other pathways in flame A.

To identify the reactions that serve as bottle-necks in the consumption of furan, a local sensitivity analysis has been performed with the proposed mechanism for the flames A and C, as displayed in Fig. 10. For brevity, C₀-C₂ reactions are not shown except for O₂ + H = OH + O which has the most important promoting effect. The sensitivity analysis indicates that the reaction furan = FA (R1) plays the key role for furan consumption in flame C. The addition of OH radical to furan giving C₂H₃CHO and CHO radical has a similar promoting effect in both flames. The decomposition of C₄H₅O-2 to give C₂H₂ and CH₂CHO radical, and the metatheses of furan with H/OH radicals to yield furyl-2/furyl-3 have a more important promoting effect in flame A than in flame C. The decompositions of FA to give CHO and C₃H₃, CHCCHCHO to H atom and CHCCHCO, the unimolecular decomposition of furan to yield C₂H₂ and CH₂CO, the metatheses of furan with O-atoms, and the ipso-addition of methyl radicals to produce methylfuran, also have a promoting effect in flame C. However, these reactions have no visible effect in flame A. The decomposition of FA to give CO and pC₃H₄ has a strong inhibiting effect on furan consumption in flame C. In the case of flame A, the decomposition of CH₂CHCHCHO to give CO and C₃H₅ radical plays a key role in the inhibition of furan consumption. While the addition of H atom to furan giving C₄H₅O-3, the H-additions to C₄H₅O-3 forming dihydrofuran, and the combination of H atom with CHCCHCHO to give CHCCH₂CHO, have only a slight inhibiting effect in flame A and no effect in flame C, the reaction CHCCHCHO = CO + C₃H₃ has a reverse tendency.

Fig. 10.

Sensitivity analysis for the conversion of furan at two equivalence ratios, (a) Φ = 1.4 (flame A, at 3.7 mm from the burner, T = 1470 K, 88.9% furan conversion) and (b) Φ = 2.2 (flame C, at 7.9 mm from the burner, T = 1609 K, 85.0% furan conversion).

4.2.3 Aromatic formation

Among the products of furan pyrolysis analyzed by Winkler et al. [16], a lot of aromatic species such as naphthalene, phenanthrene, pyrene and acenaphthylene were identified. However, even under the richest condition (flame C), only benzene, toluene, phenylacetylene (C₈H₆) and styrene (C₈H₈)were identified in the present work. This could be due to the relatively low temperature of the studied flames, as well as to the existence of O atom in furan, hindering the formation of much larger aromatics. In the following section, we will focus on the formation pathways of these species, based on the flux analysis taken at the same positions as mentioned in 4.2.2.

For all the investigated flames, the reaction fulvene + H = C₆H₆ + H is an important formation channel of C₆H₆ (36.1% for flame A and 24.2% for flame C), where fulvene is mostly formed by the combination of C₃H₃ radicals and by reaction between C₃H₃ and C₃H₅ radicals. Besides this reaction, the combination of C₃H₃ radicals is another significant source of C₆H₆ (23.4% for flame A and 71.9% for flame C). The ipso-addition of H atom to C₆H₅OH (27.8%) and the reaction C₆H₅ + H (+M) = C₆H₆ (+M) (6.2%) also contribute to the C₆H₆ formation in flame A. However, these two reactions have no contribution to C₆H₆ production in flame C. The flux analysis indicates that the formation pathway of toluene is not sensitive to the equivalence ratio. It is dominated by the combination reaction C₆H₅ + CH₃ (56.5% for flame A and 91.8% for flame C), in which C₆H₅ radicals are dominantly generated from the combination of C₃H₃ radicals. In contrast, the reaction toluene = benzyl + H is also important for toluene production in flame A (39.6%), but it is a consumption route in flame C. In flame C, C₈H₆ is formed mainly by the reactions of C₂H₂ and C₄H₂ with C₆H₅ radicals, and C₈H₈ is produced mainly by the decomposition of 2-phenylethyl radicals and by the combination reaction C₆H₅ + C₂H₃.

4.2.4 Validation of the present mechanism using pyrolysis results

To extend the validity of the present mechanism, previous pyrolysis results from Organ and Mackie (20.0 atm with initial furan concentration of 2.0%, 1.0% and 0.2% dilute in Ar) [14] and Fulle et al. (0.26 atm with furan concentration of 2.0% dilute in Ne) [15] were modeled. Considering that the pressures used in pyrolysis experiments are higher than in the flames, high pressure rate constants for reactions R1, R2, R51 and R52 that were calculated using quantum calculations with CBS-QB3 method [32] have been used in simulations.

Figure 11 compares the predicted furan and product profiles with the experimental results (shock tube, residence time 300 μs) reported by Organ and Mackie [14], in which symbols are measurements and solid, dash dot and dashed lines are respective predictions by the current model for 2.0%, 1.0% and 0.2% initial furan concentration. Also, the predictions for 2.0% initial furan concentration by the mechanism of Sendt et al. [21] are given for comparison. In general, the present model gives acceptable agreement with experimental furan profile. Particularly, in the temperature range 1450 – 1550 K, the current predictions are slightly closer to the measurements than those obtained with the model of Sendt et al. [21]. Good agreement is also obtained for C₂H₂, C₃H₄ and C₆H₆. When the temperature is higher than 1500 K, CO is somewhat underpredicted by the present mechanism under all inlet conditions. This underprediction is also observed by the model of Sendt et al. [21]. While the model of Sendt et al. [21] gave underprediction of the minor product CH₄ in the temperature range > 1500 K, the current model also tends to underpredict CH₄ under all inlet conditions. As indicated from the ROP analysis, CH₄ is mainly formed by the reaction of CH₃ radicals with C₃H₄. Since C₃H₄ is reasonably well predicted, the underprediction of CH₄ can be due to the consumption of CH₃ radicals through the reaction furan + CH₃ = methylfuran + H. C₂H₄ is fairly predicted for 0.2% inlet condition with the present mechanism. However, it is underpredicted for 2% and 1% inlet conditions, which also can result from a too large consumption of CH₃ radicals, which are a key source of C₂H₄ (CH₃ ↔ C₂H₄ ↔ C₂H₆). The model of Sendt et al. [21] shows worse prediction of C₃H₄ than ours in the temperature range of 1450 – 1525 K, but better prediction when the temperature is higher than 1525 K.

Fig. 11.

Temperature dependence of designated species in the pyrolysis of furan (dilute in Ar, 20 atm): symbols are experimental results from Organ and Mackie [14]; solid (2% furan inlet), dash dot (1% furan inlet), dash lines (0.2% furan inlet) are predictions of the present work (PW) and short dash lines (2% furan inlet) are predictions by Sendt et al. [21], respectively.

Figure 12 shows the flux analysis result for 2.0% initial furan concentration at 1527 K, corresponding to 64.8% of furan conversion, at which both propyne and benzene have peak mole fractions experimentally. As noted in the result of Sendt et al. [21], their model supported a mechanism involving two parallel furan decomposition routes to the major products CO + pC₃H₄ and C₂H₂ + CH₂CO, which is exactly the same as observed in this work. As seen in Fig. 12, furan is mainly converted to FA, which is also the same as that observed in flame C. Under pyrolysis conditions, the main products from FA are pC₃H₄ + CO, while most FA gives C₃H₃ + HCO in flame C. Besides to FA, decomposition to C₂H₂ + CH₂CO is another important consumption pathway of furan pyrolysis (25.2%). However, this channel is a minor pathway in flames even under the richest condition. In addition, 7.8% of furan disappears by reactions with H and CH₃ radicals, forming methylfuran, furyl-2, furyl-3, C₄H₅O-2 and C₄H₅O-3 radicals. Furyl-2 can decompose to C₂H₂ + HCCO and CH≡C-CH=C=O + H via CH=CH-CH=C=O radical. By β-scission to CH≡C-CH=CH-O, furyl-3 can give C₃H₃ + CO and CH≡C-CH=C=O + H. In contrast, the pathway to CH≡C-CH=C=O + H from CH=CH-CH=C=O is not observed from the flame studies. Moreover, C₄H₅O-2 and C₄H₅O-3 finally produce C₂H₂ + CH₂CHO and C₃H₅ + CO, respectively, while the formations of these two radicals are much more involved in the consumption of furan in the flames.

Fig. 12.

Rate-of-production analysis for the consumption of furan at a temperature of 1527 K and a 64.8% conversion of furan in the furan pyrolysis.

Figure 13 presents the comparison of the predicted furan and product profiles with the experimental results (2% furan/98% Ne, 1533 K, 198 Torr) reported by Fulle et al. [15], in which symbols are measured data and solid and dash lines are respective predictions by the current model and the mechanism of Fulle et al. [15]. Although CO and propyne are underpredicted slightly at the end of the observation period, a globally correct prediction can be observed for the current model. It should be noted that no other products were detected within the period of ~800 μs and only the two unimolecular dissociation reactions were involved in the model of Fulle et al. [15]. They also determined the ratio [C₂H₂]/[CO] and gave an expression [C₂H₂]/[CO] = (5.5 10⁻⁹) T^2.5 by fitting their own results and that of Lishitz et al. [12]. In this work, the predicted ratios of [C₂H₂]/[CO] are 0.45 at 400 μs and 0.44 at 800 μs, which are very close to respective 0.42 and 0.40 that are calculated using the fitted expression of Fulle et al. [15].

Fig. 13.

Species mole fractions versus residence time during the pyrolysis of furan (2% furan/98% Ne, 1533 K, 198 Torr): symbols are experimental results from Fulle et al. [15]; solid and dashed lines are predictions of the present work (PW) and Fulle et al. [15], respectively.

To analyze the difference of the rate constants calculated in this work for furan pyrolysis, it is necessary to compare them with previous measurements and calculations, as displayed in Fig. 14. The unimolecular reactions for furan pyrolysis are commonly accepted as dissociation to CO + pC₃H₄ and C₂H₂ + CH₂CO [12,14,15,18,21], while CO + pC₃H₄ is dominant at temperatures lower than 1270 K [11,13]. At temperatures higher than 1550 K, furan can generate C₃H₃ [18]. As seen in Fig. 14, only the total reaction, including routes of CO + pC₃H₄ and C₂H₂ + CH₂CO are considered. In the current model and mechanism of Sendt et al. [21], the reaction furan = FA is used since it is the rate-determining step to form CO + pC₃H₄. Generally, the rate constant of this work is in good agreement with previous ones predicted by Lishitz et al. [12], Bruinsma et al. [13], Organ and Mackie [14] and Sendt et al. [21]. The low-temperature rate constants given by Grela et al. [11] are higher than the current model and measurements of Organ and Mackie [14], which was also observed by Sendt et al. [21]. The model of Fulle et al. [15] showed good agreement with the present mechanism at temperatures higher than 1300 K, but displays a slightly lower rate constant than the current ones at lower temperatures.

Fig. 14.

Comparison of rate constants: Arrhenius plots of the rate constant for furan thermal decomposition, in which short dash line is the date of Grela et al. [11], thin solid line Lifshitz et al. [12], dot line Bruinsma et al. [13], dash dot line Organ and Mackie [14], thin dash line Fulle et al. [15], solid dash line Sendt et al. [21] and thick solid line the present work (PW).

5. Conclusions

An experimental and numerical investigation has been conducted to analyze the chemical structures of three low-pressure premixed furan/O₂/Ar flames with tunable synchrotron VUV photoionization and molecular-beam mass spectrometry. About 40 combustion intermediates and products have been identified by measurements of photoionization efficiency spectra. Mole fractions of the flame species have been calculated. A detailed furan combustion model has been developed and reasonable agreement has been obtained between experimental measurements and simulations. The current mechanism has also been successfully validated against previous data obtained for furan pyrolysis. However, further studies still remain to improve this first attempt of mechanism for the combustion of furan.

In flames, the width of the reaction zone is increased and the peak positions of most intermediates are shifted downstream with the equivalence ratio increasing; furan is consumed mainly by metatheses leading to furyl radicals, OH addition to the double bond of furan giving 2-propenal and CH=CH-CHO radicals by β-scission, isomerization forming formyl allene via 1,2-hydrogen migration; benzene is formed mainly by isomerization of fulvene which comes from the combination of the propargyl radicals. A sensitivity analysis indicates that the reaction furan =CH₂CCHCHO has a strong promoting effect, while the decomposition of CH₂CCHCHO to CO and pC₃H₄ in flame with Φ = 1.4, and CH₂CHCHCHO to CO and C₃H₅ radical in flame with Φ = 2.2 have strong inhibiting effects on furan decomposition. Under pyrolysis conditions, the major decomposition products of furan are CO + pC₃H₄ and C₂H₂ + CH₂CO. Moreover, the present rate constants of furan dissociation at high pressures based on ab initio calculations are in good agreement with previous experimental measurements and calculations.