A high temperature and atmospheric pressure experimental and detailed chemical kinetic modelling study of 2-methyl furan oxidation

Abstract

An experimental ignition delay time study for the promising biofuel 2-methyl furan (2MF) was performed at equivalence ratios of 0.5, 1.0 and 2.0 for mixtures of 1% fuel in argon in the temperature range 1200–1800 K at atmospheric pressure. Laminar burning velocities were determined using the heat-flux method for mixtures of 2MF in air at equivalence ratios of 0.55–1.65, initial temperatures of 298–398 K and atmospheric pressure. A detailed chemical kinetic mechanism consisting of 2059 reactions and 391 species has been constructed to describe the oxidation of 2MF and is used to simulate experiment. Accurate reproduction of the experimental data has been obtained over all conditions with the developed mechanism. Rate of production and sensitivity analyses have been carried out to identify important consumption pathways of the fuel and key kinetic parameters under these conditions. The reactions of hydrogen atom with the fuel are highlighted as important under all experimental conditions studied, with abstraction by the hydrogen atom promoting reactivity and hydrogen atom addition to the furan ring inhibiting reactivity. This work, to the authors knowledge, is the first to combine theoretical and experimental work to describe the oxidation of any of the alkylated furans. The mechanism developed herein to describe 2MF combustion should also function as a sub-mechanism to describe the oxidation of 2,5-dimethyl furan whilst also providing key insights into the oxidation of this similar biofuel candidate.

1 Introduction

The efficient conversion of abundant waste lignocellulosic biomass, not destined for human or animal consumption, into renewable products is a major focus of current research [1-3], as it may offer a means to reduce our reliance on fossil fuel derived products in both the fine chemicals and transportation sectors. Recent developments have focused attention on 2,5-dimethylfuran (25DMF) as a possible alternative transportation fuel, with efficient production via the highly versatile platform chemical 5-hydroxymethylfurfural now a possibility [4-7].

25DMF offers significant advantages over the current market leading biofuel, ethanol, in terms of its physicochemical properties as well as its novel production processes. Its energy density (31.5 MJ L⁻¹) [8] is greater than ethanol by some 40%, rivaling that of gasoline, with its higher boiling point (366 K) and lower aqueous solubility making it compatible in terms of transportation and storage. Recent engine tests in direct-injection spark-ignition (DISI) engines [9, 10] have shown that 25DMF, unlike ethanol, can be burned pure in current internal combustion engines with similar performance to gasoline. Measurements of specific emissions showed carbon monoxide (CO) and hydrocarbon emissions (HC) to be lower than those of gasoline, although greater than those of ethanol. Nitrous oxide and particulate matter emissions were seen to be greater than ethanol and gasoline.

2-methylfuran (2MF) has also very recently entered the fray as a possible alternative biofuel due to the development of novel production methods [11, 12]. Engine tests [13] in a DISI engine have been carried out as a result, with comparisons made to conventional research octane number (RON) 95 fuel and ethanol. HC emission reductions of up to 61% were observed when using 2MF as a fuel when compared with RON 95 with efficiency improvements of up to 9.9% observed. Like 25DMF, greater nitrous oxide emissions were measured.

From a chemical kinetic perspective, some of the earliest experimental work on the furans has focused on their pyrolysis. Grela et al. [14] determined the decomposition rates of furan, 2MF and 25DMF in a heated flow reactor at very low pressures (1 mTorr) and temperatures of 1050–1270 K, analysing the final products with online mass spectrometry. The presence of carbon monoxide amongst the decomposition products for all three reactant molecules indicated common decomposition pathways.

Similarly, Lifshitz and co-workers [15–17] carried out single pulse shock tube experiments to study the thermal decomposition of furan, 2MF and 25DMF at pressures of 2 atmospheres, in the temperature range 1050–1460 K and residence times of 2 milliseconds, using gas chromatography to analyse the post shock product distributions and developing chemical kinetic mechanisms to rationalise their results. Both Grela et al. and Lifshitz and co-workers found the rate of decomposition of these furans to increase with increasing alkylation of the furan ring. Lifshitz and co-workers also found CO to be a major decomposition product for all three reactants, again indicating similar decomposition channels.

More recent theoretical work has shone light on the decomposition channels of the furans. Sendt et al. [18] used ab initio quantum chemical methods and transition state theory to study the thermochemistry and kinetics of the thermal decomposition channels of furan. They found that 1,2-hydrogen atom migrations to form singlet cyclic carbene intermediates were thermochemically and kinetically the most favoured decomposition pathways, concluding that direct ring opening to form either singlet or triplet products was simply too energetic. In a similar work Liu et al. [19,20] reached identical conclusions.

Simmie and Curran [21] employed ab initio calculations to determine the formation enthalpies and bond dissociation energies of a range of alkylated furans, including 2MF and 25DMF. They noted the presence of considerably weak carbon–hydrogen bonds on the alkyl side-chain for these species, which readily explains the increasing reactivity observed experimentally by Grela et al. and Lifshitz and co-workers, with increasing alkylation of the furan ring.

Simmie and Metcalfe [22] also used ab initio methods to calculate energetics and kinetics of a range of unimolecular decomposition pathways and free radical reactions involving 25DMF, and to a lesser extent 2MF. They concluded, like Sendt et al. and Liu et al., that hydrogen atom migrations to form singlet carbenes play an important role in the decomposition of these species, but the presence of weak C-H bonds in the case of 2MF and 25DMF offers an important site for abstraction by free radicals (Ḣ, ȮH, ĊH₃ etc.) and a key source of reactive hydrogen atoms.

They also rationalise the formation of 2MF from 25DMF, as observed experimentally in flames [23] and shock tubes [17], via a Ḣ atom addition ĊH₃ radical elimination sequence, with a similar process capable of converting 2MF into furan, as observed by Lifshitz and co-workers [16].

Recently, the kinetics of the reaction of 25DMF with hydrogen atoms has been studied by Friese et al. [24] behind reflected shock waves from 970–1240 K and at pressures of 1.6 and 4.8 bar. It was found that the principal pathway proceeds via an addition-elimination mechanism to yield 2-methylfuran and methyl radical.

This work will focus on the combustion characteristics of 2MF, a possible biofuel candidate, a known intermediate in the combution of 25DMF and a species whose structural similarities to 25DMF should offer insight into the oxidation pathways of both furanics. This study is believed to be the first to combine experimental work, in the form of ignition delay times and laminar burning velocities, and theoretical work, in the form of a detailed chemical kinetic model, to describe the oxidation of any of these alkylated furans.

2 Experimental

2.1 Shock Tube Ignition Delay Measurements

The low-pressure shock tube facility at NUI Galway has previously been in detail by Johnson et al. [25] and will not be described further here.

Before introducing the fuel (99% purity; Sigma-Aldrich) to the mixing tanks, and to minimise the presence of atmospheric gases in the fuel, it was degassed by a series of freeze-pump-thaw cycles until no gas was observed to escape from the fuel. Oxygen (99.5% purity; BOC Ltd.) and argon (99.998% purity; BOC Ltd.) were introduced to the mixing tanks through the manifold from gas cylinders.

Three different mixtures were prepared using the method of partial pressures. Experimental ignition delay times for mixtures of 1% 2MF in 12%, 6% and 3% O2 in argon corresponding to equivalance ratios (Φ) of 0.5, 1.0 and 2.0 were obtained in the temperature range 1200-1800 K and at atmospheric pressure. Reflected shock temperatures and pressures were calculated using GasEq [26]. The driver gas used was helium (99.99% purity; BOC Ltd.).

2.2 Flat Flame Laminar Burning Velocity Measurements

The heat–flux method was first proposed by de Goey et al. [27] in 1993. This method does not require stretch correction or extrapolation of the data as stretching of the flame does not occur. The apparatus and method used in this study have very recently been described by Dirrenberger et al. [28] and only a synopsis of the experimental conditions and uncertainties are given.

Flame speeds for 2MF (≥ 98% purity; Sigma-Aldrich) in air (O₂ and N₂; 99.995% purity, Messer) have been measured at initial temperatures ranging from 298–398K and Φ = 0.55–1.65 at 1 atmosphere. Uncertainties in determination of the burning velocity are due to uncertainties in:

• mass flow measurements, with a maximum error of 0.5% per mass flow controller, as given by the manufacturer, Bronkhorst, and a maximum global error in laminar flame velocity of 1.5%.

• the thermocouples, with an error of 0.2 cm s⁻¹ in the laminar flame velocity. This error was measured by varying the gas flow rate by small amounts that did not affect the uniform temperature profile of the flame on the burner plate noticeably.

• flame distortions, for example edge effects, with an error of 0.2 cm s⁻¹ in the laminar flame velocity in the range of equivalence ratios studied. This error was measured in a similar fashion to the error in the thermocouples.

Uncertainties of around 1% were also present when determining the equivalence ratio due to mass flow effects, as given by the manufacturer. The temperature of the unburned gas mixture before and after it flowed through the plenum chamber was measured with a thermocouple. An error of 2 K was estimated. Errors in gas and liquid fuel purity were not significant as high purity compounds were used.

All experimental data is tabulated and available in electronic supplementary information.

3 Kinetic Model Development

A detailed chemical kinetic model consisting of 2059 reactions and 391 species has been developed to describe the combustion of 2MF. Detailed within this are furan [18,29] and aromatic [30] mechanisms from the literature and a sub-mechanism to describe the combustion of hydrogen and C₁–C₄ species. Details of the hydrogen/CO sub-mechanism are partially described in Keromnes et al. [31] and will be fully described in an upcoming publication [32]. C₁–C₃ chemistry is based on the work of Lowry et al. [33] with the most recent details described by Metcalfe et al. [34]. The C₄ chemistry of Healy et al. [35] is in use with chemistry for unsaturated C₄ species from Laskin et al. [36].

An in-depth ab initio study has been carried out to explore the potential energy surface and calculate kinetics for the unimolecular decomposition pathways and reactions of the hydrogen atom with 2MF. The formation of four unique carbenes and four unique Ḣ atom addition reactions are possible in the case of 2MF, given the asymmetry of the fuel. These channels are exemplified by a series of ring opening, unimolecular rearrangement and intramolecular hydrogen abstraction reactions which are too complex to discuss in detail given formatting limitations. They will form the basis of a more detailed publication which will also focus on the current kinetic model validation against the pyrolysis data of Lifshitz et al. [16] which will not be discussed here. However, the models performance against this data is presented in the supplementary material however.

The rate constant for the scission of the weak alkyl C-H bond in 2MF to give the 2-furanylmethyl radical (2MF2R, Figure 1) and the Ḣ atom has been estimated in the reverse direction, that is the recombination of two radicals, with a rate constant of 1 × 10¹⁴ cm³ mol⁻¹ s⁻¹ in accordance with Allara and Shaw [37]. The forward high pressure limiting rate constant of 2.52 × 10¹²T^0.9 exp(−42, 974/T) s⁻¹ in turn is determined from microscopic reversibility.

Fig. 1.

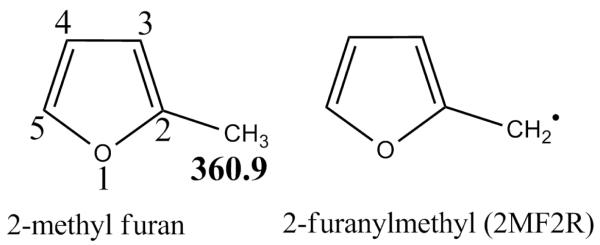
Numbering system for 2-methyl furan ring with recommended [21] bond dissociation energy (kJ mol⁻¹) of alkyl C–H bonds and structure of primary abstraction/fission product.

Scission of any of the ring-hydrogen or ring-carbon bonds has been estimated as above with rate constants of 1 × 10¹⁴ cm³ mol⁻¹ s⁻¹ and 1 × 10¹³ cm³ mol⁻¹ s⁻¹ respectively. All unimolecular decomposition channels of the fuel are further treated as pressure dependant using the high pressure limiting rate constant together with a chemical activation formulation based on Quantum Rice-Ramsperger-Kassel (QRRK) theory, as described by Dean [38].

Given the presence of weak side chain C-H bonds (Figure 1), the kinetics of the reactions of the Ḣ atom with the fuel and abstraction reactions from this site are pertinent. Rate constants for Ḣ atom addition to the ring and abstraction from the alkyl group have therefore been calculated based on CBS-QB3 [39] energetics and partition functions, with a one–dimensional hindered internal rotation approximation utilised. We calculate H atom abstraction by the Ḣ atom from the alkyl side chain to occur with a rate of 1.89 × 10⁶T^2.38exp(−2, 369/T) cm³ mol⁻¹ s⁻¹. In the final model this rate constant has been increased by a factor of two in order to improve agreement with experimental flame speeds as it is seen as a sensitive variable. This adjustment is likely within the uncertainty of our calculation.

For Ḣ atom addition at C2, C3, C4 and C5 the respective high pressure limiting rate constants (in cm³ mol⁻¹ s⁻¹) are calculated as:

$$k\left(\mathrm{C}2\right)=7.53\times {10}^8{T}^{1.51}\exp (-956.1∕T)$$

$$k\left(\mathrm{C}3\right)=1.00\times {10}^9{T}^{1.44}\exp (-2,178∕T)$$

$$k\left(\mathrm{C}4\right)=1.37\times {10}^5{T}^{2.50}\exp (-1,907∕T)$$

$$k\left(\mathrm{C}5\right)=1.29\times {10}^9{T}^{1.48}\exp (-1,026∕T)$$

Rate constants for abstraction of the methyl hydrogens by the ȮH and ĊH₃ radicals are taken as half of those calculated in the case of 25DMF [22], with the rate constant for abstraction by the HȮ₂ radical similarly determined. A simple factor of two division of the A-factor for these rate constants is appropriate given the corresponding reduction in the number of abstractable hydrogens. Rate constants for abstraction by O₂ and the Ȯ atom are based on those recently recommended in the case of toluene [30], a system which displays similar weak C-H bonds (375 +− 5 kJ mol⁻¹ [40]) which can undergo abstraction/fission to form the resonance stabilised benzyl radical.

The kinetics of n-butadienyl (Ċ₄H₅-n or ĊH = CH − CH = CH₂) pyrolysis and oxidation were found to be sensitive parameters and have been updated from those recommended by Laskin [36] based on CBS-QB3 energetics and partition functions and a QRRK treatment to account for the pressure dependency of these reactions.

At 1 atmosphere, the formation of vinylacetylene (C₄H₄) and Ḣ occurs with a rate constant of 1.02 × 10⁵¹T^−11.42exp(−27, 284/T) s⁻¹ and for the formation of C₂H₂ + Ċ₂H₃ we calculate a rate constant of 4.52 × 10⁴⁴T^−9.65exp(−25, 618/T) s⁻¹. Rate constants for the reactions of O₂ with Ċ₄H₅-n, are updated based on Marinov’s recommended kinetics for the oxidation of vinyl [41], which offers close analogy.

Thermochemistry for all species novel to the 2MF mechanism are generated based on the computational methods described above, with the THERMO application of the Multiwell Program Suite [42] used to generate both thermochemical parameters and high pressure limiting rate constants.

The complete kinetic model including species thermodynamic and transport properties is available in electronic supplementary material.

3.1 Simulation of Experiments

Simulations were carried out using Chemkin-Pro [43] with the Aurora package under constant volume conditions utilised for the simulation of shock tube ignition delay times. Flame speed simulations have been carried out using the Premix module with mixture averaged species transport equations preferred to a multi-component approach in order to reduce computational cost, given the size of the current mechanism. All flame speed simulations are carried out to a GRAD and CURV of 0.02 to offer a grid independent solution and we include effects of thermal diffusion. In the absence of experimentally determined transport properties for all novel species in the 2MF mechanism, we have estimated transport properties using the Transport Data Estimator package of the Reaction Mechanism Generator software of Green and co-workers [44].

Sensitivity analyses are carried out in order to identify the key reactions which control the ignition delay time and laminar burning velocity under the experimental conditions presented. For each reaction in the current mechanism, rate constants are multiplied by two, divided by two and the respective ignition delay times calculated in a “brute force” approach. Sensitivity coefficients (S_i) are then calculated according to equation 1:

$$S_i={\log }_{10}\left\{\right({\tau }_{k\times 2}∕{\tau }_{k∕2})∕{\log }_{10}(2∕0.5\left)\right\}$$ (1)

with a negative sensitivity coefficient indicative of a reaction which promotes reactivity and vice versa. The first order sensitivity of the mass flow rate to the A-factor of each rate constant is used to determine those reactions which control the calculated laminar burning velocities.

4 Results and Discussion

4.1 Ignition Delay Times

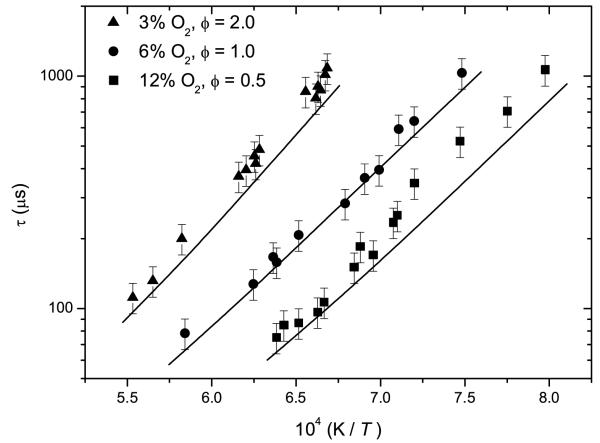
Experimental ignition delay times and those calculated by the current model are defined in Figure 2. Experimentally, the effect of increasing O₂ concentrations from 3% (Φ = 2.0) through 6% (Φ = 1.0) to 12% (Φ = 0.5) is clearly visible in the form of increased reactivity characterised by reduced ignition delay times.

Fig. 2.

Experimental ignition delay times (symbols) with 15% error bars as a function of temperature and O₂ concentration with model predictions (lines).

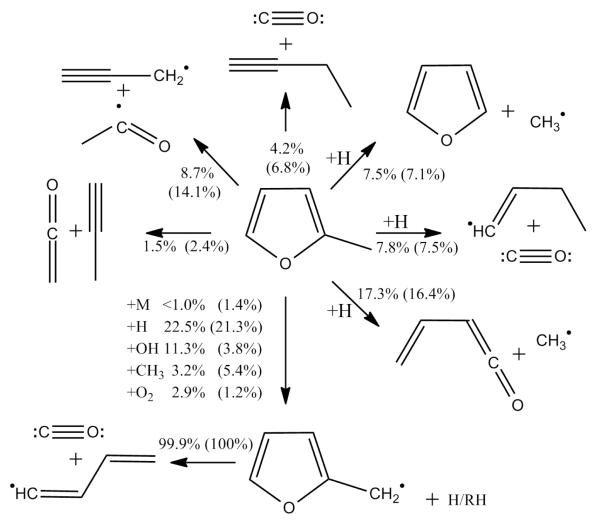
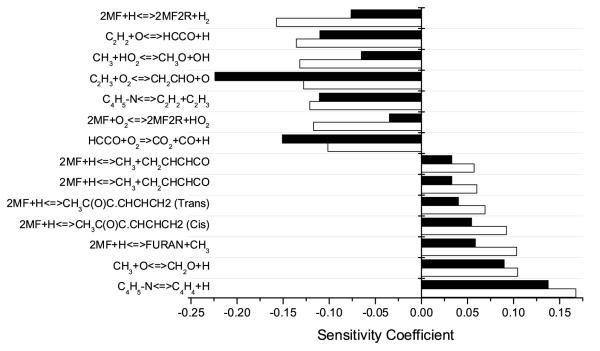
The current model reproduces the observed experimental data well under all conditions. In order to identify key reactions under varying concentrations of O₂, rate of production analyses (Figure 3) at 1500 K and at 20% fuel consumption were carried out at Φ = 0.5 and Φ = 2.0. Sensitivity analyses, visible in Figure 4, were carried out at the same temperature and equivalence ratios.

Fig. 3.

Rate of production analysis showing initial consumption reactions of 2-methyl furan. Carried out under shock tube conditions at 20% fuel consumption, 1500 K at Φ = 0.5 and Φ = 2.0 (parenthesis).

Fig. 4.

Ignition delay sensitivity analysis at 1500 K, Φ = 0.5 (open bars) and Φ = 2.0 (solid bars). Positive coefficients correspond to reactions which inhibit reactivity and vice versa. The reaction of Ḣ with O₂ to give ȮH> and Ȯ has been omitted for clarity.

Under fuel lean conditions, rate of production analysis shows a total of 39.9% of the fuel forms the 2-methylfuranyl radical (2MF2R), primarily by abstraction by the reactive Ḣ (22.5%) and ȮH (11.3%) radicals. Under fuel rich conditions we see an expected decrease in the contribution of ȮH radical abstraction (3.8%) to the consumption of the fuel, as a result of decreasing ȮH production from the reaction of Ḣ atom with O₂. 2MF2R ultimately decomposes to form CO and the Ċ₄H₅-n radical, which primarily decomposes to vinyl and acetylene or vinylacetylene and hydrogen atom.

Simple fission of the side chain C-H bond contributes very little to the fuel consumption under lean and rich conditions, despite its relative weakness, consuming only 1.4% in the latter case. The primary unimolecular decomposition pathways seen in the rate of production analyses are routed through carbene intermediates, with ultimate formation of acetyl and propargyl radicals (14.1%) or 1-butyne and CO (6.8%) under rich conditions. A 5-4 hydrogen atom migration about the ring consumes 2.4% of the fuel with ketene and propyne being formed from the subsequent elimination reaction.

Hydrogen atom addition at C₂ consumes 15.4% of the fuel at Φ = 0.5 with 7.5% of this forming furan and methyl radical and 7.8% CO and 1-buten-1-yl (Ċ₄H₇-n or ĊH = CH − CH₂ − CH₃). Hydrogen atom addition at C5 consumes 18.3% of the fuel under lean conditions, of which 17.3% ultimately forms vinyl ketene and methyl radical either directly via chemical activation (6.8%) or via an acyclic Ċ₅H_O radical ĊH₃C(O)ĊCHCHCH₂ in Figure 4) which undergoes demethylation.

Sensitivity analyses (Figure 4) have shown these hydrogen atom addition reactions to inhibit reactivity for a number of reasons. These reactions prevent Ḣ atoms from reacting with O₂ to form hydroxyl radicals and atomic oxygen by consuming 48.6% and 53.2% of the total hydrogen atoms in the system under lean and rich conditions respectively. This is clear in the increased sensitivity of these reactions under lean conditions. They also convert this reactive hydrogen atom into the less reactive methyl radical. Additionally, furan is known to be less reactive than the alkylated furans.

Little is known about the combustion of vinyl ketene in truth and we rely largely on estimated kinetics from Alzueta et al. [45] to describe it’s combustion at present. Having said this, vinyl ketene was detected in low-pressure 25DMF flames by Wu et al. [23] on the basis of it’s ionization energy, and it is not unreasonable to suggest that it’s production therein was from 2MF via this hydrogen atom addition reaction.

Whilst hydrogen atom addition reactions tend to inhibit reactivity, increasing the rate of hydrogen atom abstraction by the hydrogen atom is seen to largely promote reactivity. Although interestingly, the decomposition of the product of the abstraction channel, Ċ₄H₅-n, to C₄H₄ and the hydrogen atom, is actually seen to be the most inhibiting reaction under lean and rich conditions, despite the regeneration of hydrogen atoms observed from this reaction.

It is important to note that the decomposition of Ċ₄H₅-n to C₄H₄ and Ḣ is not active in the reverse direction and the inhibition observed is likely due to formation of the unreactive C₄H₄ species, which is a well known intermediate in the formation of soot precursors. Conversely, decomposition of Ċ₄H₅-n to C₂H₂ and Ċ₂H₃ is seen to promote reactivity as chain branching can occur from the subsequent oxidation and decomposition reactions of these species which are visible in Figure 4.

Increasing the rate of abstraction by O₂ is seen to promote reactivity, particularly under fuel lean conditions, as it provides a source of HȮ₂ radicals which can react with methyl to produce CH₃Ȯ and ȮH, with CH₃Ȯ primarily undergoing decomposition to form formaldehyde and hydrogen atom.

4.2 Laminar Burning Velocities

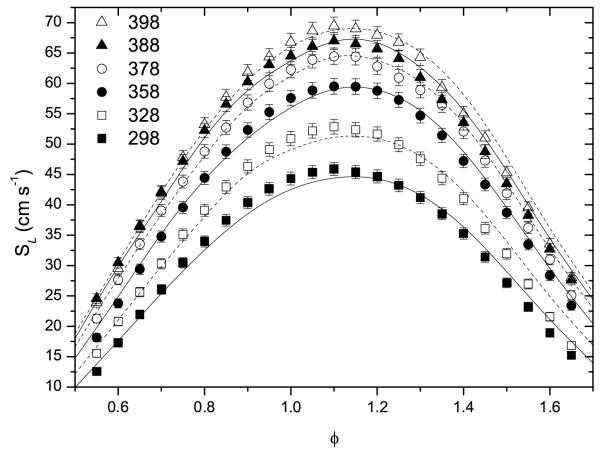
Experimental laminar burning velocities and those calculated by the current model are shown in Figure 5. Measured flame speeds are seen to increase with increasing initial temperatures, with peak reactivity for a given initial temperature occurring under conditions slightly richer than stoichiometric in all cases. The current model captures these trends well with few empirical alterations required to obtain this agreement, although current simulations are tending to overpredict the flame velocity under rich conditions.

Fig. 5.

Experimental flame speeds (symbols) with calculated errors as a function of initial temperature and equivalence ratio at pressures of 1 atmosphere and current model predictions (lines) with solid lines corresponding to closed symbols.

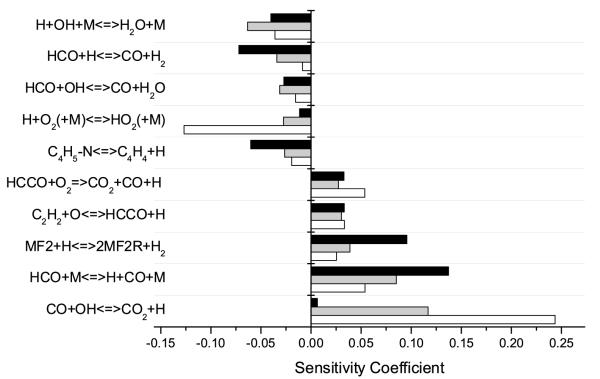
Sensitivity analyses detailing important kinetic parameters at lean (Φ = 0.6), peak flame speed (Φ = 1.1) and rich (Φ = 1.6) conditions at an initial temperature of 358 K are visible in figure 6. These sensitivity analyses exhibit that reactivity within the flame under lean and rich conditions is very much dominated by the chemistry of smaller hydrocarbons, in particular those reactions which produce and consume the hydrogen atom.

Fig. 6.

Sensitivity coefficients for reactions found to be important in predicting laminar burning velocities at Φ = 0.6 (open bars), Φ = 1.1 (grey fill) and Φ = 1.6 (black fill) at 358 K. Positive coefficients correspond to reactions which promote reactive and vice versa. The reaction of Ḣ with O₂ to give ȮH and Ȯ has been omitted for clarity.

Flame speeds are controlled by the reactions of hydrogen with molecular oxygen, although under lean conditions the oxidation of CO by the ȮH radical to produce CO₂ and the Ḣ atom is equally as important. Hydrogen atom recombinations with ȮH and O₂ to produce unreactive H₂O and HȮ₂ respectively, are amongst the most inhibiting reactions.

Formyl radical (HĊO) decomposition to carbon monoxide and hydrogen is promoting under all equivalence ratios and the abstraction reactions which therefore prevent this decomposition are seen to inhibit the overall reactivity. Acetylene oxidation by Ȯ to produce HĊCO and Ḣ is seen as promoting not only due to the direct production of Ḣ atoms, but in turn HĊCO can be oxidised by O₂ to produce a further source of this reactive species.

The majority of the kinetic parameters novel to the oxidation of 2MF are relatively insensitive and hydrogen atom abstraction by the hydrogen atom is the only reaction whose sensitivity is seen to be on a par with those of smaller hydrocarbons. This led to the adjustment of this rate constant by a factor of two as initial flame velocities were under predicted by the unaltered model. Adjustment of any rate parameters governing the combustion of these smaller species is unjustified as the kinetics of these reactions are well understood and we do not consider them candidates for optimisation against the current experimental data.

5 Conclusions

A detailed chemical kinetic model consisting of 2059 reactions and 391 species which describes the combustion of 2-methyl furan has been developed and validated against novel experimental ignition delay times and laminar burning velocities. The current model is capable of accurately reproducing the experimental data as a function of both temperature and equivalence ratio in the high temperature regime.

Sensitivity and rate of production analyses have been carried out to identify important reactions of the fuel. Kinetics of the reactions of the Ḣ atom with the fuel are seen to be amongst the most sensitive in terms of predicting ignition delay times and flame speeds under the conditions studied and are therefore important in terms of predicting the global reactivity of the system. In particular, the branching ratio between hydrogen atom abstraction and addition reactions is important, as the former promotes reactivity and the latter inhibits reactivity.

Abstraction by O₂, which is estimated as part of this work, is seen to be amongst the promoting reaction seen under fuel lean conditions in relation to ignition delay times; an experimental or theoretical determination of this rate constant would reduce the uncertainty in this estimated parameter. The kinetics of n-butadienyl radical decomposition, which have been computed as part of this work, are also highlighted as important, as it is effectively the sole product of abstraction reactions from the alkyl side chain in the high temperature regime.

Despite the excellent model agreement obtained in terms of the high temperature reactivity of 2-methyl furan, further experimental work is key to developing our understanding of this novel fuel. The gathering of shock tube ignition delay times and laminar burning velocities at elevated pressures and high temperatures are advised as a further validation of the current kinetic model. Intermediate to high temperature speciation profiles under oxidative conditions are an absolute necessity to fully understand the combustion of 2MF and further validate the mechanism proposed. Accurate quantification of furan, vinyl ketene and H₂ yields is advised as the concentrations of these species are important indicators of the kinetics of hydrogen atom addition and abstraction reactions.

The experimental and modelling work presented herein should provide a basis upon which this future work on 2MF can be built, with the inclusion of the current 2MF mechanism as a sub-mechanism to describe the combustion of 25DMF also a key output of the present study.