Genetic Estimates of Population Age in the Water Flea, Daphnia magna

Abstract

Genetic datasets can be used to date evolutionary events, even on recent time scales if sufficient data are available. We used statistics calculated from multilocus microsatellite datasets to estimate population ages in data generated through coalescent simulations and in samples from populations of known age in a metapopulation of Daphnia magna in Finland. Our simulation results show that age estimates improve with additional loci and define a time frame over which these statistics are most useful. On the most recent time scales, assumptions regarding the model of mutation (infinite sites vs. stepwise mutation) have little influence on estimated ages. In older populations, size homoplasy among microsatellite alleles results in a downwards bias for estimates based on the infinite sites model (ISM). In the Finnish D. magna metapopulation, our genetically derived estimated ages were biased upwards. Potential sources of this bias include the underlying model of mutation, gene flow, founder size, and the possibility of persistent source populations in the system. Our simulated data show that genetic age estimation is possible, even for very young populations, but our empirical data highlight the importance of factors such as migration when these statistics are applied in natural populations.

Genetic data carry a wealth of information on the history of the populations from which they are obtained. Estimable parameters include the effective population size (Waples 1989), migration rates among semi-isolated populations (Beerli 2006), the number of populations represented in a sample (Waples and Gaggiotti 2006), divergence time between incipient species (Nielsen and Wakeley 2001), mutation rates (Knowlton and Weigt 1998; Wares and Cunningham 2001), and the time that has passed since a population expansion (Rogers 1995). The accumulation of genetic diversity in expanding populations provides a means of dating the divergence between species, populations, or alleles. The same basic principles are applied whether our interest lies in estimating a neutral rate of mutation (e.g., using geminate species pairs; Knowlton and Weigt 1998), timing divergence between lineages (Robinson and Dillon 2008), or timing population expansions (Rogers 1995). These estimates are attainable because the observed diversity in the population (or divergence between groups) is a stochastic function of the number of generations since the event of interest and the mutation rate at the marker loci.

The purpose of this study was to assess the ability of two population genetic summary statistics to recover population ages from multilocus microsatellite datasets sampled from recently colonized populations. We calculated the distribution of pairwise differences among microsatellite alleles (P_K distribution, t; Shriver et al. 1997) and the variance in microsatellite allele size (s² _AS; Di Rienzo et al. 1994) to estimate population age. The distribution of pairwise differences (“mismatch distribution”) was originally studied for DNA sequences by Slatkin and Hudson (1991) and Di Rienzo and Wilson (1991), and further developed by Rogers and Harpending (1992) and Rogers (1995). The mismatch distribution has been used to date evolutionary events including the expansion of humans out of Africa (Rogers 1995), human movement to the North American continent (Bonatto and Salzano 1997), and an ancient population explosion of grayling inhabiting Lake Baikal (Koskinen et al. 2002). Shriver et al. (1997) first applied these methods to microsatellite data (the P_K distribution). More recently, similar methods have been used to estimate the age of individual Populus clones, using genetic data collected from multiple ramets (Ally et al. 2008; Ally et al. 2010).

The variance in microsatellite allele size (in units of repeats; Di Rienzo et al. 1994), like the number of pairwise differences between alleles, is expected to grow with time following a population expansion. This variance has been used as a data summary when applying approximate Bayesian computation (ABC) to microsatellite datasets (Estoup et al. 2001). One of the primary differences between estimates provided by these two statistics is the underlying model of mutation that they assume. Because the mismatch distribution was originally studied with DNA sequence data in mind, estimates based on the pairwise number of differences assume an ISM, where all mutations create novel DNA sequences. On the other hand, those based on the variance in allele size assume either a stepwise (SMM) or a two-phase mutation model (TPM), both of which account for mutations that are hidden by size homoplasy and convergence. For this reason, the ISM is not generally applicable to microsatellite data. However, because we focus on recently colonized populations, the influences of homoplasy should be minor (Estoup et al. 2002). In our study, both t and s ² _AS were applied to datasets generated through coalescent simulations and sampled from populations in the Finnish Daphnia magna metapopulation.

Our coalescent simulations were designed to assess the accuracy and precision of age estimates from these statistics (t and s ² _AS) and to determine the necessary number of marker loci needed to estimate ages in recently colonized populations. Additional simulations determined the sensitivity of the estimates to the assumptions of our model, specifically the founder size. Given the short time frames of interest in this study, we hypothesized that the mutational model assumed (ISM vs. SMM) would have little influence on estimated ages.

For the empirical dataset, we chose the well-studied Finnish D. magna metapopulation. In this system, populations of D. magna inhabit ephemeral pools on an archipelago of rocky islands off the southern coast of Finland. These freshwater crustaceans are cyclically parthenogenetic, producing genetically identical daughter clones for most of the growing season. As the conditions in habitat patches deteriorate (pools dry up, populations become crowded, etc.), Daphnia switch to sexual reproduction and produce ephippia (resting eggs). The Daphnia populations in southern Finland have been convincingly shown to exhibit dynamics consistent with a metapopulation model (Hanski and Ranta 1983), wherein individual populations are subject to local extinction with recolonization from neighboring, occupied habitat patches. Because recolonization in the Daphnia metapopulation typically is achieved by a very small number of genotypes (Haag et al. 2005), genetic diversity in these populations should correlate with the length of time since recolonization. Pools on a number of islands in the Finnish archipelago have been monitored for occupancy of three Daphnia species for nearly 30 years (Pajunen and Pajunen 2003). This long-term monitoring project provided known ages for our sampled populations, facilitating assessments of the performance of age estimation statistics in natural systems.

Conceptually, the application of these statistics to date evolutionary events is not a new idea. The same methods are applied when interspecific genetic divergence is used to estimate the time to a most recent common ancestor or when intraspecific genetic diversity is used to estimate the timing of demographic expansions. The novelty of our approach arises from two aspects of our analysis. First, we apply the t statistic, originally developed with DNA sequence data in mind (Rogers 1995), to microsatellite datasets. Second, we use multilocus microsatellite datasets to estimate ages on very recent time scales (as few as 10 generations). Furthermore, this work is unique in that we apply these statistics to an empirical system where population age is known. Our study is divided into two parts: determination of the utility of these statistics in simulated datasets and application of the same statistics in an empirical system where our assumptions should hold. The results of our simulations demonstrate the potential of these summary statistics, when calculated from multilocus genetic data, for accurately and rapidly estimating population age and define a time frame when they are most useful. Our empirical data highlight areas for future study in the D. magna system and illustrate some limitations to the application of these statistics in natural populations.

Materials and Methods

Simulations

Simulated datasets were generated under simple demographic histories using the coalescent simulator ms (Hudson 2002). The simulations were designed to model the colonization of an isolated population by a very small number of founders. Our simulations modeled population expansion from a single haplotype to eliminate the potential influence of retained ancestral polymorphisms on estimated population ages. Similarly, these populations were completely isolated in our model (i.e., no immigration) to prevent immigrant alleles from inflating age estimates. These assumptions of single founding haplotypes and no immigration are unrealistic for many natural systems. However, within-host viral populations, bacterial infections, and species introductions provide examples of systems where one or both of these assumptions might be justifiable.

Simulated histories consisted of a single step-change in effective population size, t generations in the past, decreasing N _e from the contemporary effective size to the pre-expansion size (one haplotype). We chose to use the simpler, step-change model of population expansion rather than an exponential growth model because the distribution of pairwise differences is virtually identical (Rogers and Harpending 1992). With this assumption, the timing of population expansion is the same as the age of the population. For most biological populations, the statistics we employ provide an estimate of the timing of the most recent population expansion, rather than the absolute population age. However, these values are likely to be similar in many systems (e.g., metapopulations, exotic species invasions, pathogenic infections). Mutation rate was set at 1 × 10⁻⁴ for all simulations, a moderate rate for microsatellite loci (Jarne and Lagoda 1996). Three values of contemporary effective population size (N _e = 1000, 10 000, and 1 000 000) and five population ages (t = 10, 25, 100, 250, and 1000 generations) were simulated for datasets consisting of 5, 10, and 20 microsatellite loci. All possible combinations of effective population size (3 values), age (5 values), and number of loci (3 values) were simulated, resulting in 45 parameter combinations. Each coalescent simulation consisted of a sample of 50 diploid individuals. For each of the 45 parameter combinations, we simulated 200 replicates, yielding a total of 9000 datasets.

Additionally, three extra sets of 200 replicate simulations were conducted to assess the sensitivity of the age estimation methods to the number of founding individuals (N ₀ = 10, 100, and 1000 founding haplotypes) for one combination of parameters (N _e = 1 000 000; t = 100 generations; 20 loci). Because we simulated a single population in our coalescent models, the effect of gene flow on estimation methods was not examined. The effects of increasing immigration rates should be qualitatively similar to the effects of larger founding sizes and higher mutation rates; all serve to introduce additional diversity into the population. In addition, gene flow would also affect divergence among populations in the metapopulation. We are currently investigating the combined influences of founder size and gene flow in the D. magna system using ABC (manuscript in preparation).

Simulations were also conducted to investigate the upper bounds of age estimation with microsatellite markers. The timing of the population expansion was set at 2500, 5000, or 10 000 generations ago; simulations were conducted for both 5 and 20 locus datasets, with N _e fixed at 1000. These additional simulations extended the upper bounds of one of the parameter combinations above. The expectation for this set of simulations was that the methods would underestimate population ages, as the history of the population expansion is lost after 2N _e generations (the expected time to coalescence; Di Rienzo et al. 1994). The Perl script “ms2ms.pl” (Pidugu and Schlötterer 2006) was used to convert the output of all simulations to microsatellite genotypes, assuming a strict SMM (Ohta and Kimura 1973).

Empirical Data

The long-term monitoring project in the Finnish D. magna metapopulation (Pajunen and Pajunen 2003) provided known population ages for comparisons to ages estimated using the two statistics assessed in this study. In order to conduct these comparisons, populations of D. magna were collected from 14 rock pools on the small island of Storgrundet (59.822° N, 23.261° E), near the Tvärminne Zoological Station in Finland. DNA was extracted using a Puregene (Gentra Systems Inc., Minneapolis, MN) isolation protocol and 48 D. magna individuals from each of the 14 populations were genotyped at 14 microsatellite loci (Supplementary Table 1; Colson et al. 2009).

Microsatellite amplifications were performed using a modified version of the protocol given in Colson et al. (2009). Briefly, amplifications were conducted in 12.5 µL volumes, containing 1 × GoTaq colorless buffer (Promega Corp., Madison, WI), 1.5mM MgCl₂, 800 µM dNTPs, 500 µM of each primer in the amplified group (Supplementary Table 1), and 0.5U GoTaq polymerase (Promega Corp.). All fragments were amplified using the following temperature profile: 94 °C for 4min, followed by 35 cycles of 94 °C for 30 s, 53 °C for 30 s, and 72 °C for 30 s, and a final elongation at 72 °C for 4min. Multiplexing allowed the 14 loci to be amplified in a total of 6 reactions and genotyped in 4 submissions per individual. All genotyping runs were conducted on an ABI 3730 (Applied Biosystems, Inc., Foster City, CA) at the Georgia Genomics Facility (University of Georgia) using GeneScan Rox 500 size standard (Applied Biosystems, Inc.). Microsatellite alleles were scored using panels designed in GeneMarker v. 1.6 (SoftGenetics, LLC, State College, PA). Allele calls were visually inspected and recoded where necessary. Repeat units, fluorescent tags, and multiplex groupings for the 14 microsatellite loci used in this study are provided in Supplementary Table 1.

Data Analysis

Population ages were estimated from simulated and empirical microsatellite datasets using the P_K distribution (Shriver et al. 1997) and the variance in microsatellite allele size (in units of repeats; Di Rienzo et al. 1994). For the P_K distribution, the absolute differences in the number of repeats between sampled alleles, rather than the number of mismatched bases (as in the mismatch distribution; Rogers 1995), were calculated for each pair-wise comparison in the sample. Equations 2 and 3 from Rogers (1995) were used to calculate t, a measure of the central tendency of the distribution, for each locus. Then, t values were averaged across loci to provide an estimate of population age (in generations), t, according to the relationship

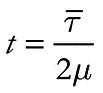() 1

where µ is the average mutation rate of the selected loci and 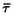is the mean t across loci (Rogers 1995).

Estimates of age based on allele size variance (s ² _AS) were obtained using the following equation (modified from Di Rienzo et al. 1994),

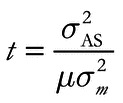() 2

where t is the time (in generations) since a population expansion, µ is the average mutation rate of the selected loci, and s ² _m is the variance in the change in the number of repeats associated with mutation. This equation can be parameterized for the particular mutational model through the latter parameter (s ² _m); for the simple SMM employed here, s ² _m = 1, but when mutations introduce changes of more than one repeat unit, s ² _m > 1 (i.e., the two-phase model; Di Rienzo et al. 1994). For multilocus datasets, s ² _AS was calculated for each locus and then averaged before applying Equation 2 to estimate population age.

For simulated datasets, age estimates for each of the 200 replicates were averaged for each of the 45 combinations of parameters. The coefficient of variation (CV), expressed as a percentage of the mean value, was calculated as a measure of the precision of the method. The relative bias of the estimator (a measure of the accuracy, also expressed as a percentage) was calculated as the difference between the simulated population age and the average estimated age (across 200 replicate datasets) divided by average estimated age. For the empirical dataset, estimated ages were tested for correlation to known ages, using a Pearson product-moment correlation. Cook’s distances were calculated to identify influential data points in our tests for correlation between estimated and known ages, using a cutoff of D _i > 4/n (Bollen and Jackman 1990), where D _i is Cook’s distance for an individual observation and n is the total number of observations. All data analyses were conducted in the R statistical computing environment (R Development Core Team 2008). All datasets, and the shell and R scripts used for data generation, processing, and analysis, are available from the corresponding author upon request.

Results

Simulations

Figure 1 illustrates the accuracy of age estimates based on t and s ² _AS for simulated datasets of 5 and 20 loci with N _e = 1000. For age estimates based on t, precision increased (CV decreased) as the age of the population or the number of sampled loci increased (Figure 2). CVs were generally lower for larger effective population sizes (Figure 2). Estimated ages for young populations (10 and 25 generations) showed low precision regardless of the effective size of the population and were far less precise when based on fewer loci (Figure 2). Although the relative bias associated with estimates from t was large for both very young and very old populations, the absolute differences between the estimated and actual population ages were small for young populations (Supplementary Table 2). A consistent downwards bias of 19–41% of the mean estimated age was evident for 1000 generation populations (Supplementary Table 2). For very young populations, simulated datasets were often monomorphic, particularly for smaller genomic samples. In these situations, estimated age was recorded as zero and included in calculations of the mean estimated age. Figure 1 plots the log of the simulated age versus the log of the estimated age, including these monomorphic datasets (see Xs in Figure 1).

Figure 1.

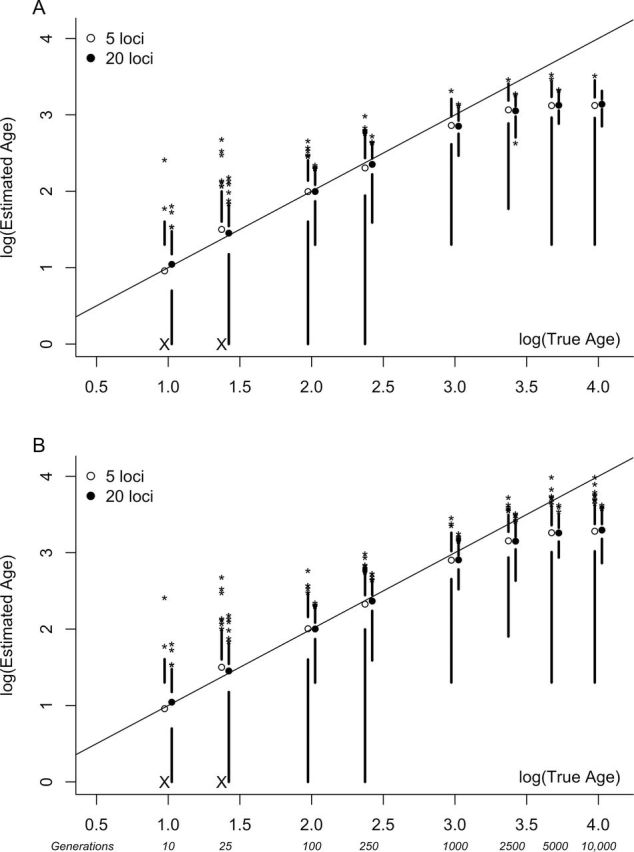
Boxplots representing the accuracy of age estimation methods: (a) P_K distribution (t) (B) variance in repeat number (s ² _AS). Means are plotted as open and filled circles for datasets of 5 and 20 loci, respectively. Lines extend from the upper and lower quartiles to the maximum and minimum values (excluding outliers), respectively. Outliers are represented as asterisks. True ages are those specified during simulations. The diagonal line indicates perfect correspondence between simulated and estimated ages. Plotted data are from simulations with N _e = 1000. Large Xs on the x axis indicate parameter combinations that frequently resulted in monomorphic datasets. In these instances, both the minimum and the lower quartile values are zero, the log of which is undefined.

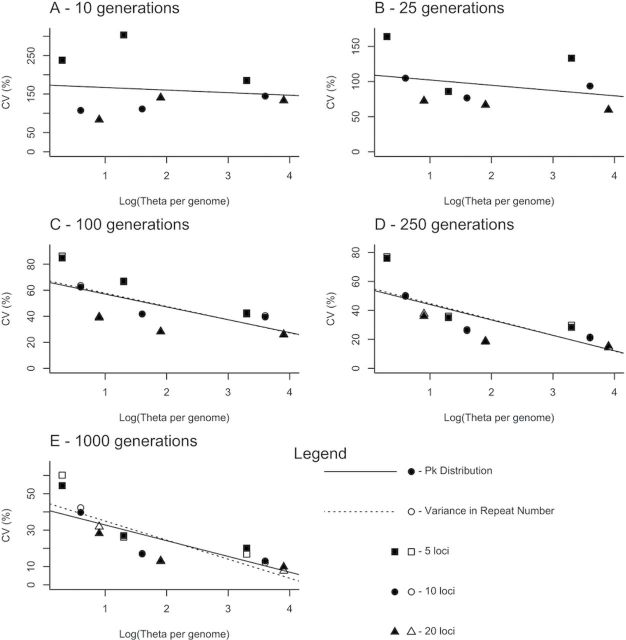
Figure 2.

Precision of the age estimation methods employed in this study. CVs are plotted against the log of genome-wide θ, defined here as the sum of the locus-specific θ values (θ _i = 4N _e µ _i). Separate plots are provided for each of the five simulated ages. Within each plot, parameter combinations sampling 5, 10, and 20 loci are indicated with squares, circles, and triangles, respectively. The relationship between CV and the informational content of the dataset [log(genome-wide θ)] is shown for each method. This relationship was assessed using a generalized linear model and trend lines for each individual method are plotted.

All else being equal, age estimates from s ² _AS for older populations were more precise when compared with younger populations (lower CVs; Figure 2). Additionally, larger datasets provided more precise estimates of population age when compared with datasets containing fewer loci. This gain in precision was primarily seen for older populations (100 generations and older). For the 20-locus dataset replicates, CV values were less than 40% of the estimated population age. For younger populations with five sampled loci, the CVs were often above this value (as high as 300%; Supplementary Table 2). Finally, s ² _AS showed a much smaller relative bias than t when older populations (1000 generations) were considered. Only the smallest simulated effective population size (N _e = 1000) produced a downward bias comparable to that seen in estimates from t. Mean estimated ages, CVs, and relative biases for simulated datasets analyzed under both of the methods outlined above are given in Supplementary Table 2.

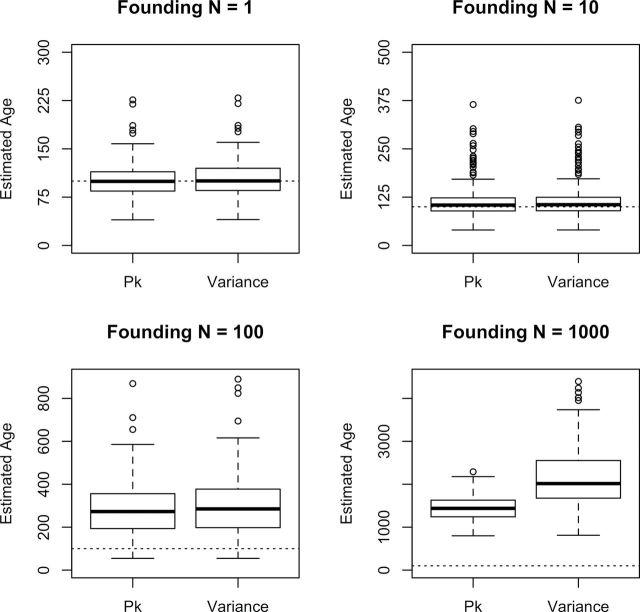
Additional simulations showed that our age estimates became biased upwards when founding populations were large (Figure 3). Estimates based on both statistics were biased for founding population sizes of 100 allele copies or more. Additionally, when these methods were applied to data from populations older than 2N _e generations, population ages were consistently underestimated (Figure 1). As expected, estimated ages reached an asymptote at approximately 2N _e generations, even when the simulated age was much greater.

Figure 3.

Boxplots of estimated ages for each of 200 replicate datasets simulated under identical conditions. Each individual simulation is composed of 20 loci sampled from a contemporary population of one million alleles. The magnitude of the population expansion was varied from the most severe case (a single founding allele) to a situation wherein 500 diploid individuals (1000 allele copies) colonize a new population. Dotted lines represent the simulated population age, 100 generations.

Empirical Data

Sampled pools encompassed the entire range of observed population ages from the studies of Pajunen and Pajunen (2003). The youngest population sampled was newly colonized in 2008 (age = 1 year), whereas the oldest populations had been occupied continuously for the entire course of the survey (age > 27 years). The mean age of the 14 sampled populations, assuming an age of 27 years for continuously occupied pools, was 10.1 years.

Sampled alleles at 7 of the 14 loci did not always differ from one another by multiples of the repeat motif. In these cases, fragments were cloned and sequenced to identify the true number of repeats. Mutations in flanking regions (including insertions in homopolymeric regions) were typically the underlying cause when noninteger differences in repeat number were observed (J Robinson, results not shown). For the purposes of age estimation, all sequenced alleles were recoded to reflect their similarity or difference with respect to the number of microsatellite repeats, ignoring differences in the flanking region.

In order to estimate ages in generations, mutation rates provided by mutation accumulation studies on the related species D. pulex (Seyfert et al. 2008) were applied to the data collected here. The rates estimated by Seyfert et al. (2008) differed between small (<30 repeats) and large (34–47 repeats) microsatellite loci. Because the markers sampled in this study all consisted of fewer than 30 repeats (Colson et al. 2009), the (slower) mutation rate for small loci (7.11 × 10⁻⁵ allele⁻¹ generation⁻¹; Seyfert et al. 2008) was employed.

Estimated ages for these 14 D. magna populations ranged from 568 to 1357 generations using t and from 693 to 8659 generations using s ² _AS. We assumed that the typical Finnish D. magna population undergoes approximately five generations per growing season (D. Ebert, personal communication). Our estimated ages are much higher, using either t (9- to 189-fold) or s ² _AS (19- to 391-fold), than the known ages given by the survey data (Figure 4). Despite this bias, estimated ages from t were significantly correlated with known ages (r = 0.5449, P < 0.05; Figure 4). This correlation may primarily be driven by the oldest populations, which also had the highest t values. Cook’s distances identified two influential data points (one of which corresponds to one of the two oldest populations) for the correlation between estimates from t and known ages. When these two observations are removed, the correlation between estimated and known ages was only marginally significant (r = 0.5133, P < 0.1). Removing only the two oldest populations also led to a correlation that was marginally significant (r = 0.5070, P < 0.1).

Figure 4.

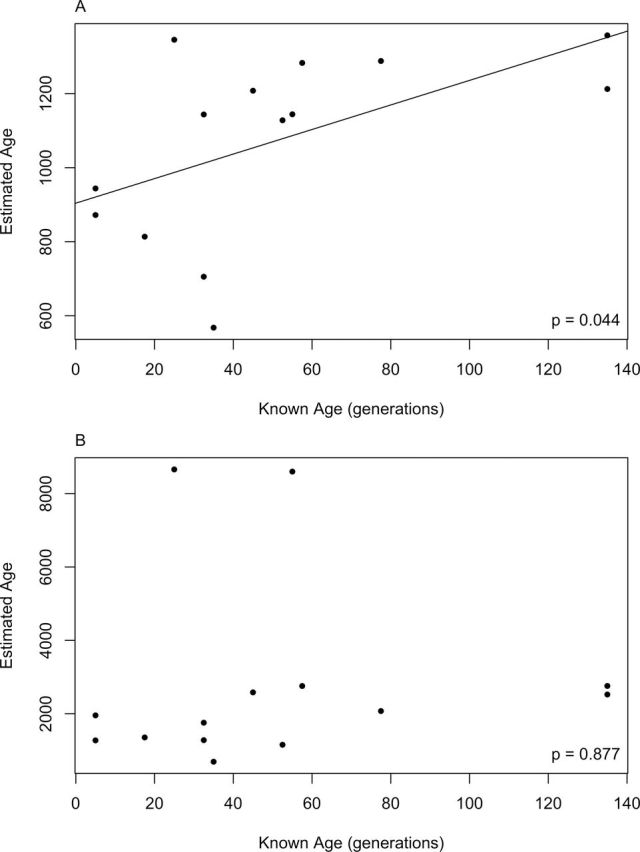
Comparison of known (survey data) and estimated (genetic data) ages in generations for the 14 sampled Finnish D. magna populations. Correlations were tested using Pearson’s product moment correlation coefficients; when significant, the correlation coefficient is reported. Estimated ages are from (a) P_K distribution (t) and (B) the variance in allele size (in units of repeats, s ² _AS).

The correlation between ages estimated from s ² _AS and known ages was not significant when all populations were considered. Cook’s distances calculated for the correlation between s ² _AS and known ages identified one of two outliers (estimated age > 8000 generations) as an influential observation, but the correlation remained insignificant when removing only this influential observation. However, when both outlier populations (true ages 25 and 55 generations; Figure 4) were removed from the analysis, a significant correlation was recovered (r = 0.6145, P < 0.05). Removal of these two populations did not affect the significance of the correlation between ages estimated from t and known ages (r = 0.6469, P < 0.05).

Discussion

The performance of the two statistics when applied to simulated data was encouraging. Both t and s ² _AS provided estimates of population age that were centered on the simulated value (Figure 1). The CVs show the precision of the estimates calculated from our replicate datasets. As expected, precision increased with the informational content of the dataset (larger genomic samples and larger sampled populations; Figure 2). For the youngest populations (10 generations), estimates were accurate, but imprecise across all sample sizes (CVs ranged from 80% to 300%; Supplementary Table 2). The CV values from our simulated datasets agree well with those obtained for repeated samples from a Poisson distribution with the number of draws equal to the total number of sampled allele copies (across loci) and a mean equal to the product of the mutation rate and the number of generations since colonization. In these samples, CVs decreased from 70% to 7% as population age increased from 10 to 1000 generations. In our simulated datasets, CVs for age estimates ranged from 83% to 140% for 20 locus datasets after 10 generations under both t and s ² _AS. After 1000 generations, CVs for estimates derived from 20 locus datasets ranged from ~8% to 32% for s ² _AS and from 10% to 28% for t (Supplementary Table 2).

The accuracy, as measured by the relative bias of our estimates, also improved with larger genomic samples, at least for recently colonized populations (less than 1000 generations old). However, as the length of time since the population was founded increased, the ability of these methods to estimate population ages eventually ceased. Our simulations define a timeframe, below which too few mutations are present in the population for accurate age estimates and above which the genetic signal of the population expansion is lost, wherein these methods are best suited for estimating population age.

The lower limit of this timeframe is set by the sampling effort and the mutation rate. In our simulations, using 20 loci, CVs were less than 40% for populations as young as 100 generations, but as high as 70% in 25 generation populations (Supplementary Table 2). Increasing sample sizes could improve the precision of these estimates. However, to achieve the level of precision attained for samples of 20 loci and 50 individuals from 100-generation-old populations (CV < 40%), more than 3-fold larger samples (160 individuals or 65 loci) would be required in very young populations (10 generations). On the other hand, the upper limit of the timeframe is set primarily by effective population size, as the signal of population expansion is lost after 2N _e generations. In our simulations, size homoplasy and convergence of microsatellite alleles led to a downwards bias in estimates provided from t before the expected asymptote at 2N _e generations (Figure 1).

In our empirical dataset, estimated ages for natural populations were higher than known ages in all instances. The upwards bias in our estimates was substantial; ages were consistently overestimated by one to two orders of magnitude. Despite this bias, age estimates from t were significantly correlated with known ages (Figure 4). This pattern was not seen when considering s ² _AS for all 14 sampled populations (Figure 4). The lack of correlation in the allele size variance dataset was driven primarily by two outlier populations. In these two populations, highly divergent alleles at 2 of the 14 loci vastly inflated s ² _AS and estimated population ages. Removal of these two populations (or of the divergent alleles) resulted in much closer relationships between estimated and known age for s ² _AS. A significant correlation (P < 0.05) between estimated and known ages was recovered when the populations were excluded, whereas a marginally significant correlation (P < 0.1) resulted when only the divergent alleles were removed. It appears that these highly divergent alleles, possibly introduced through immigration, are primarily responsible for inflating estimates derived from s ² _AS and obscuring the relationship with known ages.

The observed correlations indicate that, while insufficient as point estimates, these statistics carry useful information for the timing of population expansions. For instance, these statistics would be appropriate data summaries when using an ABC framework. Furthermore, these statistics allow for comparisons among populations, if interest lies primarily in relative ages. However, if the absolute age is of interest, it is important to insure that the assumptions behind the estimates are justifiable.

The discrepancy between the failure of our empirical application and the successes of our simulation study suggests that the assumptions of our simulation model are not all met in the D. magna system. Several of these assumptions are likely to be violated in the field. For this reason, we need to consider the possibility of deviation from the stepwise model of microsatellite evolution as well as the potential impacts of postcolonization migration, large founding sizes, and the presence of persistent source populations in the D. magna metapopulation.

The upwards bias in ages estimated for the D. magna populations could be due to aspects of our assumed mutation model. Our simulations assume a SMM, but if mutations often lead to the addition or subtraction of multiple repeat units, the TPM (Di Rienzo et al. 1994) would better explain the resulting data. Contrary to expectations, a majority (68%) of the observed mutations in D. pulex mutation accumulation lines involved changes of more than one repeat unit (Seyfert et al. 2008). If this pattern were to hold in D. magna, frequent multistep mutations would lead to an overestimation of the number of mutations separating two divergent lineages, potentially explaining the upwards bias in our estimates of population age. A mutation rate faster than the estimate from Seyfert et al. (2008) would also contribute to the upwards bias in our age estimates. Excluding outlier populations, estimates provided by the ISM and the SMM are upwards biased by on average 49- and 80-fold, respectively. A mutation rate on the order of 10⁻³ mutations per allele per generation would be required to account for the large upward bias in our population age estimates. These two explanations seem unlikely in the D. magna system. First, if the TPM were a better representation of mutation at these loci, we would expect to see gaps in the allele size distributions. Additionally, a mutation rate on the order of 10⁻³ is unlikely, as a direct estimate from long-term mutation accumulation data is 14 times lower (7.11 × 10⁻⁵) in the closely related congener D. pulex (Seyfert et al. 2008).

In essence, the bias in our estimates was the result of higher than expected levels of genetic diversity (given known ages) in our sampled populations. Both postcolonization migration and large founding sizes would serve to introduce allele copies into the sample that are not present as a result of mutations within the focal population, increasing the observed genetic diversity and inflating our population age estimates.

Haag et al. (2005) previously documented a positive correlation between population age and genetic diversity at allozyme loci. The increase in diversity at these more slowly evolving markers is most likely due to migration among occupied pools, rather than mutation. On average, 22% of empty habitat patches in the D. magna metapopulation are colonized in a given year (Pajunen and Pajunen 2003). Assuming that colonization and migration rates are equal, postcolonization migration events are not uncommon in this system. For instance, in a 10-year-old population, the probability that a migration event had not occurred since the initial colonization of the habitat patch would be (1 − 0.22)¹⁰ = 0.083 . However, migration and colonization are not completely equivalent in a population of clonally reproducing Daphnia.

After moving into an occupied habitat patch, immigrants may be vastly outnumbered, potentially limiting the persistence of their genetic contribution to future populations (Altermatt et al. 2008). Furthermore, Haag et al. (2005) found substantial genetic structure within islands (F_ST ~ 0.27), suggesting limited gene flow among pools. Nonetheless, the outbred offspring of immigrant genotypes are known to have a selective advantage in this metapopulation (Ebert et al. 2002), which would increase the probability that immigrant alleles are included in population samples, inflate the apparent rate of gene flow, and bias our age estimates upwards. The quantitative effects on our age estimates would vary depending on the rate of immigration and the nature of the immigrant alleles. If immigrant alleles are similar in size to those already segregating in the population, the effect of gene flow would be minor, in essence, similar to increasing the mutation rate. This is likely to be the case if most migration occurs between populations within islands in the archipelago. If on the other hand, highly divergent alleles move into a population, gene flow could strongly affect both the variance in repeat number (see outlier populations in Figure 4B) and the mean number of pairwise differences. In the latter case, the net effects of migration would be similar to those seen in our simulations with large founding sizes.

In our coalescent simulations, we assumed that the founding population sizes associated with recolonization were extremely small. Larger simulated founding sizes led to a substantial overestimation of population age, using either of the two statistics we employed (Figure 3). When applied to sequence data, estimates of the timing of population expansions derived from the mismatch distribution (t) take into account the effect of retained polymorphisms in the population by subtracting an estimate of the founding diversity (θ ₀) from the mean number of pairwise differences (Rogers 1995). This estimator does not adequately correct for retained polymorphisms in microsatellite datasets evolving under the SMM, leading to upwards biased results. Similarly, estimated ages provided by s ² _AS are based on the average time to coalescence in the sample, which is inflated by the presence of these polymorphisms. The influence of retained polymorphism is seen only when founding sizes are substantially larger than those assumed in our simulations. Previous research in the Finnish metapopulation suggests a propagule pool (Slatkin 1977; Wade and McCauley 1988) mode of recolonization, with very few founding genotypes (1.7 on average; Haag et al. 2005). Combined with the substantial genetic structure among populations within islands (Haag et al. 2005), these data help to justify the assumptions of our simulated expansion model. Additionally, our simulations suggest that founding size would need to be much larger (N ₀ ~ 100 allele copies) in order to explain the level of bias observed. It, therefore, seems unlikely that founding size alone is responsible for the upward bias in our estimated ages.

One other aspect of the D. magna system may also help to explain the upwards bias in our population age estimates. Of the 14 populations sampled in this study, two have persisted over the course of nearly 30 years worth of observations (Pajunen and Pajunen 2003). If these populations are inherently more stable, they might represent persistent “sources” in the metapopulation and could both harbor and distribute a large fraction of the system-wide genetic diversity. The higher genotypic diversity present in these source populations could inflate age estimates in populations colonized by their emigrants. Populations colonized from source populations would be the most likely to exhibit high-founding allelic richness. This is particularly true given the results of Haag et al. (2005), which indicate that the system most closely matches propagule-pool recolonization, wherein founders are drawn from a single occupied population (Slatkin 1977). Additionally, the sustained presence of the source populations would suggest that they are more often the source of colonists into extinct habitat patches. The genetic data we collected do not give a clear indication as to the importance of the older populations for maintaining system-wide genetic diversity. The two putative “sources” do not appear to contain a significantly larger fraction of the allelic richness in the system, when compared with younger populations (J.D.R. personal observation). The importance of these older populations for the regional diversity and their influence on our estimates of population age are, therefore, unclear.

Results from our simulations and the disconnect between Daphnia population age estimates and their known values suggests that these age estimation statistics may have limited applicability. In particular, migration among populations cannot be ignored in most biological systems. Furthermore, the assumption of monomorphic founding populations is most appropriate for clonal species. In fact, these sorts of methods have already proven their utility in clonal species. For example, Ally et al. (2008) used the accumulation of pairwise differences among microsatellite alleles (similar to our estimates from t) to estimate clone age in Populus tremuloides, by genotyping multiple ramets from the same genet. In their application, the likely causes of our biased age estimates are eliminated. Furthermore, bacteria and viruses also provide examples of systems where founding size and immigration can be safely ignored. A recent study found that across 102 patients infected with HIV-1, 76% were initially infected by a single viral particle or infected cell (Keele et al. 2011). The statistics assessed in this study could, therefore, be useful in epidemiological settings to estimate the timing of disease transmission, given within host pathogen genetic diversity data. The study by Keele et al. (2011) helps to illustrate the utility of genetic data for these purposes by using a genomic equivalent of the pairwise number of differences (the Hamming distance) to compare the coalescence time with the timing of transmission as inferred by the stage of viral progression.

From our analysis, it is apparent that the two statistics we considered carry information useful for estimating absolute population ages. Further, even when some assumptions are violated, as in the Daphnia system, estimates of relative population ages remain robust. More sophisticated statistical methods, like ABC, might be able to correct for the diversity increases associated with larger founding populations and gene flow. These methods may also make better use of the information provided by these statistics and provide a useful tool to estimate population age or other demographic parameters. The use of ABC has the potential to broaden the applicability of these statistics to systems where our assumptions are not met. When combined with these methods, the statistics employed in this study could help to better characterize the arrival and spread of invasive species or the colonization history of populations that exist in ephemeral environments.

The techniques employed in this study have typically been reserved for estimating the timing of evolutionary events that occurred thousands of generations ago, using more slowly evolving markers. Given the increasing ease with which large genetic datasets can be generated, the application of these methods has become feasible for questions on much more recent time scales. In summary, we believe that our three biological explanations (gene flow, founder size, and persistent sources) are the most likely processes underlying the upwards bias in our estimated population ages. These processes are not mutually exclusive and may interact to produce the observed bias in our age estimates.

Despite the indications from previous studies in the system, our empirical data suggest that the expansion model applied in this study was overly simplified for the D. magna system and that ecological parameters (e.g., migration rate and the number of founders) are as important to include as the complexities of the mutational process itself (i.e., the proportion of multistep mutations). Ongoing studies in our lab, using ABC, may allow the dissection of the relative influences of migration, founding size, and persistent source populations on the unexpected levels of diversity in our empirical dataset. Preliminary results of our ABC analyses show that a simulation model including persistent source populations, moderate founding sizes (~4 diploid individuals), and elevated migration rates (4Nm ~ 8) produces similar values for system-wide t and s ² _AS (Robinson 2011). It, therefore, seems likely that a combination of these factors, rather than any one individually, is responsible for the upwards bias in our population age estimates.

Supplementary Material

Supplementary material can be found at http://www.jhered.oxfordjournals.org/.

Funding

National Institutes of Health (GM07103); the Kirby and Jan Alton Graduate Fellowship from the Department of Genetics, University of Georgia; and the National Geographic Society Committee for Research and Exploration (8351-07 to J.P.W.).