Maintaining tumor targeting accuracy in real-time motion compensation systems for respiration-induced tumor motion

Abstract

Purpose: To determine how best to time respiratory surrogate-based tumor motion model updates by comparing a novel technique based on external measurements alone to three direct measurement methods.

Methods: Concurrently measured tumor and respiratory surrogate positions from 166 treatment fractions for lung or pancreas lesions were analyzed. Partial-least-squares regression models of tumor position from marker motion were created from the first six measurements in each dataset. Successive tumor localizations were obtained at a rate of once per minute on average. Model updates were timed according to four methods: never, respiratory surrogate-based (when metrics based on respiratory surrogate measurements exceeded confidence limits), error-based (when localization error ≥3 mm), and always (approximately once per minute).

Results: Radial tumor displacement prediction errors (mean ± standard deviation) for the four schema described above were 2.4 ± 1.2, 1.9 ± 0.9, 1.9 ± 0.8, and 1.7 ± 0.8 mm, respectively. The never-update error was significantly larger than errors of the other methods. Mean update counts over 20 min were 0, 4, 9, and 24, respectively.

Conclusions: The same improvement in tumor localization accuracy could be achieved through any of the three update methods, but significantly fewer updates were required when the respiratory surrogate method was utilized. This study establishes the feasibility of timing image acquisitions for updating respiratory surrogate models without direct tumor localization.

INTRODUCTION

Respiratory surrogate-based models of tumor motion relate tumor position to one or more respiratory surrogate signals in order to localize the tumor from external measurements. Such models are developed from a training dataset of concurrent tumor positions and surrogate measurements. To remain accurate, the relationship between the tumor position and the respiratory surrogate signals must remain constant over the duration of treatment.¹ However, intrafraction changes in the tumor-surrogate relationship are common,^{2, 3, 4, 5} and respiratory surrogate model accuracy tends to degrade over time.^{5, 6, 7}

To ensure accuracy over the course of treatment, models can be rebuilt during the fraction from new training data.⁷ This method has been applied clinically in the Cyberknife Synchrony^TM stereotactic radiosurgery system, which periodically (typically about once per minute) verifies its surrogate model through radiographic tumor localizations. If the tumor localization error (difference between the measured tumor position and the position predicted by the surrogate model) exceeds some user-defined threshold, the system updates the model.⁷ Note that this approach is labeled as the always update schema in this paper.

Few studies^{7, 8} have explored how best to update respiratory surrogate models to compensate for changes in the tumor-surrogate relationship. Seppenwoolde et al.⁷ explored variations on update methods for the Cyberknife Synchrony^TM system and showed that errors can be reduced through successively more frequent updates. They concluded that updating the model quickly after the tumor-surrogate relationship had changed can reduce overall residual error over the course of a fraction. However, imaging the tumor to collect data for updating the model as frequently as Seppenwoolde et al.⁷ described, every 5–25 s, may not be practical, as each image acquisition imparts nontherapeutic ionizing radiation and prolongs the overall treatment time. While Seppenwoolde et al.⁷ showed that a similar level of accuracy could be achieved by updating the model once halfway through a fraction, the magnitude of this error was not reported.

In a previous study, we evaluated a method for determining when to update a respiratory surrogate model without directly measuring tumor position.⁸ By monitoring respiratory surrogate measurements exclusively through Hotelling's T² statistic and the input variable squared prediction error, Q^(X), we were able to predict whether instantaneous respiratory surrogate-based tumor localization was accurate to within 3 mm with 95% sensitivity and 15% specificity.⁸ That initial study demonstrated the feasibility of monitoring respiratory surrogate models through external measurements alone, without explicitly measuring tumor position. However, further study is needed to determine how the model accuracy and the frequency of model updates for the surrogate monitoring method compare to that of either error-based methods or methods in which the model is updated at arbitrary intervals.

The purpose of this study was to evaluate the impact of timing model updates based on respiratory surrogate monitoring. A database of concurrent radiographic tumor localizations and respiratory surrogate measurements from a large cohort of lung and pancreas cancer patients was analyzed retrospectively. The cases we considered for determining when to update a model once treatment had commenced were: (1) never, (2) respiratory surrogate-based (when surrogate model-based tumor localization error exceeded 3 mm), (3) error-based (when either T² or Q^(X) exceeded preset confidence limits), and (4) always (in our data, this frequency corresponds to once per minute on average).

METHODS AND MATERIALS

Data

A database of Cyberknife Synchrony^TM system log files was analyzed. We considered 121 treatment fractions of lung tumor motion data from 61 patients and 45 treatment fractions of pancreas tumor motion data from 23 patients. Each log file consisted of two sets of recordings that were aligned using system-recorded timestamps: (1) measurements of tumor position, as localized through identification of the centroid of 2–3 implanted fiducial markers in stereoscopic radiographs captured once every three beams, or at an average interval of once per minute; and (2) frequent (26 Hz) measurements of the positions of a set of three LED markers affixed to a form-fitting vest. From these datasets, we were able to extract concurrent internal (tumor) and external (marker) localizations at each radiographic measurement.

Tumor motion prediction

In a previous study, we have shown that partial-least-squares (PLS) regression can be used to accurately model tumor motion from multiple respiratory surrogate signals.⁶ For each treatment fraction, a PLS regression model was created to predict tumor positions from the respiratory surrogate data. The initial model was created from the first six radiographic tumor localizations in each treatment fraction using PLS regression, as described previously.⁶

The inputs of the PLS model were three one-dimensional signals that were each derived from three-dimensional (3D) external surrogate data. One input was created from the raw data from each of the three external surrogate markers. Raw input data consisted of X_m, where X_m was a n × 3 matrix of n 3D marker position samples of surrogate marker m. To create the PLS inputs, the three-dimensional surrogate marker motion, X_m, was projected onto a single dimension to create R_m. Each row of R_m, R_mi, was calculated as $R_{mi}=(X_{mi}-{\overline{X}}_m)·P_m$, where ${\overline{X}}_m$ was the 1 × 3 matrix containing the mean of X_m along its columns and P_m was the first principal component vector of X_m. The SIMPLS PLS regression algorithm was used to create the model of tumor positions of the form $\widehat{Y}=\widehat{B}·R$ for surrogate inputs, R, estimated tumor position, $\widehat{Y}$, and regression coefficient matrix, $\widehat{B}$. The details of this regression process are provided in Malinowski et al.⁶

Model monitoring and updates

Respiratory surrogate analysis

The motion of the external respiratory surrogate markers was characterized during the model training period and was re-evaluated over the course of the treatment fraction.

For each set of six training data samples, a second PLS model based on tumor position outputs, Y, and raw (unprojected) surrogate marker positions, X, was created. This process yielded a new set of regression coefficients and tumor position estimates such that $\tilde{Y}=\tilde{B}·X$. The Hotelling's T² statistic and the input variable squared prediction error, Q^(X), were calculated for each respiratory surrogate marker position sample as described by Malinowski et al.⁸ Once the PLS model of tumor positions was created from a training dataset of six samples, the surrogate-based metrics, T² and Q^(X), were calculated from measurements of the surrogate markers exclusively and did not utilize additional gold-standard measurements of tumor position. Control limits on T² and Q^(X) were calculated as previously described⁸ from the six samples used to develop the respiratory surrogate model of tumor motion.

Model update schema

The tumor localization accuracy of the respiratory surrogate models was evaluated for four update methods. Each method was tested against 20 min of data following the initial six-sample training dataset.

Never update

Currently, despite possible intrafraction tumor-surrogate relationship changes, most clinics do not update respiratory surrogate models during motion management procedures. To simulate this case, we applied the initial model based on the first six measurements in the treatment fraction to the entire 20 min testing dataset.

Always update (approximately once per minute)

To evaluate the opposite extreme, we updated the model at each radiographic tumor localization in the dataset; the average time between successive localizations was 63 s. Specifically, 1 s after a radiographic tumor localization, the six most recent measurements were used to train a new model predicting tumor motion from external marker positions. This predictive model was then applied to predict tumor position up to the next update, 1 s after the next radiographic tumor localization.

Error-based update

The Cyberknife Synchrony^TM system is an example of a device that periodically captures radiographs in order to validate its respiratory surrogate model. The measured tumor position (using radiographs) was compared to the model-predicted tumor position. If the difference (the localization error) exceeded a user-set threshold such as 3 mm,⁷ the model was updated. To simulate this process, a new model was created each time the localization error exceeded 3 mm. An updated model was applied to data acquired 1 s after each tumor localization error that was greater than 3 mm.

Respiratory surrogate-based update

Rather than base the decision of whether to update a model on gold-standard tumor localizations, the respiratory surrogate method is based on external measurements alone. The T² and Q^(X) values were evaluated for each set of surrogate marker measurements. If either T² or Q^(X) of a sample exceeded the 70th percentile T² or Q^(X) confidence limit, then a new model was created from the previous six localizations. This model was applied to data in the fraction following 1 s after either T² or Q^(X) exceeded its confidence limit threshold.

The 70th percentile threshold for the T² and Q^(X) confidence limits was selected to balance the technique's ability to detect changes in the relationship between the model and the respiratory surrogate signals with the tendency toward false detections of such changes.

RESULTS

While updates for this dataset were limited to the times at which radiographs were acquired, the update timings differed considerably across the four methods (Fig. 1). More frequent updates did not always correspond to more accurate tumor motion prediction.

Figure 1.

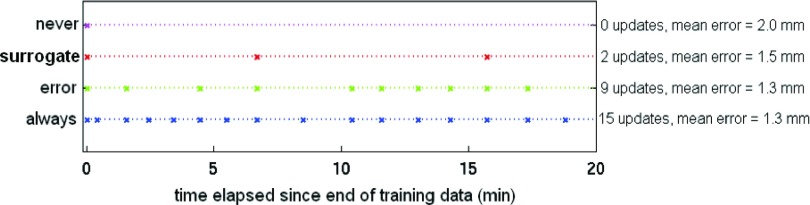
Timing of model updates for the four update methods in a representative treatment fraction. Updates are indicated by “x”s at the appropriate time. Results for this fraction for each method are summarized at right.

Model errors

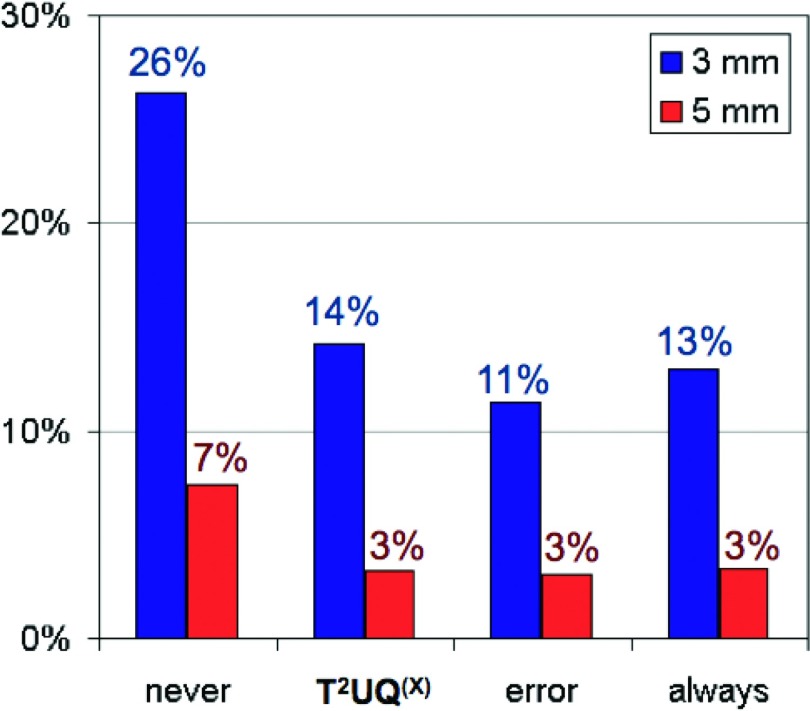
Tumor localization errors (mean ± standard deviation) for never, respiratory surrogate-based, error-based, and always update schema were 2.4 ± 1.2, 1.9 ± 0.9, 1.9 ± 0.8, and 1.7 ± 0.8 mm, respectively (Fig. 2). For never, surrogate-based, error-based, and always update methods, respectively, 7%, 3%, 3%, and 3% of tumor position prediction errors exceeded 5 mm, and 26%, 14%, 11%, and 13% exceeded 3 mm (Fig. 3). Error distributions for update schema other than never-update did not differ significantly from one another (t-test, p > 0.05). However, the never-update tumor localization errors were significantly larger (t-test, p < 0.05) than those of the other update methods.

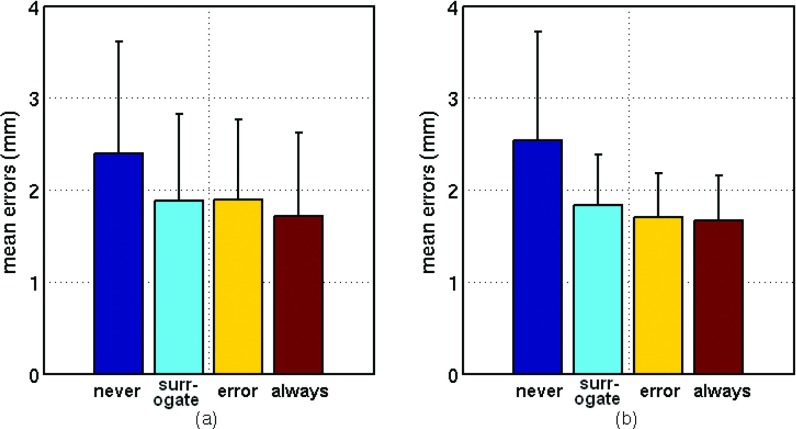
Figure 2.

(a) Lung and (b) pancreas mean and standard deviation (error bars) tumor position prediction errors over 20 min for each update method. There is no significant difference (p > 0.05) between results for surrogate-based, error-based, and always update methods.

Figure 3.

Incidence of large (>3 and >5 mm) tumor localization errors for each update method.

Update timing

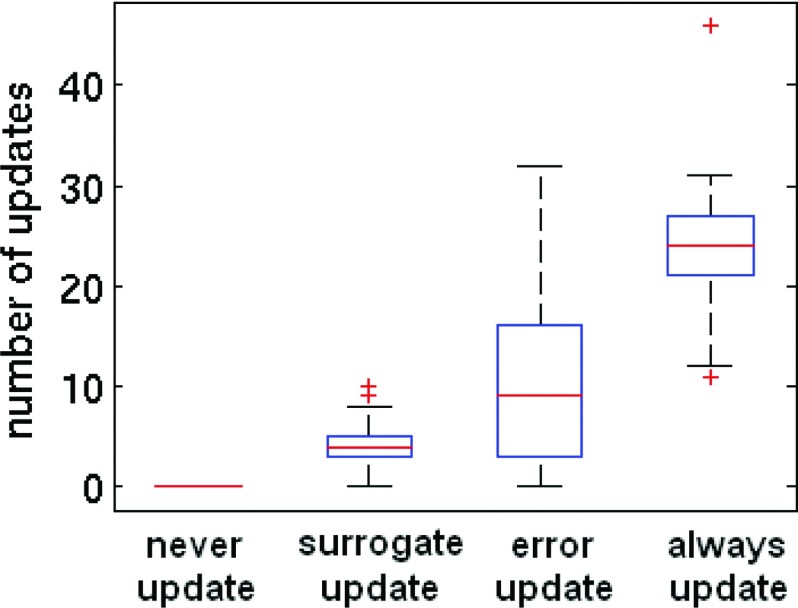
The median numbers of updates over the course of 20 min were 0, 4, 9, and 24 for never, surrogate-based, error-based, and always update schema, respectively (Fig. 4). Despite the lack of significant difference in model errors across the three update schema (Sec. 3A), there were significant (t-test, p < 0.05) differences in the numbers of updates between each of the four methods. 24% of the tumor localizations associated with an error-based update were also associated with a surrogate-based update (Fig. 4), and 55% of tumor localizations that were associated with surrogate-based updates corresponded to simultaneous error-based updates.

Figure 4.

Numbers of model updates per 20-min fraction for each update method. (Boxes denote quartile ranges, horizontal lines inside the boxes indicate the median, and any outliers greater than 1.5 times the interquartile range past the box limits are plotted as + signs.)

Site-specific results

Lung and pancreas results were compared (Fig. 2). Neither mean error nor number of updates was significantly associated with tumor site (two-way ANOVA, p > 0.05).

DISCUSSION

This study evaluated the hypothesis that knowledge-based model update timing can lead to an accurate model while limiting the necessity for frequent imaging. The results of this study indicate that more frequent updates do not guarantee a more accurate model. While any update method resulted in smaller tumor localization errors than no updates at all, errors were not significantly different across the three update methods (surrogate-based, error-based, or always). This lack of difference in tumor localization performance came about despite large differences in the mean number of updates in 20 min: 4, 9, and 24 for the surrogate-based, error-based, and always updates methods, respectively.

The prediction accuracy of respiratory surrogate-based tumor localization models degrades over the course of a treatment fraction.^{1, 2, 5, 7} In a previous study,⁸ we concluded that the T² and Q^(X) were able to predict large respiratory surrogate model errors with high sensitivity (95%) but limited specificity (15%). In this work, we have shown that instantaneous error may not be the best way to decide whether to update a model. By updating the model each time a localization error exceeded the threshold of 3 mm, many updates were carried out without significant improvement to mean model accuracy. Over the course of a fraction, the surrogate-based method was associated with more frequent localization errors >3 mm than the error-based method (14% vs 11% of localizations), but for both methods only 3% of errors were >5 mm. Despite no improvement in error, the error-based method required more than twice as many updates as the surrogate-based method. This result is in agreement with Seppenwoolde et al.,⁷ who also concluded that, while any update is valuable, more frequent updates do not necessarily lead to a more accurate model.

In both the error-based and the surrogate-based update methods, parameters can be selected to trade off between tumor localization error and number of updates. For error-based updates, 3 mm was used as the threshold, because it has been cited as a clinically relevant error threshold for the Cyberknife Synchrony^TM system.⁷ The surrogate metrics’ confidence limits were set to the 70th percentile expected value, such that the accuracy was not significantly different than the error-based method. This allowed us to compare number of updates for the two methods when localization errors were equal. For either technique, a larger localization error tolerance would necessitate fewer updates.

In this work, the number of updates was evaluated for 20 min of data. For many modern treatments, beam-on time is less than 20 min, but inroom time can be longer. At our institution, the patient is usually on the couch for approximately 15 min for conventionally fractionated treatments and for approximately 30 min for stereotactic body radiotherapy treatments. In practice, model update implementation would be implemented differently on each system, but it is likely that the process of capturing images for new model-building data during an update would take some time, potentially extending the duration of the treatment fraction. A shorter treatment would require fewer updates. Thus, even with respiration monitoring, it is important to complete a treatment fraction, including the setup process, as quickly as possible.

The surrogate-based monitoring method explored in this study was applied to PLS respiratory surrogate models. The T² and Q^(X) metrics are based on the scores developed as part of the PLS regression process. However, it would be possible to monitor any multiple-input respiratory surrogate model through these metrics. In particular, because the PLS output is very similar to that of the Cyberknife Synchrony^TM system,⁶ it is likely that the surrogate-based monitoring method evaluated in this study would be equally effective for the Cyberknife Synchrony^TM tumor localization algorithm. In any real-time tracking technology,^{7, 9, 10} accurate tumor localization is essential, and a knowledge-based method for model update timing could improve system performance. This type of monitoring would also benefit gating technologies.^{11, 12} Berbeco et al.¹¹ and Cai et al.¹³ have shown that breath-to-breath variations even in the relatively stable end-exhale position necessitate use of an internal margin for gated treatments.

The surrogate-based timing method uses respiratory surrogate measurements alone. By contrast, the error-based method requires concurrent respiratory surrogate measurements and radiographic images to validate the model directly. For this work, to allow validation of the method, updates were limited to the instances at which radiographic tumor localizations were available (about once per minute). However, because the surrogate-based method does not require internal localization, it has the potential to give early warnings of large errors by checking for updates at the surrogate measurement rate (26 Hz in this dataset). Further study is needed to determine how to best implement surrogate-based monitoring when high-frequency surrogate data are available.

CONCLUSION

When the model is never updated, mean tumor localization errors were 2.4 mm, and 26% of errors exceeded 3 mm. With the update methods, mean errors were reduced to 1.7–1.9 mm, and 11%–14% of errors exceeded 3 mm. Differences in magnitude of error between respiratory surrogate-based, error-based, and always update methods were not significant, but the number of updates in a fraction varied considerably with update method. On average, the surrogate-based method reduced the number of updates by a factor of 2.3 relative to the number required by the error-based method and by a factor of 5.9 relative to the number required by the always update method.