The electrostatic response of water to neutral polar solutes: Implications for continuum solvent modeling

Abstract

Continuum solvation models are widely used to estimate the hydration free energies of small molecules and proteins, in applications ranging from drug design to protein engineering, and most such models are based on the approximation of a linear dielectric response by the solvent. We used explicit-water molecular dynamics simulations with the TIP3P water model to probe this linear response approximation in the case of neutral polar molecules, using miniature cucurbituril and cyclodextrin receptors and protein side-chain analogs as model systems. We observe supralinear electrostatic solvent responses, and this nonlinearity is found to result primarily from waters’ being drawn closer and closer to the solutes with increased solute-solvent electrostatic interactions; i.e., from solute electrostriction. Dielectric saturation and changes in the water-water hydrogen bonding network, on the other hand, play little role. Thus, accounting for solute electrostriction may be a productive approach to improving the accuracy of continuum solvation models.

INTRODUCTION

Water plays a fundamental role in the thermodynamics of biomolecules, and the balance among intrasolute, solute-water, and water-water interactions governs such processes as protein conformational changes,¹ protein-ligand binding, and protein folding.^{2, 3, 4} Reliable models of hydration are therefore needed if one aims to predict thermodynamic driving forces or to make predictions that will be useful in drug design and protein engineering.^{5, 6, 7, 8, 9, 10} Widely used implicit solvation models based on continuum dielectric theory, e.g., the Poisson-Boltzmann (PB)^{11, 12, 13, 14} and Generalized Born (GB)^{15, 16, 17, 18, 19, 20} models, provide rapid estimates of the polar solvation free energy, a large portion of total solvation free energy of a polar molecule in water, at lower computational cost than explicit solvent models. Such models can be combined with additional terms to account for nonpolar contributions to the solvation free energy.^{21, 22, 23} An underlying approximation of continuum models is that the electrostatic reaction field of the water responds linearly to the solute's electric field. If the actual response were nonlinear, this could lead to errors in computed solvation free energies. Although some degree of sublinearity may be expected for ionic solutes, due to dielectric saturation, simulations with explicit water models have also yielded evidence of a less expected supralinear electrostatic response to neutral polar solutes,^{24, 25, 26} and we recently noticed the same phenomenon when analyzing the hydration of macrocyclic host molecules in the cucurbituril (CB) and cyclodextrin (CD) classes.

The present study aims to further characterize and account for these unexpected nonlinearities, with the long-term goal of enabling improvements in continuum solvation models. Our basic approach is to use explicit solvent molecular dynamics (MD) simulations to compute the reversible work of stepwise coupling the atomic partial charges of each solute with the water.^{27, 28, 29} The work at each step varies with the coupling constant, λ, and we are interested in the deviations from linearity in this response. We focus in particular on macrocyclic host molecules in the CB and CD classes. These miniature receptors are computationally tractable,^{30, 31} as they comprise only a few hundred atoms, yet, like protein-ligand systems, exhibit a broad range of binding affinities in aqueous solution.^{32, 33, 34} The present study thus is part of a larger effort to develop improved techniques for predicting noncovalent binding affinities.

METHODS

Structures and force-field parameters

Initial structures of cucurbiturils and cyclodextrins were obtained from the Cambridge Crystallographic Structural Database,³⁵ whereas those of small molecules, including formaldehyde, methanol, and various amino-acid side-chain analogues were obtained from the PubChem database³⁶ (http://pubchem.ncbi.nlm.nih.gov/). The structures were further refined with the PM6-DH+ energy model,^{37, 38} using the MOPAC 2009³⁹ software. Bonded (bond, angle, and torsion) and van der Waals parameters were assigned according to the OPLS-2005⁴⁰ force field using Schrodinger's MacroModel software.⁴¹ Partial charges were computed using the restrained electrostatic potential (RESP) method,⁴² from electrostatic potentials computed using Hartree-Fock method with 6-31G^* basis set. The quantum mechanical calculations were performed using GAUSSIAN 09 software.⁴³ RESP charges were obtained from the electrostatic potentials using either the Antechamber⁴⁴ program within AmberTools or the R.E.D.⁴⁵ program.

We employ the TIP3P water model, as it has been extensively validated for use in the calculation of hydration free energies^{27, 28, 46} and provides reasonable agreement with experiment for basic structural and energetic properties of liquid water.⁴⁷ This choice also provides a clear connection with prior work in which similar nonlinear responses were observed for this water model.²⁴

Explicit-water polar solvation free energies

Molecular dynamics simulations and free energy analysis were performed using the GROMACS simulation package (v. 4.5.5).⁴⁸ Electrostatic charging free energies were computed using thermodynamic integration (TI)⁴⁹ with the Bennett Acceptance Ratio (BAR) method.⁵⁰ TI was carried out using 21 windows, with the coupling parameter, λ, ranging from 0 to 1 in steps of 0.05. Polar solvation free energies and free energy differences between successive λ windows were converged to within 0.1 kcal/mol according to BAR. Each of the structures was first solvated with TIP3P⁴⁷ water in a 30 Å cubic box, except for CB[10] which, because of its greater size, was solvated in a 40 Å cubic box. The system was energy minimized using the steepest-descent algorithm and equilibrated for 500 ps under NPT conditions. Temperature was maintained at 300 K using the velocity rescaling method⁵¹ with the time constant set to 0.1 ps. An isotropic pressure of 1 bar was maintained using Berendsen's weak coupling method⁵² with the time constant set to 1.0 ps. Production runs were carried under NPT conditions for a simulation time of 5 ns for each window of TI, with the exception of the CBs and CDs, which were run for 10 ns for each window. A 2 fs integration time step with the leap-frog integration algorithm was used in all simulations. Periodic boundary conditions were applied in all three coordinate dimensions. The Particle-Mesh-Ewald (PME) method⁵³ was used for electrostatic interactions, with a direct space cutoff of 10 Å, and cubic interpolation (PME order = 4) for the calculation of long-range interactions in reciprocal space, with a Fourier transform grid of 1.2 Å maximum. Lennard-Jones (LJ) interactions were cut off at 10 Å. The solute molecule was positionally restrained to the initial geometry using harmonic restraints (23.9 kcal/mol Ų) applied to all the atoms. The bond-lengths of water molecules were constrained to their equilibrium lengths with the SHAKE algorithm,⁵⁴ allowing for a 2 fs time step.

Poisson-Boltzmann solvation

Continuum electrostatic solvation free energies based on the Poisson-Boltzmann (PB) solvation model were computed with the Adaptive Poisson-Boltzmann Solver (APBS) software.¹³ A 193 × 193 × 193 grid with a spacing of 0.15 Å was used for all the calculations. The dielectric constants of the solute and solvent regions were set to 1.0 and 78.54, respectively. The point charges of the solute were mapped to the grid using cubic B-spline discretization.⁵⁵ The solute-solvent dielectric boundary was defined as the smooth molecular surface computed using a solvent probe radius of 1.4 Å.^{56, 57} The atomic cavity radius of each solute atom, for a given value of λ, was set to the time-averaged mean distance from the atom's center to the nearest water oxygen in the corresponding explicit-water simulation, offset by a λ-independent constant designed to account for the asymmetry of the water molecule.^{58, 59} The offset was −0.84 Å for atoms having a positive charge in the fully charged (λ = 1) state, and −1.4 Å for atoms having a negative charge in the fully charged state. These offsets were established by fitting PB solvation free energies of methanol and formaldehyde against those computed using explicit-water molecular dynamics simulations. The PB electrostatic solvation free energies of methanol and formaldehyde computed using these offsets were −6.3 and −3.9 kcal/mol, respectively, which are in good agreement with the values −6.1 and −4.1 kcal/mol, respectively, computed from explicit-water molecular dynamics simulations.

RESULTS AND DISCUSSION

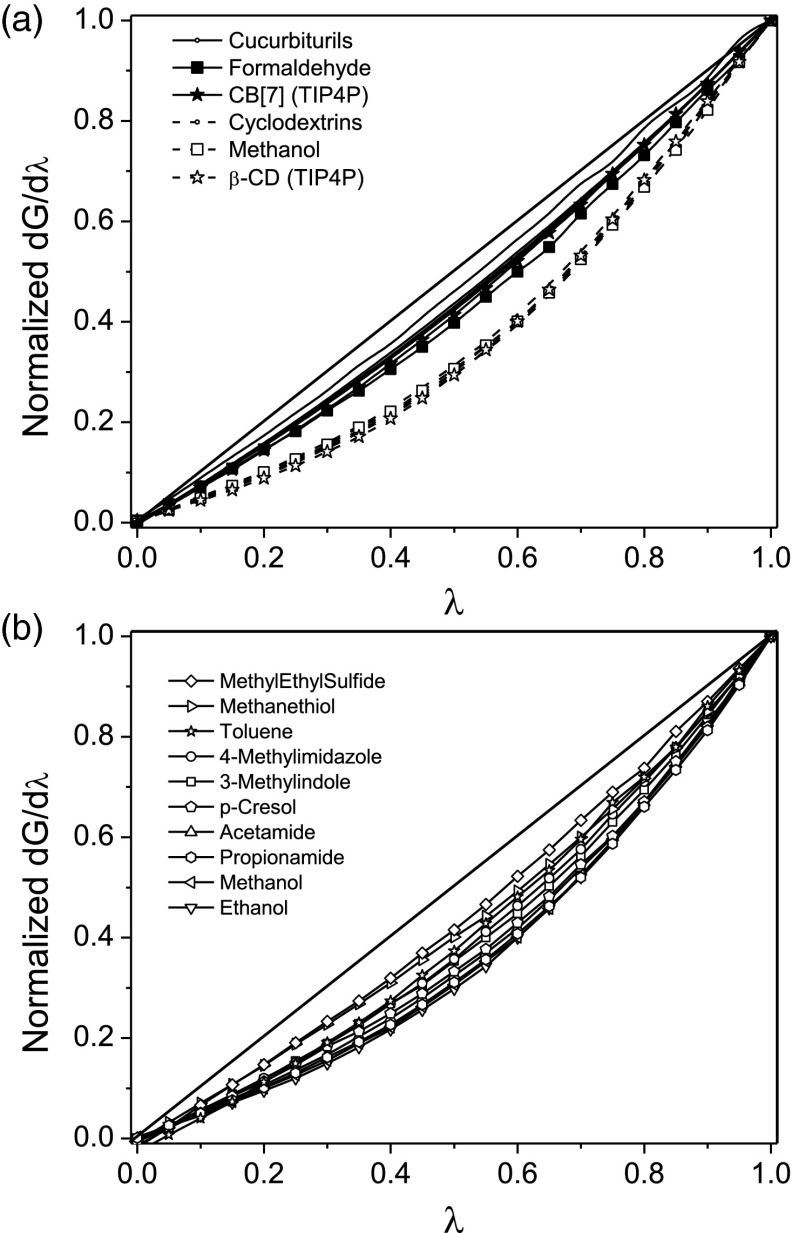
We studied the polar response of water solvating eight macrocyclic receptors: five cucurbit[n]urils (CB[n] with n = 5, 6, 7, 8, and 10), and three cyclodextrins (α-CD, β-CD, and γ-CD). The coupling of the partial atomic charges of each solute with the surrounding solvent was scaled between λ = 0 and λ = 1 in N steps of size Δλ, such that ${\lambda }_i=\frac{i}{N}$, with the solute conformation held rigid in order to isolate the solvent response. The derivative of the free energy with respect to the coupling strength, ${\left(\partial G/\partial \lambda \right)}_{{\lambda }_i}={⟨\frac{\partial H}{\partial \lambda }⟩}_{{\lambda }_i}$, was computed for each value of λ. The polar solvation free energy was then computed as $\Delta G={\sum }_i{\left(\partial G/\partial \lambda \right)}_{{\lambda }_i}\Delta \lambda$. We quantified the degree of nonlinearity with the metric α ≡ ΔG/ΔG_linear, where ΔG_linear is the polar solvation free energy computed with a linear response approximation: $\Delta G_{linear}=\frac{{\left(\partial G/\partial \lambda \right)}_{{\lambda }_N}+{\left(\partial G/\partial \lambda \right)}_{{\lambda }_0}}{2}$. Note that ${\left(\partial G/\partial \lambda \right)}_{{\lambda }_0}$ is not necessarily zero, due to the residual solvent reaction field at the solute. Values of α < 1 and α > 1 indicate supralinear and sublinear responses, respectively. In order to display the solvation responses of diverse solutes on a common scale, we provide graphs of the responses normalized to their values at λ = 1; i.e., ${\left(\partial G/\partial \lambda \right)}_{{\lambda }_i}/{\left(\partial G/\partial \lambda \right)}_{{\lambda }_N}$.

All eight receptors generate strikingly nonlinear solvation responses (Figure 1a), and in all the cases, the solvation response is supralinear, i.e., water responds more and more strongly as its electrostatic coupling with the solutes increases. It is of interest to note that the nonlinear nature of the solvent response implies non-Gaussian distributions of fluctuations in the solvent reaction field.⁶⁰ Intriguingly, the normalized response graphs in Figure 1a separate into clear families, with the CDs (dashed lines) falling into a highly nonlinear pattern (α = 0.75 ± 0.01) and the CBs (solid lines) falling onto a different curve that is more linear (α = 0.91 ± 0.02). The insensitivity of these results to receptor size (number of monomers) indicates an absence of synergy among the constituent monomers. The present observations are also insensitive to the choice of water model, as similar results are obtained with the TIP3P⁴⁷ and TIP4P⁴⁷ models for receptors CB[7] and β-CD (Figure 1a).

Figure 1.

(a) Normalized electrostatic response, i.e., ${\left(\partial G/\partial \lambda \right)}_{{\lambda }_i}/{\left(\partial G/\partial \lambda \right)}_{{\lambda }_N}$, of water to various macrocycles and representative small molecules. (b) Normalized electrostatic response of water to various amino-acid side chain analogues (listed in the order of increasing nonlinearity).

In order to test whether these nonlinearities might result from cooperative solvation among the various polar groups of these host molecules, or perhaps from the special properties of water molecules sequestered within their binding cavities,^{61, 62, 63} we ran analogous calculations for formaldehyde and methanol, whose carbonyl and hydroxyl groups match the main polar groups of the CBs and CDs, respectively. The normalized solvation responses of formaldehyde and methanol agree with those of the corresponding receptor families (Figure 1a) and yield similar nonlinearity metrics, α = 0.86 and α = 0.75, respectively. Thus, solvent sequestration does not lead to the observed nonlinearity, because formaldehyde and methanol show the same nonlinearity although they are too small to sequester water. We then examined the electrostatic responses of water to the functional groups associated with the 20 common amino acids,^{46, 64} and found a broad range of supralinear responses, with α ranging from 0.74 to 0.90 (Figure 1b). Thus, the nonlinear electrostatic response of water could play an important role in the hydration of proteins.

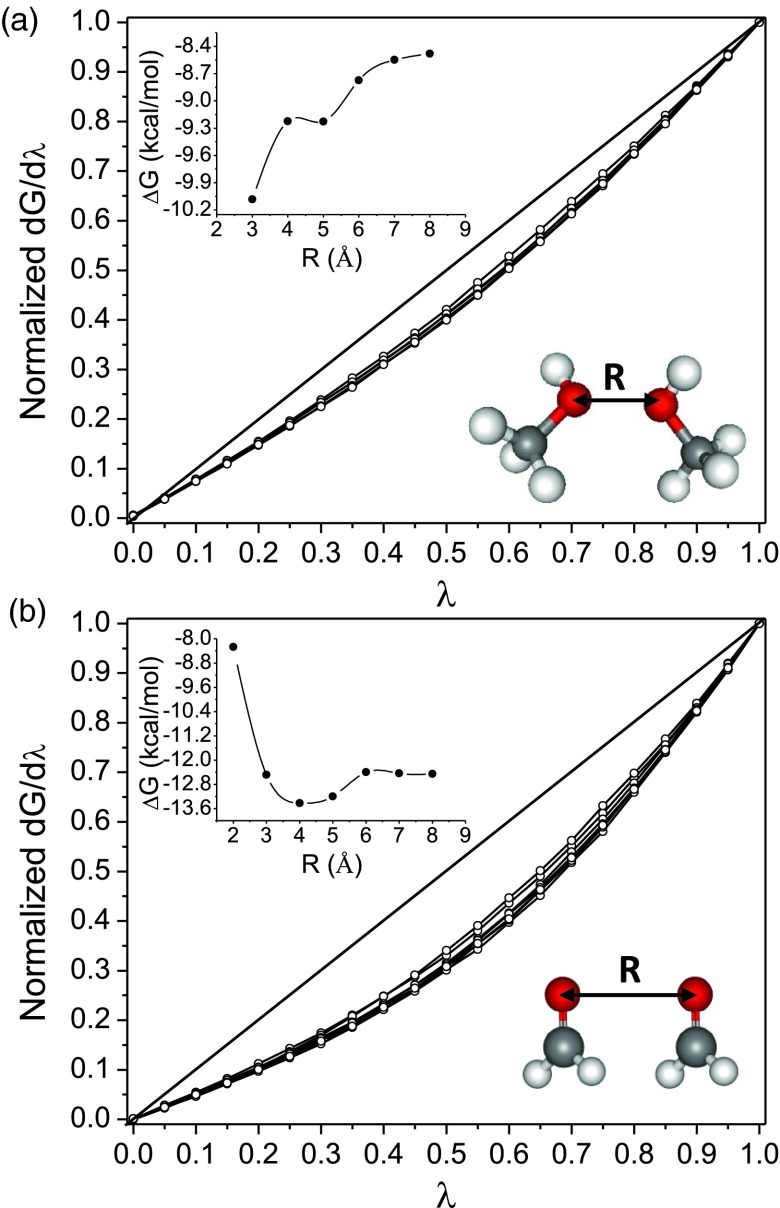
As observed here and previously,^{24, 25, 26} hydroxyl groups generate a particularly nonlinear solvation response. It has been argued that this results from a special interaction of hydroxyls with the solvent's hydrogen bonding network.²⁵ In order to test this idea, we systematically modified the hydrogen-bonding network of water around a methanol dimer by varying the intermonomer distance from 2 to 8 Å (Figure 2a). The dip in the polar solvation free energy at a distance of 4 Å (Figure 2a, inset), indicates cooperative localization (bridging) of water molecules,^{65, 66, 67} and confirms a marked alteration of the hydrogen-bonding network. Nonetheless, the nonlinearity of the solvation response is essentially constant as a function of the separation distance (α = 0.76 ± 0.02); and analogous results are found for a formaldehyde dimer (Figure 2b; α = 0.88 ± 0.01). Thus, the nonlinear solvent response cannot be attributed to any particular form of the hydrogen-bonding network.

Figure 2.

Normalized electrostatic response of methanol dimer (a) and formaldehyde dimer (b) at different intermonomer distances. The corresponding polar solvation free energies are shown in the inset.

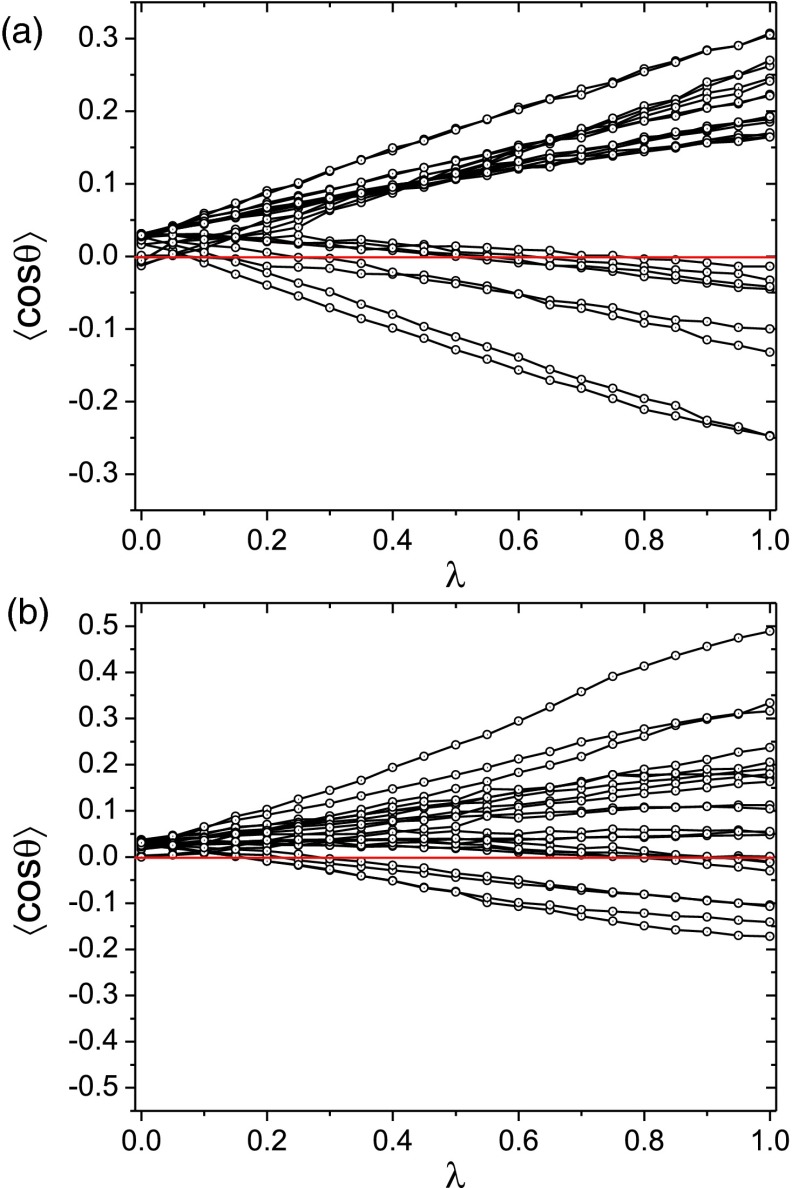
Another possible source of nonlinearity is dielectric saturation,⁶⁸ a diminishing increment in the orientational polarization of water molecules with increasing electric field, which would make the solvation response more sublinear. We examined the average orientation of water molecules at the solute surface, where the solute electric field is strongest so that saturation would be maximal, as a function of the coupling coefficient, λ. The orientation of water molecules increases almost linearly with λ around both CB[7] and β-CD (Figure 3), even near polar atoms. This linearity is consistent with the fact that the mean cosine values remain well below unity. The absence of saturation is not unexpected, because although dielectric saturation occurs at high electric fields, such as at the surface of ions,^{69, 70} little saturation is expected in the lower electric fields near the neutral polar solutes studied here.

Figure 3.

Average cosine of angle between the water dipole and the direction vector from solute atom center to the water oxygen, of the water molecules in the first hydration shell (< 4 Å from any solute atom center) as a function of solute-solvent electrostatic coupling parameter, for various atoms in CB[7] (a) and β-CD (b). Only one monomeric unit is shown here for clarity. The red line corresponds to ⟨cosθ⟩ = 0.

Finally, we considered whether the nonlinearities observed here might result from electrostriction. It is essential here to distinguish between solvent electrostriction and solute electrostriction. Solvent electrostriction refers to an increase in density of water around the solute with increasing electrostatic field strength, and is experimentally measurable with dilution experiments.⁷¹ Solute electrostriction refers to the shrinkage of the solute's solvent-excluded volume as first-shell waters are drawn closer with increased electrostatic coupling; this corresponds to a reduction in what has been termed the intrinsic volume of the solute, and is not experimentally measurable.⁷¹ While others⁷² have referred to the former as electrostriction and the latter as solute compression, we prefer the term solute electrostriction, as it emphasizes the electrostatic field as the source of the solute compression.

We first considered solvent electrostriction. An increase in solvent density around the solute would increase the dipole density (polarization) of the solvent proportionally, other things being equal, and thus should proportionally strengthen the reaction potential at the solute.^{73, 74, 75} In this way, it could lead to a supralinear electrostatic response of the solvent. Based on the slopes of the solvation response with zero (λ = 0) and full (λ = 1) electrostatic coupling, the solvent density would have to increase uniformly throughout by a factor of 6.5, in order to account for the nonlinearity observed for β-CD. An increase of this size is implausible, given the low compressibility of liquid water. Nonetheless, we examined this possibility by computing the density of water in the first solvation shell around CB[7] and β-CD with zero electrostatic coupling (Figures 4a, 4c) and with full electrostatic coupling (Figures 4b, 4d). Although turning on charge-solvent interactions increases the variation in water density across the surface, it does not appear to increase the overall density of water in the first solvation shell, because regions of increased solvent density are balanced by other regions of reduced solvent density. That said, notable localization (high density) of water molecules at specific surface sites is seen in CD[7] upon charging. The highest-density regions observed in CD[7] are those near hydroxyl hydrogens, and similarly strong localization of water is also observed near the hydroxyl group of a single methanol molecule (Figure S1 in the supplementary material⁸⁴), whose solvation nonlinearity is similar to that of CD[7] (Figure 1a). It is not clear whether this localization of water at solute hydrogen bonding sites contributes to the nonlinear electrostatic responses observed here.

Figure 4.

First solvation shell water density (relative to bulk) for cucurbit[7]uril (CB[7]) and β-cyclodextrin (β-CD), in the electrostatically decoupled (a) and (c) and coupled (b) and (d) states.

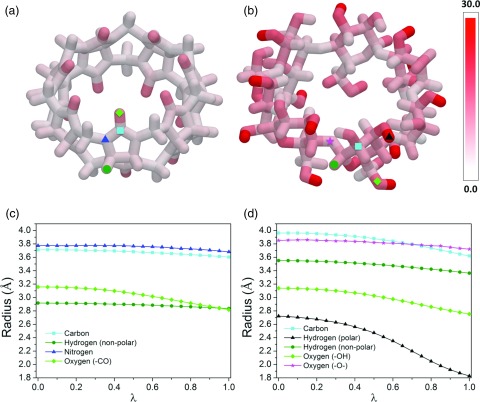
We then considered solute electrostriction, by looking for shrinkage in the radii of the first hydration shells of solute atoms, as λ rises from 0 to 1. These radii were computed as the time-averaged distance between each solute atom and the nearest water molecule's oxygen atom. Substantial reductions in these first-shell radii are in fact observed with increasing λ, particularly for CD[7] (Figure 5). The magnitude of this effect varies significantly across atoms: 2%-12% for β-CB and 1%-33% for CD[7] (Figures 5a, 5b). Similar changes in first-shell radii were also observed in the case of methanol and formaldehyde (Figure S2 and Table S1 in the supplementary material⁸⁴). Not surprisingly, the greatest reductions in first hydration shell radius occur at polar atoms, e.g., the carbonyl oxygens of β-CB and the hydroxyl hydrogens and oxygens in CD[7] (Figures 5c, 5d). Interestingly, solute atoms with identical charges and Lennard-Jones parameters can have significantly different hydration shell radii. For example, the O4 and O5 atoms (ether oxygens) of β-CD show different first-shell radii, both in the uncoupled (λ = 0) and coupled (λ = 1) cases (Figure S3 in the supplementary material⁸⁴), indicating that not only electrostatics but also the local geometry influences the preferential location of the first-shell waters. The particularly large compression of the solute near the hydroxyl hydrogens of CD[7], in both absolute and percentage terms, coincides with the pronounced nonlinear solvation response exhibited by compounds containing hydroxyl groups. This suggests that solute electrostriction might play an important role in the nonlinear solvation response of such molecules. Note that the particularly small baseline radius of the hydrogen atom makes its reaction field potential, and hence its contribution to ∂G/∂λ, particularly sensitive to changes in radius, owing to the reciprocal relationship between reaction field and radius.

Figure 5.

(a) and (b) Percent decrease in the first hydration shell radius of cucurbit[7]uril (CB[7]) and β-cyclodextrin (β-CD), respectively, upon full coupling. (c) First hydration shell radius of the representative solute atoms (marked in (a) and (b)) in CB[7] and β-CD, as a function of the coupling parameter.

We further tested the role of solute electrostriction, first by rerunning the solvation analysis of methanol with an artificially hardened LJ potential, which reduces the amount of solute electrostriction. The repulsive part of the LJ potential was changed from the standard r⁻¹² dependence to a r⁻⁴⁰ dependence, with the other LJ parameters adjusted to preserve the well depth and diameter (i.e., the distance at which the LJ potential is minimum). With this steeper repulsive potential, the first hydration shell radii of the various atoms of methanol fall by only 0.0%-7.5% as λ changes from 0 to 1, significantly less than the range of 0.6%-25.9% previously obtained with the standard Lennard-Jones potential. In particular, the solvation radii of the hardened O and H atoms fall by −0.093 and −0.219, compared with −0.380 and −0.698 Å for standard LJ parameters, and no other atoms shrink by more than 0.1 Å, even with standard LJ parameters (Table S2 in the supplementary material⁸⁴). This reduction in solute electrostriction is accompanied by a much more linear solvation response (α = 0.91) than that of unmodified methanol (α = 0.75). Thus, the artificially hardened repulsive potential lowers solute electrostriction and accordingly reduces the supralinearity of the solvation response. Note, however, that some of the reduction in nonlinearity might also result from the fact that the hardened LJ potential leads to slightly larger initial first hydration shell radii, by 0.207 Å on average.

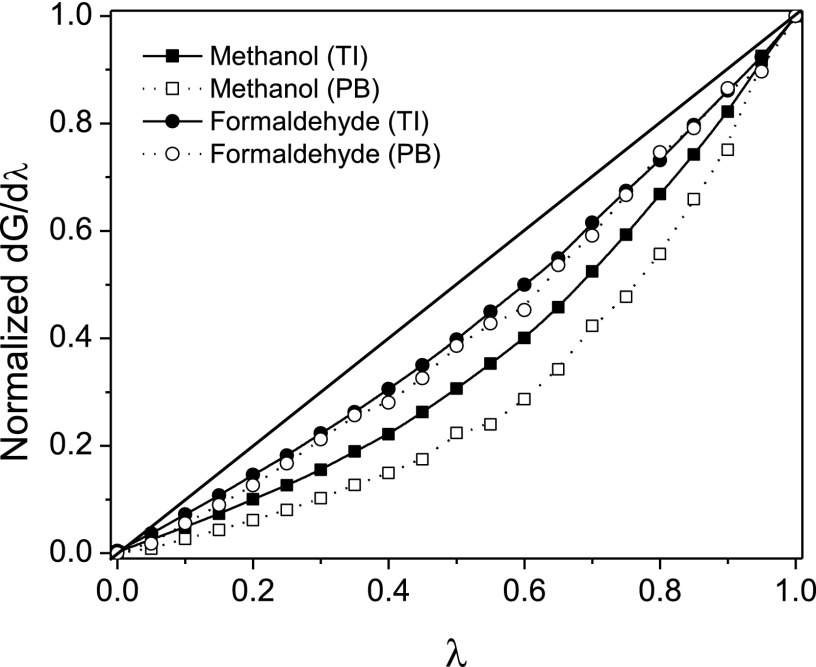
We then tested whether the solute electrostriction observed here suffices to account for the nonlinearity of the solvation response. This was done by computing the stepwise polar solvation responses of methanol and formaldehyde with continuum PB calculations, where the partial charges changed in proportion to λ, and the dielectric cavity radii were reduced from their initial values according to the mean distance of first-shell water molecules calculated from the respective explicit-water MD simulations. The initial (λ = 0) dielectric cavity radii were adjusted with different offsets for positive and negative partial charges to account for charge asymmetry of water.^{58, 59, 76} Thus, a single PB calculation with full partial charges provided an electrostatic solvation free energy in close agreement (< 0.25 kcal/mol) with the TI value. The normalized polar solvation responses calculated with the PB model (Figure 6) strongly resemble those obtained from the thermodynamic integration method using explicit-water MD simulations (Figure 1), and are equally or more supralinear. These results indicate that solute electrostriction suffices to explain the supralinear electrostatic response of water observed in the TI studies. The greater nonlinearity observed in the PB study might result in part from the fact that the PB calculations omit the repulsive LJ energy penalty implicitly associated with solute electrostriction in the TI studies.

Figure 6.

Comparison of polar solvation responses computed using thermodynamic integration (TI) method with explicit-water simulation and continuum Poisson-Boltzmann model with cavity radii at each step assigned based on the nearest water distances calculated from the respective explicit-water MD simulations.

CONCLUSIONS

In summary, strikingly supralinear solvent responses are observed for both types of host, especially for the CDs, independent of host size. These results contrast with prior observations of a linear electrostatic response of water to the charging of small ions of up to about ± 1e,^{25, 60, 77, 78} which have lent support to the validity of the linear response approximation in continuum solvation models. The distinctly supralinear pattern of the present macrocyclic hosts cannot be attributed to their ability to sequester water molecules in their binding cavities, because we observe similar nonlinearity for the small molecules formaldehyde and methanol, which bear the main polar functional groups of the CBs and CDs, respectively. In addition, we are unable to confirm the suggestion of a resonance-like interaction of polar solutes with water's hydrogen-bonding network.²⁵ Instead, the present analysis points to solute electrostriction as the main cause of this supralinearity, in agreement with a prior study limited to water treated as a solute in water.²⁶

The nearly linear electrostatic response of water to the charging of ions has been attributed to a compensating balance between solute electrostriction (supralinear) and dielectric saturation (sublinear).^{26, 77, 78} In contrast, we observe no significant dielectric saturation for neutral polar solutes. This observation agrees with prior results for solutes of similar dipole moment,²⁵ and means that the electrostriction observed here is unopposed by saturation and hence can account for the supralinear response of water to these solutes. We conjecture that the difference between water's response to ions and small dipoles derives from the fact that an ion exerts both its attractive forces (electrostricting) and its orienting torques (saturating) as a simple monopole; whereas, because a hydroxyl group (for example) is not an ideal dipole, its attractive forces on the neighboring atoms of first-shell water molecules have a strong, monopolar character, while its orienting torques, which necessarily act at longer range, have a more dipolar, and hence weaker, character.

The striking nonlinearity of water's electrostatic response to macrocyclic hosts and functional groups representative of neutral polar protein side-chains has implications for the modeling of supramolecular systems and biomolecules with continuum solvent models. For example, accuracy might be improved simply by moving away from the common practice of setting the dielectric cavity radii of atoms based only on their Lennard-Jones parameters, and instead accounting also for their partial charges or other determinants of local field strength. More advanced implicit solvent models, which seek to improve the physical description of the system^{79, 80} are also relevant in this context. In particular, variational implicit-solvent model (VISM)⁸¹ and the geometric flow model^{82, 83} are inherently capable of altering the dielectric cavity radius as a function of field strength, and may therefore capture the solute electrostriction effect identified here.