FusionArc optimization: A hybrid volumetric modulated arc therapy (VMAT) and intensity modulated radiation therapy (IMRT) planning strategy

Abstract

Purpose: To introduce a hybrid volumetric modulated arc therapy/intensity modulated radiation therapy (VMAT/IMRT) optimization strategy called FusionArc that combines the delivery efficiency of single-arc VMAT with the potentially desirable intensity modulation possible with IMRT.

Methods: A beamlet-based inverse planning system was enhanced to combine the advantages of VMAT and IMRT into one comprehensive technique. In the hybrid strategy, baseline single-arc VMAT plans are optimized and then the current cost function gradients with respect to the beamlets are used to define a metric for predicting which beam angles would benefit from further intensity modulation. Beams with the highest metric values (called the gradient factor) are converted from VMAT apertures to IMRT fluence, and the optimization proceeds with the mixed variable set until convergence or until additional beams are selected for conversion. One phantom and two clinical cases were used to validate the gradient factor and characterize the FusionArc strategy. Comparisons were made between standard IMRT, single-arc VMAT, and FusionArc plans with one to five IMRT/hybrid beams.

Results: The gradient factor was found to be highly predictive of the VMAT angles that would benefit plan quality the most from beam modulation. Over the three cases studied, a FusionArc plan with three converted beams achieved superior dosimetric quality with reductions in final cost ranging from 26.4% to 48.1% compared to single-arc VMAT. Additionally, the three beam FusionArc plans required 22.4%–43.7% fewer MU/Gy than a seven beam IMRT plan. While the FusionArc plans with five converted beams offer larger reductions in final cost—32.9%–55.2% compared to single-arc VMAT—the decrease in MU/Gy compared to IMRT was noticeably smaller at 12.2%–18.5%, when compared to IMRT.

Conclusions: A hybrid VMAT/IMRT strategy was implemented to find a high quality compromise between gantry-angle and intensity-based degrees of freedom. This optimization method will allow patients to be simultaneously planned for dosimetric quality and delivery efficiency without switching between delivery techniques. Example phantom and clinical cases suggest that the conversion of only three VMAT segments to modulated beams may result in a good combination of quality and efficiency.

INTRODUCTION

Intensity modulated radiation therapy (IMRT) and volumetric modulated arc therapy (VMAT) are advanced radiotherapy treatment delivery techniques that rely on increased degrees of freedom during optimization. Both techniques create plans that are generally considered to produce superior dose distributions compared to conventional conformal techniques for moderate to complex treatment sites. IMRT takes advantage of intensity modulation at favorable static beam angles, while VMAT exploits the extra degrees of freedom provided by increased angular sampling. While the latter may appear to increase the overall possible plan quality, there are also restrictions based on the compatibility between adjacent apertures and the speed of the dynamic delivery components. These limitations make it less clear which technique is preferable in different treatment situations.

A variety of recent publications have compared the merits of the two techniques in various treatment sites.^{1, 2, 3, 4, 5} From these studies, VMAT appears generally capable of producing plans that are dosimetrically equivalent to IMRT. VMAT plans often require fewer monitor units and can also achieve greater delivery efficiency. The improved delivery efficiency of VMAT may lead to potential reductions in patient motion and the larger area apertures generally delivered by VMAT suggest that VMAT dose distributions may be less impacted by motion and interplay effects compared to complex IMRT deliveries.⁶ However, the dosimetric quality of single-arc VMAT plans for some complex treatment geometries has failed to meet that of IMRT.^{1, 7, 8} For example, Popple et al. reported that for prostate plans, VMAT results were comparable to IMRT, but for other sites, such as head and neck, they were unable to achieve equivalent plan quality with single arc and in some cases, double arc VMAT.¹ Most notably, they saw improved target homogeneity with IMRT. Guckenberger et al. have similarly shown that target volume complexity is a factor in whether or not single arc VMAT is sufficient to reach IMRT plan quality. They noted that multiple arc VMAT can be applied at the cost of increased delivery time, monitor units, and low dose spread.⁷ In a study by Tang et al. multiple arc (IMAT), single arc (AMRT), and IMRT plans were compared.⁹ All arc plans were developed with an inhouse algorithm which assumes a VMAT capable machine with dose rate variation. The multiple arc plans achieved the highest quality of the three, while the single arc plans compromised target coverage in order to spare normal tissues. It was also noted that there are more deliverability constraints in single arc plans compared to multiple arc plans, which in turn can compromise the final results for single arc plans. As mentioned above, the use of additional VMAT arcs can lead to improved quality over single-arc VMAT, making plans comparable to IMRT.^{8, 9, 10} In certain situations, IMRT can still retain an advantage (especially in target homogeneity) for cases with multiple dose prescriptions due to the need for modulation from selected beam angles. Thus, the improved delivery efficiency of a single arc may be sacrificed for improved dosimetric quality and potentially higher monitor units, or vice versa. A system that can take advantage of the merits of both IMRT and VMAT may provide the compromise between delivery efficiency and plan quality that is needed to satisfy many clinical situations.

Chan et al. found that optimizing a VMAT plan on top of a baseline plan consisting of two manually placed 3D conformal (3DCRT) fields achieved higher dosimetric quality for an assortment of nonsmall-cell lung cancer patients compared to double-arc VMAT or 3DCRT alone with a slight increase in delivery time compared to VMAT.¹¹ Martin et al. have recently compared a similar technique in esophageal carcinoma by using four manually placed IMRT beams optimized on top of a conformal arc with a user defined dose prescription.¹² This technique was comparable to VMAT plans with one or two arcs in some cases, but the lack of inverse planning for the conformal arc, as well as the manual IMRT beam placement, may have resulted in inferior coverage and an inability to achieve some of the planning objectives.

BrainLAB (Feldkirchen, Germany) has recently introduced HybridArc, a method which combines dynamic conformal arcs with IMRT. In this system, a user defined number of IMRT beams are evenly spaced within a user defined conformal arc.¹³ Intensity values for the IMRT beams and conformal arcs are chosen based on a user-defined variable, WT_arc, that limits the relative dose contribution from IMRT beams to the total dose. However, this variable introduces the potential for a wide range of plans with varying plan quality based solely on the chosen values for WT_arc.¹⁴ A recent publication on the use of HybridArc (Robar and Thomas) found that increased conformity to the target was possible using 3–15 IMRT beams for complex cranial cases, and up to five beams for the prostate cases studied. HybridArc cranial plans required an increase in MU compared to IMRT, while MU were reduced for prostate cases.¹⁴

The current work describes a treatment planning strategy, which we call FusionArc, that has been designed to combine the merits of both VMAT and IMRT. The FusionArc strategy was implemented in an inhouse optimization system. The strategy begins with a single-arc VMAT plan as the baseline plan and then converts selected VMAT apertures into IMRT beams. The converted apertures are chosen by a metric we call the gradient factor. The gradient factor is used to predict and rank the VMAT apertures that will benefit most from modulation and thus help to advantageously combine the two techniques into one solution. In a hybrid situation, where the goal would be to utilize the minimum number of IMRT beams necessary, the placement of the IMRT beams is likely to be important. While there are usually intuitive directions that would benefit from IMRT, the prediction of the best angle for modulation may become increasingly difficult as geometries become more complex.

In this paper, we describe the FusionArc strategy, validate the gradient factor metric, characterize the plan improvement gained in several treatment sites with additional IMRT beams, and compare the plan quality and efficiency of single-arc VMAT, IMRT, and FusionArc hybrid plans.

METHODS AND MATERIALS

Hybrid VMAT/IMRT strategy and gradient factor formulation

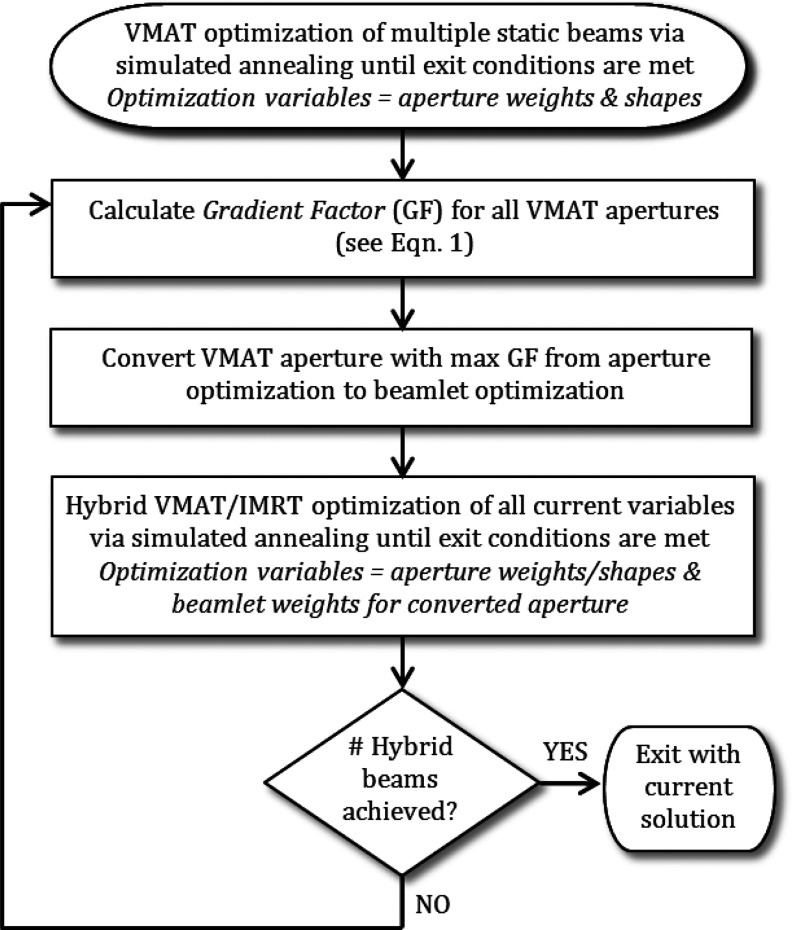
An inhouse developed beamlet-based optimization system, UMOpt,¹⁵ was enhanced to include the simultaneous optimization of both VMAT and IMRT, as shown in Fig. 1. The process begins with the optimization of a single-arc VMAT plan, using an arc approximated by many static beams and predefined beamlets. All apertures are initialized to a uniform intensity and shaped to the target. Simulated annealing is used to minimize a user-defined cost function designed with a variety of custom planning objectives.¹⁶ The optimization process proceeds for a user-defined number of iterations. Once convergence is achieved, a gradient factor (GF) is calculated for each aperture to predict the gantry angle that will give the greatest reduction in the objective function value, or cost, upon conversion to intensity modulation. The gradient factor for aperture a, GF_a, is calculated according to

$${\mathrm{GF}}_a=\sqrt{{\sum }_{i=1}^N{\left(g_i^{+}\right)}^2+{\sum }_{j=1}^M{\left(g_j^{-}\right)}^2},$$ (1)

where $g_i^{+}$ is the cost function gradient with respect to beamlet i,(∂F / ∂b_i) (i.e., the partial derivative of the cost function with respect to the intensity of beamlet i), and all beamlet intensities in set N are nonzero and have positive gradient values. The variable $g_j^{-}$ denotes the gradient with respect to beamlet j where all beamlet gradient values in the set M have negative values.

Figure 1.

Flowchart for FusionArc optimization strategy.

The first term in Eq. 1 represents the sum of squared positive-valued gradients for beamlets that are active in the current VMAT aperture. The positive-valued gradients represent beamlet intensities that would cause a reduction in the final cost function value (in the local solution) if the beamlet intensities were reduced. Since the inactive beamlets in the aperture cannot be further reduced, they are excluded from the first term in the gradient factor calculation. Similarly, the second term in the GF formulation represents the sum of squared negative-valued gradients for all beamlets in the current VMAT aperture. The negative gradient values represent beamlet intensities that would result in the cost function decreasing if their values were increased. The gradient factor is motivated by the local search method called steepest descent.¹⁷ In particular, the gradient factor for a beam can be interpreted as the maximum rate of improvement in cost function value as the current solution is modified in a feasible direction that corresponds to modulating that beam. Although the gradient factor only considers the rate of improvement rather than absolute improvement in objective function value, we hypothesize that the gradient factor will be highly correlated with the actual impact on the cost function value after allowing modulation. Therefore, we expect that beam delivery angles with a high GF will yield an increase in plan quality, and thus a reduction in the final cost, upon conversion to modulation.

Once a beam is chosen for conversion from aperture to fluence optimization based on the GF, the optimization variables for that beam angle become beamlet intensities instead of aperture intensities and shapes. All remaining VMAT apertures continue to be available for further optimization along with the IMRT, or hybrid, beams. Optimization proceeds for a fixed number of iterations or until the change in the total cost for a given number of iterations remains below a set threshold. At that time, the process can continue by converting another beam to IMRT using a new GF calculation or it can be stopped. To convert an additional beam to fluence optimization, the GF is recalculated based on the current solution (VMAT with one IMRT beam). In this situation, we have observed that the previously converted IMRT beam will have a significantly lower GF than the VMAT apertures, as would be expected. Preliminary investigation showed that plan quality was improved by adding IMRT beams one at a time, but further investigation into adding multiple beams at once may be warranted to improve optimization efficiency.

Gradient factor validation

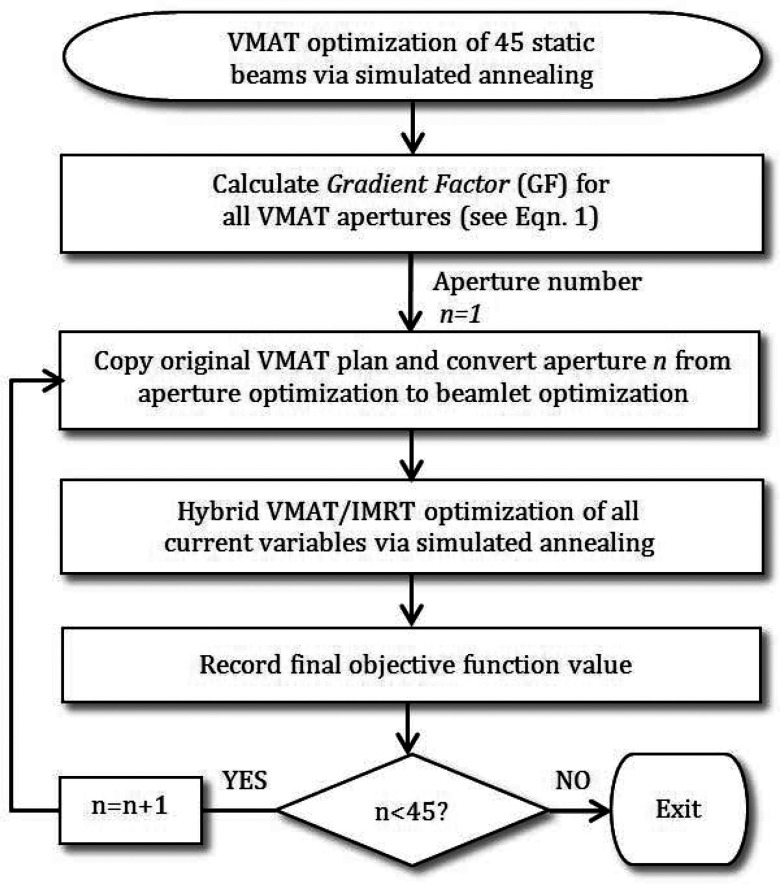
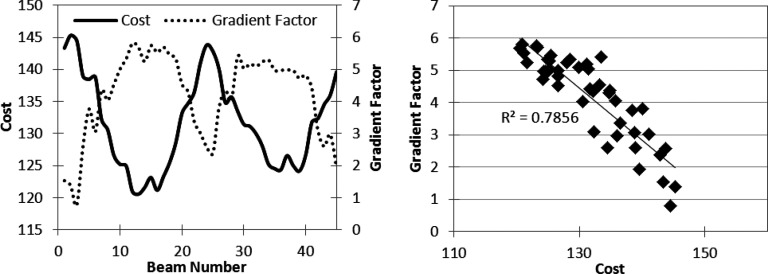
To test the correlation between the gradient factor and the benefit of modulation, single-arc VMAT plans approximated by 45 static beam angles were created and optimized separately for three cases—one phantom and two clinical examples, which are discussed in more detail in Sec. 2C. Although 8° angular spacing is large for VMAT, this value was used for the gradient factor validation since each beam was modulated one by one. After convergence, each VMAT aperture was individually converted to an IMRT beam and optimization proceeded with one hybrid IMRT beam as shown in Fig. 2. The final objective function value for each one beam hybrid plan and the gradient factor associated with the modulated beam were plotted as a function of VMAT gantry angle to determine if the gradient factor was able to predict which angles benefited the most from modulation.

Figure 2.

Flowchart for gradient factor validation strategy.

FusionArc plan comparisons

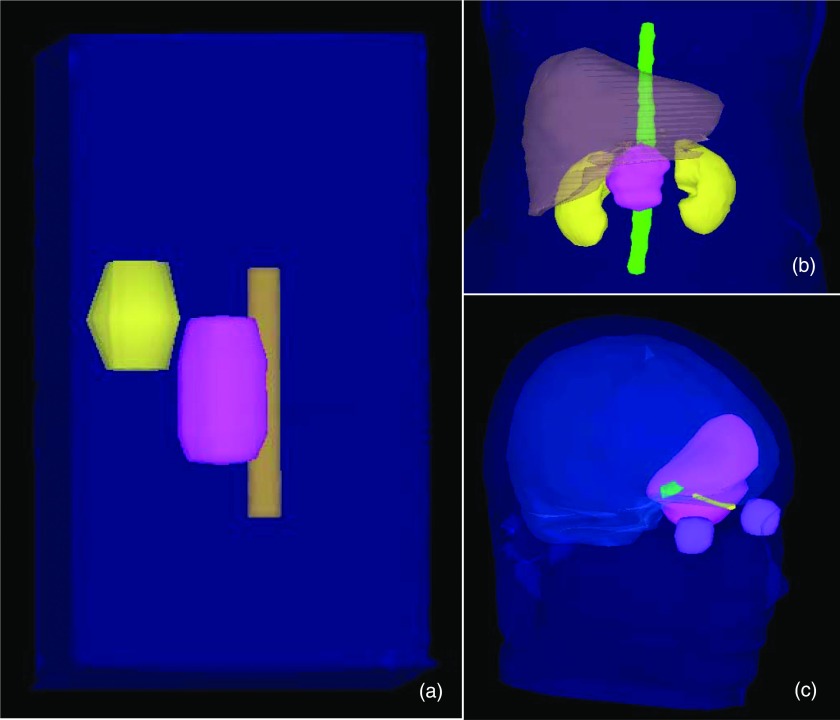
FusionArc comparisons were performed for three different cases—the TG-119 prostate phantom¹⁸ and a pancreas and brain case that had been previously treated with IMRT at our institution. All patient plans were newly created under an institutional review board approved retrospective study. Plans were evaluated quantitatively and qualitatively using a number of metrics including dose volume histograms (DVHs), dose color wash images, and plots of plan quality (or final cost) versus delivery efficiency, represented in monitor units per Gray (MU/Gy). The geometries for each case are shown in Fig. 3 and the planning goals are listed in Table 1. The planning goals for the prostate phantom case were obtained from TG-119, and objective functions for the pancreas and brain cases were based on current clinical practice at our institution.

Figure 3.

Case geometries: (a) TG-119 prostate phantom with PTV shown in pink, bladder in yellow, and rectum in brown. (b) Pancreas case with PTV in pink, liver in brown, kidneys in yellow, and cord in green (GI structures not shown for clarity). (c) Brain case with PTV shown in pink, eyes in purple, left optic nerve in yellow, optic chiasm in green, and normal brain in light blue.

Table 1.

Planning objectives for TG-119 prostate, pancreas, and brain cases.

TG119 Prostate inverse planning objectives
Structure	Objectives
PTV	79.3 Gy ± 5% (Min ≥ 75.3 Gy; Max ≤ 83.3 Gy)
Bladder	V75Gy < 10%
	V70Gy < 30%
Rectum	V75Gy < 10%
	V70Gy < 30%
Normal tissue	Minimize dose
Pancreas inverse planning objectives
Structure	Objectives
PTV	55 Gy ± 5%
Cord	D0.1cc ≤ 45 Gy
Liver	D1cc ≤ 50 Gy
Kidneys	D0.1 cc ≤18 Gy; (if cannot reach this for both kidneys, spare one)
Duodenum	D2cc ≤ 52 Gy
Small bowel	D2cc ≤ 52 Gy
Stomach	D2cc ≤ 52 Gy
Normal tissue	Minimize dose
Brain inverse planning objectives
Structure	Objectives
PTV	60 Gy ± 5%
Chiasm	D0.1cc ≤ 54 Gy
Eyes	D0.1cc ≤ 45 Gy
Optic nerves	D0.1cc ≤ 54 Gy
Normal tissue	Minimize dose

Note: All normal structure doses were minimized after the listed planning objectives were met.

In order to characterize and show the feasibility of the FusionArc planning strategy, compared to conventional IMRT and VMAT planning, each case was planned and optimized with single-arc VMAT, standard IMRT, and FusionArc with one to five hybrid beams. VMAT arcs were approximated with 45 equally spaced static beam angles (8° angular spacing) and the standard IMRT plans consisted of seven equally spaced beams. Seven beams or less are typically used at our institution for prostate, brain, and pancreas IMRT plans. All apertures were shaped to the target and made use of a 5 mm × 5 mm fluence map resolution. Limits for maximum beamlet intensities were applied to prevent undesirably hot beamlets, which can lead to increased MU with little to no improvement in plan quality.¹⁹ This strategy is consistent with clinical practice at our institution. We followed the procedure outlined in Coselmon et al.,¹⁹ using a maximum intensity ratio of 1.5–2.0 (using a standard seven beam plan).

RESULTS

A hybrid VMAT/IMRT treatment planning strategy was successfully implemented within our inhouse treatment planning system according to Fig. 1. As mentioned, the strategy utilizes a gradient factor metric to predict which VMAT beams will benefit most from added modulation. Therefore, validation results for calculation of the gradient factor are presented first, in order to characterize its use for the FusionArc plan optimization strategy. Subsequently, the results of utilizing the gradient factor to create comparisons for three cases using standard IMRT, single-arc VMAT, and FusionArc plans with one to five IMRT, or hybrid beams are presented, in order to show the ability of this hybrid strategy to provide a compromise between delivery efficiency and plan quality.

Gradient factor validation

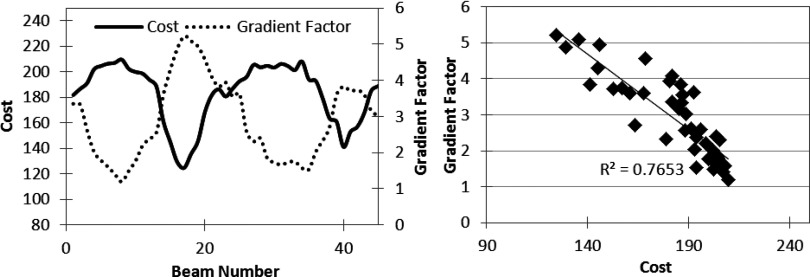
Using the strategy presented in Fig. 2, the three cases described above were optimized to create baseline VMAT plans, approximated by 45 static gantry angles. For each case, 45 one-beam hybrid plans were created by separately converting each gantry angle to fluence. Each of the 45 one-beam hybrid plans was optimized using the same number of cycles and iterations. The final cost, used here as a measure of plan quality, was recorded for each trial and plotted against the GF calculation, as seen in Figs. 456 (left). The validation tests illustrate the ability of the GF to predict the beam directions that will benefit most from modulation, where a high GF correlates with a low final objective function value, and a low GF is associated with a higher final cost. Figures 456 (right) graph the change in cost versus the gradient factor to show the quantitative correlation. The degree of linearity between the gradient factor and associated plan cost upon conversion to fluence suggests that the gradient factor calculation adequately predicts beneficial beam angles to convert to fluence optimization.

Figure 4.

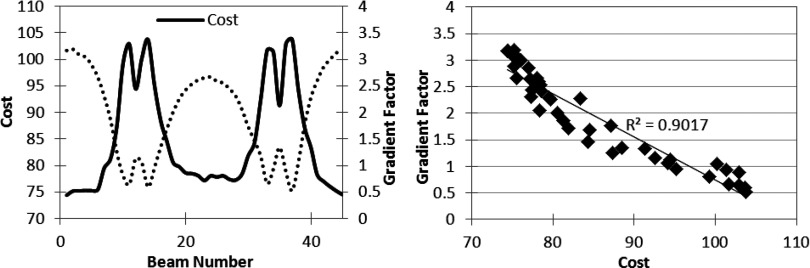
Gradient validation with TG-119 prostate case. (Left) Gradient factor validation curve. (Right) Correlation between cost vs gradient factor for data on left.

Figure 5.

Gradient validation with pancreas case. (Left) Gradient factor validation curve. (Right) Correlation between cost vs gradient factor for data on left.

Figure 6.

Gradient validation with brain case. (Left) Gradient factor validation curve. (Right) Correlation between cost vs gradient factor for data on left.

TG-119 prostate phantom case

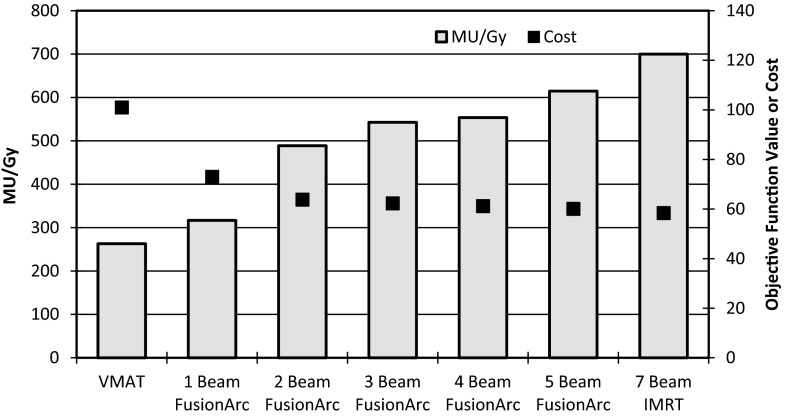
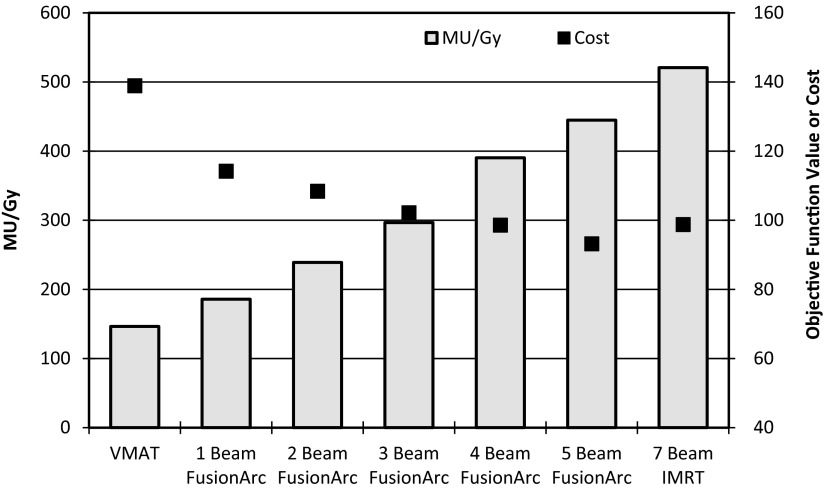
The TG-119 prostate phantom case showed substantial reductions in final cost and MU/Gy compared to the VMAT and IMRT plans, respectively, with the addition of two to three hybrid beams as seen in Fig. 7. With only two hybrid beams, the plan quality (inferred by the cost) is essentially equivalent to that of the IMRT plan, but delivery efficiency is markedly reduced. Figure 8 shows the DVHs for four of the seven final plans, demonstrating that the FusionArc plans are capable of reducing bladder and rectum mean doses. FusionArc is also capable of increasing PTV homogeneity compared to VMAT to achieve coverage similar to IMRT. A three beam FusionArc plan is capable of reducing MU/Gy by approximately 22.4% compared to IMRT, while also reducing the final cost by about 38.3% compared to the VMAT plan. Meanwhile, a five beam FusionArc plan can reduce the cost by 40.5% compared to VMAT but only achieves a 12.2% reduction in MU/Gy compared to IMRT.

Figure 7.

Plan quality (cost) and efficiency (MU/Gy) for FusionArc plans of increasing modulation for the TG-119 prostate phantom.

Figure 8.

Dose volume histograms for the TG-119 prostate phantom with seven beam IMRT, VMAT, three beam hybrid FusionArc, and five beam hybrid FusionArc plans.

Pancreas case

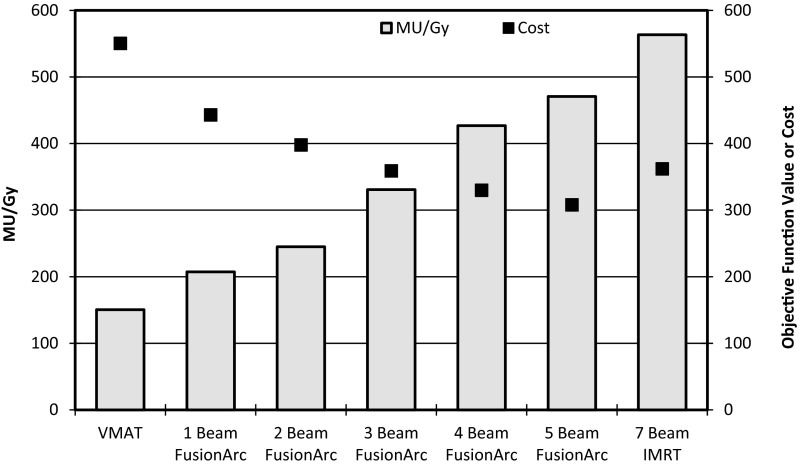
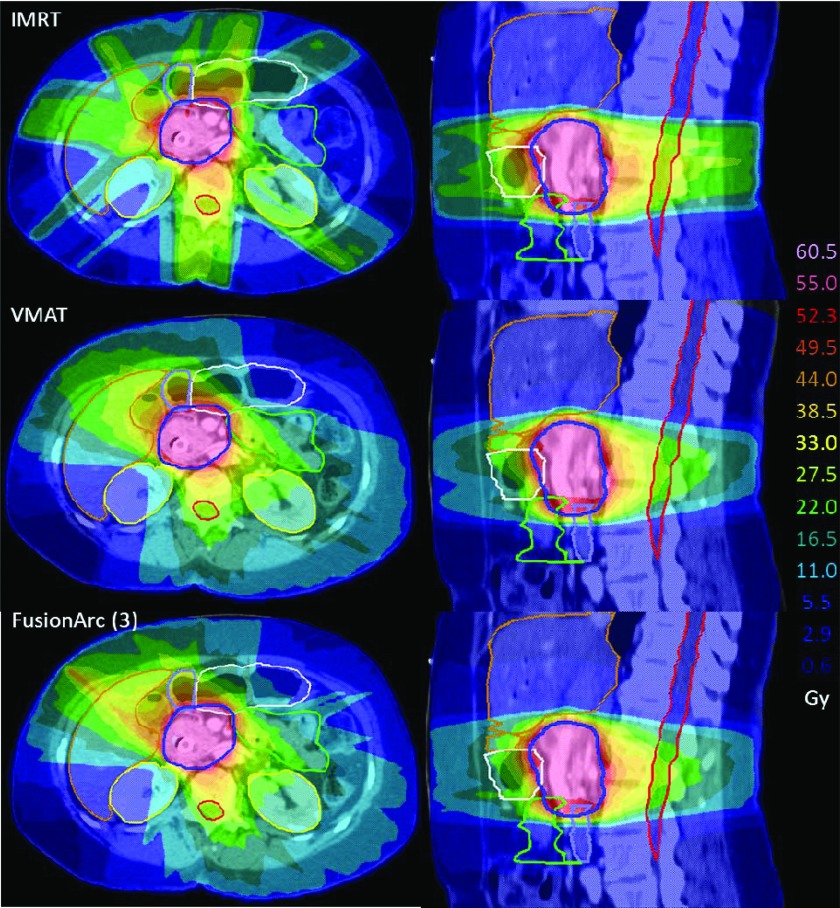
As seen in Fig. 9, the addition of only one IMRT beam yields a reduction of approximately 63.2% MU/Gy compared to IMRT, and a cost reduction of 19.5% compared to VMAT. The three beam FusionArc plan results in a decrease of 41.3% MU/Gy compared to IMRT and a 34.8% reduction in cost compared to VMAT. The three, four, and five beam FusionArc plans all showed improved plan quality (in terms of cost function value) in addition to reduced MU/Gy compared to IMRT. Dose distributions, shown in Fig. 10, illustrate some of the trade-offs made between the three techniques. For example, due to the beam arrangement, the IMRT plan gives increased dose to the stomach, but decreased dose to the small bowel compared to the rotational techniques. As is commonly seen with VMAT, there is an increase in the lower dose spread, but a decrease in the moderate to high doses to normal tissues compared to IMRT. The FusionArc plan has a slightly higher peripheral hotspot in the liver, but improved target coverage compared to both IMRT and VMAT plans.

Figure 9.

Plan quality (cost) and efficiency (MU/Gy) for FusionArc plans of increasing modulation for a pancreas patient.

Figure 10.

Dose colorwash comparisons for a pancreas case with axial (left) and sagittal (right) views. The PTV is outlined in dark blue, kidneys in yellow, spinal cord in red, stomach in white, liver in brown, small bowel in green, and duodenum in light blue. (Top) Seven beam IMRT plan. (Middle) VMAT plan. (Bottom) Three beam FusionArc plan.

Brain case

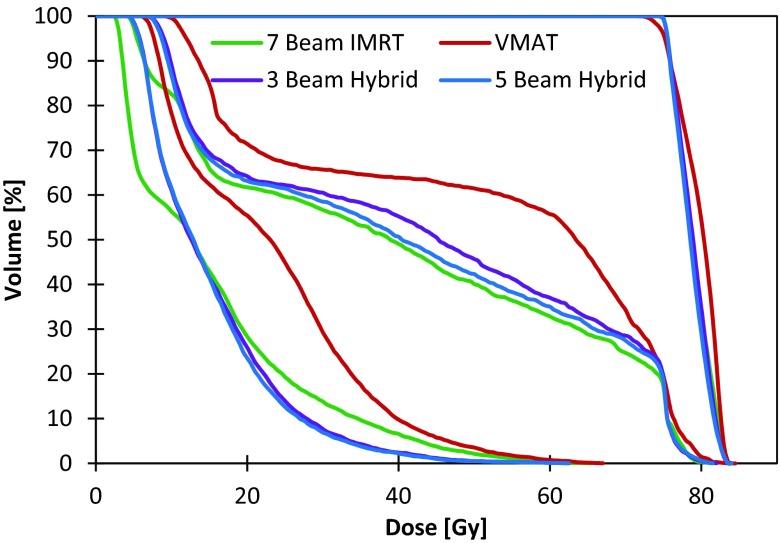
Compared to IMRT, the single-arc VMAT plans and FusionArc plans are capable of reducing MU/Gy and therefore increasing delivery efficiency. Both the four beam hybrid and the five beam hybrid plans were able to reduce the final plan cost below that of the standard IMRT plan, while maintaining lower MU/Gy. However, we recognize that the three beam hybrid in this situation offers a better compromise with a 26.4% reduction in cost compared to single-arc VMAT and approximately 43% fewer MU/Gy when compared to IMRT as seen in Fig. 11. Additionally, as seen in Fig. 12, the FusionArc plans are capable of sparing the optic structures more so than single-arc VMAT in order to meet the planning objectives in Table 1.

Figure 11.

Plan quality (cost) and efficiency (MU/Gy) for FusionArc plans of increasing modulation for a brain patient.

Figure 12.

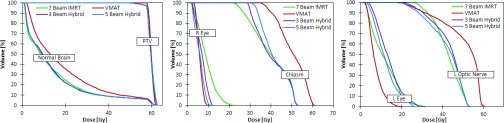
Dose volume histograms for a brain patient with seven beam IMRT, VMAT, three beam hybrid FusionArc, and five beam hybrid FusionArc plans.

DISCUSSION

IMRT and VMAT are two treatment modalities that offer increased plan quality compared to 3D conformal plans by relying on inverse planning and the many degrees of freedom inherent in each planning technique. However, the trade-offs between plan quality and delivery efficiency are not straightforward, and thus a synthesis of the two methods may provide a reasonable compromise between the efficiency of VMAT and the superior intensity modulation possible with IMRT.

In this work, a planning strategy called FusionArc has been developed and tested on a phantom and two clinical cases for two purposes: (1) to validate a GF calculation in order to select the optimal beam angle to convert to fluence and (2) to evaluate if the FusionArc optimization process offers improvements in plan quality over single-arc VMAT while offering reasonable reductions in MU/Gy compared to IMRT. The GF calculation was validated on three cases to quantitatively and qualitatively show that a higher GF correlates with a lower final cost when that beam is converted to fluence, compared to the cost associated with converting a low-valued GF beam to fluence. The results of this investigation indicate that the gradient factor effectively predicts the VMAT apertures that would benefit plan quality most upon conversion to modulation.

Each site comparison showed that FusionArc is capable of increasing plan quality with the addition of more than one hybrid beam, when compared to single-arc VMAT, while reducing MU/Gy compared to IMRT. The benefit from the first modulated beam shows the largest reduction in cost compared to VMAT, but additional modulation with more converted apertures also displays a marked decrease in plan cost. In this study, the conversion of five VMAT apertures to fluence offered final cost reductions ranging from 32.9% to 55.2% compared to VMAT. However, the associated decrease in MU/Gy, 12.2%–18.5% when compared to IMRT, was distinctly smaller. For the cases presented here, it appears that three beam FusionArc plans may offer a reasonable trade-off between final plan cost and MU/Gy, with MU/Gy reductions ranging from 22.4% to 43.7% compared to IMRT, and decreases in cost ranging from 26.4% to 48.1% compared to single-arc VMAT plans. The increased monitor units required with additional modulation suggest that clinical methods for determining the optimal compromise between quality and efficiency will need to be studied further. While a full investigation of the implications of increased MU/Gy is outside of the scope of this work, it is important to note that reducing monitor units and the associated leakage and whole body dose that can accompany complex intensity modulated deliveries may reduce the risk of secondary cancers associated with IMRT delivery as well as reduce machine wear and tear and increase department throughput.

Compared to current techniques for combining IMRT and VMAT plans, FusionArc offers the flexibility of optimizing VMAT apertures and IMRT beams concurrently, instead of requiring the user to define constraints on dose contributions from conformal arcs and IMRT beams. Additionally, the gradient factor is fundamental in determining the optimal beam angle to convert to fluence. HybridArc, which is geared toward very conformal dose distributions for radiosurgery, relies on fixed, equally spaced IMRT beams along a dynamic arc.^{13, 14} In more complex geometries, this strategy may fail to take into account geometrical considerations and could result in modulation at inappropriate angles.

A method proposed by Li and Xing²⁰ similarly demonstrates that additional modulation from “optimal” beam directions improves plan quality compared to VMAT alone. In their strategy, a large number of beam angles are used to increase the angular sampling while also simplifying the intensity modulation by eliminating the dispensable segments. That method utilizes an IMRT delivery, which could be time intensive, although some newer linear accelerator delivery systems can deliver a high number of IMRT beams much more efficiently than past designs.

It should be pointed out that inverse plan quality, whether it be for IMRT, VMAT, or conformal methods, can be highly dependent on the optimization algorithm, strategy, and cost function chosen. This is especially true if the cost function is not appropriate or the optimization algorithm allows the solution to fall into significant local minima. For example, IMRT and VMAT will not attempt to reduce dose to uninvolved normal tissue without an explicit objective to do so. This specific objective may be more important for VMAT due to the increase in angular degrees of freedom.

Our work has been initially implemented into an inhouse treatment planning system, so that we could hold as many variables consistent between the plan comparisons as possible (optimization algorithm, intensity limits, fluence resolution, calculation resolution, cost function, etc.). We believe it would be straightforward to implement the FusionArc strategy within another planning system and reproduce the relative results seen here. However, there will always be differences in the absolute and relative plan quality due to the inherent differences between inverse planning strategies, algorithms, and cost functions throughout clinical and research optimization systems.

Additional research work on the FusionArc method is warranted in several areas. Most notable is further investigation of the types of cases and geometries that will benefit most from this hybrid strategy and if multiple arcs offer added benefits over single-arc FusionArc plans. We also believe we can potentially exploit the use of the gradient factor to determine where plan perturbations are least disruptive for adaptive planning scenarios. Adaptive therapy based on physiological response to therapy is by definition based on a pattern of response of target and normal tissue to the original dose distribution. Thus, we believe that the best adaptive plan is one that will make only the minimal perturbations required to the original dose distribution to achieve the adaptive plan goals but, at the same time, not alter confidence in relying on the dose response relationships that already have been established via during-treatment feedback data and imaging relative to original treatment plans.

Other secondary tasks include improving the overall optimization efficiency and code implementation for hybrid IMRT/VMAT planning, including an investigation on the use of graphics processing units (GPU) for optimization. Additionally, while FusionArc plans could be delivered currently as two separate components—a single arc with standard step-and-shoot IMRT segments—the optimal delivery mode for hybrid plans should be determined, with the potential of co-development efforts with vendors to implement a new delivery mode for FusionArc which allows IMRT control points (with no gantry change) within a VMAT control point sequence (with gantry changes). Furthermore, a study of converting multiple beams at a time to fluence is warranted to determine when this decrease in planning and optimization time may be worth small potential increases in final cost.

CONCLUSIONS

FusionArc, a hybrid VMAT/IMRT inverse planning strategy, was designed and implemented to allow the simultaneous optimization of VMAT apertures and IMRT beams for dosimetric quality and delivery efficiency without switching between delivery techniques. As part of the optimization strategy, a gradient factor calculation was developed, validated, and implemented. We have demonstrated that the gradient factor accurately predicts the beams that will increase plan quality the most upon conversion to fluence. In the current work, the gradient factor was used to select one to five beam angles to convert to fluence for the creation of multiple FusionArc plans. Our results point to the fact that there are distinct trade-offs between efficiency and quality as increasing amounts of modulation are applied to the baseline single-arc VMAT plan. The ideal number of IMRT beams in FusionArc plans will likely vary as more clinical sites are studied. Further work will investigate the possibilities suggested by these results.