Abstract
In the last three decades, China has experienced rapid economic development and growing economic inequality, such that economic disparities between rural and urban areas, as well as coastal and interior areas have deepened. Since the late 1990s China has also experienced an ageing population which has attracted attention to the wellbeing of the rapidly growing number of elderly. This research aims to characterise province differences in health and to explore the effects of individual income and economic disparity in the form of income inequality on health outcomes of the elderly. The study is based on the Chinese Longitudinal Healthy Longevity Survey data collected in 2008 for 23 provinces. Multilevel logistic models are employed to investigate the relationship between income, income inequality and self-rated health for the elderly using both individual and province-level variables. Results are presented as relative odds ratios, and for province differentials as Median Odds Ratios. The analysis is deliberately exploratory so as to find evidence of income effects if they exist and particular attention is placed on how province-level inequality (contemporaneous and lagged) may moderate individual relationships. The results show that the health of the elderly is not only affected by individual income (the odds of poor health are 3 times greater for the elderly with the lowest income compared to those at the upper quartile) but also by a small main effect for province-level income inequality (odds ratio of 1.019). There are significant cross-level interactions such that where inequality is high there are greater differences between those with and without formal education, and between men and women with the latter experiencing poorer health.
Keywords: China, Health of elderly, Income, Income inequality, Multilevel modelling
Introduction
The relationship between income inequality and health status has been widely studied in developed countries. The “income inequality hypothesis” contends that an individual’s health is not only affected by individual income but also by the relative distribution of the income in the society where people reside (Subramanian, Blakely, & Kawachi, 2003; Wilkinson, 1997). It is argued that unequal societies lead to poorer individual health over and above the effects of individual income. Empirical work, however, has found rather mixed results (Rowlingson, 2011). Research conducted in the United States provides evidence of an association between income inequality and poor health (Blakely, Kennedy, Glass, & Kawachi, 2000; Kennedy, Kawachi, Glass, & Prothrow-Stith, 1998; Subramanian et al., 2003; Subramanian & Kawachi, 2006; Subramanian, Kawachi, & Kennedy, 2001). However, studies conducted in other developed countries (e.g. New Zealand, Finland, Sweden, UK, Denmark and Japan) found no support for the additional effect of income inequality on health over and above individual income (Blakely, Atkinson, & O’Dea, 2003; Blomgren, Martikainen, Makela, & Valkonen, 2004; Gerdtham & Johannesson, 2004; Lorgelly & Lindley, 2008; Osler et al., 2002; Shibuya, Hashimoto, & Yano, 2002). Subramanian and Kawachi (2004) argue that the more egalitarian distribution of income together with well-developed safety-net provisions in those non-USA countries is responsible for the different findings.
In terms of the mechanisms to explain the effects of income inequality on population health, three pathways have been identified: first, income inequality is linked with reduced social spending; second, inequality erodes social capital; third, inequality leads to psycho-social effects from invidious social comparisons (Kawachi & Kennedy, 1999). Subramanian and Kawachi (2004) distinguish two effects: one is the “concavity effect”, which states that the redistribution of the income from the rich to the poor will result in better overall average health as the improvement in health among the poor exceeds the health loss among the rich; the other is the “pollution effect”, an independent contextual effect which explains that the distribution of income in a society influences an individuals’ health and that an unequal society can be damaging for public health.
China has achieved tremendous economic development in the last three decades, but this has been accompanied by rising economic disparities between the coast and inland, urban and rural areas; between provinces as well as within provinces. From 1980 to 2005, China’s overall Gini coefficient (Gini coefficient is a measure of economic inequality in a society. The range of the value of Gini is between 0 and 100%, whereas 0 indicates that income is completely equally distributed and 100 means the society has the maximum income inequality) rose from 33% to 45% (Fan & Sun, 2008). Meanwhile, China’s population is ageing rapidly. The population aged over 65 is approximately 110 million (National Bureau of Statistics, 2010) accounting for about 8.3% of the total Chinese population. This proportion is estimated to reach 16% in 2030 and 23% in 2050 (United Nations, 2001).
Despite China’s remarkable economic achievement, the state provided social security coverage for the elderly is rather inadequate and inefficient (Liu & Zhang, 2004). Since the economic reforms, the public-financed and central-planned health system has turned into a more commercialised and decentralised form. The portions of both government and social spending on overall health expenditure have decreased from 28% and 56% to 16% and 23% respectively between 1980 and 2001 and the share of personal expenditure on health increased dramatically from 16% in 1980 to 61% in 2001 (Zhang & Kanbur, 2005). Moreover, only 25% of the elderly in urban areas and 4.2% of the elderly in rural areas receive financial coverage for health care from the government, collective enterprises or health insurance (Zeng & George, 2010).
Research on the relationship between income inequality and population health in China is scarce. There are in fact only two published studies. Using data from nine provinces for the early 1990’s, Li and Zhu (2006) in a multilevel analysis found an inverted-U shape association between self-rated health and community income inequality. Pei and Rodriguez (2006) in their multilevel study based in nine provinces in China during 1991–1997 found that people living in provinces with greater income inequality have a higher risk of reporting poorer health. No studies have been carried out on a more complete national survey and for the more recent period with greater differences between provinces. No research has focused on the relationship between income inequality and the health of the elderly in China. In fact, the elderly are the least researched population in income inequality studies despite the fact that their health may be more susceptible to societal income inequality, as they may be more dependent on the support of others (Muramatsu, 2003). The elderly are potentially more vulnerable to their living environment as they are less able to adapt and more reliant on resources available in the area of residence than younger adults (Robert & Li, 2001). In an unequal society, their greater awareness of their comparative socioeconomic standing, coupled with their relative isolation from the rest of the population, can result in negative emotions such as distrust, shame, and exclusion that may lead to chronic stress in their daily life (Kawachi & Kennedy, 1999). The elderly also have growing health care needs due to their advanced age and are more receptive to social spending on health care. In this context it is important to understand to what extent such inequality and individual differences in income affects the health of the elderly, an increasing but marginalised population of great policy importance.
The distinctive features of this study are:
The research is undertaken in China, a country with growing income inequality and ageing population; we pay particular attention to differences between provinces as this is becoming a marked feature of contemporary China;
The analysis is based on a large scale scientific representative survey of the elderly: the Chinese Longitudinal Healthy Longevity Survey, which allows the estimation of between province differences in self-rated health;
The methodology employs sophisticated multilevel modelling analysing the relationship between income inequality (contemporaneous and lagged) and population health at the individual and province level simultaneously so as not to commit any ecological or atomistic fallacies (Subramanian, Jones, Kaddour, & Krieger, 2009);
All the models are estimated with full Bayesian procedures which allows the exact estimation of parameters without approximations and with full uncertainty propagation (Jones & Subramanian, 2012). This is particularly important in this study as there are only 23 provinces on which to characterise regional differences and to estimate the inequality effect;
It pays particular attention to the estimation of individual income effect, as it is known that mis-specification of a level 1 predictor (assuming linearity when it is non-linear) can lead to spurious cross-level interaction effects (Bauer & Cai, 2009; Jen, Jones, & Johnston, 2009);
Attention is focussed on who might be most affected by income inequality as Rowlingson’s (2011) review finds that this aspect is very under-researched. This is achieved by a deliberate exploratory analysis of models with cross-level interactions (Jones & Duncan, 1995) whereby inequality is hypothesized to affect different types of people differentially.
Data and methods
Data
Data are from the Chinese Longitudinal Healthy Longevity Survey (CLHLS) which is a national population-based longitudinal survey initiated in 1998. It has collected extensive data on a large population of the oldest-old aged 80–112 with comparatively younger elders aged 60–79. The survey is based on a randomly selected sample of elderly Chinese from almost half of all the counties and cities of 23 out of the 31 provinces in China (Eight provinces in northwest China where ethnic minorities form a substantial proportion of the population are excluded from the CLHLS because information on self-reported age has been found to be too unreliable). These areas cover 1.1 billion people, 85 percent of the total population in China. The data used in this study is the latest 2008 survey in CLHLS which allows us to look at the lagged effects of province inequality. There are 14,744 respondents with sufficient data from the present analysis out of an original total of 16,844 interviewees. The data has a natural hierarchal structure with 14,744 individuals nested within 23 provinces. Appendix A provides a list of the provinces with the number of sampled individuals in each province. The response rate for the 2008 wave is 79.8% which is high for such a study of the elderly. The study is exempt from ethics approval since it is an analysis of secondary data.
The dependent variable in this study is Self-Rated Health (SRH). Previous studies suggest that this is a sensitive and reliable indicator of current health status with high predictive validity independent of other medical, behavioural or psycho-social factors (Idler & Benyamini, 1997; Wu & Schimmele, 2006). Interviewees self-rated their present health to the following categories: very good, good, fair, poor, and very poor. For comparability with previous studies, the categories are recoded into a binary outcome: 0 for very good, good and fair, and 1 for poor or very poor (Table 1). (Results from multiple imputation using the methods of Goldstein (2009) do not suggest that missing data substantially influences the results.)
Table 1.
Descriptive univariate information on the 2008 CLHLS sample.
| Response | |
| Poor/very poor health (n = 2395, 16.3%) | Very good, good and fair (n = 12,349, 83.7%) |
| Predictors | |
| Level 1:individuals, n = 14,744 | |
| Age | 60–116, mean = 85.7 |
| Gender | Male (6602, 44.8%), female (8142, 55.2%) |
| Education | None-schooling (8819, 59.8%); schooling (5925; 40.2%) |
| Residence | Urban (5904, 40%); rural (8840, 60%) |
| Old-age insurance | Doesn’t have (13,724, 93.1%); have (1020, 6.9%) |
| Total family income (unit: 10k Yuan) | 0–10.00, mean = 2.26 |
| Total family equivalised income | 0–10.00, mean = 1.23 |
| Level 2: province, n = 23 | |
| 2008 Gini coefficient | 27%–74%, mean = 50% |
| Level 2: province, n = 22 (Lagged inequality)a | |
| 2008 Gini coefficient | 27%–66%, mean = 49% |
| 2005 Gini coefficient | 31%–60%, mean = 46% |
| 2002 Gini coefficient | 27%–50%, mean = 45% |
| Mean of 1985–1995 Gini coefficient | 17%–28%, mean = 21% |
Note: The 2002 Gini coefficient is calculated from the family per capita income of 2002 CLHLS wave. The 2005 Gini coefficient is the mean of 2002 and 2008 Gini coefficients due to the Gini coefficients in 2005 CLHLS is out of range. The mean of 1985–1995 Gini coefficients was calculated by Xu and Zou (2000). Hainan province is a new survey area in 2008; therefore, there are only 22 provinces in the lagged inequality analysis.
Although the focus of this research is on the effects of income and inequality on the health of the elderly, it is important to control for other factors but not to over control so that the effects are diluted. It is also important to investigate moderated relationships as the effects of inequality may be different for different people. At the individual level, the key demographic, social and income predictors are age, gender, education, urban–rural residence, old-age insurance and family equivalised income1 (Table 1). At the province level, the Gini coefficient is used to measure income inequality (Fan & Sun, 2008). In the analysis, the contemporary Gini coefficient for the 23 provinces is calculated from the total family equivalised income of the respondents in 2008 wave. In China, it is the norm for old people to rely upon their adult children for financial support. Elderly from families with higher incomes will have more access to better health services as well as more personalized care to improve their health status. As a result, the health outcomes of the elderly are more directly affected by their family income instead of personal income. This research will use total family equivalised income to measure income inequality and explore its relationship with the self-rated health for the elderly.
It is also important to consider lagged effects of inequality (Li & Zhu, 2006; Subramanian & Kawachi, 2006). Consequently, in addition to the Gini coefficients derived contemporaneously from the 2008 survey, Gini values were also derived from previouswaves of the study in 2005 and 2002. Fully comparable data before that are scarce and we were forced to use the estimates (averaged over the 1985–1995 period) of Xu and Zou (2000) which are based only on urban residents. While comparisons are difficulty, Table 1 shows there was much less between province differences at this earlier period so that these values include the beginning stage of the rising inequality in China.
Methods: hierarchical analysis with multilevel logistic model
Multilevel statistical techniques provide an analytical framework for data with a hierarchical structure (Duncan, Jones, & Moon, 1998). They estimate the variability between individuals and between places simultaneously (Hox, 2002; Jones, 1991; Snijders & Bosker, 1999). As the response of self-rated health is binary, a multilevel logistic model based on a logit-link function will be used. ‘Very good, good and fair health’ is used as the base category. Individuals constitute the lower level and the provinces form the upper level of the model. All the models are estimated by the MLwiN software (Rasbash, Charlton, Jones, & Pillinger, 2009). Because of the discrete nature of the outcome and the rather small number of higher level units, Bayesian MCMC estimation is used for more robust estimation (Browne & Draper, 2006).
A simple main-effects multilevel non-linear probability model is shown below as:
| (1) |
where the observed response Yij is 1 if the individual i in province j is in poor health; 0 otherwise. The underlying proportion of being in poor health π;ij is non-linearly related to income at the individual level (X1ij) and income inequality at the province level (X2j). This model is linearized by a logit transformation:
| (2) |
There are three fixed parameters in this model that capture the average relationship across all respondents and provinces. The β0 parameter is the overall intercept log-odds for elderly across provinces of being in poor health. The β1 parameter captures the ‘micro’ individual income effect, and the β2 parameter captures the ‘macro’ income inequality effect at the province level. The u0j terms are the random differential intercepts which represent province-level residual differences after taking account of individual income and income inequality; they are on the logit scale and assumed to be Normally distributed with mean of 0 and variance of. This variance term summarises the residual between province variations on the logit scale. The level 1 variance, because of the binary outcome, is assumed to come from a Bernoulli distribution in which the variance is determined by the underlying mean proportion.
The Median Odds Ratio (MOR) (Merlo et al., 2006) is used to portray the higher-level variance in a more readily interpretable form. It translates the province level variance into an odds ratio scale, the same scale as the individual effects, which are conventionally expressed as relative odds ratios. The MOR is the median value of the odds ratio between the province at highest propensity of poor health and the province of lowest propensity when randomly picking two provinces. Therefore, the MOR can be conceptualised as the increased propensity that would result (in the median) if a respondent moved to another province with a higher propensity of poorer health. The MOR formula is:
| (3) |
where is the estimated level 2, between province variance on the logit scale; and φ−1 (0.75) is the 75th percentile of the cumulative distribution function of the standard Normal distribution. It is possible to derive a confidence interval for this ratio as a by-product of the MCMC estimation (Jones & Subramanian, 2012).
Models are estimated with full Bayesian procedures which allow the exact estimation of parameters without approximations and with full uncertainty propagation so that the imprecision associated with one parameter is taken into account in characterising the uncertainty of another parameter (Jones & Subramanian, 2012). This is particularly important in the present study as there are only 23 provinces on which to characterise regional differences and to estimate the inequality effect. The models are estimated using the MLwiN 2.25 software with full Bayesian MCMC methods with minimally informative priors. They are based on initial maximum likelihood estimation, a discarded burn-in of 500 simulations and a further fifty thousand monitoring simulations according to the good-practice recommendations of Draper (2006).
Results
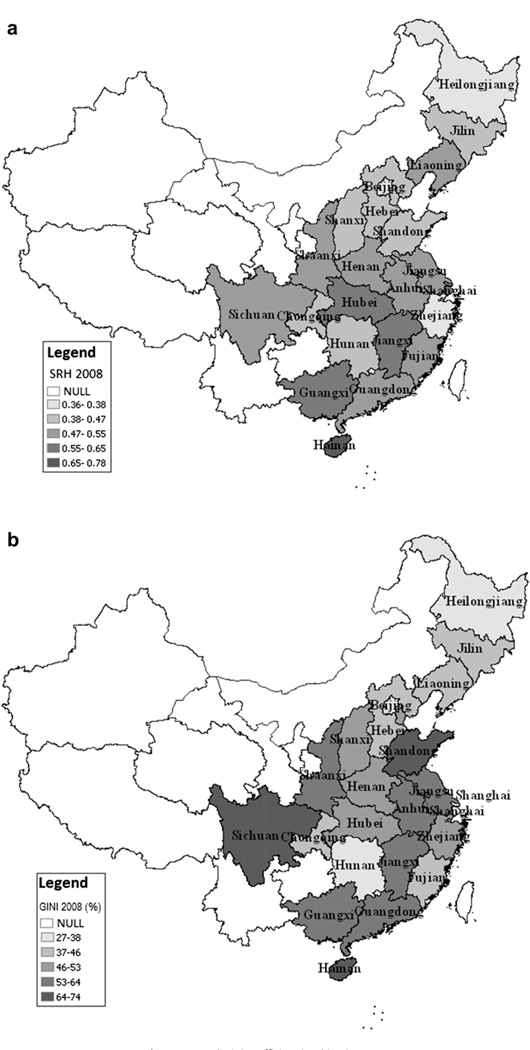
Fig. 1(a) shows the average un-modelled SRH as the proportion in poor health in 2008 at the provincial level with the darker colour indicating poorer SRH. Elderly in Hubei, Jiangxi, Shanghai and Guangxi tend to be in poorer health with the worst being found in Hainan. Fig. 1(b) presents the Gini coefficient for 2008. The darker colour indicates a higher Gini coefficient, signifying larger income inequality. Hainan, Sichuan and Shandong have the highest Gini coefficient in China. From Fig. 1(a) and (b), Jiangxi, Guangxi and Hainan present poor self-rated health and high Gini coefficient. In contrast, Heilongjiang, Jilin, Beijing, Hebei and Hunan have good self-rated health and a low Gini coefficient in 2008. The differences between provinces in their 2008 Gini coefficients are very large with the most equal province having a Gini of 27% which is equivalent to egalitarian Scandinavian countries while the most unequal with values in excess of 60% are comparable to southern Africa. If the arguments are correct about the “pollution” effect operating at the large geographical scale, then they should be found in this study.
Fig. 1.
SRH and Gini coefficient in China in 2008.
The analysis consists of a sequence of eight models of growing complexity, from a model with simple demographic characteristics of the elderly initially, then adding individual level variables, followed by inequality variable and then cross-level interactions between inequality and individual characteristics. The cross-level interactions analysis is deliberately exploratory as no previous studies report the effects of inequality on the health of the elderly in China and there is a need to be alert to what may be important effects; we need to avoid committing Type I errors. This paper guards against the problem of induction and Type II errors by being open about what models are estimated, evaluating the models for parsimony, and showing the comparative size of the effects.
The results are presented in the form of logits (Table 2). Also given in the table are the residual variances between provinces after including variables in the fixed part of the model. The overall fit of different models is evaluated by using The Deviance Information Criterion (DIC), a badness-of-fit measure that is penalized for model complexity (Spiegelhalter, Best, Carlin, & van der Linde, 2002). Any reduction in the DIC is an improvement in the fit of the model, and better fits are shown by larger reductions in the DIC. To improve estimation all the continuous variables are centred on their grand mean so that the estimated constant is then not a value outside the range of the observed data.
Table 2.
Logit multilevel regression estimates.
| Null |
Model 1 |
Model 2 |
Model 3 |
Model 4 |
||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Estimate(SE) | P-value | Estimate(SE) | P-value | Estimate(SE) | P-value | Estimate(SE) | P-value | Estimate(SE) | P-value | |
| Fixed part | ||||||||||
| Constants | −1.748(0.101) | <0.001 | −1.708(0.119) | <0.001 | −2.19(0.155) | <0.001 | −2.113(0.145) | <0.001 | −2.298(0.145) | <0.001 |
| Age | −0.007(0.002) | <0.001 | −0.009(0.002) | <0.001 | −0.009(0.002) | <0.001 | −0.008(0.002) | <0.001 | ||
| Age2 | −0.001(0.000) | <0.001 | −0.001(0.000) | <0.001 | −0.001(0.000) | <0.001 | −0.001(0.000) | <0.001 | ||
| Female (ref: male) | 0.201(0.044) | 0.029 | 0.126(0.053) | 0.02 | 0.123(0.052) | 0.018 | 0.139(0.052) | 0.009 | ||
| Non-schooling (ref: schooling) | 0.176(0.06) | 0.002 | 0.173(0.057) | 0.016 | 0.097(0.056) | 0.058 | ||||
| Rural (ref: urban) | 0.129(0.051) | 0.012 | 0.121(0.051) | 0.002 | −0.006(0.053) | 0.79 | ||||
| No insurance (ref: have insurance) | 0.371(0.109) | <0.001 | 0.373(0.109) | <0.001 | 0.285(0.108) | 0.008 | ||||
| Gini | 0.024(0.008) | 0.003 | ||||||||
| Log income | −0.34(0.036) | <0.001 | ||||||||
| Log income2 | 0.187(0.02) | <0.001 | ||||||||
| Log income3 | −0.017(0.002) | 0.005 | ||||||||
| Random part | ||||||||||
| Level 2 | ||||||||||
| Between province | 0.268(0.133, 0..517) | 0.278(0.140, 0.528) | 0.253(0.127, 0.483) | 0.171(0.08,0.34) | 0.208(0.102, 0.397) | |||||
| DIC | 12757.537 | 12692.068 | 12665.429 | 12664.435 | 12550.461 | |||||
| Change in DIC | 65.469(1 vs Null) | 26.639 (2 vs 1) | 0.994 (3 vs 2) | 114.968 (4 vs 2) | ||||||
| Model 5 |
Model 6 |
Model 7 |
Model 8 |
|||||
|---|---|---|---|---|---|---|---|---|
| Estimate(SE) | P-value | Estimate(SE) | P-value | Estimate(SE) | P-value | Estimate(SE) | P-value | |
| Fixed part | ||||||||
| Constants | −2.113(0.142) | <0.001 | −2.111(0.146) | <0.001 | −2.107(0.143) | <0.001 | −2.098(0.148) | <0.001 |
| Age | −0.008(0.002) | <0.001 | −0.008(0.002) | <0.001 | −0.008(0.002) | <0.001 | −0.008(0.002) | <0.001 |
| Age2 | −0.001(0.000) | <0.001 | −0.001(0.000) | <0.001 | −0.001(0.000) | <0.001 | −0.001(0.000) | <0.001 |
| Female (ref: male) | 0.143(0.053) | 0.009 | 0.142(0.053) | 0.007 | 0.136(0.052) | 0.009 | 0.123(0.054) | 0.02 |
| Non-schooling (ref: schooling) | 0.101(0.058) | 0.113 | 0.101(0.058) | 0.08 | 0.094(0.058) | 0.113 | 0.104(0.057) | 0.057 |
| Rural (ref: urban) | 0.012(0.052) | 0.77 | 0.009(0.052) | 0.86 | 0.016(0.052) | 0.77 | 0.01(0.052) | 0.84 |
| No insurance (ref: have insurance) | 0.295(0.108) | 0.01 | 0.298(0.108) | 0.006 | 0.283(0.112) | 0.01 | 0.285(0.109) | 0.008 |
| 2008 Gini | 0.019(0.008) | 0.016 | 0.018(0.008) | 0.021 | 0.011(0.008) | 0.14 | 0.012(0.008) | 0.127 |
| Log income | −0.274(0.043) | 0.043 | −0.277(0.043) | <0.001 | −0.275(0.043) | <0.001 | −0.276(0.044) | <0.001 |
| Log income2 | 0.113(0.015) | 0.015 | 0.112(0.014) | <0.001 | 0.111(0.014) | <0.001 | 0.112(0.014) | <0.001 |
| Log income3 | 0.028(0.01) | 0.006 | 0.027(0.01) | 0.007 | 0.028(0.01) | 0.006 | 0.028(0.01) | 0.05 |
| Gini*income | 0.001(0.002) | 0.53 | ||||||
| Gini*non-educated | 0.011(0.005) | 0.023 | ||||||
| Gini*female | 0.011(0.004) | 0.017 | ||||||
| Random part | ||||||||
| Level 2 | ||||||||
| Between province | 0.159(0.075, 0.324) | 0.164(0.078, 0.325) | 0.155(0.071, 0.307) | 0.158(0.076, 0.310) | ||||
| DIC | 12550.01 | 12550.7 | 12546.93 | 12546.27 | ||||
| Change in DIC | 114.425(5 vs 3) | −0.69 (6 vs 5) | 3.08 (7 vs 5) | 3.74 (8 vs 5) | ||||
The DIC for the null model is 12757.537. Model 1 includes gender and a quadratic term for age to estimate the log-odds of being in poor health. The DIC decreases by 65.469 from the null model. There is no evidence to suggest a cubic age term or an interaction between gender and age. Model 2 additionally includes 3 socio-economic variables: urban/rural residence, schooling/non-schooling, and with/without old-age insurance. It results in further substantial improvement with a 26.639 reduction in the DIC. Model 3 adds contemporaneous 2008 Gini coefficient as a main effect. In multilevel analysis, the standard error of the estimate will reflect the 23 values at provincial level for this variable and not the apparent, but incorrect 14,700 observations. The addition of this term results in a small decrease in the DIC. It means that the inclusion of the main effect for Gini consumes an additional degree of freedom and has additional predictive power. The sign of this coefficient is positive supporting the relative income hypothesis that people from unequal places experience poorer health. Model 4 builds upon model 2 and adds a cubic polynomial term for the natural log of family income which results in a very substantial reduction in the DIC of 114.9682.
Model 5 includes the Gini coefficient and the cubic form of family logged income with a reduction of 114.425 in the DIC from model 3. The next three models include interactions that are specified between inequality and family income (in its linear logged form), education and gender. While an improvement was not found for including the interaction with income and inequality, there was evidence for cross-level interaction for the other two models with the largest improvement found in the model with the cross-level interaction between gender and Gini. The results of the last two models suggest that the effect of inequality is different for different groups of people in a society. In contrast, no compelling evidence was found to include interactions between inequality and urban/rural residence, old-age insurance, or age in the model.
In order to appreciate the nature and the relative size of the effects, the logits are converted into relative odds ratios with the base category – the lowest likelihood to report poor health-being set to one. The logits in Table 2 are known as cluster-specific estimates, of which the fixed part estimates (the averages) are conditional on the higher-level random effects for provinces (Jones & Subramanian, 2012). Using the simulation-based procedures of the MLwiN Customised predictions (Rasbash, Steele, Browne, & Goldstein, 2009) the logits are transformed into odds ratios so that the estimates represent the relative odds for individuals living in a province that is typical (that is the median) in terms of experiencing poor health. The predictions are made so that they show the effect of each variable in turn while controlling for all the other predictors in the model which are set at their mean value.
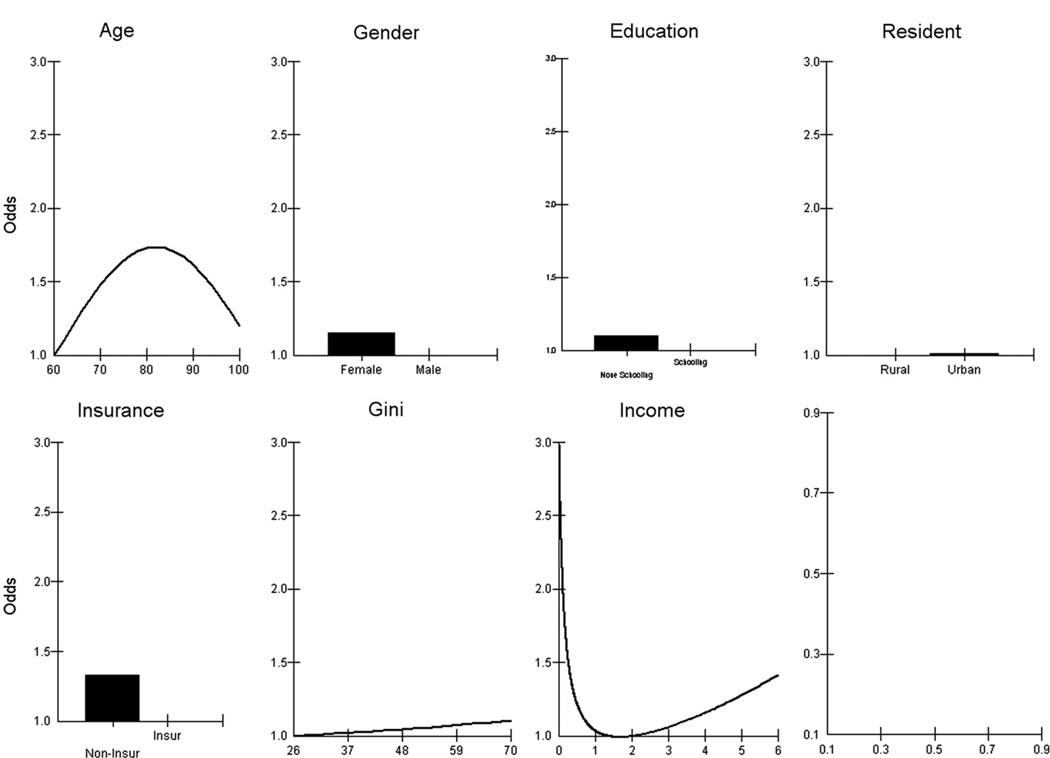
Fig. 2 depicts the median odds for model 5. The vertical axes of all seven graphs are on the same scale so that they are directly comparable. Over the range of the plotted predictor variables, the largest effect is found for individual income. It shows a marked curvilinear relationship such that the greatest odds for reporting poor health is found for those with the lowest income who are 3 times more likely to be in poor health than those with an equivalised income of 13,300 Yuan which conveniently represents the division between the bottom three quarters of the income distribution and the top quarter. This richest top quarter of the distribution experiences, in contrast, worsening odds of poor health as income increases. There are also curvilinear effects for age. The relative odds of reporting poor health increases with age from 60 years and reaches its maximum at 82 years and then starts to decline. The odds for 82 years are 70 percent higher than that for the 60 years and the odds for 100 years is similar to that of 65 years. The next largest effect is for old-age insurance. People without old-age insurance are 33% more likely to be in poor health than those with such support. Gender has a relatively modest overall effect: females are 15% more likely to report poor health than males. Those without schooling are 9 percent higher in reporting poor health whereas the differences between urban and rural are negligible once other variables are taken into account. For the income inequality effect, as the Gini coefficient increases by 1%, the odds raises by 0.019.
Fig. 2.
Results from Model 5: The odds of poor health.
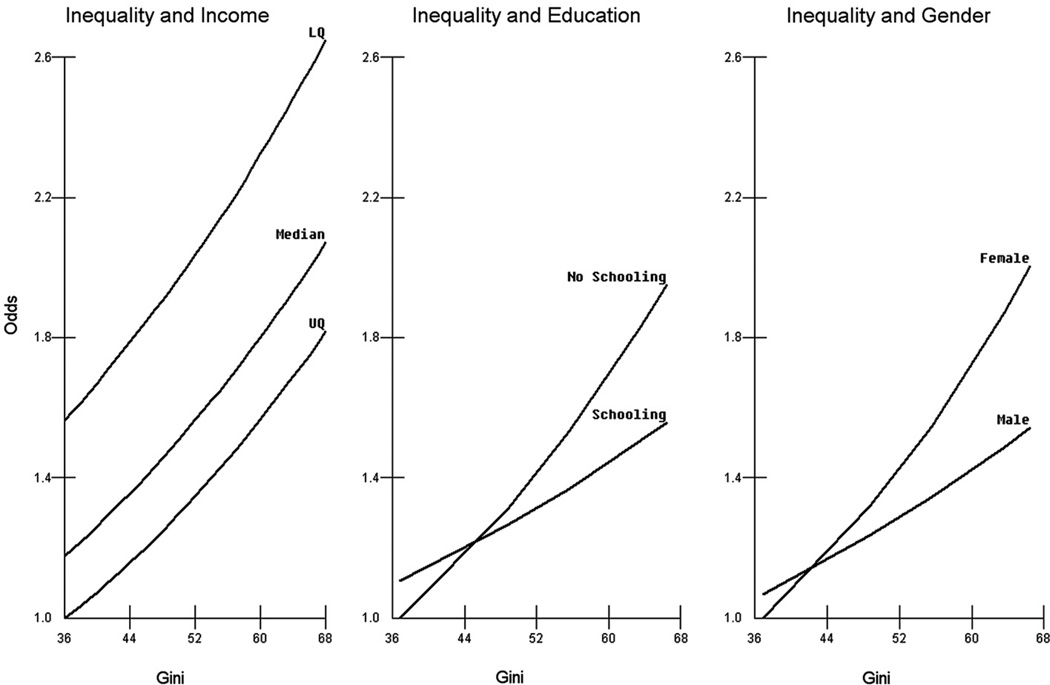
Fig. 3 portrays the relative odds for each of the cross-level interactions from models 6, 7 and 8. Again the vertical axis has been scaled for comparability. The horizontal axis is the Gini coefficient and the displayed values range from the 10% percentile to the 90% percentile. The income effects are plotted for respondents at three levels of individual income, the lower quartile, the median, and the upper quartile, respectively. The effects for individuals at different levels of income are very evident and this is unsurprising given the results from Fig. 2. However, there is also an additional effect for inequality, so that for each group there are increased odds of reporting poor health as the Gini coefficient increases. The ‘close-to-parallel’ lines on the odds scale is due to the differential Gini-income being insignificant. The effect for education is such that in provinces with the least unequal income, there is little difference between schooling and non-schooling, but this gap grows with greater inequality as the increase is most marked for the non-schooling. A similar pattern is found for gender as there is effectively no gender gap when inequality within a province is low; but this widens as the Gini increases with females having higher odds of reporting poor health.
Fig. 3.
Cross level interactions with inequality (derived from models 6, 7 and 8).
Table 2 also shows the results for the level 2 residual and credible intervals accounting for the between-province variance for all eight models. The largest unexplained level 2 variance is found in model 1, the demographic model. The variance declines after the inclusion of the socioeconomic variables and a further decline in the unexplained variance is occasioned by the inclusion of the Gini term and polynomial function for family income. A further reduction in the unexplained province variance results from the inclusion of the cross-level interactions, so that the lowest unexplained variance is for model 7 with the Gini by Education interaction.
The MOR statistic can be used to appreciate the nature of these province differentials and compare them with the relative odds ratios of the fixed part of the model. In Model 1, the variance of 0.278 translates to a MOR of 1.65 with 95% confidence intervals of 1.43 and 2. Thus, there are significant differences between provinces, and if respondents are selected from two randomly chosen provinces, the odds of being in poorer health in the province with the worse health is 65% higher. This is greater than the main effects for education, old-age insurance, gender and urban/rural residence. In model 7 the between-province variance has decreased to 0.155. This equates to a MOR of 1.44 with 95% confidence intervals of 1.23–1.70. This means that significant differences still exist between provinces even after taking account of the main effects and the Gini-education cross-level interaction, with typical relative odds between randomly chosen provinces exceeding those of the individual effects of gender, insurance and education of the main effects in the model.
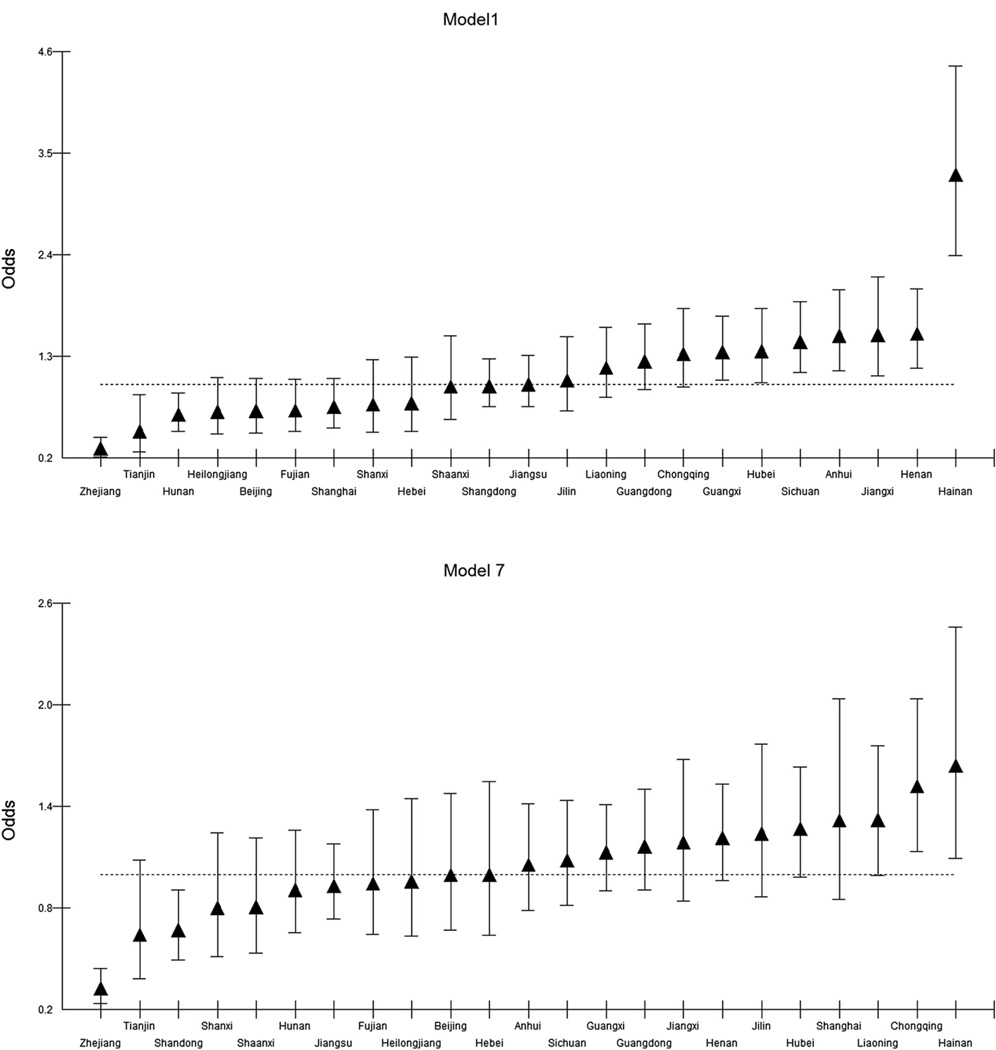
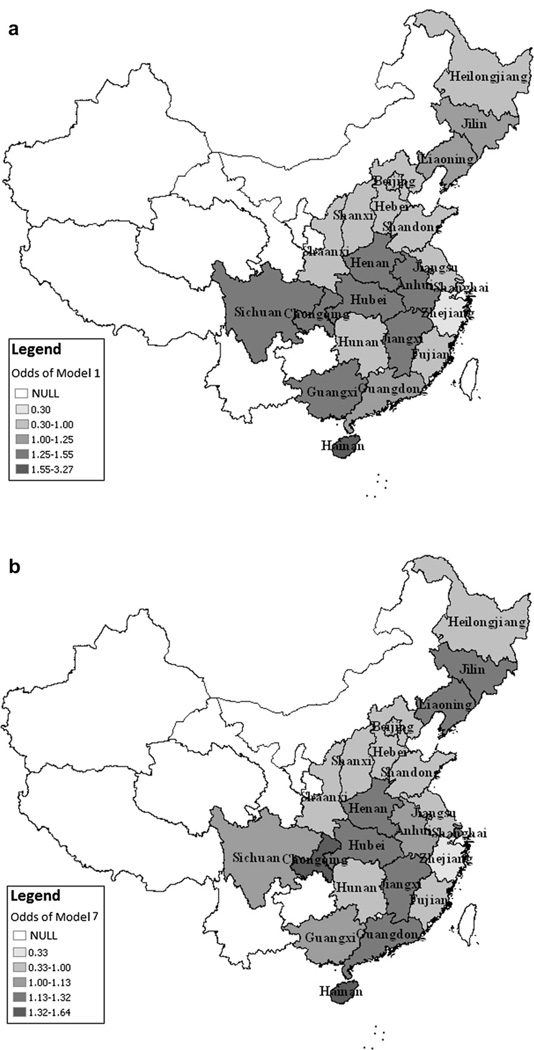
In order to appreciate the scale of the differences, Fig. 4 plots the province differentials on an odds scale for both Models 1 and 7, with the value 1 representing the all-province level of poor health conditional on the terms included in the fixed part of the model. The graph also shows the 95% comparative confidence intervals. The differential odds in model 1 are very substantial with a number of provinces being significantly high or low. The extremes are represented by Hainan whose relative odds are over three times the national rate of poor health and Zhejiang, the province with the best rate which is only a third of the national average. The differential odds for model 7 are smaller with Hainan remaining the highest province but only 1.6 times the national rate. The best health province is again Zhejiang whose risk of reporting poor health is only a third of the national average. Interestingly Zhejiang is also one of the richest provinces in China with a larger proportion of well-developed private enterprises (Wei & Ye, 2004) while Hainan’s economy is predominantly agricultural and tourism. Fig. 5 maps the differential odds for model 1 and 7. In the demographic model (Fig. 5(a)), the coastal provinces (not including Hainan province) have better health than inland provinces; however, after adjusting for income inequality, family income and gender (model 7), the differential odds between coastal provinces and inland provinces becomes less obvious (Fig. 5(b)). From model 1 and 7, it is clear that people in the northern China have better health than those from the middle and south parts of China (not including Liaoning and Jilin provinces).
Fig. 4.
Differential relative odds for provinces derived from models 1 and 7 compared to the national average set at 1.
Fig. 5.
Maps of odds of poor health for provinces derived from model 1 and model 7.
The above results illustrate a small but significant contemporaneous effect of provincial income inequality on the health of the elderly. Table 3 shows the results when lagged Gini values are included one at a time in a model equivalent to Model 3 of Table 2. (In the CLHLS, Hainan province is newly included in the 2008 wave; therefore, only 22 provinces are included in the lagged inequality analysis.) After controlling for the individual predictors, 3-year and 6-year lagging effects of provincial income inequality appear to be significantly associated with the health of the elderly, and are not substantially different from the contemporaneous effect. The longer term effects, however, are substantially bigger (odds of 1.04 for a unit increase in Gini) but are not significant reflecting the lack of power to detect effects when there is small variation in a predictor variable; provinces differed much less in their inequality in 1985–1995. These results are generally similar to Pei and Rodriguez (2006) and Subramanian and Kawachi (2006), in that there are some lag effects, but they are not substantially different to those for contemporary Gini. Indeed in further analysis not shown here, this effect for contemporary Gini was found for the 2002 and 2005 waves when the health status was measured concurrently.
Table 3.
Logit multilevel regression estimates on model 3 for 2008, 2005, 2002 and mean 1985–1995 province income inequality (Random parts are not shown).
| Fixed part | 2008 |
2005 |
2002 |
8595 |
||||
|---|---|---|---|---|---|---|---|---|
| Estimate(SE) | P-value | Estimate(SE) | P-value | Estimate(SE) | P-value | Estimate(SE) | P-value | |
| Constants | −2.215(0.152) | <0.001 | −2.135(0.131) | <0.001 | −2.159(0.132) | <0.001 | −2.191(0.134) | <0.001 |
| Age | −0.01(0.002) | <0.001 | −0.01(0.002) | <0.001 | −0.01(0.002) | <0.001 | −0.01(0.002) | <0.001 |
| Age2 | −0.001(0.000) | <0.001 | −0.001(0.000) | <0.001 | −0.001(0.000) | <0.001 | −0.001(0.000) | <0.001 |
| Female (ref: male) | 0.112(0.052) | 0.032 | 0.102(0.053) | 0.056 | 0.101(0.053) | 0.058 | 0.1(0.054) | 0.063 |
| Non-schooling (ref: schooling) | 0.160(0.057) | 0.005 | 0.165(0.057) | 0.004 | 0.167(0.058) | 0.004 | 0.171(0.058) | 0.058 |
| Rural (ref: urban) | 0.13(0.05) | 0.009 | 0.125(0.051) | 0.015 | 0.127(0.052) | 0.014 | 0.131(0.052) | 0.012 |
| No insurance (ref: have insurance) | 0.422(0.116) | <0.001 | 0.383(0.107) | <0.001 | 0.384(0.108) | <0.001 | 0.386(0.11) | <0.001 |
| 2008 Gini | 0.017(0.008) | 0.006 | ||||||
| 2005 Gini | 0.020(0.008) | 0.013 | ||||||
| 2002 Gini | 0.015(0.009) | 0.10 | ||||||
| 85–95 Gini | 0.041(0.04) | 0.32 | ||||||
Discussion and conclusions
We have found that there are substantial geographical differences in the self-reported health of the elderly in contemporary China, with some seven-fold difference between the worst (Hainan) and best (Zhejiang) provinces. These are to a large extent accounted for by income, income inequality and other socioeconomic measures (education and insurance), but some differences remain particularly the relatively good health of the elderly in Zhejiang province. Initial models show that the elderly in urban areas have better health than rural but these differences attenuate and become insignificant when family income is taken in to account. The most substantial effect is that for family income with those belonging to a family at the bottom of the scale having treble the odds of poor health compared to those are at the upper-quartile of income. Over and above these direct income effects there is additional worse experience if the elderly has not received schooling and if they do not have insurance to support their old age. The main effect for income inequality is relatively small but there is some evidence of a general effect such that unequal provinces have poorer health even when account is taken of individual family income. The models with cross-level interactions find that some groups in society are more affected by province inequality. This operates in such a way that the least advantaged in a society (those with no schooling and are females) experience a greater chance of reporting poor health in a similar manner to Norwegian results (Dahl, Elstad, Hofoss, & Martin-Mollard, 2006). The lagging effect of income inequality in this study is consistent with Pei and Rodriguez (2006). We found similar effects of contemporaneous income inequality as at 3 and 6 years previously.
In terms of the demographic variables, women in general have a worse health experience than men and there is a marked nonlinear relationship with age that affects both sexes. Younger elderly, below around 80 years old, have greater odds of being in poor health as age increases, but for older elderly, their odds of being in poor health reduces as age increases. This potentially counter-intuitive result has in fact been found by others. Liu and Zhang (2004) researched Chinese aged over 80, finding that there is positive health status when elderly are at advanced age. This may be explained by the Chinese cultural values that revere the elderly and the institutional support that is available for the oldest-old. Elderly aged 80+ are entitled to special support and care from the local government. Cohort effects and differential survival may also play a role in this complex relationship with age, and we plan to investigate this further with longitudinal data. This is important given that the study has a substantial sample size of the old elderly and that similar positive attitudes to health have been found in the oldest age groups in the very different context of the US (Ferraro, 1980).
These results support the income inequality hypothesis in two ways. First, there is a curvilinear relationship between self-rated health and total family income. (These curvilinear results were also found in further modelling of the two previous waves.) For the poorest three quarters of the sample with a family equivalised income below 13,300 Yuan, income brings about greater improvement in the health of poor than of the rich. This is direct evidence of a “concavity” effect. For the richest quarter of the sample, increased income is associated with a greater chance of having poor health. Such an apparently counter-intuitive nonlinear relationship has in fact been found in a number of studies so that the richest of all groups have poorer health and indeed die relatively young (Backlund, Sorlie, & Johnson, 1996; Der, 2001; Mackenbach et al., 2005). Second, there is some evidence of a general “social pollution” effect so that provincial income inequality has an effect over and above individual characteristics. Indeed when interactions are allowed between inequality, gender and education taking account of family income the “pollution” effect is stronger for the more marginalised groups. In more unequal provinces, there are greater differences between different fractions of society: inequality matters most for the non-educated and for females. In the more equal provinces being a man or women, having or not having an education matters less.
China is engaged in a rapid social and economic transition. The results of this study suggest that the province inequality and family income are important social determinants of the health status of the elderly. In terms of policy it is worth paying attention to the reduction of provincial income inequality and the differential growth of the family income if the elderly are to maintain or improve their health. Effective health-related policies in terms of health care, health insurance and welfare spending (Subramanian & Kawachi, 2004) are needed to mediate the relationship between rising income inequality and poorer health outcomes.
Acknowledgements
This research is self-funded and we are grateful for CLHLS (CLHLS is supported by funds from Duke University under an award from the U.S. National Institutes on Aging (NIA) (R01 AG23627-01; PI: Zeng Yi), and by the China Natural Science Foundation, China Social Science Foundation, UNFPA, and the Hong Kong Research Grant Council) to provide us with the data set. We thank Bristol Alumni Foundation to support funding the results presented in the AAG in New York in 2012. The authors would like to thank Ichiro Kawachi, S. V. Subramanian and the anonymous reviewers for their helpful comments and suggestions.
Appendix A
List of provinces along with the sample size is given in Table 4.
Table 4.
| Province | Individuals |
|---|---|
| Beijing | 285 |
| Tianjin | 117 |
| Hebei | 148 |
| Shanxi | 137 |
| Liaoning | 521 |
| Jilin | 301 |
| Heilongjiang | 257 |
| Shanghai | 429 |
| Jiangsu | 1219 |
| Zhejiang | 1049 |
| Anhui | 712 |
| Fujian | 316 |
| Jiangxi | 270 |
| Shandong | 1629 |
| Henan | 886 |
| Hubei | 653 |
| Hunan | 813 |
| Guangdong | 805 |
| Guangxi | 1928 |
| Hainan | 371 |
| Chongqing | 461 |
| Sichuan | 1273 |
| Shaanxi | 164 |
Footnotes
The equivalised income was derived by using the modified OECD equivalence scale (www.oecd.org/dataoecd/61/52/35411111.pdf) whereby the total family income is divided by a weight which depends on the number of adults and children that constitute the family. A lone household is given the weight of 1; each additional adult over 18 is 0.5 and each child receives a 0.3. The maximum weight was found to be 6.8.
The inclusion of the individual income will inherently include the effect for mean province income; we also used family income as a group (province) mean-centred variable and additionally the province mean income effect to estimate separately the within and between effects of family income in the manner of Bell and Jones (2012). The latter was insignificant and the substantive results of the analysis were unchanged. The use of the cubic polynomial of the logarithm of income was a substantial improvement of the cubic polynomial of raw income (a lower DIC of over 6).
References
- Backlund E, Sorlie PD, Johnson NJ. The shape of the relationship between income and mortality in the United States – evidence from the national longitudinal mortality study. Annals of Epidemiology. 1996;6:12–20. doi: 10.1016/1047-2797(95)00090-9. [DOI] [PubMed] [Google Scholar]
- Bauer DJ, Cai L. Consequences of unmodeled nonlinear effects in multilevel models. Journal of Educational and Behavioral Statistics. 2009;34:97–114. [Google Scholar]
- Bell A, Jones K. Explaining fixed effects: Random effects modelling of time-series cross-sectional and panel data. 2012 Downloaded from. http://polmeth.wustl.edu/media/Paper/FixedversusRandom_l_2.pdf.
- Blakely T, Atkinson J, O’Dea D. No association of income inequality with adult mortality within New Zealand: a multi-level study of 1.4 million 25–64 year olds. Journal of Epidemiology and Community Health. 2003;57:279–284. doi: 10.1136/jech.57.4.279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blakely TA, Kennedy BP, Glass R, Kawachi I. What is the lag time between income inequality and health status? Journal of Epidemiology and Community Health. 2000;54:318–319. doi: 10.1136/jech.54.4.318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blomgren J, Martikainen P, Makela P, Valkonen T. The effects of regional characteristics on alcohol-related mortality - a register-based multilevel analysis of 1.1 million men. Social Science & Medicine. 2004;58:2523–2535. doi: 10.1016/j.socscimed.2003.09.027. [DOI] [PubMed] [Google Scholar]
- Browne WJ, Draper D. A comparison of Bayesian and likelihood-based methods for fitting multilevel models. Bayesian Analysis. 2006;1:473–513. [Google Scholar]
- Dahl E, Elstad JI, Hofoss D, Martin-Mollard M. For whom is income inequality most harmful? A multi-level analysis of income inequality and mortality in Norway. Social Science & Medicine. 2006;63:2562–2574. doi: 10.1016/j.socscimed.2006.06.002. [DOI] [PubMed] [Google Scholar]
- Der G. Commentary: income and health: why are curves so appealing? International Journal of Epidemiology. 2001;30:1405–1406. doi: 10.1093/ije/30.6.1405. [DOI] [PubMed] [Google Scholar]
- Draper D. Bayesian multilevel analysis and MCMC. New York: Springer; 2006. [Google Scholar]
- Duncan C, Jones K, Moon G. Context, composition and heterogeneity: using multilevel models in health research. Social Science & Medicine. 1998;46:97–117. doi: 10.1016/s0277-9536(97)00148-2. [DOI] [PubMed] [Google Scholar]
- Fan CC, Sun MJ. Regional inequality in China, 1978–2006. Eurasian Geography and Economics. 2008;49:1–20. [Google Scholar]
- Ferraro KF. Self-ratings of health among the old and the old-old. Journal of Health and Social Behavior. 1980;21:377–383. [PubMed] [Google Scholar]
- Gerdtham UG, Johannesson M. Absolute income, relative income, income inequality, and mortality. Journal of Human Resources. 2004;39:228–247. [Google Scholar]
- Goldstein H. REALCOM-IMPUTE: Multiple imputation using MLwiN. Bristol: CMM, University of Bristol; 2009. [Google Scholar]
- Hox J. Multilevel analysis: Techniques and applications. London: Psychology Press; 2002. [Google Scholar]
- Idler EL, Benyamini Y. Self-rated health and mortality: a review of twenty-seven community studies. Journal of Health and Social Behavior. 1997;38:21–37. [PubMed] [Google Scholar]
- Jen MH, Jones K, Johnston R. Compositional and contextual approaches to the study of health behaviour and outcomes: using multi-level modelling to evaluate Wilkinson’s income inequality hypothesis. Health & Place. 2009;15:198–203. doi: 10.1016/j.healthplace.2008.04.005. [DOI] [PubMed] [Google Scholar]
- Jones K. Specifying and estimating multilevel models for geographical research. Transactions of the Institute of British Geographers. 1991;16:148–159. [Google Scholar]
- Jones K, Duncan C. Individuals and their ecologies: analysing the geography of chronic illness within a multilevel modelling framework. Health & Place. 1995;1:27–40. [Google Scholar]
- Jones K, Subramanian VS. Developing multilevel models for analysing contextuality, heterogeneity and change Vols. 1 and 2. Bristol: Centre for Multilevel Modelling; 2012. [Google Scholar]
- Kawachi I, Kennedy BP. Income inequality and health: pathways and mechanisms. Health Services Research. 1999;34:215–227. [PMC free article] [PubMed] [Google Scholar]
- Kennedy BP, Kawachi I, Glass R, Prothrow-Stith D. Income distribution, socioeconomic status, and self rated health in the United States: multilevel analysis. British Medical Journal. 1998;317:917–921. doi: 10.1136/bmj.317.7163.917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu GP, Zhang Z. Sociodemographic differentials of the self-rated health of the oldest-old Chinese. Population Research and Policy Review. 2004;23:117–133. [Google Scholar]
- Li H, Zhu Y. Income, income inequality, and health: evidence from China. Journal of Comparative Economics. 2006;34:668–693. [Google Scholar]
- Lorgelly PK, Lindley J. What is the relationship between income inequality and health? Evidence from the BHPS. Health Economics. 2008;17:249–265. doi: 10.1002/hec.1254. [DOI] [PubMed] [Google Scholar]
- Mackenbach JP, Martikainen P, Looman CW, Dalstra JA, Kunst AE, Lahelma E, et al. The shape of the relationship between income and self-assessed health: an international study. International Journal of Epidemiology. 2005;34:286–293. doi: 10.1093/ije/dyh338. [DOI] [PubMed] [Google Scholar]
- Merlo J, Chaix B, Ohlsson H, Beckman A, Johnell K, Hjerpe P, et al. A brief conceptual tutorial of multilevel analysis in social epidemiology: using measures of clustering in multilevel logistic regression to investigate contextual phenomena. Journal of Epidemiology and Community Health. 2006;60:290–297. doi: 10.1136/jech.2004.029454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muramatsu N. County-level income inequality and depression among older Americans. Health Services Research. 2003;38:1863–1883. doi: 10.1111/j.1475-6773.2003.00206.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- National Bureau of Statistics. Beijing, China: Chinese Statistics Press; 2010. [Google Scholar]
- Osler M, Prescott E, Gronbaek M, Christensen U, Due P, Engholm G. Income inequality, individual income, and mortality in Danish adults: analysis of pooled data from two cohort studies. British Medical Journal. 2002;324:13–16. doi: 10.1136/bmj.324.7328.13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pei X, Rodriguez E. Provincial income inequality and self-reported health status in China during 1991–7. Journal of Epidemiology and Community Health. 2006;60:1065–1069. doi: 10.1136/jech.2005.043539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rasbash J, Charlton C, Jones K, Pillinger R. Manual supplement to MLwiN v2.1. Bristol: University of Bristol; 2009. [Google Scholar]
- Rasbash J, Steele F, Browne WJ, Goldstein H. A user’s guide to MLwiN, version 2.10. Bristol: University of Bristol; 2009. [Google Scholar]
- Robert SA, Li LW. Age variation in the relationship between community socioeconomic status and adult health. Research on Aging. 2001;23:233–258. [Google Scholar]
- Rowlingson K. Does income inequality cause health and social problems? Joseph Rowntree Foundation; 2011. Downloaded from, http://www.jrf.org.uk/sites/files/jrf/Rowlingson-Income-eBook.pdf. [Google Scholar]
- Shibuya K, Hashimoto H, Yano E. Individual income, income distribution, and self rated health in Japan: cross sectional analysis of nationally representative sample. British Medical Journal. 2002;324:16–19. doi: 10.1136/bmj.324.7328.16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snijders TAB, Bosker RJ. Multilevel analysis: An introduction to basic and advanced multilevel modeling. London: Sage; 1999. [Google Scholar]
- Spiegelhalter DJ, Best NG, Carlin BR, van der Linde A. Bayesian measures of model complexity and fit. Journal of the Royal Statistical Society Series B: Statistical Methodology. 2002;64:583–616. [Google Scholar]
- Subramanian SV, Blakely T, Kawachi I. Income inequality as a public health concern: where do we stand? Health Services Research. 2003;38:153–167. doi: 10.1111/1475-6773.00110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Subramanian SV, Jones K, Kaddour A, Krieger N. Revisiting Robinson: the perils of individualistic and ecologic fallacy. International Journal of Epidemiology. 2009;38:342–360. doi: 10.1093/ije/dyn359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Subramanian SV, Kawachi I. Income inequality and health: what have we learned so far? Epidemiologic Reviews. 2004;26:78–91. doi: 10.1093/epirev/mxh003. [DOI] [PubMed] [Google Scholar]
- Subramanian SV, Kawachi I. Whose health is affected by income inequality? A multilevel interaction analysis of contemporaneous and lagged effects of state income inequality on individual self-rated health in the United States. Health & Place. 2006;12:141–156. doi: 10.1016/j.healthplace.2004.11.001. [DOI] [PubMed] [Google Scholar]
- Subramanian SV, Kawachi I, Kennedy BP. Does the state you live in make a difference? Multilevel analysis of self-rated health in the US. Social Science & Medicine. 2001;53:9–19. doi: 10.1016/s0277-9536(00)00309-9. [DOI] [PubMed] [Google Scholar]
- United Nations. World population prospects. New York: 2001. [Google Scholar]
- Wei YHD, Ye XY. Regional inequality in China: a case study of Zhe-jiang Province. Tijdschrift Voor Economische En Sociale Geografie. 2004;95:44–60. [Google Scholar]
- Wilkinson RG. Socioeconomic determinants of health - health inequalities: relative or absolute material standards? British Medical Journal. 1997;314:591–595. doi: 10.1136/bmj.314.7080.591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu Z, Schimmele CM. Psychological disposition and self-reported health among the ‘oldest-old’ in China. Ageing & Society. 2006;26:135–151. [Google Scholar]
- Xu LXC, Zou HF. Explaining the changes of income distribution in China. China Economic Review. 2000;11:149–170. [Google Scholar]
- Zeng Y, George L. Population aging and old-age insurance in China. London: SAGE Publications Ltd; 2010. [Google Scholar]
- Zhang XB, Kanbur R. Spatial inequality in education and health care in China. China Economic Review. 2005;16:189–204. [Google Scholar]