Summary
About a decade ago, three electron cryomicroscopy (cryo-EM) single particle reconstructions of IP3R1 were reported at low resolution. Disturbingly, these structures bore little similarity to one another, even at the level of quaternary structure. Recently, we published an improved structure of IP3R1 at ~1 nm resolution. However, this structure did not bear any resemblance to any of the three previously published structures, leading to the question of why the new structure should be considered more reliable than the original three. Here we apply several methods, including class-average/map comparisons, tilt-pair validation, and use of multiple refinement software packages, to give strong evidence for the reliability of our recent structure. The map resolution and feature resolvability are assessed with the ‘gold standard’ criterion. This approach is generally applicable to assessing the validity of cryo-EM maps of other molecular machines.
INTRODUCTION
Inositol 1,4,5-trisphosphate receptors are intracellular Ca2+ release channels that play key roles in a variety of cellular and physiological processes as diverse as fertilization, hormone secretion, gene transcription, metabolic regulation, immune responses, apoptosis, learning and memory. Understanding the molecular architecture of this class of integral membrane proteins is of broad interest to many different research communities due to the fundamental importance of IP3R channels in cellular Ca2+ signaling, which in turn impact many human diseases.
Structure determination of IP3R has been a research priority in many groups for the last two decades. Functional IP3R channels are homo or hetero-tetrameric assemblies of about 1.3 MDa. Each subunit of IP3R is about 2,700 residues and can be divided into three major functional regions: an N-terminal ligand binding region, C-terminal channel forming region, and a central regulatory region (reviewed in (Foskett et al., 2007; Taylor and Tovey, 2010)). IP3R structures have proven exceptionally difficult to realize due to their large size, their nature as integral membrane proteins functioning in lipid membrane environments, and their inherently genuine dynamics. Homotetramers of the predominant isoform from cerebellum (type 1 IP3R, IP3R1) are generally used in structural studies. Several groups have attempted to solve the structure of IP3R1, and three cryo-EM structures at 20 – 40 Å resolutions were published between 2002–2004 (Jiang et al., 2002; Sato et al., 2004; Serysheva et al., 2003). However, much to the consternation of the cryo-EM and interested biological communities, none of these structures agree even about the overall architecture of the channel. This long-standing controversy about the 3D molecular architecture of IP3R1 has been a major obstacle, substantially slowing progress of the research aiming to understand structure-functional aspects of this key protein that regulates Ca2+ levels in virtually all-eukaryotic cells. In addition, this raised the question of the credibility of cryo-EM as a tool for structural determination. Through improvements to biochemical purification of the receptor protein and optimization of cryo-specimen preparation, we have recently determined a medium resolution structure of tetrameric IP3R1 in the closed state (Ludtke et al., 2011). Yet, how can we assert the reliability of this structure in preference to earlier structures (Jiang et al., 2002; Sato et al., 2004; Serysheva et al., 2003)?
At present, the standard refinement methods used in cryo-EM lack strong built-in checks to demonstrate the veracity of the final refined density maps. When image data of a rigid molecule with strong contrast is reconstructed using standard techniques, the result is virtually always unambiguous, and all of the available reconstruction algorithms would produce equivalent structures within the limits of resolution as shown in some molecular machines (Clare et al., 2012; Ludtke et al., 2008; Milazzo et al., 2011). For such published structures, the overall quaternary structure is not controversial. However, there are three classes of molecules which are prone to produce less reliable maps: first, integral membrane proteins, which tend to produce very low-contrast cryo-EM images due to their suspension in near-CMC detergent concentrations, second, small proteins (less than ~250 kDa) without the use of contrast enhancing technologies, and third, molecules undergoing substantial motion in their solution environment. When raw particle data has too little contrast, it will still contribute to the reconstruction, producing an apparent reduction in noise level in the averaged reconstruction, but this perceived improvement can actually represent a decrease in map accuracy.
RESULTS
In this manuscript, we consider a variety of methods, which can help to validate the accuracy of cryo-EM structures at moderate resolution and assess the limiting resolution at which a map should be relied upon for biological interpretation. We apply these methods to our recent structure of IP3R1 (Ludtke et al., 2011), and demonstrate that none of the three earlier published structures (Jiang et al., 2002; Sato et al., 2004; Serysheva et al., 2003) are consistent with the current higher resolution map. Finally, we assess the resolution limits at which structural features of the recently published map can be interpreted.
Class-averages vs. Projections
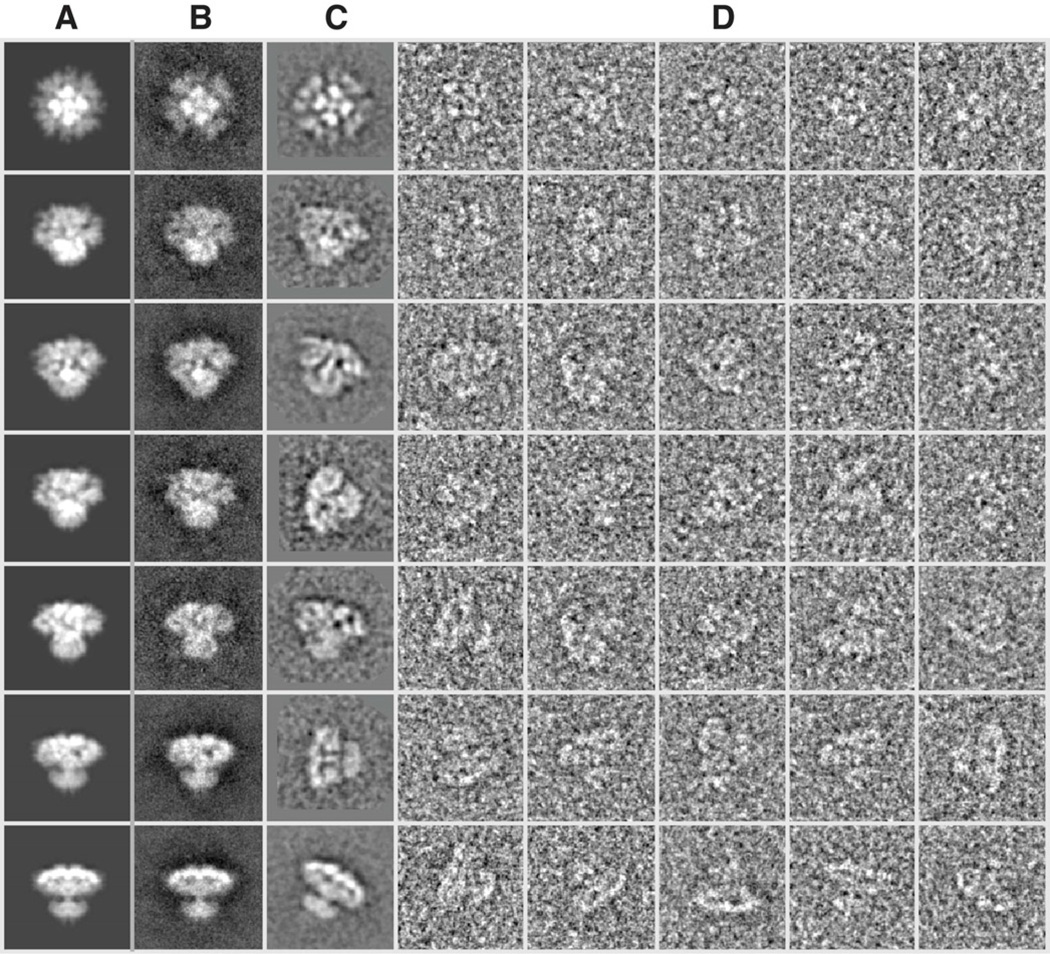
The first test normally applied to determine the reliability of a cryo-EM reconstruction is to compare computed projections of the final reconstructed map with class-averages and/or raw particles (Serysheva et al., 1995). In EMAN2 (Tang et al., 2007), two distinct types of class-averages are produced during a normal reconstruction procedure. The first type is reference-free class-averages typically generated prior to 3D reconstruction (Chen et al., 2006). These averages are produced by iterating steps of alignment, multivariate statistical analysis, and classification techniques (Chen et al., 2006; van Heel et al., 2000). This procedure makes no assumption about the data or its suitability for producing a 3D reconstruction. The second type of class-averages is produced by combining particles determined to be in a similar 3D orientation during the 3D reconstruction process. Unlike the first type of class-average, these averages are based on comparison to projections of the generated 3D map, and therefore can be template biased. It is necessary for both types of class-averages to have matching projections as a condition for a self-consistent refinement. However, even if all class-averages have a corresponding projection of the 3D map, this does not prove that the model is valid. That is, this test is a necessary, but not a sufficient condition for obtaining a valid reconstruction. This test, does, in fact, frequently fail when first starting on a new structure, and specimen conditions have not yet been optimized. That is, it remains an important initial assessment, which can catch many, but not all, common failures.
In Figure 1, we show a subset of this comparison along with individual particle images used to solve our recent IP3R1 structure (Ludtke et al., 2011). No class-averages conflicting with our map were observed. While the individual particle images are generally so noisy it is impossible to make highly detailed comparisons, at the very least, the particles are a good qualitative agreement with the 3D map.
Figure 1. Class-average self-consistency test.
Projections of the 3D map (A), reference-based class-averages (B), reference-free class-averages (unaligned, C), and selected (unaligned) individual particle images (D) are shown for comparison. Only a representative subset of the full set of projection orientations is shown, but clear qualitative agreement between the four types of images can be observed in each row.
Tilt-pair Validation
The tilt-validation method was originally proposed by Rosenthal and Henderson (Rosenthal and Henderson, 2003). In this method, additional data are collected to test the accuracy of a reconstructed map. In typical single particle experiments, a single exposure of the untilted cryo-EM grid is collected, making use of the full permissible dose. In tilt-pair validation, a separate set of experiments where two images of the same specimen area were recorded with an untilted and a 5–20 degree tilted specimen. This provides a pair of images of each particle with a known experimental rotation relating the two. The particle orientations are then independently determined computationally by comparison to the 3-D map being tested for validity. The relative orientation determined computationally by referencing the map must agree with the experimental value for a significant fraction of the particle pairs. If these orientation parameters do not agree, it implies that, either, one of the particle images is bad in some fashion (radiation damage, contamination, beam induced movement or conformationally different from the particles used for reconstruction), or that the 3D map is not correct.
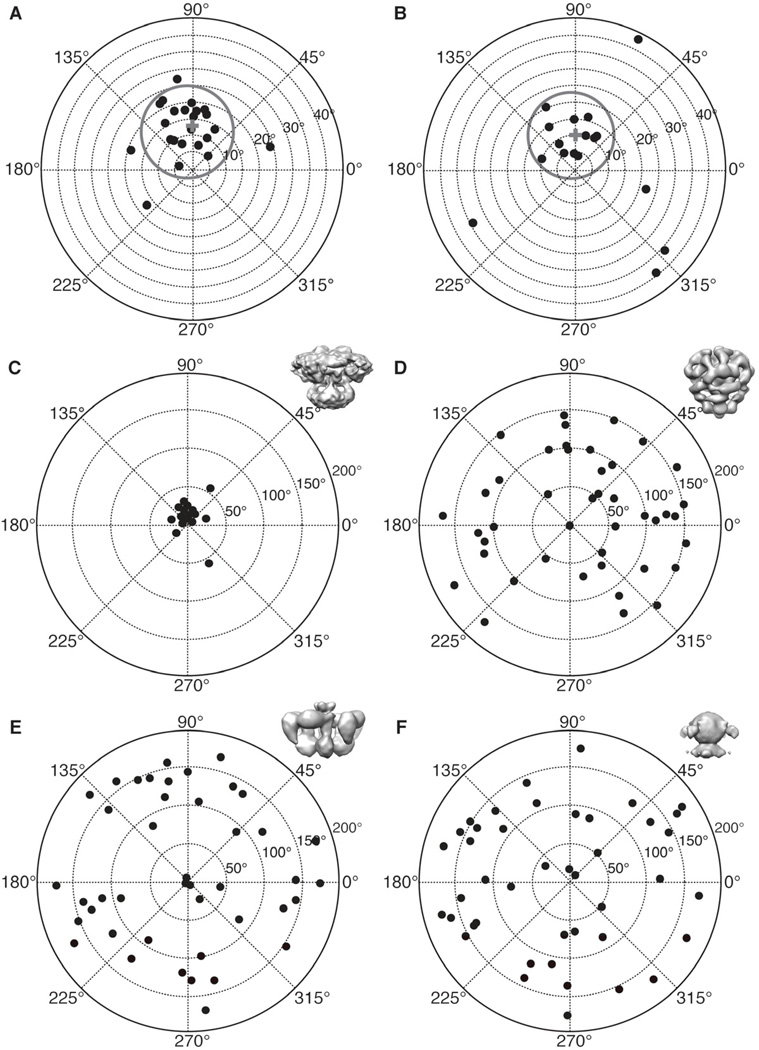
For tilt-pair validation we collected several pairs of CCD frames of tilted specimens of ice embedded IP3R1. Collecting high-resolution and high-quality tilt-pairs is, itself, a somewhat challenging experiment, as very often drift and/or charging occur in the tilted images. For particles with a fixed overall conformation, it is not necessary to have a large data set for tilt-validation, as the goal is simply to show that typical particles are self-consistent with the final structure. In the current study, we selected the two tilt-pairs with the highest contrast and the best overall image quality in both images for analysis. For these two micrograph pairs, 42 and 36 particle pairs (Table S1), respectively, were extracted using e2RCTboxer.py, and Euler angles were determined by projection matching to the current IP3R1 map (Ludtke et al., 2011). Next, the relative tilt axis and tilt angle for each particle pair were computed (see methods), and plotted in polar coordinates (Figure 2 and Table S1). These figures show that, as expected, the tilt parameters cluster around the experimental tilt angle, 10 degrees, and tilt axis, 90 degrees. 16 out of 42 particles (Figures 2A and C, Table S1), 38%, form a cluster whose mean tilt angle is 13.61 degrees and mean tilt axis is 89.46 degrees (Table S1). Given a RMSD of 4.21 degrees for the tilt angle and 5.45 degrees for the tilt axis, these values match the experimental tilt geometry. We obtain similar results for the second tilt-pair (Figure 2B and Table S1) where 13 out of 36, 36%, of the particles fall within the cluster whose mean tilt angle is 11.15 degrees and mean tilt axis is 91.86 degrees.
Figure 2. Results of tilt-pair analysis.
(A, B) IP3R1 tilt-pair validation plots for two image tilt-pairs. The grey circles denote particle pairs that cluster around the experimental tilt geometry, thus validating our IP3R1 map (EMDB-5278)(Ludtke et al., 2011). A cross indicates the center of the cluster and each point represents a single pair of particles. The radial value indicates the amount of tilt determined between the pair of particles, and azimuthal value indicates the direction of tilt. Ideally all points would fall at exactly the experimental tilt/direction. Some spread indicates the relative uncertainty in orientation determination. Note that the radial axis extends only to 40 degrees in these plots. Corresponding statistics for used tilt-pair images is given in Table S1. (C) The same plot as in (A) is shown at larger scale. Validation plots for the same tilt-pair images as in (A) were calculated against different 3D maps, (D) EMDB-1061 (Sato et al., 2004), (E) from (Serysheva et al., 2003), and (F) from (Jiang et al., 2002). Note that the three previously published maps produce a completely random distribution with no clustering. See also Table S1 and Figure S2.
While the fraction of particle pairs falling inside the cluster may seem a bit low, this is inline with previous results of similar particle mass (Henderson et al., 2011; Henderson and McMullan, 2013), and this method has been used to identify high quality particles for reconstruction and to optimize procedure for the refinement of particle orientation parameters (Henderson et al., 2011; Lau and Rubinstein, 2012) From the perspective of the first, untilted images, which would be used for a reconstruction, the results are far better than they may first appear. For a point to appear in the cluster, the orientation must be correctly determined in both of the two images. If either fails, the relative tilt also fails. If the probability of correctly determining the orientation of the first particle were 60% and the second particle was also independently 60%, this would result in only 36% of the pairs (as we observed) passing the tilt validation test. Given that the second image has suffered from additional radiation damage in this experimental protocol and is subject to charging problems often encountered in tilted specimen, the second image failure rate should actually be higher than the first image. So, despite a success rate of only about 36%, we expect that untilted particles are successfully oriented better than 60% of the time.
These results show that our recent cryo-EM map has the correct hand (Ludtke et al., 2011). If our model possessed the wrong hand, the computed mean tilt axis would be off by 180 degrees in both polar plots, directly antipodal to its present location. The success of the tilt validation demonstrates that our IP3R1 reconstruction is self-consistent, and confirms that the quaternary structure is reliable.
To further demonstrate that our tilt-pair cluster is convincing evidence for the veracity of our map, we next demonstrate what happens when tilt validation is applied to the previously published, and we assert, incorrect structures. We used the same set of tilted particles used to validate our new map, and attempted to validate the three earlier published cryo-EM structures (Jiang et al., 2002; Sato et al., 2004; Serysheva et al., 2003). As Figures 2D – F show, the computed tilt angles and tilt axes are distributed completely randomly, demonstrating that these previously published maps are not consistent with the current data in any way. It is worth mentioning, however, that one previously published structure, performed in negative stain at very low resolution, appears qualitatively self-consistent with our current structure (Hamada et al., 2003). While we lack the data to quantitatively validate this map, it qualitatively demonstrates that negative stain can still be a useful technique in validating structures of complexes, which have very low contrast in frozen, hydrated specimens.
Comparative Refinement
Another approach used to verify controversial cryo-EM reconstructions is to use the same particle data to determine the structure with two or more independent software packages, to demonstrate that the same structure can be reproduced using different computational methods, which have been successfully used in solving many cryo-EM structures. This approach has the advantage that, unlike tilt-validation, no additional data must be collected. Much like the class-average/projection comparison, this test is a necessary, but not a sufficient condition for a valid reconstruction. If a given data set does not uniquely describe a single 3D structure, due to insufficient sampling, or structural variability in solution, then different methods are likely to determine different maps from the same data, due to the unique algorithmic biases present in each software package. Additionally, this can act as a test for possible noise/model bias during refinement. Assuming that each software package determines its own independent initial model, then it is unlikely that both packages will produce exactly the same noise-biased results at high resolution. Of course, one package may produce a bona-fide better structure than another, meaning comparisons between these maps can only put a lower limit on the joint resolution of the maps. That is, one can say that both maps are reliable to at least resolution ‘X’ based on their mutual agreement.
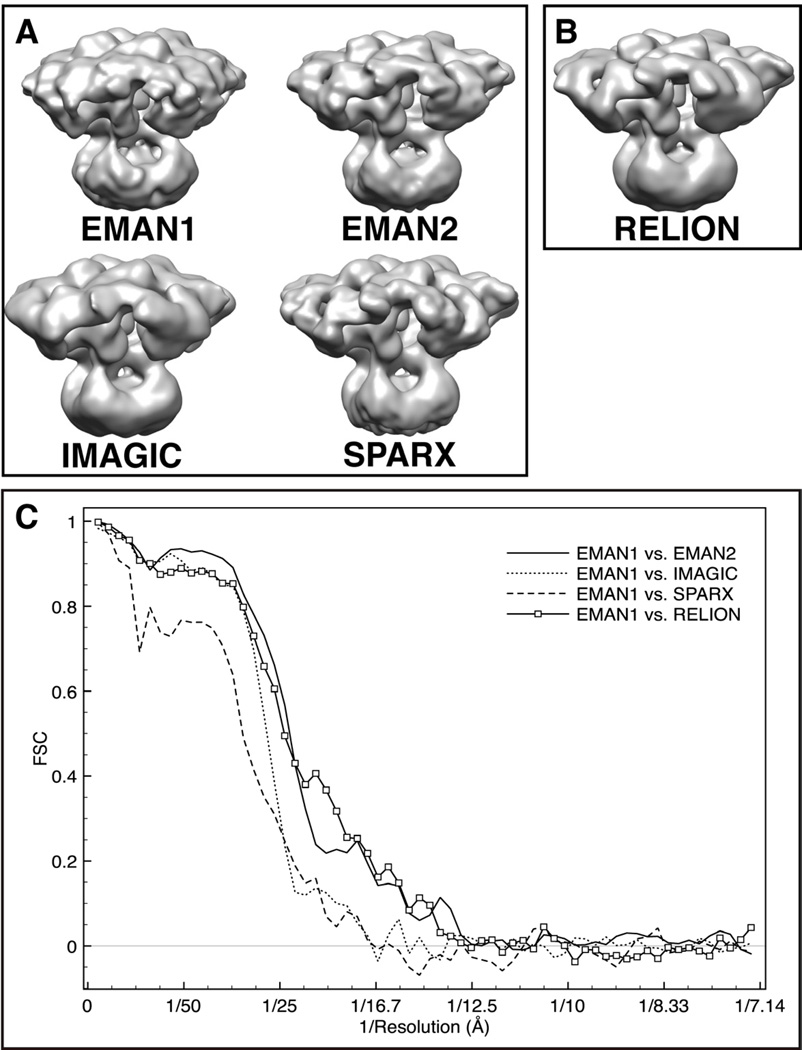
For IP3R1 we elected to do fairly exhaustive testing to not only assess the correctness of the published structure, but also to quantitatively compare the agreement among software packages as a method for placing believable limits on the interpretability of the published map. Specifically, we performed completely independent reconstructions of IP3R1 using: EMAN1, EMAN2, SPARX and IMAGIC. We also performed a refinement in RELION (Scheres, 2012), but in this case an initial model derived from the EMAN model was required to seed the refinement process. As shown in Figures 3A and B, all five maps have good qualitative agreement. These maps were all filtered to match so they can be easily compared visually, with the original unfiltered maps shown in Figure S1. Clearly the overall quaternary structure is preserved in all of the reconstructions. We will consider the question of resolution more fully in the next section.
Figure 3. 3D reconstructions of IP3R1 generated with different software packages.
Maps were calculated using the same set of cryo-EM images and a matching filter was applied to bring each to the same ~20 Å resolution, with a comparable contour level. (A) 3D reconstructions performed reference-free; (B) 3D structure reconstructed using an initial model generated from an EMAN2 structure that had been low pass filtered by RELION; (C) FSCs between the reconstructions from EMAN1 and the maps generated using other software packages. See also Figure S1 and Figure S2.
One challenge with this approach is that it requires the user to be an expert in processing with multiple 3D reconstruction packages, each of which has a substantial learning-curve. Of course, even with this knowledge, substantial additional effort is required to complete this process. Each package utilizes different data and metadata formats. Additionally, each package must also define its own symmetry and orientation conventions (Heymann et al., 2005). To help facilitate the comparative refinement process, we have integrated support for several packages into the EMAN2 graphical interface, such that, once an EMAN2 refinement has been performed, a few button presses will produce data and metadata preformatted for use for each of these programs, a script with specified options to actually run the refinement or other task, and a tool to re-integrate results back into EMAN2. This modular approach gives the user the ability to generate and integrate independent results in several places throughout the cryo-EM reconstruction pipeline. This capability can dramatically ease the process of performing such comparative refinements.
While there is excellent qualitative agreement among the five density maps, it is quite possible that our refinement attempts were not optimal in terms of resolution in all cases. With EMAN1 and EMAN2, we are confident that we have used the software to the best of our ability. The RELION and SPARX reconstructions were similarly performed under the supervision of the authors of each of those two packages. The IMAGIC reconstruction likely could have been further optimized with additional manual cycles of refinement. In this case, we stopped once it was clear that the quaternary structure agreed well with the published structure. Overall, we believe we have at least demonstrated the point that good qualitative agreement of the quaternary structure has been achieved. The convergent structure looks like the recently published map (Ludtke et al., 2011) and is different from all the earlier published maps (Jiang et al., 2002; Sato et al., 2004; Serysheva et al., 2003).
‘Gold Standard’ for Resolution Assessment of the IP3R1 Map
After a single particle reconstruction has been completed, the resolution of the map must be assessed. The most common method for this involves splitting the raw particle data into even and odd halves and computing ‘independent’ reconstructions for each half. These maps are then compared using a Fourier shell correlation (FSC) curve. The spatial frequency at which this curve falls below a specified threshold is considered the resolution of the reconstruction.
Our published IP3R1 map included such an assessment, with an evaluated resolution of ~10 Å (Ludtke et al., 2011). However, the original theory of the FSC as a measure of resolution required that the two maps being compared were fully independent (van Heel and Harauz, 1986), to avoid any bias caused by algorithms or by starting with the same initial model. However, as a community, this standard has not been widely implemented, largely due to computational expense and questions over how ‘independent’ should be properly defined. In most cases, published FSC resolution tests split the data in half at the final stage, after orientations have already been determined with respect to a common reference. This can lead to an exaggeration in resolution due to the well-known model/noise bias problem (Stewart and Grigorieff, 2004). While in many cases this bias will have a negligible impact on the measured resolution, in other cases, it can lead to resolution exaggeration, and in turn over-interpretation of the map.
At a recent meeting of the cryo-EM validation task force (Henderson et al., 2012), a more rigorous ‘gold standard’ resolution test was discussed, aimed at improving the robustness of the FSC assessment, and bringing it more in line with demonstrable feature resolvability in the map. In the current study, we have adopted this basic methodology as described in Scheres (Scheres and Chen, 2012), but with some subtle improvements.
As with the traditional FSC test, this new method begins by splitting the particle data into two even/odd subsets. However, each of these two subsets is then fully refined completely independently following normal strategies in each software package. After each iteration the two intermediate maps are compared, and refinements continue until they achieve maximal agreement. The FSC curve used to assess resolution is computed between the two final maps. We should note that there are still some subtle differences especially in defining the initial templates among the current implementations of this method in different software packages. As far as we are aware, RELION and EMAN2 are the only packages, at present, with automatic implementations of this strategy. While these implementations differ in a few subtle details, the overall strategy remains the same. To avoid bias, the starting maps for the two independent refinements are filtered beyond some threshold resolution, so they start with no high-resolution information in common. This threshold is selected to be much lower than the targeted resolution, to insure that each reconstruction has determined the high-resolution information independently.
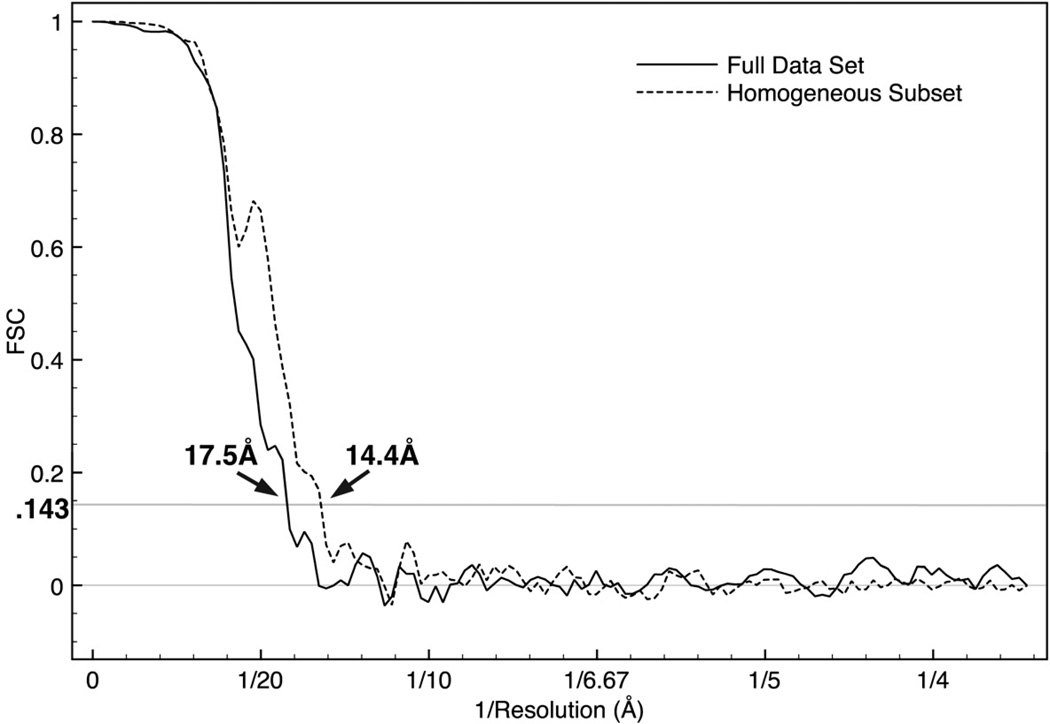
Given the independence of the refinements described here, the FSC curves produced using this approach are free of most of the artifacts which can be produced in the less rigorous FSC tests commonly used. This also means that the proposed 0.143 FSC threshold (Rosenthal and Henderson, 2003), which can sometimes produce nonsensical results with old-style FSC measurements, can be safely applied when using this test. When this test is performed in EMAN2 (Figure 4) on the full data set of IP3R1 and the phases in the final 3D map were randomized to 25 Å, we observe a resolution of roughly 17 Å, worse than the resolution we originally reported, but with minimal impact on any features we actually interpreted in the published map.
Figure 4. ‘Gold standard’ FSC plot for the EMAN2 reconstruction.
The EMAN2 refinement of the full data set produced a ‘gold standard’ resolution of about 17 Å. Splitting the data into more homogeneous subsets resulted in an additional map (not shown) with a ‘gold standard’ resolution of 14.7 Å. This demonstrates that resolution is limited by structural variability for this data set. If the data quality were limiting the resolution, splitting the data would not improve the resolution.
It is important when performing this “gold standard” test that the resolution at which the starting maps are filtered or randomized is substantially lower than the measured resolution in the test. That is, if the final resolution is measured to be 12 Å, phase randomizing to 13 Å would not be sufficient. We suggest that ~1.5x the anticipated resolution is a reasonable value, though even more initial model filtration would demonstrate map convergence even more clearly.
Though the more traditional FSC test has been widely adopted in the field to assess map resolution, as previously observed (Stewart and Grigorieff, 2004), it permits over-refinement of data with high noise levels or variable conformation. Besides the risk of over interpretation, this effect can actually produce maps of lower quality. Adding additional particles, even those with too little contrast for accurate alignment, will cause an improvement in the numerical value of the measured resolution, due to noise bias, when using the traditional FSC test. Clearly, adding incorrectly aligned particles (or pure noise) to the data set will never improve the accuracy of the final map, and in fact can degrade the map moderately. In contrast, if a proper independent FSC test with the data split at the beginning of the particle orientation refinement is used, adding ‘noise particles’ to the data set will lead to a lower measured resolution, which reflects the actual resolvability of the map. When assessing whether particles should be included or excluded from a refinement, the ‘gold standard’ test will give an accurate picture of whether the structure is improving or worsening with the data in question.
Resolution Assessment between Maps Reconstructed from Different Refinement Algorithms
As presented in Figures 3A and B, IP3R1 maps were computed from the same data set with different reconstruction algorithms. With the exception of RELION, which used the EMAN2 reconstruction filtered to 60 Å resolution, all of the other software packages were required to determine their own starting maps, using canonical methods within each package. Therefore, each of these maps was determined completely independently using the same particle data. Figure 3C shows a plot of the FSC curves computed between the published IP3R1 reconstruction (Ludtke et al., 2011) and each of the other maps in panels A and B. It is readily apparent that this cross-software FSC test is showing that the maps are consistent to only ~17 Å at FSC=0.5 in the best case. While this is not a measurement of ‘resolution’, these curves do need to be considered when deciding how much to interpret in the final reconstruction.
As an additional comparison, we also performed tilt-pair validation for each of these five different maps, using EMAN2’s tilt-pair validation software (Figure S2). All of the structures exhibit a clear cluster, as expected. There is some variability in the outliers, which represent particles that have at least one of the two orientations incorrectly determined.
Local Resolution and Motion
While the resolution in the present estimate is clearly worse than our original published estimate (Ludtke et al., 2011), the quaternary structure described in our original manuscript was fundamentally correct, and higher resolution features had little impact on our biological interpretation. The only α-helices we attempted to interpret in the original structure were the pore-lining helices in the trans-membrane domain. These were interpreted as a similarity in overall density pattern in the pore region as compared to the same region in the crystal structure of the Kir2.2 channel (PDB ID: 3JYC). Since the FSC is an average over the entire map, it does not indicate if one region has higher variability than another. As the resolved helices are in proximity to the 4-fold symmetry axis, where uncertainty in particle orientation has less impact, it is possible that this region is somewhat better resolved than the map as a whole. For example, the lumenal turret regions identified in IP3R1 channel and resembling the extracellular turrets in Kir-type K+ channels (Ludtke et al., 2011), seem to be uniformly present in these reconstructions. Nonetheless, as we discussed in our original publication, it is clear that a rigorous subnanometer resolution map is required to unambiguously identify and interpret densities corresponding to all secondary structure elements throughout the entire 1.3 MDa channel protein complex.
We next consider why there is such a significant resolution discrepancy in this channel. The explanation for this begins with the variance map published with our original structure (Ludtke et al., 2011), which demonstrates there are regions of very high variability within the map. We also demonstrated that sub-classifying particles in particular orientations implied internal motions as large as 20 Å in this channel.
We also used EMAN2 to split the full data set into two subsets with more structural homogeneity, by performing multi-model refinement (e2refinemulti.py). This refinement was seeded with two similar previously generated structures, then refined to convergence, with each particle allowed to move between references in each refinement cycle (Chen et al., 2006). After convergence, the data associated with each map was extracted into a separate set. After refining one of these sets (not shown), we achieved a structure outwardly similar to all of the other maps presented, but with an improved ‘gold standard’ resolution of 14.7 Å. If the resolution of these reconstructions were inherently limited by data quality to 17 Å resolution, then splitting the data set would not have improved the resolution in the ‘gold standard’ test. In fact, due to the reduction in particle count in each set, the resolution should have become moderately worse. The significant improvement in resolution with a smaller data set is an indication that structural variability is responsible for the limited resolution we observe.
That is, the ‘closed’ biochemical state used in these experiments seems to be undergoing significant internal motion in solution. Upon consideration, this is actually a logical, if not obvious observation. As the closed state of the channel maintained in the absence of its primary ligands, i.e. IP3 and Ca2+, would undergo multiple entropic rearrangements, ligand binding will simply restrict this rearrangement of the ion channel to a precise configuration permitting ion translocation through the conducting pore. This implies that the channel must be a naturally dynamic structure. It seems probable that the ligand-bound open state of the channel will be less dynamic than the closed state. Further experiments will be required to prove or disprove this hypothesis, but regardless, it is clear that the ligand-free closed state is highly dynamic.
Further splitting of the data did not achieve additional resolution improvements, due to decreasing particle count. However, this result is encouraging as it implies that it should be possible to achieve higher resolutions using this technique if a sufficiently large population of particles is available.
DISCUSSION
The above results show that our IP3R1 structure (Ludtke et al., 2011) is consistent with the underlying 2D cryo-images, as shown by both the self-consistency tests and the tilt-pair validation test (Henderson et al., 2011). This tilt-pair validation test is particularly important for structures at low resolutions where secondary structure elements cannot yet be unambiguously discerned. By making use of data from an additional tilt experiment on the microscope, this test provides a fairly robust experimental assessment on the validity of a structure. The primary limiting factor in this test is the relatively small proportion of total particles in each image tilt-pair, which are able to successfully pass the test, due to radiation damage, charging, conformational variants and other problems. Nonetheless, if a substantial fraction of the particles are able to pass this very stringent test, we can assume the structure is accurate. As we have demonstrated, when an incorrect structure is validated against tilt-pair data, the results exhibit a completely random distribution, with no apparent clustering.
Previously we have shown our IP3R1 sample to be biologically active based on ability of the purified receptors to form IP3-sensitive Ca2+ release channels upon reconstitution into Ca2+-loaded lipid vesicles (Ludtke et al., 2011). This observation, coupled with our validation results, demonstrates that our IP3R1 structure is biologically relevant. Furthermore, we have demonstrated that the three previously published structures (Jiang et al., 2002; Sato et al., 2004) are not compatible with our new cryo-EM data, which has demonstrably better contrast than the earlier data. Given the various challenges in pursuing structural characterization of mammalian and large ion channel, the present study shows the progress made in cryo-EM field for studying this class of macromolecular machine. Our study resolves the decade old uncertainty over the correct quaternary structure of IP3R1 channel.
Though this study addresses cryo-EM data at moderate resolution, the same standards for resolution estimation and map interpretability should be applied to cryo-EM studies determined at any resolution range. This would include even maps, which appear to resolve the C-alpha backbone, or low-resolution maps, which are obtained from post-tomographic subvolume averages. While the vast majority of cryo-EM maps published over the last decade are believed to be entirely accurate, a quantitative and rigorous approach to validating and assessing all maps would lead to more credibility for this versatile field of structural biology, as it continues to improve its resolvability and reliability for structures ranging from molecules to molecular machines either in biochemically purified states or in the cell.
METHODS
Specimen Preparation
The IP3R1 preparation for cryo-EM analysis was followed our previously published procedures (Ludtke et al., 2011).
Electron Cryomicroscopy
The published cryo-EM data for IP3R1 and the resulting 3D map (Ludtke et al., 2011) were reanalyzed in this study using different software packages. In the tilt validation experiments, vitrified IP3R1 samples were imaged using the JEOL JEM-2100 electron microscope with LaB6 filament operated at 200 keV and a Gatan 626 cryo-holder. Tilt-pair images were acquired on a Gatan 4k × 4k CCD camera at 60,000x nominal magnification of the microscope by the use of low-dose mode (~18 electron/Å2) and with defocus 1.5 – 2.0 µm.
Tilt-pair Validation
For the tilt-pair validation experiments data was collected as previously described (Ludtke et al., 2011), with the exception that 0 and 10 degree tilt pairs were collected for each region of the grid. A total of 20 tilt-pairs were collected, and the two best pairs were used for the tilt validation test. The other pairs suffered from problems with drift and charging. A total of 42 and 36 particles from two tilt pairs were used for the validation test (Table S1).
Tilt validation was performed using a set of tools developed in EMAN2, implementing the concepts described in (Rosenthal and Henderson, 2003), and now available as a standard module in e2projectmanager.py. Particle pairs were selected interactively as linked pairs using e2RCTboxer.py. Particles were then preprocessed as usual for single particle reconstruction by determining CTF parameters and performing CTF phase-flipping. Due to the small tilt angle used, the defocus gradient across the image is a negligible effect at low resolution. Euler angles for each particle of each tilt pair were determined via projection matching, using projections of the map being tested. In this case we used a 2-degree angular spacing in generating projections. For each particle pair, the tilt axis and angle were computed from the pair’s Euler angles. E2tiltvalidate was used to perform this process for all pairs and compute the tilt validation plot. If the computed tilt axis and angle are consistent and cluster around the experimental tilt axis and angle, the 3D map is deemed correct, at least to low resolution. In addition to validating the 3D map, this technique can determine if the handedness is correct, even at low resolution. If the computed tilt axis is 180 degrees out of phase with respect to the experimental tilt axis then the hand in incorrect, otherwise it is correct. This assumes, of course, that experimental knowledge of the tilt direction is pre-calibrated and accurate.
An additional complexity exists during the angle determination in the presence of symmetry. The orientation determination was made within a single asymmetric triangle, and the rotation taking place could rotate the point into a neighboring asymmetric triangle. This problem was dealt with by considering the particle to be in all possible asymmetric triangles and using only the answer which falls as close to the experimental rotation plane as possible.
Multi-Software Reconstructions
All the reconstructions with different software packages were done with the previously published data set (Ludtke et al., 2011). The EMAN1 refinement was not recomputed for this manuscript, and was performed as previously published (Ludtke et al., 2011).
The EMAN2 (blake.bcm.edu/emanwiki/EMAN2) refinement followed standard procedures in EMAN2 (Tang et al., 2007). Briefly, contrast transfer function (CTF) parameters were determined from the particles in each micrograph, including per-micrograph estimation of spectral signal to noise ratio. Phases were flipped immediately and the remaining parameters were used during alignment and averaging. An initial model was generated using e2initialmodel.py, which uses reference-free class-averages combined with randomized starting models to produce a coarse starting model (Tang et al., 2007). This model along with the phase-flipped particle data was then processed with e2refine.py. In this iterative process, particle reference-based classification of particles was performed using projections of the current 3-D map with a 2-degree angular step. Particles were aligned to references using the ‘refine’ aligner with a Fourier ring correlation similarity metric using SNR weighting and projection-based masking. Particles within each class were iteratively averaged for 2 cycles with CTF amplitude correction, with particles worse than 1 standard deviation from the mean similarity metric excluded from the 2-D average. Averages were then reconstructed in Fourier space, with additional CTF amplitude corrections. The new map was then used to generate projections for the next cycle of refinement. The final refinement, started from an intermediate resolution map, ran for 4 iterations.
The IMAGIC reconstruction was performed using IMAGIC-5 (van Heel et al., 2000). Individual particle images were boxed out and the CTF parameters were estimated and corrected using EMAN as described earlier in (Ludtke et al., 2004; Ludtke et al., 2005; Ludtke et al., 2011). Before image processing the images were normalized to have the same mean and standard deviation and were band-pass filtered with low- and high-frequency cut-offs of ~200 Å and ~9 Å, respectively, to remove background and high-frequency noise. Image processing and 3D reconstruction were performed as previously described (Serysheva et al., 1995; van Heel et al., 2000). The initial 3D reconstruction was generated using ab initio approach: the relative angular orientations of class-average images were determined by angular reconstitution using C4 symmetry constraints, and the best ~50 classes showing the lowest error at the angular search were selected to calculate the initial 3D map. The refinement of the alignment of the entire data set was then performed by using the reprojections of the initial map, the aligned images were subjected to multivariate statistical analysis and classification, and the new best class-average images were selected again to calculate the next 3D map, which was used as a new reference in the next round of refinement. The number of classes was increased in the course of the refinement to achieve more detailed classification. Within each refinement round, the quality of the 3D map was assessed using minimization of errors in the angular search, errors between input class-average images and corresponding reprojections of the 3D map, and the FSC criterion.
The 3D structure of IP3R1 with SPARX package (Hohn et al., 2007) was determined using an independent ab initio approach. First, we computed a set of 234 stable and reproducible 2D class averages using ISAC program (Yang et al., 2012). Second, we determined an initial 3D structure of IP3R1 using the set of 2D class averages and C4-symmetrized 3D distribution of Gaussian noise as an initial template in a 3D projection matching procedure iterated until convergence (Penczek et al., 1994). This step was repeated a number of times with different distributions of noise used as initial template to determine that the procedure indeed converges to the same 3D low-resolution model. Finally, the initial 3D model was refined using the entire set of original EM projection images in a 3D projection matching procedure that involved CTF correction and C4-symmetrization of the map during each iteration.
The RELION map was generated through use of tools developed within EMAN2, and integrated into EMAN2’s e2projectmanager.py graphical interface. We have also developed tools in this interface for several other inter-software conversions. For RELION, the process begins with a program called e2refinetorelion3d.py, which converts EMAN2 project data and metadata into formats suitable for RELION. Specifically, it generates an initial map, all required particle stacks, and a prototypical batch script used to launch the actual RELION refinement on a typical Linux cluster. The initial map was generated by perturbing the results of an EMAN2 refinement through a similar low-pass phase-randomization process used in the ‘gold standard’ resolution test. The particle stacks are selected by reference to a specific refinement run in EMAN2, so direct comparisons can be made. Unlike the program used to generate RELION reference free class-averages (e2refinetorelion2d.py), for which a desktop workstation suffices, the computational requirements of a 3-D RELION refinement generally require use of a Linux cluster. e2refinetorelion3d.py permits setting all of the useful RELION refinement parameters through its graphical interface, and these are propagated to the existing refinement batch script. For the IP3R1 presented here, we used several parameters other than typically required options such as symmetry group and number. RELION performs a low-pass filtering on the initial model so a value of 60 Å was used. The particle images are also masked with a soft circular mask by RELION so a diameter of 320 Å was selected. Initial values for the ‘healpix’ (7.5), ‘auto_healpix’ (1.8), ‘offsetrange’ (10.0), and ‘offsetstep’ (2.0) were provided. These numbers represent only initial values, as RELION will automatically modify them as the reconstruction converges. Unlike the other software packages which were performed completely independently, RELION necessitated the use of a reasonable initial model so the EMAN2-generated structure low-pass filtered to 60 Å was given as an initial model.
‘Gold Standard’ Resolution Test
The ‘gold standard’ resolution assessment is implemented in EMAN2 in e2refine_evenodd.py. Briefly, the particle data was divided into even and odd numbered particles. Initial models must be independent at high resolution for a valid test. To generate these models, the final refined map was Fourier transformed, and the phases were randomized beyond 25 Å, independently for the two maps. This produces two starting models identical at low resolution, but with strong high resolution noise, and no correlation beyond 25 Å.
The final resolution should be no worse than this cutoff resolution divided by ~1.5. That is, if the initial model were randomized beyond 25 Å, and the resolution were measured to be 22 Å, the test should be re-run with phases randomized to at least ~33 Å. Generally randomizing/filtering even more strongly is harmless, and improves the validity of the test, but will require more refinement cycles to converge.
Next, two independent refinements using identical parameters were performed for 4 cycles, and an FSC curve computed between the two final models. Since the initial models were completely independent at higher resolution, and independent ½ data sets were used, any high-resolution agreement between the maps is data-based, not derived from noise or model bias. Historically we have utilized the FSC=0.5 threshold for measuring resolution with the old style FSC computations. However, with the true independence of the ‘gold standard’ FSC, the original arguments for the 0.143 criterion (Rosenthal and Henderson, 2003) become valid, and this threshold provides a reasonable equivalent to the criterion applied in X-ray crystallography.
Supplementary Material
Highlights.
Five different reconstruction algorithms agree on the IP3R1 quaternary structure
IP3R1 quaternary structure is validated by tilt-pair analysis
Resolution of the IP3R1 map has been assessed using the ‘gold standard’ criterion
Acknowledgements
We are grateful to Sjors Scheres for providing 3D reconstruction of IP3R1 with RELION and for helpful discussion, and to Pawel Penczek and Zhengfan Yang for generating 3D structure of IP3R1 with SPARX. We thank Frederick Sigworth for providing cryo-EM density map of IP3R1 published in (Jiang et al., 2002). This research has been supported by NIH grants (P41GM103832, R01GM079429, R01GM072804, R01GM080139, R21AR063255) and AHA grant (12GRNT10510002).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Author contributions
S.C.M. performed 3D reconstruction of IP3R1 with RELION, comparative analysis of 3D reconstructions generated by five different software packages; J.F. – implemented tilt-pair analysis program in EMAN2, performed tilt-pair analysis; S.J.L. – EMAN2 reconstruction, assessment of resolution using “gold standard” criterion; O.B.P and I.I.S.- took tilt-pairs of cryo-EM images; I.I.S. – 3D reconstruction with IMAGIC; W.C., S.J.L., I.I.S., J.F. and S.C.M interpreted results and wrote the manuscript.
Supplemental Information
Supplemental information includes two figures and table, and can be founded with this article online.
REFERENCES
- Chen DH, Song JL, Chuang DT, Chiu W, Ludtke SJ. An expanded conformation of single-ring GroEL-GroES complex encapsulates an 86 kDa substrate. Structure. 2006;14:1711–1722. doi: 10.1016/j.str.2006.09.010. [DOI] [PubMed] [Google Scholar]
- Clare DK, Vasishtan D, Stagg S, Quispe J, Farr GW, Topf M, Horwich AL, Saibil HR. ATP-triggered conformational changes delineate substrate-binding and -folding mechanics of the GroEL chaperonin. Cell. 2012;149:113–123. doi: 10.1016/j.cell.2012.02.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foskett JK, White C, Cheung KH, Mak DO. Inositol trisphosphate receptor Ca2+ release channels. Physiol Rev. 2007;87:593–658. doi: 10.1152/physrev.00035.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamada K, Terauchi A, Mikoshiba K. Three-dimensional rearrangements within inositol 1, 4, 5-trisphosphate receptor by calcium. J Biol Chem. 2003;278:52881–52889. doi: 10.1074/jbc.M309743200. [DOI] [PubMed] [Google Scholar]
- Henderson R, Chen S, Chen JZ, Grigorieff N, Passmore LA, Ciccarelli L, Rubinstein JL, Crowther RA, Stewart PL, Rosenthal PB. Tilt-pair analysis of images from a range of different specimens in single-particle electron cryomicroscopy. J Mol Biol. 2011;413:1028–1046. doi: 10.1016/j.jmb.2011.09.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henderson R, McMullan G. Problems in obtaining perfect images by single-particle electron cryomicroscopy of biological structures in amorphous ice. J Electron Microscopy. 2013 doi: 10.1093/jmicro/dfs094. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henderson R, Sali A, Baker ML, Carragher B, Devkota B, Downing KH, Egelman EH, Feng Z, Frank J, Grigorieff N, et al. Outcome of the first electron microscopy validation task force meeting. Structure. 2012;20:205–214. doi: 10.1016/j.str.2011.12.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heymann JB, Chagoyen M, Belnap DM. Common conventions for interchange and archiving of three-dimensional electron microscopy information in structural biology. J Struct Biol. 2005;151:196–207. doi: 10.1016/j.jsb.2005.06.001. [DOI] [PubMed] [Google Scholar]
- Hohn M, Tang G, Goodyear G, Baldwin PR, Huang Z, Penczek PA, Yang C, Glaeser RM, Adams PD, Ludtke SJ. SPARX, a new environment for Cryo-EM image processing. J Struct Biol. 2007;157:47–55. doi: 10.1016/j.jsb.2006.07.003. [DOI] [PubMed] [Google Scholar]
- Jiang QX, Thrower EC, Chester DW, Ehrlich BE, Sigworth FJ. Three-dimensional structure of the type 1 inositol 1,4,5-trisphosphate receptor at 24 Å resolution. Embo J. 2002;21:3575–3581. doi: 10.1093/emboj/cdf380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lau WC, Rubinstein JL. Subnanometre-resolution structure of the intact Thermus thermophilus H+-driven ATP synthase. Nature. 2012;481:214–218. doi: 10.1038/nature10699. [DOI] [PubMed] [Google Scholar]
- Ludtke SJ, Baker ML, Chen DH, Song JL, Chuang DT, Chiu W. De Novo Backbone Trace of GroEL from Single Particle Electron Cryomicroscopy. Structure. 2008;16:441–448. doi: 10.1016/j.str.2008.02.007. [DOI] [PubMed] [Google Scholar]
- Ludtke SJ, Chen DH, Song JL, Chuang DT, Chiu W. Seeing GroEL at 6 Å Resolution by Single Particle Electron Cryomicroscopy. Structure (Camb) 2004;12:1129–1136. doi: 10.1016/j.str.2004.05.006. [DOI] [PubMed] [Google Scholar]
- Ludtke SJ, Serysheva II, Hamilton SL, Chiu W. The pore structure of the closed RyR1 channel. Structure (Camb) 2005;13:1203–1211. doi: 10.1016/j.str.2005.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ludtke SJ, Tran TP, Ngo QT, Moiseenkova-Bell VY, Chiu W, Serysheva II. Flexible architecture of IP3R1 by Cryo-EM. Structure. 2011;19:1192–1199. doi: 10.1016/j.str.2011.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milazzo AC, Cheng A, Moeller A, Lyumkis D, Jacovetty E, Polukas J, Ellisman MH, Xuong NH, Carragher B, Potter CS. Initial evaluation of a direct detection device detector for single particle cryo-electron microscopy. J Struct Biol. 2011;176:404–408. doi: 10.1016/j.jsb.2011.09.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Penczek PA, Grassucci RA, Frank J. The ribosome at improved resolution: new techniques for merging and orientation refinement in 3D cryo-electron microscopy of biological particles. Ultramicroscopy. 1994;53:251–270. doi: 10.1016/0304-3991(94)90038-8. [DOI] [PubMed] [Google Scholar]
- Rosenthal PB, Henderson R. Optimal determination of particle orientation, absolute hand, and contrast loss in single-particle electron cryomicroscopy. J Mol Biol. 2003;333:721–745. doi: 10.1016/j.jmb.2003.07.013. [DOI] [PubMed] [Google Scholar]
- Sato C, Hamada K, Ogura T, Miyazawa A, Iwasaki K, Hiroaki Y, Tani K, Terauchi A, Fujiyoshi Y, Mikoshiba K. Inositol 1,4,5-trisphosphate receptor contains multiple cavities and L-shaped ligand-binding domains. J Mol Biol. 2004;336:155–164. doi: 10.1016/j.jmb.2003.11.024. [DOI] [PubMed] [Google Scholar]
- Scheres SH. RELION: Implementation of a Bayesian approach to cryo-EM structure determination. J Struct Biol. 2012;180:519–530. doi: 10.1016/j.jsb.2012.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheres SH, Chen S. Prevention of overfitting in cryo-EM structure determination. Nature methods. 2012;9:853–854. doi: 10.1038/nmeth.2115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Serysheva II, Bare DJ, Ludtke SJ, Kettlun CS, Chiu W, Mignery GA. Structure of the type 1 inositol 1,4,5-trisphosphate receptor revealed by electron cryomicroscopy. J Biol Chem. 2003;278:21319–21322. doi: 10.1074/jbc.C300148200. [DOI] [PubMed] [Google Scholar]
- Serysheva II, Orlova EV, Chiu W, Sherman MB, Hamilton SL, van Heel M. Electron cryomicroscopy and angular reconstitution used to visualize the skeletal muscle calcium release channel. Nat Struct Biol. 1995;2:18–24. doi: 10.1038/nsb0195-18. [DOI] [PubMed] [Google Scholar]
- Stewart A, Grigorieff N. Noise bias in the refinement of structures derived from single particles. Ultramicroscopy. 2004;102:67–84. doi: 10.1016/j.ultramic.2004.08.008. [DOI] [PubMed] [Google Scholar]
- Tang G, Peng L, Baldwin PR, Mann DS, Jiang W, Rees I, Ludtke SJ. EMAN2: an extensible image processing suite for electron microscopy. J Struct Biol. 2007;157:38–46. doi: 10.1016/j.jsb.2006.05.009. [DOI] [PubMed] [Google Scholar]
- Taylor CW, Tovey SC. IP(3) receptors: toward understanding their activation. Cold Spring Harbor perspectives in biology. 2010;2 doi: 10.1101/cshperspect.a004010. a004010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Heel M, Gowen B, Matadeen R, Orlova EV, Finn R, Pape T, Cohen D, Stark H, Schmidt R, Schatz M, Patwardhan A. Single-particle electron cryo-microscopy: towards atomic resolution. Quarterly reviews of biophysics. 2000;33:307–369. doi: 10.1017/s0033583500003644. [DOI] [PubMed] [Google Scholar]
- van Heel M, Harauz G. Resolution criteria for three dimensional reconstructions. Optik. 1986;73:119–122. [Google Scholar]
- Yang Z, Fang J, Chittuluru J, Asturias FJ, Penczek PA. Iterative stable alignment and clustering of 2D transmission electron microscope images. Structure. 2012;20:237–247. doi: 10.1016/j.str.2011.12.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.