Chimera states in mechanical oscillator networks

Abstract

The synchronization of coupled oscillators is a fascinating manifestation of self-organization that nature uses to orchestrate essential processes of life, such as the beating of the heart. Although it was long thought that synchrony and disorder were mutually exclusive steady states for a network of identical oscillators, numerous theoretical studies in recent years have revealed the intriguing possibility of “chimera states,” in which the symmetry of the oscillator population is broken into a synchronous part and an asynchronous part. However, a striking lack of empirical evidence raises the question of whether chimeras are indeed characteristic of natural systems. This calls for a palpable realization of chimera states without any fine-tuning, from which physical mechanisms underlying their emergence can be uncovered. Here, we devise a simple experiment with mechanical oscillators coupled in a hierarchical network to show that chimeras emerge naturally from a competition between two antagonistic synchronization patterns. We identify a wide spectrum of complex states, encompassing and extending the set of previously described chimeras. Our mathematical model shows that the self-organization observed in our experiments is controlled by elementary dynamical equations from mechanics that are ubiquitous in many natural and technological systems. The symmetry-breaking mechanism revealed by our experiments may thus be prevalent in systems exhibiting collective behavior, such as power grids, optomechanical crystals, or cells communicating via quorum sensing in microbial populations.

In 1665, Christiaan Huygens observed that two pendulum clocks suspended on a beam always ended up swinging in exact antiphase motion (1) regardless of each pendulum’s initial displacement. He explained this self-emergent synchronization as resulting from the coupling between the clocks, which was mediated by vibrations traveling across the beam. Huygens’ serendipitous discovery has inspired many studies to establish that self-emergent synchronization is a central process to a spectacular variety of natural systems, including the beating of the heart (2), flashing fireflies (3), pedestrians on a bridge locking their gait (4), circadian clocks in the brain (5), superconducting Josephson junctions (6), chemical oscillations (7, 8), metabolic oscillations in yeast cells (9), and life cycles of phytoplankton (10).

Ten years ago, the dichotomy between synchrony and disorder was challenged by a theoretical study revealing that a population of identical coupled oscillators can attain a state where one part synchronizes and the other oscillates incoherently (11–23). These “chimera states” (13) emerge when the oscillators are coupled nonlocally (i.e., the coupling strength decays with distance between oscillators), which is a realistic scenario in many situations, including Josephson junction arrays (24) or ocular dominance stripes (25). Chimera states are counterintuitive because they occur even when units are identical and coupled symmetrically; however, with local or global coupling, identical oscillators either synchronize or oscillate incoherently but never do both simultaneously.

Since their discovery, numerous analytical studies (13, 14, 16–18) involving different network topologies (14, 19, 20) and various sources of random perturbations (21, 22) have established chimeras as a robust theoretical concept and suggest that they exist in complex systems in nature with nonlocal interactions. However, experimental evidence for chimeras has been particularly sparse so far, and it has only been achieved recently via computer-controlled feedback (26, 27). This raises the question of whether chimeras can only be produced under very special conditions or whether they arise via generic physical mechanisms. Uncovering such physical mechanisms requires analytically tractable experiments with direct analogs to natural systems.

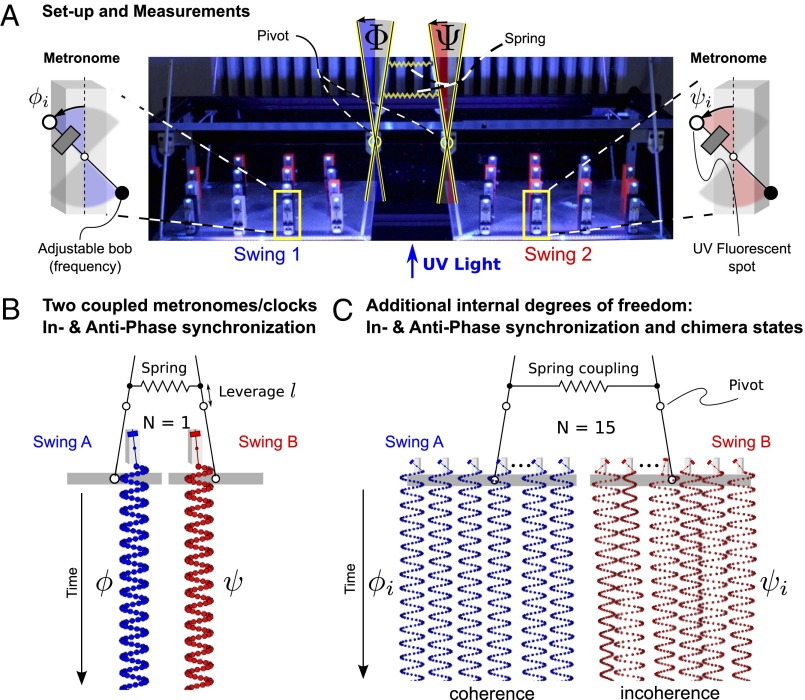
Our mechanical experiment shows that chimera states emerge naturally without the need to fine-tune interactions. We implement the simplest form of nonlocal coupling that can be achieved using a hierarchical network with two subpopulations (14, 15): Within each subpopulation, oscillators are coupled strongly, whereas the coupling strength between the two subpopulations is weaker. We place N identical metronomes (28) with a nominal beating frequency f on two swings, which can move freely in a plane (Fig. 1 and Figs. S1–S3). Oscillators within one population are coupled strongly by the motion of the swing onto which the metronomes are attached. As f is increased, more momentum is transferred to the swing, effectively leading to a stronger coupling among the metronomes. A single swing follows a phase transition from a disordered state to a synchronized state as the coupling within the population increases (28, 29). This mimics the synchronization of the gait of pedestrians on the Millennium Bridge (4) wobbling under the pedestrians’ feet. In our setup, emergent synchronization can be perceived both aurally (unison ticking) and visually (coherent motion of pendula). Finally, the weaker coupling between the two swings is achieved by tunable steel springs with an effective strength κ.

Fig. 1.

Experimental setup and measurements. Two swings are loaded with N metronomes each and coupled with adjustable springs. (A) Swing and metronome displacements are measured by digital tracking of UV fluorescent spots placed on the pendula and swings. (B) 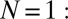Metronomes synchronize in AP or IP motion. (C) 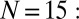Symmetry-breaking chimera states with one metronome population synchronized and the other desynchronized, or vice versa. 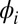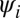The displacement angles of the pendula on the left and right swings are and , respectively.

Results

For nonzero spring coupling, 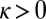, we observe a broad range of parameters in which chimeras (Fig. 1C and Movie S1) and further partially synchronized states emerge. To explore this complex behavior quantitatively, we measure the metronomes’ oscillation phase 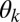, their average frequencies 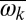, and the complex order parameter 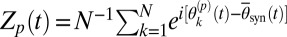, where 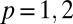denotes the left or right population and 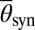is the average phase of the synchronous population ( 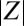quantifies the degree of synchronization: 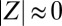for incoherent motion and 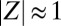for synchronous motion).

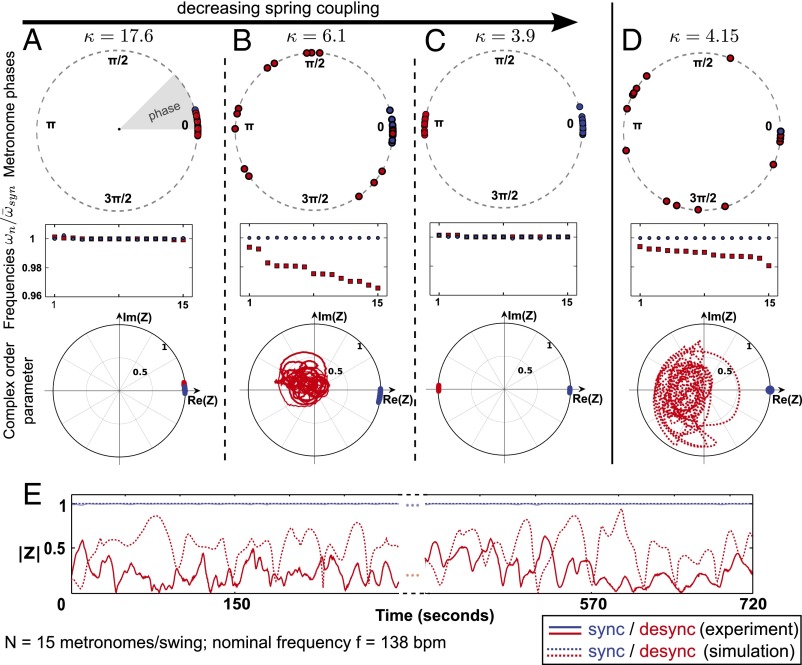
To investigate where chimeras emerge in parameter space, we have systematically varied the effective spring coupling, κ, and the nominal metronome frequency, f, while ensuring that the metronomes on uncoupled swings synchronize. The long-term behavior of the system is studied by preparing the experiments with several initial conditions (SI Text) (12–14): (i) Both populations are desynchronized [desync-desync (DD)], or (ii) one population is synchronous and the other is desynchronized [sync-desync (SD) and desync-sync (DS), respectively]. We start with a fixed frequency and gradually decrease κ. For sufficiently large κ, the spring is effectively so stiff that the two swings act like one and metronomes evolve to a synchronized in-phase (IP) motion, such that the complex order parameters overlap with (Fig. 2A and Movie S2). For low κ, we observe that the two metronome populations settle into synchronized antiphase (AP) motion, where the order parameters and phases are separated in the complex plane by 180° with 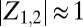(Fig. 2C and Movie S3). These synchronization modes correspond to the two eigenmodes of the swing/spring system. For intermediate κ, however, we observe chimeras (Fig. 2B and Movie S1). Whereas one of the metronome populations is fully synchronized with 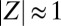, the other population is desynchronized. The trajectory of the order parameter of the desynchronized population describes a cloud in the complex plane with 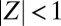. The phases of the desynchronized population are spread over the entire interval , and the time-averaged frequencies are nonidentical. As we increase κ, numerical simulations (see below) reveal that this cloud bifurcates off the AP mode, traverses the complex plane, and eventually collapses into the stable IP synchronization mode (see Fig. 4B). None of the metronomes in the desynchronized population is locked to the synchronized population either, demonstrating truly unlocked motion. Chimeras were consistently found for both SD and DS symmetries, ruling out chimeras as a result of asymmetry or pinning due to heterogeneities. Further, chimeras were not transient, such that the desynchronized population remained desynchronized (i.e., a DS or SD configuration remained for the entire duration of the experiment, typically lasting for up to 1,500 oscillation cycles).

Fig. 2.

Chimeras emerge with intermediate spring rate κ in a “competition” zone between two fully synchronous modes. With decreasing κ, we observe a transition from IP synchronization (A), over chimeras (B), to AP synchronization (C). The transition region also exhibits phase-clustered states and partial chimeras. (D and E) Simulations share all features of the experimental chimera. Data related to the synchronous and asynchronous populations are coded in blue and red, respectively. Angular frequencies are normalized with the average frequency of the synchronized population . bpm, beats per minute.

Fig. 4.

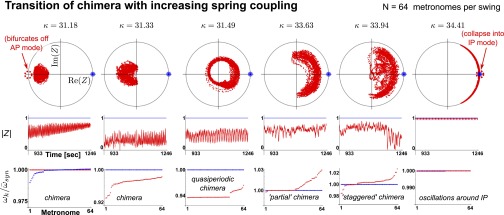
Traversal of order parameter cloud with increasing spring coupling κ. A transition through a rich spectrum of chimera states becomes evident. Numerical simulations are carried out with 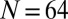metronomes (for parameters see SI Text). As κ increases, the complex order parameter 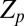bifurcates off from the AP mode at 180° and travels to the right, where it snaps into the IP synchronization mode at 0°. (Top) Complex order parameter Z is displayed. (Middle) Magnitude 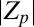is displayed. (Bottom) Angular frequencies, normalized with the average frequency of the synchronized population 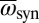, are displayed. The synchronized population is shown in blue, and the desynchronized population is shown in red.

Chimeras are sandwiched in a region between AP and IP modes consistently across various metronome frequencies (Fig. 3A). Remarkably, we also find other asynchronous states, including phase-clustered states (30) (Fig. S4); a “partial chimera,” where only a fraction of the asynchronous population is frequency-locked; and states with oscillation death (28, 31). Additionally, we observe a region of bistability of chimeras and AP synchronized motion. Closer to the edge of the IP region, we find a narrow slice where neither of the metronome populations can achieve synchrony (DD state): Even when initialized with SD or DS conditions, the system loses synchrony completely after a transient time.

Fig. 3.

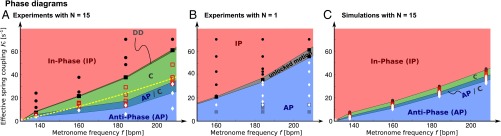
Phase diagrams from experiments for 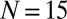(A) and 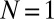(B) metronome(s) per swing and from numerical simulations with 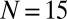metronomes (C) with metronome frequency f vs. effective spring coupling 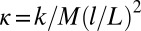. IP (red) and AP (blue) synchronization modes surround the chimera parameter region C (green) and the bistable AP/C region with chimeras and AP synchronization. Symbols represent data points (color shadings are guides only). Region C, centered around the resonance curve of the swings’ AP mode (yellow dashed line) defined by 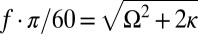, exhibits chimeras and other partially synchronized states. The bistable region AP/C exhibits chimera-like and synchronized AP states; DD represents a region where neither population synchronizes fully. For 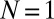, we find a similar region of unlocked motion, where the metronomes never synchronize. The phase diagram from numerical simulations for identical metronomes exhibits the same qualitative structure as the experiment, except that the width of region C is smaller (SI Text). Parameter space in experiments and simulations was sampled with varying spring coupling κ for metronome frequencies f = 138, f = 160, f = 184, and f = 208 bpm.

We have developed a mathematical model (SI Text, Fig. S5, and Table S1) that we simulated to corroborate our experimental findings and to test situations that cannot be achieved experimentally, such as large metronome populations or perfectly identical frequencies. 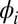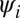The two swings are parametrized by their displacement angles from equilibrium positions, Φ and Ψ; the metronome pendula are parametrized by the displacement angles and , respectively. The metronomes are described as self-sustained oscillators with (harmonic) eigenfrequency ω, damping 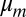with an amplitude-dependent nonlinearity 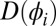due to the escapement (28, 29, 31):

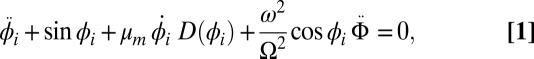where the terms represent (from left to right) pendulum inertia, gravitational force of restitution, damping, and the driving swing inertia, and the dots represent derivatives with respective to time 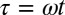. In turn, the swings of length L are described as harmonic oscillators with eigenfrequency 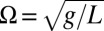and damping 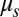. A swing is driven by the metronomes and the neighboring swing, to which it is coupled with a spring of strength κ:

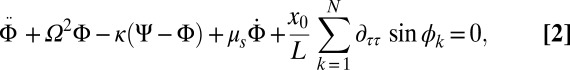where terms (from left to right) are swing inertia, force of restitution, spring coupling, friction, and the inertia summed over all metronomes on the same swing. Whereas κ determines the interpopulation coupling strength, the global coupling strength depends on the ratio of the metronome frequency and the swing eigenfrequency, 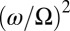. Using conditions similar to our experiments (but without frequency spread), chimeras obtained from simulations (Fig. 2 D and E) and the resulting phase diagram (Fig. 3C) agree qualitatively very well with experiments (quantitative differences are likely due to the ad hoc metronome model and potential discrepancies in parametrization as discussed in SI Text and Fig. S6). Bistability of fully synchronized (SS) and symmetry-breaking (SD and DS) states is a hallmark of the chimera instability (14), which is in distinct contrast to other symmetry-breaking scenarios mediated via supercritical transitions (13). It is therefore interesting to note that chimera states may coexist with AP synchronization modes in certain regions of the bifurcation diagram (Fig. 3 A and C).

Notably, when metronomes on each swing synchronize in an IP or AP mode, one envisages that the swings, together with the attached metronomes, collectively behave like two “giant” metronomes. These modes correspond to excitations of the eigenmodes of the swing pair with frequencies Ω (IP) and 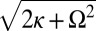(AP). Indeed, for 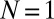metronome per swing (Fig. 1B), we find that due to momentum transfer, the swing strictly follows the motion of the attached metronome pendulum: The system behaves like Huygens’ experiment (i.e., with clocks replaced by metronomes). The metronomes settle into AP and IP synchronization modes for weak and strong coupling κ, respectively, as in modern reconstructions of Huygens’ setup (31). Additionally, we find a small region where unlocked motion is possible (Fig. 3B).

Generalizing Huygens’ experiment by adding internal degrees of freedom (i.e., metronomes) on each swing allows for much richer complex dynamics. A rich tapestry of complex states is uncovered (Fig. 4) in a transition from the AP to IP synchronization as the spring coupling κ is increased. In addition to chimeras, these include phase-clustered states (26): a “clustered chimera,” where oscillators are attracted to a clustered state but cannot quite attain frequency locking; a partial chimera, where the asynchronous population appears partially locked; and a quasiperiodic chimera (17, 18). The situation is aptly captured by the notion of “more is different” (32): Additional internal degrees of freedom open a door to unexpected complex behavior [i.e., unanticipated by mere extrapolation of simple collective behavior (32)]. Using Huygens’ term of the “odd sympathy of clocks” (1) to denote synchrony, the observed asymmetrical behavior might be described as an “antipathetic sympathy of clocks.”

Chimeras and other partly synchronous states emerge as a competition in an intermediate regime between IP and AP synchronization modes: As a result, both modes are destroyed, such that only one of the giant metronomes wins the tug-of-war and remains synchronous, whereas the other one is broken apart. The resulting asymmetry is characterized by the domination of one giant over the other [i.e., the synchronous population forces the asynchronous population (33), acting like an energy sink]. Remarkably, we find that the parameter region with chimera-like behavior is centered around the resonance curve related to the swings’ antiphase eigenmode (Fig. 3A): Near resonance, the fabric of uniform synchronization is torn.

Discussion

By devising a mechanical system composed of just two swings, a spring, and a number of metronomes (28), we have extended Huygen’s original experiment (1, 31) and demonstrated how chimeras emerge in the framework of classical mechanics. Recent experiments (26, 27) could only produce chimeras by exploiting sophisticated computer-controlled feedback, and the time delay of the coupling had to be carefully crafted in addition to tuning its strength; by contrast, in our realization, chimeras emerge generically using merely a spring, without any need to adjust parameters other than the coupling strength. Notably, our setup is composed of basic mechanical elements, such as inertia, friction, and spring rate, which have exact or generalized analogs in other areas, such as electronic (6, 34), optomechanical (35), chemical (7), and icrobial systems or genetic circuits (36). The model we propose shows that the complex synchronization patterns found in the experiments are described by elementary dynamical processes that occur in diverse natural and technological settings. This raises the question of whether chimeras may have already been observed in such systems but remained unrecognized as such. For instance, our model equations translate directly to recent theoretical studies of synchronization in power grids (37–39) and optomechanical crystals (40, 41). Consequently, as power grid network topologies evolve to incorporate growing sources of renewable power, the resulting decentralized, hierarchical networks (37) may be threatened by chimera states, which could lead to large-scale partial blackouts and unexpected behavior. On the other hand, we envision that multistable patterns of synchrony and desynchrony (19) can be exploited to build on-chip memories and computers based on arrays of micromechanical devices (35). We expect the physical mechanisms that we uncovered here will have important and far-reaching ramifications in the design and use of such technologies and in understanding chimera states in nature.

Materials and Methods

Experiments.

Two swings are suspended by four light hollow aluminum rods with a length of 50 cm (outer and inner diameters are 10 mm and 9 mm, respectively). The swings are attached to the rods via low-friction ball bearings to ensure smooth motion of the swings. The upper rod ends are attached in the same way on a large rigid support frame. The distance between the support frame and the board is set to 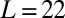cm. The motion of the two swings is constrained so that it can occur, to high precision, only in the x-y plane. Each swing is made of a 500-mm × 600-mm × 1-mm perforated aluminum plate. The total weight of each plate is 915 ± 4 g. Each swing is loaded with 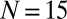metronomes with a weight of 94 g. The total weight of the swing and metronomes is 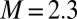kg. Two precision steel springs (Febrotec GmbH; spring constant k = 34 N/m) are firmly attached with clamps to the two adjacent swing rods (Fig. 1A) at a distance l above the pivot point. Adjusting the spring lever l changes the effective spring strength 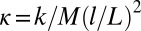. An experiment is started with a careful symmetry check of the system, by ensuring that the initial friction 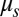is the same on both swings. The metronome’s nominal frequency is set to identical values 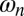. We then connect the two swings with the spring firmly set at a distance l above the pivot points. The motion of the metronomes and the swings is video-recorded under UV illumination using a Nikon D90 camera mounted with an 18- to 55-mm DX format lens. Each experiment is repeated with inverted roles of the swings (i.e., a DS experiment is followed by an SD experiment), such that the left-to-right symmetry is checked thoroughly.

Simulations.

Simulations were carried out with identical metronomes until a stationary state was reached (typically, ∼2,000 oscillation cycles). The phase diagram (Fig. 3C) was obtained by fixing the nominal metronome frequency f and then gradually increasing the effective spring rate κ (using similar parameters as in the experiment and 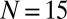metronomes per swing). For each parameter step, synchronous IP and AP states were continued quasiadiabatically, whereas simulations resulting in chimera-like states were reinitialized with randomized phases in one of the populations (SI Text).