Four dimensional deformable image registration using trajectory modeling

Abstract

A four-dimensional deformable image registration (4D DIR) algorithm, referred to as 4D local trajectory modeling (4DLTM), is presented and applied to thoracic 4D computed tomography (4DCT) image sets. The theoretical framework on which this algorithm is built exploits the incremental continuity present in 4DCT component images to calculate a dense set of parameterized voxel trajectories through space as functions of time. The spatial accuracy of the 4DLTM algorithm is compared with an alternative registration approach in which component phase to phase (CPP) DIR is utilized to determine the full displacement between maximum inhale and exhale images. A publically available DIR reference database (http://www.dir-lab.com) is utilized for the spatial accuracy assessment. The database consists of ten 4DCT image sets and corresponding manually identified landmark points between the maximum phases. A subset of points are propagated through the expiratory 4DCT component images. Cubic polynomials were found to provide sufficient flexibility and spatial accuracy for describing the point trajectories through the expiratory phases. The resulting average spatial error between the maximum phases was 1.25 mm for the 4DLTM and 1.44 mm for the CPP. The 4DLTM method captures the long-range motion between 4DCT extremes with high spatial accuracy.

1. Introduction

Four dimensional computed tomography (4DCT), developed for radiotherapy treatment planning, is an imaging technique that allows for the acquisition of time-varying 3D image sequences of the thorax through the respiratory cycle (Vedam et al., 2003; Pan et al., 2004; Ford et al., 2003). 4DCT images contain motion and acquisition related artifacts, are noisy due to low radiation dose acquisition techniques, and are acquired at lower spatial resolution. The resulting 4DCT image set also contains the respiratory-induced CT characteristics of the pulmonary parenchyma that reflect the regional changes in air content (Guerrero et al., 2006; Reinhardt et al., 2008). Since the lungs expand and contract non-uniformly with breathing, extracting quantitative motion or physiological information from 4DCT image sets requires deformable image registration (DIR).

Two categories of DIR algorithms exist divided by the data on which they operate, image content (e.g. image features, landmark-based, segmentation-based, etc.) or voxel properties (Maintz and Viergever, 1998). Li refers to this dichotomy as geometric versus intensity approaches and introduces a hybrid approach combining the two (Li et al., 2008). The DIR algorithms that utilize sets of registered landmark point pairs and interpolation schemes to determine the displacement vectors between image pairs are examples of image content based DIR (Schaefer et al., 2006; Kaus et al., 2007; Al-Mayah et al., 2008; Bookstein, 1989). Landmark pairs are determined from each of the two images either manually or using an automated method. An interpolation scheme is applied to the point pairs to determine the displacement of all voxels within the region (or organ) of interest. These point-based approaches have the advantage that they avoid the problem of solving large systems of equations, and are independent of the image content. However, manually selecting corresponding points is impractical for clinical use and automating their selection has thus far proven unreliable.

Deformable model methods are an example of intensity approaches in which a mathematical model is derived to represent the displacement between images in terms of a partial differential equation (PDE). PDEs analogous to fluid flow equations, compressible or incompressible, form the basis of the optical flow class of methods first described by Horn and Schunck (Horn and Schunck, 1981). Surveys of these methods are available in the literature (Barron et al., 1994; Beauchemin and Barron, 1995). Sarrut (Sarrut, 2006) surveys a number of DIR methods suitable for computing deformations between pairs of 3D CT images of the lungs. Compressible flow equations have been used in prior studies to model the apparent displacement of lung tissue due to respiratory motion in 4DCT images (Castillo, 2007; Li et al., 2008; Castillo et al., 2009a). It is known for optical flow algorithms that small displacements result in reduced spatial error versus large displacements due to many factors including the linear approximations made in their formulation (Barron et al., 1994). Approaches designed to work with larger displacements, such as the algorithm proposed by Lucas and Kinades (Lucas and Kanade, 1981), have greater accuracy with smaller displacements. Remeshing or down sampling the original images and smoothing to reduce the spatial frequency content of the images, are methods utilized to extend the displacement range to the displacements found between the maximum inhale/exhale 4DCT components. However, smaller displacements are present in the 4DCT components between the maximum inhale/exhale images and may be utilized advantageously.

A 4D DIR algorithm should simultaneously consider all phases of the 4D image set and constrain the spatiotemporal attributes of the displacement fields concurrently during the registration process. Klein et al used 4D DIR to sum 4D cardiac PET images into a single 3D motion compensated composite image volume (Klein and Huesman, 2002). They calculated the displacement from each image to a reference image using the incremental motion fields between adjacent time frames, then combined the incremental steps following the displacement trajectories to form long distance displacements. Their implementation alternated between optimization of incremental and long distance displacements in an ad hoc approach. Computational memory constraints limited Klein et al in their implementation to only minimize cost functions associated with the motion field between individual pairs of image volumes at any point in the calculation. Other approaches to 4D DIR have been reported. Sundar et al (Sundar et al., 2009) report on using the hierarchical attribute matching mechanism 4D DIR algorithm to estimate myocardial motion from cine MRI cardiac images. The original 4D image sequence was registered with a fictitious image sequence consisting of replicated end-diastolic images, the sequential net displacements from end-diastole were determined. Schreibmann et al utilized an automated 4D-4D DIR algorithm to find the spatiotemporal match between two 4D data sets, registering 4DCT to 4D cone beam CT and temporally separated 4DCT to 4DCT (Schreibmann et al., 2008).

For the evaluation of DIR algorithms, image similarity and expert determined landmarks point pairs have each been proposed as standard methods (Sharpe and Brock, 2008; Castillo et al., 2009b). However, investigators have found image similarity does not guarantee good spatial registration of the underlying anatomy (Crum et al., 2003; Shen and Davatzikos, 2002; Castillo et al., 2009b; Li et al., 2008). Similarity measures operate in the intensity domain and not in the spatial domain, thus, they do not evaluate the correctness of registration, the magnitude of registration errors, and the spatial distribution of errors. A number of recent studies have utilized sets of expert-determined landmark features to evaluate DIR spatial accuracy in the lung. The uncertainty of spatial error estimates was found to be inversely proportional to the square root of the number of landmark point pairs and directly proportional to the standard deviation of the spatial errors (Castillo et al., 2009b). The number of landmark points required to achieve a desired uncertainty in the spatial error estimate can be estimated from the desired uncertainty and the expected standard deviation between cases. Comparative evaluation based on fewer than the required validation landmarks results in misrepresentation of the relative spatial accuracy. For thorough and unbiased characterization of DIR spatial accuracy performance, it is necessary to ensure that the validation landmark sets adequately sample the volume of interest not only spatially, but also in terms of the clinically relevant variables that could potentially affect DIR output. A large number of landmark points also makes possible estimates of the average spatial error with sub-voxel accuracy.

In this study, we develop and validate a DIR approach based on the idea of recovering parameterized voxel trajectories which represent the paths taken by voxels though space as functions of time. The method utilizes the full set of expiratory phase 4DCT component image data simultaneously while performing the calculation, and inherently determines the displacement between the maximum exhale/inhale pair. The numerical implementation of the method approximates image intensity values on a variable grid by 3D cubic-splines (removing local discontinuities), which reduces the effects of image noise and artifacts in the calculation of local derivatives. Next, utilizing a cubic path assumption, the parameterized trajectory of each voxel is calculated by performing a nonlinear least squares fit to a local compressible flow equation. These values are retained only for those voxel that achieve a goodness of fit criteria. The displacements for those voxels that do not achieve the criteria are determined using neighboring values and moving least squares interpolation (Schaefer et al., 2006). The bulk of the computational workload is represented by a series of small, nonlinear least squares problems which are solved in parallel by a gradient-based optimization routine, utilizing the smooth b-spline image representations. We utilize manually selected large landmark point pairs to characterize the performance of our 4D DIR, referred to as 4D local trajectory modeling (4DLTM), and compare it with a component phase to phase (CPP) 3D DIR.

This paper is organized as follows: sections 2-4 describe the mathematical theory and implementation of our 4D DIR. Section 5 discusses the image acquisition and expert-determined landmark validation sets. Sections 6 and 7 provide the demonstration of improved spatial accuracy using anatomic pulmonary landmarks. The 4D method is compared with two 3D methods currently in use. Finally, our future work is discussed in section 7 and our conclusions in section 8.

2. Registration Across 4D Image Sets: Trajectory Modeling

DIR methods designed to register image pairs typically utilize modeling approaches based on an Eulerian coordinate system. This approach is natural given the voxel grid discretization inherent to image volumes, and the fact that a single image pair provides only a small amount of information from which to determine the registration. As such, the simplest general entity with the ability to encode the registration of a single voxel, that is, a three dimensional displacement vector, is the quantity most often sought after by current methods.

However, registration across a 4D image set requires knowledge of each voxel's spatial location at each time step in the sequence. The simplest approach for computing this type of registration is to apply any standard 3D image registration method to each temporally sequential image pair in the set. The result is one full displacement field for each image in the sequence. The mapping relating the position of any given voxels in the first image to its counterpart in the last image is then determined by “connecting the dots”, that is, by following the piecewise linear path given by temporally traversing the calculated displacement fields. The main strength as well as the main drawback to the sequential registrations approach is the decoupling of the 4D registration problem into several 3D registration problems. Though the decoupling reduces the complexity of the full 4D problem, the approach fails to utilize all available temporal information as a whole. Consequently, errors in the registration at any particular time step result in a deviation from the correct trajectory, and propagate through the remaining time steps.

Registration across a 4D image set is essentially the recovery of each voxel's spatial trajectory as a function of time. Within this context, it is natural to adopt a Lagrangian coordinate framework.

The temporal image set we wish to register is assumed to be a collection of snap shots taken from an unknown density function:

$$\rho (\mathbf{\text{x}}(\xi ,t),t)\in ℝ,t\in [0,1],\mathbf{\text{x}}(\xi ,t)\in \Omega ,$$ (1)

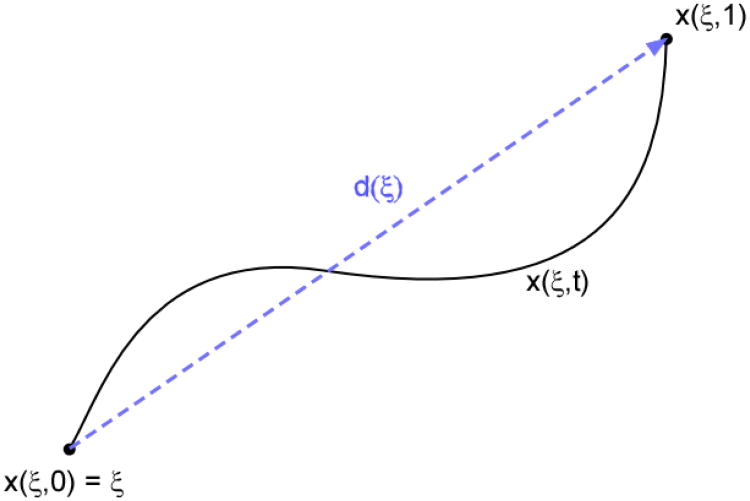
where x(ξ, t)∈ ℝ³ is the Lagrangian coordinate of the particle located at ξ for t = 0, and Ω is the region of interest captured by the image set. Specifically, the function x(ξ, t) represents the trajectory of the particle originally located at ξ, through Ω as a function of time (Figure 1). Naturally, knowledge of the path implies knowledge of the displacement vector d(ξ):

Figure 1. Displacement versus Lagrangian path.

The Lagrangian coordinate of the particle located at ξ for t = 0, is given by the function x(ξ, t), which represents the trajectory of the particle originally located at ξ, through Ω as a function of time. The displacement vector, d, is the vector difference x(ξ, t_final) − x(ξ, 0).

$$\begin{array}{l}\mathbf{\text{x}}(\xi ,0)=\xi ,\\ \mathbf{\text{x}}(\xi ,1)=\mathbf{\text{d}}(\xi )+\xi .\end{array}$$

The goal now is to develop an image registration framework based on recovering the path x(ξ,t). The first step in this process is identifying a parametric class of functions with the capacity to capture the true physical behavior of thoracic 4DCT voxel motion, while at the same time remaining simplistic enough for the associated parameter recovery to remain computationally tractable.

As stated earlier, image pair registration is based on calculating displacement vectors. Accordingly, most existing DIR methods assume voxel trajectories are straight lines:

$$\mathbf{\text{x}}(\xi ,t)=t\mathbf{\text{d}}(\xi )+\xi .$$ (2)

However, such a restricted motion may not be appropriate for modeling thoracic voxel motion (see Figure 2). On the other hand, 4DCT image acquisition inherently is noisy and results in image artifacts due to respiratory variation. There is also the potential to over fit the trajectories when using high order polynomials. Over fitting in the presence of image noise and artifacts can cause physically nonrealistic trajectories (Figure 3). The choice of the parameterization also depends on the amount of temporal image information available. For example, given only an image pair, the linear path/displacement approach is appropriate since image information at intermediate time steps is not available, and a high order parameterization cannot be fully utilized. In the best case scenario where the exact position of the voxel is known at each time step, a well-posed polynomial curve fitting to the position data requires that the number of time steps be greater than the degree of the polynomial space.

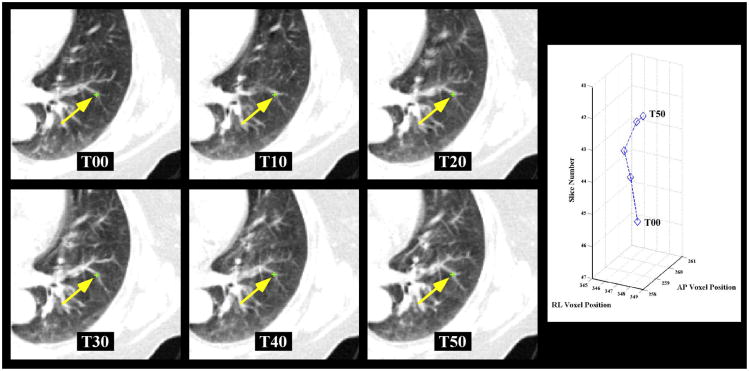
Figure 2. 4D Landmark point trajectories.

4D landmark point sets were utilized to test the adequacy of the trajectory model and spatial accuracy of the DIR algorithms studied. a) The 4DCT image sets used in this study consisted of the 6 images spanning the expiratory phases from maximum inhalation (T00) to maximum exhalation (T50). 75 landmark point sets were identified on 10 cases as shown for the example point. Each 4D landmark point was identified (yellow arrow) for phases T00 through T50 as shown. b) A sample 4D trajectory of the landmark point depicted is plotted. Note that the T30 and T40 points overlay each other.

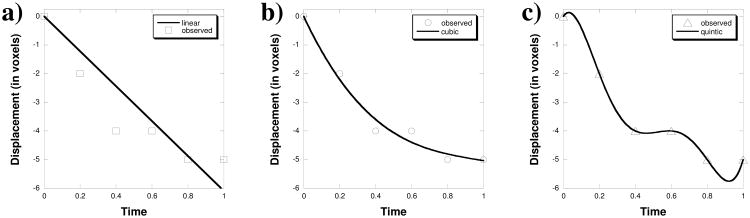
Figure 3. Trajectory modeling with polynomials.

4D landmark point sets were utilized to test the adequacy of the trajectory modeling across the 6 images spanning the expiratory phases (from T00 to T50). a) A linear model of the z-displacement is shown versus a sample landmark point displacement. b) A cubic model of the z-displacement is shown versus a sample point. c) A quintic (5^th order polynomial) model of the z-displacement is shown versus a sample landmark point displacement.

In this study, we will consider general polynomials up to degree N for voxel trajectory modeling, where N + 1 is the number of 3D images in the 4D set. Representing the motion of each component with a one dimensional N^th order polynomial parameterizes x(ξ,t) with 3N coefficients.

$$\mathbf{\text{x}}(q;\xi ,t)=\left[\begin{array}{c}{q}_1{t}^N+q_2{t}^{N-1}\dots +q_{N}t\\ q_{N+1}{t}^N+q_{N+2}{t}^{N-1}\dots +q_{2N}t\\ q_{2N+1}{t}^N+q_{2N+2}{t}^{N-1}\dots +q_{3N}t\end{array}\right]+\xi ,$$ (3)

Note that linear paths (2) are contained within the full space of paths described by equation (3).

3. Trajectory Recovery via Compressible Flow

In addition to the voxel trajectory model, as is the case for all DIR methods, an image intensity model is required to relate the intensity of a voxel at the initial time step to its intensity at all other times. The simplest and most commonly employed models are based on the assumption that each voxel's intensity is constant with respect to time:

$$\rho (\mathbf{\text{x}}(\xi ,t),t)=\rho (\mathbf{\text{x}},0)=\text{constant},$$ (4)

an idea first proposed by Horn and Schunck for the original optical flow method. For instance, coupling the constant intensity assumption with linear path trajectories reduces equation (4) to the familiar intensity matching criteria:

$$\rho (\mathbf{\text{x}}+\mathbf{\text{d}}(\mathbf{\text{x}}),1)=\rho (\mathbf{\text{x}},0).$$ (5)

The original optical flow method of Horn and Schunck (Horn and Schunck, 1981) utilizes the partial differential equation obtained by differentiating equation (4) with respect to time, commonly referred to as the optical flow equation:

$$\frac{d\rho }{\mathit{\text{dt}}}={\rho }_t+\nabla \rho \cdot \mathbf{\text{v}}=0,$$ (6)

where v(x) is voxel velocity.

However, a more general assumption is that mass is conserved:

$${\int }_{\Omega }\rho (\mathbf{\text{x}},0)d\Omega ={\int }_{\Omega }\rho (\mathbf{\text{x}},1)d\Omega ={\int }_{\Omega }\rho (\mathbf{\text{x}},t)d\Omega ,t\in (0,1).$$

This property is modeled by the continuity (conservation of mass) equation:

$${\rho }_t+\nabla \rho \cdot \mathbf{\text{v}}+\rho \text{div}(\mathbf{\text{v}})=0.$$ (7)

and is derived elsewhere in the literature (Leveque, 2002; Song and Leahy, 1991). Substituting the optical flow equation (6) into the conservation of mass equation (7) implies that the velocity field is divergence free:

$$\text{div}(\mathbf{\text{v}})=0,$$

or equivalently, that the flow modeled by equations (5) and (6) is incompressible, whereas equation (7) represents compressible flow. Though slightly more complicated, intensity models based on equation (7) have the virtue of accounting for voxel intensity variations without a priori manipulation of the data (as in (Sarrut et al., 2006)), and are suitable for a more general class of registration problems.

3D Optical flow DIR methods based on partial differential equations (6) or (7) determine the registration by computing a velocity field describing the apparent motion depicted in an image pair. Assuming the time step between image pairs to be unity, the voxel velocity vector is equivalent to the displacement vector. In the case of trajectory modeling, a compressible flow model given in terms of x(t) is obtained by converting equation (7) into its integrated form.

Substituting equation (6) into equation (7) results in the ordinary differential equation:

$$\frac{d\rho (\mathbf{\text{x}}(\xi ,t),t)}{\mathit{\text{dt}}}=-\rho (\mathbf{\text{x}}(\xi ,t),t)\text{div}(\mathbf{\text{v}}(\xi ,t)),$$

the solution of which is given by:

$$\rho (\mathbf{\text{x}}(\xi ,t),t)=\rho (\xi ,0)e^{-{\int }_0^t\text{div}(\mathbf{\text{v}}(\mathbf{\text{x}}(\xi ,\tau ))d\tau }$$ (8)

as described in Corpetti et al (Corpetti et al., 2002). Note that for incompressible flow, the velocity field is divergence free and equation (8) is equivalent to equation(4).

We decouple the integral of the divergence from the exponential by applying the natural log to both sides of the equation, which yields our compressible flow, voxel trajectory DIR model for a given initial voxel location ξ:

$$\mathit{\text{R}}(\xi ,t)=0,\text{for all}t\in [0,1],$$ (9)

where

$$\mathit{\text{R}}(\xi ,t)\equiv \text{ln}(\rho (\mathbf{\text{x}}(\xi ,t),t))+\left[{\int }_0^t\text{div}(\mathbf{\text{v}}(\mathbf{\text{x}}(\xi ,\tau ))d\tau \right]-\text{ln}(\rho (\xi ,0)).$$

For the case where x(t) is restricted to a class of functions parameterized by a vector q, formulation (9) includes the parameterization variables:

$$R(q,\xi ,t)=\text{ln}(\rho (\mathbf{\text{x}}(q;\xi ,t),t))+\left[{\int }_0^t\text{div}(\mathbf{\text{v}}(\mathbf{\text{x}}(q;\xi ,\tau ))d\tau \right]-\text{ln}(\rho (\xi ,0))=0.$$ (10)

Equation (9) defines the relationship between the initial intensity of a voxel ξ and its intensity at any time t, under the assumption that mass is conserved. However, given the inherent noise typical of 4DCT and the density fluctuations caused by perfusion, equation (10) should not be enforced as a hard constraint. Rather, describing x(q; ξ, t) as a least squares fit to equation (9) is more appropriate:

$$\underset{q}{\text{min}}{\int }_0^1\mathit{\text{R}}{(q,\xi ,t)}^2\mathit{\text{dt}}.$$ (11)

In general, equation (11) does not provide enough information to uniquely determine x(q; ξ,t). Moreover, equation (11) only depends on the image information located on the path x(ξ,t). Augmenting the formulation to incorporate local neighborhood information improves the model and results in a well-posed, nonlinear least squares problem, the solution of which is the solution to the trajectory recovery problem for the initial voxel location ξ:

$$\underset{q}{\text{min}}{\int }_{\Omega }\delta (\xi ,\gamma )({\int }_0^1\mathit{\text{R}}{(q,\gamma ,t)}^2\mathit{\text{dt}})d\gamma ,$$ (12)

where δ_s(ξ, γ) is a Gaussian centered on ξ with standard deviation s, evaluated at γ.

Calculating a parameterized trajectory for the initial point ξ based on formulation (12), utilizes all available spatial and temporal image information from a local neighborhood centered on ξ. In addition, the Gaussian δ acts as a window function that easily allows for the development of a local DIR methodology where the full DIR is calculated by solving a series of smaller, simpler registration problems, similar to the Lucas and Kanade method (Lucas and Kanade, 1981) and the linear local compressible method described in Castillo et al (Castillo et al., 2009a).

4. Numerical Implementation

Our numerical implementation is based on recovering polynomial path trajectories (3) from 4D image sets by applying a Levenberg-Marqurdt, gradient-based, nonlinear least squares solver to a discretized version of problem (12) for a subset of all voxel locations chosen from a coarse grid. A full DIR is computed from the coarse grid via moving least squares interpolation (Schaefer et al., 2006). In this way, the registration is computationally tractable despite the size of thoracic 4DCT image sets, and the methodology easily lends itself to an efficient, parallel implementation.

However, two key issues must be addressed with this approach. First, the gradient based optimization routine requires image information from non-grid locations. Consequently, a smooth, continuous representation of each image in the 4D set is required. Second, due to the nonlinear nature of the formulation, it is possible for the optimization routine to get stuck in local minima. This problem is alleviated by supplying the optimization routine with a dependable initial guess of the solution. For this purpose, we have also implemented a pairwise, displacement recovery method based on (12). The initial guess for the cubic problem is then the piecewise linear trajectory provided by applying the pairwise algorithm to each temporally sequential image pair.

4.1. Image Representation

The image set we wish to register is assumed to contain snapshots, ρ_k(x), of the unknown density function ρ(x(t),t):

$${\rho }_k(\mathbf{\text{x}})=\rho (\mathbf{\text{x}},t_k),k=0,1,\dots ,n,t_0=0,t_n=1.$$ (13)

A smooth representation of the image can be obtained via interpolation. Cubic b-splines are a popular choice for image interpolation due to their inherent smoothness properties and the minimal computational overheard resulting from their compact support. Thus, for each image in the set ρ_k, we compute an associated cubic b-spline representation P_k.

4.2. Trajectory Recovery for General Parameterization

The discretized analog to problem (12) is based solely on the discretization inherent to the image set. Specifically, for a particular voxel ξ_j, the discretized trajectory formulation is given by:

$$\underset{q}{\text{min}}\sum _{{\xi }_i\in {\Omega }_j}{w}_i(\sum _{k=1,2,\dots n}\mathit{\text{R}}{({\xi }_i,q,t_k)}^2),$$ (14)

where Ω_j is an isotropic box centered on ξ_j, and w_i is computed from the Gaussian distribution δ_s. The lengths of the box are chosen to be equal to 2/3 the standard deviation s. Thus, the contributions from voxels outside Ω_j are negligible.

Evaluation of the image terms present in equation (10) is straightforward given the b-spline images P_k. The difficulty lies in calculating

$${\int }_0^t\text{div}(\mathbf{\text{v}}(\mathbf{\text{x}}(q;\xi ,\tau )))d\tau .$$ (15)

For fixed t, the Eulerian position of the particle ξ is given by g = x(q; ξ,t) and

$$\text{div}(\mathbf{\text{v}}(\mathbf{\text{g}},t))=\frac{\partial {\nu }_1(\mathbf{\text{g}},t)}{\partial x}+\frac{\partial {\nu }_2(\mathbf{\text{g}},t)}{\partial y}+\frac{\partial {\nu }_3(\mathbf{\text{g}},t)}{\partial z}.$$

Approximating the divergence with forward finite differences yields:

$$\text{div}(\mathbf{\text{v}}(\mathbf{\text{g}},t))\approx {\nu }_1(\mathbf{\text{g}}+{\mathbf{\text{e}}}_1,t)-{\nu }_1(\mathbf{\text{g}},t)+{\nu }_2(\mathbf{\text{g}}+{\mathbf{\text{e}}}_2,t)-{\nu }_2(\mathbf{\text{g}},t)+{\nu }_3(\mathbf{\text{g}}+{\mathbf{\text{e}}}_3,t)-{\nu }_3(\mathbf{\text{g}},t),$$ (16)

where e_i is the unit coordinate vector. Since the path x(ξ,t) is assumed to have a simple parameterized form, the values for the velocity components at the location g are easily obtained by differentiating x(ξ,t) with respect to time. However, approximation (16) cannot be fully localized without removing its dependence on the velocity information from neighboring voxels, namely the ν_i(g + e_i) terms.

The introduction of an auxiliary scalar function φ(t), accounting for the velocity information from neighboring voxels at time t, is the cost of the localization:

$$\text{div}(\mathbf{\text{v}}(g,t))\approx \varphi (t)-{\nu }_1(g,t)-{\nu }_2(g,t)-{\nu }_3(g,t).$$ (17)

Substituting the divergence approximation (17) and the b-spline image representations into the compressible flow trajectory formulation (10) gives:

$$\mathit{\text{R}}(\xi ,q,t_k)\approx \text{ln}({\mathit{\text{P}}}_k(\mathbf{\text{x}}(q;\xi ,t_k)))-\text{ln}({\mathit{\text{P}}}_0(\xi ,0))+{\int }_0^{t_k}[\varphi (q_{\varphi };t)-{\nu }_1(\mathbf{\text{x}}(q;\xi ,\tau )),-{\nu }_2(\mathbf{\text{x}}(q;\xi ,\tau ))-{\nu }_3(\mathbf{\text{x}}(q;\xi ,\tau ))]d\tau .$$ (18)

Note that the development of a numerical method based on (18) requires that the auxiliary function φ(t) also be parameterized by a vector variable q_φ. For the case where polynomials are utilized to model the trajectory components as well as the auxiliary function, the integral can be computed analytically and reduced to an inner product between the unknown parameter vector

$$\widehat{q}=\left[\begin{array}{c}{q}_{\varphi }\\ q\end{array}\right],$$

and a vector a_k containing multiples of powers of t_k. Thus, for the polynomial case, the general formulation (12) reduces to the following nonlinear least squares problem:

$$\underset{\widehat{q}}{\text{min}}\sum _{{\xi }_i\in {\Omega }_j}{w}_i(\sum _{k=1,\dots n}{[\text{ln}({\mathit{\text{P}}}_k(\mathbf{\text{x}}(q;{\xi }_i,t_k)))+a_k^T\widehat{q}-c_i]}^2).$$ (19)

where c_i =ln(P₀(ξ_i)).

4 .3 Linear Path Recovery for Pairwise Image Registration

For a linear path trajectory x(ξ,t) = td(ξ), the associated velocity of x(ξ,t) is constant with respect to time and equivalent to the displacement vector d. Moreover, for a pairwise DIR there are only two time steps to consider, t = 0 and t = 1. In this case, knowledge of the auxiliary function φ is only required at t = 1, and can therefore be considered an unknown constant as opposed to an unknown function. Applying these conditions to problem (18) results in the linear path compressible flow problem:

$$\underset{\widehat{\mathbf{\text{d}}}}{\text{min}}\sum _{{\xi }_i\in {\Omega }_j}{w}_i{(\text{ln}({\mathit{\text{P}}}_1({\xi }_i+\mathit{\text{d}}))+a^T\widehat{\mathit{\text{d}}}-c)}^2,$$ (20)

with a = (1,−1,−1,−1)^T, d̂ = (φ,d₁,d₂,d₃)^T, and c = P₀(ξ). The pairwise linear path registration of the voxel ξ is then represented by the solution to problem (20). Problem (20) is a standard nonlinear least squares problem, for which many solvers are available. Given the simplicity of the objective function and the b-spline image representation, gradient information can be easily calculated analytically and supplied to the solver.

4.4 Polynomial Path Recovery for Registration Across a 4D Image Set

N^th degree polynomial trajectory recovery is based on the nonlinear least squares problem (19) and the parameterization q given by the trajectory model (3). The auxiliary scalar function φ (t) is also parameterized as an N^th degree polynomial:

$$\varphi (q_{\varphi };t)=[t^N{t}^{N-1}\cdots t1]\cdot q_{\varphi },q_{\varphi }\in {ℝ}^{N+1}.$$ (21)

Thus, recovering the trajectory for a given voxel ξ requires solving problem (19) for the 4N +1 total unknowns parameters contained in the associated q̂ corresponding to the N^th degree polynomial path parameterization. Given the nonlinear nature of problem (19), it is possible for optimization routines to converge to local minima. This issue can be addressed by supplying a dependable initial guess to the optimization routine. The piecewise linear path given by solving problem (20) for each temporally sequential image pair serves as this initial guess. Our polynomial path trajectory recovery method software is written in C++, utilizing the Levenberg-Marquardt method implementation provided by the MINPACK FORTRAN library to solve problem (20).

The full 4DLT registration method solves problem (19) for each voxel on a coarse grid subset of all image voxels. The magnitude of the objective function is monitored after convergence of the optimization routine to ensure the quality of the solution. If the optimization routine converges to an unacceptable local minimum, the solution for that voxel is disregarded. A displacement field relating the voxels in the first image to those in the last image is extracted from the trajectory recovery by first evaluating x(q; ξ, 1) for each voxel in the coarse grid subset. The “holes” in the coarse grid solution caused by local minima are then filled in by a moving least squares interpolation utilizing information from voxels with reliable solution to problem (19). A full resolution, dense displacement field is then created form the coarse grid via standard interpolation, such as trilinear or moving least squares.

5. Materials and Methods

5.1. 4DCT image data

Ten patients, treated for thoracic malignancies (esophagus or lung cancer) in the Department of Radiation Oncology at The University of Texas M. D. Anderson Cancer Center, who received 4DCT imaging as part of their treatment planning were selected from the patient database for this retrospective study. The patient identifiers were removed in accordance with the retrospective study protocol approved by our Institutional Review Board (RCR 03-0800). Each patient had undergone a treatment planning session where a 4DCT image of the entire thorax and upper abdomen was obtained at 2.5-mm slice spacing on a PET/CT scanner (Discovery ST; GE Medical Systems, Waukesha, WI) with a 70-cm bore (Figure 2). The images had been acquired with the patients in the supine position with normal resting breathing. The 4DCT acquisition technique using the respiratory signal from the Real-Time Position Management Respiratory Gating System (Varian Medical Systems, Palo Alto, CA) has been previously described (Pan et al., 2004). Five of the 4DCT image sets (labeled patients 1 – 5 below) were cropped to include the entire ribcage and sub-sampled in the transverse plain (Castillo et al., 2009b). The patient and 4D image characteristics of the ten cases utilized in this study are given in table 1.

Table 1.

Patient characteristics for the 10 test cases.

Patient	Resp. period (sec)	Tidal volume (mL)	Malignancy	Tumor-location	GTV (mL)	Image Dimension	Voxel Dimension (mm)
1	∼2.4	191	Eso ca.	Mid eso	30.2	256 × 256 × 94	0.97 × 0.97 × 2.50
2	∼4.4	423	Eso ca.	Distal eso	25.9	256 × 256 × 112	1.16 × 1.16 × 2.50
3	∼3.5	406	Eso ca.	GE jxn	41.4	256 × 256 × 104	1.15 × 1.15 × 2.50
4	∼5.3	412	Eso ca.	Distal eso	65.6	256 × 256 × 99	1.13 × 1.13 × 2.50
5	∼3.3	269	Eso ca.	GE jxn	112.9	256 × 256 × 106	1.10 × 1.10 × 2.50
6	∼4.0	673	SCLC	LLL	132	512 × 512 × 128	0.97 × 0.97 × 2.50
7	∼5.4	635	Eso ca.	GE jxn	16.7	512 × 512 × 136	0.97 × 0.97 × 2.50
8	∼5.1	897	NSCLC	LUL	2.24	512 × 512 × 128	0.97 × 0.97 × 2.50
9	∼2.9	255	Eso ca.	Distal eso	54.1	512 × 512 × 128	0.97 × 0.97 × 2.50
10	∼3.4	431	NSCLC	RLL	211.1	512 × 512 × 120	0.97 × 0.97 × 2.50

Abbreviations: Eso ca. = esophagus cancer; SCLC = small cell lung cancer; NSCLC = non-small cell lung cancer; LLL = left lower lobe; LUL = left upper lobe; RLL = right lower lobe; GE jxn = gastro-esophageal junction; GTV = gross tumor volume. Volumes presented in milliliters (mL).

5.2. Displacement test data

Measurements of DIR spatial accuracy for each case were obtained using manually identified sets of prominent anatomical landmark feature pairs identified across multiple consecutive respiratory phase images, from the maximum inhalation phase (designated T00) to the maximum exhalation phase (designated T50). A Matlab-based software interface named APRIL (Assisted Point Registration of Internal Landmarks), previously described (Castillo et al., 2009b), was utilized to facilitate manual selection of landmark feature pairs between volumetric images. Basic features of the software include separate window and level settings for each display, visualization of equivalent voxel locations in the orthogonal plains, and interactive tools for segmentation of lung voxels from the image data. To determine corresponding feature points the user must manually designate the feature correspondence via mouse click on the target image. For all cases, a reference set of pulmonary landmark feature pairs was generated using the maximum inhale/exhale component phase images from the 4DCT set. No implanted fiducials or added contrast agents were used to aid in the selection of landmark features, which typically included vessel and bronchial bifurcations. Source feature points were selected systematically on the 10 test image pairs by an expert in thoracic imaging, beginning at the apex of the lung.

For the first 5 test image pairs the expert selected >10 features points for each lung per axial slice, these images were described in our prior publication (Castillo et al., 2009b) and are available on the Internet (www.dir-lab.com). For the second 5 image pairs, points were selected with an initial goal of >3 feature points for each lung per axial image slice. This approach ensured the collection of >1100 validation point pairs for the first 5 cases and >400 for the subsequent 5 cases. Following feature selection for a given case, all landmark pairs were visually reviewed by the primary reader a second time and the location adjusted on the exhale image if necessary. The verification step was required before the initial registration process, performed by the primary reader, was considered complete. The points were then used to test the spatial accuracy of DIR algorithms for this study. For each of the 10 cases a subset of 75 landmark features were propagated across the expiratory phases T00 to T50, as shown in the example in Figure 2.

5.3. Polynomial trajectory modeling

The 4DLTM algorithm is applied to the 10 image cases using 1st (linear) through 5th order (quintic) polynomial trajectory models and evaluated for spatial accuracy over the landmarks as reported earlier (Castillo et al., 2009b). The spatial accuracy of the 4DLTM algorithm, using the 5 differing polynomial trajectory models, was compared using the Friedman rank sum test. This nonparametric test was used to test the equality of the mean error of the five methods. Next, a rank based pair-wise comparison is made between the best (and worse) performing method and the remaining methods as well. 4DLTM with cubic trajectory models is employed for the formal spatial accuracy comparison with the component phase-to-phase registration approach.

5.4. DIR spatial accuracy assessment

The registration spatial error is defined as the difference between the calculated output and the designated reference standard displacements. In this case, large sets of manually delineated feature pairs serve as the primary validation data. The observer selects at the voxel level, creating integer displacements between landmark points. To make the evaluation of manual and calculated landmark registration equivalent, the comparison with calculated positions is performed on the same integer grid. This is achieved simply by rounding the final displaced position of each coordinate of interest to the nearest integer. As described in Castillo et al (Castillo et al., 2009b), we are able to estimate the average error of each registration algorithm with sub-voxel accuracy due to the large measurement sample sizes. The mean errors determined from the rounded and floating point DIR positions will, in a statistical sense, likely be similar. This is due to the fact that on average approximately equal quantities of test voxels are rounded toward their respective reference target position as are rounded away.

Point registration error was quantified as the three-dimensional Euclidean distance between target voxels in the primary data set, and those determined by applying the calculated DIR transformation to the corresponding source feature location. Mean registration error and corresponding standard error were determined for both DIR algorithms over the set of validation landmarks, providing a global measure of spatial accuracy performance for each case. Mean errors were also determined over the combined set of expert-determined feature points for all cases. Additionally, errors were assessed separately for individual right-left (RL), anterior-posterior (AP), and superior-inferior (SI) component directions.

5.5. Statistical methods

The primary endpoint of this study is the comparison of the 4DLTM and the CPP algorithms mean spatial errors, where the spatial errors are the differences between the calculated and reference displacements. Summary statistics are provided for individual RL, AP, and SI component displacements, the 3D Euclidean displacement, and the associated spatial errors. Other statistical analyses will be carried out as appropriate. Respiratory parameters for the test cases are also summarized. Continuous variables (lung volumes, tidal volume, and displacements) were summarized in the form of mean (SD, range). Categorical variables (tumor location, and tumor histology) were summarized in the form of frequency tables. The Wilcoxon rank sum test was used to compare the mean spatial errors between the two DIR algorithms for each, and across all 10 cases. All tests were two-sided with p-values ≤ 0.05 considered significant. Statistical analysis was performed with SAS version 9 (SAS Institute, Cary, NC) and S-Plus version 7 (Insightful Co., Seattle, WA).

6. Results

6.1. 4DCT image properties

The patient clinical and 4DCT characteristics of the 10 test cases utilized in this study are given in table 1. Respiratory periods were estimated directly from the RPM respiratory trace data acquired for each patient at the time of image acquisition. Estimates are seen to range from ∼2.4 - ∼5.4 sec., suggesting a variable cross-section of breathing patterns included in the reference data. Tidal volumes were similarly approximated and obtained from binary mask images of the segmented lung voxels. For each case, lung masks were generated based on three-dimensional connectivity and global histogram thresholds of [-1000 -250] HU. Visible airway and esophagus structures were removed from all masks prior to tidal volume calculation. As described above, the reference data are comprised of both sub-sampled and full resolution clinical patient images.

Characteristics of the reference landmark data are given in table 2. For the first 5 test image pairs the expert aimed to select ≥10 features points for each lung per axial slice; these images were described in our prior publication (Castillo et al., 2009b) and are available on the Internet (www.dir-lab.com). For the second 5 images pairs, points were selected with an initial goal of ≥3 feature points for each lung, per axial image slice (Figure 4a). This approach resulted in the collection of 8832 individual reference landmark pairs between the maximum inhale and exhale component phase images for the set of reference image sets. Estimates of landmark reproducibility were obtained by repeat registration of uniform subsets of T00 landmark positions for each case. For patient cases 6 -10, three independent observers manually registered subsets of 150 of the primary landmark features. Each observer performed the manual registration utilizing the APRIL software, without prior knowledge of the original registration performed by the primary reader. Mean repeat registration error (and pooled standard deviation) for the combined set of observers ranged from 0.70 (0.99) - 1.13 (1.27) mm. Average (and standard deviation) displacement of the reference landmark features varied substantially among the reference cases, ranging from 4.01 (2.91) - 15.16 (9.11) mm.

Table 2.

Summary of manual displacements for the 10 test cases.

Patient	Number of landmarks	Intraobserver Error (mm)	Average displacements (Standard deviation) (all in mm)
			3D-Euclidean	Right-left	Anterior-posterior	Superior-inferior
1	1280	0.85 (1.24) mm	4.01 (2.91)	0.58 (0.62)	0.67 (0.79)	3.68 (3.04)
2	1487	0.70 (0.99)	4.65 (4.09)	0.72 (0.85)	0.72 (0.88)	4.09 (4.37)
3	1561	0.77 (1.01)	6.73 (4.21)	1.17 (1.05)	1.28 (1.23)	6.10 (4.49)
4	1166	1.13 (1.27)	9.42 (4.81)	0.94 (1.21)	1.42 (1.22)	8.98 (5.04)
5	1268	0.92 (1.16)	7.10 (5.15)	0.86 (0.96)	1.74 (1.66)	6.30 (5.45)
6	419	0.97 (1.38)	11.10 (6.98)	2.15 (1.89)	2.53 (2.10)	10.21 (6.97)
7	398	0.81 (1.32)	11.59 (7.87)	1.28 (1.17)	2.13 (1.54)	10.85 (8.29)
8	476	1.03 (2.19)	15.16 (9.11)	2.29 (1.72)	3.78 (3.25)	13.62 (9.71)
9	342	0.75 (1.09)	7.82 (3.99)	1.25 (1.02)	2.98 (1.93)	6.45 (4.51)
10	435	0.86 (1.45)	7.63 (6.54)	0.93 (0.91)	1.90 (1.91)	6.97 (6.60)

Displacements presented in millimeters (mm) with pooled standard deviations (SD) in parentheses.

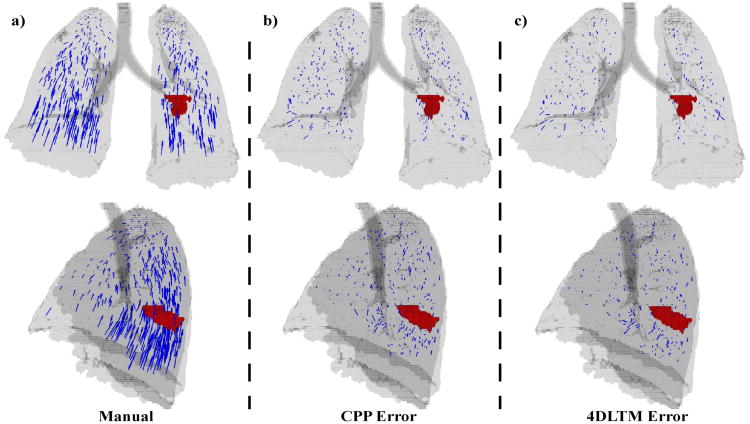
Figure 4. Landmark points and DIR errors.

Manually identified landmark point sets were utilized to compare the spatial accuracy of the DIR algorithms studied. a) 419 manually determined displacement vectors are shown in anterior (top row) and lateral (bottom row) projection for a sample case. The lung silhouette is in gray and the gross tumor volume is shown in red. Residual error vectors are also shown for b) 4DLTM and c) CPP DIR algorithms. Each error vector points from the manually delineated feature location in the target image to that determined from the respective DIR transformation.

6.2. Polynomial trajectory modeling

The 4DLTM algorithm was applied to the ten 4DCT image test cases using 1st (linear) through 5th order (quintic) polynomial trajectory models and evaluated for spatial accuracy over the 8832 landmark points. The resulting 3D Euclidean mean spatial errors and standard deviations are summarized in Table 3. The 5 models were compared using the nonparametric Friedman rank sum test to determine if there was a difference in the mean spatial error between the five polynomial models. A significant difference was found (p = 6.36×10^-6) between the five models. Upon performing a rank based pair-wise test the linear model performed worse than the other four models. There was no difference between the remaining four models. We chose the third order (cubic) polynomial model for further evaluation as a compromise between added flexibility versus simplicity of the model. Therefore, the cubic model was implemented for the formal spatial accuracy comparison with the component phase-to-phase registration approach.

Table 3.

Polynomial trajectory model spatial accuracy.

	Polynomial Order
	linear	quadratic	cubic	quartic	quintic
3D Euclidean Error p-value*	1.89 (1.76) 6.36 × 10-6	1.27 (1.41)	1.25 (1.43)	1.23 (1.42)	1.22(1.42)

Mean errors presented in millimeters (mm) with pooled standard deviations (SD) in parentheses.

^*Tested using the nonparametric Friedman rank sum test.

6.3. Performance of the CPP algorithm

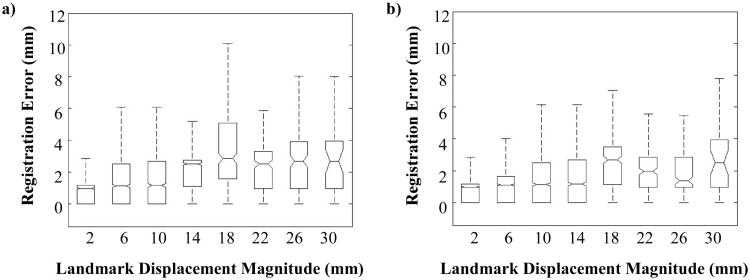
A qualitative evaluation of the CPP algorithm for one case is illustrated by the error vectors shown in Figure 4b, which demonstrates the spatial distribution of the errors. Quantitative spatial accuracy performance of the CPP algorithm is summarized in table 4. For the set of ten reference cases, mean (and standard deviation) three-dimensional Euclidean magnitude registration errors ranged from 0.99 (1.12) - 1.96 (2.33) mm. Mean magnitude component errors were consistently largest in the SI direction, ranging from 0.49 (1.02) - 1.35 (1.62) mm. Over the combined set of 8832 reference measurements, all mean component errors were less than 1 mm, while the weighted 3D Euclidean magnitude error (and pooled standard deviation) was 1.44 (1.54) mm. Figure 5a shows a box plot of registration error versus landmark displacement magnitude for the set of reference point pairs. Displacement magnitudes were binned into 4 mm increments, with the plotted data shown overlain each bin center. Notches indicate the median of error measurements within the associated bin, while the box edges reflect the 25^th and 75^th percentiles. ‘Whiskers’ are shown extending to the most extreme data points not considered outliers, where outlier points are categorized as those measurements e_i in the range e_i < q₁ − 1.5(q₃ − q₁) or e_i > q₃ + 1.5(q₃ − q₁), with q₁ and q₃ corresponding to the 25^th and 75^th percentiles, respectively. Two-tailed Spearman rank correlation was calculated to quantify correlation between registration error and landmark displacement magnitude, with ρ = 0.3297 (p-value = 0).

Table 4.

Spatial accuracy performance of the two algorithms CPP and 4DLTM.

Patient	Number of landmarks	Algorithm	Average spatial error of image registration
			3D-Euclidean	Right-left	Anterior-posterior	Superior-inferior
1	1280	CPP	1.07 (1.10)	0.32 (0.49)	0.34 (0.51)	0.61 (1.12)
		4DLTM	0.97 (1.02)	0.32 (0.49)	0.34 (0.50)	0.49 (1.01)
		p-value	1.36e-4
2	1487	CPP	0.99 (1.12)	0.35 (0.57)	0.36 (0.62)	0.49 (1.02)
		4DLTM	0.86 (1.08)	0.31 (0.55)	0.32 (0.60)	0.38 (0.95)
		p-value	5.91e-10
3	1561	CPP	1.23 (1.32)	0.38 (0.59)	0.40 (0.64)	0.73 (1.29)
		4DLTM	1.01 (1.17)	0.37 (0.58)	0.36 (0.61)	0.48 (1.09)
		p-value	0
4	1166	CPP	1.51 (1.58)	0.52 (0.74)	0.58 (0.80)	0.81 (1.52)
		4DLTM	1.40 (1.57)	0.52 (0.76)	0.54 (0.79)	0.70 (1.48)
		p-value	2.93e-5
5	1268	CPP	1.95 (2.02)	0.64 (0.92)	0.69 (0.88)	1.24 (1.96)
		4DLTM	1.67 (1.79)	0.58 (0.82)	0.69 (0.96)	0.92 (1.66)
		p-value	1.42e-13
6	419	CPP	1.94 (1.72)	0.60 (0.95)	0.59 (0.81)	1.35 (1.62)
		4DLTM	1.58 (1.65)	0.54 (0.93)	0.61 (0.88)	0.93 (1.44)
		p-value	2.30e-8
7	398	CPP	1.79 (1.46)	0.55 (0.64)	0.68 (0.87)	1.11 (1.49)
		4DLTM	1.46 (1.29)	0.47 (0.61)	0.58 (0.70)	0.82 (1.30)
		p-value	2.39e-6
8	476	CPP	1.96 (2.33)	0.64 (0.94)	0.71 (1.07)	1.25 (2.19)
		4DLTM	1.77 (2.12)	0.53 (0.82)	0.68 (0.92)	1.08 (2.05)
		p-value	2.43e-3
9	342	CPP	1.33 (1.17)	0.41 (0.56)	0.59 (0.70)	0.67 (1.17)
		4DLTM	1.19 (1.12)	0.41 (0.57)	0.51 (0.62)	0.57 (1.10)
		p-value	6.31e-3
10	435	CPP	1.84 (1.90)	0.48 (0.66)	0.71 (0.89)	1.21 (1.89)
		4DLTM	1.59 (1.87)	0.45 (0.66)	0.65 (0.96)	0.95 (1.77)
		p-value	1.86e-5
Avg		CPP	1.44 (1.54)	0.46 (0.70)	0.51 (0.75)	0.85 (1.49)
		4DLTM	1.25 (1.43)	0.43 (0.67)	0.48 (0.74)	0.65 (1.34)
		p-value	0.001953

Spatial errors presented in millimeters with standard deviation (SD) in parentheses. The Wilcoxon rank sum test was performed as described above, with corresponding p-values shown. Abbreviations: Avg=average, CPP=incremental 3D local compressible flow, 4DLTM= 4D local compressible flow.

Figure 5. Spatial error versus displacement magnitude.

The absolute distances between the reference landmark displacement vectors and the a) 4DLTM and the b) CPP algorithms were tallied for the set of 8832 landmarks versus size of the displacement in 4 mm increments. Though the complete set of landmark measurements was used to generate the box plots shown, outlier data points have been removed from the figure for clarity.

6.4. Performance of the 4DLTM algorithm

A qualitative evaluation of the 4DLTM algorithm for one case is illustrated by the error vectors shown in Figure 4c, which demonstrates the spatial distribution of the errors. Quantitative spatial accuracy performance of the cubic 4DLTM algorithm is summarized in table 4. For the set of ten reference cases, mean (and standard deviation) three-dimensional Euclidean magnitude registration errors ranged from 0.86 (1.08) - 1.77 (2.12) mm. Mean magnitude component errors were consistently largest in the SI direction, ranging from 0.38 (0.95) - 1.08 (2.05) mm. Over the combined set of 8832 reference measurements, all mean component errors were less than 0.75 mm, while the weighted 3D Euclidean magnitude error (and pooled standard deviation) was 1.25 (1.43) mm. A box plot of registration error versus landmark displacement magnitude is shown in Figure 5b for the set of reference landmark point pairs. Corresponding two-tailed Spearman rank correlation coefficient is ρ = 0.2653 (p-value = 0), indicating weak but statistically significant correlation.

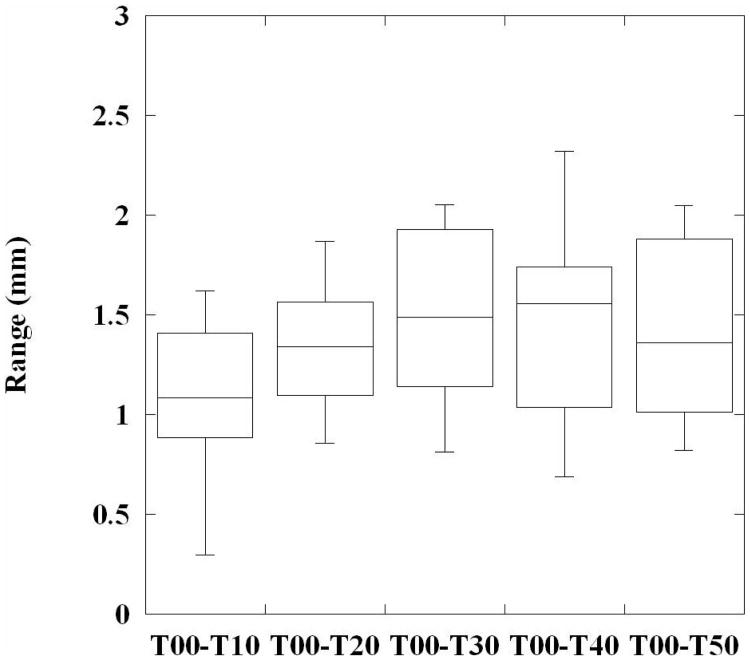
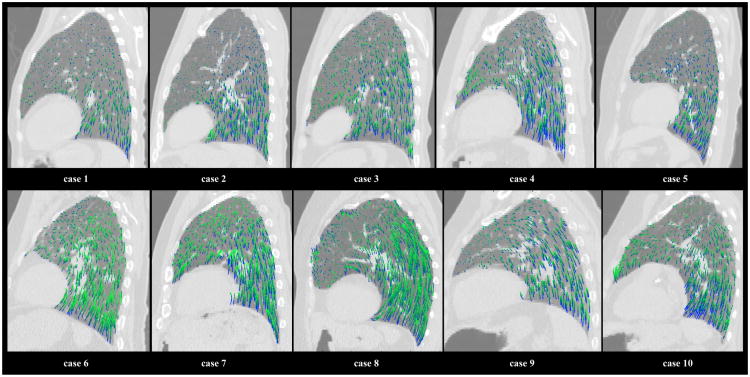
For each case, the 75 sampled 4D reference landmark trajectories were used to evaluate the registration error at each incremental phase displacement. Figure 6 shows a box plot of the error range at each step, using the cumulative set of sampled positions for all 10 cases. A trend toward increasing magnitude error with phase increment is visually apparent, consistent with the statistically significant correlation between error and displacement magnitudes described above. Figure 7 shows an illustration of the calculated in-plane motion fields over an example T00 sagittal slice for each reference case. The calculated trajectories were plotted for randomly chosen voxel positions within the lung field, and are color-coded to indicate their temporal sequence. The initial T00→T10 displacements are shown in blue, while each subsequent displacement gradually changes shade towards dark green. The recovered motion fields show large variation in overall displacement magnitude, motion nonlinearity, and temporal distribution of magnitude motion, suggesting adequate flexibility of the cubic 4DLTM model to accurately measure breathing patterns from clinically acquired 4DCT patient images.

Figure 6. Phase-step registration errors.

A box plot is shown illustrating the range of 4DLTM cubic magnitude registration errors at each phase increment. The 75 sampled 4D reference trajectories for each case were combined to pool the measured errors, resulting in 750 error measurements for each phase bin.

Figure 7. Calculated temporal motion sequences.

For each reference case, an example T00 sagittal view is shown with a random sample of the corresponding in-plane trajectories calculated using the cubic 4DLTM algorithm. The plotted trajectories are color-coded to indicate their temporal sequence. The initial T00 →T10 displacements are shown in blue, while each subsequent displacement gradually changes shade towards dark green. The calculated motion sequences are seen to vary widely across the 10 reference cases, both in time and space. The corresponding quantitative error assessment for each case is shown in Table 4.

6.5. Comparison of spatial accuracies

The two-sided Wilcoxon signed rank test was performed for each case in order to assess the statistical significance of differences between the spatial accuracy performance of the CPP and cubic 4DLTM algorithms, with p-values for each test shown in table 4. For each case, the improvement in spatial accuracy achieved by the cubic 4DLTM algorithm was regarded as statistically significant with p-values ranging from (0 to 6.31 × 10^-3). Over the cumulative set of measurements for all cases, the statistical test yields a double-sided p-value of 0. However, this approach is not strictly valid because it assumes that each error observation is independent, which is not true since observations are patient dependent. In order to apply the statistical test over the cumulative set of measurements across all cases, we instead use the mean values for each case as the data. In this case, the observations are independent and the resulting p-value is 0.001953. Although the larger p-value is much more conservative, it still reflects a statistically significant difference between the two algorithms over the combined set of data, which is consistent with the results for each individual case.

Figure 4a shows an isosurface rendering of the T00 lung volume of an example case (patient #6), overlain with the corresponding set of 419 reference displacement vectors mapping landmark features from their T50 to T00 coordinate positions. The GTV located in the left lower lobe is also shown. The dependence of landmark displacement magnitude with relative position within the lung is visibly clear in the image. Figures 4(b & c) show the residual error vectors for the 4DLTM and CPP algorithms, respectively. Visually, both sets of residual error vectors appear small and approximately uniformly distributed, with the largest errors occurring in the inferior aspect of the right and left lower lobes. These regions correspond with the largest displacements. This is consistent with the Spearman correlation coefficients, which showed small but statistically significant correlation of the registration errors for both algorithms with landmark displacement magnitude. For the case depicted, respective mean (and standard deviation) registration errors for 4DLTM and CPP were 1.58 (1.65) and 1.94 (1.72), with p-value = 2.3 × 10^-8.

7. Discussion

Deformable image registration (DIR) is an enabling image analysis tool in radiotherapy (Sarrut, 2006) with applications to multi-modality image fusion (Kessler, 2006), image analysis (Pizer et al., 1999), semi-automated image segmentation (Ragan et al., 2005), 4D dose estimation (Guerrero et al., 2005; Kang et al., 2007), and 4D image-guided radiotherapy (Keall, 2004). DIR registration between the component phase images of 4D CT provides a link for extraction of the motion (Guerrero et al., 2004; Yaremko et al., 2008) and physiological information such as cardiac wall motion or ventilation (Guerrero et al., 2006; Song and Leahy, 1991). In this study, we derived and validated a 4D DIR algorithm, the 4DLTM algorithm, based on the idea of recovering parameterized voxel trajectories that represent the paths taken by the voxels through space as functions of time to link all the expiratory phase component images. The method utilizes a compressible flow voxel intensity model, and operates on the full set of expiratory phase 4DCT component image data simultaneously while performing this calculation. The numerical implementation of the method approximates image intensity values using 3D cubic-splines which reduces the effects of image noise and artifacts in the calculation of local derivatives. In this implementation only voxels that achieved a goodness of fit criteria were retained. The displacements for those voxels that did not achieve the criteria were determined using neighboring values and a moving least squares interpolation.

The piecewise linear path obtained by registering temporally sequential component phases, in a manner similar to a methodology described in (Boldea et al., 2008), served as the initial guess for the polynomial trajectory recovery. Not surprisingly, the polynomial based trajectory modeling yielded a significant increase in the spatial accuracy over the piecewise linear initial guess. Specifically, the results of testing polynomial spaces of up to degree 5, for spatial accuracy performance, indicate that linear paths (2) produce substantially poorer spatial accuracies than those of higher order polynomials, indicating that voxel trajectories are nonlinear; i.e. voxels do not travel along a straight line throughout the breath cycle. This result is based on performing a Friedman rank sum test, which indicated that the mean error of all methods is not equal with a p-value of 6.36×10^-6. The result of a rank based pair-wise comparison between the linear polynomial performance and the performance of the remaining polynomial degrees allows us to conclude that linear paths produce a larger error than the other polynomial spaces with a family wise level of significance of 10%. The variation in the performance of 4DLTM across the remaining orders was not statistically significant, a result that is not surprising considering that the space of all quintic polynomials contains all quadratics, cubics, and quartics. However, based on the registration results and the examination of expert-determined landmarks across 4D data set, cubic polynomials provide sufficient flexibility, computational tractability, and high spatial accuracy for describing the point trajectories through the expiratory phases. The resulting average spatial error between the maximum 4DCT component phases of 4DLTM with cubic polynomial trajectory modeling were 1.25 mm for the 4DLTM, while the average spatial error for piecewise linear paths (CPP method) was 1.44 mm.

Expert-determined sets of anatomical landmark feature pairs have become a common utility for evaluating DIR spatial accuracy, particularly in the context of clinically-acquired thoracic images (for example, see (Brock et al., 2005; Pevsner et al., 2006; Rietzel and Chen, 2006; Sarrut et al., 2006; Boldea et al., 2008; Li et al., 2008; Wu et al., 2008; Castillo et al., 2009a; Castillo et al., 2009b)). However, variability among reference datasets, particularly with regard to both the quantity and spatial uniformity of selected landmark features, can potentially yield numerical results that are misrepresentations of the true spatial accuracy, from which erroneous conclusions regarding the relative performance characteristics of multiple algorithms or implementations can be drawn. Thus, the current lack of consistency among evaluation strategies confounds formal quantitative comparison of published numerical DIR spatial accuracy assessments. In addition, inconsistencies among reference cases, such as arising from individual patient motion characteristics, motion and image reconstruction artifacts, variable disease states, image size, and voxel dimension further contribute to the inherent uncertainty associated with conclusions regarding relative performance drawn from metanalysis of the available literature. The expert-determined landmark features used to evaluate DIR spatial accuracy in this study were made publically available on the Internet at our laboratory website (http://www.dir-lab.com). This DIR reference database consists of ten 4DCT image sets and corresponding manually identified landmark points between the maximum phases. A subset of points are propagated through the expiratory 4DCT component images. We hope the availability of this DIR reference database will allow a common framework on which to compare the performance of DIR algorithms in the future.

The use of trajectory modeling as a DIR method for thoracic 4DCT images is a natural extension of prior studies on measuring and modeling lung trajectories, such as those of Seppendwoolde et al (Seppenwoolde et al., 2002), Shirato et al (Shirato et al., 2004), and Boldea et al (Boldea et al., 2008). In those studies, a 2-mm gold fiducial was implanted in or near the lung tumor to perform real-time target tracking for gated radiotherapy treatment delivery (Shirato et al., 2000). The fiducial tracking was performed using two fluoroscopic units, capturing the trajectory at a sampling rate of 30 frames per second through the entire radiotherapy treatment sessions. In Seppendwoolde et al (Seppenwoolde et al., 2002) a parameterized sinusoidal function was utilized to model the measured lung or tumor motion trajectories through multiple respiratory cycles. Boldea et al used piecewise linear trajectory modeling based DIR, an approach that is essentially equivalent to the initial guess we supply to our 4DLTM algorithm, to extract, evaluate, and quantify motion non-linearity and hysteresis across 4DCT images (Boldea et al., 2008). They found non-linear and hysteresis was more pronounced for longer trajectories and achieved average spatial accuracies of 2.3mm and 2.5mm for two 4D based methods. The findings of these studies suggest improvements in our 4DLTM algorithm should be explored through the use of non-polynomial models and adaptive modeling. The later, includes the use of differing model forms for cranial-caudal motion versus transaxial motion and differing forms based on estimates of regional displacement. Improvement may also result from using the full 4DCT image set, which would ensure round-trip consistency and allow evaluation of sinusoidal versus elliptical functions for trajectory models.

The 4DLTM algorithm calculations were all performed in the local neighborhood of each voxel, as such, the algorithm should readily port to graphics processing units (GPUs) for improved computational speed. Due to their emerging use as a highly multi-threaded coprocessor, GPUs are especially well-suited for data-parallel computational problems such as the 4DLTM presented here. These affordable yet powerful computational resources will likely find significant use in the radiotherapy clinical environment. GPUs have been reported to accelerate computational tasks such as cone-beam CT reconstruction, DIR calculation, and radiation dose calculation by one to two orders of magnitude over CPU implementations (Sharp et al., 2007; Xu and Mueller, 2007; Samant et al., 2008; Noe et al., 2008; Hissoiny et al., 2009). We anticipate a significant reduction (20 to 100 times) in overall computational time for the 4DLTM algorithm on a GPU such as the NVIDIA Tesla. Calculations times in the less than 2 minutes range on a single PC with GPU would expand the potential use of the 4DLTM algorithm to many applications.

8. Conclusions

In this study, a new methodology for DIR based on trajectory modeling (4DLTM) was developed and evaluated using a publically available 4DCT image and landmark points database. Polynomials trajectory models from linear through quintic were tested, linear trajectory modeling performed significantly (p-value = 6.36×10^-6) worse than higher order polynomial models. The 4DLTM DIR algorithm utilizing cubic trajectory modeling was then compared with piece-wise component phase to phase (CPP) DIR to calculate the displacement from the maximum exhale to inhale 4DCT component images through the expiratory phase. The 4DLTM performed significantly better, the resulting average spatial error between the maximum phases was 1.25 mm for the 4DLTM and 1.44 mm for the CPP. The 4DLTM method captures the long-range motion between 4DCT extremes resulting in high spatial accuracy.