Abstract
In this work, development and evaluation of a three dimensional (3D) finite element model (FEM) based on the diffusion approximation of time-domain (TD) near-infrared fluorescence light transport in biological tissue is presented. This model allows both excitation and fluorescence temporal point-spread function (TPSF) data to be generated for heterogeneous scattering and absorbing media of arbitrary geometry. The TD FEM model is evaluated via comparisons with analytical and Monte Carlo (MC) calculations and is shown to provide a quantitative accuracy which has less than 0.72% error in intensity and less than 37 ps error for mean-time. The use of the Born-Ratio normalized data is demonstrated to reduce data-mismatch between MC and FEM to less than 0.22% for intensity and less than 22 ps in mean-time. An image reconstruction framework, based on a 3D FEM formulation, is outlined and simulation results based on a heterogeneous mouse model with a source of fluorescence in the pancreas is presented. It is shown that using early photons (i.e. the photons detected within the first 200 picoseconds of the TPSF) improves the spatial resolution compared to using continuous-wave signals. It is also demonstrated, as expected, that the utilization of two time-gates (early and latest photons) can improve the accuracy both in terms of spatial resolution and recovered contrast.
Keywords: Light propagation in tissues, turbid media, fluorescence, time-resolved imaging, image reconstruction
1. Introduction
Time domain near infrared (NIR) fluorescence imaging is a molecular imaging technique whereby a region of interest is irradiated by a red or NIR excitation light source and the emitted fluorescence light, together with the transmitted and/or reflected light at excitation, is used to determine the spatial distributions of fluorescent tracers and/or other fluorescent structures in biological tissue (Arridge et al., 1993; Gao et al., 2006; Gao et al., 2008; Kumar et al., 2006; Lam et al., 2005; Leblond et al., 2009; Niedre and Ntziachristos, 2010; Patterson and Pogue, 1994; Soloviev et al., 2007; Vishwanath and Mycek, 2005). Although the comparison between the different data collection strategies is largely under debate, continuous-wave (CW) and frequency domain (FD) systems have to date been relatively inexpensive, less complex to develop and have provided relatively shorter time scans, whereas time domain (TD) systems are slow (due to photon counting nature) but highly sensitive. It is also well accepted that since TD and FD systems provide time-resolved information, it is possible to independently measure the distribution of both scattering and absorption coefficients, as well as fluorescence lifetime (O’Leary et al., 1996). Additionally, a theoretical analysis of the moments of the forward problem in fluorescence diffuse optical tomography through use of different data types for TR fluorescence reconstruction has demonstrated the increasing sensitivity of moments to noise (Ducros et al., 2009). However, since TD measurement data implicitly contains a weighted sum of modulation frequencies from the FD data types, it can in principle provide much more information regarding the underlying optical properties of the tissue being interrogated (Marjono et al., 2008).
The benefits of using early-arriving photons have been long known (Wu et al., 1997), and a number of researchers have previously studied and developed TD based image reconstruction strategies that utilize time-gated data to extract optical properties from the domain being imaged (Kumar et al., 2005; Gao et al., 2002). The use of early photons can potentially lead to a better imaging resolution, through the reduction in thickness of the photon measurement density function (PMDF) for early sampling times (Schweiger and Arridge, 1995). Additionally, there has been some work describing the use of a gradient-based iterative reconstruction scheme with multiple time-gates over the full TD curve (Hielscher et al., 1999). More recently, Niedre et al. (Niedre et al., 2008; Li and Niedre, 2011) have demonstrated that improvements in resolution can be achieved by the use of early photons for fluorescence tomographic imaging of lung tumors in mice in vivo. Further studies have shown that when transmitted through the torso of a mouse, early photons were significantly less diffuse than quasi-CW photons which allowed an improved visualization of fluorescent targets for individual optical projections and reconstructed tomographic images (Niedre and Ntziachristos, 2010). Leblond et al. (Leblond et al., 2009) have also demonstrated that early photon data allows the improvement of spatial resolution, since it allows the retention of imaging singular modes corresponding to higher spatial frequencies in the image reconstruction problem.
For clinical applications, TD imaging can potentially be used to develop a non-invasive in vivo molecular imaging technique that not only allows real-time viewing of cellular activity but also is able to extract time-related patho-physiological information from biological tissue (Luker and Luker, 2008; Zhang et al., 2007; Massoud et al., 2004). The technique could be applied for diseases such as cancer detection and diagnosis at a very early stage in comparison with other imaging or detection modalities that require months or years for tumors to grow to be detectable (Palmedo et al., 2002; Houston et al., 1988; Warner et al., 2001). This provides the advantages for faster treatment of the diseases and better therapeutic monitoring and outcomes. In addition, the model in practice could also potentially be used to accelerate drug discovery and development due to it is ability of nearly real-time viewing of cellular activity in-vivo (Luker and Luker, 2008; Rudin and Weissleder, 2003; Gross and Piwnica-Worms, 2006).
To date, much work relating to time domain fluorescent modelinghas been done; however, they are mostly centered on 2D light transport models (Gao et al., 2006; Gao et al., 2008), and most have been developed for frequency domain systems (Jiang, 1998; Lee and Sevick-Muraca, 2002). The algorithms and techniques presented in this paper are developed for 3 Dimensional (3D) fluorescent models using Finite Element Models (FEM) for time domain propagation of NIR light in turbid media. In addition, analytical solutions (Lam et al., 2005; Patterson and Pogue, 1994; Hattery et al., 2001) and Monte Carlo (MC) (Vishwanath and Mycek, 2005) models have also been used for simulations of 3D fluorescent light propagation in time domain that can provide model verification. However, analytical solutions provide fast and computationally efficient solutions but typically suffer from the drawback that they can only be applied for simple homogeneous geometries, although some developments of analytical solutions based on the Kirchoff’s approximation for Fluorescence models have been reported (Ripoll et al., 2002). MC models, on the other hand, can be applied for complex geometries; however these approaches are more time consuming and computationally expensive to achieve stable responses (Preisa et al., 2009; Fang and Boas, 2009), but with the advent of Graphics Processing Unit (GPU) and parallel processing implementation the processing time has been dramatically improved (Fang and Boas, 2009; Jin et al., 2011). The FEM model introduced in this paper combines the strengths of both these approaches, providing a fast technique that can be applied for complex heterogeneous geometries.
In this paper, we outline in detail the implementation of 3D time domain FEM-based Fluorescence model and its validation via MC and analytical simulations. Specifically, we demonstrate the accuracy of the application of Fluorescence time domain FEM using the Diffusion Approximation (DA), as compared to both an analytical model (also based on the DA) and an MC model using a 3D slab reflectance model. The measured Temporal Point Spread Function (TPSF) for both the excitation and emission data are compared against the two models (i.e., analytical and MC) to demonstrate the limits of the DA on TD data, as well as to outline the benefits of using the so-called Born-Ratio (emission normalized with respect to excitation) data. When compared to MC, the FEM Born-Ratio data is shown to provide a greater degree of accuracy in terms of data match than the FEM fluorescence data alone. Data is also presented showing that the early time-bin intensity measurements as acquired from a TD model, are a function of the source/detector separation, though this does not necessarily imply that the accuracy of shorter time-bins increases with source/detector separation. Finally, the FEM-based image reconstruction algorithm that can be used for time-gated intensity data is also presented in detail together with the incorporation of multiple time-bins for 3D tomographic imaging of a complex mouse model. The models and algorithms presented were developed using the NIRFAST software (Dehghani et al., 2008), which is an open source software package designed for light transport modeling and image.
2. Methods and Results
2.1 FEM solutions to the time-dependent diffusion equation
Although generally well known and understood, in order to outline the implementation of both the forward and inverse model for TD fluorescence within the FEM framework, we will first define the diffusion approximation. In the following, the subscripts x and m denote the excitation and fluorescence emission wavelengths, respectively, of a light field propagating within a heterogeneous turbid medium, Ω. The medium is excited using an ultra-short point source, which is modeled using a delta-function source, δ(r-rs,t), along the space and time dimensions. The propagation of both excitation and emission light in the medium can be modeled by two coupled time-dependent diffusion equations:
| (1) |
| (2) |
where ϕv(r,rg,t)(v∈[x,m], g∊[s,d]) are the time-dependent photon density functions at time t and position r. The field ϕx(r, rs, t) is the impulse/tissue response to a delta-function source of wavelength λx located at position rs. On the other hand, ϕm(rd, r, t) models the light signal detected at position rd resulting from fluorescence emitted by a fluorophore distribution with absorption coefficient μaf(r) located at position r. The photon density functions depend non-linearly on the effective tissue optical properties, namely, the absorption coefficient, μav(r), and the diffusion coefficient, Kv(r, t) = 1/[3(μav(r)+μ’sv(r)], where μ’sv(r) is the reduced scattering coefficient. The photon density at the excitation wavelength, ϕx(r, rs, t), is also a non-linear function of the fluorophore absorption coefficient, μaf(r); however, it is customary, when using diffused fluorescence to image tissue, to assume that the fluorophore absorption coefficient is much smaller than that associated with other chromophores such as hemoglobin and water. As a consequence, equation (1) is often solved assuming that the fluence functions are independent of μaf(r) (Gao et al., 1998; Lam et al., 2005; Niedre et al., 2008); whereas, in this work the potential non-linear dependence of ϕx(r, rs, t) on μaf(r) is accounted for. It is assumed that there is negligible overlap between the excitation and emission spectra of the fluorophore at λm and therefore the emission photon density is assumed to be independent of μaf(r). The other physical parameters characterizing the fluorophores are the lifetime, τ(r), and the quantum efficiency, η(r). In equation (2), e(τ, t) = e−t/τ(r)U(t), where U(t) is a unit-step function and the operator, ⊗, is the temporal convolution operator. Solutions to the equations above are obtained using Type III boundary conditions, which has been shown to accurately account for index of refraction mismatch at the air/tissue boundary (Schweiger et al., 1995).
Here, the excitation (equation (1)) and emission (equation (2)) equations are each solved at time step k based on FEM. According to the work from Arridge et al. (Arridge et al., 1993), equation (1) can be discretized – temporally and spatially – and written as:
| (3) |
which, in order to isolate the 0th order term, can be re-written as:
| (4) |
where
| (5) |
K, C and M are the FEM matrices and Q is the FEM representation of the source term in equation (1). These matrices are given by:
| (6) |
where ψ is the basi funcion and i,j = 1,2,3,…,N, N is the number of nodes within the FEM volume mesh. FEM solutions to equation (1) are obtained by solving equation (4) through matrix inversion, which is achieved using a bi-conjugate gradient solver with a pre-conditioner based on one Choleski factorization of the matrix, Ax.
Solutions for the emission case are obtained in a manner similar to the excitation case with the exception of the source term, which is now a function of the FEM fields ϕx(k). First, equation (2) is written in the form:
| (7) |
where
| (8) |
Equation (7) can be then re-written as:
| (9) |
where the structure of the matrices, Am and Bm, is the same as those defined in equation (5), with the exception that the optical properties that are used to evaluate the matrices are those associated with the emission wavelength, λm.
The main difference between equations (4) and (9) is the source term on the right-hand-side. For the excitation case, the laser source is approximated by a delta function. However, the source term for the emission case depends on the physical properties of the fluorescent molecules as well as on the spatial and temporal distribution of the excitation field, ϕx. In order to obtain FEM solutions for the excitation field, the first time-step intensity (ϕx(1)) is initially obtained by solving equation (4) with the delta function source. Then, as shown by inspection of equation (4), the calculated solution at time-step, k = 1, is used as the source term for calculating the intensity in the next time-step (k = 2). This process is repeated iteratively in order to compute the modeled light intensity for every time-step until the end of the modeled photo-detection time window. For the emission case, the first time-step intensity, ϕm(1), is obtained by solving equation (9). Prior to solving this equation, however, a time convolution operation between the mathematical objects ϕx(1) and e(τ, t) is numerically performed. Then, the resulting time-vector is multiplied by the ratio of the quantum efficiency and the lifetime, η(r)/τ(r). The light intensities for all time steps are then derived using a similar approach as defined for the excitation case.
Validation of the TD algorithm presented was achieved by direct comparison of the time-dependent FEM solutions against both analytical solutions and Monte Carlo (MC) simulations. The particular analytical and MC models used here have been shown in the past to accurately model light transport in tissue for epi-illumination detection geometries (see, e.g., Ref. (Leblond et al., 2010a) for a description of the various detection geometries used in diffuse fluorescence imaging). As such, those methods can be considered gold standards for light transport simulations in biological tissue. The analytical model is a closed-form solution to the time-dependent diffusion equation assuming extrapolated boundary conditions (ECB) consistent with a single-layer semi-infinite turbid medium and are based on the work of Patterson and Pogue (Patterson and Pogue, 1994). The MC model used here was developed by Vishwanath and Mycek (Vishwanath and Mycek, 2005), and is able to simulate TD signals (i.e., TPSF’s) at both excitation and fluorescence emission wavelengths in a multi-layered semi-infinite turbid medium. However, contrary to numerical FEM solutions and analytical modeling, MC simulations are obtained using a statistical approach. As such, the requirement for acceptable levels of signal-to-noise imposes that each simulation keeps track of large numbers of photons typically of the order of 1×106 and more. This explains why MC simulations can result in prohibitively large computational times and memory requirements when compared to numerical FEM and analytical approaches, although with the current advent of low cost GPU computation these computational times have improved (Fang and Boas, 2009).
Bench-marking of the FEM model against the analytical and MC solutions were achieved assuming an epi-illumination photo-detection geometry. Tissue excitation was modelled as a narrow beam laser source and light detection was modelled at a single point located a distance d away from the light source. The geometry of a semi-infinite homogeneous turbid medium was used for the analytical and MC solutions; whereas, the FEM numerical solutions were obtained using the mesh of a rectangular cuboid. The physical dimensions of the cuboid were Δx = 135 mm, Δy = 40 mm , Δz = 60 mm with a mesh resolution of 0.85 mm. More precisely, the ranges of the cuboid spatial coordinates were: x = [50mm : −85mm], y = [0mm : −40mm], and z = [−30mm : 30mm], with a nodal spacing of 0.85 mm.
For all simulations (analytical, statistical, and numerical), the excitation laser source was modeled on the surface at (x,y,z) = (0,0,0) mm, i.e., on the same surface where measurements are made for source-detector distances of d = 3, 5, 10, 15, 26 mm. The optical properties and fluorophore physical parameters used for the three types of simulations (analytical, statistical and numerical) are shown in Table 1, where g represents the scattering anisotropy factor used only for MC simulations. The time-dependent FEM and analytical solutions were obtained using a time-window of T = 40 ns with a TPSF time resolution dt = 20 ps, whereas for the MC model the time resolution was also kept at 20 ps for a total of 1 billion photons.
Table 1.
Optical properties and fluorophore physical parameters associated with the tissue-mimicking numerical phantom used for epi-illumination photodetection simulations. The reduced scattering coefficient used for the FEM and analytical simulations is given as μs’ = (1-g) μs
| Epi-illumination Numerical Phantom Optical Properties | ||
|---|---|---|
| Physical parameter | Symbol | Measured value |
| Absorption coefficient (excitation) | μ ax | 0.035 mm−1 |
| Absorption coefficient (emission) | μ am | 0.035 mm−1 |
| Scattering coefficient (excitation) | μ sx | 10.0 mm−1 |
| Scattering coefficient (emission) | μ sm | 10.0 mm−1 |
| Scattering anisotropy factor (excitation) |
gx | 0.9 |
| Scattering anisotropy factor (emission) |
gm | 0.9 |
| Fluorophore absorption coefficient (excitation) |
μ af | 0.0019 mm−1 |
| Fluorophore Quantum yield | η | 0.1 |
| Fluorophore lifetime | τ | 1 ns |
| Index of refraction | n | 1.52 |
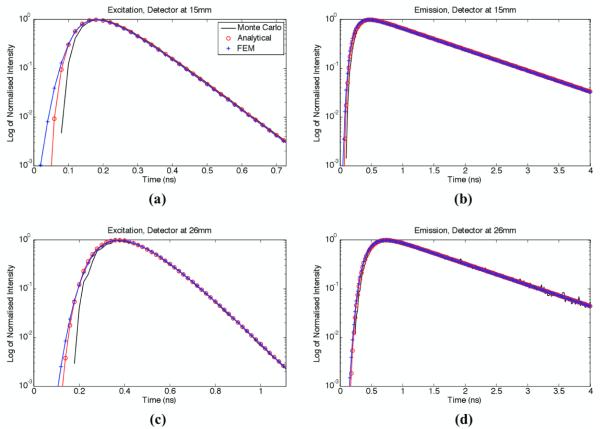
Figure 1 shows modelled TPSF’s generated from FEM, analytical, and MC simulations in an epi-illumination photo-detection geometry. The simulations were performed using the optical and fluorophore properties shown in Table 1 for source-detector separations of d = 15 mm (Figure 1(a) and 1(b)) and d = 26 mm (Figure 1(c) and 1(d)). Moreover, TD curves were generated at wavelengths for both excitation (Figure 1(b) and 1(d)) and fluorescence emission (Figure 1(a) and 1(c)). For comparison purposes, all TD curves were normalized with respect to their maximum value. This normalization procedure was employed because the relative amplitude of TPSF’s generated with different models is physically irrelevant for simulations. Also, in order to better convey the photon count information in the low signal time bins (e.g., early photons), the y-axes of the curves are shown on a logarithmic scale.
Figure 1.
Normalised TPSF’s for the three light transport simulation models considered: (a) reflected excitation field for a source-detector separation d = 15 mm, (b) fluorescence emission for a source-detector separation d = 15 mm, (c) reflected excitation field for a source-detector separation d = 26 mm, (d) fluorescence emission for a source-detector separation d = 26 mm. The y-axis of all curves is shown on a logarithmic scale.
The FEM and analytical models are solutions to the diffusion equation and as such, they are not expected to effectively capture the physics of the early-photons. This component of the light signal is associated with early time bins (typically time < 500 ps in Figure 1) and corresponds to photons for which the light paths were too short for randomization to have occurred. However, because it is modelling the phenomenon of radiation transport, the validity of the MC solutions is not limited to diffused photons and is therefore, in principle and as shown experimentally, a more appropriate method for early-photon simulations (Niedre et al., 2010). As expected, the highest discrepancy in Figure 1 can be seen for the early arriving photons, specifically for the smaller source-detector separation. For the emission case, it can be seen from Figure 1(b) and (d) that the mismatch between all models appears minimal, except for the MC case, where the limited number of photons simulated led to high levels of noise, which highlights a weakness of MC simulations. Additionally, in order to show the level of agreement between the various simulations for late arriving photons, Figure 1(b) and (d) are shown for data up to 4 ns; whereas, to demonstrate the discrepancies for early arriving photons, Figure 1(a) and (c) are limited to 0.72 ns and 1.1 ns, respectively.
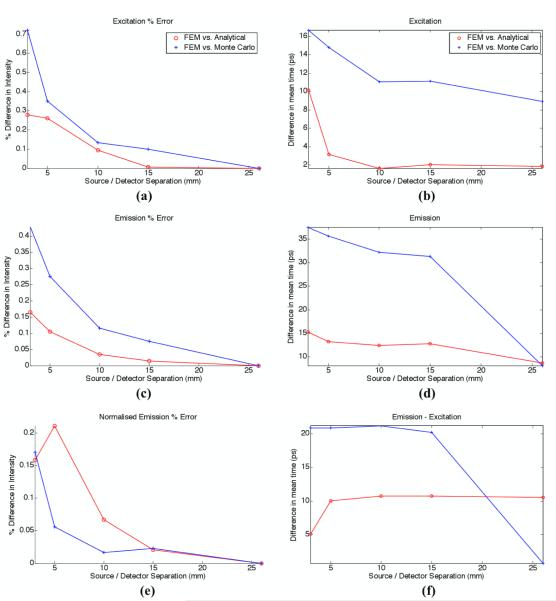
In order to allow for a more quantitative analysis to be performed, the TPSFs from all three light transport models were used to calculate two point-spread function data-types commonly used to reconstruct optical images based on time-domain data (Riley et al., 2007; Schweiger and Arridge, 1999). For each TPSF the total intensity and mean-time of flight were computed for all source-detector separations (see Ref. (Hillman, 2002) for details relating to the computation of optical data-types). Using these calculated data-types for each simulation model, a relative error was calculated between the values obtained using the FEM model and those computed based on the analytical and MC solutions. The results are presented in Figure 2(a) – (d) where the intensity difference is shown as a percentage while mean-time results are shown as absolute differences in picoseconds. For excitation-emission intensity and mean-time, the error between the FEM solutions and those obtained using an analytical model were significantly smaller when compared to the error between FEM and MC. In fact, the excitation-emission intensity errors between the FEM and analytical model were less than 0.3% while the percentage error with the MC solutions were close to 0.72% when the source-detector separation was smaller than d = 5 mm. Increased agreement between FEM and analytical models is understandable since they are both solving the diffusion equation. Also, increased mismatch between FEM and MC solutions for smaller source-detector distances can be explained by the inability of diffusion modelling to capture the physics of short light-path photons. For the mean-time of flight, the error between the FEM and MC are greater for the emission data, seen to be 32 ps at 15 mm, whereas the corresponding error at the excitation was 12 ps. In all cases the smallest error was observed at the larger source-detector separation.
Figure 2.
Percentage error for (a) excitation intensity and (b) excitation mean-time of flight, (c) emission intensity and (d) emission mean-time of flight, (e) normalized intensity of emission (ratio of emission with respect to excitation) and (f) difference in meantime between emission and excitation. All plots represent the difference of FEM model with respect to analytical or Monte Carlo model.
In applications such as diffuse fluorescence tomography, the conventional treatment of optical data consists of using a ratiometric technique to mitigate the impact of unknown experimental factors (Soubret et al., 2005; Leblond et al., 2010b). This method consists of normalising the emission intensity data by the excitation intensity data, the so-called Born-Ratio data. However, when considering the mean-time, normalisation consists in taking the difference between the emission mean-time and the excitation mean-time of the TPSF’s (Hillman, 2002). Figures 2(e) and (f) show the error between these normalised data-types computed as relative differences between the FEM solutions and the other two gold-standard light simulation models. In the case of normalised intensity, it can been seen that even in the case of d = 5 mm, the difference between the FEM and MC data were reduced from more than 0.27% (for emission) to less than 0.06% (for normalised emission). In the case of mean-time of flight data, the corresponding error was seen to be reduced from 35 ps to 22 ps, demonstrating a significant benefit in the use of normalised data as a means to reduce the burden put on accurate light transport modelling.
As discussed earlier, many research groups have previously presented the use of early time-bin intensity data for image reconstruction. It is therefore crucial to analyse the accuracy provided by the presented FEM time-domain fluorescence model with respect to MC, not only as a function of source/detector separation, but also the time-bins utilized. Figure 3a shows the percentage error between simulated FEM and MC ‘normalised Born-Ratio’ data, for different integrated time-bins as a function of source/detector separations for the optical parameters shown in Table 1. Interestingly, at the shortest source/detector separations, the percentage error was smallest for the earliest time-gates. This can be explained by the fact that at shorter source/detector distances more early photons will be detected due to a shorter mean photon path, thus improving the statistics of the early photon gate. This is of important consideration, since most work published to date has considered a unique set of integrated time-bins for all source/detector combinations for image reconstruction, whereas this result indicates that the best method may also be a function of source/detector separation. In all cases, the percentage error reduces to less than 2% for integrated time-bins of more than 1 ns.
Figure 3.
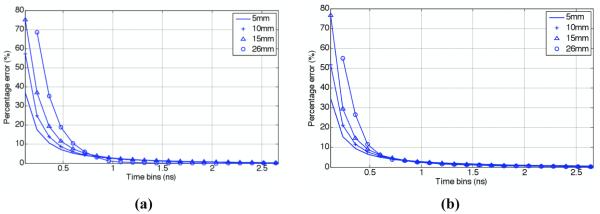
Percentage error for normalized Born-Ratio data between MC and FEM, for a range of integrated time-bins of intensity data for models for (a) optical parameters as shown in Table 1 and (b) μax, = 0.104 mm−1, μsx = 7.25 mm−1, μam, = 0.0672 mm−1, μsx = 6.91 mm−1, g = 0.9, μaf, = 0.01 mm−1, quantum yield = 0.33 and life-time = 1 ns. Early time-bin data for 26 mm is not shown due to low SNR within the MC data.
Further models were simulated (not shown) to represent realistic bulk tissue optical properties of more absorption dominant organs such as the liver and spleen: μax, = 0.104 mm−1, μsx = 7.25 mm−1, μam, = 0.0672 mm−1, μsm = 6.91 mm−1, g = 0.9, μaf, = 0.01 mm−1, quantum yield = 0.33 and lifetime = 1 ns, which correspond to the properties of liver at excitation wavelength of 635 nm and emission wavelength of 660 nm. Similar trends as those shown in Figures 1 and 2 were seen, with the maximum percentage difference for intensity measurement between MC and FEM being less that 2.5% and mean-time of flight less than 37 ps. The corresponding numbers for the Born-Ratio data for intensity measurements and mean-time were found to be less than 0.45% and 22 ps, respectively. Figure 3b shows the percentage error between FEM and MC ‘normalised Born-Ratio’ data, for different source/detector separations, as a function of different integrated time-bins for these higher optical parameters, displaying the same trends as those seen in Figure 3a.
2.2 Image reconstruction
The goal of the inverse problem is to recover the unknown optical properties (in this case the absorption due to the fluorophore, μaf) using the measured boundary data (in this case normalized Born-Ratio). We are limiting our discussion for the normalized Born-Ratio data, since it is generally agreed, and as we have show earlier, that this strategy can improve the accuracy as compared to MC models; however, adaptation of our findings can be translated to emission-only data. Image reconstruction is achieved by minimizing the difference between some measured boundary data and modeled data, for a given specified time-gate (Dehghani et al., 2009). Specifically, assuming that the total Born-Ratio intensity data for a specific integrated time-bin is used, the image reconstruction becomes an optimization problem where we seek to minimize an objective function
| (10) |
where y is the integrated time-binned intensity and F(μ) is the corresponding modelled data for a set of optical parameters, μ. The image reconstruction then becomes an iterative process, whereby the update equation is given by:
| (11) |
where δμ is the update parameter (μaf), δϕ is the difference between the modelled and measured data at each iteration, and λ is the regularisation parameter. The Jacobian matrix, J, is the matrix that relates a small change in the log of measured normalised Born-Ratio boundary data to a small change in μaf for a given time-bin (from t1 to t2), and is given by:
| (12) |
where is the adjoint emission field at position, r, at time, ti, from the adjoint source field originating from the detector at position, d; Φx (r,s,ti) is the excitation field at position, r, at time, ti, originating from a source at position, s; and . In the FEM framework, the convolution in equation (12) is not a direct multiplication, since the density and distribution of spatial nodes within a problem may not be homogeneous, and therefore the effect of associated shape functions for each spatial node and its associated neighboring nodes must be taken into account (Arridge and Schweiger, 1995).
For the case of using multiple time-bin intensity data, equation (11) is simply modified whereby
| (13) |
where δϕt2-t1 is the rate of change in measured data between time-bins t1 and t2 and Jt2-t1 is the associated Jacobian for time-bins. In the case of utilizing the Born-Ratio data, δϕ in equation (11) then becomes:
| (14) |
where superscripts, exp and mod, correspond to experimental and modeled data, respectively.
In order to demonstrate the capabilities of the developed image reconstruction algorithm, together with the benefits of using early time-bins as compared to total intensity data (i.e., total integrated TPSF), a heterogeneous mouse model based on the Digimouse — Figure 4(a) (Dogdas et al., 2007) — has been created that consists of 46,468 nodes corresponding to 222,262 linear tetrahedral elements, with optical properties as shown in Table 2. Excitation (635 nm) and emission (660 nm) data were simulated using 25 sources placed directly under the abdomen, proximal to the major abdominal organs, and 25 detectors were simulated directly on the surface above the same region: Figure 4(b). For the forward model, the pancreas was assumed to contain a fluorescence absorption of 0.002 mm−1 with a quantum efficiency of 0.33 and a lifetime of 1 ns, and the TD data were modeled for a total of 3 ns at 50 ps time steps. The computational time for the forward data was 330 seconds using the MATLAB Parallelization Toolbox on a workstation containing 6 dual core Opteron 2427 processors and 16 GBytes of RAM, running on 8 ‘workers’.
Figure 4.

(a) Heterogeneous mouse model where each region (as in table 2) is represented by different colour and (b) location of the source (underneath) and detectors (above) over the abdomen.
Table 2.
The seven regions of anatomy used within the heterogenous mouse model, Figure 1, together with chromophore concentrations and scattering properties used (Alexandrakis, 2005)
| Region | Total hemoglobin (mM) |
Oxygen Saturation (%) |
Water concentration (%) |
Scatter amplitude |
Scatter power |
|---|---|---|---|---|---|
| Adipose | 0.0033 | 70 | 50 | 0.98 | 0.53 |
| Bones | 0.0049 | 80 | 15 | 1.4 | 1.47 |
| Muscles | 0.07 | 80 | 50 | 0.14 | 2.82 |
| Stomach | 0.01 | 70 | 80 | 0.97 | 0.97 |
| Lungs | 0.15 | 85 | 85 | 1.7 | 0.53 |
| Kidneys | 0.0056 | 75 | 80 | 1.23 | 1.51 |
| Liver | 0.3 | 75 | 70 | 0.45 | 1.05 |
| Pancreas | 0.3 | 75 | 70 | 0.45 | 1.05 |
For image reconstruction, three sets of time-bins have been considered; (1) the total intensity from 0 – 0.2 ns, (2) the total intensity from 0 – 3 ns and (3) the total intensity from 0 – 0.2 ns as well as the total intensity from 2 – 3 ns. The Jacobian for each time-bin was calculated assuming a homogenous model consisting of purely homogenous tissue (μax = 0.0115 mm−1, μam = 0.0075 mm−1, μs’x = 1.36 mm−1 and μs’m = 1.32 mm−1) and images were reconstructed for fluorescence absorption only, using normalised Born-Ratio data. In all cases, to avoid the inverse crime, a second mesh consisting of 42,301 nodes corresponding to 210,161 linear tetrahedral elements was used with a regularisation parameter 10 times the maximum diagonal of the matrix JJT (see equation (11)). The corresponding images at iteration 10 are shown in Figure 5 with reconstructed parameters shown in Table 3.
Figure 5.
Target and reconstructed images for Fluorophore absorption within the mouse model pancreas using different time-bins. All reconstructed images are displayed as the threshold of 50% reconstructed peak value.
Table 3.
The expected and reconstructed peak values, FWHV of the fluorophore absorption of the pancreas in the heterogeneous mouse model, together with computation time per iteration
| Peak μaf (mm−1) |
FVHM (mm) |
Iteration time (s) |
|
|---|---|---|---|
| Target | 0.002 | 7.8 | - |
| 0 – 0.2 ns | 0.000048 | 30.8 | 184 |
| 0 – 3 ns | 0.000056 | 284.3 | 804 |
| 0 – 2 ns and 2 – 3 ns |
0.000052 | 99.4 | 804 |
As evident from the images in Figure 5, reconstructed images in all cases located the prostate well, with the peak reconstructed value using the ‘early’ time-bins (0 – 0.2 ns) = 0.000048 mm−1, using ‘early and late’ time-bins (0 – 0.2 ns and 2 – 3 ns) = 0.000052 mm−1, and the corresponding values for ‘late’ time-bin (0 – 3 ns) = 0.000056 mm−1. The size of the reconstructed object was also larger for the 0 – 3 ns time-bins. Using either the ‘early’ or ‘early and late’ time-bins appears to have maintained better resolution, which is in line with previous studies (Li and Niedre, 2011; Leblond et al., 2010a; Kumar et al., 2006; Jin et al., 2011). The low recovered value of the fluorophore can be due to multiple factors, with the main effect being the homogenous lower optical property assumption of the model. In this presented example, the whole mouse model used for reconstruction is assumed to consist of purely homogenous tissue, which inherently has a much lower optical attenuation, as compared to the model used for simulated data, as shown in Figure 4(a).
3. Discussion
A three-dimensional finite element model (3D FEM) implementation of the time domain (TD) fluorescence light propagation in soft tissue based on the diffusion approximation has been developed and has been evaluated using both analytical and MC simulation. Using the analytical solution for the TD model based on a semi-infinite medium of given optical properties (Table 1), the data using a 3D FEM model was evaluated and shown to provide a match with an associated error of 0.29% and 0.16% for excitation and emission intensity data, respectively, and less than 10 ps and 15 ps for the respective mean-time data (Figure 2). Similar results were found for varying optical parameters (not shown).
Acknowledging the fact that both the analytical and FEM solutions are based on the diffusion approximation, a MC model was also utilised to provide an additional tool for the evaluation of both the FEM and the analytical solution: Figures 1 and 2. Temporal point spread function (TPSF) data generated for both the excitation and emission light propagation from a homogenous medium (Table 1) provided a good match between all different simulation types (FEM, analytical, and MC). As seen from Figure 1, the FEM and analytical solutions did not model the early photon propagation well, owing to the inaccuracy of the diffusion approximation in this regime. Nonetheless, the overall agreement for the TPSFs between these 3 different models is found to be good in terms of the expected shape and responses.
To provide a more quantitative evaluation of the models, the total intensity and mean-time of flight was calculated for all models as a function of source-detector separation (Figure 2). The largest error in the intensity data was observed between the MC and FEM models for the smallest source-detector separation, especially in the emission data. This was primarily due to the fact that the diffusion equation is not adequate for modelling the early photons, which travel a more ballistic, i.e., non-diffuse, path. For the mean-time of flight data-type, the largest error was also observed between MC and FEM; however, in this case, the emission mean-time of flight showed a larger mismatch compared to the excitation. In all models and for both data types, either for intensity or mean-time of flight, the mismatch diminished as the source-detector distance was increased. Demonstrating the utility of normalising emission data, Figure 2(e) and (f) display the difference between normalised data-sets for FEM and MC models. For both intensity and mean-time of flight, the data mismatch is greatly reduced using Born normalization, supporting the use of such normalisation for routine fluorescence image reconstruction using experimental data. However, further work is needed to investigate the effect of different heterogeneous optical properties at excitation and emission wavelengths, and whether such normalisation would still provide better information about imbedded fluorescence markers.
In the simulation comparison experiment, the analytical model and the FEM model showed the strongest correlation, likely because both models rely on the Diffusion Approximation. The major difference between these models is the type of boundary conditions employed. The FEM employs type III boundary conditions, which have been shown to more accurate than the extrapolated boundary conditions employed by the analytical model (Schweiger et al., 1995).
The accuracy of integrated time-bin normalized Born-Ratio data between the FEM and MC demonstrated that for small source/detector separations the mismatch for early time-bins (< 1 ns) is lower than for later arriving photon time-bins: Figure 3. Although this finding may be intuitive, it does demonstrate the need to take into account source/detector distance-specific time-bins for imaging, using the diffusion approximation, and not a globally specified early photon time-bin, to improve accuracy of image reconstruction.
Finally, the general framework for image reconstruction using 3D FEM for TD time-gated data is presented. Using a complex heterogeneous mouse model, it is shown that early time-bin data can provide better localization and a combination of early and late time-bins can further improve contrast as compared to total intensity data (Figure 5 and Table 3). However the reconstructed peak values shown in this paper do not reach the expected values, which is primarily due to the incorrect homogeneous assumption of the optical properties within the image reconstruction. This can be further improved by the utilization of additional reconstruction steps, whereby the background optical properties may be approximated using the excitation and emission data prior to fluorescence reconstruction, together with utilization of a-priori structural information from dual modality systems (Davis et al., 2007; Kepshire et al., 2009).
4. Conclusion
In this paper, a 3D FEM based diffuse time domain model for near-infrared light transport in biological tissue is presented and validated using both analytical and Monte Carlo solutions. This new functionality allows simulation of both excitation and fluorescence TPSFs for heterogeneous scattering and absorbing media in arbitrary geometries. The paper focused on the development of the model and evaluations were performed theoretically via comparisons with analytical and MC. The TPSF data-types presented in the comparisons include the TPSF curves for a range of source/detector separations, the normalised light fluence, the mean time of photon arrival, the absolute difference of the mean-time, and the percentage error between measured and simulated intensity.
It has been demonstrated that using a 3D FEM implementation of the TD diffusion-based light propagation model, both the excitation and emission photon transport in a phantom can be modelled to create time dependant information with the lowest accuracy seen at the very early arriving photons. Model based image reconstruction based on FEM implementation has been outlined together with the utilisation of multiple integrated time-bin intensity data demonstrating the benefits of incorporating early and late time-bins for the improvement of image accuracy.
Acknowledgments
This work has been funded by the National Institutes of Health (NIH) grants RO1 CA132750, RO1 CA120368 and K25 CA138578 through the National Cancer Institute (NCI). The TD FEM code is distributed as part of the NIRFAST modeling software at http://www.nirfast.org.
References
- Alexandrakis G, Rannou FR, Chatziioannou AF. Tomographic bioluminescence imaging by use of a combined optical-PET (OPET) system: a computer simulation feasibility study Phys. Med. Biol. 2005;50:4225–41. doi: 10.1088/0031-9155/50/17/021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arridge SR, Schweiger M. Photon-measurement density functions. Part2: Finite-element-method calculations. Applied Optics. 1995;34:8026–37. doi: 10.1364/AO.34.008026. [DOI] [PubMed] [Google Scholar]
- Arridge SR, Schweiger M, Hiraoka M, Delpy DT. A Finite Element Approach for Modeling Photon Transport in Tissue. Med. Phys. 1993;20:299–309. doi: 10.1118/1.597069. [DOI] [PubMed] [Google Scholar]
- Davis SC, Dehghani H, Wang J, Jiang S, Pogue BW, Paulsen KD. Image-guided diffuse optical fluorescence tomography implemented with Laplacian-type regularization. Optics Express. 2007;15:4066–82. doi: 10.1364/oe.15.004066. [DOI] [PubMed] [Google Scholar]
- Dehghani H, Eames ME, Yalavarthy PK, Davis SC, Srinivasan S, Carpenter CM, Pogue BW, Paulsen KD. Near Infrared Optical Tomography using NIRFAST: Algorithms for Numerical Model and Image Reconstruction Algorithms. Communications in Numerical Methods in Engineering. 2008 doi: 10.1002/cnm.1162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dehghani H, Srinivasan S, Pogue BW, Gibson A. Numerical modelling and image reconstruction in diffuse optical tomography. Phil. Trans. R. Soc. A. 2009;367:3073–93. doi: 10.1098/rsta.2009.0090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dogdas B, Stout D, Chatziioannou AF, Leahy RM. Digimouse: a 3D whole body mouse atlas from CT and cryosection data. phys med biol. 2007;52:577–87. doi: 10.1088/0031-9155/52/3/003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ducros N, Herve L, Da Silva A, Dinten JM, Peyrin F. A comprehensive study of the use of temporal moments in time-resolved diffuse optical tomography: part I. Theoretical material. Physics in Medicine and Biology. 2009;54:7089–105. doi: 10.1088/0031-9155/54/23/004. [DOI] [PubMed] [Google Scholar]
- Fang Q, Boas DA. Monte Carlo simulation of photon migration in 3D turbid media accelerated by graphics processing units. Opt Express. 2009;17:20178–90. doi: 10.1364/OE.17.020178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao F, Niu H, Zhao H, Zhang H. The forward and inverse models in time-resolved optical tomography imaging and their finite-element method solutions. Image and Vision Computing. 1998;16:703–12. [Google Scholar]
- Gao F, Zhao H, Tanikawa Y, Yamada Y. A linear, featured-data scheme for image reconstruction in time-domain fluorescence molecular tomography. Opt Express. 2006;14:7109–24. doi: 10.1364/oe.14.007109. [DOI] [PubMed] [Google Scholar]
- Gao F, Zhao H, Yamada Y. Improvement of image quality in diffuse optical tomography by use of full time-resolved data. Applied Optics. 2002;41:778–91. doi: 10.1364/ao.41.000778. [DOI] [PubMed] [Google Scholar]
- Gao F, Zhao H, Zhang L, Tanikawa Y, Marjono A, Yamada Y. A self-normalized, full time-resolved method for fluorescence diffuse optical tomography. Opt Express. 2008;16:13104–21. doi: 10.1364/oe.16.013104. [DOI] [PubMed] [Google Scholar]
- Gross S, Piwnica-Worms D. Molecular imaging strategies for drug discovery and development. Curr Opin Chem Biol. 2006;10:334–42. doi: 10.1016/j.cbpa.2006.06.028. [DOI] [PubMed] [Google Scholar]
- Hattery D, Chernomordik V, Loew M, Gannot I, Gandjbakhche A. Analytical solutions for time-resolved fluorescence lifetime imaging in a turbid medium such as tissue. J Opt Soc Am A Opt Image Sci Vis. 2001;18:1523–30. doi: 10.1364/josaa.18.001523. [DOI] [PubMed] [Google Scholar]
- Hielscher AH, Klose AD, Hanson KM. Gradient-based iterative image reconstruction scheme for time-resolved optical tomography. Ieee Transactions On Medical Imaging. 1999;18:262–71. doi: 10.1109/42.764902. [DOI] [PubMed] [Google Scholar]
- Hillman EM. Experimental and theoretical investigations of near infrared tomographic imaging methods and clinical applications. University College; London: 2002. [Google Scholar]
- Houston ST, Jones LW, Waluch V. Nuclear magnetic resonance imaging in detecting and staging prostatic cancer. Urology. 1988;31:171–5. doi: 10.1016/0090-4295(88)90050-7. [DOI] [PubMed] [Google Scholar]
- Jiang HB. Frequency-domain fluorescent diffusion tomography: a finite-element-based algorithm and simulations. Applied Optics. 1998;37:5337–43. doi: 10.1364/ao.37.005337. [DOI] [PubMed] [Google Scholar]
- Jin J, Venugopal V, Intes X. Monte Carlo based method for fluorescence tomographic imaging with lifetime multiplexing using time gates. Biomedical Optics Express. 2011;2:871–86. doi: 10.1364/BOE.2.000871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kepshire D, Mincu N, Hutchins M, Gruber J, Dehghani H, Hypnarowski J, Leblond F, Khayat M, Pogue BW. A microcomputed tomography guided fluorescence tomography system for small animal molecular imaging. rev Sci Inst. 2009;90 doi: 10.1063/1.3109903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar AT, Skoch J, Bacskai BJ, Boas DA, Dunn AK. Fluorescence-lifetime-based tomography for turbid media. Opt Lett. 2005;30:3347–9. doi: 10.1364/ol.30.003347. [DOI] [PubMed] [Google Scholar]
- Kumar ATN, Raymond SB, Boverman G, Boas DA, Bacskai BJ. Time resolved fluorescence tomography of turbid media based on lifetime contrast. Optics Express. 2006;14:12255–70. doi: 10.1364/oe.14.012255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lam S, Lesage F, Intes X. Time Domain Fluorescent Diffuse Optical Tomography: analytical expressions. Opt Express. 2005;13:2263–75. doi: 10.1364/opex.13.002263. [DOI] [PubMed] [Google Scholar]
- Leblond F, Davis SC, Valdes PA, Pogue BW. Pre-clinical whole-body fluorescence imaging: Review of instruments, methods and applications. J Photochem Photobiol B. 2010a;98:77–94. doi: 10.1016/j.jphotobiol.2009.11.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leblond F, Dehghani H, Kepshire D, Pogue BW. Early-photon fluorescence tomography: spatial resolution improvements and noise stability considerations. J Opt Soc Am A Opt Image Sci Vis. 2009;26:1444–57. doi: 10.1364/josaa.26.001444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leblond F, Tichauer KM, Pogue BW. Singular value decomposition metrics show limitations of detector design in diffuse fluorescence tomography. Biomedical Optics Express. 2010b;1:1514–31. doi: 10.1364/BOE.1.001514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee J, Sevick-Muraca EM. Three-dimensional fluorescence enhanced optical tomography using referenced frequency-domain photon migration measurements at emission and excitation wavelengths. JOSA A. 2002;19:759–71. doi: 10.1364/josaa.19.000759. [DOI] [PubMed] [Google Scholar]
- Li Z, Niedre M. Hybrid use of early and quasi-continuous wave photons in time-domain tomographic imaging for improved resolution and quantitative accuracy. Biomedical Optics Express. 2011;2:665–79. doi: 10.1364/BOE.2.000665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luker GD, Luker KE. Optical imaging: current applications and future directions. J Nucl Med. 2008;49:1–4. doi: 10.2967/jnumed.107.045799. [DOI] [PubMed] [Google Scholar]
- Marjono A, Yano A, Okawa S, Gao F, Yamada Y. Total light approach of time-domain fluorescence diffuse optical tomography. Opt Express. 2008;16:15268–85. doi: 10.1364/oe.16.015268. [DOI] [PubMed] [Google Scholar]
- Massoud TF, Paulmurugan R, Gambhir SS. Molecular imaging of homodimeric protein-protein interactions in living subjects. FASEB J. 2004;18:1105–7. doi: 10.1096/fj.03-1128fje. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niedre M, Ntziachristos V. Comparison of fluorescence tomographic imaging in mice with early-arriving and quasi-continuous-wave photons. Opt Lett. 2010;35:369–71. doi: 10.1364/OL.35.000369. [DOI] [PubMed] [Google Scholar]
- Niedre M, Valim N, Brock J. Experimental measurement of time-dependant photon scatter for diffuse optical tomography. Journal of Biomedical Optics. 2010;15 doi: 10.1117/1.3523371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niedre MJ, deKleine RH, Aikawa E, Kirsch DG, Weissleder R, Ntziachristos V. Early photon tomography allows fluorescence detection of lung carcinomas and disease progression in mice in vivo. Proc Natl Acad Sci U S A. 2008;105:19126–31. doi: 10.1073/pnas.0804798105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Leary MA, Boas DA, X.D. L, Chance B, Yodh AG. Fluorescence lifetime imaging in turbid media. Opt. Lett. 1996;21:158–60. doi: 10.1364/ol.21.000158. [DOI] [PubMed] [Google Scholar]
- Palmedo H, Hensel J, Reinhardt M, Von Mallek D, Matthies A, Biersack HJ. Breast cancer imaging with PET and SPECT agents: an in vivo comparison. Nucl Med Biol. 2002;29:809–15. doi: 10.1016/s0969-8051(02)00342-6. [DOI] [PubMed] [Google Scholar]
- Patterson MS, Pogue BW. Mathematical model for time-resolved and frequency-domain fluorescence spectroscopy in biological tissues. Appl. Opt. 1994;33:1963–74. doi: 10.1364/AO.33.001963. [DOI] [PubMed] [Google Scholar]
- Preisa T, Virnaua P, Paul W, Schneidera JJ. GPU accelerated Monte Carlo simulation of the 2D and 3D Ising model. Journal of Computational Physics. 2009;228:4468–77. [Google Scholar]
- Riley J, Hassan M, Chernomordik V, Gandjbakhche A. Choice of data types in time resolved fluorescence enhanced diffuse optical tomography. Med Phys. 2007;34:4890–900. doi: 10.1118/1.2804775. [DOI] [PubMed] [Google Scholar]
- Ripoll J, Nieto-Vesperinas M, Weissleder R, Ntziachristos V. Fast analytical approximation for arbitrary geometries in diffuse optical tomography. Opt Lett. 2002;27:527–9. doi: 10.1364/ol.27.000527. [DOI] [PubMed] [Google Scholar]
- Rudin M, Weissleder R. Molecular imaging in drug discovery and development. Nat Rev Drug Discov. 2003;2:123–31. doi: 10.1038/nrd1007. [DOI] [PubMed] [Google Scholar]
- Schweiger M, Arridge SR. Near-infrared imaging: Photon measurement density functions. Proc. SPIE. 1995;2389 [Google Scholar]
- Schweiger M, Arridge SR. Application of temporal filters to time resolved data in optical tomography. phys med biol. 1999;44:1699–717. doi: 10.1088/0031-9155/44/7/310. [DOI] [PubMed] [Google Scholar]
- Schweiger M, Arridge SR, Hiroaka M, Delpy DT. The Finite Element Model for the Propagation of Light in Scattering Media: Boundary and Source Conditions. Med. Phys. 1995;22:1779–92. doi: 10.1118/1.597634. [DOI] [PubMed] [Google Scholar]
- Soloviev VY, Tahir KB, McGinty J, Elson DS, Neil MA, French PM, Arridge SR. Fluorescence lifetime imaging by using time-gated data acquisition. Appl Opt. 2007;46:7384–91. doi: 10.1364/ao.46.007384. [DOI] [PubMed] [Google Scholar]
- Soubret A, Ripoll J, Ntziachristos V. Accuracy of fluorescent tomography in the presence of heterogeneities: study of the normalized Born ratio. IEEE Trans Med Imaging. 2005;24:1377–86. doi: 10.1109/tmi.2005.857213. [DOI] [PubMed] [Google Scholar]
- Vishwanath K, Mycek MA. Time-resolved photon migration in bi-layered tissue models. Opt Express. 2005;13:7466–82. doi: 10.1364/opex.13.007466. [DOI] [PubMed] [Google Scholar]
- Warner E, Plewes DB, Shumak RS, Catzavelos GC, DiProspero LS, Yaffe MJ, Goel V, Ramsay E, Chart PL, ColeD EC, Taylor GA, Cutrara M, Samuels TH, Murphy JP, Murphy JM, Narod SA. Comparison of breast magnetic resonance imaging, mammography, and ultrasound for surveillance of women at high risk for hereditary breast cancer. Journal of Clinical Oncology. 2001;19:3524–31. doi: 10.1200/JCO.2001.19.15.3524. [DOI] [PubMed] [Google Scholar]
- Wu J, Perelman L, Dasari RR, Feld MS. Fluorescence tomographic imaging in turbid media using early-arriving photons and Laplace transforms. Proc Natl Acad Sci U S A. 1997;94:8783–8. doi: 10.1073/pnas.94.16.8783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang L, Lee KC, Bhojani MS, Khan AP, Shilman A, Holland EC, Ross BD, Rehemtulla A. Molecular imaging of Akt kinase activity. Nat Med. 2007;13:1114–9. doi: 10.1038/nm1608. [DOI] [PubMed] [Google Scholar]