Skip to main content
PMC home page
Astrobiology logoLink to Astrobiology
. 2011 Mar;11(2):105–114. doi: 10.1089/ast.2010.0475

Testing Anthropic Selection: A Climate Change Example

Dave Waltham 1,✉
PMCID: PMC3697027  PMID: 21401338

Abstract

Planetary anthropic selection, the idea that Earth has unusual properties since, otherwise, we would not be here to observe it, is a controversial idea. This paper proposes a methodology by which to test anthropic proposals by comparison of Earth to synthetic populations of Earth-like planets. The paper illustrates this approach by investigating possible anthropic selection for high (or low) rates of Milankovitch-driven climate change. Three separate tests are investigated: (1) Earth-Moon properties and their effect on obliquity; (2) Individual planet locations and their effect on eccentricity variation; (3) The overall structure of the Solar System and its effect on eccentricity variation. In all three cases, the actual Earth/Solar System has unusually low Milankovitch frequencies compared to similar alternative systems. All three results are statistically significant at the 5% or better level, and the probability of all three occurring by chance is less than 10−5. It therefore appears that there has been anthropic selection for slow Milankovitch cycles. This implies possible selection for a stable climate, which, if true, undermines the Gaia hypothesis and also suggests that planets with Earth-like levels of biodiversity are likely to be very rare. Key Words: Planetary habitability and biosignatures—Intelligence—Paleoenvironment and paleoclimate—Co-evolution of Earth and life—Complex life. Astrobiology 11, 105–114.

1. Introduction

This paper concerns a simple but important question: Is our world a typical product of planetary formation processes, or does it exhibit an unusual combination of properties that were necessary preconditions for the emergence of intelligent life? Any such prerequisites must be present on Earth, even if they are extremely rare in the general population of planets, since “what we can expect to observe must be restricted by the conditions necessary for our presence as observers” (Carter, 1974). Clearly, this is a near tautology; so the interesting question is not whether it is true, but rather, whether its effects are significant. Critically for astrobiology, if these effects are significant, then planets that have Earth-like levels of biodiversity may be very rare.

The application of such “anthropic selection” ideas, to Earth, is not new (Carter, 1983; Barrow and Tipler, 1986; Ward and Brownlee, 2000), but anthropic selection remains controversial (Kasting, 2001), partly because it is a difficult hypothesis to test (Larson, 2007). Another reason for skepticism is the often unspoken assumption that Darwinian natural selection can account for any apparent life-friendliness of the environment, that is, life is fine-tuned to the environment rather than the environment's being fine-tuned for life. Another issue for anthropic selection is that many of its effects would also be mimicked if the Gaia hypothesis is correct, that is, that life modifies the environment in ways which are beneficial to itself (Lovelock and Watson, 1982; Lovelock and Whitfield, 1982), since this would again lead to apparent fine-tuning of the environment. However, even with allowance for these alternate interpretations, there are limits to the adaptability of organisms and to the ability of organisms to adapt their environment as shown, for example, by the low biological activity of the very dry Atacama Desert (Navarro-González et al., 2003). Thus, there must be anthropic selection effects at some level.

This paper proposes a methodology with which to investigate anthropic selection claims and illustrates the approach by analyzing whether Earth has an unusually high (or low) rate of Milankovitch-driven climate change. The objectives are, therefore, to demonstrate that anthropic ideas can be tested and, by doing so for a specific case, to demonstrate that anthropic selection effects can be significant.

The paper begins by expanding upon Carter (1983) and Waltham (2007), in which Bayesian statistics were used to describe how the ensemble properties of inhabited worlds will differ from those of the general population of planets. In particular, links between this Bayesian framework and the use of computer models to generate artificial ensembles of alternate worlds will be introduced. Also, the manner in which rapid climate change may help, or inhibit, the emergence of intelligent life will be briefly described, followed by a more specific examination of Milankovitch-cycle mechanisms for climate change, since these are amenable to computer modeling. With this background established, it will be shown that the properties of the Earth-Moon system and the architecture of the entire Solar System suggest that there has been anthropic selection for slow Milankovitch cycles.

2. Bayesian Framework

Bayes' theorem gives an elegant way to express the concept of anthropic selection (Carter,1983; Waltham, 2007). The probability distribution of a relevant planetary property (e.g., water mass fraction, surface temperature, magnetic field strength) will, in general, be expected to be different for inhabited worlds than for a wider population of planets. These two different probability distributions are linked by Bayes' theorem

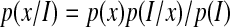graphic file with name M1.gif (1)

where p(x/I) is the distribution of property x for inhabited planets, p(x) is the probability distribution for a wider population of planets, p(I/x) is the probability that a planet having property x will be inhabited, and p(I) is a normalization constant (i.e., not dependent upon x) given by the fraction of planets that are inhabited.

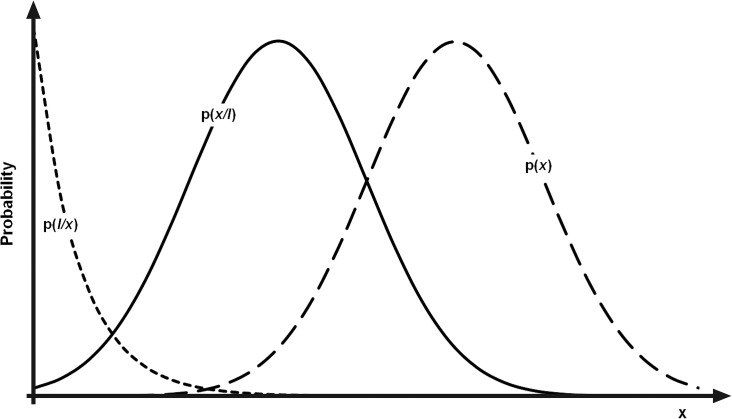
Figure 1 shows schematically how this expression behaves for the example of a property that discourages the emergence of intelligent life, that is, a property where p(I/x) reduces with increasing x. Under these conditions, the product p(x) · p(I/x) in Eq. 1 has a peak at low x compared to p(x), so p(x/I) also peaks at relatively low x. Thus, inhabited worlds have a probability distribution that is shifted to small x relative to the distribution for planets in general. For the opposite case, where higher values of x encourage the appearance of intelligent life, the peak in p(x/I) will shift up instead of down. Some properties will not influence the appearance of intelligent life at all, in which case p(I/x) will be constant for all significant values of p(x) and hence p(x/I) will have exactly the same form as p(x). Finally, planetary properties may have a more complex influence where, for example, p(x/I) peaks at some value (e.g., for surface temperatures there is probably a peak at values which promote long-lived liquid water); nevertheless, the effect of Eq. 1 will be to give inhabited worlds a different probability distribution for such properties than the general planetary population.

FIG. 1.

FIG. 1.

Open in a new tab

Schematic illustration of Bayes' Theorem as applied to anthropic selection. p(x) is the probability distribution of property x for a general population of planets. p(I/x) models how the probability of the emergence of intelligence varies with x. In the case illustrated here, intelligence is most likely when x is small. p(x/I) is the resulting probability distribution of x for the subset of planets which happen to be inhabited. Note that the most likely value of x is smaller for inhabited worlds, that is, there is an anthropic selection effect.

Given this framework, it is clear that significant anthropic selection will manifest itself as a change in the probability distribution of an anthropically affected property for inhabited worlds compared to the equivalent distribution for a more general planetary population. However, measurement of such distributions is not currently possible since our sample for general planets is highly biased by planet-searching techniques (e.g., the radial velocity method is biased toward large planets in small orbits), while our knowledge of inhabited worlds is limited to a single specimen (i.e., Earth). This last problem is not too serious, since all we need do is demonstrate that Earth is unlikely to be drawn from p(x), for example, by showing that it differs significantly from the mean. This is a much less sensitive test than, say, a chi-squared comparison of two complete distributions, but it will still show up any strong anthropic effects. The real problem lies in estimating p(x). In this paper, I propose side-stepping the issue by using computer modeling as described in the next section.

3. Computer Model Estimation of Local Distribution Functions

The previous section was slightly vague about the population of planets used to calculate the global distribution function p(x). In fact, any sensible and well-defined subset of planets can be used. For example, if p(x) is estimated for all terrestrial planets, the resultant function p(x/I) will be the equivalent probability distribution for all inhabited terrestrial planets. It is therefore valid to define the wider population in any convenient fashion provided it is remembered that the resultant p(x/I) applies only to an appropriately defined subset of all inhabited worlds. In the remainder of this paper, I will use synthetic “Earth-like” populations of planets to define p(x), that is, I will compare Earth to other very similar planets.

This approach therefore compares the true Earth to other nearby (in parameter space) systems and can be thought of as doing a local, rather than global, comparison. Nevertheless, the comparison is still useful because anthropic processes, by selecting globally, will also necessarily select locally; that is, if there is an anthropic bias, it will show up locally, too. This may be thought of as analogous to finding a local minimum in an optimization problem; it does not prove that a global minimum has been found, but it does demonstrate that optimization has occurred.

Furthermore, using Earth-like populations of planets is clearly a reasonable choice in the sense that we know that at least one such system exists. Indeed, if it is not a sensible choice (i.e., because such systems are exceedingly rare), then this itself supports the proposal that Earth has been influenced by significant anthropic selection.

4. Climate Change and Intelligent Life

Later in this paper, the methodology outlined above will be used to discern a possible anthropic influence on Earth's rate of climate change. Here, I will briefly outline ways in which climate change may influence the evolution of complex life in general and the emergence of intelligent life in particular.

It is widely recognized that regions of Earth that have stable temperatures (e.g., tropical rainforests) have high levels of biodiversity (see review by Wilson, 2001). The hypothesis that this link is direct and causal is reinforced by the observation that the deep ocean seafloor also has high biodiversity (Sanders, 1968), even though the conditions are, stability excepted, poor and biological productivity therefore low. Further evidence of a link between rapid climate change and loss of species richness has been gleaned from studies of Earth's glacial-interglacial cycles. The most recent ice ages have resulted in reduced biodiversity within the temperate zones where the greatest changes in climate occurred (see review by Hewitt, 2004). There are, therefore, two independent lines of evidence that support the proposition that biodiversity is, in general, lower when climate change is significant.

Given this link between climate change and species diversity, it is plausible that planets with high climate variability may be less likely to produce intelligent observers than planets with more stable conditions. However, it is also arguable that the ultimate emergence of intelligent species is actually encouraged by adverse conditions because these help to clear ecological niches (cf. the adaptive radiation of mammals following demise of the dinosaurs) and because evolutionary innovations may be particularly advantageous during testing times [cf. the emergence of Homo sapiens during the relatively unstable Neogene (Calvin, 1991, 2002; Stanley, 1996) and the emergence of multicellular life around the time of the Neoproterozoic glaciation (Hyde et al., 2000; Kirschvink et al., 2000)]. There may be truth in both views; that is, the probability of emergence of intelligence may be maximized by a combination of high biodiversity and occasional adversity. In this context, it is worth noting that, following mass extinction events on Earth, it typically took ∼10 million years for full biodiversity to be restored (Kirchner and Well, 2000; Sahney and Benton, 2008), and this timescale may control the minimum length of typical stable periods necessary to provide the raw materials for natural selection during subsequent times of hardship.

In summary, there are good arguments to suggest that the emergence of intelligent observers may be encouraged by rapid climate change, but there are equally good arguments that suggest the opposite or, even, that climate change has no significant effect whatsoever. Based upon existing studies of life on Earth, therefore, it is far from clear whether climate stability is good, bad, or broadly neutral in encouraging the eventual evolution of intelligence. However, the methodology proposed in this paper can be used to distinguish between these three possibilities.

To make further progress, I concentrate on the climatic influence of Milankovitch cycles, that is, the periodic variations in Earth's climate that are induced by changes in Earth's orbit and orientation in space. The key factors here are axial precession (time varying axis orientation), orbital precession (time varying orbital orientation), and time variation in orbital eccentricity (circularity of the orbit). Note that changes in obliquity (the tilt of Earth's axis relative to its orbit) are the consequence of interaction between axial precession and orbital precession, and this important factor is therefore included in the following analyses.

The evidence that Milankovitch cycles affect Earth's climate is secure. Isotopic analyses of deep-sea sediment cores (Shackleton and Pisias, 1985; Zachos et al., 2001) and ice cores (Petit et al., 1999) have shown convincing evidence of periodic ice volume and temperature changes which correlate well with the frequencies of insolation-variation produced by Milankovitch cycles. The detailed processes that allow subtle orbital changes to affect global climate remain uncertain (e.g., Lisiecki et al., 2008), but the general mechanism is clear: the intensity of Earth's seasons is controlled by obliquity variations, eccentricity variations, and the slowly changing relationship between solstices and perihelion (Ruddiman, 2000). These small changes in seasonal intensity alter the overall climate of Earth via feedback mechanisms [e.g., ice-albedo feedback (Kellog, 1973; Curry and Schramm, 1995)]. There is evidence in the rock record that the resulting climate cycles operated throughout Earth's history (e.g., Grotzinger, 1986) and that they have a particularly profound effect during cooler times when they drive glacial-interglacial transitions (Shackleton and Pisias, 1985; Zachos et al., 2001).

5. Earth Axis Precession Example

One of the key frequencies driving Earth's current ice ages is a ∼41,000 year oscillation in its obliquity, over the range 22.1–24.5°, which shows up clearly in frequency analyses of deep-sea sediment cores (Shackleton and Pisias, 1985; Zachos et al., 2001) and ice cores (Petit et al., 1999). Obliquity variation, in turn, results from the interaction between Earth axis precession (dominantly at 50.5″/y) and Earth orbit precession (dominated by an oscillation at − 18.7″/y), which add to give a dominant obliquity frequency of 31.8″/y (equivalent to a periodicity of 40,700 years). The rate at which Earth's axis precesses is therefore an important indirect factor that controls the frequency of Ice Ages.

I will now examine whether the actual precession rate for Earth is unusually low (or high) compared to other, suitably defined Earth-like systems. More formally, the null hypothesis to be tested is that there is no difference between the precession rate probability distribution of inhabited Earth-like systems compared to the probability distribution for all Earth-like systems. As discussed earlier, the comparison can be made between the Earth and a “local” probability distribution which, in this case, will be defined by “Earths” which are identical in every way to our own world except that differences in the Moon-forming collision (Canup and Asphaug, 2001) 4.52 billion years ago (Lee et al., 1997; Kleine et al., 2005) resulted in a different present-day precession rate.

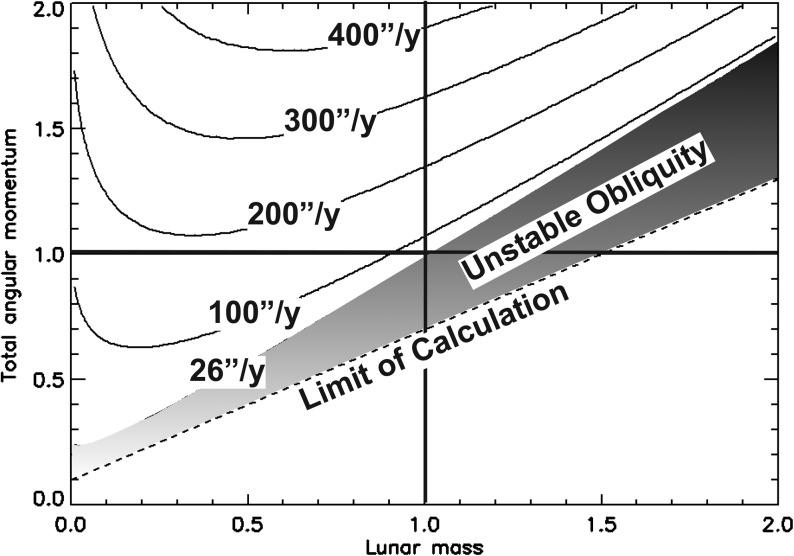
Earth's precession rate is controlled by its rate of spin and by the size of tidal forces exerted by the Sun and Moon on its equatorial bulge. Waltham (2004) examined how present-day precession rates (i.e., after 4.52 billion years of Earth-Moon system evolution) would change had the Moon-forming collision resulted in a different-sized Moon or a different total angular momentum in the Earth-Moon system, or both. The calculations are bounded by a minimum lunar mass of zero, the requirement that there be enough angular momentum for the Moon to be in orbit, and the requirement that there not be so much angular momentum that Earth breaks up. Further details of these calculation boundaries are given in Waltham (2004). One further important boundary appears in these calculations and is shown in Fig. 2. As tidal drag slows Earth's rotation over time and, hence, the precession rate, a critical value of 26″/y is crossed, at which point resonant interactions with the major planets of the Solar System render our obliquity chaotically unstable (Laskar et al., 1993; Tomasella et al., 1996). Hence, all Earth-Moon systems to the right of this limit have passed through this chaotic region before reaching the modeled age of 4.52 billion years. In addition, as Laskar and Robutel (1993) showed, below this threshold there are a large number of further resonances, that is, 26″/y is merely the first to be reached. All Earth-Moon systems to the right of this line will therefore have experienced one or more periods of rapid and dramatic change in obliquity.

FIG. 2.

FIG. 2.

Open in a new tab

The precession rates for Earth-like planets 4.52 billion years after a moon-forming impact. Axes show the total angular momentum and lunar mass resulting from the impact and are normalized by the true values for the actual Earth-Moon system. Note that a moderately different angular momentum, or lunar mass, results in either an unstable obliquity (where precession <26″/y) or more rapid precession than that of the true Earth (i.e., >50″/y). Thus, the actual Earth-Moon properties are apparently fine-tuned to give slow Milankovitch cycles. For further details see Waltham (2004).

This result may seem at variance with the widely held belief that a large Moon increases Earth's axial stability. The direct result of increasing the Moon's mass is indeed to increase tidal torque on Earth's equatorial bulge and hence increase the precession rate (and hence avoid chaotic instability). However, the increased tidal drag associated with a larger Moon also has the effect of slowing Earth's rotation, which reduces the equatorial bulge. In addition, the increased tidal drag causes the Moon to recede more rapidly, and this also reduces the tidal torque. The overall result of these processes is that a larger Moon actually decreases Earth's precession rate (and axial stability) given sufficient time. This result has been widely reported (e.g., Ward, 1982; Kasting 2001; Waltham 2004), but the idea that a large Moon increases axial stability remains ingrained in much astrobiology literature. The more correct statement that Earth's Moon is close to the maximum size compatible with axial stability is of much greater astrobiological interest and deserves wider recognition.

Figure 2 shows that precession rates increase as lunar mass drops or angular momentum increases. Hence, the minimum rates of change in axial orientation lie immediately adjacent to the chaotic-obliquity boundary. Critically, as shown in Fig. 2, this is the region occupied by the true Earth-Moon system, which therefore has an unusually low precession rate compared to most other, similar, systems. This can be explained as resulting from anthropic selection for slow obliquity change. Above and to the left of this region there is high precession (and hence high rates of obliquity change), whereas below and to the right of this region the obliquity becomes chaotic (and hence changes rapidly). Note that this is a simpler and more consistent explanation for this remarkable coincidence than that given in Waltham (2004).

To recast this result in the language of probability distributions introduced earlier, it is necessary to assume that all lunar-mass/angular-momentum combinations within the calculated region of Fig. 2 are equally probable. Simulation results for moon-forming impacts over a wide range of possible conditions have not yet been reported in the literature since, understandably, work has concentrated upon finding impact conditions that reproduce the Earth-Moon system (e.g., see Canup and Asphaug, 2001; Canup et al., 2001; Canup, 2004; Morishima and Watanabe, 2004). However, it is relevant to note that most simulations tend to either produce moons that are too small or systems with too much angular momentum (Canup et al., 2001; Morishima and Watanabe, 2004). This implies that lunar-mass/angular-momentum combinations above and to the left of the actual Earth-Moon location in Fig. 2 are the most likely outcomes of the moon-forming collision. Hence, assuming uniform probability probably overestimates the likelihood of outcomes near the chaotic-instability boundary of Fig. 2. Note also that this analysis has excluded all outcomes to the right of the instability boundary; and, since there is no reason to think these will be excluded in reality, this also means that the probability derived below is likely to be an overestimate.

Given this conservative uniform probability assumption, it is a simple matter to estimate the likelihood of a system emerging with a precession rate as low, or lower, than that of the true Earth-Moon system. Of 20,900 simulated systems used to model the allowed lunar-mass/angular-momentum pairs, 160 simulations have a precession rate below 50.5″/y. Hence, the probability of the Earth-Moon system having a precession rate less than or equal to 50.5″/y by chance is 0.77%. The hypothesis that inhabited Earth-like systems have the same probability distribution for precession rate as the population of all Earth-like systems can therefore be rejected at the 1% significance level. In plain English, the precession rate of the Earth is unusually small compared to that of typical products of moon-forming collisions.

6. Orbital Precession Rates and the Architecture of the Solar System

In an attempt to demonstrate that the result above is not a coincidence but, rather, the consequence of anthropic selection for slow rates of Milankovitch-driven climate change, Earth's orbit will be considered now, which will give an independent test, since variations in orientation of Earth's orbit are controlled by different factors to those that control variation in the orientation of Earth's axis.

The most important controls on the rates of orbital change are the overall size of the solar system and the typical masses of the planets within it. Waltham (2007) showed that anthropic selection should result in planets within our system being relatively light or widely spaced compared to the planets of most other systems. This is a prediction that will be directly tested in coming decades as the results of space-based exoplanet searches become available, but it is worth noting that, already, micro-lensing surveys indicate that there are fewer solarlike planetary systems than would be expected if all planetary systems are analogues of our own (Gould et al., 2010).

However, a more subtle effect than that due to scale and mass is considered here: given a sample of planetary systems with the same scale (as set by the Sun-Neptune separation) and the same planetary masses as ours, do the specific planetary separations in our system give rise to unusually slowly precessing orbits? To answer this question, a population of solarlike planetary systems was simulated by altering the locations of the major planets so that the Milankovitch cycles of these systems can be compared to those of the Solar System.

In a simple planetary system consisting of a single planet orbiting a single star, the orbit shape and orientation is fixed for all time (neglecting relativistic effects and effects due to nonspherical bodies). However, as additional planets are introduced, mutual gravitational interactions result in orbits whose shapes and orientations vary in a quasi-cyclic manner. Techniques for modeling the resulting evolution of planetary orbits were developed by Laplace and Lagrange around the end of the 18th century. These Laplace-Lagrange secular equations produce a set of frequencies (denoted here by fi, 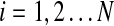Inline graphic where N is the number of planets) that governs the rate of change of orbital orientations and another set (denoted gi, 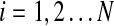Inline graphic) that governs the rate of change of orbital eccentricities. The Laplace-Lagrange equations, together with the masses and semimajor axes for the eight planets in our Solar System, therefore produce 16 fundamental frequencies. Following the procedure given in Murray and Dermott (1999, chapter 7), these are given in Table 1 along with the equivalent frequencies calculated by Brouwer and van Woerkom (1950), who included extra resonance and solar obliquity terms and Laskar (1985) who computed frequencies by Fourier transformation of direct computer simulations of planetary orbits. Note that the frequencies given by all three calculations are broadly comparable. The major differences lie in g5 and g6 as a result of a near resonance between Jupiter and Saturn not included in the simple calculations used in the present paper. In principle, such resonances could be added into the analysis by using the Brouwer and van Woerkom approach (1950) or modern numerical methods (e.g., those in Laskar, 1985), but such approaches would be prohibitively expensive given the many thousands of hypothetical systems modeled below. Fortunately, Table 1 gives confidence that the first-order approximations provided by the simple Laplace-Lagrange approach are adequate for the purposes of this paper.

Table 1.

Precession and Eccentricity Frequencies in the Solar System

  BW1950 La2004 MD1999 1.1aJ
f1 (″/y) −5.201 −5.590 −5.186 −4.351
f2 (″/y) −6.571 −7.050 −6.556 −5.545
f3 (″/y) −18.74 −18.85 −18.66 −17.09
f4 (″/y) −17.63 −17.76 −17.59 −13.75
f5 (″/y) 0.000 0.000 0.000 0.000
f6 (″/y) −25.73 −26.35 −25.98 −36.90
f7 (″/y) −2.902 −2.992 −2.907 −3.149
f8 (″/y) −0.678 −0.692 −0.679 −0.725
Mean f −9.681 −9.910 −9.695 −10.19
g1 (″/y) 5.463 5.590 5.447 4.972
g2 (″/y) 7.344 7.452 7.325 5.962
g3 (″/y) 17.33 17.37 17.27 13.73
g4 (″/y) 18.00 17.92 17.95 16.07
g5 (″/y) 4.296 4.257 3.730 4.330
g6 (″/y) 27.77 28.25 22.50 32.83
g7 (″/y) 2.719 3.088 2.706 2.944
g8 (″/y) 0.633 0.673 0.634 0.677
Mean g 10.44 10.58 9.695 10.19
Open in a new tab

Column 1: From Brouwer and van Woerkom (1950). Column 2: From Laskar et al. (2004). Column 3: Simple Laplace-Lagrange approach following Murray and Dermott (1999). Column 4: Simple Laplace-Lagrange approach with Jupiter orbital radius increased by 10%.

Regardless of which computational methods are used, a significant problem emerges when they are used to consider orbital evolution for Earth over billions of years (as required in this paper). As shown by Laskar (1999) and Laskar et al. (2004), it is not computationally feasible to reproduce the orbital elements of the inner four planets more than about 50 million years into the past. Beyond that, inevitable small measurement uncertainties in the present-day elements magnify to the point where the predicted elements become unusable.

Fortunately, this level of modeling detail is not necessary for the needs of this paper. In the Laplace-Lagrange method, the amplitudes and phases of the sinusoids associated with each of the frequencies from Table 1 vary from planet to planet and vary through time, and it is these that cannot be accurately tracked over billions of years. However, provided the masses and orbital radii remain unchanged, the fundamental frequencies themselves are fixed. Furthermore, all planets have significant components from all the frequencies, so the average frequency is an indication of the order of magnitude for orbital change rates for all the planets in our Solar System. This average may be expressed by the mean g-frequency or the mean f-frequency, but for the simple approach used here, these two are equal in magnitude but opposite in sign. Thus, the average g-frequency is sufficient to characterize the typical magnitude of either set. The resulting mean g-frequency is a property of the entire Solar System and is a single number that characterizes the rate of eccentricity change for all the planets in the Solar System.

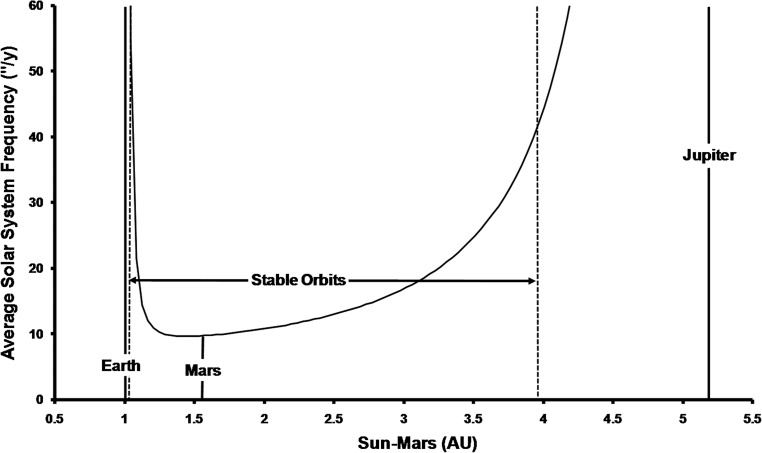
Table 1 shows what happens to the Laplace-Lagrange frequencies and the mean frequency if Jupiter is placed 10% farther from the Sun, while leaving all other planets in their true positions. All the characteristic frequencies alter, and the resulting mean frequency climbs to 10.189″/y. Similar analyses can be repeated for any planetary configuration. As an example, Fig. 3 shows how the mean frequency of the Solar System varies as Mars is moved through a range of locations with the orbital radii for all other planets fixed at their true values. Note that the minimum possible frequency occurs very close to the true location of Mars.

FIG. 3.

FIG. 3.

Open in a new tab

Mean eccentricity-change frequency of the entire Solar System as a function of Mars location. The actual location of Mars in our Solar System is shown, and this is very close to the location which gives minimum mean frequency. Thus, Mars' location is apparently fine-tuned to give slow Milankovitch cycles.

Further progress requires appropriate assumptions about the probability distribution for the Sun-Mars separation. Not all locations for Mars will be equally likely since interactions with other planets (especially Jupiter) will make some locations unstable. Studies of orbital stability (Gladman, 1993) have suggested that the orbit of a low-mass test particle (e.g., Mars) is stable if its minimum separation from a massive inner planet (Earth) or outer planet (Jupiter) is greater than 3.5 Hill radii with the Hill radii, Rh, given by

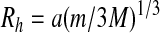graphic file with name M4.gif (2)

where a is the semimajor axis, m is the planet mass, and M is the central star mass. The locations of the resulting excluded zones are shown in Fig. 3. Further constraints on planetary locations will be considered later in this paper; but, for now, if all remaining locations are assumed to be equally probable, then only 5.0% of all possible locations for Mars result in an average frequency for the Solar System that is smaller than that found in the true Solar System.

However, this result for Mars is not particularly impressive since eight planets are under consideration and a probability this low should occur by chance for about one planet in 20. It is therefore necessary to look at all the planets. Similar analyses can be undertaken for each of the other planets except Mercury and Neptune (see Table 2). Mercury and Neptune set the overall scale of the system, and moving them gives a monotonic change in frequency rather than a minimum.

Table 2.

Probability That Moving an Individual Planet Will Reduce the Mean Eccentricity-Change Frequency of the Solar System

Venus 36.2%
Earth 32.6%
Mars 5.0%
Jupiter 0.8%
Saturn 82.2%
Uranus 34.7%
Open in a new tab

Mars and Jupiter have very low probability, whereas the other planetary locations are not statistically significant. Note that the probability of 2 (or more) results below 5% out of 6 planets is 3.2%.

In Table 2, only Mars and Jupiter have locations that appear to be statistically interesting, that is, have a probability ≤5% of occurring by chance. The probability that two or more planets out of six will fall below 5% can be calculated by using the binomial distribution, which yields an overall probability of 3.2%. Hence, the precise locations of the individual planets in the Solar System do result in a rate of change of eccentricity that is small compared to that typical of planetary systems constructed by making small modifications to the Solar System's architecture.

This is an encouraging result; but, in detail, the results in Table 2 are surprisingly variable, since it is easier to get a low average frequency by getting all planets in approximately the right locations than it is by getting some very precisely positioned (e.g., Jupiter) while having others with far-from-optimal placement (e.g., Saturn). One possible explanation is that the positions of individual planets are not independent variables. If there are dynamic constraints on relative locations of planets, then it may not be possible to get all planets simultaneously into “good” positions. This possible explanation for the anomalies in Table 2 will be investigated next.

7. Near-Commensurability

It has been known for several decades that there is a preference, within the Solar System, for near-commensurabilities in orbital period. For example, the time taken for Jupiter to orbit twice around the Sun (59.3 years) is almost the same as five times Saturn's orbital period (58.9 years). Statistical analysis of all such pairings (including those in the giant planet–satellite systems) by Roy and Ovenden (1954) showed that near-commensurabilities comfortably exceeded the number expected by chance at the 0.44% significance level (chosen to be equivalent to a 3σ deviation). More recent observations of near-commensurability in extrasolar planetary systems (Udry et al., 2007) suggest that this may be a common property in many planetary systems.

Goldreich (1965) attempted to explain near-commensurabilities for satellite systems. In his theory, tidal dissipation leads to evolution of satellite orbits at differing rates, so that, at some point in time, satellite pairs by chance approach near-commensurability. Once this occurs, perturbation theory indicates that satellites can exchange significant angular momentum. The evolution of the two satellites then becomes coupled, and the near-commensurability is locked in. Tidal dissipation is too small for this process to explain planetary (rather than satellite) near-commensurabilities, but Goldreich (1965) pointed out that “the stability proof discussed in this paper would apply equally well to other phenomena which might produce secular changes in semi-major axes.” He goes on to speculate that such forces were probably present during the formation of the Solar System and that this would explain planetary near-commensurabilities. More recent numerical modeling studies (e.g., Thommes et al., 2008) support this idea that effects such as gas-drag and planet-planet scattering in the early stages of planetary system formation produce evolution toward a relatively stable state in which there are near-commensurabilities in orbital periods.

Hence, both observation and theory support the idea that near-commensurability is a natural outcome of the evolution of planetary systems. This may explain the unexpected discrepancies seen in Table 2 and discussed earlier. To investigate this possibility, and following Roy and Ovenden (1954), the remainder of this section will assume that pairs of adjacent planets have orbital radii that give rise to orbital periods with ratios near n:m where 1 ≤ n ≤ 6 and 2 ≤ m ≤ 7, which gives rise to 15 distinct ratios. The overall scale of the resulting planetary systems will be fixed, as before, by keeping Neptune in its true location, and the ratios given above are then used to specify the orbits of the remaining seven planets. This gives rise to 157 ∼ 170 million alternate solar systems, which is far too many to model exhaustively; hence, specimen systems will be picked randomly from this population (i.e., Monte Carlo modeling is undertaken).

There is one further difficulty that must be discussed before the results of this modeling are presented. Strictly speaking, the simple Laplace-Lagrange method addressed breaks down when pairs of planets approach commensurability, since additional terms then become necessary in the equations, and these have the effect of greatly increasing the frequencies. This explains why the frequencies given in column 3 of Table 1 are slightly underestimated compared to those in columns 1 and 2 (which have some compensation for near-commensurability). Fortunately, the resulting resonance peaks are very sharp so that, as Table 1 demonstrates for the Solar System, this complication can be ignored as a first approximation, provided planets are merely close to, rather than precisely at, such locations. Hence, although the systems modeled below assume exact commensurability, the results actually approximate those for planetary systems where the semimajor axes have been modified slightly to move away from these resonance peaks.

Given this caveat, the mean frequency for each of the alternate solar systems described above can be calculated and compared to the mean frequency for the system closest to our Solar System (Table 3) that has a mean precession frequency of 10.2″/y (cf. 9.7″/y in Table 1). After modeling 10,000 randomly chosen systems, 3.9% ( = 386) of these have frequencies less than or equal to 10.2″/y. Thus, the particular configuration of near-commensurabilities in this system has an unusually low frequency compared to most alternate systems that have different combinations of near-commensurabilities. Furthermore, these results support the proposal given above that Saturn, in particular, is far from its individual optimal position because of additional constraints imposed on the structure of the Solar System by planetary formation processes and subsequent evolution.

Table 3.

Nearest Approximation to the Solar System Assuming That Orbital Periods of Adjacent Planets Are in the Exact Ratio n:m and That Neptune's Location Is Fixed to Set the Overall Scale

Inner planet Outer planet n m a true (AU) a predicted (AU)
Mercury Venus 2 5 0.39 0.36
Venus Earth 3 5 0.72 0.67
Earth Mars 1 2 1.00 0.94
Mars Jupiter 1 6 1.52 1.50
Jupiter Saturn 2 5 5.20 4.94
Saturn Uranus 1 3 9.54 9.11
Uranus Neptune 1 2 19.19 18.94
Neptune       30.07 30.07
Open in a new tab

8. Discussion

8.1. Milankovitch timescale sensitivity

The general methodology outlined in this paper is capable of discriminating between anthropic selection for slow climate change, anthropic selection for rapid climate change, or the possibility of no significant anthropic effect at all. Three separate tests for an anthropic effect on Milankovitch timescales have been attempted here, and all three show a clear preference in the true Earth for slow climate change compared to similar, alternate systems. Firstly, consideration of the properties of the Earth-Moon system suggests that only 0.77% of alternate models have slower precession (and hence obliquity) change. Secondly, treating the locations of the major planets as independent variables suggests that only 3.2% of alternate solar systems have slower average frequencies (hence slower rate of change of eccentricity). Finally, the assumption that the Solar System's structure can be approximated by one in which adjacent planets have simple relationships between their periods leads to the conclusion that only 3.9% of alternate structures have slower frequencies. The probability that the results from all three of these tests are purely coincidental is less than one in 105.

The motivation for looking at Milankovitch cycles is that demonstration of their optimization is a tractable problem. This approach was chosen despite the fact that Milankovitch cycles are a second-order influence on climate and of far less significance than factors such as solar (Newmann and Rood, 1977), biological (e.g., Gray, 1993), and geological processes (Walker et al., 1981). Given this, it is perhaps surprising that the Milankovitch-selection effect appears to be so strong.

The explanation for this surprisingly strong effect may lie in the particular periodicities typical of Milankovitch cycles (i.e., ∼104 to 106 years), since populations of organisms may be particularly sensitive to climate change on these particular timescales. Climate changes on much shorter timescales (i.e., ∼102 years) are comparable to large-organism lifetimes, so organisms must have adaptations to cope with such changes (e.g., hibernation as an adaptation to seasonal variations). On very long timescales (i.e., >106 years), on the other hand, climate change is sufficiently slow that organisms simply co-evolve with the climate by Darwinian selection. However, problems might occur on intermediate timescales where change may be too fast to allow Darwinian evolution but too slow for the full range of conditions to be experienced during the lifetime of an individual organism. Under these circumstances, organisms that happened to be adapted to a wide range of temperatures would be out-competed by organisms more closely adapted to current conditions. Closely adapted organisms might therefore flourish at the expense of climate generalists, but their descendants would be too specialized to cope with subsequent changes in conditions. In other words, on these interim timescales, there is no evolutionary stable strategy (Smith and Price, 1973), and organisms are unable to adapt effectively to medium-term changes in climate.

8.2. Alternate mechanisms

This paper has presented preliminary evidence that Earth's Milankovitch cycles are significantly slower than might be expected on a randomly chosen Earth-like planet in a randomly chosen solarlike planetary system and has suggested that this is the result of anthropic selection for slow climate change. One potential flaw in the foregoing arguments is that it is possible that Milankovitch-rate minimization is a general property of all dynamically stable planetary systems. The presently known small, incomplete, and highly biased sample of extrasolar planetary systems does not yet allow this alternate hypothesis to be directly tested, although this may become possible as the results from currently planned exoplanet-finding programs become available over the next few decades. This possibility could also be tested by using advanced planetary system modeling programs [e.g., “Mercury” developed by Chambers (1999)] to examine the long-term stability of a small sample of the systems generated for this paper. However, it is worth pointing out that the discovery that stable planetary systems have minimized Milankovitch frequencies would represent a major breakthrough in a celestial mechanics problem that has remained unsolved for centuries; namely, the problem of proving the stability of the Solar System. Proof of the stability of the Solar System has eluded Newton, Laplace, and Poincaré, among others, and such a simple solution seems far less likely than the explanation promoted in the present paper, that is, that this is a peculiar property of our Solar System and a consequence of anthropic selection. It is also worth mentioning that the dynamical stability explanation also fails to explain why the properties of the Earth-Moon system also show near minimization of Milankovitch-cycle frequencies.

Nevertheless, the anthropic selection explanation of the results from this paper is likely to be a controversial proposal, and further work will be required to confirm or refute this idea. Such work could use improved models of tidal-drag evolution and more detailed models of planetary orbit evolution. Future extrasolar planet search programs should also help to resolve the outstanding issues.

9. Conclusions

  • (1) Anthropic proposals can be tested by comparing Earth's properties to those of synthetic populations of Earth-like worlds generated with computer modeling.

  • (2) Investigation of Earth's Milankovitch cycles shows that these are relatively slow, and this may indicate anthropic selection for slow climate change.

  • (3) The Gaia hypothesis may have confused cause and effect, that is, climate stability might be a precondition for a complex biosphere rather than climate stability being the consequence of a complex biosphere.

  • (4) Planets with Earth-like levels of biodiversity may therefore be rare in the Universe.

References

  1. Barrow J.D. Tipler F.J. The Anthropic Cosmological Principle. Oxford University Press; Oxford: 1986. [Google Scholar]
  2. Brouwer D. van Woerkom A.J.J. Astronomical Papers Prepared for the Use of the American Ephemeris and Nautical Almanac. Vol. 13. The Nautical Almanac Office, U.S. Naval Observatory; Washington, DC: 1950. The secular variations of the orbital elements of the principal planets; pp. 81–107. [Google Scholar]
  3. Calvin W.H. The Ascent of Mind: Ice Age Climates and the Evolution of Intelligence. Bantam Books; New York: 1991. [Google Scholar]
  4. Calvin W.H. A Brain for All Seasons: Human Evolution and Abrupt Climate Change. University of Chicago Press; Chicago: 2002. [Google Scholar]
  5. Canup R.M. Simulations of a late lunar-forming impact. Icarus. 2004;168:433–456. [Google Scholar]
  6. Canup R.M. Asphaug E. Origin of the Moon in a giant impact near the end of the Earth's formation. Nature. 2001;412:708–712. doi: 10.1038/35089010. [DOI] [PubMed] [Google Scholar]
  7. Canup R.M. Ward W.R. Cameron A.G.W. A scaling relationship for satellite-forming impacts. Icarus. 2001;150:288–296. [Google Scholar]
  8. Carter B. Confrontation of Cosmological Theories with Observational Data. IAU Symposium No. 63; Reidel, Dordrecht: 1974. Large number coincidences and the anthropic principle in cosmology; pp. 291–298. [Google Scholar]
  9. Carter B. The anthropic principle and its implications for biological evolution. Philos Transact A Math Phys Eng Sci. 1983;310:347–363. [Google Scholar]
  10. Chambers J.E. A hybrid symplectic integrator that permits close encounters between massive bodies. Mon Not R Astron Soc. 1999;304:793–799. [Google Scholar]
  11. Curry J.A. Schramm J.L. Sea ice-albedo climate feedback mechanism. J Climate. 1995;8:240–247. [Google Scholar]
  12. Gladman B. Dynamics of systems of two close planets. Icarus. 1993;106:247–263. [Google Scholar]
  13. Goldreich P. An explanation of the frequent occurrence of commensurable mean motions in the Solar System. Mon Not R Astron Soc. 1965;130:160–181. [Google Scholar]
  14. Gould A. Subo Dong. Gaudi B.S. Udalski A. Bond I.A. Greenhill J. Street R.A. Dominik M. Sumi T. Szymański M.K. Han C. Allen W. Bolt G. Bos M. Christie G.W. DePoy D.L. Drummond J. Eastman J.D. Gal-Yam A. Higgins D. Janczak J. Kaspi S. Kozłowski S. Lee C.-U. Mallia F. Maury A. Maoz D. McCormick J. Monard L.A.G. Moorhouse D. Morgan N. Natusch T. Ofek E.O. Park B.-G. Pogge R.W. Polishook D. Santallo R. Shporer A. Spector O. Thornley G. Yee J.C. (The μFUN Collaboration); Kubiak M. Pietrzyński G. Soszyński I. Szewczyk O. Wyrzykowski Ł. Ulaczyk K. Poleski R. (The OGLE Collaboration); Abe F. Bennett D.P. Botzler C.S. Douchin D. Freeman M. Fukui A. Furusawa K. Hearnshaw J.B. Hosaka S. Itow Y. Kamiya K. Kilmartin P.M. Korpela A. Lin W. Ling C.H. Makita S. Masuda K. Matsubara Y. Miyake N. Muraki Y. Nagaya M. Nishimoto K. Ohnishi K. Okumura T. Perrott Y.C. Philpott L. Rattenbury N. Saito TO. Sako T. Sullivan D.J. Sweatman W.L. Tristram P.J. von Seggern E. Yock P.C.M. (The MOA Collaboration); Albrow M. Batista V. Beaulieu J.P. Brillant S. Caldwell J. Calitz J.J. Cassan A. Cole A. Cook K. Coutures C. Dieters S. Dominis Prester D. Donatowicz J. Fouqué P. Hill K. Hoffman M. Jablonski F. Kane S.R. Kains N. Kubas D. Marquette J.-B. Martin R. Martioli E. Meintjes P. Menzies J. Pedretti E. Pollard K. Sahu K.C. Vinter C. Wambsganss J. Watson R. Williams A. Zub M. (The PLANET Collaboration); Allan A. Bode M.F. Bramich D.M. Burgdorf M.J. Clay N. Fraser S. Hawkins E. Horne K. Kerins E. Lister T.A. Mottram C. Saunders E.S. Snodgrass C. Steele I.A. Tsapras Y. (The RoboNet Collaboration); Jørgensen U.G. Anguita T. Bozza V. Calchi Novati S. Harpsøe K. Hinse T.C. Hundertmark M. Kjærgaard P. Liebig C. Mancini L. Masi G. Mathiasen M. Rahvar S. Ricci D. Scarpetta G. Southworth J. Surdej J. Thöne C.C. (The MiNDSTEp Consortium) Frequency of solar-like systems and of ice and gas giants beyond the snow line from high-magnification microlensing events in 2005–2008. Astrophys J. 2010;720:1073–1089. [Google Scholar]
  15. Gray J. Major Paleozoic land plant evolutionary bio-events. Palaeogeogr Palaeoclimatol Palaeoecol. 1993;104:153–169. [Google Scholar]
  16. Grotzinger J.P. Upward shallowing platform cycles: a response to 2.2 billion years of low-amplitude, high frequency (Milankovitch band) sea level oscillations. Paleoceanography. 1986;1:403–416. [Google Scholar]
  17. Hewitt G.M. The structure of biodiversity—insights from molecular phylogeography. Front Zool. 2004;1:4–19. doi: 10.1186/1742-9994-1-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Hyde W.T. Crowley T.J. Baum S.K. Peltier W.R. Neoproterozoic ‘snowball Earth’ simulations with a coupled climate/ice-sheet model. Nature. 2000;405:425–429. doi: 10.1038/35013005. [DOI] [PubMed] [Google Scholar]
  19. Kasting J.F. Peter Ward and Donald Brownlee's “Rare Earth”. Perspect Biol Med. 2001;44:117–131. [Google Scholar]
  20. Kellog W.W. Climatic feedback mechanisms involving the polar regions. In: Weller G., editor; Bowling S.A., editor. Climate of the Arctic. Geophysical Institute; Fairbanks, AK: 1973. pp. 111–116. [Google Scholar]
  21. Kirchner J.W. Well A. Delayed biological recovery from extinctions throughout the fossil record. Nature. 2000;404:177–180. doi: 10.1038/35004564. [DOI] [PubMed] [Google Scholar]
  22. Kirschvink J.L. Gaidos E.J. Bertani L.E. Beukes N.J. Gutzmer J. Maepa L.N. Steinberger R.E. Palaeoproterozoic snowball Earth: extreme climatic and geochemical global change and its biological consequences. Proc Natl Acad Sci USA. 2000;97:1400–1405. doi: 10.1073/pnas.97.4.1400. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Kleine T. Palme H. Mezger K. Halliday A.N. Hf-W chronometry of lunar metals and the age and early differentiation of the Moon. Science. 2005;310:1671–1674. doi: 10.1126/science.1118842. [DOI] [PubMed] [Google Scholar]
  24. Larson G.L. Perspectives on current issues. Is “anthropic selection” science? Physics in Perspective. 2007;9:58–69. [Google Scholar]
  25. Laskar J. Accurate methods in general planetary theory. Astron Astrophys. 1985;144:133–146. [Google Scholar]
  26. Laskar J. The limits of Earth orbital calculations for geological time-scale use. Philos Transact A Math Phys Eng Sci. 1999;357:1735–1759. [Google Scholar]
  27. Laskar J. Robutel P. The chaotic obliquity of the planets. Nature. 1993;361:608–612. [Google Scholar]
  28. Laskar J. Joutel F. Robutel P. Stabilization of the Earth's obliquity by the Moon. Nature. 1993;361:615–617. [Google Scholar]
  29. Laskar J. Robutel P. Joutel F. Gastineau M. Correia A.C.M. Levrard B. A long-term numerical solution for the insolation quantities of the Earth. Astron Astrophys. 2004;428:261–285. [Google Scholar]
  30. Lee D. Halliday A.N. Snyder G.A. Talylor L.A. Age and origin of the Moon. Science. 1997;278:1098–1103. [Google Scholar]
  31. Lisiecki L.E. Raymo M.E. Curry W.B. Atlantic overturning responses to Late Pleistocene climate forcings. Nature. 2008;456:85–88. doi: 10.1038/nature07425. [DOI] [PubMed] [Google Scholar]
  32. Lovelock J.E. Watson A.J. The regulation of carbon dioxide and climate: Gaia or geochemistry? Planet Space Sci. 1982;30:795–802. [Google Scholar]
  33. Lovelock J.E. Whitfield M. Lifespan of the biosphere. Nature. 1982;296:561–563. [Google Scholar]
  34. Morishima R. Watanabe S. Co-accretion of the Earth-Moon system after the giant impact: reduction of the total angular momentum by lunar impact ejecta. Icarus. 2004;168:60–79. [Google Scholar]
  35. Murray C.D. Dermott S.F. Solar System Dynamics. Cambridge University Press; Cambridge: 1999. [Google Scholar]
  36. Navarro-González R. Rainey F.A. Molina P. Bagaley D.R. Hollen B.J. de la Rosa J. Small A.M. Quinn R.C. Grunthaner F.J. Cáceres L. Gomez-Silva B. McKay C.P. Mars-like soils in the Atacama Desert, Chile, and the dry limit of microbial life. Science. 2003;302:1018–1021. doi: 10.1126/science.1089143. [DOI] [PubMed] [Google Scholar]
  37. Newmann M.J. Rood R.T. Implications of solar evolution for the early Earth's atmosphere. Science. 1977;198:1035–1037. doi: 10.1126/science.198.4321.1035. [DOI] [PubMed] [Google Scholar]
  38. Petit J.R. Jouzel J. Raynaud D. Barkov N.I. Barnola J.-M. Basile I. Bender M. Chappellaz J. Davis M. Delaygue G. Delmotte M. Kotlyakov V.M. Legrand M. Lipenkov V.Y. Lorius C. Pépin L. Ritz C. Saltzman E. Stievenard M. Climate and atmospheric history of the past 420,000 years from the Vostok ice core, Antarctica. Nature. 1999;399:429–436. [Google Scholar]
  39. Roy A.E. Ovenden M.W. On the occurrence of commensurable mean motions in the Solar System. Mon Not R Astron Soc. 1954;114:232–241. [Google Scholar]
  40. Ruddiman W.F. Earth's Climate: Past and Future. W.H. Freeman; New York: 2000. [Google Scholar]
  41. Sahney S. Benton M.J. Recovery from the most profound mass extinction of all time. Proc Biol Sci. 2008;275:759–765. doi: 10.1098/rspb.2007.1370. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Sanders H.L. Marine benthic diversity: a comparative study. Am Nat. 1968;102:243–282. [Google Scholar]
  43. Shackleton N.J. Pisias N.G. Atmospheric carbon dioxide, orbital forcing, and climate. In: Sundquist E.T., editor; Broecker W.S., editor. The Carbon Cycle and Atmospheric CO2: Natural Variations Archean to Present, Proceedings of the Chapman Conference on Natural Variations in Carbon Dioxide and the Carbon Cycle, Tarpon Springs, FL, January 9–13, 1984, (A86-39426 18-46) AGU Geophysical Monograph 32, American Geophysical Union; Washington DC: 1985. pp. 303–317. [Google Scholar]
  44. Smith J.M. Price G.R. The logic of animal conflict. Nature. 1973;246:15–18. [Google Scholar]
  45. Stanley S.M. Children of the Ice Age: How a Global Catastrophe Allowed Humans to Evolve. Harmony Books; New York: 1996. [Google Scholar]
  46. Thommes E.W. Bryden G. Wu Y. Rasio F.A. From mean motion resonances to scattered planets: producing the Solar System, eccentric exoplanets, and late heavy bombardments. Astrophys J. 2008;675:1538–1548. [Google Scholar]
  47. Tomasella L. Marzari F. Vanzani V. Evolution of the earth obliquity after the tidal expansion of the Moon orbit. Planet Space Sci. 1996;44:427–430. [Google Scholar]
  48. Udry S. Fischer D. Queloz D. A decade of radial-velocity discoveries in the exoplanet domain. In: Reipurth B., editor; Jewitt D., editor; Keil K., editor. Protostars and Planets V. University of Arizona Press; Tucson: 2007. pp. 685–700. [Google Scholar]
  49. Walker J.C.G. Hays P.B. Kasting J.F. A negative feedback mechanism for the long-term stabilization of Earth's surface temperature. J Geophys Res. 1981;86:9776–9782. [Google Scholar]
  50. Waltham D.A. Anthropic selection for the Moon's mass. Astrobiology. 2004;4:460–468. doi: 10.1089/ast.2004.4.460. [DOI] [PubMed] [Google Scholar]
  51. Waltham D.A. The large-moon hypothesis: can it be tested? International Journal of Astrobiology. 2007;5:327–331. [Google Scholar]
  52. Ward W.R. Comments on the long-term stability of the Earth's obliquity. Icarus. 1982;50:444–448. [Google Scholar]
  53. Ward P.D. Brownlee D. Rare Earth. Copernicus; New York: 2000. [Google Scholar]
  54. Wilson E.O. The Diversity of Life. Penguin; London: 2001. [Google Scholar]
  55. Zachos J. Pagani M. Sloan L. Thomas E. Billups K. Trends, rhythms and aberrations in global climate 65 Ma to present. Science. 2001;292:686–693. doi: 10.1126/science.1059412. [DOI] [PubMed] [Google Scholar]

Articles from Astrobiology are provided here courtesy of Mary Ann Liebert, Inc.

RESOURCES