Mechanical Compromise of Partially Lacerated Flexor Tendons

Short abstract

Tendons function to transmit loads from muscle to move and stabilize joints and absorb impacts. Functionality of lacerated tendons is diminished, however clinical practice often considers surgical repair only after 50% or more of the tendon is lacerated, the “50% rule.” Few studies provide mechanical insight into the 50% rule. In this study cyclic and static stress relaxation tests were performed on porcine flexor tendons before and after a 0.5, 1.0, 2.0, or 2.75 mm deep transverse, midsubstance laceration. Elastic and viscoelastic properties, such as maximum stress, change in stress throughout each test, and stiffness, were measured and compared pre- and post-laceration. Nominal stress and stiffness parameters decreased, albeit disproportionately in magnitude, with increasing percent loss of cross-sectional area. Conversely, mean stress at the residual area (determined using remaining intact area at the laceration cross section) exhibited a marked increase in stress concentration beginning at 47.2% laceration using both specified load and constant strain analyses. The marked increase in stress concentration beginning near 50% laceration provides mechanical insight into the 50% rule. Additionally, a drastic decrease in viscoelastic stress parameters after only an 8.2% laceration suggests that time-dependent mechanisms protecting tissues during impact loadings are highly compromised regardless of laceration size.

Introduction

Tendons connect muscle to bone and transmit loads from muscle to move and stabilize joints and absorb impacts. They stretch up to 4%–6% strain during in vivo loading [1–3] and display both elastic and viscoelastic behaviors. Tendons with tears and lacerations exhibit diminished mechanical properties compared to normal. Lacerations have been shown in vitro to decrease ultimate load [4–9] and stiffness [6,7] and increase compliance (defined as increased strain under a given load) [4,10] compared to normal tendons. Clinically, it has been suggested that tendons torn more than 50% should be surgically repaired [11–16]. This “50% rule” was originally developed for hand surgery, but has grown to become the standard surgical recommendation for many other tendons, such as rotator cuff [17]. However, little evidence is present to confirm the practice's accuracy or predictive ability [17], and few studies have investigated the mechanical basis of this guideline, and those studies that have, report conflicting results. For example, Mazzocca et al. demonstrated that strain reached during cyclic loading to 100 N does not increase significantly compared to a normal tendon until a 50% rotator cuff tear is present and therefore provided a mechanical basis for the 50% rule [4]. However, Bey et al. reported that extrapolation of their strain data, taken when a constant load of 31 N was applied to normal and 33% cut human cadaver rotator cuff tendons, did not support the 50% rule because the increase in strain would be less than 50%, with the value still falling below the estimated failure strain in vivo [10].

Tear size criteria for surgical repair of digital flexor tendons is debated in the literature, and few studies have addressed the effect of partial tears on the mechanical properties of flexor tendons. Separate clinical studies have concluded that tendons with tear sizes of up to 30% [8], 60% [18], 80% [9], and 95% [19] can be treated successfully without repair and utilizing early mobilization. Bishop et al. concluded that tendons with lacerations up to 60% of the cross-sectional area should be conservatively treated without surgical repair and with early mobilization. This was determined by comparing ultimate load, energy absorption, and stiffness of repaired to nonrepaired lacerated tendons [7]. Supporting Bishop's claim of only considering surgical repair at cut sizes greater than 60%, McCarthy et al. compared the mechanical properties of lacerated tendons to previously measured in vivo forces [6]. This approach, comparing mechanical properties of a lacerated tendon to forces measured in vivo by Schuind [20], was also completed by Manning et al. and Hariharan et al. to demonstrate that surgical repair should be considered with cuts greater than 90% [21] and 75% [5], respectively.

The guideline for the 50% rule is generally supported by clinical trials [11,13–15], and the differing surgical criteria for digital flexor tendons are based primarily on ultimate strength [5–9,21] without consideration of remaining tissue behavior under physiologic loads. A robust mechanical study investigating the elastic and viscoelastic properties of partially torn tendons at physiologic load levels has not yet been reported, although such a study would add insight into the early, post-laceration mechanical behavior for the 50% rule. This study will therefore analyze the effects various laceration sizes have on mechanical properties, both elastic and viscoelastic, in flexor tendons. Based on a damage parameter defined by Lemaitre as the difference between the total area and the effective resisting area divided by the total area [22], we hypothesize that laceration will decrease nominal tendon mechanical properties and percent decrease will be equal in magnitude to percent loss of cross-sectional area.

Methods

Specimen Preparation.

Thirty-two digital flexor tendons were carefully dissected from porcine lower limbs obtained from a local abattoir. Based on previous work in our lab, the following preparation and testing protocols were performed [23,24]. The tendons were cleaned of muscle and extraneous connective tissue but the distal bone insertion site was left intact. The distal bone (excluding the tendon insertion site) was potted in lightweight polyester resin filler in a mold matching the internal dimensions of the testing grip to prevent unwanted movement during testing. Width and thickness of the unloaded specimens were measured using an electronic digital caliper in three places along the tendon and averaged. Care was taken to ensure minimal contact of the calipers with the tendon and measure perpendicular to the long axis of the tendon to prevent inaccurate measurements. An elliptical shape was assumed for calculation of the cross-sectional area. Throughout specimen preparation, hydration was maintained with physiologic buffered saline solution.

Mechanical Testing.

Specimens were loaded into a servohydraulic mechanical testing system (MTS) for testing (Bionix 858; MTS, Minneapolis, Minnesota). The proximal (muscle) end of the tendon was gripped by a soft tissue grip with interlocking, rough surfaces. The distal (bone) end was held in a custom grip (Fig. 1(a)). Load was measured using a 4450 N (1000 lb) load cell (Honeywell Model 060-0571-06, Morrison, New Jersey) and displacement was controlled by the MTS. Time, displacement, and load data were output to a PC with Labtech Notebook software (Laboratory Technology Corporation, Fort Collins, Colorado).

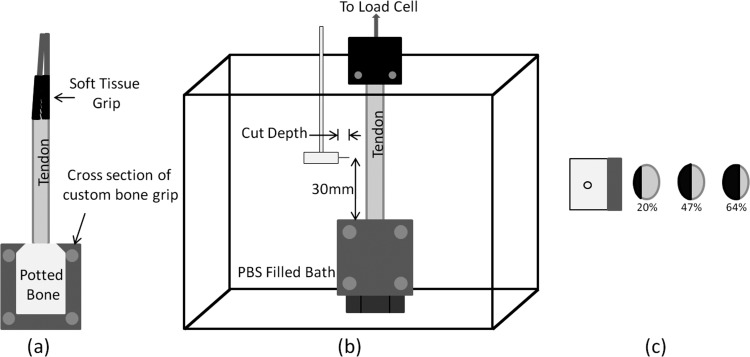
Fig. 1.

(a) Diagram of tendon gripped in soft tissue and bone grip. The soft tissue grip contains two rough surfaces to clamp the muscle side of the tendon and the potted bone fits snugly into the custom bone grip. (b) Diagram of the gripped tendon placed in a saline filled bath. The cut was produced 30 mm from the bone grip by the cutting tool shown. (c) Diagram showing the top view of the cutting tool and cross sections of three different tendons. The black section and percentages shown correspond to the cut area percentage.

A preload of 1 N was slowly placed on the tendon for a quasistatic starting point. After allowing the tendon to equilibrate, initial grip-to-grip length was measured and preconditioning was performed. Preconditioning was completed with a sinusoidal displacement from 0% to 2% strain at 0.5 Hz for 10 cycles. A rest period of 600 s was allotted before beginning further testing to allow for viscoelastic recovery. This rest period and all subsequent rest periods were completed with the tendon under preload.

Mechanical investigation began with testing utilizing a cyclic strain input (referred to for the remaining of the paper only as “cyclic testing”) at the same frequency and duration as the preconditioning waveform from 0% to 4% strain. After 1000 s rest, step strain input testing (referred to simply as “relaxation testing” for the remainder of the paper) was completed, 4% strain held for 100 s. Rise time to 4% strain was 40 ms for the relaxation test. After completion of the relaxation test, a transverse, midsubstance laceration was made 30 mm from the distal insertion site with the tendon in the grips and under preload (Fig. 1(b)). The laceration was made with a 0.5, 1.0, 2.0, or 2.75 mm blade as shown in Figs. 1(b) and 1(c) (n = 8 for each group). Laceration sizes were controlled using a backed cutting tool to prevent the blade from cutting beyond the desired depth (Fig. 1(b)). The 0.5, 1.0, 2.0, and 2.75 mm laceration corresponded to approximately 10%, 20%, 50%, and 65% of the cross-sectional area, respectively (each group n = 8). After laceration, another 1000 s was allowed for rest, after which cyclic and relaxation tests were repeated in the same manner as before. Cyclic and relaxation tests were 20 and 100 s, respectively, to ensure comparative viscoelastic changes were due to tendon laceration instead of fatigue or other strain history effect.

Parameter Calculation.

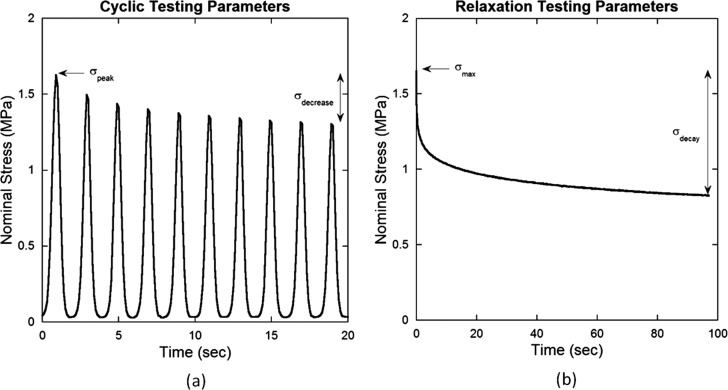
Nominal stress for cyclic and relaxation tests before and after laceration was calculated by dividing the force data by the initial, average cross-sectional area. Maximum stress was defined as an elastic property, σ_peak for cyclic tests and σ_max for relaxation tests (Fig. 2). Cyclic maximum, σ_peak corresponded, to the peak value of the first cycle. Maximum stress during relaxation testing, σ_max always corresponded to initial stress, and was recorded at t = 2.5t_r (t_r = rise time) with the zero time point defined halfway through the rise time as recommended by Lakes [25]. Viscoelastic effects were described for cyclic testing by σ_decrease, defined as the difference in peak stress between the first and last cycles (Fig. 2(a)). The relaxation test viscoelastic parameter, σ_decay, was defined as the decrease in stress from beginning to end of the 100 s (Fig. 2(b)). Post-laceration stress values were modified for additional analysis by dividing the measured force by the intact area at the laceration location (referred to as “residual area” for the remainder of the paper) to obtain mean stress at the residual area (MRA stress) parameters, denoted with a prime (${\sigma }_{\mathrm{peak}}^{\text{'}}$, ${\sigma }_{\mathrm{decrease}}^{\text{'}}$, ${\sigma }_{\max }^{\text{'}}$, and ${\sigma }_{\mathrm{decay}}^{\text{'}}$). MRA stress parameters define average stress within the residual area, but do not account for stress concentrations that may be present.

Fig. 2.

Mechanical testing parameters for (a) cyclic testing (σ_peak, σ_decrease) and (b) relaxation testing (σ_max, σ_decay)

Analysis of specimen behavior at a specified load below the highest load that all specimens reached during cyclic testing was performed. This load criterion was used to allow use of all specimens while still providing the largest strain and stress differences between laceration groups. At the specified load of 6.5 ± 0.05 N, strain, nominal stress (σ_nominal), and MRA stress (σ_MRA) were determined from data of each test. Nominal and MRA stresses were calculated using the areas specified above. Linear interpolation between the data points immediately above and below the load of interest was used to calculate parameters at the correct load. Displacement and initial length data were used to calculate the grip-to-grip strain.

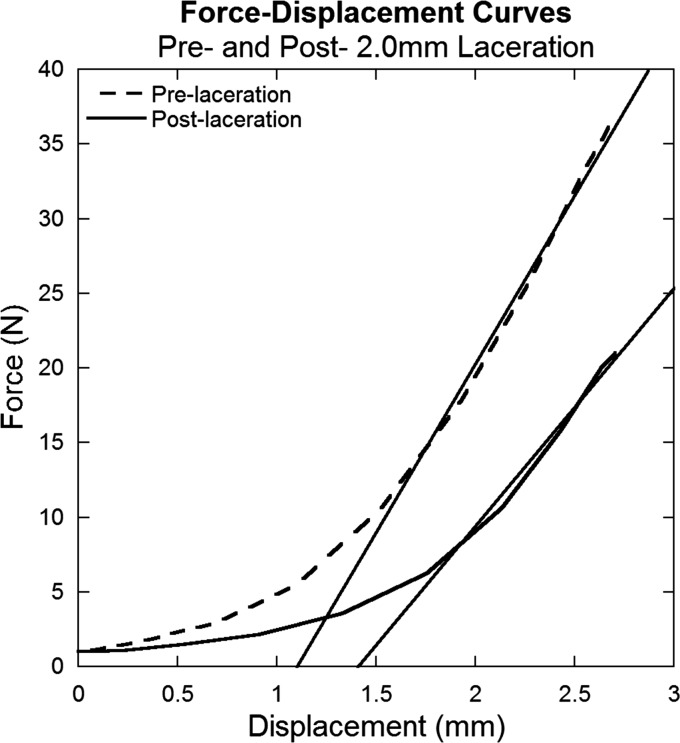
Stiffness was calculated by determining the slope of the linear region of the force-displacement curve for the initial pull of the cyclic test. The most linear region was determined to correspond to data between 2% strain and the peak of the pull (4% strain) for all cyclic tests (Fig. 3).

Fig. 3.

Representative force-displacement curves for pre- and post-laceration data for a tendon subjected to a 2.0 mm laceration. Data were obtained from the initial pull of the cyclic testing. The slopes of the linear regions of each curve (curve fits shown) were used to determine stiffness.

The post-laceration percentage of the intact tendon stress or stiffness was reported as

$$\frac{\mathrm{Stress}\hspace{1em}\mathrm{or}\hspace{1em}\mathrm{stiffness}\hspace{1em}\mathrm{post}\text{-}\mathrm{laceration}}{\mathrm{Stress}\hspace{1em}\mathrm{or}\hspace{1em}\mathrm{stiffness}\hspace{1em}\mathrm{pre}\text{-}\mathrm{laceration}}*100$$ (1)

Statistics.

Changes in parameter values after laceration for each laceration size, reported as a percentage of the intact tendon value, were statistically compared for each parameter by completing a one-way ANOVA. Additionally, within each parameter, a Fisher's least significant difference post hoc test was completed to determine specific differences between laceration sizes.

Significance between pre- and post-laceration values for each laceration size within each parameter was then calculated using a separate paired Student's t test. Significance was defined as p ≤ 0.05.

Results

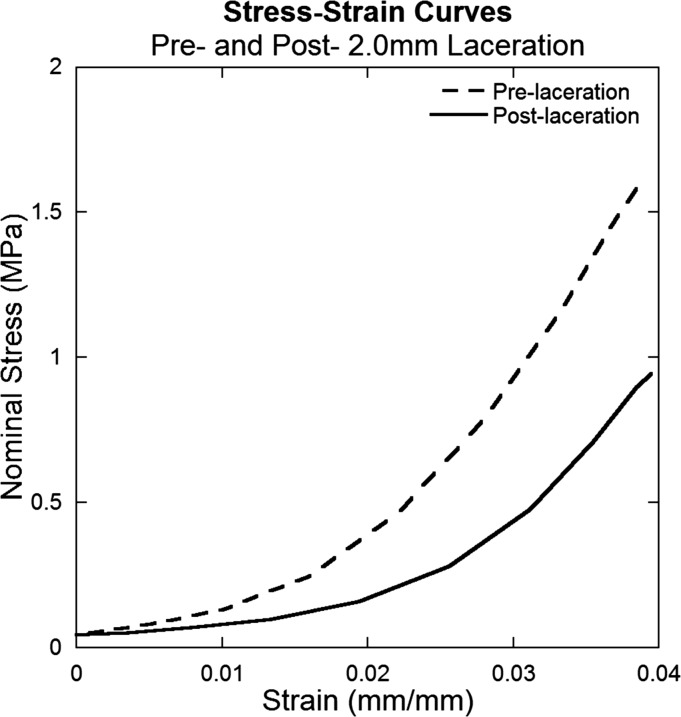
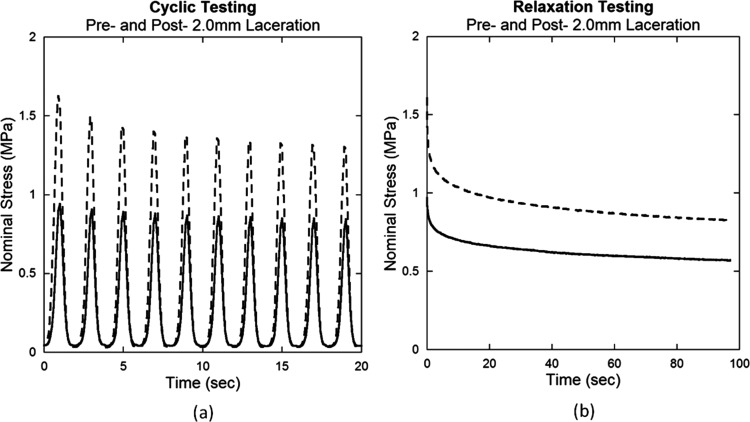
Tendon damage induced by laceration can be observed by the change in mechanical behavior during cyclic and relaxation tests. Stress-strain curves demonstrate that lacerated tendons are more compliant and therefore require greater muscle shortening to bear an equivalent load (Fig. 4). Decreased nominal stress for displacement controlled testing is also observed after laceration in cyclic and relaxation tests (Fig. 5).

Fig. 4.

Representative stress-strain curves for pre- and post-laceration data for a tendon subjected to a 2.0 mm laceration. Data were obtained from the initial pull of the cyclic testing. Initiation of stress application occurs at a larger strain and nominal stress (force divided by original cross-sectional area) decreases post-laceration.

Fig. 5.

Representative pre- and post-laceration data for (a) cyclic and (b) relaxation testing of a tendon subjected to a 2.0 mm laceration. Nominal stress decreased after laceration for both tests.

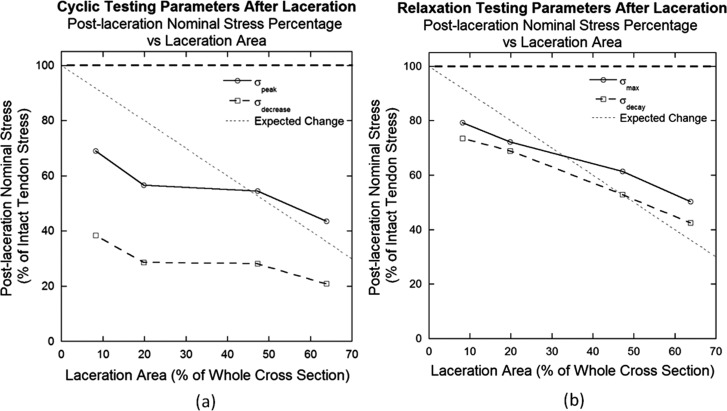
Calculated percent cross-sectional area lacerated corresponded to laceration size as shown in Table 1. These laceration sizes were significantly different from each other (p < 0.0001). Post-laceration nominal stress percentages of each parameter were compared to percent cross-sectional area lacerated. Percentages for all parameters decreased with increasing percent laceration area (Fig. 6). Cyclic testing demonstrated a near-plateau region between the 19.8% and 47.2% lacerations in both parameters, σ_peak and σ_decrease (Fig. 6(a)). Relaxation testing displayed a linear decrease for its parameters, σ_max and σ_decay, after laceration (Fig. 6(b)). However, no parameter demonstrated a percent decrease exactly predicted by the percent loss in cross-sectional area (relationship shown as “Expected Change” in Fig. 6).

Table 1.

Laceration depth and its corresponding area displayed as a percentage of the intact tendon cross-sectional area. The percent area lacerated is given as mean ± standard deviation.

Laceration depth (mm)	0.50	1.00	2.00	2.75
% Area lacerated	8.2 ± 0.8	19.8 ± 1.6	47.2 ± 4.7	63.8 ± 6.7

Fig. 6.

Post-laceration nominal stress expressed as a percentage of pre-laceration stress plotted against the laceration area for (a) cyclic and (b) relaxation testing parameters. The expected change shown is based on the prediction that a proportional, linear correlation exists between damage and laceration area. Relaxation parameters exhibit a more linear relationship between post-laceration nominal stress percentage and laceration area.

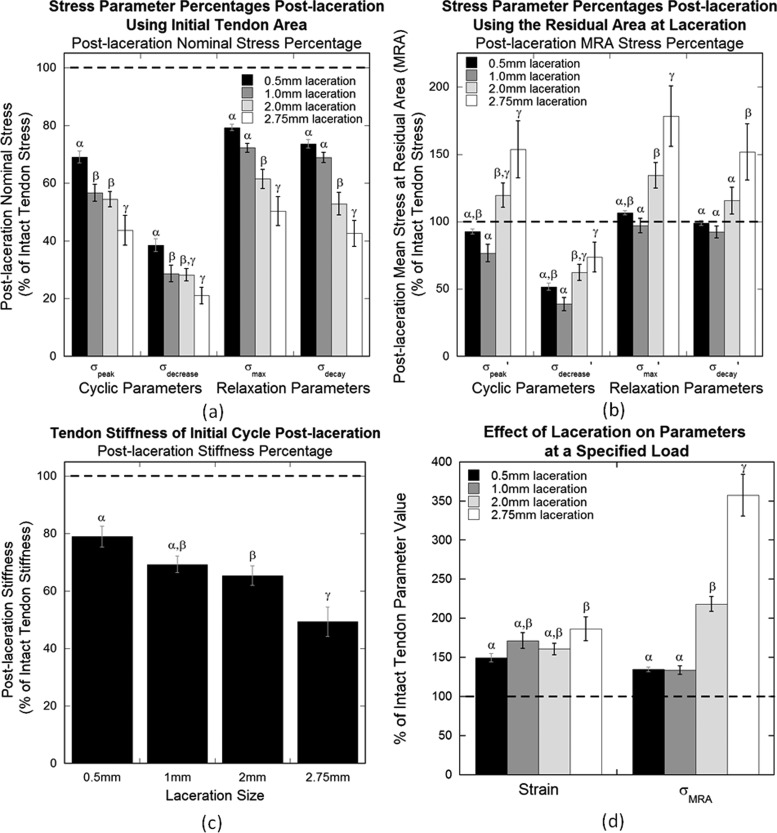
A transverse laceration injury decreased nominal elastic and viscoelastic stress properties of tendon in cyclic and relaxation tests. Post-laceration values of σ_peak, the elastic cyclic property, decreased with increasing laceration size (Table 2, Fig. 7(a)). A significant difference was found between post-laceration percentages of the intact value for all laceration groups within this parameter, determined by an ANOVA (p = 0.0002). Student's t tests additionally demonstrated significance between pre- and post-laceration stress values for the 1.0 (p = 0.011), 2.0 (p = 0.004), and 2.75 mm lacerations (p = 0.013), however the 0.5 mm laceration did not demonstrate a significant difference post-laceration (p = 0.08). The average peak stress of the intact tendons was 2.17 ± 0.93 MPa (average ± standard deviation). Post-laceration values of σ_decrease, the viscoelastic cyclic property, also decreased with increasing laceration size (Table 2, Fig. 7(a)). Significance was found between post-laceration percentages of the intact value for all groups (p = 0.0006) and between pre- and post-laceration values for each laceration size (p < 0.008 for all groups). The average stress decrease of the intact tendons was 0.46 ± 0.23 MPa.

Table 2.

Parameter values post-laceration reported as a percentage of pre-laceration values for each laceration depth. Values reported are mean percentage ± standard deviation and the asterisk indicates a significant difference between pre- and post- laceration values for each group (p < 0.05).

Laceration depth		0.5 mm	1.0 mm	2.0 mm	2.75 mm
Nominal stress parameters
Cyclic parameters	σpeak	69.0 ± 5.9	56.7 ± 8.3*	54.5 ± 7.5*	43.7 ± 14.5*
σdecrease	38.5 ± 6.3*	28.6 ± 8.2*	28.2 ± 6.1*	21.0 ± 8.2*
Relaxation parameters	σmax	79.3 ± 3.0	72.2 ± 4.5	61.5 ± 9.4*	50.3 ± 14.2*
σdecay	73.6 ± 4.1	38.9 ± 5.2	52.9 ± 11.2*	42.6 ± 12.7*
MRA stress parameters
Cyclic parameters	σ′peak	92.6 ± 5.4	76.5 ± 18.3	119.6 ± 25.3	153.6 ± 60.1
σ′decrease	51.6 ± 7.8*	38.8 ± 13.8*	62.2 ± 17.0*	73.7 ± 31.1
Relaxation parameters	σ′max	106.5 ± 4.1	97.0 ± 15.1	134.4 ± 26.4	178.3 ± 63.2
σ′decay	98.8 ± 5.3	92.2 ± 12.5	115.7 ± 28.3	151.8 ± 59.3
Stiffness parameter
	Stiffness	79.0 ± 10.3	69.3 ± 8.3	65.4 ± 9.5*	49.3 ± 14.5*
Specified load parameters
	Strain	149.4 ± 15.4*	171.4 ± 28.4*	160.9 ± 21.1*	186.7 ± 42.8*
σMRA	134.7 ± 8.5*	134.0 ± 15.0*	218.2 ± 27.2*	357.6 ± 75.4*

Fig. 7.

Post-laceration parameter percentage of pre-laceration values for (a) nominal stress parameters, (b) MRA stress parameters, (c) stiffness, and (d) specified load parameters. (a) Nominal stress percentages decrease for both cyclic and relaxation parameters. (b) MRA stress parameters begin to increase at 2.0 mm laceration. (c) Stiffness decreases with increasing laceration size. (d) Strain and MRA stress increase post-laceration. Error bars represent standard error (n = 8) and differing Greek letters (α, β, γ) represent significant differences between laceration groups within each parameter determined by the Fisher's least significant difference post hoc analysis (p < 0.05).

Percent of intact tendon stress for σ_max, the elastic relaxation property, demonstrated larger decreases with larger lacerations (Table 2, Fig. 7(a)). Percentages of intact values post-laceration for all laceration groups were significantly different from each other (p < 0.0001). Post-laceration values for 2.0 and 2.75 mm lacerations were significantly different than pre-laceration values (p = 0.011 and 0.024, respectively), but not for the 0.5 or 1.0 mm laceration (p = 0.246 and 0.115, respectively). The average intact value of the maximum stress was 1.90 ± 0.79 MPa. The viscoelastic relaxation parameter, σ_decay, also decreased with increasing laceration size (Table 2, Fig. 7(a)). Percentages of intact values post-laceration for all laceration groups were significantly different from each other (p < 0.0001). Post-laceration values were significantly different than pre-laceration values for 2.0 (p = 0.002) and 2.75 mm (p = 0.006) lacerations, while 0.5 and 1.0 mm lacerations did not demonstrate a significant difference (p = 0.175 and 0.125, respectively). Average stress decay of the all intact tendons was 0.91 ± 0.37 MPa.

Elastic and viscoelastic MRA stress parameters for constant strain analysis for cyclic and relaxation testing, ${\sigma }_{\mathrm{peak}}^{\text{'}}$, ${\sigma }_{\mathrm{decrease}}^{\text{'}}$, ${\sigma }_{\max }^{\text{'}}$, and ${\sigma }_{\mathrm{decay}}^{\text{'}}$, initially decrease with increasing laceration size but begin to increase at 2.0 mm laceration (Table 2, Fig. 7(b)). Post-laceration percentages of intact values for all groups were significantly different from each other for all parameters (p < 0.009).

Stiffness of the tendon decreased with increasing laceration size (Table 2, Fig. 7(c)). Percentages of intact values post-laceration for all laceration sizes were significantly different from each other (p < 0.0001). Post-laceration values were significantly different than pre-laceration values for 2.0 (p = 0.03) and 2.75 mm (p = 0.02) lacerations, while 0.5 and 1.0 mm lacerations did not demonstrate a significant difference (p = 0.18 and 0.06, respectively).

The maximum load reached by all specimens during cyclic testing was 6.71 N. Therefore, 6.5 ± 0.05 N was chosen as the load range for the specified load analysis. Strain percentages of the intact tendon values post-laceration for all laceration groups were not significantly different from each other (p = 0.087), but post-laceration values for each laceration size were significantly greater than pre-laceration values (p < 0.007 for all groups) (Table 2, Fig. 7(d)). Similar to the constant strain MRA stresses, constant load analysis MRA stress, σ_MRA, post-laceration percentages began to increase at 2.0 mm laceration (Table 2, Fig. 7(d)). Post-laceration percentages of the intact values for all groups were significantly different from each other (p < 0.0001), and post-laceration values were significantly greater than pre-laceration values for each group (p < 0.002 for all groups).

Discussion

Due to the tendons' complex composition, structure, and hence mechanical behavior, investigation of normal and damaged behaviors is important for understanding function and diagnosing and treating injuries. The goal of this study, motivated by the 50% rule, was to determine the effects of different laceration sizes on elastic and viscoelastic mechanical properties of tendons. Nominal stress and stiffness analyses predictably demonstrate an increased mechanical compromise with increasing tendon lacerations. The average peak stress, σ_peak, for all intact tendons (2.17 ± 0.93 MPa) was within 1.60 MPa of peak stresses reported in the literature found during tests to similar strains, 4% [24] and 5% [26]. Analyses of MRA stress parameters reveal a change in behavior when the tendon is lacerated 50%, providing further insight into the 50% rule.

Nominal elastic parameters, σ_peak and σ_max, were increasingly compromised with increasing laceration size. Results are consistent with several studies that demonstrate the load-to-failure elastic property decreases with increasing tendon laceration size [4–9]. Decreases in elastic properties indicate that less force is required to reach damaging strain. Therefore lacerated tendons have greater compliance than healthy tendons. Hence, large lacerations will provide a lower resistance to motion than small lacerations. Physiologically this will increase risk of large strains, which may cause further damage or complete tendon rupture.

Similar to elastic parameters, nominal viscoelastic parameters, σ_decrease and σ_decay, decreased with increasing laceration size. Time dependent variables are therefore compromised and the tendons' ability to absorb, store, and transfer energy is affected. In addition, responses to various loading conditions over time are altered. This effect may be a result of changes in interaction between extracellular components and collagen within the tendon.

Nominal cyclic parameters, σ_peak and σ_decrease, decrease more after laceration (regardless of size) than relaxation parameters σ_max and σ_decay. This may be due to differences in strain rate during initial loading to 4% strain. Fast strain rate application in relaxation tests likely limits reorganization of extracellular components (i.e., collagen fibers) during loading. Hence, after laceration, entangled, lacerated fibers that would not be loaded during slower strain rate applications which allow for fiber reorganization may interact and share load with adjacent intact fibers. These additional loaded fibers during relaxation testing would increase overall stress after laceration compared to cyclic testing, and may explain the smaller decreases in relaxation parameters.

In contrast to our hypothesis, neither cyclic nor relaxation parameters change proportionally to residual intact area. Relaxation parameters are affected in a more linear manner with increasing laceration size than cyclic parameters. This indicates relaxation behavior may better predict laceration size.

Tendon stiffness decreases after laceration, decreasing more with larger laceration sizes. A decrease in stiffness after tendon laceration is demonstrated in studies completed by McCarthy et al. [6] and Bishop et al. [7]. A stiffness decrease after injury results in laxity and less stabilization. A limitation of this measurement, however, is that overall stiffness is reported based on grip-to-grip displacement and whole tendon load. In reality, displacement and load within the tendon, especially a lacerated tendon, will likely vary considerably resulting in local differences in stiffness [27]. Therefore future studies will benefit from considering this during data collection and analysis.

Mechanical property variations throughout a lacerated tendon were briefly addressed by considering stress at the smallest cross-sectional area, the residual area at the location of laceration. Interestingly, MRA stress parameters decreased between the 8.2% and 19.8% laceration groups but began to rapidly increase at the 47.2% laceration group. This behavior is caused by opposing effects on tendon stress due to decreases in force and cross-sectional area. Decreasing force for increasing laceration sizes decreases stress, while decreasing cross-sectional area conversely increases stress. Therefore results demonstrate that force decrease dominates MRA stress results below 47.2% laceration, but decreasing cross-sectional area dominates above this threshold. This mechanical analysis indicates that MRA stress concentrates at the laceration location during physiologic tendon motion, and therefore, to diminish the risk of further injury, surgical repair or immobilization may need to be considered.

The specified load analysis, performed at 6.5 N, may be more physiologically relevant and was completed to determine effects of laceration on strain and MRA stress. Although absolute results would have differed had other specified load values been chosen for this analysis, the observed trends in tendon compromise would likely remain the same. Strain values increased post-laceration. Results confirm an increase in tendon strain at the specified load with lacerations as small as 8.2% of the tendon area. A strain increase during load control tests after laceration has also been reported by Bey et al. [10] and Mazzocca et al. [4]. Because tendon failure has been shown to repeatedly fall in the strain range of 8%–11% [28–31], an increase in strain at any load level may cause greater risk of further cellular damage or ECM failure under normal load applications. Likewise, MRA stress determined using the specified load analysis, σ_MRA, increased after all lacerations, but, as also demonstrated in the constant strain analysis, reveals a more significant increase beginning with the 47.2% laceration group. Overall, these results confirm the complexity of the composite material in that it neither behaves as a homogeneous material, nor does it behave as a set of independent fibers.

Although this study provides insight into the mechanical behavior of partially lacerated tendons, it contains several methodological limitations. We assumed the initial cross sections were elliptical, which may introduce some inaccuracies into the stress values. However, this assumption was consistent among groups for statistical comparison. Additionally, if heterogeneities exist within the tendon (e.g., canine flexor tendons exhibited two dense sections that are separated by a less dense section [8]), results would be affected by which fibers are lacerated. Finally, in determining the viscoelastic parameters, the tendons were not allowed to reach complete equilibrium during the cyclic and relaxation tests. However, because consistency was kept in the test durations, groups provided comparable data to test laceration effects.

To decide whether surgical treatment is required when 50% or greater of the tendon is lacerated, other factors (e.g., patient activity level, adhesion formation, flap formation, and gapping within the repair [7,9]) need to be taken into account. Tan et al. suggested lacerations greater than 80% be surgically repaired to primarily prevent gapping at the laceration [9]. In addition, the injury mechanism, tear or laceration, will affect function of intact fibers. Provenzano et al. demonstrated that cellular damage, specifically necrosis, occurs at the onset of strain application and increases with increasing strain [32]. Therefore, intact fibers of a tendon torn by overstretch will contain more damaged cells and induce more remodeling than a lacerated tendon, likely increasing the temporal mechanical compromise. In vivo healing response to tendon damage and repair also needs to be considered. Kubota et al. reported a 25% weakening of mechanical properties of chicken flexor tendons during the first two weeks after laceration [33], demonstrating that healing processes may further compromise tendon mechanical properties during this time period. Additionally, surgical repair of tendon has been shown to decrease tendon properties due to the disruption of the blood supply by the sutures [7].

This in vitro study contributes a more robust mechanical description of effects of different size lacerations on elastic and viscoelastic properties of flexor tendons. Our results demonstrate a decrease in nominal elastic, viscoelastic, and stiffness parameters with increasing laceration size measured during cyclic and relaxation testing. Relaxation parameters demonstrate a linear correlation to laceration area, making it easier to relate laceration size to relaxation behavior. Nominal stress parameters, by themselves, are insufficient to support or refute the 50% rule, however, this study demonstrated that a laceration as small as 8.2% of the cross-sectional area can cause a decrease of more than 60% (more than a sixfold difference between laceration size and compromise) in a viscoelastic parameter. A prior study completed with a similar testing protocol on the same type of specimens in our lab demonstrated that relaxation values are repeatable and not dependent on the testing order [23]; this suggests that the reported parameter decrease is a direct result of the laceration and not of our repeated measures methodology. The decrease in the viscoelastic parameter suggests that time-dependent mechanisms protecting tissues during impact loadings are highly compromised by laceration. In addition, post-laceration strain values determined using a specified load analysis are nearly 150% of the pre-laceration values after an 8.2% laceration, indicating a significant increase in compliance. MRA stress parameters at the laceration location, ${\sigma }_{\mathrm{peak}}^{\text{'}}$, ${\sigma }_{\mathrm{decrease}}^{\text{'}}$, ${\sigma }_{\max }^{\text{'}}$, and ${\sigma }_{\mathrm{decay}}^{\text{'}}$, demonstrate increased stress beginning with the 47.2% laceration group, providing insight to the 50% rule. Increases beginning at 50% laceration suggest that larger lacerations exhibit a marked increase in stress concentration within the tendon. MRA stress, σ_MRA determined at a specified load also begins to further increase when the tendon is 50% lacerated, confirming the effect of the marked increase in stress concentration. This suggests tendons with laceration sizes of 50% or greater are at higher risk of laceration propagation than tendons with smaller lacerations due to the marked increase in stress concentration, indicating surgical repair may need to be more strongly considered at this level of damage.