Synergy in Binary (MWNT, SLG) Nano-Carbons in Polymer Nano-Composites: A Raman Study

Abstract

Load transfer and mechanical strength of reinforced polymers are fundamental to developing advanced composites. This paper demonstrates enhanced load transfer and mechanical strength due to synergistic effects in binary mixtures of nano-carbon/polymer composites. Different compositional mixtures (always 1 wt. % total) of multi-wall carbon nanotubes (MWNTs) and single-layer graphene (SLG) were mixed in polydimethylsiloxane (PDMS), and effects on load transfer and mechanical strength were studied using Raman spectroscopy. Significant shifts in the G-bands were observed both in tension and compression for single as well binary nano-carbon counterparts in polymer composites. Small amounts of MWNT_0.1 dispersed in SLG_0.9/PDMS samples (subscripts represents weight percentage) reversed the sign of the Raman wavenumbers from positive to negative values demonstrating reversal of lattice stress. A wavenumber change from 10 cm⁻¹ in compression to 10 cm⁻¹ in tension, and an increase in elastic modulus of ~103% was observed for MWNT_0.1SLG_0.9/PDMS with applied uniaxial tension. Extensive scanning electron microscopy revealed the bridging of MWNT between two graphene plates in polymer composites. Mixing small amounts of MWNTs in SLG/PDMS eliminated the previously reported compressive deformation of SLG and significantly enhanced load transfer and mechanical strength of composites in tension. The orientation order of MWNT with application of uniaxial tensile strain directly affected the shift in Raman wavenumbers (2D band and G-band) and load transfer. It is observed that the cooperative behavior of binary nano-carbons in polymer composites resulted in enhanced load transfer and mechanical strength. Such binary compositions could be fundamental to developing advanced composites such as nano-carbon based mixed dimensional systems.

1.0 Introduction

An important application of graphitic nano-carbons is their use as reinforcers/fillers in polymer composites for enhanced mechanical strength and load transfer. In this respect, use of carbon nanotubes has been effective due to their high tensile strength, high aspect ratio, and one-dimensional (1D) nature leading to directional stress transfer and compatibility with surface functionalization techniques [1–23]. Recently, two-dimensional (2D) graphitic nano-carbon, namely few layer graphene nanoplatelets (GNPs), have shown impressive load transfer both in tension and compression when acting as reinforcers in polymer composites [24]. A surprising observation was that for large strains (>1.5%), GNP fillers went into compression under uniaxial tensile deformation [24]. Similarly, under uniaxial compressive load, the Raman signature was one that of tension in the lattice. This effect although intriguing is not yet well understood. Further, lack of clear understanding of how mechanical strength and load transfer are affected in binary mixtures of nano-carbon/polymer composites warrants further investigation.

Recent reports have shown extraordinary synergy in binary nano-carbon mixtures consisting of single wall carbon nanotubes (SWNT) and nano-diamonds (ND), and few layer graphene (FLG) and ND in matrix of polyvinyl alcohol (PVA) [25]. The nano-carbons (ND, SWNTs and FG) were surface functionalized using acid treatment to form carboxyl and hydroxyl groups that could better interact with the PVA matrix [25]. The ~400% enhancement in elastic modulus of PVA was reported due to the inducement of crystallization of the polymer with addition of nano-materials [25]. Since that impressive study, further studies have shown synergistic effects of increased toughness resulting from the combination of SWNTs and reduced graphene oxide (GO) flakes in solution-spun polymer fiber [26]. Similarly, not only mechanical strength, synergistic effects in thermal conduction has been reported in hybrid graphite nano-platelet-MWNT fillers in epoxy composites. Thermal conductivity enhancement of ~800% at ~10 wt. % loading of hybrid nano-carbons in epoxy was demonstrated [27]. Synergistic effects of SWNT and GO composite fibers coagulated from acidic PVA solution exhibited both high strength and high conductivity and was reported to be promising candidates for actuation applications [28]. While these studies are quite impressive and show the synergy between use of binary mixtures of nano-carbons in polymers affecting mechanical strength, interfacial thermal conductivity, and device actuation, Raman spectroscopy has not been previously employed to investigate actual change in lattice expansion or contraction due to cooperative effects of binary mixtures of nano-carbons for load transfer/mechanical strength/interfacial thermal conduction.

Over the years, Raman spectroscopy has emerged as a powerful method in understanding load transfer and mechanical properties of single nano-carbon/polymer composites. It was Ajayan et al., who demonstrated load transfer in a MWNT/epoxy system using Raman spectroscopy [2]. The enhanced shift in Raman G′ mode during compression demonstrated higher interfacial shear stress and load transfer to the nanotubes [2]. Since then, numerous reports have emerged on the use of Raman spectroscopy for studying load transfer and mechanical strength of nano-carbon reinforced polymer composites using both G-band shifts and 2D-band shifts [1, 2, 5, 20, 29–32]. However, there are no studies on how load is transferred in polymer composites consisting of binary nano-carbon mixtures using Raman spectroscopy.

Raman spectroscopy studies on binary mixtures of nano-carbons polymer composites in tension and compression can give us a deeper understanding of how strains are developed in the lattice and the synergy of two carbons in different dimensional states aiding load transfer. The use of binary mixtures of nano-carbon as reinforcers in polymer matrix could have different impacts on load transfer and mechanical strength. Extraordinary synergy is only achieved at a specific concentration of the nano-carbons in the polymer matrix and therefore is not an additive property. One can envision different scenarios of mixing binary mixtures of nano-carbons in polymer matrix: 1) load could be shared equally by both the nano-carbons (this could potentially occur at equal weight percentages or same dimensional state), 2) load could be shared predominantly by one nano-carbon, thereby eliminating influence of the second carbon, 3) one of the nano-carbons may limit the deformation of the other in the matrix resulting in selective and directional load transfer, 4) shape induced anisotropy of the nano-carbons can result in enhancement in stiffness and mechanical strength, and 5) adding binary mixtures of nano-carbons and subsequent polymerization of the composite can lead to smaller segmental chain length and limited extensibility of polymer chains. Finally, dimensionality and mechanical properties of individual nano-carbons should also play a significant role in enhancing interfacial interactions in determining collective composites properties. Therefore, we investigated load transfer and mechanical strength of binary mixtures of nano-carbon fillers in PDMS matrix using Raman spectroscopy. PDMS was used in this study due to its high significance in many day to day industrial applications. PDMS belongs to the group of silicones and is a common polymer used in industries, such as medical, food, aerospace, tribological, lithographic, cosmetics and microfluidics. Recently nano-carbons in PDMS have found applications as photo-thermal polymerization agents [33] and photomechanical actuators [34–38]. Such actuators have found applications in MEMS as micro-actuators [39], micro-mirrors [40], and micro-grippers [41, 42] utilizing photomechanical actuation principle [38–41] for non-contact and remote controlled actuation. Therefore, the present investigations could make an impact in the above mentioned areas where synergy between nano-carbons can be exploited for actuation applications. Our results suggest small amounts of MWNT_0.1 in SLG_0.9/PDMS matrix (for simplicity we refer wt. % of nano-carbon as subscripts) eliminates the previously reported compressive deformation (GNP in PDMS) [24], thereby reversing the sign of the Raman wavenumber changes (from positive to negative) in uniaxial tension. This resulted in load transfer to SLG and almost fourfold increase in elastic modulus compared to single nano-carbon SLG_1.0/PDMS and MWNT_1.0/PDMS counterparts. We discuss a mechanism where strain induced orientational order of MWNT and the shorter segmental length and the limited configuration of the polymeric chain on MWNT addition can result in the synergistic effect of eliminating the compressive deformation of SLG in direction perpendicular to the applied strain thereby changing the sign of Raman wavenumbers and increasing the elastic modulus.

2.0 Results and Discussion

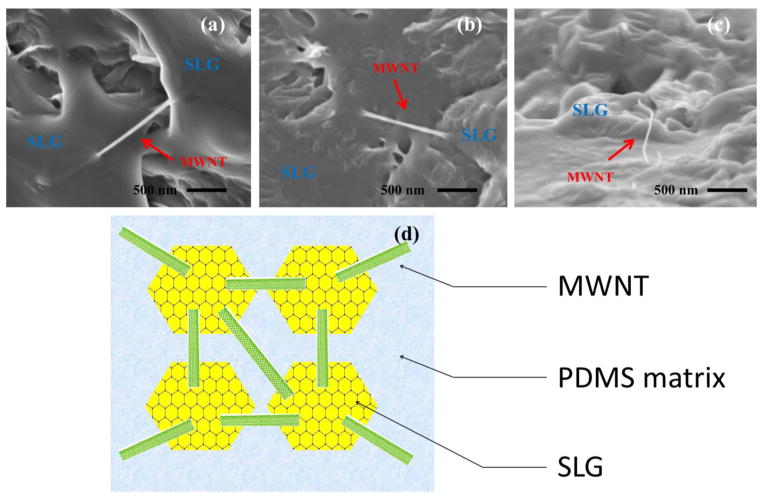
Figures 1(a – c) presents cross-sectional SEM images and Raman spectroscopy for MWNT_1.0SLG_0.0/PDMS, MWNT_0.0SLG_1.0/PDMS, and MWNT_0.5SLG_0.5/PDMS respectively. The SEM image for MWNT_1.0SLG_0.0/PDMS (Figure 1(a)), clearly shows dispersion of MWNTs in the matrix. One end of the MWNT appears stretched out of the matrix while the other end is embedded in the matrix. This is indicative of strong interfacial adhesion between the nanotube and PDMS polymeric chains [4]. The SEM image of MWNT_0.0SLG_1.0/PDMS (Figure 1(b)) shows that the plate-like morphology is retained in the polymer matrix. The SEM image of the MWNT_0.5SLG_0.5/PDMS (Figure 1(c)) shows a combination of the retention of SLG morphology and nanotube stretched out of the polymer. There are places where the nanotube polymer is seen to bridge the gap between two SLG/PDMS plate structures (arrow in Figure 1(c)). The SEM images clearly show MWNTs covered in PDMS acting as bridges between two SLG plates. Even in the mixtures, one end of the MWNT is seen to stretch out of the matrix while the other end is anchored in the SLG/PDMS matrix (Figure 2(c)). This demonstrates strong interfacial adhesion of the MWNT filler in the mixtures.

Figure 1.

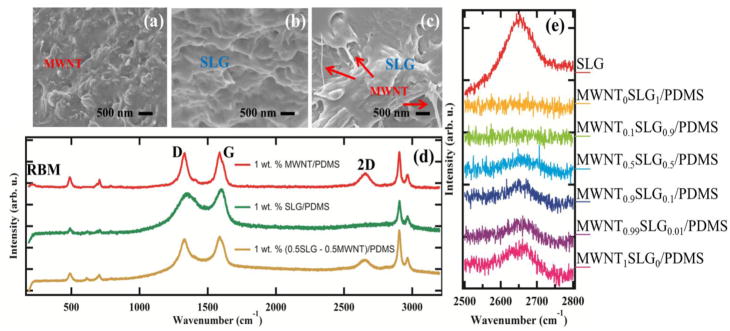
SEM images of (a) MWNT₁SLG₀/PDMS, (b) MWNT₀SLG₁/PDMS, (c) MWNT_0.5SLG_0.5/PDMS, Scale bar: 500 nm. (d) Raman spectra of (a–c) samples, (e) Comparison of 2D peaks for pure SLG and SLG mixed in PDMS and small additions of MWNT to SLG/PDMS.

Figure 2.

(a–c) SEM images of MWNT_xSLG_1-x/PDMS matrix, (d) schematic representation of SLG-MWNT/polymer system based on the SEM images above.

In the Raman spectrograph (Figure 1(d)), one can see all 9 peaks associated with PDMS in the samples. The Radial Breathing Mode (RBM) ~219.3 cm⁻¹, the disorder induced D band (~1,329 cm⁻¹), tangential mode G-band (~1,588 cm⁻¹), and 2D or G′-band (~2,657 cm⁻¹) of the MWNT are seen in the MWNT_1.0SLG_0.0/polymer samples, demonstrating high purity of sample preparation. For the MWNT_0.0SLG_1.0/PDMS samples, the D-band (~1,344 cm⁻¹) and the G-band (~1,596 cm⁻¹) are evident in the PDMS matrix. Past Raman studies on monolayer graphene on PDMS has shown a G-band position of ~ 1581.6 15.6 cm⁻¹ [43]. Therefore, our measured values for the G-bands are within the measured fluctuations for monolayer graphene. Now investigating the 2D band, this is faint in these samples. The 2D band was seen at 2680 cm⁻¹ but however very faint or lower intensities. The low intensity of the 2D resonance and broadening of the G and the D band indicates high functionalization densities of graphene as seen in past report [44]. This suggests higher level interaction of SLG with the polymer. Figure 1(e) presents the evolution of the 2D band for pure SLG and SLG/PDMS mixtures with MWNT. For the binary mixtures the 2D peak was seen to increase in intensity with addition of MWNT. Ideally, lack of any defect centers of SLG will lead to no D-band. The presence of D-band in the polymer samples, its broadening and the lower intensity of 2D peaks may suggest folding of the graphene sheet during the evaporative mixing process [45]. The spatial in-homogenous curvature of the SLG in polymer can act as a smooth one dimensional defect line along the fold and therefore can result in D-band peak for SLG/PDMS [45]. The direct contact of the polymer to the SLG and the process of mixing over 24–36 h inside the polymer can result in folds, kinks, as well as doping and functionalization of the graphene sheet all of which can induce a D-band, broaden G band and lower the relative intensity of 2D band. While this warrants further investigation, the lower intensity of 2D band suggest that the electronic properties of SLG are directly affected by mixing in the polymer. Decrease or increase in I_G/I_2D compared to the pure samples may be indicative of hole or electron doping respectively. Based on the intensity values, the I_G/I_2D =10.5 was calculated for SLG samples and, the I_G/I_2D = 132.2 was calculated for SLG/PDMS. This may not be the case for few layer graphene (FLG) as only the top layer comes in contact when mixed with the polymer and keeps the layers in between in pristine condition. Therefore, the 2D band is expected to have higher intensities even when mixed in polymers for FLG compared to their SLG counterparts or no change in the electronic properties. For FLG, we found I_G/I_2D =3.1 and for FLG/PDMS, I_G/I_2D =3.0 was found from our measurements. This show when mixing in polymers SLG is affected more by the polymer compared to the FLG. The lack of variation of I_G/I_2D for FLG and FLG/PDMS is remarkable and show that the electronic properties for FLG are not affected by mixing with the polymer. A fundamental result observed in this study is that mixing SLG in polymers can have a profound effect on its Raman bands and could have significance in fabrication and characterization of advanced composites. Finally, in the Raman spectrum of the binary mixture, MWNT_0.5SLG_0.5/PDMS, the D-band (1,344 cm⁻¹), G-band (1593 cm⁻¹) and 2D-band (2,654 cm⁻¹) are clearly visible. The appearance of 2D band in binary mixtures may suggest that the electronic properties of carbon nanotubes are unaffected by curvature effects [46]. The similarity of the 2D peak compared to pure MWNT/PDMS samples with lower relative intensity may suggest the MWNT entanglement atop graphene sheet, similar to the decrease in relative intensity of 2D peaks with increase in number of graphitic layers (FLG) [46]. This is quite reasonable as the SEM investigation also suggest entanglement of MWNT on the SLG plates. Based on the RBM mode of the nanotube/polymer sample, the diameter of the nanotube was calculated using equation ν_RBM = A/d +B, where A = 233 cm⁻¹ nm and B =10 cm⁻¹ are constants giving us an inner diameter of MWNT ~1.06 nm. The diameter value based on the RBM mode in the nanotube/polymer samples demonstrates lack of bundling of the MWNTs, and excellent dispersions within the polymer samples using the evaporative mixing and the NIR cross-linking process [33]. Lack of bundling and smaller diameters may also indicate higher level nanotube/polymer interaction, resulting in better interfacial adhesion and strength.

Figure 2 presents the SEM images of MWNT_0.5SLG_0.5/PDMS from three different areas. In all three areas, nanotubes are seen to bridge the SLG plates in the polymer matrix. The SEM images show a density of 1–2 MWNT or small bundle bridging adjacent SLG samples. This is reasonable given the small weight fractions of MWNT additive. Figure 2(d) presents a schematic model based on the SEM observations of how MWNT arrange themselves between graphene plates. The 1D nature of MWNT can cause entanglement of the individual tubes between the mesh like SLG lattice in the polymer. The long evaporative mixing, and subsequent polymerization cause the MWNT to be entangled in the SLG lattice permanently by the polymeric chains. This may warrant further investigation as long or short chain polymers can have different effects on the entanglement of MWNT that may affect the overall properties of the composites.

Raman spectroscopy has been used many groups in the past to measure strains in nanoscale fillers such as carbon nanotubes and graphene [2, 3, 5, 6, 19, 47–50]. When a strain is applied, interatomic distances change resulting in shifts in the vibrational frequencies. The G-band (~1,588 cm⁻¹) and G′-band (~2,700 cm⁻¹) in the Raman signatures are known to shift with applied strains both for MWNT and SLG [24]. The larger shift in Raman peak position of the G-band or G′-band is indicative of larger load carried by the nano-carbon. Recent studies on graphene/polymer composites have shown the G-band shift of ~10 cm⁻¹/strain % for few layer graphene sheets strained on top of different substrates [24]. In this paper we have used the G-band to investigate effects of load transfer as the 2D bands were faint in SLG/PDMS as shown in Figure 1(c). An increase in G-band wavenumbers with strain means in-plane lattice compression, while a decrease in G-band wavenumbers with strain means tensile forces on the nano-carbon lattice. Characterizing the shift in G-peak in the samples under tension and compression may indicate the strength of the nanotube-polymer interface. Finally, characterizing the shift in Raman peak position in binary nano-carbon/polymer composites knowing how they shift in single nano-carbon/PDMS composites can bring out an in-depth understanding of the synergistic effects.

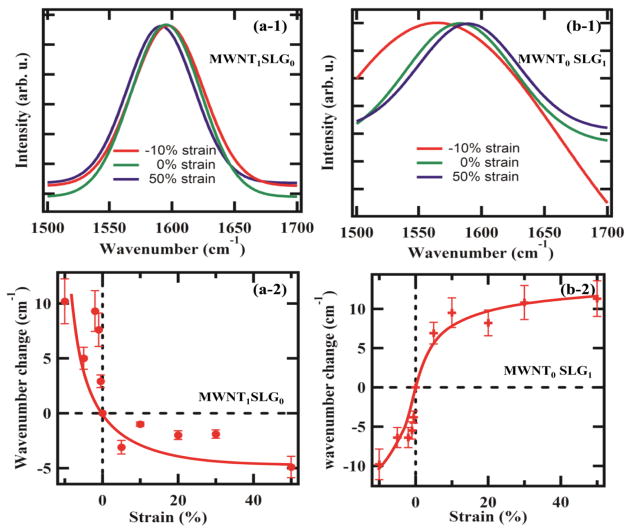
In order to investigate synergistic effects in the G-band, Raman spectroscopy was conducted on MWNT₁SLG₀/PDMS and MWNT₀SLG₁/PDMS separately in tension and compression. Figure 3 ((a-1) & (b-1)) presents the shift in G-band peak position from −10% to 50% strain. The G-band corresponding to 0% strain is seen at ~1,588 cm⁻¹. At ~10% uniaxial compression, the G-band is shown to shift right and at ~50% uniaxial tension, the G-band is shown to shift left for MWNT₁SLG₀/PDMS, similar to past reports on MWNT [33]. On the other hand, the MWNT₀SLG₁/PDMS (Figure 3(b-1)) showed highly interesting results. At 10% uniaxial compression, the G-band shifted left (indicating tensile strains) and at 50% uniaxial tension, the G-band shifted right (compression), which is in line with recent reports of GNP polymer composites [24]. This suggests application of uniaxial tension in one direction resulted in compression of the SLG lattice in the other as the Raman signature suggest. This may be due to the polymeric chains extending in the direction of the strain owing to the lower glass transition temperature and rubbery elasticity [24]. Figures 3((a-2) & (b-2)) show the change in wavenumber as a function of strain for MWNT₁SLG₀/PDMS and MWNT₀SLG₁/PDMS. The shift in wavenumbers of ~10 cm⁻¹ for compression, and ~5 cm⁻¹ in tension show that more load is transferred to the MWNT filler in compression (Fig. 3(a-2)). For the MWNT₀SLG₁/PDMS, there was ~10 cm⁻¹ change in wavenumbers in both tension (50%) and compression (10%), but in the opposing direction as MWNT fillers (Fig. 3 (b-2)). Again, the shift in wavenumbers was 1 cm⁻¹/% strain in compression and 0.2 cm⁻¹/% strain in tension suggesting that load is transferred more in compression. It should be noted that there is no linear relationship in Raman wave number changes between tension and compression and these numbers are non-linear.

Figure 3.

(a-1) & (b-1): Raman intensity versus shift in wavenumbers in uniaxial tension and compression for MWNT₁SLG₀ and MWNT₀SLG₁ respectively; (a-2) & (b-2) change in wavenumber versus strain in uniaxial tension and compression for MWNT₁SLG₀ and MWNT₀SLG₁ respectively

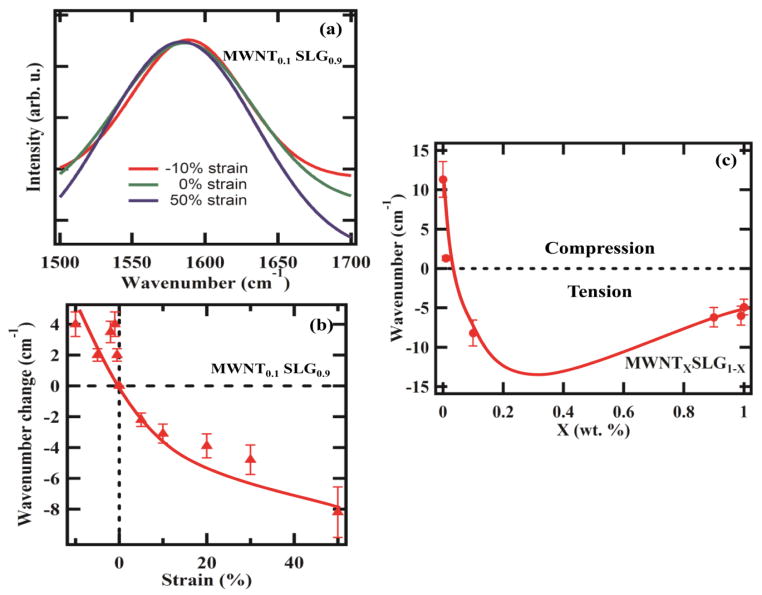
Investigating the Raman signatures of the binary mixtures (Figure 4), the synergistic effects of load transfer were seen for MWNT_0.1SLG_0.9/PDMS (9:1 ratio) samples. First in looking at the Raman signature at −10% strain (Fig. 4a), the G-band shifted to the right (signaling compression or increase in wavenumbers with uniaxial applied compression) compared to the un-strained position. Similarly, at ~50% tensile strain, the G-band is shifted to the left (signaling lattice tension or decrease in wavenumbers with uniaxial applied tension). This is unexpected as MWNT₀SLG₁/PDMS (Figure 3 (b-2)) showed the opposing effect. So, it was observed that at 9:1 binary nano-carbon mixtures of SLG/MWNT, the Raman signature completely changed signs from compression to tension which is intriguing. Figure 3(b) presents the wavenumber change versus percentage strain for the mixed sample. A 4 cm⁻¹ increase in wavenumber for 10% compression and ~8 cm⁻¹ decrease in wavenumbers for 50% tension is observed.

Figure 4.

Load transfer (G-band) in SLG_0.9MWNT_0.1/PDMS: (a) Raman intensity versus wavenumber; (b) change in wavenumber as a function of percentage strain; and (c) change in wavenumber versus weight fraction of nano-carbon under 50% uniaxial tension.

Figure 4(c) presents transition in wavenumbers as a function of MWNT-SLG wt. % ratios in the sample under 50% uniaxial tension. Positive wavenumbers at 0–0.01 wt. % of MWNTs in SLG/PDMS suggest compressive forces dominate the SLG lattice under uniaxial tension, similar to results in Figure 3 (pure 1 wt. % SLG/PDMS). At ~0.1 wt. % MWNTs, wavenumbers shift to the left or decrease, suggesting lattice tension with applied tensile strain. The complete reversal in wavenumber signs with small amounts of MWNTs suggests synergy between SLG and MWNT. Further increase in MWNTs, wavenumbers do not shift signs, keeping the samples under tension. At 0.8–1.0 wt. % MWNTs, saturation is reached in wavenumbers. The total change in wavenumbers of ~20 cm⁻¹ per 0.1 wt% MWNT or 200 cm⁻¹/wt. % is quite remarkable transformation of the Raman signal given the small weight fractions used.

A plausible mechanism of how MWNTs aids in limiting deformation of SLG in the direction of applied strain is suggested. Without any MWNTs, the collective Raman signature of MWNT₀SLG₁/PDMS is one of compression. This was also seen in recent report on FLG/polymer composites [24]. The mobile large chain PDMS network in the direction of applied strain can result in compressive forces on SLG resulting in net Raman signature that of compression [24]. While the earlier understanding was that force on one direction can cause the graphene plates to compress in the other, this may be possible for small strains. It is more plausible that wrapping of the polymer chains around SLG can make it fold there by causing SLG to compress. The D band in the Raman signature of SLG/PDMS may suggest folding of SLG lattice where the fold can appear as a defect center for scattering [45]. One or more folding of the SLG sheet can thus exert a net compressive stress on the SLG lattice.

Stretching the polymer sample results in an increase in useful work that will available to the sample upon release. Therefore, the elastic free energy or also called the Helmhotz free energy (A), of the sample should increase where A = U − TS [51]. Since internal energy (U) and temperature (T) of the polymer system are both assumed to remain constant, the entropy (S) of the system must decrease. This makes qualitative sense as well, as stretching the sample results in polymeric chains going from a high entropically disordered state (unstrained configuration), to a lower entropic ordered state (strained configuration) [51]. Assuming the entropy of the system to be equal S = S₀ + k · LnW(r), where S₀ is the initial entropy, k is the Boltzmann constant, and W(r) is the density distribution of the end-to-end polymeric chains [51]. Substituting these results into A, the A = U − T(S₀ + k · LnW(r)). In other words, the elastic free energy is dependent on the density distribution of the end to end polymeric chains. Assuming that the polymeric chain length follows a Gaussian distribution, the density distribution is the number of configurations allowable to the polymeric chain. Shorter chains result in a stiffer polymer [51]. While the mechanism of molecular reinforcement is poorly understood [51], we believe addition of the two carbon nanostructures to the polymer results in different polymeric chain/carbon configurations. Because of the 2D mesh-like structure of SLG, it is likely that the polymer chains can be entangled in the mesh or warp around SLG. The polymer chains wrapping around the SLG can fold the SLG or make the lattice go to a net compressive state which is seen in the Raman data. Carbon nanotubes however, likely present a different mechanism for shortening the polymeric chains. Due to their high aspect ratio, 1D CNTs likely present opportunities for polymeric chains to become much more entangled along the axis of the nanotube. The CNTs cannot fold as the SLG’s and therefore always remain in tension on application of uniaxial tension. Therefore, for the same wt. % additive, CNT/PDMS composites should be stiffer than SLG/PDMS composites, which have been confirmed experimentally by our results in the next section. The expression for true strain can therefore be written as ${\tau }_x=V^{-1}{\lambda }_x{\sum }_{i=1}^3(\partial \mathrm{\Delta }{A}_{el}/\partial {\lambda }_i^2)\partial {\lambda }_i^2/\partial {\lambda }_x$ and can be evaluated for the x, y and z dimensions [51]. The shorter polymeric chains due to the CNTs could result in limiting the strain in the x and y directions (assuming uniaxial tension is applied in the z direction). Since the chains are polymerized from inside by NIR illumination, the effective segmental length must decrease with addition of MWNT or making it stiffer. The entanglement of the MWNT onto the SLG as the SEM suggest can also make the net polymeric chain length shorter during the polymerization process.

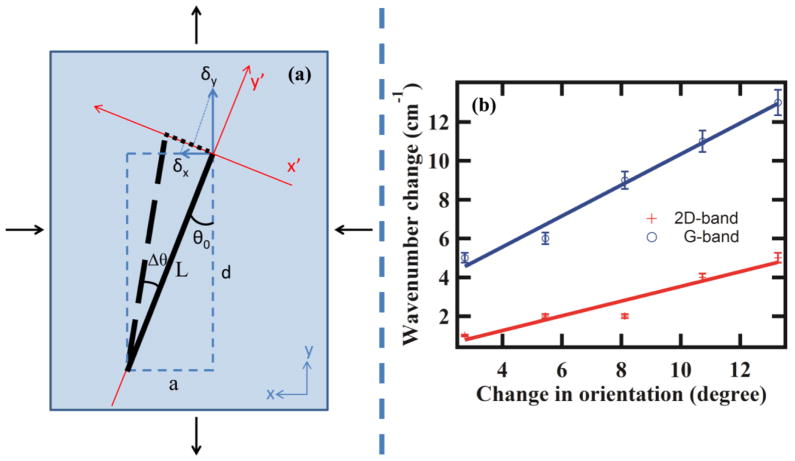
One another aspect that may affect the load transfer and the mechanisms is the orientational order of the nano-carbon in the presence of strain. By using nanotube as an example, we developed a 2D model to calculate the change in angular orientation of the nanotube with shift in Raman wavenumbers. Orientation of the nanotube should play an important role in load transfer. When a uniaxial tensile strain is applied to MWNT/PDMS composite, the MWNT will align itself or undergo change in orientation in the direction of the strain. This has been shown to improve photomechanical stresses in the past for actuation applications [37, 38]. Figure 5 presents the shift in Raman wavenumbers (measured) versus the orientational angle (calculated) of the carbon nanotubes. The calculation is based on the model that describes the movement of a rigid rod in polymer matrix as shown in Figure 5(a). The average change in angular orientation of the nanotube in polymer matrix can be written as:

$$<\mathrm{\Delta }\theta >=\underset{0}{\overset{\frac{\pi }{2}}{\int }}arctan(\frac{{\delta }_{x^{\prime }}}{L})P({\theta }_0){d^{\theta }}_0$$

where δ_x′ = δ_y · sinθ₀ + δ_x · cosθ₀, is the change in length in the x′ axes on change in orientation of the nanotube in the presence of uniaxial tension; δ_y = ε_y · d, δ_x = v · ε_y · a, P(θ₀) is the orientational probability distribution of the nanotube and this is a flat distribution of $\frac{1}{\pi /2}$. The change in orientational angles can therefore be calculated based on the applied uniaxial tensile strain using the equation above.

Figure 5.

(a) Model describing the change in orientation of the nanotube in polymer on application of a uniaxial tensile strain, (b) change in Raman wavenumbers for G and 2D band (measured) versus change in orientation angle (calculated) for different uniaxial tensile strains applied to the sample.

Figure 5(b) presents the shift in Raman wavenumbers versus the calculated change in orientation angles using the model above. Surprisingly a linear relationship is established between calculated angles and the actual measured Raman values. The linear relationship between orientation angles and Raman wavenumber shift for both G and 2D band suggest load transfer due to orientation ordering of carbon nanotubes in the matrix. For SLG, similar angle change can be expected if it is treated as a rigid 2D sheet on a 2D plane. However, for the mixtures, a 3D model might be required to take into account the entanglement of carbon nanotubes between 2 SLG plates as observed in the SEM images. This is beyond the scope of this paper and future atomistic modeling can bring out the actual synergy between the nano-carbons and how orientation of the carbons affects the synergy. Nevertheless, the model described here gives some insights into the change in Raman wavenumbers as a function of calculated orientation angles. Such change in Raman wavenumbers with orientation angles could in principle be useful for design of nanoelectronic devices based on strains. Further, 1D MWNT are better reinforcers compared to 2D SLG sheets in polymer composites for uniaxial tension. The single dimensionality and high strength of the nanotubes can be expected to exhibit much higher load transfer along the axial direction compared to 2D SLG sheets in tension.

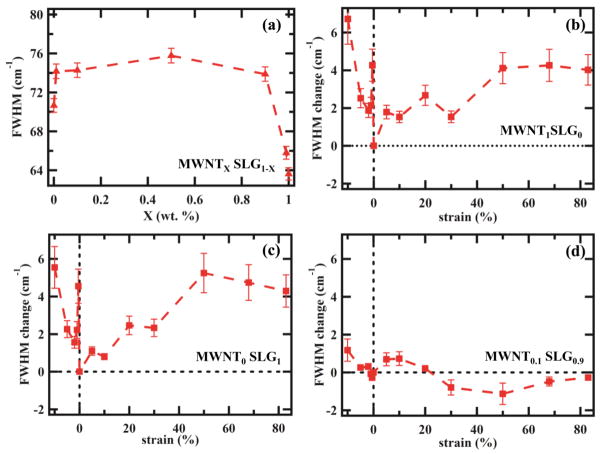
Investigating further, the Full Width Half Maximum (FWHM) of the G peak could indicate the measure of stress distribution of the nano-carbon in the composite. Slippage is expected and the Raman G bands are expected to broaden due to the high level of strains used in these experiments and the viscoelastic nature of the polymer. It should be noted that past reports on load transfer of nano-carbon composites using Raman spectroscopy has investigated only limited uniaxial tension and compression (±20%) [2, 3, 5, 6, 19, 47–50]. Figure 6(a) presents the FWHM versus weight fraction of the nano-carbon. The FWHM is almost a constant for all the weight fractions of the binary mixtures in PDMS changing as we approach one of the weight fractions of the nano-carbons without strain. Figure 6(b) presents the change in FWHM versus strain for MWNT₁SLG₀/PDMS sample. Smaller change in FWHM means uniform stress distribution and no slippage on applied tension or compression. In Figure 6(b) one can see change in FWHM of almost 6 cm⁻¹ (<10% of actual FWHM of 74 cm⁻¹) from 10% compression to the unstrained state. The change in FWHM data in tension is better (4 cm⁻¹, <5.4% of actual FWHM) suggesting less slippage in tension and more uniform stress distribution achieving saturation in the values with increasing strain. One can see that the FWHM change is almost constant between −5% to 30% at ~2 cm⁻¹ suggesting uniform load transfer at these strain values. Figure 6(c) presents the FWHM versus strain for MWNT₀SLG₁/PDMS sample. Similar trends are seen here in compression accompanied by slippage and in tension more uniform stress distribution. Although we see values of 6 cm⁻¹ for FWHM change in compression, it should be noted that the change in FWHM is less than ~10% of the actual FWHM values (74 cm⁻¹) presented in Figure 6(a). Therefore, this is not a significant effect and load is still transferred in compression more than in tension. Figure 6(d) presents the FWHM versus strain for the synergistic mixture MWNT_0.1SLG_0.9/PDMS. This sample shows that the FWHM is almost constant in both uniaxial compression and tension. The FWHM change is seen to be reduced by 3 times (from 6 cm⁻¹ change in FWHM for MWNT₀SLG₁/PDMS to 2 cm⁻¹ change for (MWNT_0.1SLG _0.9)/PDMS). This is only ~2.7% of the actual FWHM values and can be practically considered as no slippage. The change in FWHM in tension for all strains is almost zero suggesting no slippage and stress distribution remaining constant throughout the matrix or the same as un-strained sample. The use of binary nano-carbons therefore minimized slippage and made the stress distribution constant throughout with narrow FWHM change. This can only happen if the effective segmental chain is reduced and severe entanglement of MWNT and SLG with the polymeric chains giving the chains limited extensibility. It should be noted that even the 6 cm⁻¹ values of FWHM for pure samples is still narrow (<10%) suggesting uniform load transfer and minimum slippage in both compression and tension.

Figure 6.

Full Width Half Maximum (FWHM) data for the different compositions of MWNT_xSLG_1-x/PDMS: (a) FWHM versus weight fraction of the nano-carbon; (b) change in FWHM versus percentage strain for MWNT₁SLG₀/PDMS; (c) change in FWHM versus strain for MWNT₀SLG₁/PDMS; and (d) change in FWHM versus strain for MWNT_0.1SLG_0.9/PDMS.

One property that may support the Raman results on enhanced load transfer or synergistic effects of binary nano-carbon mixtures is the measurement of elastic moduli for both the samples and their comparison. Table 1 presents elastic modulus values of pure PDMS, MWNT₁SLG₀/PDMS, MWNT_0.99SLG_0.01/PDMS, MWNT_0.9SLG_0.1/PDMS, MWNT_0.5SLG_0.5/PDMS, MWNT_0.1SLG_0.9/PDMS, MWNT_0.01SLG_0.99/PDMS and MWNT₀SLG₁/PDMS. Elastic modulus values were measured to be ~ 0.96 MPa ±0.03 for pure PDMS, ~1.72 MPa ± 0.04 for MWNT₁SLG₀/PDMS, ~1.19 MPa ± 0.03 for MWNT₀SLG₁/PDMS and finally ~1.95 MPa ± 0.06 for the MWNT_0.1SLG_0.9/PDMS samples. Table 1 also presents change in elastic modulus for all the samples. An impressive increase of ~103% was seen in the synergistic sample compared to the pristine polymer. By comparison, the elastic modulus value increase of MWNT₀SLG₁/PDMS was only ~26% compared to the pristine polymer. This may be due to the defects, kinks and folding of SLG in the polymer that lowers the elastic modulus values in tension. The change in elastic modulus value for all the other mixtures are reported to be ~55–94%. It is seen that with increase in MWNT, the change in elastic modulus increase, reach a maximum and then decrease suggesting, the synergy is maximum between the 2 nano-carbons at ~0.1 wt. % MWNT. Since elastic modulus values were measured in tension, compressive deformation of SLG due to folding could lower the increase in elastic modulus. Adding small amounts (~0.1 wt. %) of MWNTs limits this deformation and therefore increases the elastic modulus value of almost ~4 times. This means, adding small amounts of MWNT must make the effective segmental chain length smaller due to severe entanglement and lead to stiffer SLG/PDMS matrix. In other words, MWNTs limit deformation of SLG, enabling larger load transfer in tension, minimum slippage and enhanced elastic modulus values.

Table 1.

Synergistic effects in elastic modulus of MWNT_xSLG_1-x/PDMS composites.

Composite	Elastic modulus (MPa)	Elastic modulus change
PDMS	0.96 ± 0.03	0
MWNT1SLG0/PDMS	1.72 ± 0.04	76%
MWNT0.99SLG0.01/PDMS	1.56 ± 0.05	63%
MWNT0.9SLG0.1/PDMS	1.49 ± 0.04	55%
MWNT0.5SLG0.5/PDMS	1.57 ± 0.03	64%
MWNT0.1SLG0.9/PDMS	1.95 ± 0.06	103%
MWNT0.01SLG0.99/PDMS	1.87 ± 0.05	94%
MWNT0SLG1/PDMS	1.19 ± 0.02	26%

Investigating further, one can use simple models to predict the change in elastic modulus of the composites based on rule of mixtures and Halpin-Tsai equations as done in the past [52]. Using simple rule of mixture approach, we predict the Young’s modulus of the MWNT_XSLG_1-X/PDMS composites by assuming the composite to be an isotropic and elastic matrix filled with binary nano-carbons. In the case of rule of mixtures, it is assumed both SLG and MWNT are well bonded and homogenously dispersed. The strain is assumed to be the same and equally distributed in both the nano-carbons. The Young’s modulus of SLG (from reduced graphene oxide) is ~250 GPa [53], MWNT is ~300 GPa [54] and PDMS is 0.96 MPa (measured). The elastic modulus of the composite using rule of mixtures can be written as:

$$E_m=({\eta }_o{\eta }_l·E_{\mathit{MWNT}}-E_{\mathit{PDMS}})·w_{\mathit{MWNT}}+({\eta }_o{\eta }_l{\eta }_f·E_{\mathit{SLG}}-E_{\mathit{PDMS}})·w_{\mathit{SLG}}+E_{\mathit{PDMS}}$$

η_o is orientation efficiency factor, η_l is the length efficiency factor and η_f is the topological index factor. Since SLG can undergo folding or change in topology, this may affect the eventual elastic modulus values and therefore is quite reasonable to have such efficiency factors. The η_l is the length efficiency factor is described by the equation:

$${\eta }_l=1-\frac{\mathit{Tanh}(a·L/D)}{a·L/D}$$

where a can be described as:

$$a=\sqrt{\frac{-3·E_{\mathit{PDMS}}}{2·E_{\mathit{carbon}}·ln(w_{\mathit{carbon}})}}$$

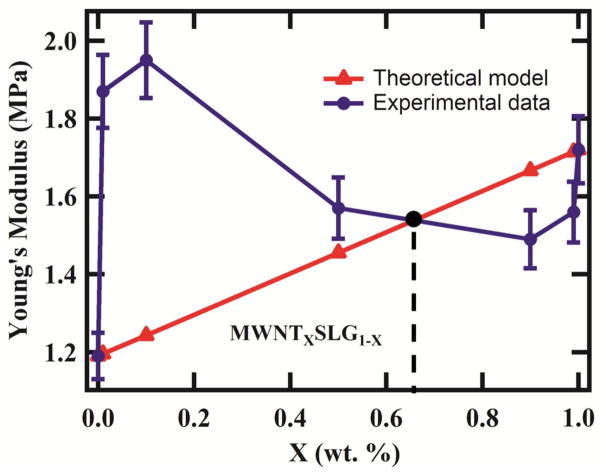
The length efficiency factor approaches unity as aL/D becomes large. This suggests that high aspect ratio fillers give better elastic modulus values. Since the elastic modulus values of the both MWNT_1.0SLG_0.0/PDMS and SLG _1.0MWNT_0.0/PDMS are known, these experimental values can be used in these theoretical equations to arrive at L/D and L/W values. The L/D for MWNT was calculated as ~61 and for SLG L/W of ~10 was used [55]. Assuming SLG to be rolled out CNT, and setting D = W/π, gives us L/D for SLG = 31.4. In both cases the L/D values of >10 underscores that both MWNT and SLG are good choices as reinforcers for polymer composites. The orientation efficiency factor is assumed to be 0.2 for randomly aligned fibers and the topological index factor η_f is suggested to be 0.9. The topological index factor assumes that SLG retains most of its plate like configuration and the defects are quite small. Geometric rolling or folding can increase or decrease the topological index factor. As the number of defects increase, the η_f values will decrease. One can then develop a relationship between defect density and topological index that could be included in the model for future calculations. Further, a relationship based on the Raman D band intensity or ratio of G to D band can be developed that can predict the topological index more accurately depending on the defects, folds, kinks and doping. However, such complex model accompanied by TEM imaging of graphene sheets with different defect densities is beyond the scope of the present paper. Figure 7 presents the elastic modulus of the MWNT_xSLG_1-x/PDMS versus weight fraction of the nano-carbon using the above described theoretical model. The actual experimental data is also plotted for comparison. Surprisingly, a linear relationship is established for the Young’s modulus of the composite with different fractions of MWNT and SLG. The linear relationship will be highly useful for design of nanocomposites based on 2 nano-carbons. However, looking at the experimental values, the model cannot accurately predict synergy between 2 nano-carbons. There is a cross-over point shown in dotted lines where the model and the experimental values agree between 0.5–0.7 wt. % MWNT. There are several reasons why the model does not accurately agree with the experimental values for other weight fractions. Composite models such as rule of mixtures assumes invariability of elastic properties of the nano-carbon and cannot predict events such as folding of graphene sheets affecting load transfer and mechanical strength, dimensionality of the sheets affecting mechanical strength and how MWNT may be bridging between 2 graphene sheets thereby eliminating the compressive deformation. While, these physical events are reflected in the Raman data, highly sophisticated atomistic simulations are needed to predict events such as synergy. These results also suggest that simple models that were previously used to predict mechanical properties of single nano-carbon fiber in polymer composites cannot be fully extended to the use of 2 nano-carbons if there is synergy between the nano-carbons. Nevertheless, the theoretical equation above is still quite useful for predicting the Young’s modulus of the composite with 2 nano-carbons where synergy may not be involved (Ex: nano-carbons of the same dimensional states but different elastic properties such as carbon nanotube and carbon nano-fiber). The experimental results show that use of 2 nano-carbons is better than one nano-carbon and that could be a fundamental basis on which both the model and experimental data agree. Again, it should be made clear that synergy may only be observed with 2 nano-carbons of different dimensional states in polymer composites.

Figure 7.

Elastic modulus versus weight percentage of nano-carbon filler for MWNT_xSLG_1-x/PDMS composite calculated using the rule of mixtures and compared to the experimental data.

Looking forward, synergy between two or more nano-carbon fillers could enhance load bearing capability, limit deformation, and improve mechanical properties of polymer composites. Graphene is a 2D structure and therefore entanglement of the polymer during the mixing process can result in folding of the lattice thereby exerting a net compressive stress. This could mean reduced/increased overall mechanical properties depending on tension/compression. Small amount of MWNT entangled in SLG during mixing and subsequent polymerization reduced the chain length and eliminated the folding of SLG completely. The method of using NIR polymerization as reported here could also be useful in improving interfacial shear strength and mechanical properties of nano-composites. While surface chemical functionalization of nanotubes/graphene are quite attractive for better interaction with polymers, recent reports have shown that improvement in interfacial adhesion due to surface functionalization of nanotubes does not always promote substantial improvement in mechanical properties [32]. This is due to surface degradation of nanotubes/graphene during functionalization. Realization of advanced mechanical properties in graphene based composites may depend on the extent to which folding of the SLG can be minimized in polymers.

3.0 Conclusions

In conclusion, this paper reports how synergy is achieved in binary nano-carbon mixtures using Raman spectroscopy and polymer physics principles. Significant shifts in the G-bands were observed both in tension and compression for single as well binary nano-carbon mixtures in polymer composites. Addition of small amounts of MWNT (~0.1 wt. %) dispersed in SLG (0.9 wt. %)/PDMS samples reversed the sign of the Raman wavenumbers from positive to negative values demonstrating complete reversal of lattice stress. A wavenumber change from 10 cm⁻¹ in compression to 10 cm⁻¹ in tension was observed for MWNT_0.1SLG_0.9/PDMS with applied uniaxial tension. MWNTs limited the deformation of SLG in one direction by providing limited extensibility to the chains and thereby improving the elastic modulus by ~103% compared to pristine polymer. Raman wave numbers shifts with angular orientation of the nanotube suggest linear relationship between change in Raman G and 2D band and MWNT orientation on application of strains. A simple rule of mixtures was used to theoretically predict the elastic modulus values of the binary nano-composite. This modeling yielded several interesting insights. A linear relationship was established between the change in elastic modulus of the nano-composite and weight fraction of the nano-carbons. Such linear relationship is ideal for fabrication of nanocomposites based on two nano-carbons. While the rule of mixtures could be used conveniently for predicting elastic modulus and stress in binary nano-carbon composites, the model could not accurately describe the observed experimental elastic modulus values which were larger. The only range in which the model and experimental values agreed were in between 0.5 to 0.7 wt. % of MWNT, which is equal mixtures and slightly larger ratio of the nano-carbons. There are several reasons for this. Composite models based on rule of mixtures assume the invariability of dimensionality, elastic constants and deformation. However in reality, synergy is the cooperative effect between two nano-carbons that results in increase in elastic modulus of the composite greater than the sum of the individual contributions. In these experiments it is seen that graphene sheets fold inside the polymer giving rise to a net compressive stress on uniaxial tension. Adding small quantities of MWNT eliminated the compressive deformation due to entanglement and stretched the SLG/PDMS matrix (observed in SEM images) resulting in complete reversal of lattice stress (Raman shifts) and enhancement in mechanical strength (Young’s modulus). Such impressive results suggest cooperative action of two nano-carbon fillers is better than single nano-carbon for better interfacial strength, mechanical properties and load transfer. Synergy between 2 nano-carbons in polymer materials could be highly useful in development of sensors, actuators, and in general mixed dimensional systems based on carbon [34]. One interesting experiment for the future may be to probe the synergy between 3 nano-carbons (0D buckyballs, 1D MWNT and 2D SLG) of different dimensionality, mechanical strength and load transfer capabilities. Such experiments might bring in additional insights and some unexpected discoveries in the future.

4.0 Methods

4.1 Materials

SLG (2D ACS Material, ~92% carbon, < 8% oxygen, produced via thermal exfoliation reduction and hydrogen reduction of single layer graphene oxide) and MWNTs (1D-Cheap Tubes, diameter: 1–10 nm, length 0.6–1 μm) were chosen due to their different dimensional states. Commercially available SYLGARD (R) 184 elastomer from Dow Corning Corporation was used as the polymer base compound. SYLGARD (R) 184 elastomer curing agent from Dow Corning Corporation was used as the cross-linker. The base compound:cross-linker was maintained at 10:1 as suggested by manufacturer. By changing the ratio of the binary nano-carbon mixtures in the polymer matrix, evolution of load transfer was investigated.

4.2 Sample preparation

Homogenous dispersions totaling 1 wt. % of nano-carbon fillers of MWNTs, SLG and their binary mixtures (different ratio of SLG/MWNT totaling 1 wt. %) were prepared using an evaporative mixing method that involved sonication of the nano-carbon fillers in isopropyl alcohol (IPA) solution for 4 h, evaporative mixing of PDMS base compound with the nano-carbon-IPA suspension for 24 h at 65C, addition of cross-linker (base compound: curing agent ratio of 10:1) and subsequent degas, cross-linking and polymerization using NIR light for 240 min, and finally post-bake relaxation for 12 h. Process times and NIR dose was optimized to achieve saturation of elastic modulus values of pure PDMS. Near-infrared (NIR) cross-linking and polymerization of samples through optical absorption and subsequent heating of the fillers to cross-link is a paradigm that has been shown recently to improve both mechanical properties and interfacial shear strength without degradation to nano-fillers [33]. Unlike conventional crosslinking processes where samples are heated in a vacuum oven between ~90–120C for 30 min, the NIR polymerization enables heating of nanotubes inside the polymer matrix by illumination with NIR light (700–1100 nm). This has been reported to significantly strengthen the nanotube/polymer interface and enable higher load transfer [33]. Samples using evaporative mixing and cross-linking were manufactured in batches. Each batch yielded 5 different samples both for characterization and mechanical property testing. Following sample preparation, scanning electron microscopy (SEM) was used to investigate sample cross-sections and nano-carbon/polymer interface. SEM images were taken in atleast 5–10 different spots and most of the SEM images were representative of the images presented here ensuring homogenous mixing.

4.3 Raman spectroscopy

Raman spectroscopy was used to ascertain shift in the wavenumbers with increasing strains to compare the load transfer between adding single nano-carbon filler or binary mixtures of nano-carbon fillers in polymer matrix. The ~632.8 nm line beam of helium-neon laser in an inVia RENISHAW micro-Raman spectrometer was focused onto the sample surface with 50× objective lens, thus forming a laser spot ~3 μm in diameter. Tensile strains were applied to samples under the micro-Raman spectrometer by stretching the samples to pre-determined lengths using a linear actuator. Compressive strains were applied by anchoring one end of the sample and pushing the other end using a linear actuator to a pre-determined length. Raman measurements were conducted in at least 4–5 different locations in each sample for statistically confident values. A Gaussian profile was used to fit the Raman bands. Finally, samples containing various fractions (0–1 wt. %) of MWNTs, SLG and combinations of SLG-MWNTs in PDMS were prepared and their elastic moduli (E) tested.

4.4 Young’s modulus calculation

Synergistic effects in elastic modulus were studied by comparing change in E values for pure PDMS, MWNT_1.0/PDMS, SLG_1.0/PDMS and various ratio of MWNT-SLG mixtures wt. % (totaling 1 wt. %). Young’s modulus of the samples were determined by measuring stress change with application of a 0–5% pre-strain in 1% increments for 4–5 different samples [36]. Change in elastic modulus was calculated based on the original elastic modulus of pure PDMS, and the percentage change reported for each sample. All the samples had linear elastic behavior in this region.