On-line corrections for visuomotor errors

Abstract

This study was designed to determine how visual feedback mediates error corrections during reaching. We used visuomotor rotations to dissociate a cursor, representing finger position, from the actual finger location. We then extinguished cursor feedback at different distances from the start location to determine whether corrections were based on error extrapolation from prior cursor information. Results indicated that correction amplitude varied with the extent of cursor feedback. A second experiment tested specific aspects of error information that might mediate corrections to visuomotor rotations: rotation angle, distance between the finger and cursor positions and the duration of cursor exposure. Results showed that corrections did not depend on the amplitude of the rotation angle or the amount of time the cursor was shown. Instead, participants corrected for the cursor–finger distance, at the point where cursor feedback was last-seen. These findings suggest that within-trial corrections and inter-trial adaptation might employ different mechanisms.

Introduction

During reaching tasks, target acquisition is mediated largely by sensory information about target location. However, information pertaining to the current hand position is also used to formulate and execute accurate movements; the visual system provides information about hand location with respect to the target, while proprioceptive sensors provide information about limb position and state. Consequently, task accuracy and precision suffer when these cues are disrupted or prevented (Elliott and Allard 1985; Carson et al. 1992, 1993; Sainburg et al. 1993; Gordon et al. 1995). However, the relative contributions of vision and proprioception have been shown to vary across movement directions, target modalities, and phases of planning (van Beers et al. 2002; Sober and Sabes 2003, 2005; Sarlegna and Sainburg 2007), making it difficult to distinguish the specific roles of these sensory signals during movement.

Previous studies have utilized distortions, provided by virtual reality environments, to dissociate the roles of vision from proprioception during reaching. For example, visuomotor rotations impose an angular dissociation between a cursor representation of the finger position and the actual finger position, with respect to a start location. Upon initial exposure to the distortion, participants aim their finger toward the target at movement initiation. This results in large cursor errors that must be corrected on-line in order to accurately complete the task. With repeated exposure to the rotation, participants gradually learn to adjust their initial movement direction, such that the rotation is accounted for at movement onset. Following adaptation, this learned angle generalizes across limbs, workspace, and arm configurations, and can be used to extrapolate accurate final positions from targets located at distances outside the training workspace (Krakauer et al. 2000; Sainburg and Wang 2002; Wang and Sainburg 2005). While such angle-based compensations account for adaptation across trials, it is not clear what aspects of visual errors are corrected during ongoing movements. In a recent study, Saunders and Knill (2004) exposed subjects to visuomotor perturbations that altered the position of the screen cursor or the motion (i.e. direction) of the screen cursor, relative to the finger location. They found that subjects responded to both manipulations at similar latencies, suggesting that position and direction-based information can be utilized to mediate corrections within a given trial. However, Saunders and Knill (2004) provided subjects with the screen cursor during target acquisition, allowing continuous updating of the corrective response throughout the final stages of movement. We now explore how information about movement error might be used to predict emerging errors during the course of motion, when the visual feedback is no longer available. Removing visual information after the error is displayed allows the assessment of the correction strategy, unaffected by such updating, and provides an indication of the degree to which errors might be extrapolated during continued movement.

The current study was designed to determine what features of visual errors mediate on-line corrections to visuomotor rotations. In the first experiment, we examined whether the angle of visuomotor rotation might lead to extrapolation of errors after the cursor is removed. To examine this question, we used a randomized paradigm, in which, we introduced constant angle rotations, but removed cursor feedback at different points in the movement. We reasoned that if angle-based information mediates the extrapolation of errors, then the amplitude of corrections should remain constant across trials with different extents of feedback. The results of this first experiment revealed that the amplitudes of corrections to rotations varied systematically with the extent of cursor feedback, suggesting that errors are not extrapolated from previous cursor information. The results of this first experiment were consistent with the idea that subjects corrected for the distance between the finger trajectory and cursor trajectory at the time that visual feedback was removed (CF distance). However, it also remained possible that corrections depended on the perceived reliability of sensory information within each trial (Kording and Wolpert 2004). In other words, as the duration of cursor exposure decreased, it is plausible that within-trial sensory information was deemed less reliable, thereby causing subjects to rely more heavily on their previous, baseline, experience.

In order to test this idea, we specifically varied different features of the error information. We hypothesized that the amplitude of corrections might depend on (1) the CF distance, (2) the duration of cursor exposure, or (3) the amplitude of the rotation angle. Additionally, it is possible that correction amplitude depended on an interaction between these factors. In order to address these questions, we utilized a 2 × 2 (rotation angle × CF distance) design, such that rotating the cursor by a small and large rotation angle imposed both a small and a large CF distance. This design dictated that the extent of cursor exposure was different for each of the conditions. Our results indicated that the amplitudes of corrections did not depend on the amplitude of the rotation angle or the duration of cursor exposure, but did depend on CF distance. Linear regression analysis, conducted within and across conditions, showed that correction amplitude was not predicted by the amount of time that the cursor was available. In summary, our results indicated that corrections to visuomotor rotations are not extrapolated from angular error information, as occurs across trials during the adaptation process. Rather, a seemingly simpler process of correcting for the most recent CF distance is implemented within the trial.

Methods

Subjects

A total of 16 neurologically intact adults (8 females, 8 males), aged from 18 to 28 years were recruited for these studies. Handedness was determined using a 35-item version of the Edinburgh inventory (Oldfield 1971), and only those classified as right-handers were used for the experiment. Of the 16 volunteers, 8 participated in the first experiment and 8 participated in the second experiment. All participants gave informed consent prior to the start of the experiment. This study was approved by the Biomedical Institutional Review Board (IRB #15084) of the Pennsylvania State University, and has been performed in accordance with the ethical standards laid down in the 1964 Declaration of Helsinki.

Experimental setup

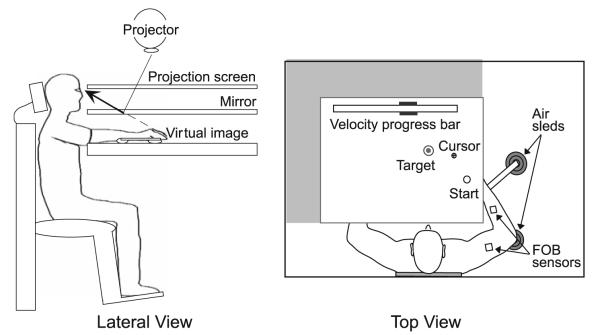
Figure 1 depicts the experimental setup. Participants sat facing the experimental apparatus, and their right arm, positioned just below shoulder height, was supported by an air jet system that reduced the effects of gravity and friction. Participants were fitted with an adjustable arm brace that stabilized the wrist and fingers. A start circle, target, and cross-hair cursor representing index fingertip position were projected on a horizontal back-projection screen just above the arm. A mirror, located below this screen, reflected the visual display such that it was perceived to be in the same horizontal plane as the arm and fingertip. In order to assure that this projection was veridical, the screen was calibrated prior to the start of the experiment. Positions and orientations of the measured segments were sampled using a Flock-of-Birds (FoB; Ascension-Technology) magnetic 6 degree-of-freedom movement-recording system. One FoB sensor was attached to the upper arm segment via an adjustable plastic cuff, and a second sensor was fixed to the forearm support. Each sensor was approximately positioned at the center of each arm segment. The positions of three bony landmarks (index fingertip, the lateral epicondyle of the humerus and the acromion, directly posterior to the acromio-clavicular joint) were digitized using a stylus that was rigidly fixed to a FoB sensor. These positions remained constant throughout the experimental session, relative to the sensors attached to each arm segment. The cross-hair cursor (1.5 cm in diameter) was projected on the screen at a rate of 85 Hz, which was fast enough to maintain the cursor on the fingertip throughout the sampled movements. During the experiment, the arm was covered and the lights were turned off so that participants were unable to view their movements. Data were digitized at 100 Hz using a Macintosh computer, which controlled the sensors through separated serial ports, and stored on disk for further analysis. Custom computer algorithms for experiment control and data analysis were written in REAL BASIC™ (REAL Software, Inc.), C (CodeWarrior™) and IGOR Pro™ (WaveMetrics, Inc.).

Fig. 1.

Lateral and top views of the experimental setup. Participants sat facing the experimental apparatus with their right arm supported by air sleds. A start circle, target and screen cursor, representing index fingertip position, was projected on a horizontal back-projection screen. A mirror, located below this screen, reflected the visual display such that it was perceived to be in the same horizontal plane as the arm and fingertip. Flock-of-Bird (FoB) sensors were attached to the upper arm segment and to the forearm support. A velocity progress bar was displayed at the top of the screen and target speeds were indicated with black rectangles

Experimental task: general

At the beginning of each session, a target and start location were presented on the screen. The position of the index finger was provided in real time as a screen cross-hair cursor. Participants were instructed to bring the cursor into the start circle at the beginning of each trial. Following a period of 300 ms, an audiovisual signal prompted the beginning of the trial and participants were instructed to move directly to the target. Between trials, cursor feedback was restricted to within 2 cm of the start center. During a baseline session, participants were familiarized to the experimental setup. Feedback regarding peak velocity was provided as a progress-bar display, and participants were trained to produce peak velocities ranging from 0.8 to 1.2 m/s. Points were awarded for final position accuracy when the movement also satisfied the peak velocity requirement. The target was 2 cm in diameter, final position errors of less than 1 cm were awarded 10 points, those between 1 and 2 cm were awarded 3 points, and final position errors between 2 and 3 cm were awarded 1 point. During the experimental sessions, the velocity progress bar was not shown, but participants were still required to produce peak velocities in the specified range to receive points.

Cursor manipulations

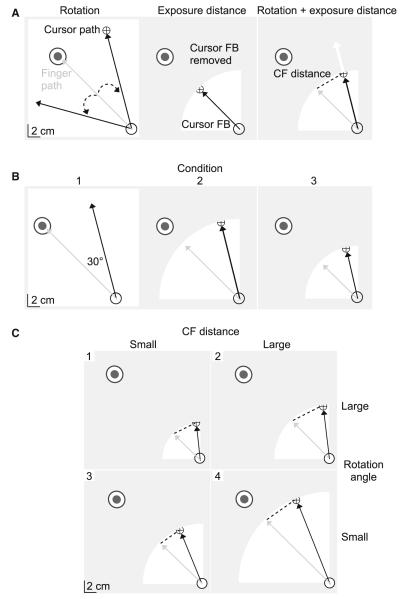
Two manipulations were used during the experimental sessions: visuomotor rotations and “cursor exposure distances”. During trials with a visuomotor rotation, the position of the cursor, corresponding to the index fingertip, was rotated relative to the start circle by a specified angle in either the clockwise (CW) or the counterclockwise (CCW) direction (Fig. 2a, left). As a result, the initial portion of the finger path was generally directed at the target (gray) and reflected the desired initial trajectory, while the cursor path (black) was directed away from the target. In order to bring the cursor accurately to the target, participants were required to initiate corrective responses that were opposite in direction to the rotation. The primary goal of this study was to assess the quality of corrections to visual errors. Therefore, participants were instructed to respond to the errors imposed by the visuomotor rotations at a comfortable speed. The second manipulation, cursor exposure distance, was defined with respect to the center of the start location and represented a distance, beyond which, cursor feedback was removed within each trial. As depicted by the shading in Fig. 2a (middle), when the index finger was within the cursor exposure distance, cursor feedback was permitted (white). However, as the index finger crossed the cursor exposure distance, the cursor was removed (gray). When both manipulations were applied simultaneously, participants received early information regarding the angle of rotation, but would be required to extrapolate from the previous cursor information within that trial in order to fully correct for the rotation (white arrow; Fig. 2a, right). Additionally, the combination of cursor manipulations resulted in a displacement between the last-seen cursor position and the actual finger position (CF distance; dotted line). CF distance varied systematically with the cursor exposure distance and with the amplitude of the rotation angle. Larger cursor exposure distances and/or rotation angles resulted in larger CF distances than smaller cursor exposure distances and/or rotation angles.

Fig. 2.

Experimental manipulations. Each frame depicts the start location (open circle), target location, finger path (gray arrow), screen cursor (cross-hair), and/or cursor path (black arrow). a Visuomotor rotations introduced a discrepancy in cursor and finger information by rotating the screen cursor, indicating index fingertip position, relative to the start location by a specified angle (dotted arrow; left). Cursor exposure distances controlled the amount of error information in each trial by limiting cursor feedback to within a certain distance from the start location (white; middle). When the visuomotor rotation and cursor exposure distance were applied simultaneously, participants were required to extrapolate from previous cursor information in order to fully compensate for the rotation (white arrow; right). Additionally, the distance between the cursor and finger (CF distance; dotted line) varied systematically with the amplitude of the cursor exposure distance and rotation angle. b Experiment 1. All perturbation trials were rotated by 30°, such that each condition varied by the amplitude of the cursor exposure distance. The first three conditions are shown. c Experiment 2. A small (4 cm; left) and large (6 cm; right) CF distance was created by rotating the cursor by either a large (top; 39°) or small (bottom; 23°) rotation angle

Experimental task: experiment 1

The first experiment consisted of a baseline session with 25 trials and an experimental session with 6 blocks, each having 55 trials. The target, located 16 cm and 135° from the start location, was similar for all trials. During each block in the experimental session, a 30° visuomotor rotation was randomly applied every 3–4 trials in either the CW or the CCW direction. This resulted in eight rotations per direction per block. During the first experimental block, full cursor feedback was shown within each trial. However, for the remainder of the experimental session, a different cursor exposure distance was applied to all trials within each block (12, 8, 4, 2, 1 cm). These blocks were performed in sequential order, resulting in six conditions that varied with the cursor exposure distance (Table 1). The first three conditions are shown in Fig. 2b. Because the first experimental block permitted full cursor feedback, the CF distance was determined at the target distance, rather than the point that cursor feedback was removed.

Table 1.

Experimental conditions of experiment 1

Condition	Rotation angle (°)	Cursor exposure distance (cm)
1	30	16
2	30	12
3	30	8
4	30	4
5	30	2
6	30	1

Experimental task: experiment 2

Experiment 2 consisted of 1 practice session with 25 trials and 1 experimental session with 230 trials. All trials were to a single target, located 20 cm and 135° from the start circle. In contrast to experiment 1, where cursor exposure distances were applied to all trials within each block, both manipulations were randomly presented within a single experimental session for experiment 2. Every 3–4 trials, participants were exposed either to a cursor exposure distance or to both a cursor exposure distance and a visuomotor rotation. Rotations occurred in either the CW or the CCW direction. The second experiment was designed to determine whether within-trial corrections to visuomotor rotations depended on the amplitude of the rotation angle, CF distance, and duration of cursor exposure or some combination of these factors. Thus, we systematically varied the angle of the visuomotor rotations and the cursor exposure distances, such that small (4 cm) and large (6 cm) CF distances were imposed by both a small (23°) and a large (39°) rotation angle (Fig. 2c). In order to achieve this 2 × 2 (CF distance × rotation angle) design, cursor exposure distances were different for each condition (15, 10, 9, 6 cm). As summarized in Table 2, this resulted in four conditions that varied with the amplitude of the rotation angle, cursor exposure distance, and CF distance.

Table 2.

Experimental conditions of experiment 2

Condition	Rotation angle (°)	Cursor exposure distance (cm)	CF distance (cm)
1	39	6	4
2	23	10	4
3	39	9	6
4	23	15	6

Kinematic data: general

The 3D position of the index finger was calculated from the sensor position and orientation. All kinematic data were low-pass filtered at 8 Hz (3rd-order, dual pass Butterworth) and differentiated to yield velocity and acceleration values. Peak velocity was calculated as the maximum in tangential velocity. The onset of movement was defined by the last minimum (<3% peak tangential finger velocity) prior to the maximum in tangential finger velocity, while movement termination was similarly defined by the first minimum (<3% peak tangential finger velocity) following the maximum in tangential finger velocity or the peak corrective response.

While the hand paths of baseline and rotated trials were generally directed toward the target at movement onset, corrections to visuomotor rotations were directed perpendicular to the initial movement direction. Thus, we utilized the mean baseline performance of each subject as a standard for classifying rotation trials, normalizing correction amplitude and determining the earliest measurable response to the rotation. Baseline trials were taken as the median trial between two rotation trials and never directly followed a rotation trial. Mean perpendicular displacement for the baseline and rotation trials was determined for each of the cursor exposure distances (8 trials each). Perpendicular displacement was calculated at movement termination with respect to the initial movement direction, which was determined by the line joining the center of the start location and the position of the finger at peak velocity. Negative values indicated hand paths that were directed CW to the initial movement direction, while positive values indicated hand paths that were directed CCW to the initial movement direction. Thus, the perpendicular displacements of baseline movements were near zero, while corrections showed perpendicular displacements that varied predictably with the direction of rotation. A trial was classified as showing a reliable correction if the perpendicular displacement fell outside that of the comparable baseline mean ± 1 standard deviation, and the correction was directed opposite to the rotation. Trials that did not show corrections, quantified in this manner, were removed from the analysis. We then determined the minimum cursor exposure distance that resulted in frequent and reliable error corrections to the rotation. For each participant, the percentage of trials corrected [(number of trials with a reliable correction/total number of trials) × 100] was determined for each cursor exposure distance. Regression analysis was conducted to determine the dependence of the percentage of trials corrected on the cursor exposure distance. Similar to perceptual discrimination analysis, we then determined the cursor exposure distance for which 33% of trials were corrected or what would be predicted by chance alone (choosing either baseline movement, CCW correction, or CW correction). Baseline performance was also used to normalize correction amplitude, so as to account for the natural curvature of each participant’s baseline movements. Mean baseline perpendicular displacement for each cursor exposure distance was subtracted from the perpendicular displacement of each rotation trial with the same cursor exposure distance. Correction amplitude was calculated as the absolute value of the normalized perpendicular displacement. Finally, in order to determine the earliest measurable response to the rotation, we utilized a routine that was modified from one previously used to identify corrective responses to mechanical perturbations in kinematic, kinetic, and electromyo-graphic data (Mutha et al. 2008). We calculated the difference in the perpendicular velocity of mean baseline performance and each rotation trial. Perpendicular finger velocity was calculated by differentiating perpendicular displacement. As shown in Fig. 4b, peak response to the rotation (black line) was indicated by the maximum in perpendicular velocity (change from baseline). The last minimum prior to peak perpendicular velocity (change from baseline) that was <20% of the peak response was taken as the earliest measurable response to the rotation (indicated by an arrow). Correction time was calculated as the time from the onset of movement to the earliest measurable response to the rotation. Additionally, cursor exposure duration was calculated from movement onset to the point where the index finger crossed the cursor exposure distance and movement duration was calculated from the onset of movement to the end of movement.

Fig. 4.

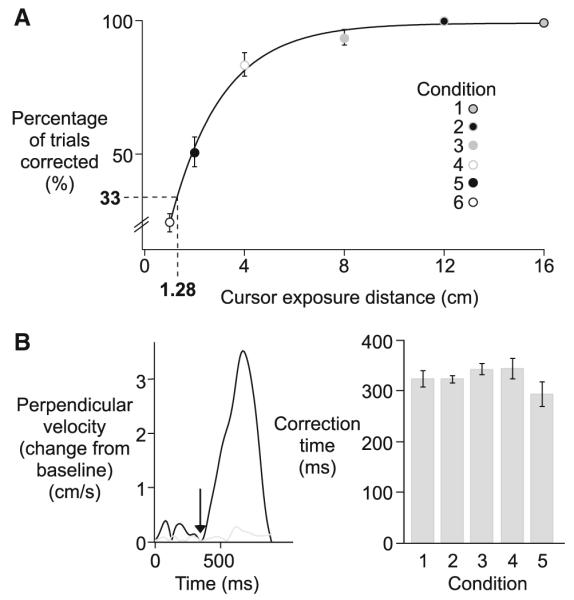
Experiment 1. a Percentage of trials corrected (means ± standard errors, across subjects) is plotted as a function of cursor exposure distance for each condition (exponential line-fit; y = 99.053 – 122.15e^{(−0.48208x)}; black line). b Perpendicular velocity (change from baseline) for a sample corrected (black) and uncorrected (gray) trial, with the first measurable response of the corrected trial indicated with an arrow (left). Correction time (mean values ± standard errors, across subjects) for each condition (right)

Statistical analysis

There were six conditions in experiment 1, which varied with the cursor exposure distance. Thus, we utilized one-way repeated-measures ANOVA with cursor exposure distance (16, 12, 8, 4, 2, 1 cm) as the within-subject factor. Post hoc analysis was done using the Tukey–Kramer HSD (Honestly Significant difference) test. The average percentage of trials corrected across subjects decreased exponentially as CF distance decreased. Thus, we utilized nonlinear regression analysis (exponential fit) to assess the dependence of the average percentage of trials corrected on the CF distance. Exponential fits have previously been used to describe changes in motion perception during a body rotation task (Vingerhoets et al. 2006). A within-subject linear regression analysis was used to assess the dependence of the average correction amplitude on the CF distance.

In experiment 2, four conditions varied with two independent measures of interest, rotation angle and CF distance. We utilized a two-way repeated-measures ANOVA with rotation angle (23°, 39°) and CF distance (4, 6 cm) as within-subject factors. Post hoc analysis was done using the Tukey–Kramer HSD (Honestly Significant difference) test. Additionally, within-subject linear regression analysis was used to assess the dependence of correction amplitude on cursor exposure duration for each CF distance and for each condition separately. Comparison of correlation coefficients was accomplished by converting r-values to z-scores using Fisher’s z’ transformation. For linear regression analysis conducted within each CF distance, we subjected Fisher’s z-scores and slope values to a one-way repeated-measures ANOVA with CF distance (4, 6 cm) as the within-subject factor. For linear regression analysis conducted within each condition, we utilized a one-way repeated-measures ANOVA with condition (1, 2, 3, 4) as the within-subject factor.

Results

Experiment 1

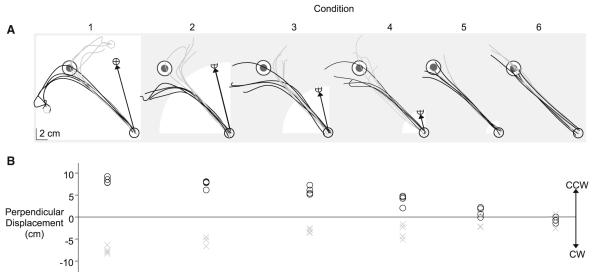
Figure 3a shows sample hand paths from visuomotor rotation trials separated by condition for a representative subject. Movements tended to be directed toward the target at movement onset, and changed direction during the course of motion so as to compensate for the rotation. CW rotations predominantly resulted in CCW corrections (black), while CCW rotations predominantly resulted in CW corrections (gray). Additionally, the number of trials with distinguishable corrections varied across condition. This trend is also illustrated in Fig. 3b, which shows the perpendicular finger displacement of the sample trials in Fig. 3a. All trials in the first four conditions showed considerable perpendicular displacements that were opposite in direction to the imposed rotation. However, when cursor feedback was restricted to within 2 cm of the start circle, as was the case for conditions 5 and 6, the frequency and consistency of corrections were considerably decreased. These trials showed little perpendicular displacement with respect to the initial movement direction (black line). Furthermore, as indicated by the overlap of markers (gray, black), corrections were not consistently directed, and as a result, did not necessarily compensate for the rotation.

Fig. 3.

Experiment 1. a Hand paths of corrective responses to clock-wise (black) and counterclockwise (gray) rotations for each condition from a representative subject. The cursor exposure window (white), the cursor path direction for clockwise rotations (black arrow), and the position the finger would need to terminate in order to bring the cursor to the target center (open gray circle) are shown for reference. b Perpendicular finger displacements of the clockwise (black) and counterclockwise (gray) rotation trials for each condition in Fig. 3a. Negative perpendicular displacements indicate responses that were directed clockwise (CW), while positive values indicate responses that were directed counterclockwise (CCW)

Visuomotor rotations introduce an error between the cursor and intended target that increases as a function of the distance from the start location. As a result, this cursor error was small for conditions where cursor feedback was removed early in the movement. When few corrections to the visuomotor rotation were evident, it is plausible that there was not enough time for error detection to take place, or the error between the target and cursor was too small to be detected. Consequently, cursor errors imposed by the dissociation would not be available and corrections would not be adaptive. Thus, we determined the minimum cursor exposure distance that resulted in reliable error corrections to the rotation. The cursor exposure distance for which 33% of trials were corrected represents chance prediction for a three-condition task (choosing baseline movement, CCW correction, or CW correction). Figure 4a shows the percentage of trials corrected across subjects for the cursor exposure distance in each condition. Corrections were defined by the amplitude and direction of perpendicular displacement with respect to baseline trials (see methods). For cursor exposure distances >8 cm (conditions 1, 2, and 3), more than 90% of all rotation trials were corrected. However, the percentage of trials corrected considerably decreased with cursor exposure distances <2 cm (conditions 5, 6). By interpolating from the exponential line-Wt (y = 99.053 – 122.15e^{(−0.48208x)}), shown in Fig. 4a, we determined that approximately 33% of rotation trials should be corrected for a cursor exposure distance of 1.28 cm. This finding indicates that the cursor must travel a greater distance than 1.28 cm from the center of the start circle for reliable error corrections to occur more frequently than what would be predicted by chance. Because further analysis will focus on error correction trials, trials from condition 6, which introduced a cursor exposure distance less than this distance threshold (1 cm), will be excluded from the remainder of the analysis.

As is depicted in the hand paths in Fig. 3a, corrections to visuomotor rotations occurred near the target location and were directed perpendicular to the initial movement trajectory. In order to determine the earliest response to the rotation, we calculated the difference in perpendicular finger velocity of each rotation trial from that of mean baseline performance (see methods). Figure 4b (left) shows the perpendicular velocity (change from baseline) from a sample corrected (black) and uncorrected (gray) trial. As was expected, perpendicular finger velocity (change from baseline) for the uncorrected trial was small compared to that of the corrected trial. By searching backwards from the peak in the corrective response, we determined the earliest measurable correction time to be approximately 350 ms (indicated by an arrow) for the sample corrected trial.

Figure 4 (right) shows the mean values and standard errors of correction time across subjects for each condition. On average, correction onset occurred 325 ± 8 ms following movement initiation, which is a reasonable correction time for this type of task (Shabbott and Sainburg 2008). Additionally, correction time was not Significantly different across cursor exposure distances (F_4,35 = 2.0851; p = 0.11), indicating that removing visual feedback about hand position during the course of motion did not affect the latency of visually mediated corrections. It should be noted that this study was designed to assess the quality of visual-mediated corrections, and as a result, the current response time reflects a paradigm in which participants were instructed to respond to errors at a comfortable speed. Therefore, the ~325 ms correction time, measured in this study, does not necessarily reflect the absolute minimum latency at which visual information can be used.

The next question that we addressed was how subjects corrected for the visuomotor rotations when the extent of cursor feedback was manipulated. While the latency of corrections to visuomotor rotations was similar across conditions, the quality of corrections, indicated by perpendicular finger displacement, varied systematically with the cursor exposure distance, as is shown in Fig. 3a and b. Interestingly, the extent of cursor feedback appeared to directly determine the amplitude of the correction, which was measured as the absolute value of the normalized perpendicular finger displacement. This trend was consistent across subjects (Fig. 5, left) and is reflected by our ANOVA, which revealed a main effect of cursor exposure distance (F_4,35 = 42.3255; p < 0.0001). This suggests that participants did not correct for the angle of the visuomotor rotation. Instead, corrections varied systematically with the cursor exposure distance. Figure 5 (middle) shows that correction amplitude increased as a function of the cursor exposure distance for the representative subject shown in Fig. 3 (black), in addition to all other subjects (gray). This relationship is further indicated by the mean results of the within-subject regression analysis, which shows a strong dependence of correction amplitude on cursor exposure distance across subjects (Fig. 5, right; r = 0.91 ± 0.02; slope = 0.32 ± 0.02). However, given that peak velocity was similar for all conditions (F_4,35 = 0.2645; p = 0.90), the CF distance also varied systematically with the distance of cursor exposure. Therefore, it is not possible to determine from this study whether the amplitude of within-trial corrections to visuomotor rotations depends on the cursor exposure duration, CF distance, amplitude of the rotation angle, or some interaction between these factors. We thus, designed our next experiment to dissociate these factors.

Fig. 5.

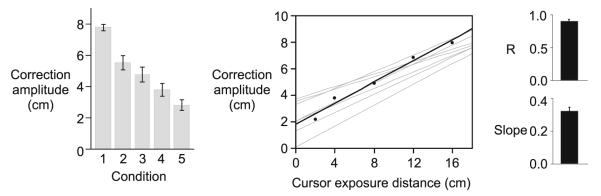
Experiment 1. Correction amplitude (mean values ± standard errors, across subjects) for each condition (left). Mean correction amplitude is plotted as a function of cursor exposure distance from a representative subject (black; middle). Linear regressions for all other subjects are shown in gray. The correlation coefficient (mean ± standard error, across subjects) and slope (mean ± error, across subjects) for mean correction amplitude versus cursor standard exposure distance (right)

Experiment 2

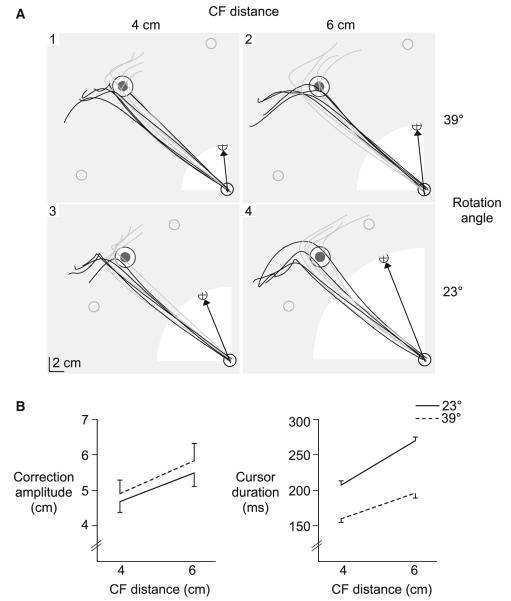
In order to address the apparent confounds in experiment 1, we designed an experiment to specifically test what aspects of visual information are most important for correcting visuomotor rotations within a given trial. In experiment 2, we systematically varied the cursor exposure distance and the angle of rotation, such that a small (23°) and large (39°) rotation angle resulted in both a small (4 cm) and large (6 cm) CF distance (2 × 2 design). We predicted that if subjects corrected for the CF distance, then the amplitude of the response would vary with the CF distance, and not the angle of rotation. This should result in a main effect of CF distance on correction amplitude. However, if correction amplitude depended on the amplitude of the rotation angle, then we would expect a main effect of rotation angle, but not CF distance. Figure 6a shows hand paths from a representative subject for each condition. The amplitude of corrections tended to vary with the amplitude of the CF distance, but not the angle of rotation.

Fig. 6.

Experiment 2. a Hand paths of corrective responses to clockwise (black) and counter-clockwise (gray) rotations for each condition from a representative subject. The cursor exposure distance (white), the cursor path direction for clockwise rotations (black arrow) and the position the finger would need to terminate in order to bring the cursor to the target center (open gray circle) are shown for reference. b Correction amplitude (mean values ± standard errors, across subjects), and c Cursor exposure duration (mean values ± standard errors, across subjects) for the 4 and 6 cm CF distance is displayed for the small (23°; solid line) and large (39°; dotted line) rotation angle

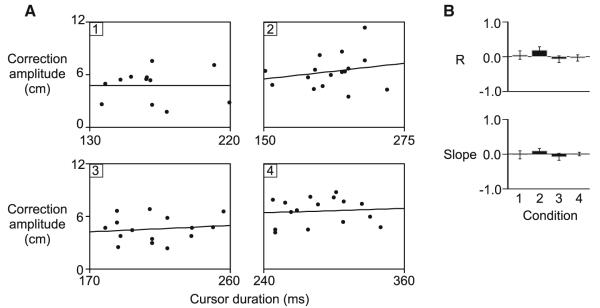
Correction amplitude is shown across subjects for each condition in Fig. 6b (left). Corrections to the 4 cm CF distance (4.8 ± 0.2 cm) were significantly smaller than corrections to the 6 cm CF distance (5.7 ± 0.3 cm), irrespective of the angle of rotation. This is reflected by a main effect of CF distance (F_1,28 = 24.5464; p < 0.0001) and lack of an effect of rotation angle (F_1,28 = 2.4589; p = 0.13) or interaction of CF distance with rotation angle (F_1,28 = 0.1207; p = 0.73). Interestingly, the amplitudes of corrections tended to be slightly larger for the larger rotation angle than the smaller rotation angle, despite the fact that cursor exposure duration (Fig. 6b, right) was Significantly shorter for the larger rotation angle (178 ± 9 ms) than the shorter rotation angle (238 ± 9 ms) (main effect of rotation angle; F_1,28 = 580.6876; p < 0.0001). This pattern is in direct opposition to what would be expected if cursor exposure duration determined correction amplitude. This trend is further illustrated in Fig. 7 (left), which shows correction amplitude plotted as a function of cursor exposure duration, for the representative subject shown in Fig. 6a. Given the main effect of CF distance on correction amplitude, a separate linear regression was conducted for each CF distance. Across subjects, the mean correlation coefficient (−0.018 ± 0.03) and slope value (−0.017 ± 0.01) from the within-subject regression analysis was near zero (Fig. 7, right), and was not Significantly different for the 4 and 6 cm CF distance (Fisher’s z-score, F_1,28 = 0.5325; p = 0.49; slope, F_1,28 = 1.8404; p = 0.22). This indicates that correction amplitude did not depend on the amount of time that the cursor was available.

Fig. 7.

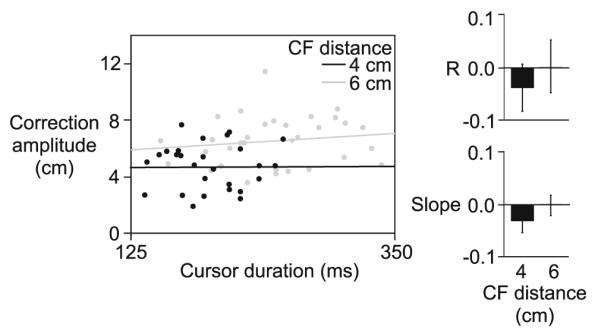
Experiment 2. Correction amplitude is plotted as a function o f cursor duration for the 4 cm (black) and 6 cm (gray) CF distance, for a representative subject (left). Correlation coefficients (mean values ± standard errors, across subjects) and slopes (mean values ± standard errors, across subjects) are displayed for the small (4 cm) and large (6 cm) CF distance (right)

An alternative hypothesis is that correction amplitude within a given rotation trial depended on an interaction between two or more of the factors of interest (rotation angle, CF distance, cursor exposure duration). In fact, as shown in Fig. 6b (right), and as reflected by the results of our ANOVA, there was an interaction of rotation angle with CF distance for cursor exposure duration (F_1,28 = 27.5107; p < 0.0001). As such, the pattern of correction amplitudes shown in Fig. 6b (left) could also be interpreted as being dependent on the amplitude of the rotation angle, modulated by the amount of time that the cursor was available. In other words, the representation of the angular dissociation in the cursor and felt position of the finger might decay as the cursor is removed at earlier points in the movement. This idea is consistent with previous work, which has shown that the contributions of sensory modalities are often weighted in a task-specific manner, so as to maximize accuracy and precision (van Beers et al. 2002; Bagesteiro et al. 2006; Sarlegna and Sainburg 2007). To test this hypothesis, we examined whether correction amplitude varied with cursor exposure duration for each separate condition. As shown in Fig. 8a, in which correction amplitude is plotted as a function of cursor exposure duration for each condition from a representative subject, this does not appear to be the case. The lack of dependency of correction amplitude on cursor duration is further indicated by the mean correlation coefficient (−0.027 ± 0.05) and slope value (−0.004 ± 0.04) from the linear regression analysis across subjects (Fig. 8b). These values were near zero and similar for all conditions (Fisher’s z-score, F_3,28 = 1.2241; p = 0.33; slope, F_3,28 = 0.6414; p = 0.60). It should be noted that the range of cursor durations, within each condition, was ~100 ms. Given that the mean movement duration of baseline movements was 662 ± 14 ms, the variance in cursor exposure durations within each condition was >10% of the total movement duration for baseline movements. In summary, these findings indicate that correction amplitude is not dependent on the angle of rotation, modulated by the duration of cursor exposure.

Fig. 8.

Experiment 2. a Correction amplitude is plotted as a function of cursor duration from a representative participant for each condition (1, 2, 3, 4). b Correlation coefficients (mean values ± standard errors, across subjects) and slopes (mean values ± standard errors, across subjects) are displayed for each condition (right)

Discussion

Following adaptation to visuomotor rotations, participants are able to extrapolate from the experience in order to generalize the rotation angle across distances, spatial locations, and limbs (Krakauer et al. 2000; Sainburg and Wang 2002; Wang and Sainburg 2005). It is, however, currently unknown what aspects of error information are used for within-trial corrections to visuomotor rotations. In order to address this question, we exposed participants to visuomotor rotations on random trials and removed cursor feedback at different points in the movement. Our results showed that the amplitude of corrections varied systematically with the extent of cursor feedback, suggesting that errors are not extrapolated from angle-based information after the cursor is removed. We next examined whether the amplitudes of corrections depended on the duration of cursor exposure, distance between the cursor and finger positions at the time that feedback was removed, amplitude of the rotation angle, or some interaction between these factors. In a second experiment, we varied the extent of cursor feedback such that we exposed participants to large and small rotation angles that resulted in both large and small distance errors between the finger and cursor. Results indicated that the amplitude of corrections depended on the amplitude of the cursor–finger error, but not the angle of rotation, duration of cursor exposure nor an interaction between these factors. In summary, participants apparently correct for the most recently detected displacement of the cursor from the finger location, but do not extrapolate from the angle of rotation. This suggests that corrections elicited during an ongoing movement and during inter-trial adaptation might employ distinct control mechanisms, possibly localized in separate areas of the brain.

During targeted-reaching tasks, final positions tend to be more accurate when visual feedback about hand position is available than when the view of the hand is prevented (Elliott and Allard 1985; Carson et al. 1990, 1992, 1993). This advantage, in part, likely reflects better planning prior to movement start, provided by a more accurate representation of the initial state of the arm relative to the target (Prablanc et al. 1979; Rossetti et al. 1994; Desmurget et al. 1995). However, given inaccuracies in the movement plan or unexpected changes to task goals, visual feedback of hand position can further improve accuracy by mediating modifications to ongoing movements. Still, it remains unclear how visual information is assessed and corrected during the course of motion. A number of studies have indicated that task accuracy only improves when hand position is provided near the vicinity of the target (Carlton 1981; Temprado et al. 1996), and that the acceleration phase of motion is unaffected by visual feedback (van der Meulen et al. 1990; Heath et al. 1998). Such results have been interpreted in support of Woodworth’s (1899) early proposition that visual-based error corrections are limited to the later phases of motion. However, other studies have shown improvements in reaching accuracy when visual feedback of hand position was provided much earlier in a movement (Blouin et al. 1993a, b; Bedard and Proteau 2004; Ma-Wyatt and McKee 2007). In a recent set of studies, Saunders and Knill (2003, 2005) used cursor perturbations to determine the temporal characteristics of visual-based corrections during movement. They reported that corrections for early perturbations had similar latencies to those of late perturbations, suggesting that the use of visual feedback was not confined to the end phases of motion. Results also suggested that the extent of on-line corrections varied with the duration of cursor feedback, a finding consistent with other studies (Komilis et al. 1993; Nijhof 2003). Thus, it appears that visual feedback is used very early in movement, to formulate error corrections on-line.

The results of the current study support the finding that early visual information is used for error correction processes, and substantially extends previous findings by showing that corrections implemented late in movement can reflect errors that were detected as early as 112 ms following movement onset (2 cm from the start location). In our second experiment, we showed that the amplitude of the error imposed by the displacement of the cursor from the finger, and not the duration of visual feedback, is the limiting factor for on-line corrections to visuomotor rotations. During our 30° visuomotor rotations, frequent and reliable error corrections were evident when the cursor travelled beyond 1.28 cm from the center of the start location; at this point, the distance between the cursor and finger was 0.66 cm. Thus, it is plausible that participants only corrected for the imposed displacement of the cursor from the finger when that distance was >0.66 cm, which is within the normal width of an adult fingertip. However, it remains possible that this threshold differs across tasks.

Visuomotor rotations have often been employed to study the process of trial-to-trial adaptation to novel visuomotor conditions. While large on-line corrections are typically found upon initial exposure to visuomotor rotations, these corrections are reduced over the course of many trials, as the movement plan is adapted to account for the rotation at movement onset, a process that is mediated by implicit processes (Mazzoni and Krakauer 2006). Previous results from our laboratory have indicated that subjects gradually develop a model of the imposed rotation direction; following adaptation, subjects generalize the direction and amplitude of the rotation, as opposed to remapping the position space of the task (Wang and Sainburg 2005). Consistent with these findings, other studies have shown that subjects generalize learning across limb configurations, distances, workspace, and even from one arm to the other, and that this generalization is based on rotation angle (Krakauer et al. 2000; Sainburg and Wang 2002; Wang and Sainburg 2005). When the rotation is removed after learning, these angle-based transformations often persist in the form of ‘after-effects’ (Ghilardi et al. 1995; Mazzoni and Krakauer 2006; Zarahn et al. 2008), directional errors that are opposite to the rotation. Thus, during trial-to-trial adaptation of visuomotor rotations, there is little doubt that subjects develop a model of the angle of rotation, in order to plan subsequent movements.

The results of the current experiment indicate that on-line corrections to visuomotor rotations are likely based on a different strategy that does not depend on the angle of rotation. Participants do not extrapolate from angle-based cursor information, as is seen following adaptation. Additionally, the current results showed that the representation of the rotation angle is not strengthened with the duration of exposure to the rotation. This strategy, again, is unlike the adaptation process, where the angle of rotation is incrementally learned over the course of many trials. The current results strongly suggest that participants corrected for the last-available cursor error, imposed by the displacement of the cursor from the finger position. Taken together, these results suggest that feedback-mediated corrections within a given trial and during the adaptation process could employ separate control strategies. This is consistent with a number of other studies, which have shown that adaptation does not rely on on-line corrections, supporting the idea that these two strategies are related to different underlying control mechanisms (Klassen et al. 2005; Tseng et al. 2007; Hinder et al. 2008). Conversely, Saunders and Knill (2004) recently showed that the latencies of corrective responses for a given trial were similar whether the direction or the position of the cursor, relative to the finger, was manipulated. Thus, the authors concluded that both positional and directional information is used to formulate within-trial corrections to visuomotor errors. However, it should be noted that when the position of the cursor was manipulated, there was a noticeable trend for responses to occur at shorter latencies than when the direction of the cursor was manipulated. While this difference was not statistically significant, it is possible that the longer latency responses for direction perturbations (>20 ms longer than the latency for responses to the position perturbation) allowed sufficient time for a detectable distance error between the cursor and finger to emerge. This would be consistent with the findings of the current experiment. Moreover, when position and direction perturbations were combined in such a way that the position error was minimized mid-movement, response time were Significantly prolonged relative to other conditions (Saunders and Knill 2004). Therefore, while the direction perturbation was present, information about the position of the cursor appeared to be the dominant source of error information used in formulating the corrective response. This finding emphasizes the importance of position-based errors during within-trial error corrections. Finally, unlike the current experiment, Saunders and Knill (2004) provided subjects with cursor information during target acquisition. As a result, the initial corrective responses shown in that study could represent a more immediate process that does not involve the formulation of the full response. While direction-based errors might mediate such responses, the results of the current experiment showed that this information is not used to predict emerging errors, after the cursor is removed.

The idea that corrections within and across trials might be strategically different, suggests that these processes could be controlled by distinct areas of the brain and thus, differentially affected by disease. Previous imaging studies have suggested a possible role for the cerebellum in visual-based on-line corrections (Inoue et al. 1998; Diedrichsen et al. 2005), as well as trial-to-trial adaptation (Shadmehr and Holcomb 1997; Krakauer et al. 2004). These findings corroborate work in nonhuman primates, which has indicated that cerebellar purkinje cells encode desired final positions and movement errors (Kitazawa et al. 1998), and that the firing patterns of these cells tend to correlate with improvements in performance across sequential trials (Gilbert and Thach 1977). Another major structure involved in visuomotor adaptation is the posterior parietal cortex. This region was shown to be active during motor learning tasks, including adaptation to visuomotor rotations (Inoue et al. 1997; Shadmehr and Holcomb 1997; Ghilardi et al. 2000; Inoue et al. 2000; Krakauer et al. 2004). These studies have suggested a role of posterior parietal cortex in carrying out transformations between eye-centered and hand-centered coordinates (Buneo et al. 2002). While both cerebellum and posterior parietal cortex appear to be important for motor adaptation, studies in patient populations have provided evidence that specific circuits involving both areas (Clower et al. 2005) might differentially control corrections to ongoing movements, and inter-trial adaptations.

A striking double-dissociation in motor deficits has been shown in patients with disorders that affect the basal ganglia, such as Huntington’s and Parkinson’s disease (Albin et al. 1989), and those with lesions in the cerebellum. In a comprehensive study by Smith and Shadmehr (2005), patients with Huntington’s disease showed disrupted on-line corrections when exposed to a novel dynamic environment, but substantial learning across trials. Conversely, cerebellar patients showed on-line corrections, but modifications between trials were abnormal and thus, adaptation was incomplete. Across a wide variety of tasks, feedback-mediated adjustments to ongoing movements tend to be affected in patients with Parkinson’s and Huntington’s disease (Smith et al. 2000; Desmurget et al. 2004; Tunik et al. 2004), while the ability to adapt over sequential trials remains intact (Agostino et al. 1996; Fernandez-Ruiz et al. 2003). In contrast, patients with cerebellar lesions show problems during a variety of motor learning tasks (Sanes et al. 1990; Martin et al. 1996; Chen et al. 2006; Tseng et al. 2007), but sustain the ability to adjust movements on-line (Day et al. 1998). Taken together, these results suggest a distinct role for the basal ganglia in feedback-mediated corrections within trials, and for the cerebellum in inter-trial adaptation. Our current findings support these studies by demonstrating that angle-based cursor information is not used to extrapolate errors on-line, evidence that on-line error correction processes are distinct from those employed between trials during the adaptation process. Additionally, we suggest that the results of the current experiment extend these ideas by demonstrating two qualitatively distinct classes of visuomotor corrections that occur within a single trial, and across multiple trials, respectively.