A Correlated Random Effects Model for Non-homogeneous Markov Processes with Nonignorable Missingness

Abstract

Life history data arising in clusters with prespecified assessment time points for patients often feature incomplete data since patients may choose to visit the clinic based on their needs. Markov process models provide a useful tool describing disease progression for life history data. The literature mainly focuses on time homogeneous process. In this paper we develop methods to deal with non-homogeneous Markov process with incomplete clustered life history data. A correlated random effects model is developed to deal with the nonignorable missingness, and a time transformation is employed to address the non-homogeneity in the transition model. Maximum likelihood estimate based on the Monte-Carlo EM algorithm is advocated for parameter estimation. Simulation studies demonstrate that the proposed method works well in many situations. We also apply this method to an Alzheimer's disease study.

1. Introduction

Multi-state life history data arise in many research areas such as medicine, social sciences and public health, and multi-state models provide a convenient way to characterize the movement of individuals among distinct states. With continuous time multi-state models, transition intensities are often of primary interest, and these are perhaps most widely modeled by Markov models (e.g., Bartholomew 1983; Singer and Spilerman 1976a, 1976b; Wasserman 1980). Various methods based on Markov models have been proposed in literature, including discrete time (e.g., Albert and Waclawiw 1998) and continuous time models (Andersen et al. 1993; Kalbfleish and Lawless 1985, 1989; Cook et al. 2004; Cook, Kalbfleisch and Yi 2002).

Most applications assume a homogeneous Markov process; that is, the transition probabilities only depend on the elapsed time between observations. This assumption is not satisfied when transition probabilities depend on previous times. Limited work has been devoted to deal with non-homogeneous Markov process models. Kalbfleisch and Lawless (1985) proposed a method for modeling non-homogeneous multi-state data under panel observations, in which the non-homogenous intensity matrix is a product of a baseline homogeneous intensity matrix and a function of time. Gentleman et al. (1994) considered piecewise constant transition intensities to deal with non-homogeneous models. A number of authors have used piecewise homogeneous processes to model temporal homogeneity with applications (e.g., Saint-Pierre et al. 2003; Ocana-Riola 2005; Perez-Ocon, Ruiz-Castro and Gamiz-Perez 2001). Hubbard, Inoue and Fann (2008) considered a time transformation method to deal with the non-homogeneity. This method allows the time-varying transition intensity matrix by assuming the transition intensity to be the product of a baseline transition intensity matrix and a scalar function of time. This method requires fewer parameters to estimate than piecewise methods, and hence is appealing when a smaller number of subjects or shorter observation periods are available, and the computation burden is less.

In many situations, multi-state life history data arise in clusters. For example, in studies of Alzheimer's disease (AD) conducted by the National Alzheimer's Coordinating Center (NACC), the data were collected from 29 Alzheimer's disease centers, and follow-up visits for subjects in each cluster are scheduled at one year-interval. Subjects in the same cluster may have correlations due to some common features. Appropriate analysis should take the correlations into account. A general method to deal with the clustered data is the random effects model (Laird and Ware 1982), in which the correlations are incorporated through the assumption that the cluster-specific effects are to be random.

In cohort studies, clinical assessments may be scheduled before the study, but patients may choose when they want to visit clinics for clinical examinations according to their degree of disease activity. This creates a problem somewhat akin to incomplete data arising in longitudinal studies. In this case, data may be missing at random (MAR) (Little and Rubin 2002) if missing status depends on observed (typically past) responses, or missing not at random (MNAR), where the missing status may depend on the latent disease status.

Grüger et al. (1991) discussed the informative sampling in multi-state models. Chen, Yi and Cook (2010) proposed a piecewise constant transition model to handle the non-homogeneity in a progressive process with informative observations. Sweeting, Farewell, and De Anglis (2010) developed a multi-state Markov model for disease progression in the presence of informative examinations by using a more regularly observed auxiliary variable. Both the methods of Chen, Yi and Cook (2010) and Sweeting, Farewell, and De Anglis (2010) do not consider the clustered data. Little work in the literature has addressed incomplete clustered data under the framework of a non-homogenous Markov process. Under a MAR or MNAR mechanism, the naïve analysis method such as the complete case analysis can give biased inferences. In this paper, we provide a general method to handle incomplete clustered data for the non-homogeneous Markov processes when data are MAR and MNAR. The time transformation method (Hubbard, Inoue and Fann 2008) is employed to address the non-homogeneity, and the correlated random effects models are employed to address the MNAR or nonignorable mechanism. This method is very appealing in that it can deal with missing not at random mechanism and allow time-varying intensities under the framework of non-homogeneity for the clustered life history data. Furthermore, using the nonparametric time transformation model, we can accommodate temporal non-homogeneity without assuming that transition intensities follow any particular functional form of time. Thus, our proposed method is more flexible than previous methods dealing with non-homogeneity. Maximum likelihood methods are used with parameter estimation carried out via the Monte-Carlo EM algorithm, and variance estimation is performed using the Louis's method (Louis 1982).

The remainder of this paper is organized as follows. In Section 2, we describe models and estimation for continuous time models. In Section 3, we develop methods for parameter estimation when data are MAR and MNAR. Empirical studies including the simulation studies and sensitivity analyses are implemented in Section 4. Data arising from a dementia disease study are analyzed using the proposed method in Section 5. We conclude the paper with a general discussion in Section 6.

2. Notation and Model Formulation

2.1. Non-homogeneous Random Effects Markov Process Model via Time Transformation

Suppose there are K states, 1, 2, …, K, and let Y_ij(u) be the state occupied for subject j at time u in cluster i, i = 1, …, n, j = 1, …, n_i. To incorporate the correlations among the clusters in the transitions among these states, random effects models are often employed in the Markov transition intensity function. To be specific, the transition intensity function at time u for transitions from state $\tilde{k}$ to state k for subject j in cluster i, given the random effect δ_1i, is

$$\begin{array}{cc}\hfill q_{ij\tilde{k}k}^{\ast }(u\mid {\delta }_{1i})& =\underset{\Delta u\to 0}{\lim }\frac{P\left(Y_{ij}\right(u+\Delta u)=k\mid Y_{ij}(u)=\tilde{k},{\delta }_{1i})}{\Delta u},\tilde{k}\ne k,\hfill \\ \hfill q_{ij\tilde{k}\tilde{k}}^{\ast }(u\mid {\delta }_{1i})& =-\sum _{k\ne \tilde{k}}{q}_{ij\tilde{k}k}^{\ast }(u\mid {\delta }_{1i}),\hfill \end{array}$$

where δ_1i is often assumed to come from a density function f(δ_1i|Σ₁) with parameter Σ₁. The use of the random effect δ_1i on u (through the intensity function) is one way of introducing correlation within the ith cluster. To model the dependence of the transition intensities on risk factors, we may introduce covariates by expressing the transition intensities as functions of time (in the non-homogeneous case) and covariates. For a given individual j in cluster i, we often adopt models of the form

$$q_{ij\tilde{k}k}^{\ast }(u\mid {\mathbf{X}}_{ij\tilde{k}k},{\delta }_{1i})=q_{0\tilde{k}k}^{\ast }\left(u\right)\exp ({\mathbf{X}}_{ij\tilde{k}k}^T{\beta }_{\tilde{k}k}+{\mathbf{Z}}_i^T{\delta }_{1i}),$$

where $q_{0\tilde{k}k}^{\ast }\left(u\right)$ is the baseline transition intensity with all explanatory variables ${\mathbf{X}}_{\mathit{ij}\tilde{k}k}$ and random effect δ_1i being zero, ${\mathbf{X}}_{\mathit{ij}\tilde{k}k}$ is the time-invariant covariate vector, δ_1i is a random effect vector for cluster i and is often assumed to follow a normal distribution with mean 0 and covariance matrix Σ₁, and Z_i is a covariate vector for random effect δ_1i. Furthermore, we assume δ_1i and δ_1i′ are independent for i ≠ i′. A simple example is the frailty model that is commonly used in practice if we take Z_i as a scalar one. Let ${\mathbf{X}}_{\mathit{ij}}={({\mathbf{X}}_{\mathit{ij}\tilde{k}k}^T,\tilde{k},k=1,\dots ,K)}^T$, ${\mathbf{X}}_i={({\mathbf{X}}_{i1}^T,\dots ,{\mathbf{X}}_{{\mathit{in}}_i}^T)}^T$, ${\delta }_1={({\delta }_{11}^T,\dots ,{\delta }_{1n}^T)}^T$.

A multi-state model for subject j in cluster i with state space {1, 2, …, K} can then be described via the transition intensity matrix ${\mathbf{Q}}_{\mathit{ij}}^{\ast }(u\mid {\delta }_{1i})$ with elements $q_{\mathit{ij}\tilde{k}k}^{\ast }(u\mid {\delta }_{1i})$, $\tilde{k}$, k = 1, …, K. Let P_ij(u, u + v|δ_1j) denote the K × K cluster-specific transition probability matrix from time u to time v + u for subject j in cluster i, given δ_1i. For a homogeneous process the transition intensity matrix ${\mathbf{Q}}_{\mathit{ij}}^{\ast }(u\mid {\delta }_{1i})$ does not depend on time u, and the transition probability $P_{\mathit{ij}\tilde{k}k}(u,u+v\mid {\delta }_{1i})=P\left(Y_{\mathit{ij}}\right(u)=\tilde{k},Y_{\mathit{ij}}(v+u)=k\mid {\delta }_{1i})$ depends only on the time interval v, so we denote it as $P_{\mathit{ij}\tilde{k}k}(v\mid {\delta }_{1i})$, $\tilde{k}$, k = 1, …, K. In the matrix form, we have

$${\mathbf{P}}_{ij}(\upsilon \mid {\delta }_{1i})=\exp \left({\mathbf{Q}}_{ij}^{\ast }\right({\delta }_{1i}\left)\upsilon \right),$$

where P_ij(v|δ_1i) is the K × K cluster-specific transition matrix with element $P_{\mathit{ij}\tilde{k}k}(v\mid {\delta }_{1i})$. For a non-homogeneous process, we do not have an explicit form between the transition intensity matrix and transition probability matrix. However, we can do some proper time scale transformation such that the process is homogeneous afterwards (Hubbard et al. 2008). Specifically, let t = h(u) be a time transformation on which the process is homogeneous with intensity matrix Q_ij(δ_1i) given the random effect δ_1i, then

$${\mathbf{P}}_{ij}(u_1,u_2\mid {\delta }_{1i})=P(t_2-t_1\mid {\delta }_{1i})=\exp \left\{{\mathbf{Q}}_{ij}\right({\delta }_{1i}\left)\right(t_2-t_1\left)\right\},$$

where t_m = h(u_m), m = 1, 2. It is easy to show that ${\mathbf{Q}}_{\mathit{ij}}^{\ast }(u\mid {\delta }_{1i})={\mathbf{Q}}_{\mathit{ij}}\left({\delta }_{1i}\right)\mathit{dh}\left(u\right)∕\mathit{du}$, which implies that time scale transformations leading to a time homogeneous Markov process are possible if the non-homogeneity in the process is due to a time-varying multiplicative change in the matrix of transition intensities.

Here we assume, after the time scale transformation t = h(u), the transition intensity matrix for subject j in cluster i given the random effect δ_1i does not depend on time. Then, the model becomes

$$q_{ij\tilde{k}k}(t\mid {\delta }_{1i})=q_{0\tilde{k}k}\exp ({\mathbf{X}}_{ij\tilde{k}k}^T{\beta }_{\tilde{k}k}+{\mathbf{Z}}_i^T{\delta }_{1i}),$$

where $q_{\mathit{ij}\tilde{k}k}$ is the $\tilde{k}k\text{th}$ element of the homogeneous intensity matrix Q_ij(δ_1i) for subject j. Let ${\mathbf{P}}_{\mathit{ij}\tilde{k}k}(t\mid {\delta }_{1i})$ denote the transition probability with an elapse time t for subject j in cluster i from state $\tilde{k}$ to k given the covariate ${\mathbf{X}}_{\mathit{ij}\tilde{k}k}$, and the random effect δ_1i. Let β denote the unknown parameter vector in the transition intensity matrix Q_ij(δ_1i).

The choice of h(·) is very flexible, and we require h(u) ≥ 0 and dh(u)/du ≥ 0, since h(u) defines a time scale. Two common methods in practice for selecting the h(·) are the exponential time transformation h(u) = uϕ^u and the nonparametric time transformation h(u) = uξ(u), where

$$\begin{array}{c}\hfill \xi \left(u\right)=\sum _{m=1}^{d}c\left(u\right){\varphi }_m\left\{\frac{1}{\gamma }K\left(\frac{u-u_i}{\gamma }\right)\right\},\hfill \\ \hfill c\left(u\right)={\left\{\sum _{k=1}^d\frac{1}{\gamma }K\left(\frac{u-u_k}{\gamma }\right)\right\}}^{-1},\hfill \end{array}$$

K(·) is a kernel function, and γ is a bandwidth. This kernel smoother has knots at u_k, k = 1, …, d; smoothing parameter ϕ satisfies constraints ϕ_k > 0. To make identifiability, we often assume ϕ₁ = 1 or ξ(0) = 0.

We comment that not all non-homogeneous models can be so transformed to homogeneity, but through selection of the transformation function, the proposed method can cover various non-homogeneity cases that are often used in practice. For example, using the nonparametric time transformation model can accommodate temporal non-homogeneity without assuming that transformation intensities follow any particular functional form of time, which is more flexible than previous method dealing with non-homogeneity. The exponential transformation form has several advantages. First, it has a good interpretation: if ϕ > 1, it means a (ϕ − 1) × 100% increase in the rate of all transitions per year (assuming a yearly time unit); if ϕ < 1, it means a (1 − ϕ) × 100% decrease in the rate of all transitions per year (assuming a yearly time unit); ϕ = 1 means the process is homogeneous on both the original and transformed time scales. Second, it requires estimation of fewer parameters, and hence can reduce the computation burden and can also be employed even when a smaller number of subjects or shorter observation periods are available.

2.2. Independent Inspection Process for Complete Data

With continuous time models and observation schemes, the response process {Y(u), u > 0} may be observed at any time point u over the period observation. If the time of assessment u does not depend on the state of the underlying response process Y, we can base inference on the response process conditional on the assessment times (Grüger, Kay and Schumacher 1991), and this is typically an implicit assumption in standard analyses. In this paper, we consider the problem in which subjects are scheduled to be examined at pre-specified assessment times denoted u₁ < u₂ < … u_M, where M is the number of pre-specified assessment times. This reflects many common clinical settings where patients are expected to return for regular follow-up assessment, say, on annual basis. This enables us to adopt a convenient frame work employed to describe incomplete longitudinal data since it is then only necessary to indicate whether each assessment is made.

Let Y_ij = (Y_ij(u₁), …, Y_ij(u_M))^T be a health state vector for subject j in cluster i at all observation time points, where each element of Y_ij may take values 1, …, K, i = 1, …, n, j = 1, …, n_i. Define ${\mathbf{Y}}_i={({\mathbf{Y}}_{i1}^T,\dots ,{\mathbf{Y}}_{{\mathit{in}}_i}^T)}^T$.

3. Estimation and Inferences

3.1. Maximum Likelihood Estimation with Complete Data

Let θ = (β, ϕ, Σ₁). We can maximize the observed data log-likelihood given the initial state,

$$\ell \left(\theta \right)=\sum _{i=1}^n\log \left[\int \prod _{j=1}^{n_i}\prod _{m=2}^{M}P\left(Y_{ij}\right(h\left(u_m\right))\mid Y_{ij}(h\left(u_{m-1}\right)),{\delta }_{1i})f\left({\delta }_{1i}\right)d{\delta }_{1i}\right],$$

to solve for the parameter θ. However, there is no explicit form for this likelihood, thus the maximization procedure is hard to implement. Alternatively, we can employ the Monte-Carlo EM (MCEM) algorithm (McLachlan and Krishnan 1997), which is easy to implement. To do this, we regard the random effect δ₁ as a missing value, and the complete data log-likelihood of (y, δ₁) is

$$\ell (\theta ;\mathbf{y},{\delta }_1)=\sum _{i=1}^n{\ell }_i(\theta ;{\mathbf{y}}_i,{\delta }_{1i}),$$

where ${\ell }_i(\theta ;{\mathbf{y}}_i,{\delta }_{1i})={\sum }_{j=1}^{n_i}{\sum }_{m=2}^M\left[\log \right\{P\left(Y_{ij}\right(h\left(u_m\right))\mid Y_{\mathit{ij}}(h\left(u_{m-1}\right)),{\delta }_{1i})\}+\log \{f\left({\delta }_{1i}\right)\left\}\right]$, $\mathbf{y}={({\mathbf{y}}_1^T,\dots ,{\mathbf{y}}_n^T)}^T$, and y_i is a realization of Y_i, i = 1, …, n.

In the E step, given the value θ^(t), we calculate

$$\begin{array}{cc}\hfill Q_i(\theta \mid {\theta }^{\left(t\right)})& =E\left[{\ell }_i\right(\theta ;{\mathbf{y}}_i,{\delta }_{1i})\mid {\mathbf{y}}_i,{\theta }^{\left(t\right)}]\hfill \\ \hfill & =\int {\ell }_i(\theta ;{\mathbf{y}}_i,{\delta }_{1i})\times f({\delta }_{1i}\mid {\mathbf{y}}_i,{\theta }^{\left(t\right)})d{\delta }_{1i}.\hfill \end{array}$$

This step also involves the integration, and in general, there is no explicit form. In practice, the Monte-Carlo method is often used to approximate this integration. To do this, we sample ${\delta }_{1i}^{\left(1\right)},\dots ,{\delta }_{1i}^{\left(B_i\right)}$ from the conditional distribution f(δ_1i|y_i, θ^(t)) via Gibbs sampler, where the conditional distribution

$$f({\delta }_{1i}\mid {\mathbf{y}}_i,{\theta }^{\left(t\right)})\propto f({\mathbf{y}}_i\mid {\delta }_{1i},{\theta }^{\left(t\right)})f({\delta }_{1i}\mid {\theta }^{\left(t\right)}).$$

Given the B_i samples,

$$Q_i(\theta \mid {\theta }^{\left(t\right)})\approx \frac{1}{B_i}\sum _{b=1}^{B_i}{\ell }_i(\theta ;{\mathbf{y}}_i,{\delta }_{1i}^{\left(b\right)}).$$

In the M step, we maximize ${\sum }_{i=1}^n{Q}_i(\theta \mid {\theta }^{\left(t\right)})$ via the Fisher-scoring algorithm to solve for the parameter θ. Iterate the E and M steps until convergence. Denote the limit as $\widehat{\theta }$.

For the variance estimate, we use Louis's (1982) formula. The information matrix of θ is given by

$$\mathbf{I}\left(\widehat{\theta }\right)=\sum _{i=1}^n\frac{{\partial }^2{Q}_i(\widehat{\theta };\widehat{\theta })}{\partial \theta \partial {\theta }^T}-\sum _{i=1}^n\sum _{b=1}^{B_i}\frac{1}{B_i}\left(\frac{\partial {\ell }_i(\widehat{\theta };{\mathbf{y}}_i,{\delta }_i^{\left(b\right)})}{\partial \theta }\right){\left(\frac{\partial {\ell }_i(\widehat{\theta };{\mathbf{y}}_i,{\delta }_i^{\left(b\right)})}{\partial \theta }\right)}^T+\sum _{i=1}^n\left(\frac{\partial Q_i(\widehat{\theta };\widehat{\theta })}{\partial \theta }\right){\left(\frac{\partial Q_i(\widehat{\theta };\widehat{\theta })}{\partial \theta }\right)}^T,$$

and the covariance matrix of $\widehat{\theta }$ is $\mathbf{I}{\left(\widehat{\theta }\right)}^{-1}$.

3.2. Maximum Likelihood Estimation with Incomplete Responses which are Missing at Random

With incomplete response under the missing at random (MAR) mechanism, we may also employ the MCEM algorithm to solve for the parameter θ. For simplicity, we let y_i = (y_i,obs, y_i,mis), where y_i,obs and y_i,mis denote the observed and missing parts for the response y_i. To implement the MCEM algorithm, the log-likelihood of (y, δ) is

$$\begin{array}{cc}\hfill \ell (\theta ;\mathbf{y},\delta )& =\sum _{i=1}^n{\ell }_i(\theta ;{\mathbf{y}}_{i,\mathit{obs}},{\mathbf{y}}_{i,\mathit{mis}},{\delta }_{1i})\hfill \\ \hfill & =\sum _{i=1}^n\left[\sum _{j=1}^{n_i}\sum _{m=2}^M\log \right\{P\left(Y_{ij}\right(h\left(u_m\right))\mid Y_{ij}(h\left(u_{m-1}\right)),{\delta }_{1i})\}+\log \{f\left({\delta }_{1i}\right)\left\}\right].\hfill \end{array}$$

In the E step, given θ^(t), we calculate

$$\begin{array}{cc}\hfill Q_i(\theta \mid {\theta }^{\left(t\right)})& =E\left[{\ell }_i\right(\theta ;{\mathbf{y}}_{i,\mathit{obs}},{\mathbf{y}}_{i,\mathit{mis}},{\delta }_{1i})\mid {\mathbf{y}}_{i,\mathit{obs}},{\theta }^{\left(t\right)}]\hfill \\ \hfill & =\int \int {\ell }_i(\theta ;{\mathbf{y}}_{i,\mathit{obs}},{\mathbf{y}}_{i,\mathit{mis}},{\delta }_{1i})\times f({\delta }_{1i},{\mathbf{y}}_{i,\mathit{mis}}\mid {\mathbf{y}}_{i,\mathit{obs}},{\theta }^{\left(t\right)})d{\mathbf{y}}_{i,\mathit{mis}}d{\delta }_{1i}.\hfill \end{array}$$

Similarly, we use Monte-Carlo method to approximate the above integration. To do this, we sample $({\delta }_{1i}^{\left(1\right)},{\mathbf{y}}_{i,\mathit{mis}}^{\left(1\right)}),\dots ,({\delta }_{1i}^{\left(B_i\right)},{\mathbf{y}}_{i,\mathit{mis}}^{\left(B_i\right)})$ from the joint distribution f(δ_1i, y_i,mis|y_i,obs, θ^(t)) via Gibbs sampler, where the full conditional distributions are given by

$$\begin{array}{cc}\hfill f({\delta }_{1i}\mid {\mathbf{y}}_i,{\theta }^{\left(t\right)})& \propto f({\mathbf{y}}_i\mid {\delta }_{1i},{\theta }^{\left(t\right)})f({\delta }_{1i}\mid {\theta }^{\left(t\right)})\hfill \\ \hfill f({\mathbf{y}}_{i,\mathit{mis}}\mid {\mathbf{y}}_{i,\mathit{obs}},{\delta }_{1i},{\theta }^{\left(t\right)})& \propto f({\mathbf{y}}_i\mid {\delta }_{1i},{\theta }^{\left(t\right)}).\hfill \end{array}$$

Given the B_i samples,

$$Q_i(\theta \mid {\theta }^{\left(t\right)})\approx \frac{1}{B_i}\sum _{b=1}^{B_i}{\ell }_i(\theta ;{\mathbf{y}}_{i,\mathit{obs}},{\mathbf{y}}_{i,\mathit{mis}}^{\left(b\right)},{\delta }_{1i}^{\left(b\right)}).$$

In the M step, we maximize ${\sum }_{i=1}^n{Q}_i(\theta \mid {\theta }^{\left(t\right)})$ via the Fisher-scoring algorithm to solve for θ. Iterate the E and M steps until convergence. Denote the limit as $\widehat{\theta }$.

For the variance estimate, we use Louis's (1982) formula. The information matrix of θ is given by

$$\mathbf{I}\left(\widehat{\theta }\right)=\sum _{i=1}^n\frac{{\partial }^2{Q}_i(\widehat{\theta };\widehat{\theta })}{\partial \theta \partial {\theta }^T}-\sum _{i=1}^n\sum _{b=1}^{B_i}\frac{1}{B_i}\left(\frac{\partial {\ell }_i(\widehat{\theta };{\mathbf{y}}_{i,\mathit{obs}},{\mathbf{y}}_{i,\mathit{mis}}^{\left(b\right)},{\delta }_i^{\left(b\right)})}{\partial \theta }\right){\left(\frac{\partial {\ell }_i(\widehat{\theta };{\mathbf{y}}_{i,\mathit{obs}},{\mathbf{y}}_{i,\mathit{mis}}^{\left(b\right)},{\delta }_i^{\left(b\right)})}{\partial \theta }\right)}^T+\sum _{i=1}^n\left(\frac{\partial Q_i(\widehat{\theta };\widehat{\theta }}{\partial \theta }\right){\left(\frac{\partial Q_i(\widehat{\theta };\widehat{\theta })}{\partial \theta }\right)}^T,$$

and the covariance matrix of $\widehat{\theta }$ is $\mathbf{I}{\left(\widehat{\theta }\right)}^{-1}$.

3.3. Maximum Likelihood Estimation with Incomplete Response which are Missing not at Random

With incomplete responses under the missing not at random (MNAR) mechanism, we must model the missing data process appropriately to obtain a valid inference. To do this, we let R_ijm be the missing indicator of Y_ij(u_m), which equals 1 if Y_ij(u_m) is observed and 0 otherwise. Let R_ij = (R_ij1, …, R_ijM)^T, ${\mathbf{R}}_i={({\mathbf{R}}_{i1}^T,\dots ,{\mathbf{R}}_{{\mathit{in}}_i}^T)}^T$, and we use the lower case letter to denote the realization of the random variable. To incorporate the cluster effects in the missing data model, we may also employ a random effects model, as follows,

$$\mathrm{logit}{\lambda }_{ijm}={\tilde{X}}_{ijm}^T\alpha +{\tilde{Z}}_i^T{\delta }_{2i},$$ (1)

where ${\lambda }_{\mathit{ijm}}=P(R_{\mathit{ijm}}=1\mid {\stackrel{‒}{\mathbf{R}}}_{\mathit{ijm}},{\mathbf{X}}_i,{\delta }_{2i})$, ${\stackrel{‒}{\mathbf{R}}}_{\mathit{ijm}}=\{R_{\mathit{ij}1},\dots ,R_{\mathit{ij},m-1}\}$, δ_2i is a random effect vector in the missing data model with density f(δ_2i|Σ₂), Σ₂ is an unknown parameter vector, ${\tilde{X}}_{\mathit{ijm}}$ may include the function of $\{{\mathbf{X}}_i,{\stackrel{‒}{\mathbf{R}}}_{\mathit{ijm}}\}$, and ${\tilde{\mathbf{Z}}}_i$ is a cluster-level covariate vector. Denote ${\delta }_i={({\delta }_{1i}^T,{\delta }_{2i}^T)}^T$. To accommodate for the correlation between δ_1i and δ_2i, we let Σ₁₂ = cov(δ_1i, δ_2i). We further make the assumption that the missing data process and the response process are independent given the random effect δ_i. Let $\delta ={({\delta }_1^T,\dots ,{\delta }_n^T)}^T$.

Let θ = (β, ϕ, Σ₁, Σ₂, Σ₁₂, α). We also implement the MCEM algorithm for solving for the parameter θ. The log-likelihood of (r, y, δ) is

$$\begin{array}{cc}\hfill & \ell (\theta ;\mathbf{r},\mathbf{y},\delta )=\sum _{i=1}^n{\ell }_i(\theta ;{\mathbf{r}}_i,{\mathbf{y}}_{i,\mathit{obs}},{\mathbf{y}}_{i,\mathit{mis}},{\delta }_i)\hfill \\ \hfill =& \sum _{i=1}^n\left[\log f\right({\mathbf{r}}_i\mid {\mathbf{y}}_i,{\delta }_i)+\log f({\mathbf{y}}_i\mid {\delta }_i\left)\right\}+\log \left\{f\right({\delta }_i\left)\right\}],\hfill \end{array}$$

where

$$\begin{array}{c}\hfill f({\mathbf{r}}_i\mid {\mathbf{y}}_i,{\delta }_i)=f({\mathbf{r}}_i\mid {\delta }_i)=\prod _{j=1}^{n_i}\prod _{m=2}^M{\lambda }_{ijm}^{r_{ijm}}{(1-{\lambda }_{ijm})}^{1-r_{ijm}}\cdot f(r_{ij1}\mid {\delta }_i),\hfill \\ \hfill \text{and}f({\mathbf{y}}_i\mid {\delta }_i)=\prod _{j=1}^{n_i}\prod _{m=2}^{M}P\left(Y_{ij}\right(h\left(u_m\right))\mid Y_{ij}(h\left(u_{m-1}\right)),{\delta }_i).\hfill \end{array}$$

In the E step, given θ^(t), we calculate

$$\begin{array}{cc}\hfill Q_i(\theta \mid {\theta }^{\left(t\right)})& =E\left[{\ell }_i\right(\theta ;{\mathbf{r}}_i,{\mathbf{y}}_{i,\mathit{obs}},{\mathbf{y}}_{i,\mathit{mis}},{\delta }_i)\mid {\mathbf{r}}_i,{\mathbf{y}}_{i,\mathit{obs}},{\theta }^{\left(t\right)}]\hfill \\ \hfill & =\int \int {\ell }_i(\theta ;{\mathbf{r}}_i,{\mathbf{y}}_{i,\mathit{obs}},{\mathbf{y}}_{i,\mathit{mis}},{\delta }_i)\times f({\delta }_i,{\mathbf{y}}_{i,\mathit{mis}}\mid {\mathbf{r}}_i,{\mathbf{y}}_{i,\mathit{obs}},{\theta }^{\left(t\right)})d{\mathbf{y}}_{i,\mathit{mis}}d{\delta }_i.\hfill \end{array}$$

To approximate the above integration using Monte-Carlo method, we sample $({\delta }_i^{\left(1\right)},{\mathbf{y}}_{i,\mathit{mis}}^{\left(1\right)}),\dots ,({\delta }_i^{\left(B_i\right)},{\mathbf{y}}_{i,\mathit{mis}}^{\left(B_i\right)})$ from the joint distribution f(δ_i, y_i,mis|r_i, y_i,obs, θ^(t)) via Gibbs sampler, where the full conditional distributions are given by

$$\begin{array}{cc}\hfill f({\delta }_i\mid {\mathbf{r}}_i,{\mathbf{y}}_i,{\theta }^{\left(t\right)})& \propto f({\mathbf{r}}_i\mid {\delta }_i,{\theta }^{\left(t\right)})f({\mathbf{y}}_i\mid {\delta }_i,{\theta }^{\left(t\right)})f({\delta }_i\mid {\theta }^{\left(t\right)}),\hfill \\ \hfill \text{and}f({\mathbf{y}}_{i,\mathit{mis}}\mid {\mathbf{r}}_i,{\mathbf{y}}_{i,\mathit{obs}},{\delta }_i,{\theta }^{\left(t\right)})& \propto f({\mathbf{y}}_i\mid {\delta }_i,{\theta }^{\left(t\right)}).\hfill \end{array}$$

Given the B_i samples,

$$Q_i(\theta \mid {\theta }^{\left(t\right)})\approx \frac{1}{B_i}\sum _{b=1}^{B_i}{\ell }_i(\theta ;{\mathbf{r}}_i,{\mathbf{y}}_{i,\mathit{obs}},{\mathbf{y}}_{i,\mathit{mis}}^{\left(b\right)},{\delta }_i^{\left(b\right)}).$$

In the M step, we can maximize ${\sum }_{i=1}^n{Q}_i(\theta \mid {\theta }^{\left(t\right)})$ via the Fisher-scoring algorithm to solve for θ. Iterate the E and M steps until convergence. Denote the limit as $\widehat{\theta }$.

For the variance estimate, we can use Louis's (1982) formula. The information matrix of θ is given by

$$\mathbf{I}\left(\widehat{\theta }\right)=\sum _{i=1}^n\frac{{\partial }^2{Q}_i(\widehat{\theta };\widehat{\theta })}{\partial \theta \partial {\theta }^T}+\sum _{i=1}^n\left(\frac{\partial Q_i(\widehat{\theta };\widehat{\theta })}{\partial \theta }\right){\left(\frac{\partial Q_i(\widehat{\theta };\widehat{\theta })}{\partial \theta }\right)}^T-\sum _{i=1}^n\sum _{b=1}^{B_i}\frac{1}{B_i}\left(\frac{\partial {\ell }_i(\widehat{\theta };{\mathbf{r}}_i,{\mathbf{y}}_{i,\mathit{obs}},{\mathbf{y}}_{i,\mathit{mis}}^{\left(b\right)},{\delta }_i^{\left(b\right)})}{\partial \theta }\right){\left(\frac{\partial {\ell }_i(\widehat{\theta };{\mathbf{r}}_i,{\mathbf{y}}_{i,\mathit{obs}},{\mathbf{y}}_{i,\mathit{mis}}^{\left(b\right)},{\delta }_i^{\left(b\right)})}{\partial \theta }\right)}^T,$$

and the covariance matrix of $\widehat{\theta }$ is $\mathbf{I}{\left(\widehat{\theta }\right)}^{-1}$.

Here we comment that the Louis's method for variance of the parameter estimate $\widehat{\theta }$ works fine for low dimensional parameters, but it becomes inconvenient if one has high dimensional parameter or a mixed fixed effect coefficient and random covariance matrix since the second derivatives of Q(·) function are not easy to obtain. For high dimensional cases, a better choice is the method by Jamshidian and Jennrich (1993).

4. Simulation Studies

4.1. Performance of the Proposed Method

Here we consider a three-state transition process with transition intensity given by

$$q_{ij\tilde{k}k}=q_{0\tilde{k}k}\exp (X_{ij}{\beta }_{\tilde{k}k}+{\delta }_{1i})$$

for $\tilde{k}\ne k$ after the time transformation h(u) = uϕ^u, where ${\delta }_{1i}~N(0,{\sigma }_1^2)$, and X_ij is a time independent covariate generated from N(0, 1). We will study the performance of the proposed method when the transformation function is correctly specified/ misspecified in the following. The true parameters are q₀₁₂ = 0.2, q₀₁₃ = 0.1, q₀₂₁ = 0.2, q₀₂₃ = 0.1, β₁₂ = 1.0, β₁₃ = 0.5, β₂₁ = −0.5, β₂₃ = 1.0, ${\sigma }_1^2=0.01$, and ϕ = 1.2. The observation time points are uniformly on (0, 3) with equal space interval 1. At the first observation time point, subjects are equally likely to be in state one or two. The number of clusters is set to be 30, and the number of subjects is 50 in each cluster.

The missing data model is

$$\mathrm{logit}{\lambda }_{ijm}={\alpha }_0+{\alpha }_1{X}_{ij}+{\delta }_{2i}$$ (2)

for j = 2, 3, …,where ${\delta }_{2i}~N(0,{\sigma }_2^2)$. The true values are α₀ = 1.0, and ${\sigma }_2^2=0.01$. We vary α₁ to adjust the missing proportions. We also assume ρ = corr(δ_1i, δ_2i) and change it to adjust the dependence between the response and missing indicators. One thousand simulations are run for each parameter configuration.

First, we consider that the transformation function h(·) is correctly specified. Here we compare three methods. One is the proposed method; the second, called “Independence”, is the method that we ignore the correlation between the two random effects δ_1i and δ_2i, i.e. we set ρ = 0 although it is not; the third, called “Marginal”, is the method that we ignore the cluster level effect in the intensity, i.e. we set ${\sigma }_1^2=0$ although it is not. Tables 1 to 3 report the result, where BIAS is the percent relative bias; SD is the empirical standard deviation; CP is the 95% coverage probability. It is seen that the proposed method gives satisfactory results with negligible finite sample biases and good coverage probabilities. However, the independence method yields large biases and poor coverage probabilities when ρ ≠ 0. When ρ = 0, the independence method gives very close results to the proposed method. For the marginal method, it yields larger biases for all cases.

Table 1.

Empirical performance of the proposed method and naive methods with correctly specified and misspecified transformation function: α₁ = −1.0, about 40% missing

		Proposed Method			Independence			Marginal			Misspecified
ρ	Para.	BIAS%	SD	CP%	BIAS%	SD	CP%	BIAS%	SD	CP%	BIAS%	SD	CP%
0.6	q 012	−1.2	0.032	94.3	−26.9	0.031	5.6	−26.7	0.030	5.0	7.1	0.045	85.1
0.6	q 013	−0.8	0.020	94.1	−24.2	0.017	8.2	−24.4	0.016	6.7	−2.2	0.023	89.8
0.6	q 021	1.3	0.068	93.7	20.0	0.089	76.1	19.0	0.079	75.2	84.4	0.126	6.0
0.6	q 023	−0.9	0.043	94.3	−36.5	0.044	35.3	−35.3	0.041	33.0	12.8	0.073	83.8
0.6	β 12	−0.2	0.162	95.3	0.1	0.161	94.5	1.0	0.156	89.0	−9.6	0.135	76.7
0.6	β 13	−1.6	0.140	95.7	−3.7	0.141	94.1	−9.1	0.148	87.5	−31.2	0.153	68.0
0.6	β 21	1.8	0.307	94.3	−3.1	0.308	94.6	−6.4	0.306	86.2	28.5	0.283	76.7
0.6	β 23	−0.8	0.429	94.4	−2.9	0.425	93.5	−8.1	0.300	84.9	−16.2	0.278	75.1
0.2	q 012	−0.9	0.029	94.7	−26.7	0.028	4.0	−26.3	0.030	4.4	7.2	0.048	83.8
0.2	q 013	−1.7	0.019	94.0	−24.3	0.016	7.9	−24.2	0.016	7.0	−0.8	0.025	88.0
0.2	q 021	1.9	0.064	93.7	19.9	0.075	77.9	19.9	0.087	73.9	87.3	0.136	4.9
0.2	q 023	−0.3	0.041	94.6	−36.3	0.040	34.9	−35.7	0.041	36.2	12.1	0.074	83.8
0.2	β 12	−0.8	0.155	94.8	−0.2	0.152	94.3	−1.0	0.146	86.6	−8.9	0.146	77.8
0.2	β 13	−0.8	0.139	95.2	−3.2	0.142	93.8	−8.5	0.135	86.2	−26.0	0.150	77.1
0.2	β 21	1.2	0.308	93.5	−5.7	0.308	93.4	−4.1	0.286	85.3	22.3	0.282	82.0
0.2	β 23	−0.7	0.315	94.3	−8.2	0.310	93.6	−7.2	0.279	86.0	−17.6	0.311	73.6
0.0	q 012	−1.2	0.032	94.2	−2.2	0.029	93.5	−27.3	0.028	3.3	7.4	0.044	82.4
0.0	q 013	−1.5	0.019	94.2	−2.6	0.014	94.5	−24.5	0.016	5.3	−1.1	0.023	88.9
0.0	q 021	2.2	0.082	94.0	1.3	0.082	94.8	18.7	0.083	74.6	84.3	0.139	8.7
0.0	q 023	−0.6	0.046	94.0	−1.3	0.039	94.2	−34.8	0.039	33.9	12.7	0.068	85.7
0.0	β 12	−0.4	0.162	94.2	−0.5	0.159	93.9	−0.4	0.149	94.1	−8.9	0.135	80.9
0.0	β 13	−1.3	0.130	94.7	−0.4	0.130	96.4	−10.2	0.130	89.3	−26.4	0.150	71.6
0.0	β 21	0.9	0.321	94.6	−1.3	0.317	94.5	−3.7	0.303	84.5	26.2	0.276	80.5
0.0	β 23	−0.9	0.271	95.1	−1.3	0.12464	94.0	−9.0	0.259	87.5	−18.1	0.348	73.8

Table 3.

Empirical performance of the proposed method and naive methods with correctly specified and misspecified transformation function: α₁ = 4.0, about 15% missing

		Proposed Method			Independence			Marginal			Misspecified
ρ	Para.	BIAS%	SD	CP%	BIAS%	SD	CP%	BIAS%	SD	CP%	BIAS%	SD	CP%
0.6	q 012	−1.0	0.028	94.1	17.2	0.052	49.7	26.7	0.740	51.5	69.7	0.074	0.5
0.6	q 013	−1.3	0.021	94.4	−7.1	0.028	79.2	−6.3	0.030	78.3	12.3	0.043	72.7
0.6	q 021	0.5	0.064	94.1	−12.2	0.079	69.5	3.8	1.210	69.1	34.4	0.120	50.5
0.6	q 023	−1.0	0.039	94.7	4.5	0.050	81.9	4.7	0.048	86.7	79.0	0.087	23.9
0.6	β 12	−0.1	0.164	95.7	−2.5	0.166	94.6	−5.5	0.199	81.0	−13.0	0.143	64.8
0.6	β 13	−0.7	0.229	94.2	3.1	0.223	94.0	27.7	0.210	66.8	−12.6	0.217	86.6
0.6	β 21	1.2	0.426	95.5	4.1	0.419	93.5	24.2	0.394	72.9	47.2	0.362	67.7
0.6	β 23	−1.7	0.268	94.2	4.3	0.261	94.4	1.0	0.385	87.1	−4.6	0.197	80.2
0.2	q 012	−0.6	0.029	95.3	16.8	0.045	49.9	17.7	0.055	50.7	70.9	0.075	0.2
0.2	q 013	−1.3	0.019	94.4	−6.4	0.025	82.2	−7.6	0.028	77.4	10.2	0.041	78.2
0.2	q 021	0.0	0.067	94.5	−12.0	0.074	69.2	−11.3	0.096	67.9	32.6	0.118	51.8
0.2	q 023	−1.5	0.041	93.9	4.6	0.043	86.5	5.3	0.048	84.2	82.5	0.086	20.4
0.2	β 12	0.0	0.148	94.4	−3.6	0.148	92.9	−3.1	0.157	82.6	−11.9	0.146	69.1
0.2	β 13	−1.4	0.193	94.7	2.7	0.188	93.7	24.4	0.211	75.8	−16.8	0.222	85.0
0.2	β 21	1.4	0.397	94.6	1.8	0.396	94.0	18.8	0.418	76.9	51.1	0.388	62.8
0.2	β 23	0.1	0.189	94.0	4.4	0.188	93.5	2.1	0.239	85.7	−5.4	0.189	75.9
0.0	q 012	−1.5	0.057	95.1	1.0	0.055	94.1	17.7	0.050	48.4	72.3	0.094	0.9
0.0	q 013	−0.6	0.027	95.0	−1.3	0.026	94.8	−7.2	0.027	77.7	9.0	0.045	78.0
0.0	q 021	2.0	0.096	94.1	−1.5	0.099	94.5	−10.2	0.088	70.9	35.3	0.168	53.0
0.0	q 023	−1.6	0.040	95.2	0.4	0.042	93.9	7.9	0.052	81.8	85.6	0.089	17.2
0.0	β 12	−0.3	0.170	95.1	−2.8	0.167	95.1	−3.3	0.166	81.1	−11.6	0.154	67.0
0.0	β 13	−1.5	0.221	96.4	2.4	0.215	94.9	27.6	0.210	68.2	−16.8	0.243	83.0
0.0	β 21	0.6	0.411	93.9	1.9	0.406	94.5	14.4	0.413	73.4	48.9	0.380	66.1
0.0	β 23	−0.1	0.352	94.8	2.0	0.13644	94.0	1.3	0.335	84.5	−8.6	0.338	76.8

Next, we consider that the transformation function is misspecified to h(u) = u, i.e., we model the homogeneous process although it is not. The last method in Tables 1 to 3, labeled “Misspecified”, records the results. As expected, this method gives biased estimates for parameters, indicating that the estimate of the proposed method is sensitive to the misspecification of transformation function.

4.2. Model Selection and Assessment

As a parametric method, the proposed method for the estimation of β is sensitive to misspecification of the missing data and time transformation models. Therefore, careful assessment of these models is warranted. We now discuss some model selection and assessment procedures for the transition intensity, transformation and missing data models.

In general, a likelihood ratio test is used to compare the fit of two models, one of which is nested within the other. This often occurs when testing whether a simplifying assumption for a model is valid, as when two or more model parameters are assumed to be related. Both models are fitted to the data and their log-likelihood recorded. The test statistic is twice the difference in these log-likelihoods. In many cases, the probability distribution of the test statistic can be approximated by a Chi-squared distribution with k degrees of freedom, where k is the difference of the number of parameters between the full model and the reduced model. The model with more parameters will always fit at least as well (have a greater log-likelihood). Whether it fits significantly better and should thus be preferred can be determined by deriving the p-value of the obtained test statistic. The standard likelihood ratio test applies well when testing some fixed effects in the transition intensity. A cautionary note is that the standard likelihood ratio test may be somewhat problematic since the transition intensities are nonnegative (for example, when testing the baseline intensity), or model comparisons involve variance components that are bounded at zero when testing random effects, thus the standard likelihood ratio test does not apply. However, as indicated by Self and Liang (1987) the likelihood ratio test for testing an effect that is bounded at zero (e.g., testing baseline transition intensity that is equal to zero or a random effect that is equal to zero) has an asymptotic distribution of a mixture of a point at mass zero and a ${\chi }_1^2$ distribution. Testing whether more baseline transition intensities are simultaneously zero or both a transition intensity and a random effect are simultaneously zero are more complex. This situation can be avoided by testing these parameters sequentially (Saint-Pierre et al. 2003). For non-nested models, people may consider Akaike Information Criterion (AIC) or Bayesian Information Criterion (BIC), etc.

Alternatively, Gentleman et al. (1994), Aguirre-Hernandez and Farewell (2002) and Saint-Pierre et al. (2003) discuss the use of empirical and predicted state occupancy to assess goodness-of-fit for Markov process models. The idea is that we compare the observed and predicted prevalence of states at each time point, which would allow us to assess if the transition intensity model, time transformation model or the missing data model is reasonable.

5. Application to an Alzheimer's Disease Study

We apply the proposed method to the National Alzheimer's Coordinating Center (NACC) Uniform Data Set (UDS), which is an ongoing longitudinal database of subjects seen at one of the National Institute on Aging's 29 funded Alzheimer's Disease Centers (ADC) located throughout the USA.

Some studies have found amnestic mild cognition impairment (MCI) to be transient because future evaluations could yield a reversion to normal cognition (here we group normal and “impaired, not MCI” and denote by normal cognition for simplicity) as opposed to progression to dementia. In this section, we implement our proposed method to investigate the risk factors for transitions among normal cognition, MCI, dementia and death. There are 7932 subjects from 29 Alzheimer's Disease Centers included at the entry of this study. Follow-up visits for subjects are scheduled at approximately one-year intervals, with up to four clinical visits at present. There are 6722 subjects with complete data observed.

In this analysis, we treat death as an absorbing state but allow transitions between all other states. Risk factor vector X_i includes: sex, congestive heart failure (CVCHF, yes/no), geriatric depression score (GDS), family history of dementia (fhdem, yes/no), diabetes (yes/no), hypertension (yes/no), education (years), Mini-Mental State Examination (MMSE) score, and age. The MMSE score is a screening scale that evaluates orientation to place, orientation to time, registration (immediate repetition of three words), attention and concentration (spelling D-L-R-O-W), recall (recalling the previously repeated three words), language (naming, repetition, reading, writing, comprehension), and visual construction (copy two intersecting pentagons). The MMSE is scored as the number of correctly completed items, with lower scores indicative of poorer performance and greater cognitive impairment.

For simplicity, the four states, normal cognition, MCI, dementia and death, were coded as 1, 2, 3 and 4, respectively. The multiplicative models for transition $\tilde{k}$ to k after the exponential transformation are

$$q_{ij\tilde{k}k}(t\mid {\delta }_{1i})=q_{0\tilde{k}k}\exp ({\mathbf{X}}_{ij}^T{\beta }_{\tilde{k}k}+{\delta }_{1i})$$

for $\tilde{k}$, k = 1, 2, 3, 4, $\tilde{k}\ne k$, and we assume ${\delta }_{1i}~N(0,{\sigma }_1^2)$.

For the missing data model, we assume

$$\mathrm{logit}{\lambda }_{ijm}={\alpha }_0+{\mathbf{X}}_{ij}^T{\alpha }_x+{\alpha }_2{r}_{ij,m-1}+{\delta }_{2i},$$

where ${\delta }_{2i}~N(0,{\sigma }_2^2)$. We further assume the correlation between δ_1i and δ_2i is ρ.

For the time transformation model, we assume an exponential transformation of the form h(u) = uϕ^u.

As discussed in Section 4.2, we first do model selections. For the transition intensity and missing data models, the likelihood ratio test is employed. Final results for the transition intensity and missing data models are reported in Tables 4 and 5. To investigate the goodness-of-fit for our time transformation, missing data and transition intensity models, we compare the expected and observed state occupancies, which is shown in Table 6. The expected number in state j at time t after the start is obtained by multiplying the number of individuals under observation at time t by the product of the proportion of individuals in each state at the initial time and the transition probability matrix in the time interval t. Here we use mean values of the covariates in the population in intensities. Pearson's Chi-squared test (Aguirre-Hernandez and Farewell 2002) shows that there is no significant difference (p-value=0.14) between the observed and expected state occupancies, indicating that the time transformation, missing data and transition intensity models are reasonable here.

Table 4.

Comparisons of two methods for the multiplicative effects on the transition intensities in the studies of Alzheimer's disease: hazard ratios and 95% confidence intervals

	Proposed Method			Naive Analysis
Parameter	HR	95%LCL	95%UCL	HR	95%LCL	95%UCL
Normal → MCI:
SEX(F)	0.972	0.795	1.200	1.022	0.827	1.292
fhdem	1.275	1.032	1.570	1.372	1.087	1.720
MMSE	1.020	0.981	1.030	1.011	1.006	1.021
AGE	1.026	1.013	1.040	1.033	1.014	1.041
MCI → Dementia:
SEX(F)	0.708	0.580	0.865	0.712	0.572	0.877
fhdem	1.246	1.012	1.534	1.191	0.955	1.380
MMSE	0.997	0.984	1.011	0.999	0.988	1.024
AGE	1.023	1.011	1.035	1.020	1.007	1.033
Dementia → Death:
SEX	0.660	0.549	0.794	0.614	0.515	0.732
fhdem	1.077	0.887	1.307	1.117	0.928	1.345
MMSE	0.875	0.864	0.886	0.986	0.877	0.996
AGE	1.045	1.033	1.056	1.046	1.035	1.058

Table 5.

Missing data model in the analysis of Alzheimer's disease

Parameter	Estimate	SE	p-value
Intercept	4.822	0.363	<0.001
SEX(F)	−0.196	0.058	<0.001
CVCHF	0.149	0.155	0.338
GDS	−0.027	0.011	0.017
fhdem	−1.366	0.062	<0.001
diabete	−0.145	0.086	0.090
hypert	0.093	0.059	0.118
EDUC	0.005	0.004	0.169
MMSE	−0.007	0.003	0.033
AGE	−0.006	0.003	0.060
r m−1	−1.932	0.183	<0.001

Table 6.

Observed and expected state occupancies at each clinic visit

	State Occupancies (observed/expected)
visit	Normal	MCI	Dementia	Death
1	301/301	143/143	295/295	6/6
2	2482/2475	1089/1080	1805/1799	150/172
3	2883/2866	1202/1183	2276/2258	336/389
4	1493/1483	516/510	1200/1188	254/281

Table 4 lists risk factors of interest for the transitions from normal to MCI, MCI to dementia and dementia to death. Here, we compare two methods: the proposed method and the naive method that ignores the missing data and the clustering effects. The estimates of ϕ in the transformation function are 1.040 with 95% confidence interval (1.021, 1.059) for the complete case analysis and 1.048 with 95% confidence interval (1.031, 1.066) for the proposed method. Both reveal that the process exhibits significant non-homogeneity, and the rate of evolution of the process is increasing as a function of time.

The estimates of the variance of the random effects are ${\widehat{\sigma }}_1^2=0.477$ (p-value=0.222), and ${\widehat{\sigma }}_2^2=0.475$ (p-value=0.491), indicating that there are no significant cluster effects in both the response and the missing data processes. Significance of the correlation ($\widehat{\sigma }=-0.235$, p-value< 0.001) between δ_1i and δ_2i indicates that the missing not at random mechanism is perhaps reasonable.

For risk factors, the naive analysis and the proposed methods give different estimates. In the transition from normal cognition to MCI, family history of dementia and age are significant, indicating that older people and people who have a family history of dementia have higher risk of transition from normal cognition to MCI. MMSE is significant in the naive analysis, but it is not significant in the proposed method analysis. In the transition from MCI to dementia, sex, fhdem, and age are significant, indicating that older people, people with family history of dementia or males have higher risk of transition from MCI to dementia. However, naive analysis shows that family history of dementia has no significant effect on this transition. In the transition from dementia to death, sex, MMSE and age are significant, indicating that a person has higher risk to death if he/she has a lower MMSE score or with an older age, and women has lower risk of transition from dementia to death comparing to men.

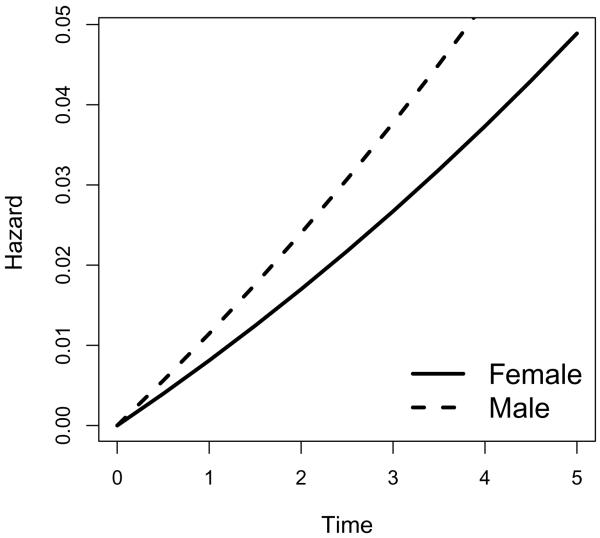
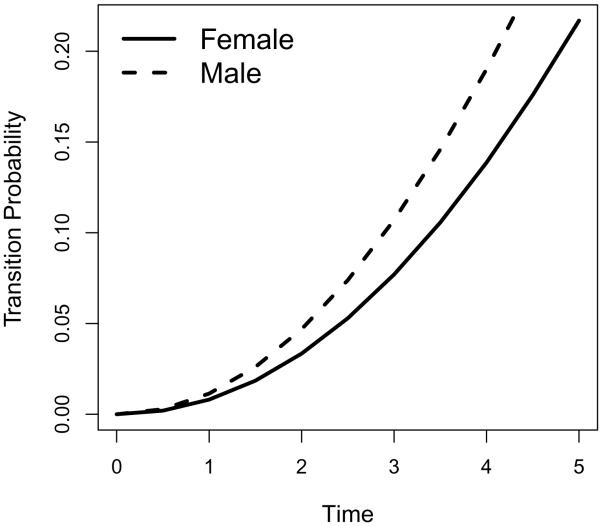
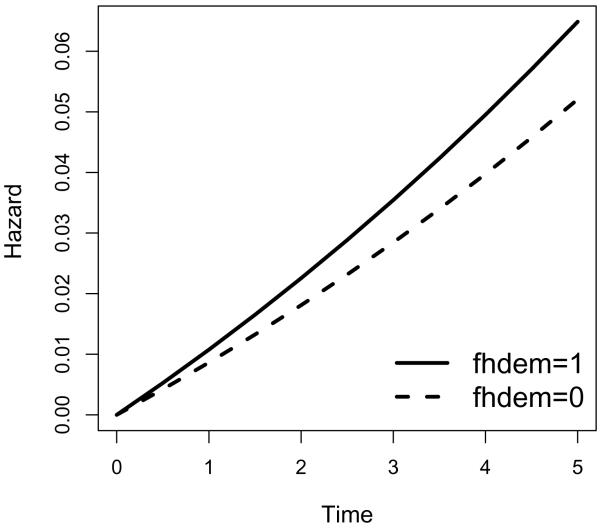
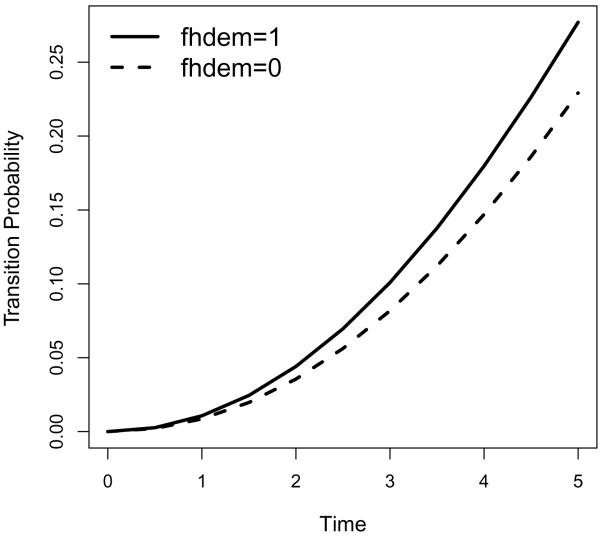
In practice, interests often lie in the transition from MCI to dementia. Figures 1 and 2 list the transition intensities and transition probabilities from MCI to dementia for sex groups adjusted for covariates fhdem, MMSE and age, where we use the mean value overall subjects for each covariate being adjusted. As is expected, males have higher risk of transition from MCI to dementia (hence higher transition probabilities from MCI to dementia) compared to females. Similarly, we plot the the transition intensities and transition probabilities from MCI to dementia for family history of dementia groups adjusted for covariates sex, MMSE and age, where we use the mean value overall subjects for each covariate being adjusted. As is expected, people with family history of dementia have higher risk of transition from MCI to dementia (hence higher transition probabilities from MCI to dementia) compared to those without family history of dementia.

Figure 1.

Transition intensities for sex groups from MCI to Dementia

Figure 2.

Transition probabilities for sex groups from MCI to Dementia

6. Discussion

In this paper we propose a likelihood-based method for the analysis of incomplete observations arising in clusters under the framework of non-homogeneous Markov processes using the time transformation model. To deal with the missing not at random mechanism and clustering effects, we employ a correlated random effects model for the response and missing data processes. Simulation studies demonstrate that the proposed method works well in a variety of situations.

Note that, to obtain consistent parameter estimates under MNAR, both the transition model and the model for the missing data process must be correctly specified. In practice, we aim to build a model which provides useful insight into the response process and observation process. Our strategy is therefore to build models that contain a large number of covariates, carry out tests of fit of nested models, and ultimately find a parsimonious model using standard procedures for model selection. The need for generalizations to deal with more complex models can be assessed by model expansion and the use of general model selection procedures such as the likelihood ratio test.

In this paper, we only consider that the time-transformation function is independent of the cluster. This method can be easily extended to consider a different transformation for any cluster. However, the number of parameters to be estimated will be inflated, especially when the number of clusters is big. So, careful selection of the transformations is warranted. To reduce the number of parameters, model selection procedures introduced in Section 4.2 such as the likelihood ratio test can be employed.

One limitation of our method is that it assumes that covariates are time independent. Time dependent covariates are not a problem if they are piecewise-constant, more problematic if they are known at all time points but continuously changing (e.g. age), and very problematic if they are only known at their observation times (e.g. biomarkers). Relatively little work has been done on fitting multi-state regression models with time-dependent covariates. In the special case of a single interval-censored covariate that indicates the development of a particular condition, Goggins et al. (1999) develop methods for Cox regression for a right censored event time. Chen and Cook (2003) considered models and methods to deal with an interval-censored progressive covariate processs in recurrent event analyses. Cook, Zeng, and Lee (2008) consider an extension to the bivariate setting where both the covariate and failure times are interval-censored. The more general problem of interval-censored time varying covariates remains relatively open and worthy of future research.

Figure 3.

Transition intensities for family history of dementia (fhdem) groups from MCI to Dementia.

Figure 4.

Transition probabilities for family history of dementia (fhdem) groups from MCI to Dementia.

Table 2.

Empirical performance of the proposed method and naive methods with correctly specified and misspecified transformation function: α₁ = 2.0, about 25% missing

		Proposed Method			Independence			Marginal			Misspecified
ρ	Para.	BIAS%	SD	CP%	BIAS%	SD	CP%	BIAS%	SD	CP%	BIAS%	SD	CP%
0.6	q 012	−0.4	0.030	94.2	−9.3	0.043	59.7	−8.6	0.038	65.0	33.7	0.066	12.9
0.6	q 013	−1.5	0.018	94.3	−17.3	0.020	34.9	−17.4	0.020	33.0	2.8	0.035	82.5
0.6	q 021	0.6	0.068	94.0	3.6	0.095	86.7	4.1	0.079	86.7	57.0	0.152	21.9
0.6	q 023	−0.8	0.042	94.2	−23.9	0.044	51.8	−22.0	0.044	57.1	38.5	0.081	63.0
0.6	β 12	−0.9	0.140	93.9	−1.0	0.136	93.6	−0.6	0.130	86.7	−10.6	0.139	73.5
0.6	β 13	−1.4	0.160	94.9	5.1	0.158	93.6	6.4	0.169	85.1	−19.3	0.199	75.9
0.6	β 21	1.3	0.341	94.0	3.4	0.334	93.8	4.9	0.319	82.4	35.1	0.320	73.7
0.6	β 23	−0.2	0.392	94.4	3.4	0.388	93.8	0.8	0.346	88.7	−10.0	0.342	77.2
0.2	q 012	−0.9	0.031	94.6	−8.3	0.040	62.9	−9.5	0.036	61.2	32.4	0.058	12.6
0.2	q 013	−0.8	0.019	95.3	−17.5	0.019	35.8	−17.1	0.020	38.3	3.6	0.033	83.6
0.2	q 021	1.5	0.076	94.7	4.6	0.084	83.7	2.2	0.085	83.6	57.2	0.153	24.7
0.2	q 023	−1.2	0.041	94.2	−23.0	0.042	54.3	−22.7	0.042	56.7	36.1	0.084	56.8
0.2	β 12	−0.5	0.139	94.4	0.0	0.144	93.8	−1.2	0.144	84.8	−9.8	0.137	71.0
0.2	β 13	−1.1	0.158	94.2	2.4	0.160	94.2	9.1	0.160	81.6	−19.1	0.176	79.2
0.2	β 21	0.6	0.333	94.1	−0.7	0.328	94.5	7.5	0.356	78.0	33.5	0.344	71.9
0.2	β 23	−0.6	0.288	95.1	3.3	0.287	93.6	1.1	0.325	86.1	−7.6	0.365	72.4
0.0	q 012	2.3	0.040	94.9	−1.6	0.039	94.1	−8.5	0.041	60.7	33.4	0.059	11.2
0.0	q 013	−4.6	0.021	94.0	−1.2	0.024	94.6	−17.0	0.020	37.3	1.7	0.033	86.8
0.0	q 021	0.7	0.099	95.0	2.8	0.092	94.3	3.9	0.089	83.2	56.7	0.135	24.8
0.0	q 023	−1.7	0.042	94.1	−2.5	0.045	94.4	−24.5	0.043	51.1	35.8	0.079	63.1
0.0	β 12	−0.7	0.154	93.7	0.3	0.150	95.6	−0.5	0.155	85.4	−10.1	0.128	71.6
0.0	β 13	0.4	0.181	94.2	1.3	0.181	93.7	9.1	0.184	85.2	−25.0	0.185	76.7
0.0	β 21	1.6	0.371	94.9	−1.4	0.364	94.1	1.8	0.377	76.0	34.9	0.313	70.9
0.0	β 23	−1.2	0.487	94.6	0.8	0.14579	94.9	0.2	0.418	86.9	−5.9	0.272	77.2