A Stochastic Evolutionary Model for Protein Structure Alignment and Phylogeny

Abstract

We present a stochastic process model for the joint evolution of protein primary and tertiary structure, suitable for use in alignment and estimation of phylogeny. Indels arise from a classic Links model, and mutations follow a standard substitution matrix, whereas backbone atoms diffuse in three-dimensional space according to an Ornstein–Uhlenbeck process. The model allows for simultaneous estimation of evolutionary distances, indel rates, structural drift rates, and alignments, while fully accounting for uncertainty. The inclusion of structural information enables phylogenetic inference on time scales not previously attainable with sequence evolution models. The model also provides a tool for testing evolutionary hypotheses and improving our understanding of protein structural evolution.

Introduction

The study of biopolymers has long relied heavily on alignment. Alignment algorithms identify regions of similarity between proteins and nucleic acids as a means of identifying common function and inferring homology. Sequence alignment also plays a key role in the reconstruction of phylogenies, a task with application to diverse areas such as drug design and resistance, epidemic monitoring, forensics, and anthropology. Alignment is vital for reconstruction because when sequences share a common ancestor, the degree of similarity between them can be used to estimate evolutionary distances. In such situations, formal statistical inference and proper accounting for uncertainty rely on a model of the evolutionary process. Incorporation of alignment uncertainty has been shown to be crucial for proper characterization of uncertainty in phylogenetic reconstruction (Lunter et al. 2008; Wong et al. 2008). Improved phylogenetic estimation therefore relies in part on reducing alignment uncertainty through more informative evolutionary modeling.

An enormous literature on statistical alignment and phylogeny exists, and we do not attempt a comprehensive summary in this study. Felsenstein (2003) provides a broad overview. Evolutionary models involve stochastic processes for mutation (Dayhoff et al. 1978; Jones et al. 1992) and insertion/deletion (Thorne et al. 1991, 1992; Miklós et al. 2004) and when combined these provide a model suitable for use in Bayesian or maximum likelihood alignment calculations (Bishop and Thompson 1986; Hein et al. 2000). Use of such models for Bayesian phylogenetics is widespread (Holmes and Bruno 2001; Huelsenbeck et al. 2002; Lunter et al. 2005).

Existing evolutionary models for proteins focus on primary structure, treating each protein as a sequence of amino acid characters. (Some work has attempted to incorporate structure-induced dependence among sequence positions—see, e.g., Robinson et al. 2003; Rodrigue et al. 2009— but these models nevertheless operate at the sequence level.) However, it is well known that protein tertiary structure is conserved over much longer time scales than sequence. This is because selective pressure occurs at the level of function; because a large percentage of sequence positions contribute to function only through their role in structure formation; and because of the significant redundancy in sequence space of protein folds. As a result, many homologous proteins may share limited sequence similarity, placing them in the “twilight zone” for sequence alignment.

When protein tertiary structure information is available, structural alignment algorithms can often be used to obtain highly accurate alignments in the absence of significant sequence similarity. Many such algorithms have been developed, typically based on optimizing a similarity score, including minimization of the sum of squared distances between aligned C_α coordinates or corresponding pairwise C_α distances. See Eidhammer et al. (2000) and Hasegawa and Holm (2009) for comprehensive reviews. However, as these algorithms are entirely based on optimization of heuristic score functions, most provide little or no accounting for uncertainty or confidence in the resulting alignment and no possibility of formal statistical inference procedures. In addition, structural scores such as root-mean-square deviation (RMSD) give only indirect information about evolutionary distance (Chothia and Lesk 1986; Panchenko et al. 2005; Zhang et al. 2010).

Rodriguez A and Schmidler SC (unpublished data) have developed a probabilistic approach to structure alignment (see also Schmidler 2006 and Wang R and Schmidler SC, unpublished data) and shown that some other structural alignment algorithms are special cases of their model. This provides many advantages, including full accounting for uncertainty in the alignment, enabling adaptive estimation of alignment parameters, and making explicit the statistical assumptions implicit in commonly used score functions. Rodriguez A and Schmidler SC (unpublished data) also provide a joint sequence–structure model and show significant improvements over a sequence-based approach alone in approximate estimation of evolutionary distances by selecting point accepted mutation (PAM) distances. However, these approaches use a gap-penalty formulation and as such do not serve as a formal, reversible evolutionary stochastic process suitable for use in phylogenetic applications. Gutin and Badretdinov (1994) and Grishin (1997) explore spatial diffusion processes to describe structural evolution and derive equations relating RMSD to sequence identity and evolutionary distance, but in both cases, the alignment is assumed to be given. In the absence of an indel process, these methods do not provide an explicit evolutionary model for alignment or phylogeny.

In this article, we build on these approaches to develop what we believe to be the first stochastic evolutionary process for protein sequence and structural drift simultaneously, suitable for protein alignment and phylogenetic estimation. We show that the inclusion of structural information effectively stabilizes inference of alignments and evolutionary distances for distant relationships. We also show how the model may be used to test evolutionary hypotheses. We conclude with a discussion of several possible extensions to the model to incorporate greater biophysical realism.

Materials and Methods

Evolutionary Model

Our evolutionary model is formulated as a continuous time Markov process composed of three components: an insertion/deletion (indel) model, an amino acid substitution model, and a structural drift model. The indel component follows the Links model of Thorne et al. (1991). The sequence mutation component follows a standard substitution rate matrix. Finally, the structural component models the evolutionary drift of individual amino acids (represented by C_α coordinates) in three-dimensional space using an Ornstein–Uhlenbeck (OU) process (Uhlenbeck and Ornstein 1930; Karlin and Taylor 1981). In what follows we denote by S^X the sequence of amino acid characters, and by C^X the 3D atomic coordinates, of protein X.

Indel Model

Let X and Y represent two proteins, with X an evolutionary ancestor of Y. The indel model describes the process of residues being added to and deleted from X. Thorne et al. (1991) have previously developed a birth–death model for this process known as the Links model. The model assumes a constant birth rate λ and death rate μ through time and across the length of the protein chain, with independence from site to site. Amino acid survival probabilities can be determined from the Links model for any values of λ, μ, and time interval t (e.g., Holmes and Bruno 2001):

(1)

(2)

(3)

Here α(t) is the probability of ancestral survival, β(t) is the probability of insertions given at least one surviving descendant, and γ(t) is the probability of insertions given ancestral death. These probabilities can be represented as a transition matrix for a pair hidden Markov model (HMM, Durbin et al. 1998) with emitting states match, insertion, and deletion, and null start and end states (Holmes and Bruno 2001). (See Appendix for details.) Let M denote the alignment matrix between X and Y, defined as the adjacency matrix of an order-preserving bipartite matching; then P(M|μ,λ,t) is given by the corresponding product of probabilities in this transition matrix.

Although the Links model is the most commonly used, alternative models that allow for larger indel events (Thorne et al. 1992; Miklós et al. 2004) may also be substituted.

Sequence Model

Using the Links model for indels, a complete evolutionary sequence model is obtained by specification of an amino acid substitution rate matrix. Several such matrices exist in the literature; for the examples in this article, we use the JTT 1992 matrix (Jones et al. 1992) as adjusted by Kosiol and Goldman (2005). We make the standard assumption that the substitution process is in equilibrium and that insertions arise according to the equilibrium distribution. Letting S^X and S^Y represent the sequences of X and Y, the joint likelihood of S^X, S^Y, and an alignment M is:

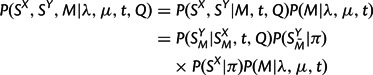where S_M^X and S_M^Y denote the matched (aligned) positions of S^X and S^Y, 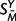the unmatched positions of S^Y, Q the substitution rate matrix, and π the equilibrium distribution of characters. P(S_M^Y | S_M^X , t, Q) is given by a product of independent substitution probabilities at each site, obtained by exponentiation of tQ; 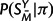and P(S^X|π) are products of the appropriate entries of π; and P(M|λ,μ,t) is described in the preceding section. This specifies a complete model for sequence evolution of the type used by many researchers (e.g., Holmes and Bruno 2001 and references therein).

Structural Model

We define a model for protein structure evolution analogously, building a structural drift process on top of the Links indel process. Let C^X and C^Y be n_X × 3 and n_Y × 3 matrices containing the Euclidean coordinates of the C_α's of X and Y respectively, where n_X is the number of amino acids in X. Where the sequence model uses a continuous-time, finite-state Markov process, the structure model uses a reversible diffusion process in 3D space modeling drift and fluctuation in the amino acid positions (represented by their C_α coordinates). We model positions as drifting independently in space according to an OU process, or Brownian motion with a mean reversion coefficient. (Unlike standard Brownian motion, the OU process has a stationary distribution and thus can be used as a component in a reversible stochastic process.) If C_ij^(t) is the jth coordinate of the ith C_α at time t, this process is described by the stochastic differential equation

(4)

where dB is standard Brownian motion, ζ is the mean of the process, and θ represents the strength of the reversion toward the mean. We set ζ = 0 for convenience, as we are concerned with shape and thus location is arbitrary (see the Rotation and Translation section). This process has the advantage of permitting closed-form expression of the equilibrium distribution

(5)

and conditional distribution at time t, given time s:

(6)

Therefore, again assuming that the parent structure C^X and insertions in C^Y follow the equilibrium distribution, the joint likelihood of two structures and an alignment between them can be expressed in a form analogous to the sequence model:

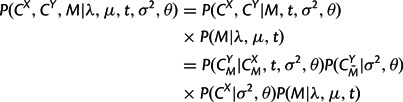(7)

with 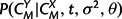calculated according to equation (6), 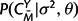and P(C^X|σ²,θ) according to equation (5), and P(M|λ,μ,t) as the appropriate product of transition probabilities from matrix (9) in the Appendix. In addition, the marginal likelihood of the observed structures, P(C^X,C^Y|λ,μ,t,σ²,θ), can be obtained by summing across all possible alignments M using a dynamic programming forward algorithm for pair HMMs (Durbin et al. 1998).

Note that this diffusion process assumes no significant structural reorganization and is best viewed as a model of structural drift within the basin of attraction of a particular fold. Evolution between folds is likely a discontinuous event with slowly accumulating sequence changes suddenly crossing into the basin of an alternative fold; our model currently does not account for such between-fold evolutionary events.

The model also assumes independence among sites, as with most commonly used sequence evolution models. Site independence is necessary to maintain analytical tractability of equations (5) and (6) after convolving with the indel process, whereas mean reversion of the OU process (as opposed to Brownian motion) ensures existence of the equilibrium distribution, equation (5). Independence does mean that the insertion distribution is diffuse, allowing insertions to arise anywhere in the protein (as dictated by the variance of C^X), without regard to the locations of neighboring amino acids. As a result of these assumptions the model is inadequate as a generative model for physically realistic protein structures but behaves well for inference conditional on observed structures. Possible extensions of the model toward additional biophysical realism are described in the Discussion section.

Rotation and Translation

For simplicity, we have introduced the structural component of the model under the assumption that X and Y share a common coordinate frame. In practice, the coordinates C^X and C^Y are obtained through experimental methods in which the coordinate frame is arbitrary. Thus, when comparing C^Y with C^X, we should not distinguish between elements of the set:

containing all possible rotations and translations of C^Y, where SO(3) denotes the special orthogonal group of 3 × 3 rotation matrices. It is possible to resolve this by treating equivalence classes of protein coordinates (shape spaces) using Procrustes transformations (Rodriguez A and Schmidler SC, unpublished data). However, as the optimal transformation depends on the full alignment, the likelihood over all alignments cannot be decomposed recursively as required for the HMM forward–backward algorithms. Instead, we treat R and η as uncertain parameters to be estimated (Green and Mardia 2006; Schmidler 2006) and calculate likelihoods conditional on a given rotation and translation. Then equation (7) becomes

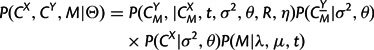with Θ representing the entire parameter set (λ,μ,t,σ²,θ,R,η).

Joint Sequence and Structure Model

The combined model is obtained by assuming independence between the sequence substitution and structural diffusion processes, conditional on the indel process. Thus, the full likelihood of the combined model is simply the product of the individual model likelihoods.

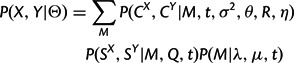(8)

with Θ again representing the entire parameter set. Each factor of the product in equation (8) is provided by one of the preceding sections.

Parameter Estimation and Computation

We take a Bayesian approach to parameter estimation, with the posterior distribution obtained by Markov chain Monte Carlo (MCMC) simulation. Parameters are updated by a random walk Metropolis–Hastings (Metropolis et al. 1953; Hastings 1970), with acceptance probability involving the marginal likelihood, equal to P(X,Y|λ,μ,t,σ²,θ,R,η) given by (8). In practice, it is best to update λ and μ together, similarly for R and η, to account for dependence in the posterior. All examples reported below use vague Gamma(1.01,.01) priors for t,λ,μ,σ², and θ, a uniform distribution on rotations for R, and an improper uniform prior for η.

Rotation/Translation Sampling

A random walk for R and η can be constructed as follows. Propose R′ from R by generating an axis v uniformly from the unit sphere and angle ϕ from a von Mises distribution with high concentration around 0, and form R′ as the composition of R and (v, ϕ). Then propose η′ ∼ N(η,τ²I), and accept or reject the pair R′,η′ together.

The mixing of R and η can be slow. To remedy this, an independence step is interspersed with the random walk, with proposal distribution constructed as a mixture with components centered at a “library” of plausible transformations. This library is created by computing the least-squares transformation between each pair of consecutive n-residue subsequences between X and Y (Rodriguez A and Schmidler SC, unpublished data) and excluding all such transformations with RMSD > δ, where the threshold δ is chosen to arrive at a manageable number of mixture components. Each component of the mixture is the product of a von Mises–Fisher distribution centered on the axis of rotation, a von Mises distribution centered on the angle of rotation, and a normal distribution centered on the translation. Then the probability density of this distribution at any rotation R′ and translation η′ is

where vMF (v′;v_i,κ₁) is the density of the von Mises–Fisher distribution evaluated at v′, the axis of rotation of R′; vM (ϕ′;ϕ_i,κ₂) is the density of the von Mises distribution evaluated at ϕ′, the angle of rotation of R′; N (η′;η_i,τ²I) is a multivariate normal distribution centered at η_i and evaluated at η′; and k is the number of components in the mixture. Mardia and Jupp (2000) provide general information regarding spherical distributions. An algorithm for generating samples from the von Mises–Fisher distribution is provided by Wood (1994). The proposed pair (R′,η′) is then accepted or rejected according to the Metropolis–Hastings criterion.

Monitoring Convergence

Convergence of the MCMC algorithm was established by the following protocol in all analyses reported in the Results section later. Multiple independent MCMC chains of 50,000 iterations were run from overdispersed starting points, with 10,000 iterations discarded as burn-in. We used eight chains for the sequence model and 16 chains for the combined model (to account for larger state space due to additional parameters). Convergence was tested by the Gelman and Rubin (1992) diagnostic on the marginal posterior distribution for each parameter.

Results

Inference for Distantly Related Proteins

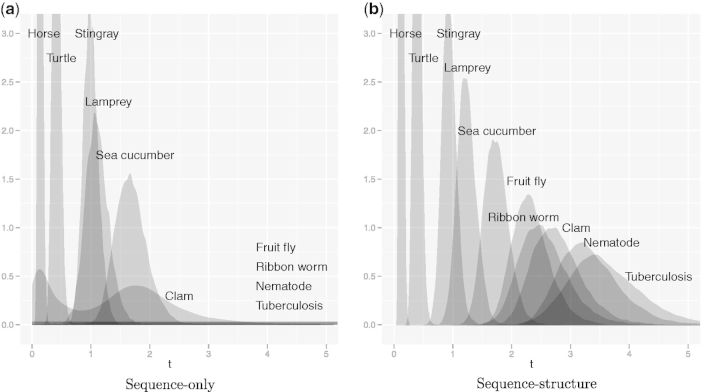
The joint sequence–structure evolutionary model described in the Evolutionary Model section enables improved alignment and estimation of evolutionary distance and rates between distantly related proteins. To illustrate this on a well-understood protein family, we applied both the sequence-only model and the combined sequence–structure model to estimate the evolutionary distance between the human hemoglobin α subunit and globins from a series of increasingly distant species (table A1). Figure 1 shows the resulting marginal posterior distributions for evolutionary distance t. In both models, the posterior distribution of t accounts for alignment uncertainty, which is critical for phylogenetic applications (Lunter et al. 2008; Wong et al. 2008). The two models yield comparable results for the pairs with short evolutionary distances and hence high sequence similarity, but as similarity decreases the uncertainty in sequence alignments grows. For sequences with very low similarity, many alignments have virtually equal probability, and the sequence-only likelihood becomes essentially flat for sufficiently large t. The inclusion of structural information by the combined model dramatically reduces this alignment uncertainty, allowing better use to be made of the sequence information, and also contributes additional information about evolutionary distance through the simple model of structural drift.

Fig. 1.

Posterior distributions for evolutionary distance between human hemoglobin α and a series of increasingly distant globins, obtained by (a) sequence-only model and (b) combined sequence–structure model. Distributions obtained from both models are nearly identical for the closest three orthologs (horse, turtle and stingray) but begin to diverge beyond this point. The sequence–structure model stochastically orders the proteins according to generally accepted taxonomy, whereas the sequence model begins to underestimate distances with the lamprey and sea cucumber and yields completely flat, uninformative posteriors for the fruit fly, ribbon worm, nematode, and tuberculosis.

This “range” extension of the model through the addition of structure is significant. The sequence-only model begins to differ from the combined model at distances of only 1.5 expected substitutions per site, becoming completely uncertain by 2.5 expected substitutions, whereas the combined model continues to provide informative posteriors to distances of at least 3.5 expected substitutions. In addition, the sequence model parameters (t,λ,μ) become confounded even at modest evolutionary distances (see also fig. 3 later). In contrast, the combined model has no difficulty simultaneously estimating all parameters (t,λ,μ,σ²,θ,R,η) with no loss of precision in t.

Fig. 3.

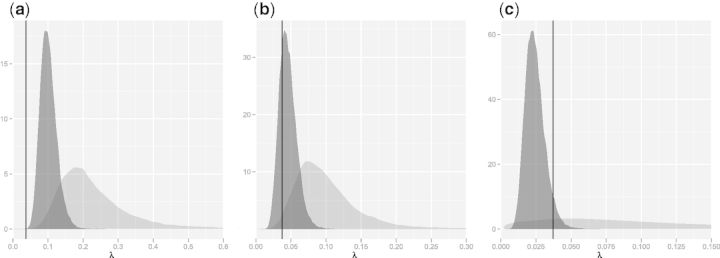
Posterior distributions of birth rate (λ) between globins of human and (a) lamprey, (b) sea cucumber, and (c) clam obtained under sequence-only (light) and sequence–structure (dark) models. Increasingly diffuse indel rate posteriors lead to underestimated evolutionary distance estimates; λ =0.03718 estimated previously by Hein et al. (2000) is given as a reference (vertical line).

Delaying the Phase Transition

The sharp increase in entropy of the posterior distribution under the sequence model is suggestive of the phase transition discussed by Mossel (2003, 2004) (see also Daskalakis et al. 2011), who shows that if the substitution rate is above a threshold, it is impossible to recover either ancestral sequences or phylogenetic topology over large evolutionary distances using sequence evolution models. Empirically, we see the transition even earlier (at shorter distances) than suggested by Mossel's bounds, between t = 1.5 and t = 2; this is explained principally by the fact that Mossel's result assumes a fixed alignment, while accounting for uncertainty in the alignment (and indel rates) causes the uncertainty to grow much faster.

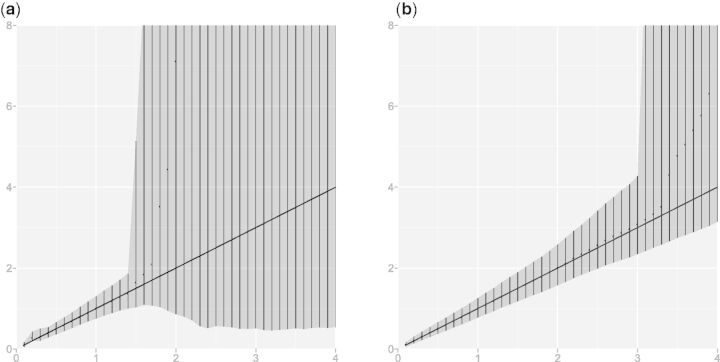
To examine the effect of alignment uncertainty on evolutionary distance estimation, we simulated (under the JTT substitution model, with no indels) the evolution of 100 independent sequence descendants from human hemoglobin α up to time t = 4 and another 100 descendants involving indels (using the Links model with rates λ =.05 and μ =.0504). We estimated the evolutionary distance from the ancestral sequence to each of the 200 descendants, over the time interval t ∈ [0,4] at increments of 0.1, using the MCMC algorithm described above and treating all parameters as unknown, but with the alignment fixed for the first 100 (no indel) sequences. Figure 2 shows the quantiles of the posteriors averaged across the 100 simulations. When the alignment is known, the sequence model displays a sharp transition in posterior uncertainty (credible interval width) at t = 3; beyond this point, the data inform only that the sequences are not closely related. This transition occurs much earlier (around t = 1.5) when the alignment is unknown and its uncertainty must be accounted for. In this case, when λ,μ, and t are simultaneously estimated the model swiftly loses identifiability, resulting in completely uninformative posterior distributions.

Fig. 2.

Average 95% credible intervals and medians from 100 simulated descendants of human hemoglobin α. The sequence model with unknown alignment (a) has a sharp transition at t = 1.5. Removal of alignment uncertainty (b) delays the transition to three expected substitutions. For our combined sequence–structure model, we witness this transition still later, at times > 3.5 (fig. 1).

The addition of structural information in the combined sequence–structure model dramatically reduces uncertainty in the alignment, which should therefore push the transition back to where it occurs for sequences with known alignment. Additionally, the structural drift model, while simplistic, does provide some information about distance. The results in figure 1 indicate that the transition for the combined model does not occur until after t = 3.5, confirming that the structural information does add some information beyond just the alignment. This suggests that the range of the model may be extended to even longer evolutionary distances by improving the realism of the structural diffusion model to include stronger information about t and not just M.

Estimating Indel Rates

With the alignment known, the sequence model is able to provide a useful lower bound even after the transition, but this is no longer true when the uncertainty arising from an unknown alignment is accounted for (compare fig. 2a and b). In particular, underestimation of evolutionary distance occurs due to overestimation of the indel rates λ and μ: as sequence similarity decreases, differences become as likely to be explained by rapid insertions and deletions over a short time period as by substitutions, so deflated estimates of t can result. Around t = 2 in figure 2a, approximately half of the simulated proteins exhibited high variance while the other half had narrower posteriors which underestimated the evolutionary distance; thus it is not enough to obtain a concentrated posterior from the sequence model, as larger values of t are likely to be underestimated.

Figure 1 contains three examples of this: 2LHB (lamprey), 1HLB (sea cucumber), and 1B0B (clam). For each of these, the sequence-only model gives significantly smaller estimates of distance than the combined sequence–structure model. Examination of the posteriors for λ (fig. 3) confirms that indel rates have been overestimated by the sequence model, with underestimation of t particularly extreme in the case of 1B0B as a result of a very diffuse posterior for λ. In fact, the long tailed posterior for λ leads to a second mode, near zero, in the posterior for t (fig. 1). A previous treatment of the Links model based on human α and β globins estimated the insertion rate at 0.03718 (Hein et al. 2000), and this value was confirmed by Knudsen and Miyamoto (2003); it is provided in figure 3 for reference. Combined model estimates of indel rates are much more stable between protein pairs and much closer to the results obtained by Hein et al. (2000).

Phylogeny Estimation

The uncertainty of evolutionary sequence models with respect to evolutionary distance can dramatically impact the ability to accurately estimate phylogenies (Lunter et al. 2008; Wong et al. 2008). As our joint sequence–structure model drastically reduces this uncertainty, we expect it will have significant impact on stabilizing phylogenetic estimation. Here, we explore this impact by estimating pairwise evolutionary distances and applying neighbor-joining methods (Saitou and Nei 1987; Howe et al. 2002). In the future, the combined model will be integrated into a full Bayesian simultaneous alignment and phylogeny estimation model, for which it is naturally suited and directly applicable.

Figure 4a shows the estimated phylogeny for the hemoglobin α subunits of 24 organisms (table A1) including near and distant relationships (pairwise sequence identity 12–87%), obtained by applying neighbor-joining to the set of pairwise posterior mean distances. Commonly accepted taxonomy from the National Center for Biotechnology Information (NCBI) Taxonomy Database (Sayers et al. 2009; Benson et al. 2009) is given in figure 4b. The phylogeny estimated similarly (neighbor-joining with posterior mean distances) under the sequence-only model is shown in figure 4d, albeit with unit distances (see below).

Fig. 4.

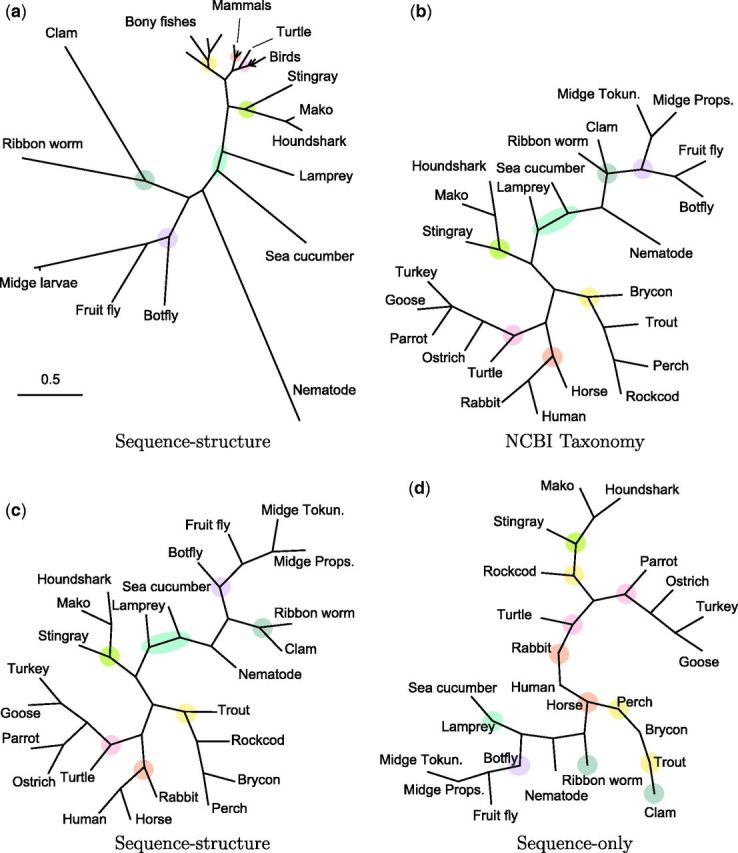
Phylogenies for a group of 24 globins (table A1, pairwise sequence identity 12–87%) obtained by different methods. Branch lengths in (b), (c), and (d) have been normalized for topology comparison. (a) Neighbor-joining tree using pairwise posterior mean evolutionary distances under sequence–structure model. (b) Accepted taxonomy (NCBI Taxonomy Database). (c) Topology of (a). Estimated topology closely matches NCBI taxonomy (b), with small differences. (d) Topology of neighbor-joining tree using pairwise posterior mean evolutionary distances under sequence-only model. Some groups are incorrectly separated and several species appear as zero-branch-length intermediate points. Figures are created with TreeView (Page, 1996).

The reconstructed phylogeny obtained using the combined sequence–structure model (fig. 4a) replicates the established taxonomy almost perfectly. All subgroups are correctly formed, including grouping of the only reptile (turtle) with the birds but as the most distant member. There are minor differences in the topologies within groups where branch lengths are small and minor changes in length can result in topology changes. A fully Bayesian approach to phylogeny estimation would yield a posterior distribution over competing topologies as well—here, our intent is merely to indicate the potential of our sequence–structure model for this purpose.

Using the sequence-only model, many of the pairwise distance posterior distributions remain essentially unchanged from the prior, resulting in broad posterior support and very large posterior means under diffuse gamma priors. In such situations, point estimates have little meaning, and posterior intervals convey a near-total lack of information about the evolutionary distance between the two proteins. A phylogeny based solely on the sequence model therefore tends to form clusters of closely related proteins with very large intercluster distances and arbitrary relative placement of the groups. Intergroup branch lengths are so long that visualization of the phylogeny is challenging; for this reason, the sequence-based phylogeny is given with unit branch lengths (fig. 4d), so that topology can be easily examined. The topology contains multiple inconsistencies with the established taxonomy (fig. 4b). The lamprey is separated from other vertebrates, as well as the rockcod from other bony fishes. The mammals do not appear as a clade, but as zero-branch-length points between subtrees.

Comparison to Multiple Sequence Alignment

Our sequence–structure model dramatically outperforms the analogous evolutionary sequence model on a pairwise basis, as demonstrated. However, simultaneous multiple sequence alignment (MSA) algorithms can also reduce alignment uncertainty, albeit to a lesser extent, through sharing of information. In addition, many phylogenetic methods in common use do not attempt to account for alignment uncertainty. We used MAFFT (Katoh et al. 2005) as a representative, widely used MSA algorithm, and compared the resulting tree with that estimated under our model for the group of 24 globins of figure 4. Default parameters were used for MAFFT. There are no major differences between the trees estimated by MAFFT and our model, indicating that the combination of MSA and selective use of multiply conserved positions used by MAFFT also does a good job of stabilizing the tree. Note, however, that these procedures, while adding robustness, do not correspond to an explicit evolutionary model as in our case.

More importantly, MSA algorithms rely on the presence of close homologs. There are several closely related groups in the set of 24 globins, making this well suited for an MSA approach. We performed the comparison again after removing the closely related proteins to arrive at a subset of eight mutually distant globins (pairwise sequence identity 12–43%); figure 5 compares the resulting phylogeny under our sequence–structure model with that produced by MAFFT. The phylogeny from our model remains consistent with the established taxonomy and with the tree obtained using the full set of globins, with only a minor shift in the placement of the nematode. The MAFFT phylogeny, however, becomes unstable, separating the lamprey from the other vertebrates. Changing the MAFFT default substitution matrix from BLOSUM62 to BLOSUM30 (more appropriate for distant homologs) has little effect, while modifying the gap penalty parameter caused MAFFT to perform worse.

Fig. 5.

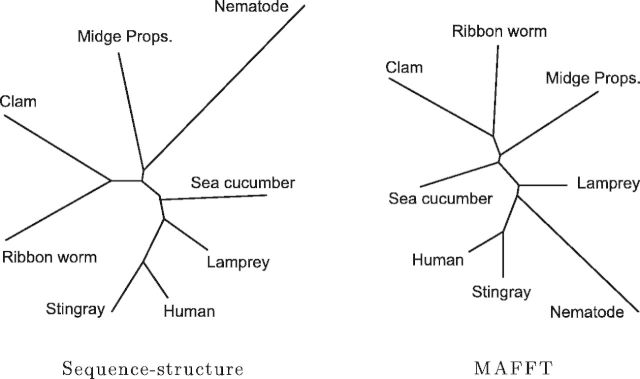
Estimated phylogenies for a subset of eight mutually distant globins (pairwise sequence identity 12–43%). The sequence–structure model still closely matches the established NCBI taxonomy, whereas MAFFT begins to exhibit significant differences. Additionally, the MAFFT phylogeny has become more sensitive to parameter choice, whereas the sequence–structure model estimates appropriate parameters from the data.

To further examine the different potential of the sequence–structure model and MSA approaches to analyze distantly related proteins, we simulated 10 sets of 6 pairwise-distant descendants of the α subunit of the human globin at the leaves of a symmetric tree (top of fig. 6) with inner branch lengths 0.35 and outer lengths 1.2 (pairwise sequence identity 13–17% on average). Simulation parameters were (λ = 0.03, μ = 0.0302, σ² = 0.7, θ = 0.005) — values typically estimated from observed globins. To further challenge our structure model, insertions in simulated structures were placed at the midpoint of their neighbors, as the independence of the insertion distribution equation (5) would otherwise make them easier to identify than naturally occurring insertions. For each of the 10 simulated data sets, we estimated the underlying phylogeny using MAFFT with default parameters and using our joint model as before (neighbor-joining on pairwise posterior means). The results are shown in figure 6. The sequence–structure model arrives at the correct topology in 6 of the 10 cases and preserves correct nearest neighbors in three of the other four. MAFFT only estimates the topology correctly in one instance and mismatches neighbors in all of the rest. The principal difficulty for the multiple sequence algorithm is insufficient sequence information to resolve the alignment when sequences are highly divergent. The problem is exacerbated by reliance upon a single optimal alignment which is highly uncertain. Our model benefits from both the Bayesian averaging over all possible alignments and also especially from the dramatic reduction of alignment uncertainty upon incorporating structural information, resulting in significantly improved phylogeny estimation.

Fig. 6.

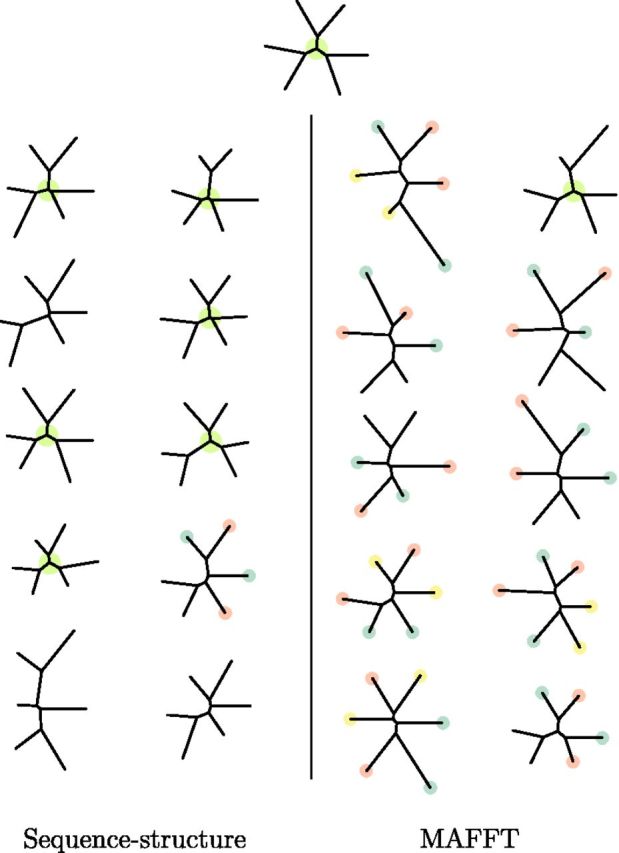
Phylogenies estimated from simulated highly divergent data sets (average pairwise sequence identity 13–17%). Top: true tree used to simulate data. Left: sequence–structure model estimates. Right: MAFFT estimates. Central green circle indicates correct topology, whereas red, blue, and yellow identify correct pairs where mismatches are made. The sequence–structure model estimates the correct toplogy in 6 of 10 simulations and preserves correct pairings of the proteins in all but one. MAFFT produces the correct topology in only one data set and in all other cases matches pairs incorrectly.

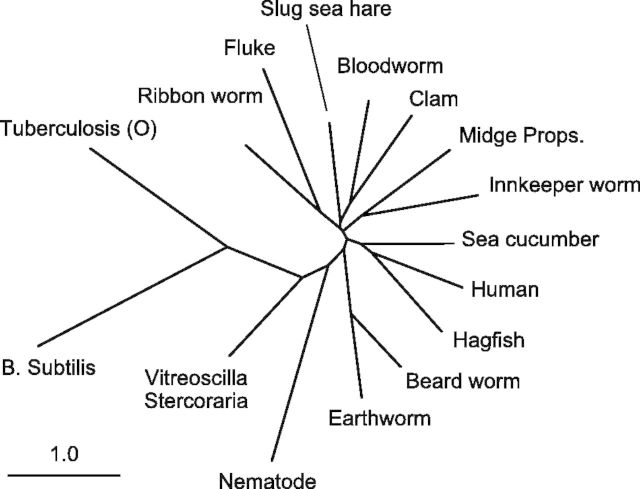
Indeed, the effect of this stabilization extends to sets of proteins for which MSA fails completely. With a broader set of globin-like proteins (pairwise sequence identity 9–32%, table A2), MAFFT returns an error message that a reliable phylogeny cannot be produced. Our model continues to be effective at these distances; the phylogeny is given in figure 7. The tree continues to correctly preserve the subtree containing the human globin, with the hagfish and sea cucumber as nearest neighbors. The extracellular giant hemoglobins of the earthworm and beardworm are placed together, and the nematode is the last multicellular organism before arriving at the microbes. This tree is not intended as a definitive estimate—a fully Bayesian treatment involving phylogeny sampling instead of neighbor-joining would be preferable to deal with the multiple near polytomies in the tree—but these results nevertheless illustrate the significant improvement available from the joint sequence–structure model.

Fig. 7.

Phylogenetic tree estimated under the sequence–structure model on a highly divergent set of proteins (pairwise sequence identity 9–32%), from which MAFFT is unable to reconstruct a phylogeny.

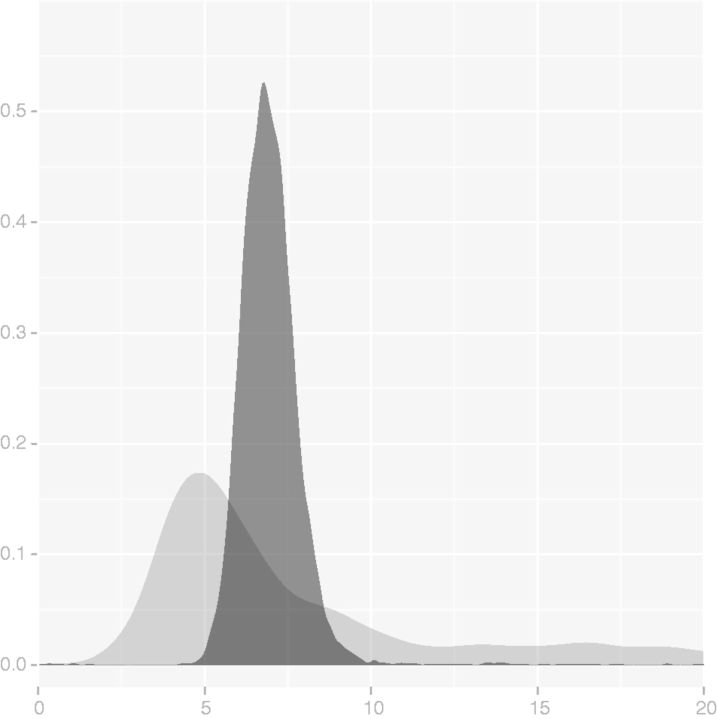
At extreme evolutionary distances (7% sequence identity) even the sequence–structure model becomes nearly unidentifiable, even when proteins share a common fold, for the following reason: as illustrated in figure 2, there is a sharp threshold past which sequence information provides only a lower bound on evolutionary distance, even in the case of fixed alignment. Beyond this threshold, sequences are effectively in equilibrium and no longer provide any information for estimating t. At this point, the structure component of the model provides all information about t, but the OU process by itself is identifiable only up to the product σ²t. (At shorter distances, Q serves to determines the scale for t, making σ² and t simultaneously estimable.) Figure 8 demonstrates the relative precision of σ²t to t on these time scales, for comparing the β subunit of phycocyanin from red alga with the α subunit of human hemoglobin. Thus at the farthest within-fold distances, a structure-only approach based on σ²t as a measure of distance between proteins can still provide some information about evolutionary relationships, but we would need to fix σ² (analogous to scaling Q to one expected substitution per time unit) to estimate t itself.

Fig. 8.

Posterior distributions of t (light) and σ²t (dark) between phycocyanin β chain of red alga and human hemoglobin α obtained under sequence–structure model. At such large distances (7% sequence identity), sequence provides no information about t and only the product σ²t may still be reliably estimated through structural information.

Reconstruction Regimes

Our results highlight the existence of multiple “regimes” of reconstructability, depending on divergence times of the input proteins. When sequence is sufficiently well conserved that pairwise alignments are easily resolved, neighbor-joining works well. As divergence increases into the “twilight zone” of sequence similarity, pairwise alignments begin to fail but can be recovered by pooling information across the set of sequences using MSA. However, as demonstrated earlier, a third regime exists when sequence information is inadequate for even MSA. In this case, our model demonstrates that structural information can still resolve the alignment, and conditional on alignment the sequences still contain sufficient similarity to infer evolutionary distance. Finally, as sequences become widely divergent, we enter a fourth regime where even though structural similarity may resolve the alignment, sequences are effectively in equilibrium and provide essentially no information about either the alignment or the evolutionary distance. In this last situation, our structural model may still be used to estimate divergence times t, but only if σ² is fixed by other means (fig. 8), analogous to scaling sequence substitution models to one expected substitution per time unit.

Discussion

We have described a stochastic process model for combined protein sequence and structure evolution, suitable for use in likelihood-based alignment and phylogeny estimation. Results on example protein families indicate that the inclusion of structural information can dramatically decrease uncertainty due to alignment and as a result significantly stabilize reconstructed phylogenies. The current model has certain shortcomings, and we briefly describe them in this study, along with possible extensions for future investigation.

Availability of Structural Data

Clearly the benefits of our approach are reliant on availability of experimental structural data for the proteins of interest. However, the number of known structures continues to grow rapidly as a result of high-throughput structure determination efforts. Moreover, our results suggest that availability of structures for even a subset of the sequences can significantly stabilize the reconstructed tree, by informing rate parameters (through a hierarchical model) and decreasing uncertainty in key evolutionary distances that may drive topology uncertainty. It may also be possible to incorporate high-accuracy predicted structures, such as those based on homology modeling, for sequences of unknown structure.

Improving the Structural Evolution Model

Intuitively, the inclusion of structure adds quantitative information (compared with the discrete characters of sequence models): the diffusion process penalizes large displacements of atoms in Euclidean 3-space. This helps identify homologous residues by favoring indel scenarios that best preserve the relative positions of residues present in both ancestor and descendant.

As mentioned in the Structural Model section, the diffusion model of structural drift does not account for significant structural reorganization leading to discontinuous changes in fold. Descendant proteins are centered around ancestral structures, slowly losing fold information, without the ability to significantly reorganize into new structurally distinct stable folds. Interesting preliminary work by Herman J, Taylor W, and Hein J (personal communication) provides a possible approach to modeling such large scale events using transitions between discrete states and may be useful in combination with our model to provide a process that diffuses locally but has potential for discrete transitions.

In addition, the independent-site assumption in the OU process lacks certain realistic biophysical features such as excluded volume/repulsion and bond length constraints, which give rise to dependence among positions. The challenge in incorporating such effects is analytical tractability: for a general (e.g., repulsive) potential U(X), the stationary distribution is known only up to a normalizing constant but that constant is required to evaluate changes in model size due to the indel process, and moreover, the conditional distribution is generally not analytically tractable. Incorporation of some site dependence may be achieved by the addition of a between-site covariance matrix to the OU process, but the conditional and stationary distributions again become problematic when convolved with the Links indel process. The current independent site OU process was chosen to provide simplicity and computational tractability, at the expense of some physical realism. However, since inference is performed conditional on observed structures, these limitations may be less important. Still, it is worth noting that a more realistic evolutionary process model for the structure might help provide additional information about evolutionary distance, since as mentioned in the Results section, we believe that in the current model, structural information serves primarily to dramatically reduce alignment uncertainty, with information about t coming primarily from the sequence model.

Structure-Specific Indel and Substitution Processes

Currently, the model assumes constant insertion/deletion rates (λ and μ), structural diffusion rate (σ²), and substitution matrix (Q) at all sites along the protein. A more realistic model would take advantage of the known structure, by allowing different rates according to secondary structure, solvent accessibility, location in an active site or binding site, etc. Although this seems straightforward, some care is required to preserve reversibility under indels. Structure-specific substitution matrices have been used successfully in sequence alignment and sequence–structure alignment (threading) and should improve the realism and information content of the model.

Dependence among Sequence and Structure

Currently, the sequence and structural information are combined by assuming conditional independence of substitutions and structural deviations given the alignment. This is easily extended to incorporate dependence. The magnitude of dependence may be explored by estimating the conditional mean and variance of atom coordinate changes given sequence substitution from a database of hand alignments.

Fully Bayesian Structural Phylogenetic Tree Reconstruction

Finally, the outcomes in the Results section relate to pairwise evolutionary distances and phylogenies constructed using neighbor-joining methods. We are currently incorporating the model into fully Bayesian simultaneous alignment-and-phylogeny estimation, as done for sequence evolution models by Lunter et al. (2005) and Redelings and Suchard (2005). The incorporation of structural data may go a long way toward resolving the significant uncertainty reported in simultaneous estimation models involving sequence only (Lunter et al. 2008; Wong et al. 2008), particularly when the phylogeny involves long time scales.

Despite these shortcomings, outcomes reported in the Results section with the current model show significant improvements over sequence-only models commonly used in current practice. As such, the model provides an additional tool for phylogenetic studies, especially those involving distant relationships or rapidly changing sequences, by extending the applicability of evolutionary protein models to longer time scales.

Appendix

The transition matrix for the pair HMM used to compute the marginal likelihood across all alignments. Parameters λ and μ and functions α(t),β(t), and γ(t) are given in the Indel Model section.

(9)

Table A1.

Protein Data Bank (PDB) entries and corresponding species from figures 1, 3, 4, and 5.

PDB ID	Species	Common name
1ASH	Ascaris suum	Nematode
1B0B	Lucina pectinata	Lucine clam
1CG5	Dasyatis akajei	Stingray
1GCV	Mustelus griseus	Houndshark
1HBH	Pagothenia bernacchii	Emerald rockcod
1HLB	Caudina arenicola	Sea cucumber
1HV4	Anser indicus	Bar-head goose
1IDR	Mycobacterium tuberculosis	Tuberculosis
1OUT	Oncorynchus mykiss	Rainbow trout
1X3K	Tokunagayusurika akamusi	Midge larva
1XQ5	Perca flavescens	Perch
2BK9	Drosophila melanogaster	Fruit fly
2C0K	Gasterophilus intestinalis	Botfly
2DHB	Equus caballus	Horse
2DN2	Homo sapiens	Human
2LHB	Petromyzon marinus	Lamprey
2RAO	Oryctolagus cuniculus	Rabbit
2XKI	Cerebratulus lacteus	Milky ribbon worm
2ZFB	Psittacula krameri	Parrot
3A59	Struthio camelus	Ostrich
3A5B	Propsilocerus akamusi	Midge larva
3AT5	Podocnemis unifilis	Side-necked turtle
3BCQ	Brycon cephalus	Red-tailed brycon
3K8B	Meleagiris gallopavo	Turkey
3MKB	Isurus oxyrinchus	Shortfin mako

Table A2.

PDB entries and corresponding species from figure 7.

PDB ID	Species	Common name
1ASH	Ascaris suum	Nematode
1B0B	Lucina pectinata	Clam
1H97	Paramphistomum epiclitum	Fluke
1HLB	Caudina arenicola	Sea cucumber
1IT2	Eptatretus burgeri	Inshore hagfish
1ITH	Urechis caupo	Innkeeper worm
1MBA	Aplysia limacina	Slug sea hare
1NGK	Mycobacterium tuberculosis	Tuberculosis
1OR6	Bacillus subtilis	Bacillus subtilis
1VHB	Vitreoscilla stercoraria	Vitreoscilla stercoraria
1X9F	Lumbricus terrestris	Earthworm
2D2M	Oligobrachia mashikoi	Gutless beard worm
2DN2	Homo sapiens	Human
2HBG	Glycera dibranchiata	Bloodworm
2XKI	Cerebratulus lacteus	Milky ribbon worm
3A5B	Propsilocerus akamusi	Midge larva