Higher order chromatin structure: bridging physics and biology

Abstract

Recent advances in microscopy and genomic techniques have provided new insight into spatial chromatin organization inside of the nucleus. In particular, chromosome conformation capture data has highlighted the relevance of polymer physics for high-order chromatin organization. In this context, we review basic polymer states, discuss how an appropriate polymer model can be determined from experimental data, and examine the success and limitations of various polymer models of high-order interphase chromatin organization. By taking into account topological constraints acting on the chromatin fiber, recently-developed polymer models of interphase chromatin can reproduce the observed scaling of distances between genomic loci, chromosomal territories, and probabilities of contacts between loci measured by chromosome conformation capture methods. Polymer models provide a framework for the interpretation of experimental data as ensembles of conformations rather than collections of loops, and will be crucial for untangling functional implications of chromosomal organization.

Introduction

The organization of a long DNA molecule or a chromatin fiber inside a cell is rich with opportunities for the application of concepts from polymer physics. Recently developed experimental techniques and powerful computer simulations now make it possible to test whether various hypotheses about chromatin architecture are consistent with experiments [1-4]. Polymer models have the promise to unite diverse experimental observations into a coherent conceptual and physical framework. Moreover, insights from polymer physics call for a shift from the existing paradigm of regularly looped models of chromatin organization to a view where higher-order chromatin organization is considered in terms of probabilistic models, or ensembles, of polymer conformations. A conformational ensemble probabilistically describes contacts between genomic loci and distributions of spatial locations for individual loci. The view of chromatin in terms of ensembles highlights the importance of entropy for understanding nuclear organization (Figure 1). A similar physics-based approach revolutionized our understanding of protein folding [5].

Figure 1.

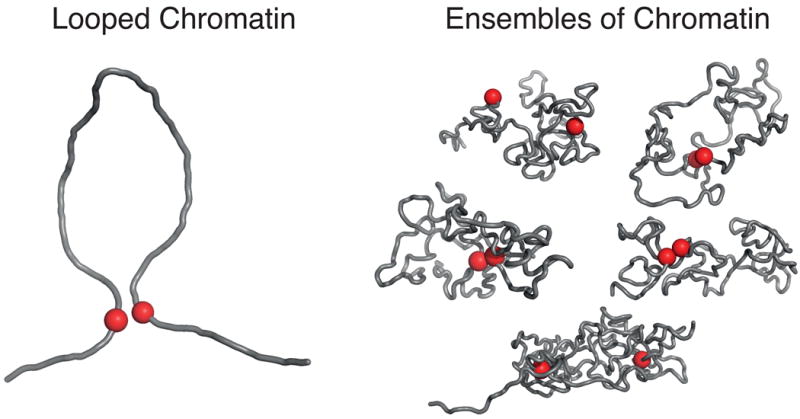
Looped vs. ensemble view of chromatin organization. An ensemble view is important for capturing the experimentally observed variability in high-order chromatin organization. Looped chromatin and the conformations in the ensemble of chromatin both show the same small piece of a longer chromatin fiber; red spheres highlight two potentially contacting loci on the chromatin fiber.

The first level of eukaryotic chromatin organization, packing of DNA into an array of nucleosomes, is relatively well understood [6]. Building upon this consensus, recent studies extended our understanding of the nucleosomal array by considering the structural and functional implications of DNA-encoded sequence signals [7,8], active modifying and remodeling machinery [9], and the interplay between nucleosomes and gene expression [10,11].

In the classical textbook view, nucleosomes are subsequently folded into a regular, 30nm fiber [12]. However, recent experiments including cryo-electron microscopy, electron spectroscopy, and small-angle x-ray scattering have cast doubt on the pervasiveness of the 30-nm fiber during interphase and metaphase [13-15], and argue strongly against the presence of any regular fiber beyond the 10nm fiber formed by nucleosomal arrays in the majority of cell types.

Higher levels of chromatin organization have been traditionally thought of as various arrangements of loops formed by an underling fiber [12]. Here we argue that despite its visual appeal and simplicity, understanding high-order chromatin organization in terms of regularly folded loops falls short of explaining experimental observations. Locations of genomic loci in the nucleus and distances between genomic loci are highly variable [16,17], and individual genomic loci come in contact with a diverse set of genomic loci [1,18]. In light of the variability of high-order chromatin organization, ensembles of polymer conformations provide a natural framework for understanding chromatin organization.

Polymer Physics

In polymer physics, three conformational ensembles: the random coil (random walk, RW), the swollen coil (self-avoiding walk, SAW), and the equilibrium globular state (EG), are the foundation for understanding more complex polymer systems [19-21]. These three ensembles are equilibrium states for an individual homopolymer (i.e. a polymer with identical monomers) in a solvent. These ensembles are characterized by various relationships between the observable measures, or scalings, and include: the characteristic size of the whole polymer R(N) (i.e. its root mean squared end-to-end distance <R_ee²>^1/2, or a mean radius of gyration) as a function of its length N, the mean spatial distance between loci (sub-chain size) R(s) as a function of distance s between these loci along the polymer (genomic distance), and the contact probability between loci P(s) (See Figure 2).

Figure 2.

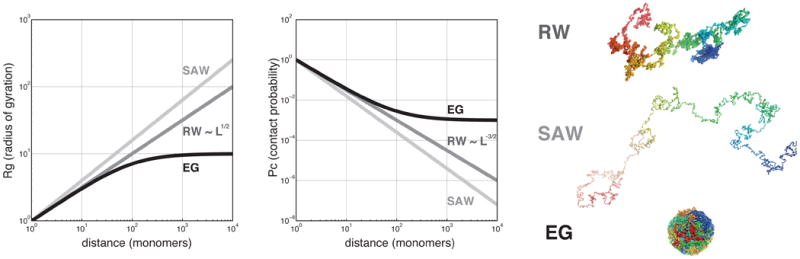
Basic polymer states. A: scaling for spatial distance R(s) between two loci as a function of genomic distance s between them. B: scaling for the contact probability P(s). C. Sample conformations for each of the states. Conformations illustrate the random coil (random walk, RW) state, the extended swollen coil state (self-avoiding random walk, SAW) and the compact equilibrium globular state (EG).

Random (Gaussian) coil

If steric repulsions between monomers of the polymer are negligible, are balanced by interactions with the solvent or screened by other polymers in a melt, and if topological constrains are disregarded, then a polymer adopts an ensemble of conformations equivalent to those of an unconfined polymer without steric interactions. Such idealized polymer is called an ideal chain. Its unconstrained conformations are well described by an ensemble of three-dimensional random walks. In the random coil state, a polymer of length N has a characteristic size of R(N)∼N^1/2. Since any part of a random walk is also a random walk, any sufficiently long sub-chain of a polymer in the random coil state has a size R(s)∼s^1/2, where s is the length of the sub-chain.

Conformations of the random coil ensemble are also characterized by the low density of monomers in the volume spanned by the whole polymer. This follows from the fact that a polymer of N monomers occupies a volume V∼R³∼N^3/2, leading to the density n∼N/V∼N^-1/2, which is small for large N.

Similarly, the contact probability between two monomers decays rapidly as P(s)∼s^-3/2 for two monomers separated by a distance s apart on a fiber for the random coil ensemble. This dependence can be understood to arise from the probability for two points to be near to each other in a volume determined by the size of the sub-chain.

Furthermore, the random coil ensemble exhibits large fluctuations in density and other observable quantities (e.g. R(s)). The relevance of fluctuations can be seen by considering the distribution of the end-to-end distance of the polymer; both the mean and the standard deviation of end-to-end distance scale as ∼N^1/2 [20], which entails large fluctuations of this quantity [21].

Importantly, these and other large-scale properties of the polymer ensemble arise irrespective of the detailed model of a polymer. At length scales exceeding several persistence lengths (i.e. length of an almost straight element) statistical properties become independent of the details of the model. An example of two models that converge at large scales are a Gaussian chain of monomers connected by springs and a worm-like chain model with a constant bending rigidity [20].

Swollen coil

If steric repulsion of excluded volume between monomers of the polymer plays a significant role, then a different ensemble is required to describe the statistical properties of the polymer. In the swollen coil, the characteristic size of the polymer grows as R(N)∼N^0.6, more quickly than in a random walk. A swollen coil has a similarly low and non-uniform density. Polymers in the swollen coil state are largely unknotted [22]. Note, however, that introducing confinement upon the swollen coil state drastically changes its properties.

Equilibrium globule

Upon confinement, sufficiently strong attractive interactions between the monomers, or repulsion from the solvent, a polymer collapses into a compact state described by yet another ensemble of conformations. The equilibrium globular state has high and uniform density and thus the characteristic size of the polymer scales quite differently with the number of monomers: R(N)∼N^1/3. This can be understood in terms of the space-filling nature of the polymer chains: the volume occupied by the polymer V∼R³∼(N^1/3)³=N increases linearly with the polymer length. However, short sub-chains of the globule are different from the whole globule and are described by random walk conformations R(s)∼s^1/2 (for s<N^2/3), since the repulsive effects of excluded volume interactions are exactly compensated by the forces which compress the polymer into the equilibrium globular state [20,21]. Longer sub-chains can be thought about as a series of random walks that “bounce” off the boundary of the globule. The size of longer sub-chains is bounded by the size of the globule leading to a hallmark plateau R(s)=const (for s>N^2/3) discussed below. Similarly, the contact probability P(s) first drops at the same rate as a random walk, and then reaches a plateau for larger s. Simulations have shown that polymers in the equilibrium globule state are highly knotted [22], making folding into the equilibrium globule an extremely slow process that requires reptation, i.e. threading of the polymer chain through the globule. The three equilibrium ensembles are related to each other; a transition from the swollen coil to the globule state occurs gradually, as a function of the strength of polymer-polymer attraction energy, with a random coil state at mid-transition.

Polymer physics also considers more complex equilibrium and non-equilibrium systems, including: melts of many polymer chains of the same and different lengths (where each chain is analogous to individual chromosomes), polymer rings (analogous to stably linked chromatin loops or circular chromosomes) [23], networks formed by multiple polymers crosslinked by strong interactions [24], branched polymers, and polymer brushes [25,26]. As with the three equilibrium homopolymer states, each polymer system has hallmark properties that can be compared with experimental measurements to select the most appropriate polymer models.

Connections between experimental data and polymer models

Two primary sources of quantitative experimental data are most widely used to discriminate between the predictions of various polymer models. First, fluorescent in-situ hybridization (FISH) and live-cell imaging provide information about spatial locations and distances between genomic loci as a function of genomic distance between them, time and cellular state [16,27]; this can then be compared to R(s) and dynamic characteristics of various polymer ensembles. Optical techniques are crucial for characterizing the cell-to-cell variability in chromosomal conformations and locations, for probing the dynamics of chromatin loci, and for their direct interpretation in terms of spatial distances. Second, measurements of average contact probabilities between genomic loci obtained via chromosome conformation capture (3C, [28]) and its high-throughput descendents (4C[18,29], 5C[30], Hi-C[1]) can be compared to the contact probabilities as a function of distance along a polymer chain, P(s), in a conformational ensemble. In 3C-based methods, DNA is crosslinked, digested, and ligated; ligation products are then read using sequencing to determine pairs of DNA fragments that are close in space. Currently, 3C techniques allow experimental interrogation of chromatin organization at unparalleled throughput and resolution, but do not provide insight into cell-to-cell variability and spatial distances. Thus, optical and 3C-based approaches offer complimentary views of chromatin folding.

Other techniques provide additional information: at the whole-nucleus scale, chromosomal territories are a key feature of the mammalian interphase nucleus [31-34], and interactions with the nuclear lamina [35] can constrain and inform polymer models. Emerging technologies such as electron spectroscopy [36], cryo-EM [14], and X-ray scattering, allow determination of the chromatin fiber's spatial distribution inside a nucleus at the resolution of individual nucleosomes. Finally, micromechanical experiments provide insight into the structure of mitotic chromosomes [37], and allow further discrimination between the assorted polymer [14,26] and biological models [38,39] of mitotic chromosomes. Since many of the latter have yet to be translated into the language of polymer physics, we focus this review on polymer models of interphase chromosomes.

Moving from Loops to Ensembles

Recent experimental data highlights the importance of moving from a regularly looped view of chromatin to an ensemble view of chromatin for understanding high-order chromatin organization. First, the monotonically decreasing scaling for contact probability P(s) obtained by Hi-C strongly argues against a preferred looping length in interphase chromosomes at observable resolutions. Second, distance along the polymer chain represented the main determinant of contact probability at longer distances; after the hundred-fold difference in contact probability due to the polymer nature of the chromatin fiber, chromosomal compartments contributed an additional few-fold preference for intra-compartment contacts. Third, at least in the cell line studied, no genomic loci separated by more than a megabase had contacts as frequently as the within-megabase contacts. Any given longer-range contact, then, is present in a minority of cells or occurs for a relatively short amount of time. This stochasticity argues for the importance of an ensemble-based view of chromatin organization at distances greater than a megabase. At shorter genomic distances, chromatin may indeed be more organized; in [40], gene expression has been linked to contacts between promoters and enhancers. However, note that enhancer-promoter contacts do not necessarily require looping out of the intervening chromatin fiber between two interacting loci, these contacts may still be quite stochastic, and an ensemble view may still be crucial.

Moreover, as follows from the diverse set of contacts for each loci in Hi-C, the observation of a contact between two loci in a population of cells does not imply that the region of the fiber between contacting loci can be thought of as a loop; the intervening fiber can readily adopt a variety of complex shapes and contact many other loci, which stands in contrast to an intuition of a looped out piece of rope (Figure 1). Also, an enriched number of contacts between two loci need not imply a specific physical or functional interaction between contacting loci: they can be brought together indirectly by other factors, including confinement of the polymer fiber or as bystanders of interactions between other loci. Finally, certain pairs of contacts may be impossible to achieve in a given conformation, necessitating a description in terms of an ensemble of conformations. An appropriate polymer model can be determined by comparing the probabilistic predictions of its ensembles with those from experimental measurements.

Models of mammalian interphase chromosome organization

As early as the observation of chromosome territories, it became evident that the basic swollen coil or random coil polymer states are poor descriptions of the conformational ensembles for mammalian interphase chromosomes. This was confirmed via FISH with the observation that mean distances R(s) between loci increase much more slowly than expected for a random coil state at genomic distances s >4Mb [41]. With this starting point, other polymer models have been proposed and explored to better fit the available data. Existing polymer models of interphase chromosomes differ in their relationships to the basic polymer states, in the types of interactions considered between monomers (e.g. excluded volume, long-range attractions), in their considerations of topological properties, and in their status as equilibrium or non-equilibrium states.

Given the failure of the random coil and the swollen coil to predict the leveling off in R(s), a logical next step was to compare experimental data to confined equilibrium polymers [41-43]. These models implicitly [41,43] and explicitly [42] account for the effects of excluded volume interactions between monomers, and indeed describe experimental data better than the random coil and swollen coil.

Long-range looping

An alternative approach towards understanding the leveling off of R(s) involves starting with the random coil polymer state and adding in interactions between monomers that are linearly distant along the chain. An early example of this approach is the Random Walk/Giant Loop (RW/GL) model [44], which was motivated by the observation of giant loop-like structures in electron microscopy images of swollen chromosomes. This model imposes long-distance (harmonic spring) interactions at regular 3Mb intervals. While these interactions understandably lead to a slower increase in R(s) than a random walk at distances greater than the loop size, the regular interactions also predict an unobserved periodicity for R(s).

The Random Loop (RL) model [45] represents a logical extension of the approach used by the RW/GL model, and has been investigated analytically [45] and computationally using Molecular Dynamics simulations [27]. As with the RW/GL model, the RL model chromatin fiber is modeled as a polymer by many long-distance (harmonic spring) interactions between the monomers. However, in the Random Loop model, monomers that attract each other are chosen at random (thereby avoiding the unobserved periodicity), using different schemes with several adjustable parameters. From a theoretical perspective, the polymer ensembles generated by the RL and the RW/GL models are expected to be similar to an equilibrium globular state. In practice, they show hallmarks of an equilibrium globule, including a greater leveling off of R(s) as compared with the random coil state for s>10Mb [27,45].

While the RL model is able to describe experimental data, a clear molecular interpretation of this model remains elusive. While introducing long-distance attractive forces (harmonic bonds) between monomers that are distant in space (i.e. microns away) may be a useful method for generating polymer ensembles with a particular scaling, these forces are difficult to interpret mechanistically when biomolecular interactions are screened at less than a nanometer [46]. It is also difficult to imagine a biomolecular mechanism that allows the affinity or probability of an interaction to vary depending upon the intervening distance in the genome, as utilized in the RL model; chemically equivalent sites for interaction-mediating molecules (e.g. CTCF) would lead to interactions that are independent of intervening genomic distance. Allowing interactions to act exclusively intra-chromosomally in the RL model is equally difficult-to-justify, since the microscopic properties of chomatin are independent of whether it is on the same or different polymer chains, and thus tempers the value of any resulting observation of chromosome territories. Finally, the number of adjustable parameters in the RL model decreases its predictive ability; this is illustrated by the authors' note that practically any value of the power v<1/2 could be obtained for the R(s)∼s^v scaling for FISH data.

The role of topological constraints

An alternative to adding long-range looping interactions is to consider the implications of topological properties of a polymer [1,4,23,47,48]. Topological constraints, i.e. the energy barrier for segments of a chain to pass through each other, can lead to formation of long-lived non-equilibrium states, or in the case of polymer rings (e.g. circular chromosomes) to a different equilibrium state. Relevantly, recent experimental data argues for the importance of steric constraints for chromatin organization in vivo [49].

In [4], the authors studied a minimal non-equilibrium model of a decondensing chromosome represented as a homopolymer model of 30nm fiber subject of excluded volume, topological constraints, and confinement into a 5um nucleus. By matching the timescale in their simulations with experimental diffusion data, they found that for realistic decondensation times their model reproduces experimentally observed scaling for R(s) for yeast, human and drosophila data, and that chromosome territories emerge naturally due to the slow intermingling of polymers. In a subsequent study, the authors find that their minimal model of decondensed chromosomes can reproduce experimental scaling for Hi-C contact probability [50]. It remains to be seen whether a similar territorial organization can be observed if the assumption of 30nm fiber is dropped and a much longer and much more flexible 10nm fiber is considered. Another outstanding question is whether the chromosomal territories observed in simulations constitute an intermediate a transient state on the way to a mixed equilibrium, or an intermediate with a long lifetime. An analogous experimental question is to determine the stability of chromosomal territories over large time scales, and to test if chromosomes display any signs of increased intermingling in very slowly dividing cells.

Topological constraints are also central to the non-equilibrium polymer state called a fractal (crumpled) globule. In contrast to earlier models which were mainly motivated by FISH data for R(s), the proposal of a fractal-globular model for chromatin organization was first motivated by the observed P(s)∼s^-1 (500kb-5Mb) scaling for contact probability in Hi-C experiments on human cells, which is inconsistent with the scaling for contact probability in an equilibrium globule. Originally proposed in 1988, the fractal (crumpled) globule was hypothesized to be a non-equilibrium state of a polymer that forms after the collapse of a homopolymer from a swollen or random coil state, yet before the polymer reaches the equilibrium globule state [51]. Simulations of polymer collapse for N=4000-100,000 monomers [1,47] confirmed the presence of the fractal globule state and demonstrated that the polymer has P(s)∼s^-1 scaling in this state. The authors then found that the fractal globule has uniform density, is unknotted, and is composed of spatially segregated domains, where the latter two features are in contrast with the equilibrium globule. The presence of compact sub-domains in the fractal globule may present a cell with a natural way to achieve intra-chromosomal compartmentalization seen in optical [52] and cryo-electron microscopy data [53]. However, a number of important questions remain regarding the interpretation of the relationship between the fractal globule model and experimental data, including: Can a fractal globule state be formed by the biologically-relevant decondensation of mitotic chromosomes rather than by polymer collapse? What is the lifetime of the fractal globule state, and what factors can stabilize this non-equilibrium state?

Related developments have considered a melt of long polymer rings [23,54], which demonstrated that, in equilibrium, unentangled rings form a state similar to the fractal (crumpled) globule state. Rings composed of spatially segregated domains, remain unentangled, and have P(s) ∼ s^-1.17. In vivo, rings may correspond to long chromosomal regions looped on or anchored to a nuclear scaffold to prevent entanglement.

In important question that can be addressed experimentally concerns the extent of topological constrains in the cell. Can and does topoisomerase II act on nucleosomal DNA during interphase? Can two chromatin fibers occasionally path through each other during interphase and how frequent as such violations of the topological constrains?

Organization of Yeast Chromosomes

Polymer physics can also shed light on differences in chromatin organization between various organisms. In [55], the authors provide a thorough and up-to-date review of yeast chromosomal organization. An immediately evident difference in chromatin organization in yeast is that, in contrast with the s^-1 decay in contact probability observed in human cell lines, contact probability in yeast decays more like s^-3/2 [28,50], and is thus consistent with a random coil or mildly confined equilibrium globule state. Further understanding of yeast chromatin organization will be achieved by incorporating known constraints about yeast chromosomes into polymer physics models. For example, 3C-based [28,56] and optical approaches [17,57] have highlighted the importance of a Rabl structure of chromatin organization [55]. An outstanding controversy in the field of yeast chromatin organization relates to the size and flexibility of the interphase chromatin fiber. To determine these parameters, experimental data is typically fit to worm-like chain polymer models [50]. An analysis of FISH data was found to be consistent with a 30nm fiber [58]. However, in order to reconcile this with 3C data [50], a computational study needed to introduce ‘kinkability’ into the fiber, increasing contact probability at short distances without changing the mean distance. Other studies [59], however, question the relevance of the 30nm fiber for yeast interphase chromatin organization, and instead suggest a more flexible and extended fiber.

Organization of Bacterial Chromosomes

Recent experimental studies in C. Cresentus [60,61] and E. Coli [62] have revealed important aspects of bacterial chromosome organization. Notably, both bacterial genomes display a fascinating linear ordering of DNA [60,62]. In [62], the authors employ a very coarse-grained model, rather than a detailed polymer model, to describe the packing of the nucleoid into an effective filament. A more recently proposed mechanism of chromosome folding by interactions between transcription factor genes and their target genes in [63] is difficult to justify: while proximity of a transcription factor gene to its target(s) is beneficial [64], there has been no evidence for specific long-range interactions that can bring and keep them specifically together in space. Furthermore, 5C data displays a unique scaling at short distances, perhaps reflecting an interesting supercoiled organization in bacterial at sub-megabase distances, and thus a polymer model consistent with 5C data and linear organization has yet to be developed. Looking forward, chain entropy and topological constraints are likely to play central roles for bacterial chromosome organization, as was suggested for a mechanism of chromosome segregation into daughter cells in E. Coli [65].

From folding to biology

Starting from the framework provided by polymer physics, an important future direction will be to leverage this framework to help understand connections between chromatin organization and genome function. For example, topological constraints may prove sufficient to explain the formation of chromosomal territories [49], but further mechanisms must be investigated to understand the spatial separation of functionally distinct chromatin compartments as uncovered by Hi-C. Chromosomal compartments in Hi-C corresponded with active and inactive chromatin, and correlated with local gene density, DNAse hypersensitivity, markers of chromatin activity [1], and even replication timing domains [66]. Similar relationships between function and spatial organization were found for lamina-associated domains [35] and nucleoli-associated domains [67]. A physical model that begins with the functional state along the chromatin fiber and produces the observed three-dimensional patterns of contacts has yet to be developed.

A challenge for polymer models of chromatin is that unlike in protein folding, where there is some understanding of the functional form for interaction energy between amino acids (e.g. mutual attraction of hydrophobic residues), much less is known about the classes and functional forms of interactions between different types of chromatin or between chromatin and various nuclear sub-compartments. Constitutive or expression-mediated interactions between specific loci or with nuclear sub-compartments including the nuclear lamina, [35], nucleoli [67], and splicing factor-rich speckles may all make important contributions to the interaction energy between regions of chromatin. Active transport of chromosomal loci may be similarly important [68]. An important future direction for polymer models of chromatin will be integrating biological information to determine the relevant functional forms for interaction energies between monomers.

Polymer physics can also provide insight into the dynamics and variability of cellular processes as a function of time, including the role of chromatin structure for constraining or facilitating protein diffusion and other molecular search processes inside the nucleus [69]. In [70], the authors show that while dense compartments of the nucleus were still accessible to diffusing proteins, slower diffusion rates were observed in heterochromatin and nucleoli. In this study, the observed sub-diffusion was attributed to the fractal nature of obstacles that chromatin can create for a protein; however, it remains to be seen whether obstacles of (>10nm) scale can constrain diffusion of small proteins (<3nm). Other computational modeling techniques, including constraint-based methods [2], may complement polymer physics approaches to the study of chromatin organization.

A polymer ensemble view of chromatin also provides a natural starting point for understanding cell-to-cell variability in gene expression [71],[72],[73]. In particular, since contacts between genomic loci separated by large genomic distances (or between different chromosomes) are much more rare than between nearby loci, a gene regulatory process that depends on these rare contacts could show additional variability due to stochastic contacts. For example, if activation of a gene requires interaction with a specific and distant enhancer, and the spatial search process describing this interaction is slow, then only those cells where the two happen to be spatially close in the chromatin ensemble will show expression. Expression in other cells may be absent or delayed by the time of search, which can in turn depend on the initial spatial distance between the gene and the enhancer. However, transcription-coupled processes may stabilize long-range chromosomal contacts and thus constrain the conformational ensemble [40]. Other cellular functions may be constrained by, or take advantage of, the stochasticity inherent in the polymer ensemble view of higher-order chromatin for processes including chromosomal inactivation [74], or the specification olfractory receptors for a neuron [68]. Experiments have begun to explore the connection between cell-to-cell variation in gene expression and chromosomal interactions [75], but significant future work will be required to reconcile the two.

Polymer physics can also suggest mechanisms of folding and dynamics that allow for the relocalization of tissue specific promoters [76], the search for homologous regions [77], the positions of active genes relative to their chromosomal territories [78], the co-localization of active genes [79], and possibly the formation of “transcription factories” [80].

Spatial chromatin organization [81,82] has also been suggested to determine the frequency of translocations [83,84] and copy-number alterations in cancer [85]. In particular, copy-number alterations were shown be consistent with a model where the frequency of an alteration between two loci depends upon their probability of being spatially proximal in a polymer ensemble that describes the chromatin fiber.

Summary

Many important future challenges await at the intersection of polymer physics and chromatin organization. Taking an ensemble-based approach to higher-order chromatin organization will be crucial for elucidating key biological activities in the nucleus. In particular, this will help uncover general organizational principles and functionally relevant interactions between genomic loci from their diverse spatial locations and lists of contacting loci.