Bayesian hierarchical distributed lag models for summer ozone exposure and cardio-respiratory mortality

SUMMARY

In this article we develop Bayesian hierarchical distributed lag models for estimating associations between daily variations in summer ozone levels and daily variations in cardiovascular and respiratory (CVDRESP) mortality counts for 19 large U.S. cities included in the National Morbidity, Mortality and Air Pollution Study (NMMAPS) for the summers of 1987–1994.

In the first stage, we define a semi-parametric distributed lag Poisson regression model to estimate city-specific relative rates of CVDRESP mortality associated with short-term exposure to summer ozone. In the second stage, we specify a class of distributions for the true city-specific relative rates to estimate an overall effect by taking into account the variability within and across cities. We perform the calculations with respect to several random effects distributions (normal, t-student, and mixture of normal), thus relaxing the common assumption of a two-stage normal–normal hierarchical model. We assess the sensitivity of the results to: (i) lag structure for ozone exposure; (ii) degree of adjustment for long-term trends; (iii) inclusion of other pollutants in the model; (iv) heat waves; (v) random effects distributions; and (vi) prior hyperparameters.

On average across cities, we found that a 10ppb increase in summer ozone level over the previous week is associated with a 1.25 per cent increase in CVDRESP mortality (95 per cent posterior regions: 0.47, 2.03). The relative rate estimates are also positive and statistically significant at lags 0, 1 and 2. We found that associations between summer ozone and CVDRESP mortality are sensitive to the confounding adjustment for PM₁₀, but are robust to: (i) the adjustment for long-term trends, other gaseous pollutants (NO₂, SO₂ and CO); (ii) the distributional assumptions at the second stage of the hierarchical model; and (iii) the prior distributions on all unknown parameters.

Bayesian hierarchical distributed lag models and their application to the NMMAPS data allow us to estimate of an acute health effect associated with exposure to ambient air pollution in the last few days on average across several locations. The application of these methods and the systematic assessment of the sensitivity of findings to model assumptions provide important epidemiological evidence for future air quality regulations.

1. INTRODUCTION

The health effects associated with short-term exposure to ambient ozone are well documented in air pollution studies (Galizia and Kinney, 1999; Devlin et al., 1991; Folinbee et al., 1988; Kinney et al., 1996; Stern et al., 1994; Levy et al., 2001; Kelsall et al., 1997; Moolgavkar, 2000; Thurston and Ito, 2001; Goldberg et al., 2001). Exposure to ozone levels less than 100ppb can irritate the respiratory tract, particularly for sensitive populations, concentrations above 300ppb can cause nose and throat irritation, and levels above 1000ppb can cause breathing problems and headaches. In addition, long-term exposure to low ozone concentrations may damage sensitive areas of skin, causing premature aging of lung tissue (Turco, 1997).

Although several time series studies in single cities have shown significant positive associations between mortality/morbidity and summer ozone levels (Kinney and Ozkaynak, 1991; Kinney et al., 1996; Burnett et al., 1997a, 1997b 1994; Moolgavkar, 2000; Goldberg et al., 2001; Kelsall et al., 1997), few multi-site time series studies have been used to estimate an average short-term effect of ozone on mortality and morbidity by combining information across several locations (Stern et al., 1994; Burnett et al., 1997a, 1997b; Thurston and Ito, 2001). Critics of single-site studies focus on: (i) inconsistencies of findings among studies; (ii) arbitrariness in the selection of the cities to be studied; and (iii) model choices that might lead to relative rates estimates biased upward. Multi-site time series studies address these criticisms because: (i) site-specific data are assembled under a common framework; (ii) the same statistical model is fitted to all the cities; and (iii) the average effect is estimated by taking into account the within-site and across-sites variability by use of hierarchical models (Dominici, 2002).

In this article we extend previous modelling approaches developed in NMMAPS for PM₁₀ (Dominici et al., 2000) to take into account the following characteristics of the summer ozone data (from 1 June to 30 September). Unlike PM₁₀, summer ozone levels are measured daily, thus allowing estimation of health effects associated with exposure to ozone in the past few days instead of health effects associated with a one day impulse in air pollution concentrations. In addition, the estimated city-specific relative rates for ozone show some outliers, indicating that a normal random effects distribution might be inappropriate.

We develop Bayesian hierarchical distributed lag models for estimating the percentage increase in cardiovascular and respiratory (CVDRESP) mortality associated with short-term changes in summer ozone levels on average across 19 cities in the United States. The distributed lag models have been used in economics after Almon (Almon, 1995) popularized them in 1965. Then, Pope, Schwartz, and others (Pope and Schwartz, 1996; Zanobetti et al., 2000; Schwartz, 2000) used these methods in environmental health studies. Building upon these methods, at the first stage, we estimate city-specific relative rates of CVDRESP mortality associated with summer ozone levels using a distributed lag Poisson regression model with natural cubic splines to take into account non-linear confounding by long-term trend, and weather. At the second stage, we combine the information across the 19 cities by assuming that the true city-specific effects are normally distributed with unknown mean and variance (Gelman et al., 1995). In addition to the usual assumption of normality, at the second stage of the hierarchical model we also assume that the ‘true’ city-specific effects are distributed as a t-student and as a mixture of two normal distributions. Third, we assign prior distributions to all the unknown parameters. Our model specification is then applied to 19 large cities of the National Morbidity, Mortality and Air Pollution Study (NMMAPS) (Samet et al., 2000a, 2000b; Dominici et al., 2003) for which ozone data were available.

We choose CVRESP mortality as the outcome to capture a population subgroup at higher susceptibility than the general population (Burnett et al., 1997a, 1997b, 1994; Kinney and Ozkaynak, 1992; Kinney et al., 1996; Galizia and Kinney, 1999). We choose ambient summer ozone levels (from 1 June to 30 September) as the exposure, since summer ozone is highest among all seasons and measured more frequently.

Controlling for confounding bias and exploring effect modification in time series studies of air pollution and mortality is challenging (Samet et al., 2000a, 2000b; Dominici et al., 2004), and requires a systematic assessment of the sensitivity of findings to model specification. For example, temperature is both a potential confounder and effect modifier of the ozone-mortality association. Ozone and mortality tend to be higher at elevated temperatures, and the health effects of ozone could be exacerbated at extreme temperatures. In addition, ozone levels can be highly correlated with other pollutants, making it difficult to disentangle its effect from those of other environmental agents. Other long-term varying factors such as influenza epidemics and weather patterns are also determinants of mortality and ozone levels, and their incorrect assessment could lead to spurious associations. We systematically explore the sensitivity of the results to the adjustment for confounding bias due to long-term trends, other pollutants, and heat waves.

2. DATA

We used data from NMMAPS including mortality counts, weather, and air pollutant concentrations for the 19 large metropolitan areas in the U.S. from 1987 to 1994. Data are available on the internet at http://ihapss.biostat.jhsph.edu/data/data.htm. See also Samet et al. (2000a, 200b); Dominici et al. (2003) for additional details.

Cause-specific mortality data, excluding non-residents and accidental deaths, were obtained from the National Center for Health Statistics. Because mortality information contained residence information at county level only to protect confidentiality, all predictor variables were aggregated at county level as well. Mortality data were classified by age (< 65, 65 to 74, and ≥ 75 years), and by cause according to the International Classification of Disease Ninth Revision. The CVDRESP mortality used in this analysis include the following ICD-9 codes: cardiovascular (codes 390–448), respiratory, including chronic obstructive pulmonary disease and related disorders (codes 490–496), influenza (code 487) and pneumonia (codes 480–486, 507). The study outcome is the daily counts of CVDRESP mortality from 1 June to 30 September for 1987–1994 (eight years of summer months).

Hourly temperature and dew point data for each site were obtained from the Earth-Info CD database (http://www.earthinfo.com). After extensive preliminary analyses that considered various daily summaries of temperature and dew point, we used 24-h averages. If a county has more than one weather station, we used the average of the measurements from all available stations.

Daily time series of ambient air pollution levels for each county were obtained from the Aerometric Information Retrieval Service (AIRS) database maintained by the U.S. Environmental Protection Agency. The daily ozone levels used in analysis for each county are obtained by the following: (i) for each day and each monitor in a county, calculating the mean ozone concentration with moving window of 365 days centering around that day, called annual mean; (ii) calculating daily residuals from the annual mean for each monitor; and (iii) to protect against outliers, calculating the 10 per cent trimmed mean of the daily residuals across all monitors in this county. Other daily pollutant data are obtained in a similar fashion. Summer daily ozone levels from 1 June to 30 September for 1987–1994 (eight years of summer months) are the exposure measures of interest.

3. METHODOLOGY

In this section we describe the two-stage hierarchical model used for estimating an overall relative rate of CVDRESP mortality associated with short-term summer ozone exposure. Let $Y_t^c$ be the daily count of CVDRESP deaths, and $x_{t-\ell }^c$ be the ambient ozone levels at lag ℓ in city c. We assume that $Y_t^c$ has a over-dispersed Poisson distribution with mean ${\mu }_t^c$ and over-dispersion parameter ϕ^c and that:

$$\text{log}{\mu }_t^c=\text{age-specific intercept}+\sum _{l=0}^6{\beta }_{\ell }^c{x}_{t-\ell }^c+\text{long-term trend}+\text{long-term trend specific to each age group}+\text{day of week}+\text{temperature and dew point}+\text{copollutants},\text{or heat wave}$$ (1)

We first provide the interpretation of the parameters of interest, that is the summer ozone health effects. At the end of the section, we describe all the potential confounders and how we adjust for confounding in our model specification. Let ${\widehat{\beta }}^c=[{\widehat{\beta }}_0^c,\dots ,{\widehat{\beta }}_6^c]$ be the vector of the estimated city-specific estimates of the lag coefficients, and let V^c be the corresponding statistical covariance matrix. Let ${\widehat{\theta }}^c={\sum }_{\ell =0}^6{\widehat{\beta }}_{\ell }^c$ be the estimated city-specific cumulative effect and let ${\widehat{v}}^c$ be the corresponding statistical variance calculated as 1′V̂^c1, where 1 is a vector of ones. We assume:

$$\begin{array}{cc}\hfill & {\widehat{\theta }}^c\mid {\theta }^c,v^c\sim \mathrm{N}({\theta }^c,v^c)\hfill \\ \hfill & {\theta }^c\mid \mu ,{\tau }^2\sim g(\mu ,{\tau }^2)\hfill \end{array}$$ (2)

The parameter ${\theta }^c={\sum }_{\ell =0}^6{\beta }_{\ell }^c$ denotes the true city-specific cumulative log-relative rate of CVDRESP mortality associated with a 10ppb increase in summer ozone level over the previous week. The detailed explanation of this interpretation is listed in Appendix 1. As an alternative, we could specify a multivariate normal_P distribution for the vector of parameters ${\beta }^c=({\beta }_0^c,\dots ,{\beta }_6^c)$ at the second stage, and then calcuate ${\theta }^c={\sum }_{\ell =0}^6{\beta }_{\ell }^c$, rather than modelling θ^c directly. However, the high collinearity of the ozone levels at different lags creates numerical problems in the lag-specific effect estimations.

The parameters μ and τ² denote the true average cumulative log-relative rate across the 19 cities and the between-city variance of the θ^cs. Our goal is to approximate the marginal posterior distributions of μ and τ².

We perform the calculations under the following assumptions for the random effects distribution g:

1. g is normal with mean μ and variance τ²

2. g is a t-student with 3 degrees of freedom and with mean μ and variance τ²

3. g is a mixture of two normals with unknown weights, that is: g(μ, τ²) = (1 – p) N(λ₁, τ²) + pN(λ₂, τ²). Then μ = (1 – p)λ₁ + pλ₂.

We fit model (2) by use of Monte Carlo Markov chain methods (MCMC) (Gelman et al., 1995) implemented by use of Winbugs (Spiegelhalter et al., 2000). As prior distributions we use the ‘default non-informative priors’: that is μ ~ N(0, 10000) and 1/τ² ~ Gamma(0.01, 0.01). In the next section, we report the sensitivity of the posterior inference on μ to the specification of the prior distribution for τ² and to the choice of the prior hyperparameters. Winbugs software is detailed in Appendix 2.

Day-to-day associations between air pollution levels and mortality counts can be confounded by time-varying factors that vary in a similar manner as pollution and mortality. Below are listed the potential confounding factors for the associations between summer ozone and CVDRESP mortality, and how they are included into the regression model to adjust relative rates estimates for confounding bias.

Age group

We have adjusted for age by adding age-specific intercepts which allow for age-specific baseline mortality rate. The variable age is a categorical variable with 3 levels: < 65, 65 to 74, and ≥ 75 years.

Yearly trend

The number of deaths for cardiovascular and respiratory mortality and ozone levels have both declined in the past few years because of improvements in medical practice and air quality regulations. We have employed an 8 degree of freedom piecewise-cubic spline over 8 years (with 4 summer months in each year and knots at the separation of each summer) to remove the yearly trend. This form of smoothing spline adjustment will allow for increases or decreases over time within each summer, which is a more flexible way of time adjustment than using yearly dummies. In addition, to further remove trends in the summer mortality time series specific to each age group, we add interaction terms between smooth functions (natural cubic spline) of time with 2.4 degrees of freedom, and the second and third of the three age groups.

Day of the week

Day of the week is a surrogate for traffic patterns and daily activity. In addition there is evidence that the daily number of deaths and pollution levels are different for weekdays versus weekends. We adjust for the potential confounding effect of day of the week by including the model a categorical variable that allows for different baseline mortality counts on the different days of the week.

Temperature and dew point temperature

Since the chemistry of ozone formation is temperature and sunlight driven (Seinfeld and Pandis, 1998), ozone levels are correlated with temperature. In addition, epidemiological studies (Curriero et al., 2002) have reported associations between summer temperatures and mortality. To account for potential confounding by weather, we included in the model natural cubic splines of daily temperature, dew point temperature, and adjusted average temperatures and dew point temperatures over the three previous days (both adjusted for current-day temperature and dew point) with six degrees of freedom.

Heat waves

Correlations between ozone and temperature and between mortality and temperature can be even higher for a subset of days with extreme temperatures (heat waves). We further explored the sensitivity of the short-term effects of summer ozone on CVDRESP mortality to the potential confounding of heat-waves. We modelled a heat-wave as a natural cubic spline of the interaction between current temperature and average temperature in the three previous days with 2 degrees of freedom.

Other pollutants

Because previous studies have found evidence of a short-term association between PM₁₀ and mortality (Samet et al., 2000a, 2000b; Dominici et al., 2003), and because both PM₁₀ and O₃ levels are correlated with ultra-fine particles, PM₁₀ might be a confounder of the ozone-mortality association. Similar arguments apply to other pollutants, including carbon monoxide (CO), sulfur dioxide (SO₂), and nitrogen dioxide (NO₂). Sensitivity analyses of the short-term effects of summer ozone on CVDRESP mortality to inclusion of copollutants were performed. To control for their potential confounding effect, we fit several multi-pollutant models within each city having as predictors the current day co-pollutant concentrations. Notice that, since PM₁₀ measurements are available only every 1 to 6 days, a distributed lag model is not appropriate to examine the potential confounding effect of PM₁₀. Therefore we explore the sensitivity of the ozone health effects to the inclusion of PM₁₀ by use of a single-lag model (we use ambient ozone exposure at lag 2). Note that only the days with available PM₁₀ measures are included in this analysis.

In summary, this article introduces the modelling approach with a focus on summer data and explores the sensitivity of the results to model choices (adjustment for confounding, random effects distributions, and prior hyperparameters). The design of the sensitivity of results to random effects distributions and prior hyperparameters is listed at the beginning of this section. Other sensitivity studies include: (i) lag structure for ozone exposure: distributed lag model versus single lag models where we included only one air pollution predictor at lags 0, 1 or 2; (ii) degree of adjustment for long-term trends: monitor the changes of model inferences to various degrees of freedoms in the natural cubit splines of time, ranging from 4 to 16 with step = 2; (iii) inclusion of other pollutants in the model; and (iv) heat waves.

4. RESULTS

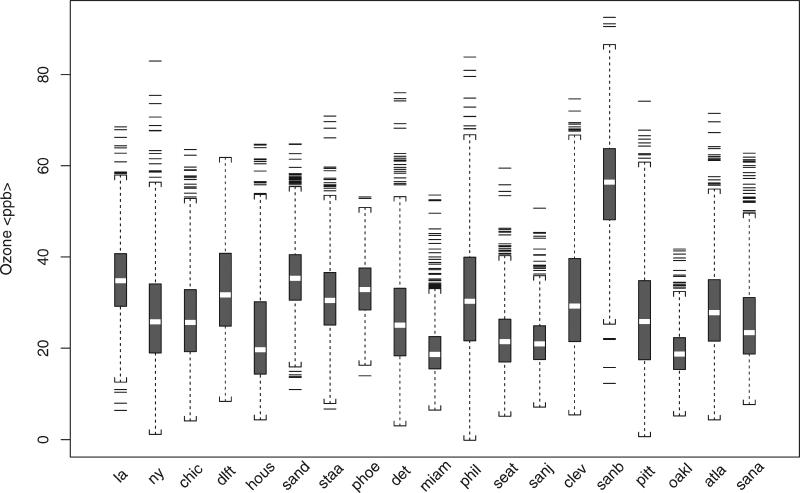
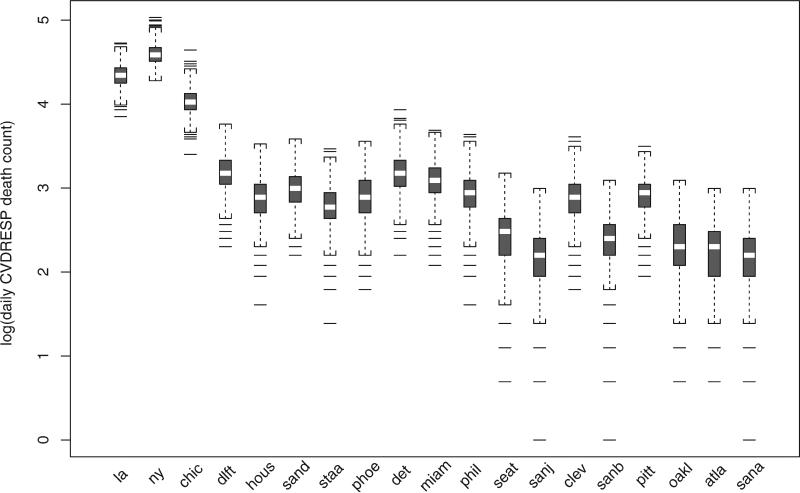
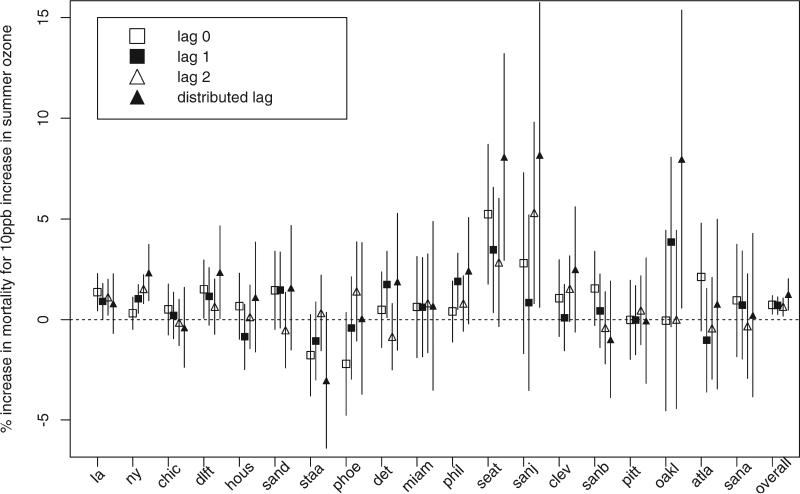
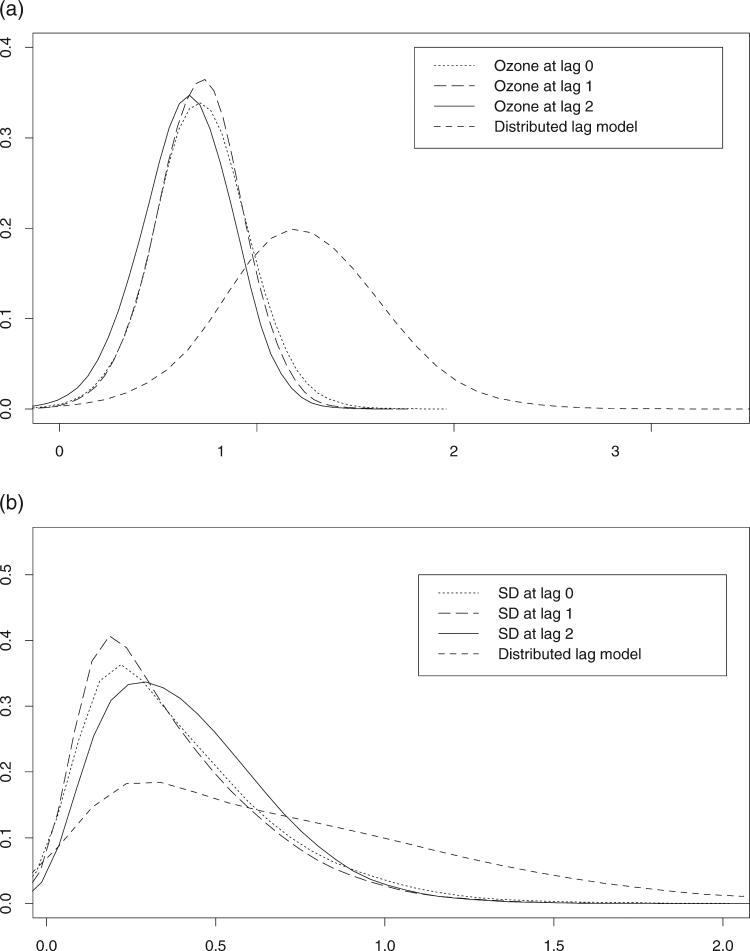
Figure 1 shows the box-plot of summer ozone levels in the 19 large U.S. cities. Daily levels of ambient ozone vary from 0 to 100ppb. Figure 2 shows the box-plot of the logarithm of the daily counts of CVDRESP mortality in the 19 large cities. The CVDRESP mortality counts in Los Angeles, New York and Chicago are much larger than others. Figure 3 shows city-specific estimates and 95 per cent posterior regions of the percentage increases CVDRESP mortality associated with a 10ppb increase in summer ozone levels at lags 0, 1, 2, and under a distributed lag model (cumulative effect in the last week). At the far right are shown the posterior means and 95 per cent posterior intervals of the corresponding overall relative rates. City-specific and overall relative rates estimates under a distributed lag model and their 95 per cent posterior regions are also reported in Table 1. Figure 4 (a and b) shows the posterior distributions of the average relative rate (μ) and of the between-city standard deviation (τ).

Figure 1.

Box-plots of summer ozone levels for 19 large U.S. cities in NMMAPS for the period 1987–1994

Figure 2.

Box-plots of log(daily CVDRESP death count) for 19 large U.S. cities in NMMAPS in summer months of 1987–1994

Figure 3.

City-specific relative rates estimates (percent increases in CVDRESP mortality associated with 10ppb increase in ozone) and their 95 per cent confidence intervals, with overall ozone effect and its 95 per cent posterior regions at the end. These effects are estimated by use of a distributed lag model for one week and at lags 0, 1 and 2 days

Table 1.

City-specific estimates of the percentage increase in CVDRESP mortality for a 10ppb increase in summer ozone levels over the previous week obtained under a distributed lag model (95 per cent confidence intervals). Last row denotes the posterior mean and the 95 per cent posterior regions of the overall effect

Los Angeles	0.79	(–0.69, 2.28)
New York	2.33	(0.93, 3.73)
Chicago	–0.39	(–2.38, 1.60)
Dallas/Fort Worth	2.35	(0.05, 4.66)
Houston	1.11	(–1.62, 3.84)
San Diego	1.58	(–1.50, 4.67)
Santa Ana/Anaheim	–3.03	(–6.40, 0.35)
Phoenix	0.05	(–3.71, 3.81)
Detroit	1.88	(–1.52, 5.27)
Miami	0.68	(–3.51, 4.86)
Philadelphia	2.42	(–0.22, 5.07)
Seattle	8.08	(2.94, 13.21)
San Jose	8.18	(0.61, 15.75)
Cleveland	2.49	(–0.62, 5.60)
San Bernardino	–0.98	(–3.87, 1.91)
Pittsburgh	–0.05	(–3.17, 3.07)
Oakland	7.97	(0.58, 15.36)
Atlanta	0.77	(–3.45, 4.99)
San Antonio	0.22	(–3.84, 4.28)
Overall	1.25	(0.47, 2.03)

Figure 4.

(a) Posterior distribution of average relative rate (μ) and (b) of the heterogeneity parameter (τ) obtained by combining city-specific relative rates estimates under a distributed lag model and single-lag models

On average across the 19 cities, we found strong evidence of an association between summer ozone levels and CVDRESP mortality under a distributed lag model, and at lags 0, 1 and 2. For example, we found that, on average across the 19 large cities, a 10ppb increase in summer ozone levels over the previous week is associated with a 1.25 per cent increase in CVDRESP mortality (95 per cent posterior regions: 0.47 per cent, 2.02 per cent). The average effects for ozone exposure at lags 0, 1, and 2 are 0.73 (95 per cent posterior regions: 0.27, 1.19), 0.70 (95 per cent posterior regions 0.26, 1.12) and 0.64 (95 per cent posterior regions 0.17, 1.07), respectively.

Notice that in several cities the estimated effects show monotonicity, with the smallest effect at lag 0 and the largest effect corresponding to the cumulative relative rate under the distributed lag model. This monotonicity suggests a consistency of findings across lag specifications with associations between ozone and mortality that persist for lags of at least 6 days. Posterior means of the heterogeneity parameter τ are similar across lag specifications with wider posterior intervals for the distributed lag model.

Table 2 summarizes the posterior means and 95 per cent posterior regions of the overall relative rates μ with respect to: (i) distributional assumptions for the random effects distribution (normal, t-student, and mixture of two normal); (ii) prior distributions on the heterogeneity variance τ² (Inverse Gamma, Jeffrey prior, uniform on the shrinkage factor); and (iii) choice of the prior hyperparameters. Posterior inference on μ are very robust to these model choices.

Table 2.

Posterior mean and 95 per cent posterior region of the overall effect μ under alternative specifications for the random effects distributions

Random effect distribution	National average estimate
Normal & 1/τ2 ~ G(0.01, 0.01)	1.25 (0.47, 2.03)
Normal & 1/τ2 ~ G(0.001, 0.001)	1.20 (0.47, 1.93)
Normal & 1/τ2 ~ G(0.0001, 0.0001)	1.20 (0.51, 1.89)
t-student with 3df & 1/τ2 ~ G(0.001, 0.001)	1.26 (0.50, 2.02)
Mixture of two normals & 1/τ2 ~ G(0.001, 0.001)	1.33 (0.51, 2.15)
Normal & 1/τ2 ∝ constant	1.29 (0.35, 2.23)
Normal & 1/τ2/(1/τ2 + 1/vc) ~ U[0, 1]	1.27 (0.37, 2.17)

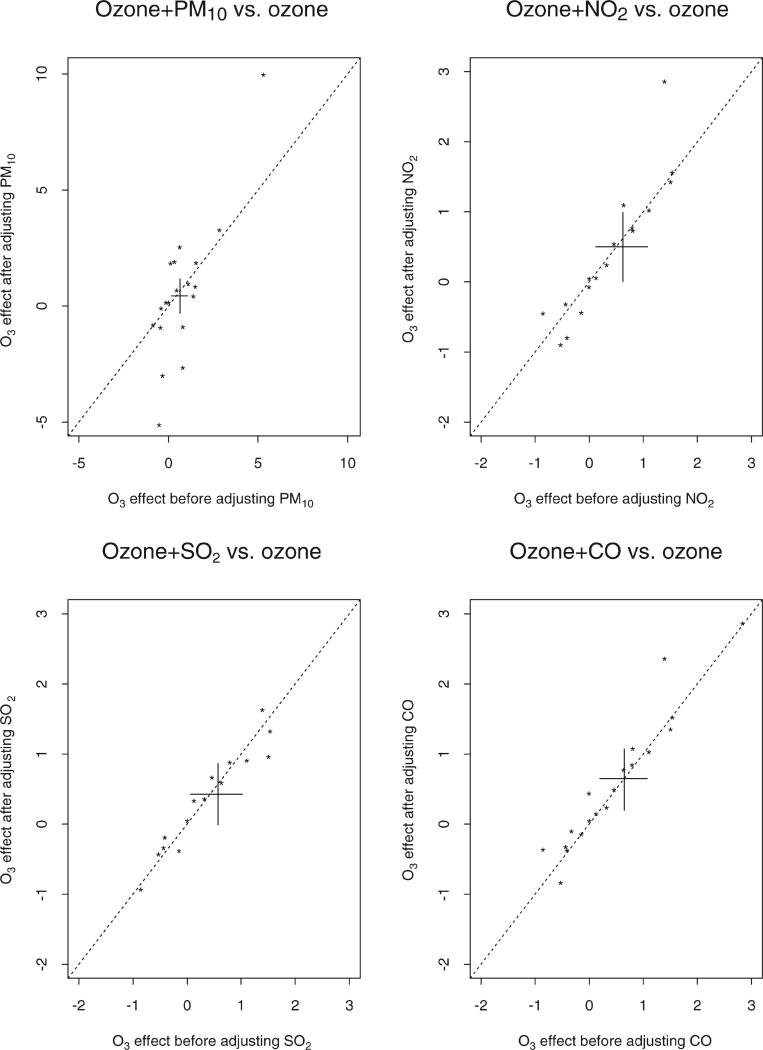
Figure 5 shows the robustness of the city-specific estimates to the inclusion of other pollutants in the model. At each panel, two sets of city-specific estimates for ozone at lag 2 are plotted against each other. On the x-axes, the estimates do not include any adjustment for other pollutants, whereas the estimates on the y-axes are adjusted for one additional pollutant. The cross mark corresponds to the overall estimates and their 95 per cent posterior regions. Notice that, except when PM₁₀ is included in the model, the two sets of estimates and their averages are very close to the diagonal line, indicating very little sensitivity of the ozone effect to the inclusion of gaseous pollutants into the model. City-specific ozone estimates vary with the adjustment for PM₁₀; however, on average the ozone effect estimate remains positive and significant. Since PM₁₀ measurements are available only every 1 to 6 days and only the days with available PM₁₀ measures are included in the analysis, the sensitivity of the ozone health effects to the inclusion of PM₁₀ in the model might indicate a true confounding effect or might be attributed to higher statistical uncertainty due to the lack of daily PM₁₀ measurements. The average relative rates under the several bi-pollutant models are summarized in Table 3.

Figure 5.

City-specific ozone relative rates estimates at lag 2 adjusted by another pollutant (PM₁₀, NO₂, SO₂ or CO), plotted against ozone relative rates estimates at lag 2. The cross is plotted corresponding to the two overall relative rates (adjusted versus unadjusted) and their 95 per cent posterior regions

Table 3.

Percentage increase in CVDRESP mortality associated with a 10ppb increase in ozone, adjusting for co-pollutants (95 per cent posterior regions)

O3 effect	O3	O3 + PM10	O3 + NO2	O3 + SO2	O3 + CO
O3 lag 0	0.73 (0.27, 1.19)	0.74 (–0.33, 1.72)	0.60 (0.11, 1.10)	0.51 (0.01, 1.03)	0.69 (0.20, 1.18)
O3 lag 1	0.70 (0.26, 1.12)	0.69 (–0.01, 1.38)	0.63 (0.15, 1.12)	0.49 (0.06, 0.95)	0.65 (0.21, 1.08)
O3 lag 2	0.64 (0.17, 1.07)	0.46 (–0.32, 1.17)	0.50 (0.01, 0.099)	0.42 (–0.01, 0.86)	0.65 (0.20, 1.07)

Note: All pollutants and ozone are at the same lag structure. The availability of PM₁₀ measurements is only every 1 to 6 days; Seattle and San Antonio do not have any NO₂ measurements; Miami, Seattle, San Jose, Oakland and San Antonio do not have any SO₂ measurements

To assess the confounding effect of heat waves, we fit the distributed lag model within each city by including a smooth function of interaction between current day temperature and average temperature in the last three days. The average relative rate is robust to the inclusion of this interaction term and moved from 1.25, 95 per cent posterior regions (0.47, 2.03) to 1.11,95 per cent posterior regions (0.38, 1.86), as listed in Table 4.

Table 4.

Percentage increase in CVDRESP mortality associated with a 10ppb increase in ozone, adjusting for heat wave (95 per cent posterior regions)

O3 effect	O3	O3 + heat wave
Distributed lag (DL)	1.25 (0.47, 2.03)	1.11 (0.38, 1.86)

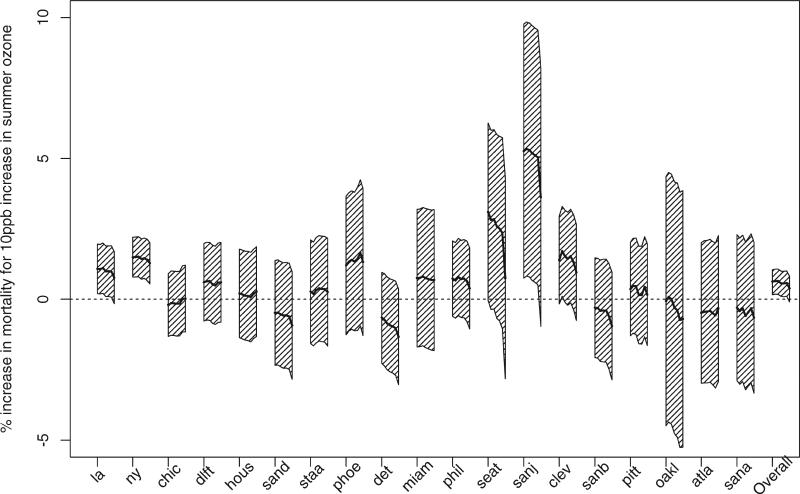
Figure 6 shows the robustness of ozone effects at lag 2 to the degrees of freedom in the smooth functions of time. More specifically, the midline of each box denotes the relative rate estimates as we vary the number of degrees of freedom in the smooth function of time from 4 to 16 with increasing step = 2, and the polygon captures the corresponding confidence intervals. The polygon at the far right shows the posterior means of the overall relative rates and their 95 per cent posterior regions. The picture shows that the average relative rate estimates are somewhat sensitive to the selection of the number of degrees of freedom in the smooth function of time.

Figure 6.

Sensitivity analysis of the city-specific effects at lag 2 with respect to the degrees of freedom in the smooth functions of time. The number of degrees of freedom vary from 4 to 16 with increasing step = 2. Each polygon captures the change in the city-specific relative rates estimates with their corresponding 95 per cent confidence intervals. The last polygon captures the change of overall ozone effect estimates with its 95 per cent posterior regions

In summary, we found strong evidence of associations between short-term summer exposure to ozone and CVDRESP mortality on average across 19 large cities in the U.S. We found that this association persists at different lags and it is robust to the adjustment for long-term trend, temperature, heat waves, and other pollutants.

5. DISCUSSION

In this article, we extend modelling approaches developed as part of the NMMAPS by introducing Bayesian hierarchical distributed lag models with non-normal random effects distributions for estimating associations between short-term variations in ozone and CVDRESP mortality. On average across the 19 large cities in the U.S., we found that a 10ppb increase in summer ozone levels over the previous week is associated with a 1.25 per cent increase in CVDRESP mortality (95 per cent posterior region: 0.47, 2.03). Results were robust to: (i) distributional assumptions on the random effects distribution; (ii) inclusion of other gaseous pollutants (CO, SO₂ and NO₂) in the model; (iii) potential confounding effects of long-term trend, temperatures, and heat waves; (iv) lag specification; and (v) prior distributions.

Our methods have recently been applied to a more extensive NMMAPS analysis on ozone and mortality, which includes 95 large cities in the U.S. for the period 1987–2000 (Bell et al., 2004). While this article focuses on summer mortality, Bell et al. (2004) focuses on yearly mortality. These more extensive ozone analyses found a strong association between short-term variations in ozone and mortality. In fact, Bell et al. (2004) report a national average equal to 0.64 per cent (95 per cent posterior region: 0.31, 0.98) in CVDRESP mortality for a 10ppb increase in the preceding week's ozone levels, using a constrained distributed lag model.

Our results provide additional evidence in support of an association between ozone and mortality and are consistent with the literature. Epidemiological studies have found associations between low ozone levels and: (i) decline in pulmonary functions (Galizia and Kinney, 1999; Folinbee et al., 1988; Kinney et al., 1996; Devlin et al., 1991); (ii) increase in hospital admissions for asthma, especially among children (Stern et al., 1994; Galizia and Kinney, 1999); and (iii) congestive heart failure among the elderly (Burnett et al., 1997b). Positive associations between short-term 1-h maximum ozone levels and mortality, adjusted for the potential confounding effects of other pollutants and weather, have been found in Los Angeles and New York (Kinney and Ozkaynak, 1991; Kinney et al., 1996). In addition, a multi-site time-series study of 16 Canadian cities showed a significant positive association between respiratory admissions and summer daily 1-h maximum ozone levels at lag 1 (Burnett et al., 1997a).

The strengths of our approach are: (i) the use of routinely collected data on air pollution, mortality and weather; (ii) the implementation of Bayesian hierarchical models for combining information across locations and for estimating the average relative rate accounting for within-city statistical uncertainty and heterogeneity of the effects across locations; and (iii) the systematic assessment of the sensitivity of findings to adjustment for confounding bias and model choice.

This analysis has the following limitations. First, the 24-h daily average of hourly ozone measurements is used as the exposure variable. Because of the volatile nature of ozone, with the maximum generally appearing in the early afternoon and lowest levels at night, the 24-h average might not be an adequate summary measure of the ozone exposure. Therefore additional work is needed to explore the sensitivity of our results with respect to other summary measures, such as the daily 1-h and 8-h maxima. Bell et al. (2004) investigated multiple metrics of ozone concentration, and found all to be significantly associated with mortality. Second, we use ambient levels of ozone as a surrogate for exposure without taking into account potential exposure measurement error. Third, our model-based methods for adjusting for confounders, although extensive, cannot completely rule out confounding bias in the estimated associations. In this article we used 1 degree of freedom per summer to adjust for trend. Therefore the lack of a more severe adjustment for long-term trend might have biased some of our relative rate estimates. However, when we repeated the analyses by using 2 degrees of freedom per summer, we still found a positive association between ozone and mortality with a national average estimate equal to 0.93 per cent (95 per cent posterior region: (–0.06, 1.99)). Unfortunately, no data-driven method exists to estimate an optimal number of degrees of freedom for removing confounding due to long-term trends. This issue has been discussed extensively by Dominici et al. (2004). Fourth, the association between ozone and mortality might also be confounded by other pollutants which are not currently measured in NMMAPS. For example, ozone contributes to the secondary formation of organic aerosols, which are a large source of ultra-fine particles (Andreae and Crutzen, 1997; Seinfeld and Flagan, 1997).

These results provide evidence to policy-makers on the harmful effects of ozone on human health. Such epidemiological evidence is central to the regulatory process, including the setting of the National Ambient Air Quality Standards (NAAQS) for ozone. Regulations are designed to protect human health with an adequate margin of safety for susceptible populations, such as those with cardiovascular or respiratory disease. This research extends earlier time-series analysis and indicates that summer ozone levels adversely impact cardiovascular and respiratory mortality.

APPENDIX 1

To illustrate why the log-relative rate θ^c can be interpreted as the percentage increase in CVDRESP associated with a 10ppb increase in summer ozone levels over the previous week, we consider the following:

$$\begin{array}{c}\hfill \text{log}{\mu }_t^c=\sum _{l=0}^6{\beta }_{\ell }^c{x}_{t-\ell }^c+\text{all other covariates}\hfill \\ \hfill \text{log}{\mu }_t^{c^{\ast }}=\sum _{l=0}^6{\beta }_{\ell }^c(x_{t-\ell }^c+1)+\text{all other covariates}\hfill \\ \hfill \text{log}{\mu }_t^{c^{\ast }}-\text{log}{\mu }_t^c=\text{log}\frac{{\mu }_t^{c^{\ast }}}{{\mu }_t^c}=\sum _{l=0}^6{\beta }_{\ell }^c={\theta }^c\hfill \end{array}$$

$$\begin{array}{cc}\hfill \frac{{\mu }_t^{c^{\ast }}}{}=e^{\theta c}& \approx 1+{\theta }^c,1\text{st-order approximation using Taylor expansion}\hfill \\ \hfill \frac{{\mu }_t^{c^{\ast }}-{\mu }_t^c}{{\mu }_t^c}& \approx {\theta }^c\hfill \\ \hfill 100\times \frac{{\mu }_c^{c^{\ast }}-{\mu }_t^c}{{\mu }_t^c}& \approx (1000\times {\theta }^c)∕10\hfill \end{array}$$

In summary, 1000 × θ^c, which is consistently reported in the article, indicates the percentage increase in CVDRESP mortality associated with 10ppb increasing in summer ozone levels every day for the previous week. This interpretation used in this article is consistent with other time series studies published in the literature (Moolgavkar, 2000; Zeghnoun et al., 1990; Goldberg et al., 2001).

APPENDIX 2

model {
for (i in 1:N) {
ozone[i]< -y[i,1]
sigma[i]< -y[i,2]
prec[i]< -1/(sigma[i]*sigma[i])
ozone[i]~dnorm(beta[i],prec[i])
beta[i]~dnorm(mu,tau)
}
mu~dnorm(0,0.0001)
tau~dgamma(0.01,0.01)
sig.O< -1/sqrt(tau)
} ##mixture of two normal distributions
model { for (i in 1:N) {
ozone[i]< -y[i,1]
sigma[i]< -y[i,2]
prec[i]< -1/(sigma[i]*sigma[i])
ozone[i]~dnorm(beta[i],prec[i])
beta[i]~dnorm(mu[i], tau)
mu[i]< -lambda[T[i]]
T[i]~dcat(P[])
}
P[1:2]~ddirch(alpha[])
theta~dnorm(4, 1.0E-6)I(0.0,)
lambda[2]< -lambda[1]+theta
lambda[1]~dnorm(–2, 1.0E-6)
tau~dgamma(0.001, 0.001)
sig.O< -1/sqrt(tau)
tot< -P[1]*lambda[1]+P[2]*lambda[2]
}