Abstract
Complete genome sequences contain valuable information about natural selection, but this information is difficult to access for short, widely scattered noncoding elements such as transcription factor binding sites or small noncoding RNAs. Here, we introduce a new computational method, called Inference of Natural Selection from Interspersed Genomically coHerent elemenTs (INSIGHT), for measuring the influence of natural selection on such elements. INSIGHT uses a generative probabilistic model to contrast patterns of polymorphism and divergence in the elements of interest with those in flanking neutral sites, pooling weak information from many short elements in a manner that accounts for variation among loci in mutation rates and coalescent times. The method is able to disentangle the contributions of weak negative, strong negative, and positive selection based on their distinct effects on patterns of polymorphism and divergence. It obtains information about divergence from multiple outgroup genomes using a general statistical phylogenetic approach. The INSIGHT model is efficiently fitted to genome-wide data using an approximate expectation maximization algorithm. Using simulations, we show that the method can accurately estimate the parameters of interest even in complex demographic scenarios, and that it significantly improves on methods based on summary statistics describing polymorphism and divergence. To demonstrate the usefulness of INSIGHT, we apply it to several classes of human noncoding RNAs and to GATA2-binding sites in the human genome.
Keywords: molecular evolution, population genetics, noncoding DNA, regulatory sequences, probabilistic graphical models
Introduction
Evolutionary modeling has become an essential tool in genomic analysis, particularly for the study of noncoding elements in eukaryotes, which tend to be sparsely annotated, poorly understood, and difficult to examine experimentally. So far, most evolutionary analyses of such elements have been based on patterns of sequence divergence between genomes that diverged millions of years ago (Boffelli et al. 2003; Thomas et al. 2003; Cooper et al. 2005; Siepel et al. 2005; Pollard et al. 2010). However, numerous confounding factors limit the utility of this approach. For example, evolutionary “turnover” (gain and loss of functional elements) can be prominent on these time scales (Dermitzakis and Clark 2002; Moses et al. 2006) and can distort patterns of sequence divergence. In addition, positive and negative selection can sometimes act on the same sequences and have partially canceling effects on divergence. Finally, technical challenges such as orthology identification and genomic alignment are nontrivial on these time scales, and errors in these procedures can produce spurious inferences of natural selection.
In principle, data describing genetic polymorphism within species could help to address these limitations. Patterns of polymorphism reflect evolutionary processes on relatively short timescales, during which turnover should be much less prevalent. Orthology identification and alignment are also much more straightforward on these time scales. Furthermore, it is well known that patterns of polymorphism within a species and divergence between species can be used to tease apart the signatures of positive and negative selection (McDonald and Kreitman 1991; Sawyer and Hartl 1992; Bustamante et al. 2005).
In practice, however, it is technically challenging to extract useful information about natural selection from patterns of polymorphism and divergence in noncoding elements. Many of the elements of interest, such as transcription factor binding sites and small noncoding RNAs, are quite short (at most tens of bases in length), and polymorphisms tend to be sparse. As a result, many elements of interest typically contain no informative sites whatsoever, whereas most others contain just one or two. This problem can be addressed by pooling data from multiple elements (Andolfatto 2005), but variation across loci in mutation rates and coalescence times can lead to difficulties in interpreting such pooled data sets (Smith and Eyre-Walker 2002; Stoletzki and Eyre-Walker 2011). Finally, the confounding influence of demography on patterns of polymorphism is a persistent problem when attempting to draw conclusions about natural selection (Nielsen et al. 2007).
Here, we describe a new computational method, called Inference of Natural Selection from Interspersed Genomically coHerent elemenTs (INSIGHT), that is designed to address these challenges. INSIGHT uses the general strategy of contrasting patterns of polymorphism and divergence in a collection of elements of interest with those in flanking neutral regions, thereby mitigating biases from demography, variation in mutation rates, and differences in coalescence time. In this way, it resembles McDonald–Kreitman (MK)-based methods for identifying departures from neutrality (McDonald and Kreitman 1991; Sawyer and Hartl 1992; Smith and Eyre-Walker 2002; Andolfatto 2005). Unlike these methods, however, INSIGHT is based on a generative probabilistic model, accommodates weak negative (WN) selection (Charlesworth and Eyre-Walker 2008), and allows diffuse information from many short elements across the genome to be pooled efficiently, in a manner that avoids statistical pitfalls arising from pooling counts of site classes. Our modeling approach also fully integrates phylogenetic information from multiple outgroup species with genome-wide population genetic data.
The main purpose of this article is to detail the probabilistic model and inference strategy underlying the INSIGHT method. We also compare our full probabilistic model with summary-statistic-based methods similar to those used in a number of previous polymorphism-and-divergence studies (Fay et al. 2001; Smith and Eyre-Walker 2002; Andolfatto 2005), demonstrating several advantages of our methods across a range of simulation parameters. In a parallel submission (Arbiza L, Gronau I, Aksoy BA, Hubisz MJ, Gulko B, Keinan A, Siepel A, in revision), we report the use of INSIGHT in a large-scale analysis of transcription factor binding sites in the human genome, based on chromatin-immunoprecipitation-and-sequencing (ChIP-seq) data for 78 human transcription factors (Dunham et al. 2012). Here, we further demonstrate the breadth of applicability of the method by applying it to several classes of human noncoding RNAs and using it to carry out a position-specific analysis of GATA2-binding sites in the human genome.
Materials and Methods
General Approach
The central goal of INSIGHT is to characterize the aggregate influence of natural selection on a collection of elements having some arbitrary genomic distribution (fig. 1). The collection of elements is assumed to be reasonably homogeneous and coherent but can be defined in many different ways. For example, it might include all binding sites of a particular transcription factor, all noncoding RNAs of a particular type, all binding sites near genes of a particular functional category, or all paired bases in a group of RNAs (see Discussion). We assume the individual elements are fairly short, ranging from a single nucleotide to perhaps a few hundred bases in length. The key modeling challenge is to integrate sparse information from many such elements in a manner that accounts for variation along the genome in properties such as mutation rate and coalescence time. Rather than attempting to fully describe the relationships among selection, polymorphism, and divergence—which is complex and demography-dependent—our model works by contrasting patterns of polymorphism and divergence in the elements of interest with those in nearby neutral sites.
Fig. 1.
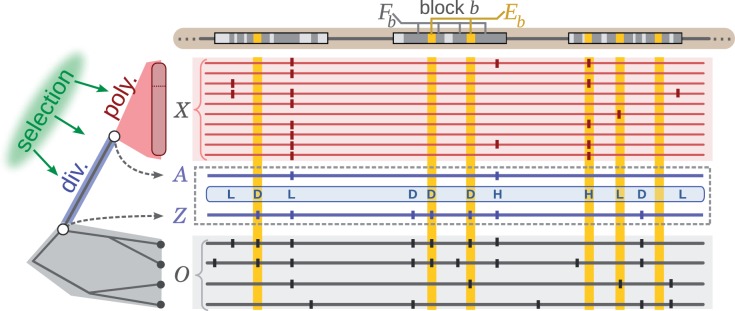
Schematic description of INSIGHT. The method measures the influence of natural selection by contrasting patterns of polymorphism and divergence in a collection of genomic elements of interest (gold) with those in flanking neutral sites (dark gray). Nucleotide sites in both elements (Eb) and flanks (Fb) are grouped into genomic blocks of a few kilobases in length (b) to accommodate variation along the genome in mutation rate and coalescence time. The model consists of phylogenetic (gray), recent divergence (blue), and intraspecies polymorphism (red) components, which are applied to genome sequences for the target population (X, red) and outgroup species (O, gray). At each nucleotide position, the alleles at the MRCA of the samples from the target population (A) and of the target population and closest outgroup (Z) are represented as hidden variables and treated probabilistically during inference. The allele Z determines whether monomorphic sites are considered to be divergent (D). Polymorphic sites are classified as having low- (L) or high- (H) frequency–derived alleles based on A and a frequency threshold f. The labels shown here are based on a likely setting of Z and A. Vertical ticks represent single nucleotide variants relative to an arbitrary reference. Inference is based on differences in the patterns of polymorphism and divergence expected at neutral and selected sites.
We assume that genome-wide polymorphism data are available for a particular target population, in a form that allows polymorphic sites to be reliably distinguished from invariant sites and provides reasonably accurate information about allele frequencies. At present, this is most easily achieved using high-coverage individual genome sequences, although our methods could also be adapted to make use of statistically inferred genotype frequencies based on low-coverage sequence data (Yi et al. 2010). We further assume that genomic sequence data are available for one or more outgroup species. Although the method can be used with a single outgroup genome, better information about ancestral alleles can be obtained by using two or more minimally distant outgroups that diverged from one another prior to the divergence of either one from the target population.
We assume that each nucleotide site evolves according to one of four possible selective modes: neutral drift (neut), strong negative (SN) selection, WN selection, or positive selection (P). This coarse-grained, categorical approach to modeling the distribution of fitness effects (DFE) is motivated by observations indicating that the data contain only limited information about the full DFE (Boyko et al. 2008; Wilson et al. 2011). The key to our approach is that these four selective modes have qualitatively distinct effects on patterns of polymorphism and divergence (cf., Bierne and Eyre-Walker 2004). In particular, SN and positive selection will generally cause mutations to reach fixation or be lost rapidly, and therefore will mostly eliminate observable polymorphisms. By contrast, WN selection will allow polymorphisms to persist for longer periods of time, but will tend to hold derived alleles at low frequencies. In addition, negative selection (either strong or weak) will largely prohibit the eventual fixation of derived alleles. Therefore, we make the following three assumptions about nucleotide sites under selection: 1) only positively selected sites make nonnegligible contributions to divergence; 2) only WN sites make nonnegligible contributions to polymorphism; and 3) any polymorphisms must have low derived allele frequencies. (Neutral sites, of course, may also contribute to divergence and polymorphism.) Together, these assumptions allow the fraction of sites under selection to be estimated. As it turns out, they are not sufficient to fully disentangle the contributions of all four selective modes, but they do allow us to obtain indirect information about the contributions of positive and WN selection at selected sites (discussed later).
In addition, we classify every site as monomorphic (M), polymorphic with a
low-frequency–derived allele (L), or polymorphic with a high-frequency–derived
allele (H), where the distinction between L and H sites depends on a designated
low-frequency threshold f (typically 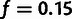 ).
Information about selection comes from the relative frequencies of these labels in the
elements of interest relative to the flanking neutral sites, together with patterns of
divergence with respect to the outgroup genomes. A minor complication is that in some
cases, the derived allele class depends on the ancestral allele, which is not known. We
address this problem by treating the ancestral allele as a hidden (latent) random variable
and integrating over possible values as needed. The use of this low-dimensional projection
of the SFS is intended to buffer our method from the effects of recent demographic changes
in the target population. In the simulation analyses reported later, we examine the extent
to which our inferences are robust to demography. We also examine their dependence on the
threshold f.
).
Information about selection comes from the relative frequencies of these labels in the
elements of interest relative to the flanking neutral sites, together with patterns of
divergence with respect to the outgroup genomes. A minor complication is that in some
cases, the derived allele class depends on the ancestral allele, which is not known. We
address this problem by treating the ancestral allele as a hidden (latent) random variable
and integrating over possible values as needed. The use of this low-dimensional projection
of the SFS is intended to buffer our method from the effects of recent demographic changes
in the target population. In the simulation analyses reported later, we examine the extent
to which our inferences are robust to demography. We also examine their dependence on the
threshold f.
Probabilistic Model
Our model assumes that the genomic regions under study are partitioned into a collection
of blocks, B. The nucleotide sites within each block
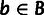 are further partitioned into sites within
the elements of interest, Eb, and the associated neutral
flanking sites, Fb (cumulatively E and
F, respectively). Each block is assigned a population-scaled mutation
rate (
are further partitioned into sites within
the elements of interest, Eb, and the associated neutral
flanking sites, Fb (cumulatively E and
F, respectively). Each block is assigned a population-scaled mutation
rate (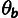 ), a neutral divergence scale factor
(
), a neutral divergence scale factor
(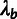 ), and an outgroup divergence scale factor
(
), and an outgroup divergence scale factor
(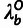 ). In addition, the model has four global
parameters: the fraction of sites under selection in elements (ρ),
the relative divergence (η) and polymorphism
(γ) rates at selected sites, and
). In addition, the model has four global
parameters: the fraction of sites under selection in elements (ρ),
the relative divergence (η) and polymorphism
(γ) rates at selected sites, and 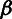 ,
a multivariate parameter summarizing the neutral site frequency spectrum (table 1). The full set of parameters is denoted
by
,
a multivariate parameter summarizing the neutral site frequency spectrum (table 1). The full set of parameters is denoted
by 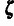 .
.
Table 1.
Model Parameters.
| Parameter | Type | Description |
|---|---|---|
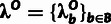 |
Neutral | Block-specific neutral scaling factor for the outgroup portion of
the phylogeny, used when computing the prior distributions for the deep
ancestral allele 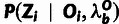 . . |
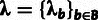 |
Neutral | Block-specific neutral scaling factor for divergence. |
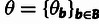 |
Neutral | Block-specific neutral polymorphism rate. |
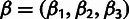 |
Neutral | Relative frequencies of the three derived allele frequency
classes, 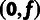 , , 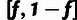 , and , and 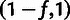 , within neutral polymorphic sites. , within neutral polymorphic sites. |
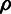 |
Selection | Fraction of sites under selection within functional elements. |
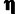 |
Selection | Ratio of divergence rate at selected sites to local neutral divergence rate. |
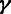 |
Selection | Ratio of polymorphism rate at selected sites to local neutral polymorphism rate. |
Each site i is associated with a set of aligned bases from the outgroup
genomes (Oi) and the polymorphism data for the target
population (Xi). Xi is further
summarized as 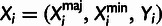 , where
, where 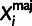 and
and 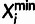 are the observed major and minor alleles,
and
are the observed major and minor alleles,
and 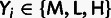 is the minor allele frequency class
(
is the minor allele frequency class
(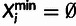 when
when 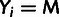 ).
The entire data set is denoted by
).
The entire data set is denoted by 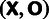 .
Yi is defined by the observed minor allele frequency
mi and the specified low-frequency threshold,
.
Yi is defined by the observed minor allele frequency
mi and the specified low-frequency threshold,
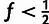 ; in particular,
; in particular,
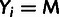 when
when 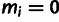 ,
,
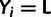 when
when  ,
and
,
and 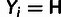 when
when 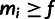 .
Note that the minor allele frequency is observed, whereas the derived allele frequency
depends on the identity of the hidden population ancestral allele
(Ai) and is thus inferred probabilistically by the model.
Sites with three or more alleles are discarded in preprocessing. Each site is also
associated with three hidden variables: a selection class (
.
Note that the minor allele frequency is observed, whereas the derived allele frequency
depends on the identity of the hidden population ancestral allele
(Ai) and is thus inferred probabilistically by the model.
Sites with three or more alleles are discarded in preprocessing. Each site is also
associated with three hidden variables: a selection class ( ), a “deep” ancestral allele at the most recent common
ancestor (MRCA) of the target population and closest outgroup
(Zi), and a population ancestral allele
(Ai) (table
2).
), a “deep” ancestral allele at the most recent common
ancestor (MRCA) of the target population and closest outgroup
(Zi), and a population ancestral allele
(Ai) (table
2).
Table 2.
Model Variables Associated with Site i.
| Variable | Type | Description |
|---|---|---|
| Oi | Observed | Set of aligned bases from outgroup species |
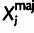 |
Observed | Base for major allele in target population |
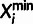 |
Observed | Base for minor allele in target population
( for monomorphic sites) for monomorphic sites) |
| Yi | Observed | MAF class for site i: “M” for monomorphic sites (MAF = 0) |
“L” for
polymorphic sites with MAF 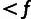
| ||
“H” for
polymorphic sites with MAF 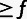
| ||
| Si | Hidden | Selection class: “ ” for neutral sites ” for neutral sites |
“ ” for sites under selection ” for sites under selection | ||
| Zi | Hidden | Ancestral allele at the MRCA of the target |
| Population and the closest outgroup | ||
| Ai | Hidden | Ancestral allele at the MRCA of samples from the target population |
We assume independence of blocks, conditional independence of the nucleotide sites within each block given the model parameters, conditional independence of the variables describing the target population (Ai, Si, and Xi) from the outgroups (Oi) given the deep ancestral allele (Zi), and independence of the site-wise selection classes (Si), as shown graphically in figure 2. The same graphical model applies to all sites, except that the selection class is fixed to “neut” for the flanking sites. Thus, a likelihood function for the model, conditional on the outgroup data, can be written as follows:
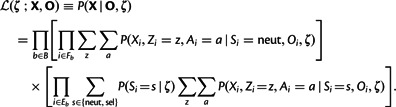 |
(1) |
Furthermore, each term of the form 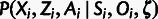 can be factorized as follows:
can be factorized as follows:
| (2) |
Fig. 2.
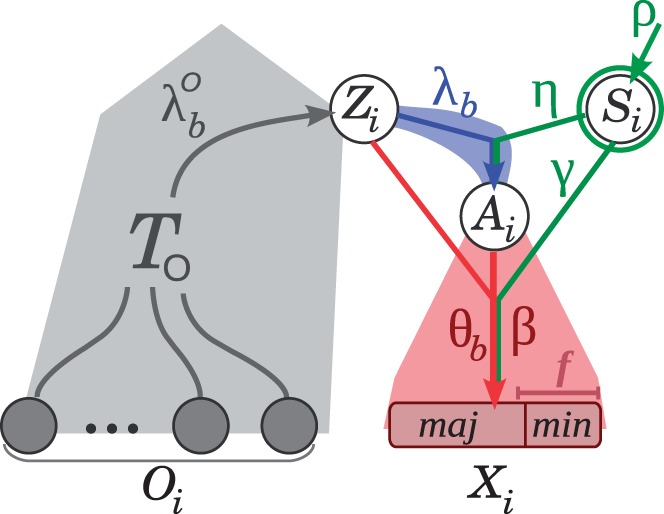
Graphical model for an
individual nucleotide site i. As in figure 1, the phylogenetic portion of the model is shown in
gray, the divergence component in blue, and the polymorphism component in red.
Observed variables are represented by solid circles and hidden variables by empty
circles. The observed alleles in the target population and outgroups are represented
by Xi and Oi, respectively.
Xi consists of a major
( ) and minor
(
) and minor
( ) allele, as well as the minor allele
frequency class (Yi; not shown). The selection class is
denoted Si, and the ancestral alleles are denoted
Zi and Ai, as described
in figure 1. Conditional dependence
between the variables is indicated by directed edges, in the standard manner for
probabilistic graphical models. Model parameters are shown alongside the associated
conditional dependency edges. The selection parameters
) allele, as well as the minor allele
frequency class (Yi; not shown). The selection class is
denoted Si, and the ancestral alleles are denoted
Zi and Ai, as described
in figure 1. Conditional dependence
between the variables is indicated by directed edges, in the standard manner for
probabilistic graphical models. Model parameters are shown alongside the associated
conditional dependency edges. The selection parameters
 are highlighted in
green.
are highlighted in
green.
This likelihood function is composed of four conditional probability distributions, corresponding to the variables Si, Zi, Ai, and Xi. The distribution for Si is needed only for element sites and is given by a two-component mixture model with coefficient ρ:
| (3) |
The conditional distribution for Zi given the outgroup data,
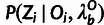 , is based on a standard statistical
phylogenetic model and is computed using existing software. Notice that our model assumes
that the phylogenetic model for the outgroups is independent of the selection class,
Si. This assumption is not strictly warranted (sites under
selection are likely to evolve at different rates in the outgroups), but it dramatically
simplifies the inference procedure by allowing us to pre-estimate the outgroup scale
factors (
, is based on a standard statistical
phylogenetic model and is computed using existing software. Notice that our model assumes
that the phylogenetic model for the outgroups is independent of the selection class,
Si. This assumption is not strictly warranted (sites under
selection are likely to evolve at different rates in the outgroups), but it dramatically
simplifies the inference procedure by allowing us to pre-estimate the outgroup scale
factors (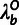 ) and the site-wise distributions for
Zi (see Parameter Inference). In practice, this
simplifying assumption is of little consequence, because it only affects the prior
distribution for Zi, which is fairly insensitive to
evolutionary rates in outgroup lineages as long as the branches of the phylogeny are not
too long.
) and the site-wise distributions for
Zi (see Parameter Inference). In practice, this
simplifying assumption is of little consequence, because it only affects the prior
distribution for Zi, which is fairly insensitive to
evolutionary rates in outgroup lineages as long as the branches of the phylogeny are not
too long.
The third conditional distribution, 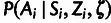 ,
describes the process of sequence divergence on the lineage leading to the target
population. Given a global neutral branch length t for this lineage (in
substitutions per site), we assume a nucleotide substitution rate of
,
describes the process of sequence divergence on the lineage leading to the target
population. Given a global neutral branch length t for this lineage (in
substitutions per site), we assume a nucleotide substitution rate of
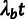 for neutral sites and
for neutral sites and
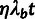 for sites under selection. Note that
η can be driven downward by negative selection or upward by
positive selection, so that it may be greater or less than one, depending on the DFE.
Because we are primarily interested in cases in which t is quite small
(e.g.,
for sites under selection. Note that
η can be driven downward by negative selection or upward by
positive selection, so that it may be greater or less than one, depending on the DFE.
Because we are primarily interested in cases in which t is quite small
(e.g., 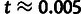 for the case of humans and chimpanzees), we
use the following approximation for the probability of divergences under a Poisson
substitution model:
for the case of humans and chimpanzees), we
use the following approximation for the probability of divergences under a Poisson
substitution model:
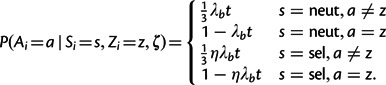 |
(4) |
Finally, the fourth conditional distribution, 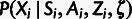 ,
describes the patterns of polymorphism in the target population given the ancestral
alleles and selection class. The definition of this distribution is somewhat more
involved. Briefly, we assume that the neutral polymorphism rate for each genomic block
b is determined by a block-specific population-scaled mutation rate,
,
describes the patterns of polymorphism in the target population given the ancestral
alleles and selection class. The definition of this distribution is somewhat more
involved. Briefly, we assume that the neutral polymorphism rate for each genomic block
b is determined by a block-specific population-scaled mutation rate,
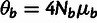 , which allows the model to accommodate both
variable mutation rates and selection from linked sites (background selection or
hitchhiking). The probability of observing a polymorphic nucleotide position is taken to
be
, which allows the model to accommodate both
variable mutation rates and selection from linked sites (background selection or
hitchhiking). The probability of observing a polymorphic nucleotide position is taken to
be 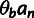 , where n is the number of
haploid genomes sampled and
, where n is the number of
haploid genomes sampled and 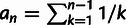 (Watterson 1975). In the absence of
missing data, an is a constant of no consequence in the
inference procedure, but it can be used to accommodate sites with small amounts of missing
genotype data if desired (see Discussion and supplementary methods, Supplementary Material online). Given a neutral polymorphism, the
probabilities of low-, intermediate-, and high-frequency–derived allele are given by
(Watterson 1975). In the absence of
missing data, an is a constant of no consequence in the
inference procedure, but it can be used to accommodate sites with small amounts of missing
genotype data if desired (see Discussion and supplementary methods, Supplementary Material online). Given a neutral polymorphism, the
probabilities of low-, intermediate-, and high-frequency–derived allele are given by
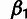 ,
, 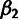 ,
and
,
and 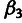 , respectively
(
, respectively
(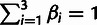 ). The situation is similar for sites under
selection, except that they are assumed to have population-scaled mutation rates of
). The situation is similar for sites under
selection, except that they are assumed to have population-scaled mutation rates of
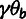 and only low-frequency derived alleles are
permitted. It is possible to derive closed-form expressions for this distribution for all
cases of interest (supplementary table S1, Supplementary Material online). In addition, the conditional distributions
and only low-frequency derived alleles are
permitted. It is possible to derive closed-form expressions for this distribution for all
cases of interest (supplementary table S1, Supplementary Material online). In addition, the conditional distributions
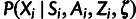 and
and 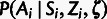 can be combined into a single conditional distribution table,
can be combined into a single conditional distribution table,
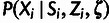 , by integrating over possible values of
Ai. This integration is simplified by assuming an infinite
sites model for the time since the population-level MRCA, which implies
, by integrating over possible values of
Ai. This integration is simplified by assuming an infinite
sites model for the time since the population-level MRCA, which implies
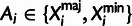 (table 3).
(table 3).
Table 3.
Conditional Distribution Table for
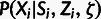 .
.
| S | y |
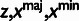 a a
|
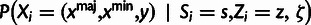 |
|---|---|---|---|
 |
M | 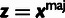 |
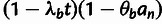 |
 |
M | 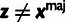 |
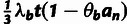 |
 |
L | 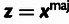 |
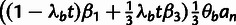 |
 |
L | 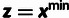 |
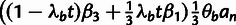 |
 |
L | 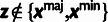 |
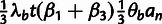 |
 |
H | 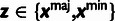 |
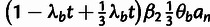 |
 |
H | 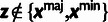 |
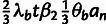 |
 |
M | 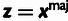 |
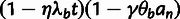 |
 |
M | 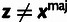 |
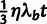 |
 |
L | 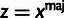 |
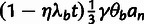 |
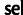 |
L | 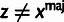 |
0 |
 |
H | — | 0 |
aRelationships among variables. It is implicit that
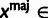 {A, C, G, T} and
{A, C, G, T} and
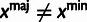 in all cases. In addition,
in all cases. In addition,
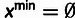 when
when 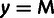 .
.
Parameter Inference
The main objective of the inference procedure is to produce maximum likelihood estimates
(MLEs) of the selection parameters, ρ, η, and
γ, but to do so, the neutral parameters
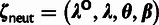 must also be estimated. In principle, an
expectation-maximization (EM) algorithm could be used to jointly estimate all model
parameters. However, this approach is impractical for genome-wide applications involving
millions of nucleotide sites. Instead, we take advantage of the “loose
coupling” between the phylogenetic outgroup model and the remaining portions of the
model, and between the portions of the model concerned with the elements and the flanking
sites, to decompose the inference procedure into separate stages, each of which can be
performed fairly simply and efficiently.
must also be estimated. In principle, an
expectation-maximization (EM) algorithm could be used to jointly estimate all model
parameters. However, this approach is impractical for genome-wide applications involving
millions of nucleotide sites. Instead, we take advantage of the “loose
coupling” between the phylogenetic outgroup model and the remaining portions of the
model, and between the portions of the model concerned with the elements and the flanking
sites, to decompose the inference procedure into separate stages, each of which can be
performed fairly simply and efficiently.
Our inference procedure is based on the observation that the likelihood function can be
expressed as a product of a function of the flanking sites and a function of the element
sites (eq. 1). The first function
depends only on the neutral parameters, whereas the second function depends on both the
neutral and the selection parameters. However, because the flanking sites are expected to
significantly outnumber the sites within the elements, the information about the neutral
parameters comes predominately from the first function, and they can be estimated to a
good approximation by maximizing this function only. The selection parameters can then be
estimated by conditionally maximizing the second function. By making some additional minor
simplifying assumptions, the first stage of inference can be further divided into two
separate steps, one concerned with estimation of the phylogenetic parameters,
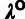 and
and 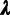 ,
and one concerned with estimation of the population genetic parameters,
,
and one concerned with estimation of the population genetic parameters,
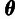 and
and 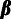 .
Our inference procedure thus consists of the following three distinct stages (supplementary methods, Supplementary Material online):
.
Our inference procedure thus consists of the following three distinct stages (supplementary methods, Supplementary Material online):
Phylogenetic Model Fitting: The divergence scale factors
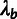 and
and 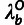 are estimated by fitting a pre-estimated neutral phylogenetic
model to putative neutral sites in each genomic block using standard phylogenetic
fitting procedures (Hubisz et al.
2011). The fitted phylogenetic model for the outgroup species is then used to
compute the prior distribution for ancestral alleles,
are estimated by fitting a pre-estimated neutral phylogenetic
model to putative neutral sites in each genomic block using standard phylogenetic
fitting procedures (Hubisz et al.
2011). The fitted phylogenetic model for the outgroup species is then used to
compute the prior distribution for ancestral alleles,
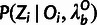 , at all sites in the
block.
, at all sites in the
block.Neutral Polymorphism Model Fitting: MLEs of the block-specific polymorphism rate parameters,
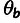 , and the global parameter
, and the global parameter 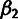 are obtained using simple closed-form expressions. Global
parameters
are obtained using simple closed-form expressions. Global
parameters 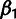 and
and 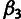 are estimated by a simple EM algorithm (they do not have
closed-form estimators due to ancestral uncertainty).
are estimated by a simple EM algorithm (they do not have
closed-form estimators due to ancestral uncertainty).Selection Inference: The selection parameters ρ, η, and γ are estimated conditional on the pre-estimated neutral parameters and ancestral priors by maximizing the likelihood of the element sites only by EM.
Extracting Information about the Modes of Selection
Although the INSIGHT model does not permit direct estimation of the fractions of sites
under WN, SN, or positive selection, the estimated model parameters can be used to obtain
indirect measures of the impact of WN and positive selection. A useful measure of positive
selection is 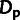 , the number of divergence events driven by
positive selection (sometimes called “adaptive substitutions”), and a similar
measure pertaining to WN selection is
, the number of divergence events driven by
positive selection (sometimes called “adaptive substitutions”), and a similar
measure pertaining to WN selection is 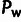 ,
the number of polymorphic sites subject to selection. Expected values for
,
the number of polymorphic sites subject to selection. Expected values for
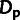 and
and 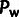 can be obtained by summing over site-wise posterior probabilities associated with the
variable configurations
can be obtained by summing over site-wise posterior probabilities associated with the
variable configurations 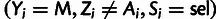 and
and 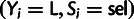 , respectively (supplementary methods, Supplementary Material online). To allow comparisons between sets of
different sizes, we normalize
, respectively (supplementary methods, Supplementary Material online). To allow comparisons between sets of
different sizes, we normalize  and
and 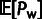 by dividing them by the total number of
nucleotide sites considered (in kilobases). By dividing
by dividing them by the total number of
nucleotide sites considered (in kilobases). By dividing 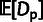 by the total (expected) number of divergences, one can alternatively obtain an estimate of
the fraction of substitutions driven by positive selection, a quantity known as
α (Smith and Eyre-Walker
2002; Andolfatto 2005) (supplementary methods, Supplementary Material online).
by the total (expected) number of divergences, one can alternatively obtain an estimate of
the fraction of substitutions driven by positive selection, a quantity known as
α (Smith and Eyre-Walker
2002; Andolfatto 2005) (supplementary methods, Supplementary Material online).
Confidence Intervals and Likelihood Ratio Tests
The probabilistic nature of the model allows us to estimate standard errors for the
estimated selection parameters using the curvature method (Lehmann and Casella 1998), based on an approximate Fisher
information matrix derived from the 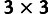 matrix of second derivatives for the log-likelihood function for ρ,
η, and γ (eq. 1) at the joint MLE (supplementary methods, Supplementary Material online). In addition, likelihood ratio tests (LRTs)
can be used to evaluate evidence for selection in general (
matrix of second derivatives for the log-likelihood function for ρ,
η, and γ (eq. 1) at the joint MLE (supplementary methods, Supplementary Material online). In addition, likelihood ratio tests (LRTs)
can be used to evaluate evidence for selection in general (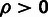 ), positive selection (
), positive selection (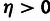 ), and WN selection (
), and WN selection (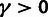 ). The LRTs are performed by fitting the model to the data twice, once
with no restrictions on the free parameters, and once with a parameter of interest fixed
at zero. Twice the difference in log likelihoods is then treated as a test statistic and
compared with an appropriate asymptotic distribution. The tests for
). The LRTs are performed by fitting the model to the data twice, once
with no restrictions on the free parameters, and once with a parameter of interest fixed
at zero. Twice the difference in log likelihoods is then treated as a test statistic and
compared with an appropriate asymptotic distribution. The tests for
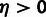 and
and 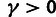 involve nested models in which the null hypothesis falls at a boundary of the alternative
hypothesis. The associated test statistics therefore have asymptotic null distributions
equal to a 50:50 mixture of a
involve nested models in which the null hypothesis falls at a boundary of the alternative
hypothesis. The associated test statistics therefore have asymptotic null distributions
equal to a 50:50 mixture of a 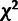 distribution with one degree of freedom and a point mass at zero (Chernoff 1954; Self and
Liang 1987). The case of ρ is more complex, because a value
of
distribution with one degree of freedom and a point mass at zero (Chernoff 1954; Self and
Liang 1987). The case of ρ is more complex, because a value
of 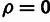 causes η and
γ to become irrelevant to the likelihood function. Therefore, we
used an empirical distribution to determine the cutoff for this LRT and found this to be
consistent with a
causes η and
γ to become irrelevant to the likelihood function. Therefore, we
used an empirical distribution to determine the cutoff for this LRT and found this to be
consistent with a 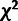 distribution with three degrees of freedom (see Results).
distribution with three degrees of freedom (see Results).
Implementation and Software
The INSIGHT software consists of several modules. The main module is a C program,
INSIGHT-EM, for the two EM algorithms used for inference: the main one for the selection
parameters and a simpler one for 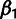 and
and 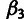 . The phylogenetic model fitting stage is
implemented separately using procedures from RPHAST (Hubisz et al. 2011), and additional scripts are used for
processing and filtering the polymorphism data. The INSIGHT website (http://compgen.bscb.cornell.edu/INSIGHT/, last accessed February 15, 2013)
provides source code, documentation, and sample files for running the EM algorithm. The
website also provides access to a server that can be used to run INSIGHT on any collection
of human genomic elements, using our precomputed summaries of human polymorphism data
(discussed later).
. The phylogenetic model fitting stage is
implemented separately using procedures from RPHAST (Hubisz et al. 2011), and additional scripts are used for
processing and filtering the polymorphism data. The INSIGHT website (http://compgen.bscb.cornell.edu/INSIGHT/, last accessed February 15, 2013)
provides source code, documentation, and sample files for running the EM algorithm. The
website also provides access to a server that can be used to run INSIGHT on any collection
of human genomic elements, using our precomputed summaries of human polymorphism data
(discussed later).
Estimators Based on Summary Statistics
For comparison with our model-based estimates, we made use of simple estimators for the
fraction of sites under selection (ρ) and the number of adaptive
substitutions (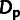 ). These estimators are based on the numbers
of polymorphisms in element and flanking sites, denoted PE and
PF, respectively, and the numbers of divergence events in
element and flanking sites, denoted DE and
DF, respectively. They include a divergence-based
estimator for ρ introduced by Kondrashov and Crow (1993),
). These estimators are based on the numbers
of polymorphisms in element and flanking sites, denoted PE and
PF, respectively, and the numbers of divergence events in
element and flanking sites, denoted DE and
DF, respectively. They include a divergence-based
estimator for ρ introduced by Kondrashov and Crow (1993),
| (5) |
a parallel estimator based on polymorphism rates,
| (6) |
and
an estimator for 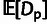 based on the McDonald and Kreitman (1991)
test, adapted from Smith and Eyre-Walker
(2002):
based on the McDonald and Kreitman (1991)
test, adapted from Smith and Eyre-Walker
(2002):
| (7) |
In comparison with our model-based estimates, the divergence-based estimator
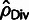 ignores the effect of positive selection,
and the estimators
ignores the effect of positive selection,
and the estimators 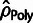 and
and 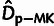 both implicitly assume that no
polymorphisms occur in selected sites, and thus ignore the effects of WN selection. All
three estimators share the limitation of pooling counts across elements in a manner that
does not account for variable mutation rates across loci.
both implicitly assume that no
polymorphisms occur in selected sites, and thus ignore the effects of WN selection. All
three estimators share the limitation of pooling counts across elements in a manner that
does not account for variable mutation rates across loci.
Simulations
We conducted a series of experiments on simulated data to assess the validity of our
modeling assumptions and to evaluate the accuracy of the inference method. Simulated
elements and flanking regions were generated with the forward simulator SFS_CODE (Hernandez 2008), assuming various mixtures of
selective modes for the elements. We simulated data for human populations and chimpanzee,
orangutan, and rhesus macaque outgroups, using parameters based on previous studies. Each
simulated block consisted of a 10 bp element, reflecting a typical binding site, and 5,000
flanking neutral sites on each side. We assumed a constant recombination rate and a
randomly varying mutation rate, and each nucleotide position was assigned to one of four
selection classes: neutral evolution (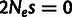 ), SN selection (
), SN selection (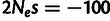 ), WN selection (
), WN selection (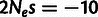 ), and positive selection (
), and positive selection (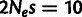 ). The choices of population-scaled selection coefficients were
approximately based on several other recent studies (Eyre-Walker et al. 2006; Boyko et al. 2008; Wilson et al.
2011). Selection at WN and SN sites was held constant across the phylogeny,
whereas for P sites, we assumed an interval of positive selection followed by WN selection
on the lineage leading to the human population, to simulate selective sweeps rather than
recurrent positive selection (see supplementary methods, Supplementary Material online, for complete details). The 10 kb flanking
sites were all assigned to the neutral class, and the 10 bp of each simulated element were
allocated among the four classes by multinomial sampling. When the simulation was done,
sequence data were extracted using a single haploid sample from each of the three outgroup
populations and 50 diploid samples from the target (human) population. In addition to
assuming a range of mixtures of selective modes, we considered collections with various
numbers of elements (ranging from 10,000 to 20,000), examined four different demographic
scenarios, and perturbed the selection coefficients used for each category of selection
(see supplementary methods, Supplementary Material online, for complete details).
). The choices of population-scaled selection coefficients were
approximately based on several other recent studies (Eyre-Walker et al. 2006; Boyko et al. 2008; Wilson et al.
2011). Selection at WN and SN sites was held constant across the phylogeny,
whereas for P sites, we assumed an interval of positive selection followed by WN selection
on the lineage leading to the human population, to simulate selective sweeps rather than
recurrent positive selection (see supplementary methods, Supplementary Material online, for complete details). The 10 kb flanking
sites were all assigned to the neutral class, and the 10 bp of each simulated element were
allocated among the four classes by multinomial sampling. When the simulation was done,
sequence data were extracted using a single haploid sample from each of the three outgroup
populations and 50 diploid samples from the target (human) population. In addition to
assuming a range of mixtures of selective modes, we considered collections with various
numbers of elements (ranging from 10,000 to 20,000), examined four different demographic
scenarios, and perturbed the selection coefficients used for each category of selection
(see supplementary methods, Supplementary Material online, for complete details).
The values of ρ, 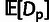 and
and 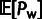 estimated by INSIGHT were compared with
“true” values for each simulation. The true value of ρ
was simply the fraction of sites assumed to be under selection during data generation. The
true value of
estimated by INSIGHT were compared with
“true” values for each simulation. The true value of ρ
was simply the fraction of sites assumed to be under selection during data generation. The
true value of 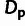 was taken to be the number of actual
divergence events that occurred in sites under positive selection. The true value of
was taken to be the number of actual
divergence events that occurred in sites under positive selection. The true value of
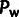 was taken to be the number of negatively
selected sites that are polymorphic. In computing this quantity, we allowed for both
strong and WN selection, because we are interested in accounting for all segregating
deleterious alleles, regardless of our modeling assumptions. For ρ
and
was taken to be the number of negatively
selected sites that are polymorphic. In computing this quantity, we allowed for both
strong and WN selection, because we are interested in accounting for all segregating
deleterious alleles, regardless of our modeling assumptions. For ρ
and 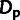 , we also compared our model-based estimates
with the simple estimates based on counts of polymorphic and divergent sites (eq. 5–7).
, we also compared our model-based estimates
with the simple estimates based on counts of polymorphic and divergent sites (eq. 5–7).
Analysis of Human Noncoding Genomic Elements
In our analysis of real data, we made use of the 69 individual human genome sequences recently released by Complete Genomics (http://www.completegenomics.com/public-data/69-Genomes/, last accessed February 15, 2013) (Drmanac et al. 2010), using data for 54 unrelated individuals. Although larger data sets are available (1000 Genomes Project Consortium 2010), this one was selected for its high coverage, which reduces the effect of genotyping error and allows singleton variants to be characterized with fairly high confidence. For outgroup genomes, we used the chimpanzee (panTro2), orangutan (ponAbe2), and rhesus Macaque (rheMac2) reference genomes. Various filters were applied to guarantee high quality alignments and variant calls (supplementary methods, Supplementary Material online). Putatively neutral sites were identified by excluding exons of known protein-coding and RNA genes plus 1 kb of flanking sites on each side, and previously predicted conserved noncoding elements plus flanking regions of 100 bp. After these filters were applied, an average of 3,881 sites per 10,000 bp block remained. Genomic blocks with <100 putative neutral sites were discarded.
We examined several classes of short interspersed noncoding elements in the human genome,
including several collections of regulatory noncoding RNAs and a collection of GATA2
transcription factor binding sites. Annotations for noncoding RNAs were taken from GENCODE
v.13 (Harrow et al. 2012) (supplementary methods, Supplementary Material online), and the GATA2-binding sites were identified
by a pipeline based on genome-wide chromatin immunoprecipitation and sequencing (ChIP-seq)
data from the ENCODE project (Dunham et al.
2012), as described separately (Arbiza L, Gronau I, Aksoy BA, Hubisz MJ, Gulko B,
Keinan A, Siepel A, in revision). To improve efficiency, we performed the phylogenetic
model fitting stage of our analysis in a preprocessing step. We fitted a neutral model
estimated from 4-fold degenerate sites to the predesignated neutral sites by estimating
two scale factors, one for the branch to the human genome
(λ) and one for the other branches in the tree
(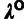 ; see Pollard et al. [2010] for details). This analysis assumed a (((human,
chimpanzee), orangutan), rhesus macaque) tree topology. The outgroup scale,
; see Pollard et al. [2010] for details). This analysis assumed a (((human,
chimpanzee), orangutan), rhesus macaque) tree topology. The outgroup scale,
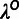 , was estimated globally using all neutral
sites genome-wide, and the human divergence scale,
, was estimated globally using all neutral
sites genome-wide, and the human divergence scale, 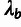 ,
was fitted separately in different genomic blocks. We used for this purpose a fixed set of
10 kb genomic windows overlapping by 5 kb and avoiding recombination hotspots. The same
blocks were used for estimating the neutral polymorphism rates,
,
was fitted separately in different genomic blocks. We used for this purpose a fixed set of
10 kb genomic windows overlapping by 5 kb and avoiding recombination hotspots. The same
blocks were used for estimating the neutral polymorphism rates,
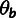 . After fitting the phylogenetic model, we
computed conditional distributions for the ancestral allele Zi
given the outgroup sequences at each nonfiltered nucleotide position i in
the genome. The estimates of
. After fitting the phylogenetic model, we
computed conditional distributions for the ancestral allele Zi
given the outgroup sequences at each nonfiltered nucleotide position i in
the genome. The estimates of 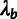 and
and 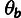 , and the distributions for
Zi, were recorded in a database and used in all subsequent
analyses.
, and the distributions for
Zi, were recorded in a database and used in all subsequent
analyses.
Results
Simulations
We applied INSIGHT to various collections of synthetic elements to assess its accuracy and to validate our modeling assumptions. This was done by comparing our model-based parameter estimates both with “true” values reflecting the simulated evolutionary histories and with values obtained using simpler estimators based on counts of polymorphisms and divergences (see Materials and Methods). We simulated data sets roughly similar to our real data (supplementary table S3, Supplementary Material online), with 10,000–20,000 blocks each consisting of a 10 bp element flanked by 5 kbp of neutral sequence on each side. We considered a range of mixtures of neutral, weak negative (WN), strong negative (SN), and positive (P) selection (see Materials and Methods).
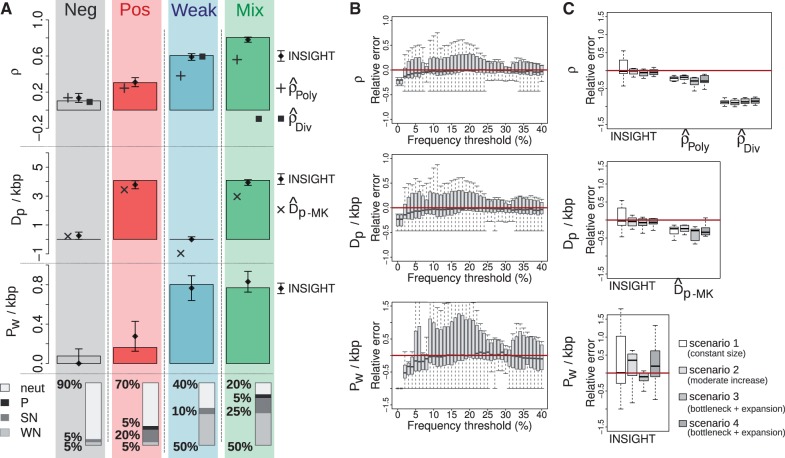
We started by examining four representative data sets (fig. 3A): 1) one with relatively few sites under
selection (10%) and negative selection only (“Neg”); 2) another with a
moderate fraction of sites under various types of selection (30%), including a
substantial fraction under positive selection (“Pos”); 3) another with a high
fraction of sites selection (60%), with mostly WN selection and no positive
selection (“Weak”); and, finally, 4) a set with a substantial fraction of
sites in each of the selective modes (“Mix”). We found that our model-based
estimates were within one standard error of the true values across all mixtures of
selective modes. The simple estimators also performed reasonably well in many cases, but
the divergence-based estimators for ρ were strongly biased by
positive selection (e.g., 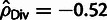 in Pos and
in Pos and 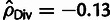 in Mix). The reason for this bias is that
these estimators implicitly attribute all divergence to neutral drift, an assumption that
is violated by nonnegligible levels of positive selection. Similarly, the
polymorphism-based estimator for ρ was biased downward in the
presence of WN selection (e.g.,
in Mix). The reason for this bias is that
these estimators implicitly attribute all divergence to neutral drift, an assumption that
is violated by nonnegligible levels of positive selection. Similarly, the
polymorphism-based estimator for ρ was biased downward in the
presence of WN selection (e.g., 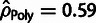 and
and 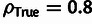 in Mix), because this estimator implicitly
assumes that selection completely eliminates polymorphism, which is not true in this case.
For similar reasons, the MK-based estimates of the number of adaptive divergences
(
in Mix), because this estimator implicitly
assumes that selection completely eliminates polymorphism, which is not true in this case.
For similar reasons, the MK-based estimates of the number of adaptive divergences
(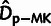 ) were also biased in the presence of WN
selection (Charlesworth and Eyre-Walker
2008).
) were also biased in the presence of WN
selection (Charlesworth and Eyre-Walker
2008).
Fig. 3.
Simulation
results. (A) Parameter estimates for four collections of 20,000
simulated elements based on different mixtures of neutral (neut), positive (P),
strong negative (SN), and weak negative (WN) selection (as indicated at bottom). The
true values of ρ, 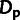 , and
, and 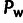 are indicated by solid bars, and estimates from INSIGHT are
indicated by diamonds, with error bars representing one standard error. For
comparison, estimates from several simpler count-based methods are also shown,
including estimates of ρ based on polymorphism
(
are indicated by solid bars, and estimates from INSIGHT are
indicated by diamonds, with error bars representing one standard error. For
comparison, estimates from several simpler count-based methods are also shown,
including estimates of ρ based on polymorphism
(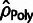 ; “+”) and divergence
(
; “+”) and divergence
(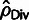 ; solid squares) rates, and estimates of
; solid squares) rates, and estimates of
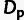 based on the MK framework
(
based on the MK framework
(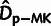 ; “×”). Adaptive
divergences (
; “×”). Adaptive
divergences (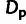 ) and deleterious polymorphisms
(
) and deleterious polymorphisms
(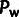 ) are shown as rates per 1,000 base
pairs (kbp). See Materials and Methods for details. (B) INSIGHT was
applied to 11 collections of 10,000 elements with various fractions of sites under
selection (see text), assuming a range of values for the low-frequency derived
allele threshold f. Relative estimation errors for
ρ,
) are shown as rates per 1,000 base
pairs (kbp). See Materials and Methods for details. (B) INSIGHT was
applied to 11 collections of 10,000 elements with various fractions of sites under
selection (see text), assuming a range of values for the low-frequency derived
allele threshold f. Relative estimation errors for
ρ, 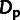 , and
, and 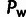 , measured as differences between the estimates and true values
normalized by the true value, are shown as a function of the frequency threshold
f. Each box plot describes the distribution of values for the 11
collections considered. Curvature-based standard errors for these experiments are
summarize in supplementary figure S2, Supplementary Material online. (C) Simulated data
sets were generated for the same 11 mixtures of selective modes × four
different demographic scenarios (supplementary table S2, Supplementary Material online), and INSIGHT parameter estimates were
compared with true values. Box plots represent the distribution of relative error
per demographic scenario. The relative estimation error for the simple count-based
estimators,
, measured as differences between the estimates and true values
normalized by the true value, are shown as a function of the frequency threshold
f. Each box plot describes the distribution of values for the 11
collections considered. Curvature-based standard errors for these experiments are
summarize in supplementary figure S2, Supplementary Material online. (C) Simulated data
sets were generated for the same 11 mixtures of selective modes × four
different demographic scenarios (supplementary table S2, Supplementary Material online), and INSIGHT parameter estimates were
compared with true values. Box plots represent the distribution of relative error
per demographic scenario. The relative estimation error for the simple count-based
estimators, 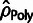 ,
, 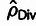 , and
, and 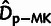 , is shown for comparison.
, is shown for comparison.
These synthetic data sets—generated by forward simulation, under fairly realistic assumptions—also enabled us to directly evaluate the assumptions underlying our model. Consistent with our assumptions, no mutations reached fixation in the 340,000 negatively selected sites (weak or strong) in our synthetic data sets. On the other hand, polymorphisms under selection were not completely restricted to WN sites, as assumed; instead, 8% of them occurred in SN sites and 9% of them in positively selected sites, with the remaining 83% in WN sites. Nevertheless, our inference procedure appeared to be robust to these violations of our assumptions, with fairly accurate estimates of all parameters in all cases. Our default threshold of f = 15% for low-frequency polymorphisms appeared to be adequate: Only 4% of selected polymorphisms exhibited derived allele frequencies exceeding this threshold, and these sites were vastly outnumbered by neutral high-frequency polymorphisms. Overall, although the simulated data did not fully support our modeling assumptions, only fairly minor violations were observed and our inference procedure seemed to be robust to them.
To test the robustness of INSIGHT to the assumed strength of selection, we conducted a
series of simulations in which we perturbed the selection coefficients used for the three
selective modes, SN, WN, and P (supplementary methods, Supplementary Material online). We found that INSIGHT performed very well
across the entire range of values assumed for SN and positive selection (supplementary fig. S1, Supplementary Material online). A clear bias in parameter estimates was
observed only when quite weak selection was assumed for the WN mode
(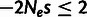 ), in which case ρ and
), in which case ρ and
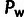 were clearly underestimated and
were clearly underestimated and
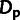 was slightly underestimated. These results
suggest that INSIGHT is generally robust to assumptions about selection coefficients, but
that negative selection has to reach a certain threshold to produce sufficient shifts in
derived allele frequencies to be detected by the method. As a result, our statements about
ρ and
was slightly underestimated. These results
suggest that INSIGHT is generally robust to assumptions about selection coefficients, but
that negative selection has to reach a certain threshold to produce sufficient shifts in
derived allele frequencies to be detected by the method. As a result, our statements about
ρ and 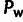 should be interpreted as including only the subset of deleterious polymorphisms that clear
this threshold (supplementary methods, Supplementary Material online).
should be interpreted as including only the subset of deleterious polymorphisms that clear
this threshold (supplementary methods, Supplementary Material online).
As mentioned earlier, f = 15% appears to be an adequate
upper bound on the derived allele frequency at negatively selected sites (Fay et al. 2001; Zhang and Li 2005; Charlesworth and Eyre-Walker 2008). In reality, of course, this threshold
depends on various factors, including the actual distribution of selection coefficients
and the demographic history of the sample. To test the robustness of our model to the
choice of f, we generated 11 collections of 10,000 elements with true
fractions of sites under selection ranging from 0 to 1 (in steps of 0.1), keeping the
proportion within selected sites in each collection constant at 45% WN, 50%
SN, and 5% PD. We then applied INSIGHT to each data set using values of
f ranging from 1% to 40% (fig. 1B). We found that very low thresholds
(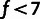 %) resulted in clear underestimation
of all model parameters, due to the presence of many selected polymorphisms with DAFs
exceeding the cutoff, whereas very high thresholds (
%) resulted in clear underestimation
of all model parameters, due to the presence of many selected polymorphisms with DAFs
exceeding the cutoff, whereas very high thresholds (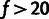 %) led to high variance due to sparse data for high-frequency
polymorphisms (supplementary fig. S2, Supplementary Material online). Importantly, however, no bias was observed
for thresholds in the range of 7–20%, indicating robustness to the specific
choice of threshold and justifying the default choice of 15%, which we used
throughout most of our analysis.
%) led to high variance due to sparse data for high-frequency
polymorphisms (supplementary fig. S2, Supplementary Material online). Importantly, however, no bias was observed
for thresholds in the range of 7–20%, indicating robustness to the specific
choice of threshold and justifying the default choice of 15%, which we used
throughout most of our analysis.
An important feature of our model is that it directly contrasts sequence patterns in
elements with those in nearby neutral sites, which should make it insensitive to the
particular demographic history of the target population. To test robustness to demography,
we simulated data sets for each of the 11 mixtures of selective modes described earlier
using four different demographic scenarios for the target population: one with constant
population size since divergence from chimpanzee, one with a moderate population
expansion, and two others with a severe population bottleneck followed by an exponential
expansion (supplementary table S2, Supplementary Material online). Inference was performed separately for each
of these 4 × 11 data sets, and the estimated parameters were then compared with
their true values and with the simple count-based estimates (fig. 1C). The divergence-based estimates,
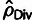 , were quite poor due to the effects of
positive selection, as discussed earlier, and the polymorphism-based estimates,
, were quite poor due to the effects of
positive selection, as discussed earlier, and the polymorphism-based estimates,
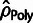 , consistently underestimated the true
values, by an average of 20–30% across the different scenarios, due to the
effects of WN selection. Similar patterns of underestimation were observed for the
MK-based estimator of the number of adaptive divergences,
, consistently underestimated the true
values, by an average of 20–30% across the different scenarios, due to the
effects of WN selection. Similar patterns of underestimation were observed for the
MK-based estimator of the number of adaptive divergences, 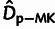 .
In contrast, our model-based estimates of ρ and
.
In contrast, our model-based estimates of ρ and
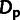 showed no apparent bias in any of the
simulated demographic scenarios. Estimates of the number of polymorphisms under selection,
showed no apparent bias in any of the
simulated demographic scenarios. Estimates of the number of polymorphisms under selection,
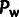 , showed somewhat greater variance, as
observed in our initial simulation study (fig.
1A), but the error in these estimates did not seem to be
affected by demography. Thus, our method appears to be capable of disentangling the
contributions of positive and negative selection even in the presence of a complex
demographic history, without the need for explicit demographic inference.
, showed somewhat greater variance, as
observed in our initial simulation study (fig.
1A), but the error in these estimates did not seem to be
affected by demography. Thus, our method appears to be capable of disentangling the
contributions of positive and negative selection even in the presence of a complex
demographic history, without the need for explicit demographic inference.
Analysis of Human Noncoding Genomic Elements
To demonstrate its application to real data, we used INSIGHT to examine several classes
of noncoding elements in the human genome, using 54 unrelated individual genomes from
Complete Genomics to define human polymorphisms, and the chimpanzee, orangutan, and
macaque genomes as outgroups (Materials and Methods). First, to assess our likelihood
ratio cutoffs and ensure that our method adequately controls for false-positive inferences
of selection, we applied INSIGHT to randomly selected “neutral”
regions—excluding genes, conserved noncoding elements, and their immediate flanks
(Materials and Methods). From the previously identified putatively neutral regions, we
sampled 500 mutually exclusive collections of approximately 30,000 “neutral
elements,” 10 bp long. For each collection, we estimated ρ and
the corresponding LRT statistic for the null hypothesis of 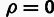 .
The 500 estimated values of ρ were generally close to zero, with a
median of 0.03 (supplementary fig. S3, Supplementary Material online) and almost no values >0.1. The
distribution of LRT statistics was roughly similar to a 50:50 mixture of a point mass at
zero and a
.
The 500 estimated values of ρ were generally close to zero, with a
median of 0.03 (supplementary fig. S3, Supplementary Material online) and almost no values >0.1. The
distribution of LRT statistics was roughly similar to a 50:50 mixture of a point mass at
zero and a 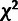 distribution with three degrees of freedom,
as expected (Materials and Methods), but did show a clear shift toward large values
relative to this distribution (fig.
4A). This shift may reflect violations of our simplifying
assumptions in real genomic data (e.g., variation in mutation rates within blocks),
contributions from alignment errors, or the inclusion of some functional sites within our
“neutral” elements. Nevertheless, we found that the use of a more conservative
(nonmixed)
distribution with three degrees of freedom,
as expected (Materials and Methods), but did show a clear shift toward large values
relative to this distribution (fig.
4A). This shift may reflect violations of our simplifying
assumptions in real genomic data (e.g., variation in mutation rates within blocks),
contributions from alignment errors, or the inclusion of some functional sites within our
“neutral” elements. Nevertheless, we found that the use of a more conservative
(nonmixed) 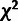 distribution with three degrees of freedom
adequately controlled for the excess in large LRT statistics. In particular, the empirical
distribution of LRT statistics shows a good fit to the tail of this distribution (fig. 4A). Thus, we use this
distribution for approximate calculations of nominal P values in our
subsequent analyses.
distribution with three degrees of freedom
adequately controlled for the excess in large LRT statistics. In particular, the empirical
distribution of LRT statistics shows a good fit to the tail of this distribution (fig. 4A). Thus, we use this
distribution for approximate calculations of nominal P values in our
subsequent analyses.
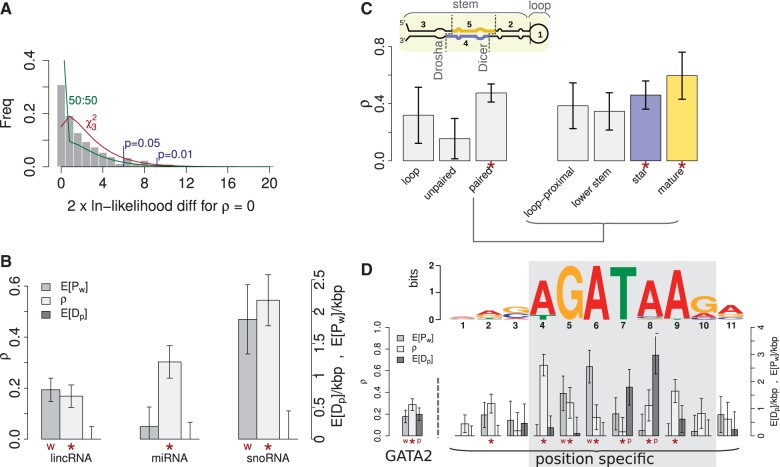
Fig. 4.
Analysis of human genomic elements. (A)
Distribution of LRT statistics for 500 sampled sets of “neutral” genomic
elements, with approximately 30,000 elements per set. Test statistics reflect a null
hypothesis that 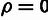 and an alternative hypothesis that
and an alternative hypothesis that
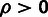 . For comparison, a
. For comparison, a
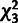 distribution (with three degrees of
freedom; red) and a 50:50 mixture of a
distribution (with three degrees of
freedom; red) and a 50:50 mixture of a 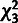 distribution and a point mass at 0 (green) are also shown.
Blue lines indicate significance thresholds for
distribution and a point mass at 0 (green) are also shown.
Blue lines indicate significance thresholds for  and
and 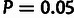 based on the
based on the 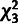 distribution. Four of the 500 data sets (0.8%) had test
statistics exceeding the
distribution. Four of the 500 data sets (0.8%) had test
statistics exceeding the 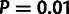 cutoff, and 24 (4.8%) exceeded the
cutoff, and 24 (4.8%) exceeded the
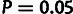 cutoff, indicating a reasonably good
fit to the tail of the distribution. The distribution of estimated values of
ρ is shown in supplementary figure S3, Supplementary Material online. (B) Model-based
estimates of ρ,
cutoff, indicating a reasonably good
fit to the tail of the distribution. The distribution of estimated values of
ρ is shown in supplementary figure S3, Supplementary Material online. (B) Model-based
estimates of ρ, 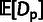 , and
, and  for three classes of noncoding RNAs (lincRNAs, miRNAs, and
snoRNAs; see Materials and Methods). Error bars indicate one standard error. Symbols
in red indicate statistical significance in LRTs for overall selection
(
for three classes of noncoding RNAs (lincRNAs, miRNAs, and
snoRNAs; see Materials and Methods). Error bars indicate one standard error. Symbols
in red indicate statistical significance in LRTs for overall selection
(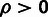 ; “*”
; “*”

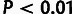 ) and WN selection
(
) and WN selection
(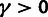 ; “w”
; “w”
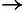
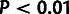 ), based on a
), based on a
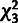 distribution for
distribution for
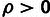 and a
and a 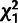 distribution for
distribution for 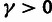 . (C) Estimates of ρ for
several structural regions of miRNAs (inset). (Left) Results for a coarse-grained
partitioning into loop bases, unpaired stem bases, and paired stem bases. (Right)
Results for a fine-grained partitioning of paired bases in the stem into
loop-proximal, lower-stem, star, and mature regions, corresponding to the regions
that undergo cropping and dicing by Drosha and Dicer (dashed lines). Estimates found
to be significantly greater than 0 (
. (C) Estimates of ρ for
several structural regions of miRNAs (inset). (Left) Results for a coarse-grained
partitioning into loop bases, unpaired stem bases, and paired stem bases. (Right)
Results for a fine-grained partitioning of paired bases in the stem into
loop-proximal, lower-stem, star, and mature regions, corresponding to the regions
that undergo cropping and dicing by Drosha and Dicer (dashed lines). Estimates found
to be significantly greater than 0 (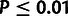 ) are highlighted (“*”). (D)
The motif inferred for GATA2 together with position-specific estimates of
ρ (left axis),
) are highlighted (“*”). (D)
The motif inferred for GATA2 together with position-specific estimates of
ρ (left axis), 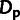 , and
, and 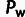 (right axis). Statistical significance is assessed and
indicated as in (B), with significant positive selection
(
(right axis). Statistical significance is assessed and
indicated as in (B), with significant positive selection
(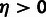 ; “P”
; “P”
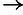
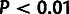 ) estimated using a
) estimated using a
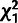 distribution. The “core”
seven positions of the motif, having IC
distribution. The “core”
seven positions of the motif, having IC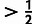 , are highlighted in gray. Estimates obtained for the joint
analysis of all seven positions of the core motif are shown as well
(left).
, are highlighted in gray. Estimates obtained for the joint
analysis of all seven positions of the core motif are shown as well
(left).
Next, we examined three classes of noncoding RNAs annotated by the GENCODE project:
microRNAs (miRNAs), small nucleolar RNAs (snoRNAs), and large interspersed noncoding RNAs
(lincRNAs). We applied INSIGHT to a high-confidence subset of annotated elements in each
of these five classes (supplementary table S3 and methods, Supplementary Material online). Our analysis considered various thresholds
for distinguishing between low and high frequency polymorphisms, but our estimates were
fairly insensitive to this threshold (supplementary fig. S4, Supplementary Material online), so we focus below on results for the default
threshold of 15%. All three classes of elements were estimated to have significant
fractions of sites under selection (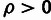 ;
;
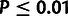 ; fig.
4B). snoRNAs showed the highest estimated value
(
; fig.
4B). snoRNAs showed the highest estimated value
(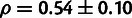 ), consistent with their essential role in
guiding chemical modifications of ribosomal and transfer RNAs (Pang et al. 2006; Matera
et al. 2007). miRNAs also showed a somewhat elevated estimate (0.3 ±
0.06). By contrast, lincRNAs were inferred to have a considerably smaller (but still
significant) fraction of sites under selection (0.17 ± 0.04), consistent with
previous observations indicating high levels of conservation are generally limited to
short segments within lincRNAs (Guttman et al.
2009; Marques and Ponting 2009;
Ulitsky et al. 2011). We also found
significant evidence of WN selection in lincRNAs (
), consistent with their essential role in
guiding chemical modifications of ribosomal and transfer RNAs (Pang et al. 2006; Matera
et al. 2007). miRNAs also showed a somewhat elevated estimate (0.3 ±
0.06). By contrast, lincRNAs were inferred to have a considerably smaller (but still
significant) fraction of sites under selection (0.17 ± 0.04), consistent with
previous observations indicating high levels of conservation are generally limited to
short segments within lincRNAs (Guttman et al.
2009; Marques and Ponting 2009;
Ulitsky et al. 2011). We also found
significant evidence of WN selection in lincRNAs (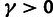 ;
;
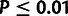 ). Furthermore, snoRNAs were estimated to
have particularly high rates of weakly selected segregating polymorphisms
(
). Furthermore, snoRNAs were estimated to
have particularly high rates of weakly selected segregating polymorphisms
(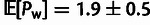 polymorphisms per kbp).
polymorphisms per kbp).
To shed additional light on the manner in which natural selection has influenced miRNA
evolution, we applied INSIGHT separately to different structural components within the
primary miRNA transcript (fig.
4C, inset). These structural classes were defined based on
predictions of hairpin secondary structures for the annotated miRNAs (supplementary methods, Supplementary Material online). We first partitioned the primary miRNA into
loop and stem regions, distinguishing between paired and unpaired bases within the stem.
Among these three partitions, paired bases in the stem region were estimated to have a
particularly high fraction of sites under selection (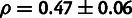 ;
;
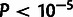 ; fig.
4C), consistent with their key role in stabilizing the hairpin
structure. In contrast, the estimates for the other two classes were not found to be
significantly greater than zero (
; fig.
4C), consistent with their key role in stabilizing the hairpin
structure. In contrast, the estimates for the other two classes were not found to be
significantly greater than zero (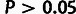 ).
We further partitioned the stem into four subregions—loop-proximal, lower stem,
star, and mature—reflecting the cleavage activity of Drosha and Dicer, the two RNase
III cleavage enzymes of primary importance in miRNA biogenesis. We obtained the highest
estimate of ρ (0.60 ± 0.16;
).
We further partitioned the stem into four subregions—loop-proximal, lower stem,
star, and mature—reflecting the cleavage activity of Drosha and Dicer, the two RNase
III cleavage enzymes of primary importance in miRNA biogenesis. We obtained the highest
estimate of ρ (0.60 ± 0.16; 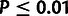 ;
fig. 4C) for the
21–22 nt mature region, reflecting its dual role in structure preservation for
efficient recognition and processing by Drosha and Dicer, and in sequence complementarity
to target mRNAs. The lower-stem and loop-proximal regions had lower estimates of
ρ, probably because they do not serve any direct regulatory role,
but are important in preserving the hairpin structure. The star region had an intermediate
estimate of ρ (0.46 ± 0.10;
;
fig. 4C) for the
21–22 nt mature region, reflecting its dual role in structure preservation for
efficient recognition and processing by Drosha and Dicer, and in sequence complementarity
to target mRNAs. The lower-stem and loop-proximal regions had lower estimates of
ρ, probably because they do not serve any direct regulatory role,
but are important in preserving the hairpin structure. The star region had an intermediate
estimate of ρ (0.46 ± 0.10; 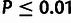 ),
perhaps because a fraction of star sequences are loaded into Argonaute complexes and carry
out functional roles, even though most are degraded (Okamura et al. 2008).
),
perhaps because a fraction of star sequences are loaded into Argonaute complexes and carry
out functional roles, even though most are degraded (Okamura et al. 2008).
Our estimates of recent selection in human miRNAs were generally concordant with previous comparative analyses in Drosophila based on patterns of divergence between species (Lai et al. 2003; Clark et al. 2007; Stark et al. 2007). They were also fairly consistent with estimates of sequence conservation across the primate phylogeny computed using phyloP scores (Pollard et al. 2010; supplementary fig. S5, Supplementary Material online). However, INSIGHT found somewhat stronger evidence for selection in the mature relative to the star region of the miRNA than did phyloP. This difference could reflect a shift toward WN selection in the star region, which is not apparent on comparative genomic time scales because selection is sufficiently strong to prohibit long-term fixation of derived alleles.
None of the analyzed noncoding RNAs showed strong evidence of positive selection, so we
turned next to a collection of elements in which we expected to find evidence of
adaptation based on other recent work (Arbiza L, Gronau I, Aksoy BA, Hubisz MJ, Gulko B,
Keinan A, Siepel A, in revision): GATA2-binding sites. Using the available ChIP-seq-based
annotations (Materials and Methods), we partitioned the nucleotides in binding sites into
11 groups, corresponding to the 11 positions in the GATA2 motif, and applied INSIGHT
separately to each group (fig.
4D). We found that the signatures of natural selection were
clearly concentrated in positions 4–10, which constitute the “core”
region of the motif (fig.
4D). Indeed, six of these seven positions, and only one other
position, were found to have significant estimates of ρ
(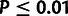 ). The 5th and 6th positions, associated with
the “GA” portion of the GATA motif, were estimated to have undergone
significant WN selection (
). The 5th and 6th positions, associated with
the “GA” portion of the GATA motif, were estimated to have undergone
significant WN selection (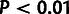 ),
whereas the signature of positive selection came primarily from the 7th and 8th positions,
which are associated with the “TA” portion of the motif. Our posterior
estimates indicated that nucleotides in these two positions contributed a total of 123
± 43 adaptive divergences across approximately 27,500 binding sites. Interestingly,
these positions (particularly the 8th) are known to play a role in modulating binding
specificity of GATA2 (Ko and Engel 1993;
Merika and Orkin 1993). They are also
critical in determining the relative binding affinities of GATA1, GATA2, and GATA3, which
regulate overlapping sets of genes and are known to serve as “switches”
between alternative modes of gene expression (Bresnick et al. 2010; Dore et al.
2012).
),
whereas the signature of positive selection came primarily from the 7th and 8th positions,
which are associated with the “TA” portion of the motif. Our posterior
estimates indicated that nucleotides in these two positions contributed a total of 123
± 43 adaptive divergences across approximately 27,500 binding sites. Interestingly,
these positions (particularly the 8th) are known to play a role in modulating binding
specificity of GATA2 (Ko and Engel 1993;
Merika and Orkin 1993). They are also
critical in determining the relative binding affinities of GATA1, GATA2, and GATA3, which
regulate overlapping sets of genes and are known to serve as “switches”
between alternative modes of gene expression (Bresnick et al. 2010; Dore et al.
2012).
Discussion
Recent advances in functional genomics have produced vast catalogs of candidate noncoding elements, including noncoding RNAs, transcription factor binding sites, RNA–binding sites, and many others (Gerstein et al. 2010; Dunham et al. 2012). Evolutionary analyses will be essential in improving annotations of these elements and revealing their functional roles. Although methods based on patterns of divergence between species have become widely used in the study of noncoding functional elements, these methods are limited by their consideration of relatively long evolutionary time scales and their sensitivity to alignment errors and other technical artifacts. INSIGHT is intended to complement these methods by detecting signatures of recent selection based on newly available population genomic data and comparative genomic data for closely related species.
INSIGHT bears some similarities to MK-based methods (McDonald and Kreitman 1991; Smith and Eyre-Walker 2002; Bierne and Eyre-Walker 2004; Andolfatto 2005), Poisson random field (PRF)-based methods (Sawyer and Hartl 1992; Bustamante et al. 2002, 2005; Williamson et al. 2005), and related methods for characterizing the DFE (Eyre-Walker et al. 2006; Boyko et al. 2008; Eyre-Walker and Keightley 2009), but it differs from previous methods in several important respects. Unlike MK-based methods, INSIGHT is based on a full generative probabilistic model, it explicitly models WN selection, and it pools information from many loci in a manner that properly accommodates differences in mutation rates and coalescence time across the genome. Unlike PRF-based methods, it does not attempt to directly model the complex relationship between allele frequencies and natural selection, but instead works by contrasting patterns of polymorphism and divergence in the elements of interest and flanking sites. INSIGHT additionally allows for straightforward LRTs of various hypotheses of interest, and it allows parameter variances to be approximately characterized using standard methods. For these reasons, we expect it to be a valuable addition to the arsenal of methods available for analysis of polymorphism and divergence data.
The INSIGHT model is designed to exploit newly available genome-scale data sets describing both candidate functional elements (Gerstein et al. 2010; Roy et al. 2010; Dunham et al. 2012) and variation within populations (1000 Genomes Project Consortium 2010; Mackay et al. 2012). Although the underlying graphical model is not complex (fig. 2), a naive approach to parameter estimation would still be prohibitively CPU-intensive with genome-wide data. We achieve major gains in efficiency by decomposing the inference procedure into three separate steps, concerned with the estimation of the phylogenetic, neutral, and selection parameters, respectively. This decomposition relies on the simplifying assumption that sites within the elements of interest contain negligible information about the neutral parameters of the model, because they are vastly outnumbered by the flanking neutral sites—a property that can typically be guaranteed by construction. It also depends on the use of a single phylogenetic model per locus in estimating the prior distribution of the ancestral allele at all sites, which should be adequate as long as relatively close outgroups are used. Notably, the first two of these steps can be performed in preprocessing and reused in the analysis of any set of loci that use the same flanking regions. Furthermore, the neutral flanks can be designed to maximize the potential for reuse (as we have done here) by defining a set of fixed genomic blocks, and associating each element with the neutral sites of the nearest block. This strategy allows the neutral and phylogenetic parameters to be pre-estimated for each block and reused in any number of subsequent analyses. Importantly, these steps dominate the running time of the inference algorithm (particularly the phylogenetic estimation step). The final stage, in which the parameters ρ, η, and γ are estimated, is independent of the number of genomes considered and typically takes less than a minute.
It is worth emphasizing that INSIGHT can be applied to any collection of genomic elements, provided each one is sufficiently short that it does not span regions having markedly different mutation rates or coalescence times, and provided each element can be associated with nearby sites likely to be free from the effects of selection. In this article, we have focused on the case of genome-wide collections of elements of a particular type, such as miRNAs or binding sites for a particular transcription factor, but many other types of analysis are possible. For example, in related work (Arbiza L, Gronau I, Aksoy BA, Hubisz MJ, Gulko B, Keinan A, Siepel A, in revision), we have examined various subsets of transcription factor binding sites, such as those associated with genes of a particular Gene Ontology category or expressed at a particular level, and those having various levels of predicted binding affinity. As we have shown here, the method can also be used to pinpoint signals of selection within elements, by partitioning them based on structural features (e.g., particular motif positions or particular miRNA structural compartments). Similar analyses could be used to contrast regions of the genome having different epigenomic marks, sequences nearby and far from genes, sequences on sex chromosomes and autosomes, or any number of other biologically significant genomic partitions.
INSIGHT could be extended in various ways to improve the fit of the model to the data and broaden the utility of the program. In this analysis, we had a sufficiently complete collection of human variation data to simply discard positions with missing data in one or more samples. In cases of more missing data, however, it may be worthwhile to use the strategy of adjusting Watterson’s constant an in the appropriate conditional distributions (table 3) based on the number of samples for which data are available at each genomic position. This simple approach should work well as long as the amount of missing data is not excessive, but it will require some care in programming to efficiently accommodate site-wise variation in an (supplementary methods, Supplementary Material online). Another useful extension would be to allow for variation across loci in the global parameters ρ, η, and γ, say, by assuming locus-specific parameters are drawn from (discretized) Beta (for ρ) or Gamma (for η and γ) distributions and estimating the hyper-parameters for these distributions from the data. This strategy should improve model fit considerably in cases of variable selection across loci, similar to phylogenetic models that allow for rate variation among sites (Yang 1994). A further extension would be to use a fully Bayesian approach and infer posterior distributions for the parameters of interest. This would also be fairly straightforward, but would most likely require Markov chain Monte Carlo sampling or variational Bayes approximations. These and other extensions would help further in using patterns of polymorphism and divergence to shed light on recent evolutionary processes, particularly in noncoding regions, and may improve predictions of the fitness effects of mutations across the genome.
Supplementary Material
Supplementary methods, tables S1–S3, and figures S1–S5 are available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).
Acknowledgments
This research was supported by a David and Lucile Packard Fellowship for Science and Engineering, National Science Foundation grant DBI-0644111, and National Institutes of Health (NIGMS) grant GM102192. Additional support was provided by a postdoctoral fellowship from the Cornell Center for Vertebrate Genomics (to L.A.).
References
- Andolfatto P. Adaptive evolution of non-coding DNA in Drosophila. Nature. 2005;437:1149–1152. doi: 10.1038/nature04107. [DOI] [PubMed] [Google Scholar]
- Bierne N, Eyre-Walker A. The genomic rate of adaptive amino acid substitution in Drosophila. Mol Biol Evol. 2004;21:1350–1360. doi: 10.1093/molbev/msh134. [DOI] [PubMed] [Google Scholar]
- Boffelli D, McAuliffe J, Ovcharenko D, Lewis KD, Ovcharenko I, Pachter L, Rubin EM. Phylogenetic shadowing of primate sequences to find functional regions of the human genome. Science. 2003;299:1391–1394. doi: 10.1126/science.1081331. [DOI] [PubMed] [Google Scholar]
- Boyko AR, Williamson SH, Indap AR, et al. (14 co-authors) Assessing the evolutionary impact of amino acid mutations in the human genome. PLoS Genet. 2008;4:e1000083. doi: 10.1371/journal.pgen.1000083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bresnick EH, Lee HY, Fujiwara T, Johnson KD, Keles S. GATA switches as developmental drivers. J Biol Chem. 2010;285:31087–31093. doi: 10.1074/jbc.R110.159079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bustamante CD, Fledel-Alon A, Williamson S, et al. (11 co-authors) Natural selection on protein-coding genes in the human genome. Nature. 2005;437:1153–1157. doi: 10.1038/nature04240. [DOI] [PubMed] [Google Scholar]
- Bustamante CD, Nielsen R, Sawyer SA, Olsen KM, Purugganan MD, Hartl DL. The cost of inbreeding in Arabidopsis. Nature. 2002;416:531–534. doi: 10.1038/416531a. [DOI] [PubMed] [Google Scholar]
- Charlesworth J, Eyre-Walker A. The McDonald-Kreitman test and slightly deleterious mutations. Mol Biol Evol. 2008;25:1007–1015. doi: 10.1093/molbev/msn005. [DOI] [PubMed] [Google Scholar]
- Chernoff H. On the distribution of the likelihood ratio. Ann Math Stat. 1954;25:573–578. [Google Scholar]
- Clark A, Eisen M, Smith D, et al. (11 co-authors) Evolution of genes and genomes on the Drosophila phylogeny. Nature. 2007;450:203–218. doi: 10.1038/nature06341. [DOI] [PubMed] [Google Scholar]
- Cooper GM, Stone EA, Asimenos G, Green ED, Batzoglou S, Sidow A. Distribution and intensity of constraint in mammalian genomic sequence. Genome Res. 2005;15:901–913. doi: 10.1101/gr.3577405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dermitzakis ET, Clark AG. Evolution of transcription factor binding sites in mammalian gene regulatory regions: conservation and turnover. Mol Biol Evol. 2002;19:1114–1121. doi: 10.1093/oxfordjournals.molbev.a004169. [DOI] [PubMed] [Google Scholar]
- Dore LC, Chlon TM, Brown CD, White KP, Crispino JD. Chromatin occupancy analysis reveals genome-wide GATA factor switching during hematopoiesis. Blood. 2012;119:3724–3733. doi: 10.1182/blood-2011-09-380634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drmanac R, Sparks AB, Callow MJ, et al. (65 co-authors) Human genome sequencing using unchained base reads on self-assembling DNA nanoarrays. Science. 2010;327:78–81. doi: 10.1126/science.1181498. [DOI] [PubMed] [Google Scholar]
- Dunham I, Kundaje A, Aldred SF, et al. (1196 co-authors) An integrated encyclopedia of DNA elements in the human genome. Nature. 2012;489:57–74. doi: 10.1038/nature11247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eyre-Walker A, Keightley PD. Estimating the rate of adaptive molecular evolution in the presence of slightly deleterious mutations and population size change. Mol Biol Evol. 2009;26:2097–2108. doi: 10.1093/molbev/msp119. [DOI] [PubMed] [Google Scholar]
- Eyre-Walker A, Woolfit M, Phelps T. The distribution of fitness effects of new deleterious amino acid mutations in humans. Genetics. 2006;173:891–900. doi: 10.1534/genetics.106.057570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fay JC, Wyckoff GJ, Wu CI. Positive and negative selection on the human genome. Genetics. 2001;158:1227–1234. doi: 10.1093/genetics/158.3.1227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerstein MB, Lu ZJ, Van Nostrand EL, et al. (131 co-authors) Integrative analysis of the Caenorhabditis elegans genome by the modENCODE project. Science. 2010;330:1775–1787. doi: 10.1126/science.1196914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guttman M, Amit I, Garber M, et al. (20 co-authors) Chromatin signature reveals over a thousand highly conserved large non-coding RNAs in mammals. Nature. 2009;458:223–227. doi: 10.1038/nature07672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harrow J, Frankish A, Gonzalez JM, et al. (41 co-authors) GENCODE: the reference human genome annotation for The ENCODE Project. Genome Res. 2012;22:1760–1774. doi: 10.1101/gr.135350.111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hernandez RD. A flexible forward simulator for populations subject to selection and demography. Bioinformatics. 2008;24:2786–2787. doi: 10.1093/bioinformatics/btn522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hubisz MJ, Pollard KS, Siepel A. PHAST and RPHAST: phylogenetic analysis with space/time models. Brief Bioinform. 2011;12:41–51. doi: 10.1093/bib/bbq072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ko LJ, Engel JD. DNA-binding specificities of the GATA transcription factor family. Mol Cell Biol. 1993;13:4011–4022. doi: 10.1128/mcb.13.7.4011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kondrashov AS, Crow JF. A molecular approach to estimating the human deleterious mutation rate. Hum Mutat. 1993;2:229–234. doi: 10.1002/humu.1380020312. [DOI] [PubMed] [Google Scholar]
- Lai EC, Tomancak P, Williams RW, Rubin GM. Computational identification of Drosophila microRNA genes. Genome Biol. 2003;4:R42. doi: 10.1186/gb-2003-4-7-r42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lehmann EEL, Casella G. Theory of point estimation. New York: Springer; 1998. [Google Scholar]
- Mackay TF, Richards S, Stone EA, et al. (52 co-authors) The Drosophila melanogaster genetic reference panel. Nature. 2012;482:173–178. doi: 10.1038/nature10811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marques AC, Ponting CP. Catalogues of mammalian long noncoding RNAs: modest conservation and incompleteness. Genome Biol. 2009;10:R124. doi: 10.1186/gb-2009-10-11-r124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matera AG, Terns RM, Terns MP. Non-coding RNAs: lessons from the small nuclear and small nucleolar RNAs. Nat Rev Mol Cell Biol. 2007;8:209–220. doi: 10.1038/nrm2124. [DOI] [PubMed] [Google Scholar]
- McDonald JH, Kreitman M. Adaptive protein evolution at the Adh locus in Drosophila. Nature. 1991;351:652–654. doi: 10.1038/351652a0. [DOI] [PubMed] [Google Scholar]
- Merika M, Orkin SH. DNA-binding specificity of GATA family transcription factors. Mol Cell Biol. 1993;13:3999–4010. doi: 10.1128/mcb.13.7.3999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moses AM, Pollard DA, Nix DA, Iyer VN, Li XY, Biggin MD, Eisen MB. Large-scale turnover of functional transcription factor binding sites in Drosophila. PLoS Comput Biol. 2006;2:e130. doi: 10.1371/journal.pcbi.0020130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen R, Hellmann I, Hubisz M, Bustamante C, Clark A. Recent and ongoing selection in the human genome. Nat Rev Genet. 2007;8:857–868. doi: 10.1038/nrg2187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okamura K, Phillips MD, Tyler DM, Duan H, Chou YT, Lai EC. The regulatory activity of microRNA* species has substantial influence on microRNA and 3′ UTR evolution. Nat Struct Mol Biol. 2008;15:354–363. doi: 10.1038/nsmb.1409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 1000 Genomes Project Consortium. A map of human genome variation from population-scale sequencing. Nature. 2010;467:1061–1073. doi: 10.1038/nature09534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pang KC, Frith MC, Mattick JS. Rapid evolution of noncoding RNAs: lack of conservation does not mean lack of function. Trends Genet. 2006;22:1–5. doi: 10.1016/j.tig.2005.10.003. [DOI] [PubMed] [Google Scholar]
- Pollard KS, Hubisz MJ, Rosenbloom KR, Siepel A. Detection of nonneutral substitution rates on mammalian phylogenies. Genome Res. 2010;20:110–121. doi: 10.1101/gr.097857.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roy S, Ernst J, Kharchenko PV, et al. (269 co-authors) Identification of functional elements and regulatory circuits by Drosophila modENCODE. Science. 2010;330:1787–1797. doi: 10.1126/science.1198374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sawyer SA, Hartl DL. Population genetics of polymorphism and divergence. Genetics. 1992;132:1161–1176. doi: 10.1093/genetics/132.4.1161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Self S, Liang K. Asymptotic properties of maximum likelihood estimators and likelihood ratio tests under nonstandard conditions. J Am Stat Assoc. 1987;82:605–610. [Google Scholar]
- Siepel A, Bejerano G, Pedersen JS, et al. (16 co-authors) Evolutionarily conserved elements in vertebrate, insect, worm, and yeast genomes. Genome Res. 2005;15:1034–1050. doi: 10.1101/gr.3715005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith NG, Eyre-Walker A. Adaptive protein evolution in Drosophila. Nature. 2002;415:1022–1024. doi: 10.1038/4151022a. [DOI] [PubMed] [Google Scholar]
- Stark A, Kheradpour P, Parts L, Brennecke J, Hodges E, Hannon GJ, Kellis M. Systematic discovery and characterization of fly microRNAs using 12 Drosophila genomes. Genome Res. 2007;17:1865–1879. doi: 10.1101/gr.6593807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stoletzki N, Eyre-Walker A. Estimation of the neutrality index. Mol Biol Evol. 2011;28:63–70. doi: 10.1093/molbev/msq249. [DOI] [PubMed] [Google Scholar]
- Thomas JW, Touchman JW, Blakesley RW, et al. (70 co-authors) Comparative analyses of multi-species sequences from targeted genomic regions. Nature. 2003;424:788–793. doi: 10.1038/nature01858. [DOI] [PubMed] [Google Scholar]
- Ulitsky I, Shkumatava A, Jan CH, Sive H, Bartel DP. Conserved function of lincRNAs in vertebrate embryonic development despite rapid sequence evolution. Cell. 2011;147:1537–1550. doi: 10.1016/j.cell.2011.11.055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watterson GA. On the number of segregating sites in genetical models without recombination. Theor Popul Biol. 1975;7:256–276. doi: 10.1016/0040-5809(75)90020-9. [DOI] [PubMed] [Google Scholar]
- Williamson SH, Hernandez R, Fledel-Alon A, Zhu L, Nielsen R, Bustamante CD. Simultaneous inference of selection and population growth from patterns of variation in the human genome. Proc Natl Acad Sci U S A. 2005;102:7882–7887. doi: 10.1073/pnas.0502300102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson DJ, Hernandez RD, Andolfatto P, Przeworski M. A population genetics-phylogenetics approach to inferring natural selection in coding sequences. PLoS Genet. 2011;7:e1002395. doi: 10.1371/journal.pgen.1002395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Z. Maximum likelihood phylogenetic estimation from DNA sequences with variable rates over sites: approximate methods. J Mol Evol. 1994;39:306–314. doi: 10.1007/BF00160154. [DOI] [PubMed] [Google Scholar]
- Yi X, Liang Y, Huerta-Sanchez E, et al. (70 co-authors) Sequencing of 50 human exomes reveals adaptation to high altitude. Science. 2010;329:75–78. doi: 10.1126/science.1190371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang L, Li WH. Human SNPs reveal no evidence of frequent positive selection. Mol Biol Evol. 2005;22:2504–2507. doi: 10.1093/molbev/msi240. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.